Generalized Kinetic Monte Carlo Framework for Organic Electronics
Abstract
1. Introduction
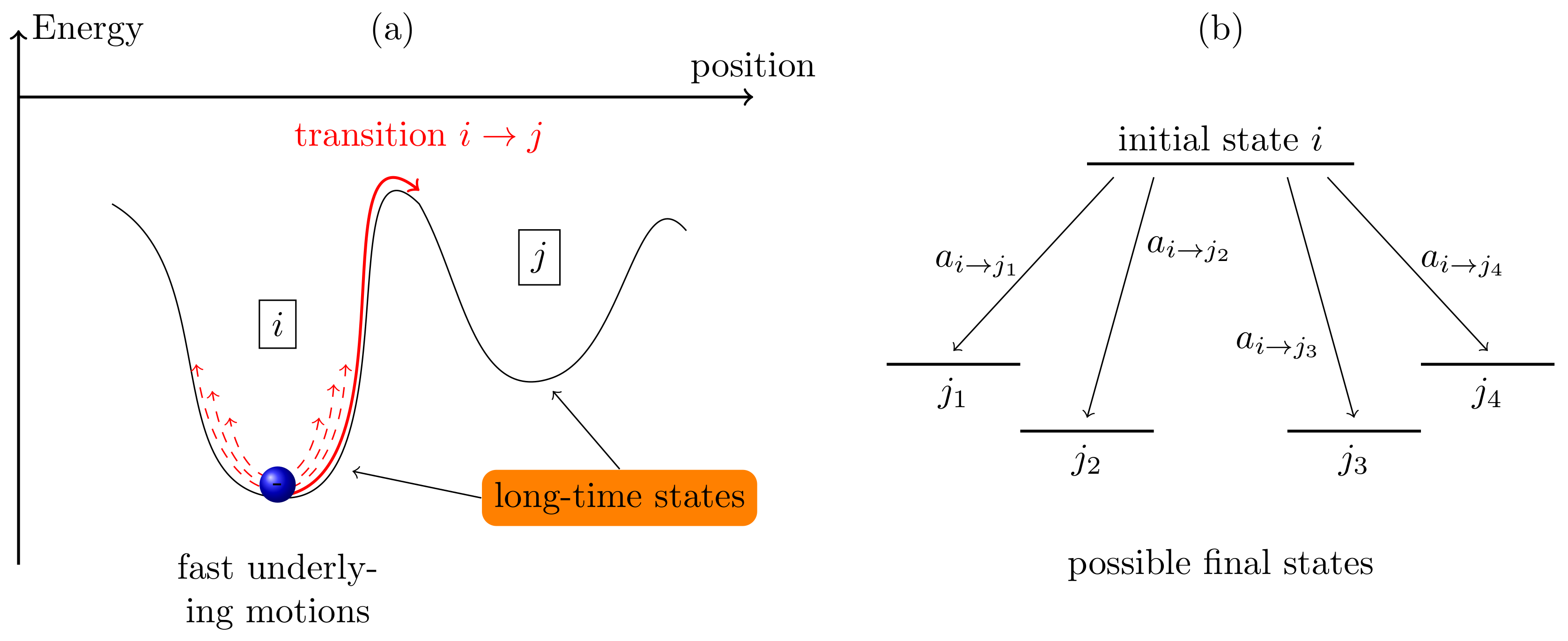
2. Kinetic Monte Carlo Method
- Initialize the system, and define all parameters that are required for the transition rates of all processes in the kMC. Define termination conditions such as the maximum simulation time .
- Identify the activated transitions for the current system state i and calculate the transition rates of all physical processes that can occur. The rates mirror the probability of the occurrence of the transition to state j. The sum of all rates is calculated.
- Two uniformly-distributed random numbers and are chosen. The first number chooses the transition from the set of events , which fulfills the condition:The second number gives the time passed before the transition is performed, given by:
- The simulation time t is advanced by , and the system configuration is updated following the transition .
- If the simulation time exceeds , the simulation stops, and all particle trajectories and the counters tracking the events are evaluated. If , the kMC loop (Step 2–4) is repeated.
3. kMC Framework for Organic Materials and Devices
3.1. Modeling of the Organic Material
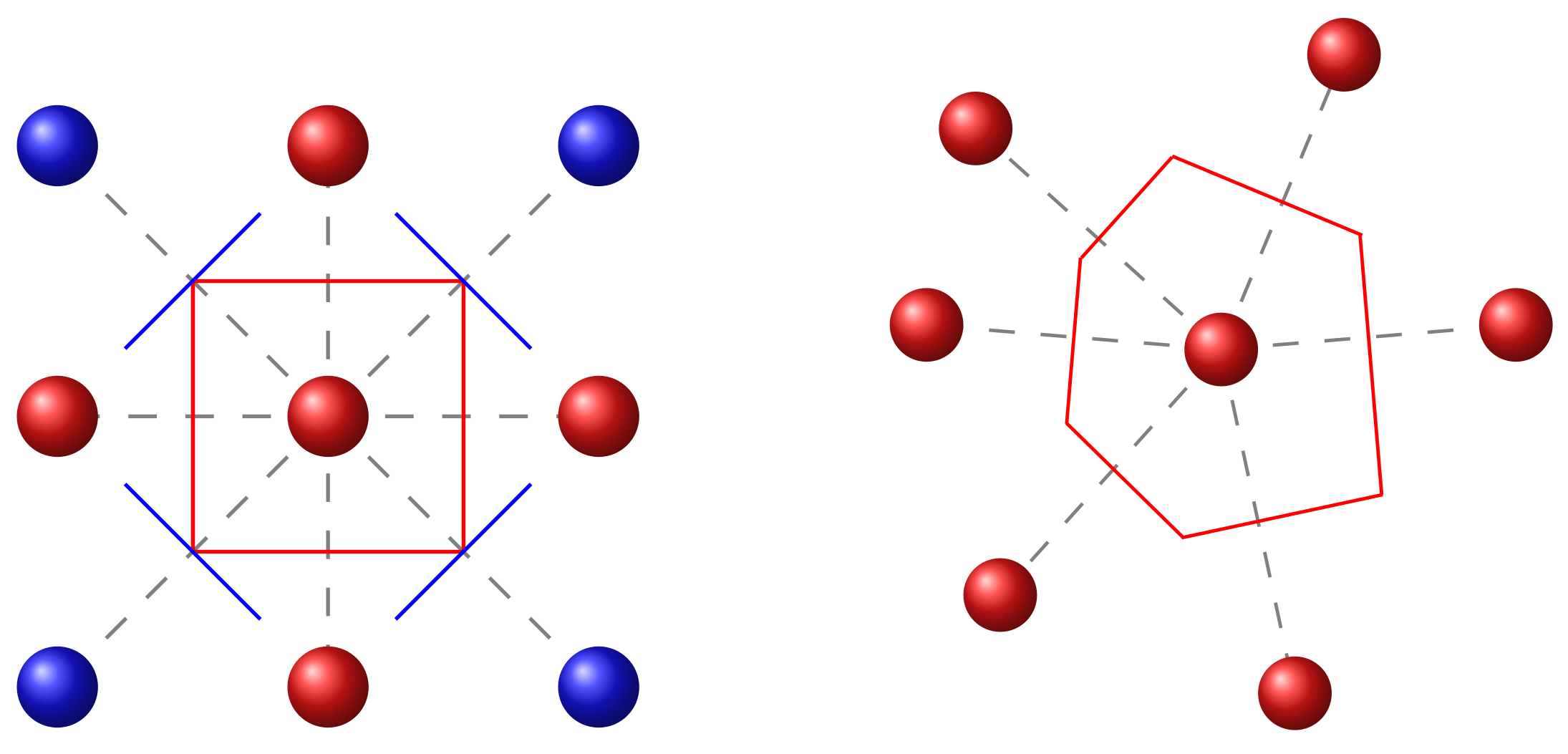
3.1.1. Voronoi Tessellation
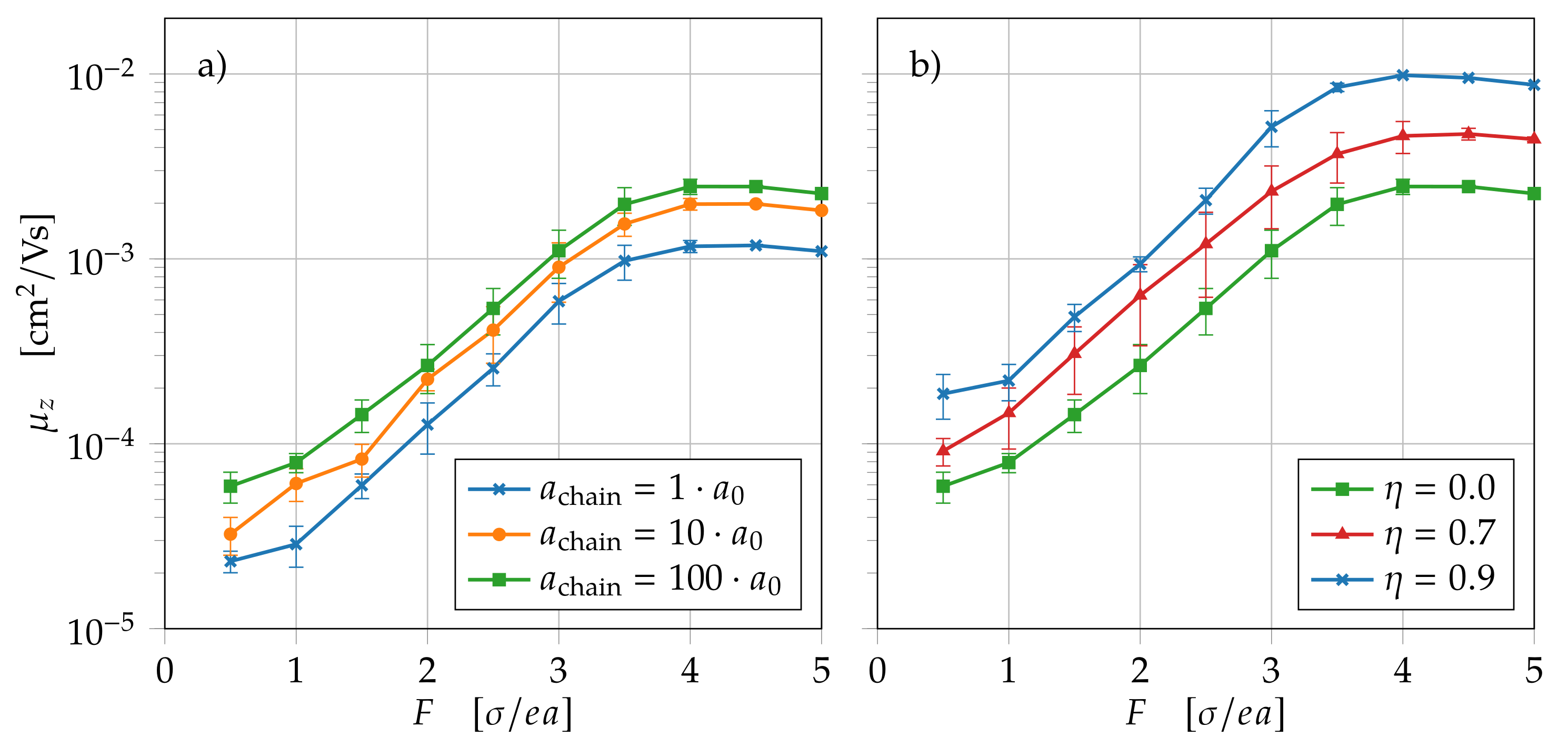
3.1.2. Polymer Chains
3.1.3. Phosphorescent Dopants
3.2. Energetic Landscape
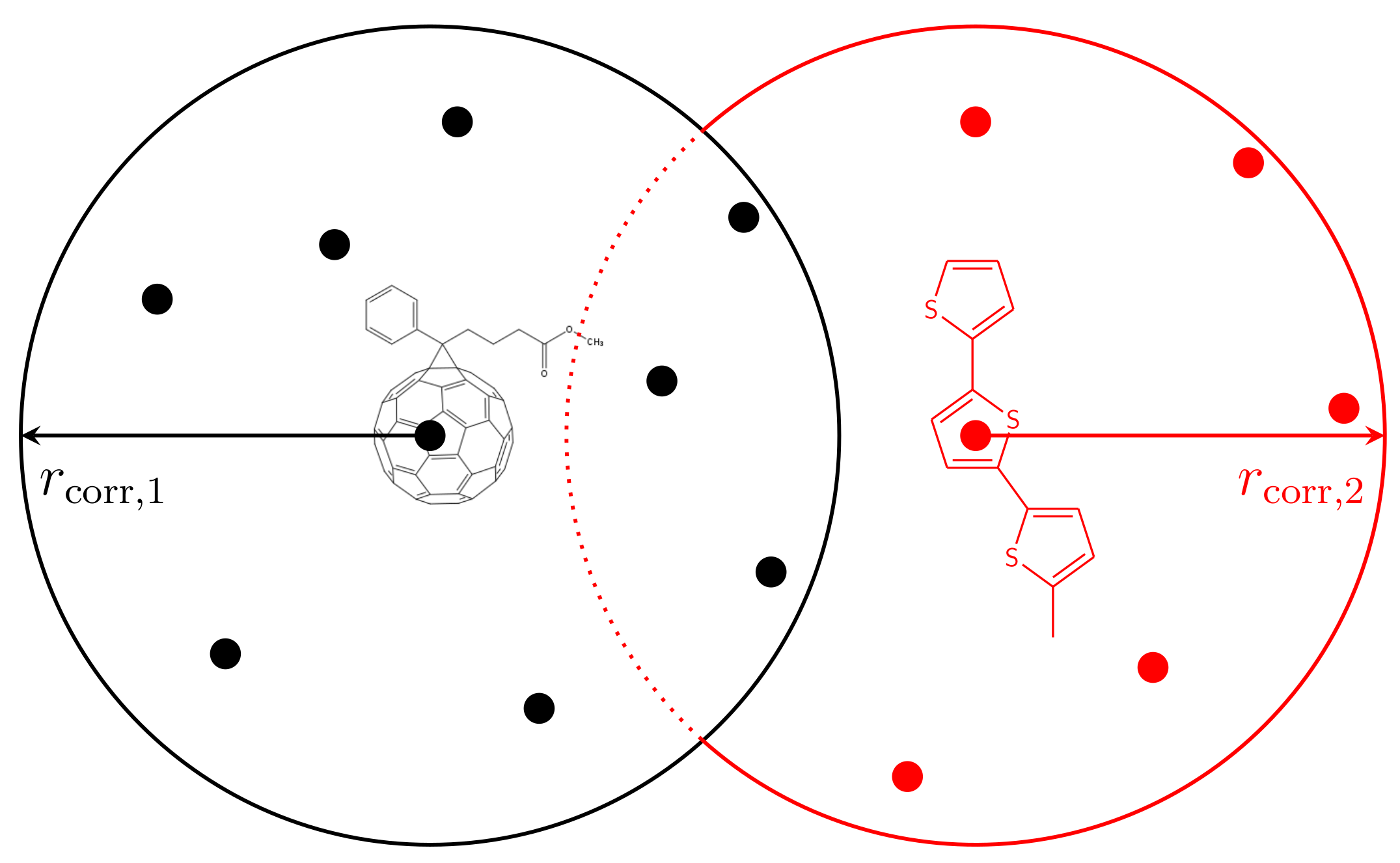
- Starting from the randomly Gaussian-distributed energetic landscape, we compute the weighted average of the energies of all sites k with for every site i using:Note that the average is only performed over sites k representing the same material as site i. The average energies are stored in an intermediate vector.
- Replace the site energies by the average energies .
- Scaling of the site energies: The averaging procedure reduces the energetic disorder. To keep the initially chosen , we compute the energetic disorder after the averaging process. Then, the site energies are scaled by:
- The level of correlation can be varied by either changing or repeating Steps 1–3.
3.3. Particles and Transitions
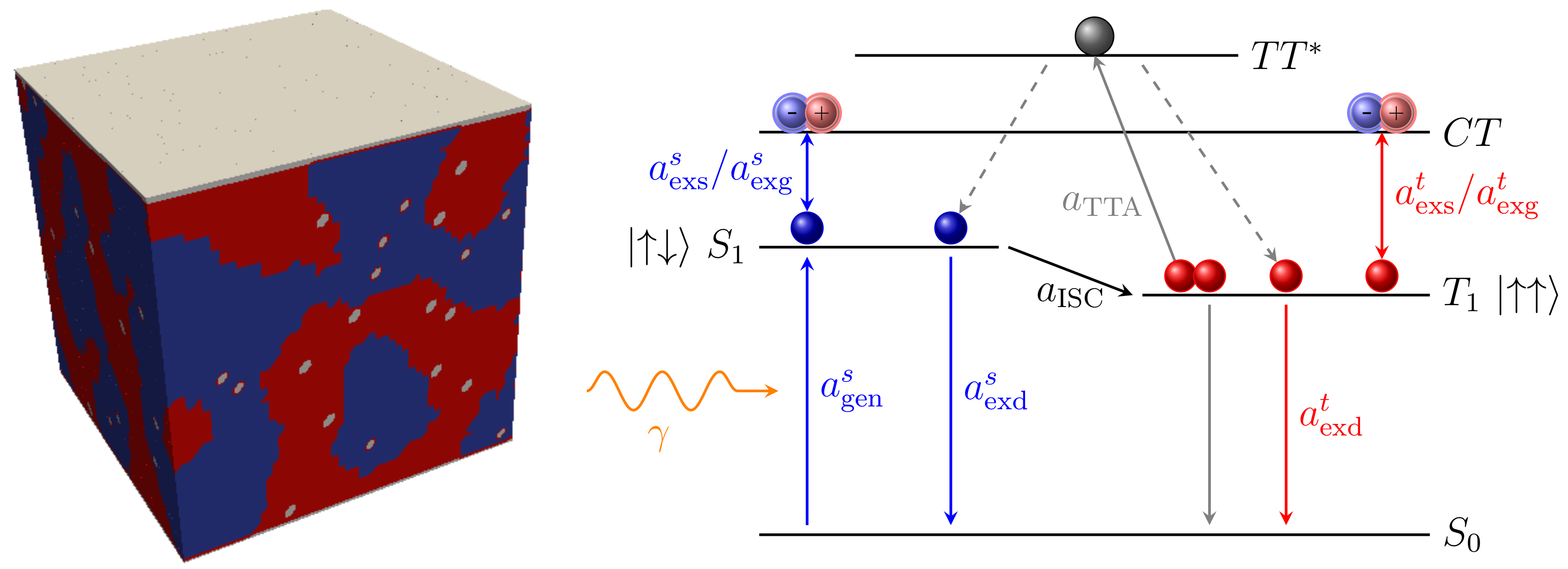
3.3.1. Charge Carriers
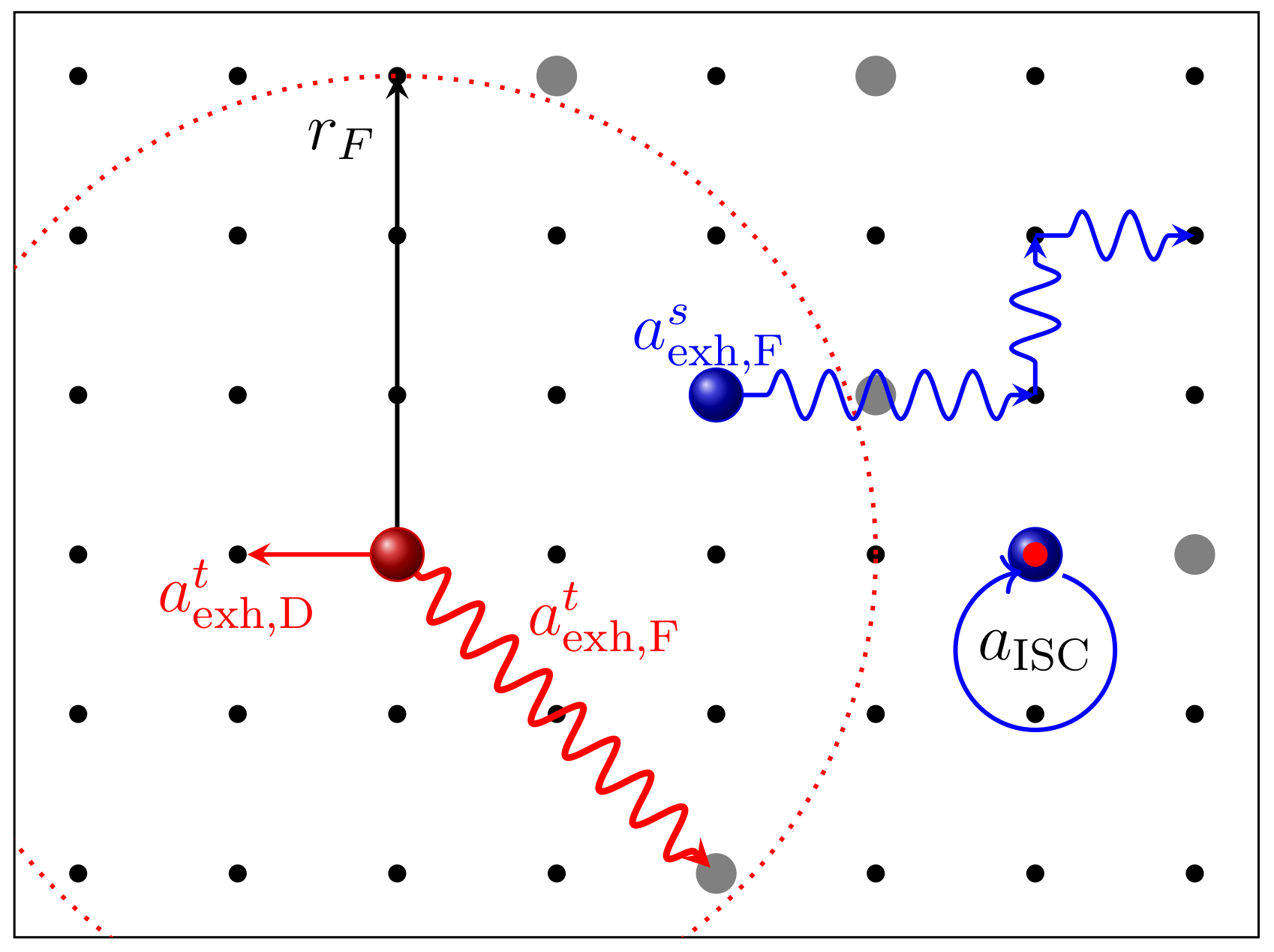
3.3.2. Excitons
4. Applications
4.1. Charge Carrier Transport through Polymer Chains
4.2. Impact of Dopant Volume Concentration on Exciton Dynamics
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Klauk, H. Organic thin-film transistors. Chem. Soc. Rev. 2010, 39, 2643–2666. [Google Scholar] [CrossRef] [PubMed]
- Dodabalapur, A. Organic light emitting diodes. Solid State Commun. 1997, 102, 259–267. [Google Scholar] [CrossRef]
- Deibel, C.; Dyakonov, V. Polymer–fullerene bulk heterojunction solar cells. Rep. Prog. Phys. 2010, 73, 096401. [Google Scholar] [CrossRef]
- Brédas, J.L.; Norton, J.E.; Cornil, J.; Coropceanu, V. Molecular understanding of organic solar cells: The challenges. Acc. Chem. Res. 2009, 42, 1691–1699. [Google Scholar] [CrossRef] [PubMed]
- Ries, B.; Bässler, H. Monte Carlo study of dispersive charge-carrier transport in spatially random systems with and without energetic disorder. Phys. Rev. B 1987, 35, 2295. [Google Scholar] [CrossRef]
- Bässler, H. Charge transport in disordered organic photoconductors a Monte Carlo simulation study. Phys. Status Solidi B 1993, 175, 15–56. [Google Scholar] [CrossRef]
- Baranovskii, S.; Zvyagin, I.; Cordes, H.; Yamasaki, S.; Thomas, P. Electronic transport in disordered organic and inorganic semiconductors. J. Non-Cryst. Solids 2002, 299, 416–419. [Google Scholar] [CrossRef]
- Köhler, A.; Bässler, H. Electronic Processes in Organic Semiconductors: An Introduction; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015. [Google Scholar]
- Groves, C.; Marsh, R.; Greenham, N.C. Monte Carlo modeling of geminate recombination in polymer-polymer photovoltaic devices. J. Chem. Phys. 2008, 129, 114903. [Google Scholar] [CrossRef] [PubMed]
- Albes, T.; Gagliardi, A. Influence of permittivity and energetic disorder on the spatial charge carrier distribution and recombination in organic bulk-heterojunctions. Phys. Chem. Chem. Phys. 2017, 19, 20974–20983. [Google Scholar] [CrossRef] [PubMed]
- Watkins, P.K.; Walker, A.B.; Verschoor, G.L. Dynamical Monte Carlo modelling of organic solar cells: The dependence of internal quantum efficiency on morphology. Nano Lett. 2005, 5, 1814–1818. [Google Scholar] [CrossRef] [PubMed]
- Casalegno, M.; Raos, G.; Po, R. Methodological assessment of kinetic Monte Carlo simulations of organic photovoltaic devices: The treatment of electrostatic interactions. J. Chem. Phys. 2010, 132, 094705. [Google Scholar] [CrossRef] [PubMed]
- Albes, T.; Lugli, P.; Gagliardi, A. Investigation of the blend morphology in bulk-heterojunction organic solar cells. IEEE Trans. Nanotechnol. 2016, 15, 281–288. [Google Scholar] [CrossRef]
- Marsh, R.; Groves, C.; Greenham, N.C. A microscopic model for the behavior of nanostructured organic photovoltaic devices. J. Appl. Phys. 2007, 101, 083509. [Google Scholar] [CrossRef]
- Kimber, R.G.; Wright, E.N.; O’Kane, S.E.; Walker, A.B.; Blakesley, J.C. Mesoscopic kinetic Monte Carlo modeling of organic photovoltaic device characteristics. Phys. Rev. B 2012, 86, 235206. [Google Scholar] [CrossRef]
- Groves, C.; Kimber, R.G.; Walker, A.B. Simulation of loss mechanisms in organic solar cells: A description of the mesoscopic Monte Carlo technique and an evaluation of the first reaction method. J. Chem. Phys. 2010, 133, 144110. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Shang, Y.; Li, Q.; Li, Y.; Zhan, X.; Shuai, Z.; Kimber, R.G.; Walker, A.B. Dynamic Monte Carlo simulation for highly efficient polymer blend photovoltaics. J. Phys. Chem. B 2009, 114, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Maqsood, I.; Cundy, L.D.; Biesecker, M.; Kimn, J.H.; Johnson, D.; Williams, R.; Bommisetty, V. Monte Carlo Simulation of Förster Resonance Energy Transfer in 3D Nanoscale Organic Bulk Heterojunction Morphologies. J. Phys. Chem. C 2013, 117, 21086–21095. [Google Scholar] [CrossRef]
- Feron, K.; Zhou, X.; Belcher, W.; Dastoor, P. Exciton transport in organic semiconductors: Förster resonance energy transfer compared with a simple random walk. J. Appl. Phys. 2012, 111, 044510. [Google Scholar] [CrossRef]
- Van Eersel, H.; Bobbert, P.A.; Coehoorn, R. Kinetic Monte Carlo study of triplet-triplet annihilation in organic phosphorescent emitters. J. Appl. Phys. 2015, 117, 115502. [Google Scholar] [CrossRef]
- Van Eersel, H.; Bobbert, P.; Janssen, R.; Coehoorn, R. Monte Carlo study of efficiency roll-off of phosphorescent organic light-emitting diodes: Evidence for dominant role of triplet-polaron quenching. Appl. Phys. Lett. 2014, 105, 156_1. [Google Scholar] [CrossRef]
- Coehoorn, R.; van Eersel, H.; Bobbert, P.; Janssen, R. Kinetic Monte Carlo study of the sensitivity of OLED efficiency and lifetime to materials parameters. Adv. Funct. Mater. 2015, 25, 2024–2037. [Google Scholar] [CrossRef]
- Mesta, M.; Carvelli, M.; De Vries, R.J.; Van Eersel, H.; Van Der Holst, J.J.; Schober, M.; Furno, M.; Lüssem, B.; Leo, K.; Loebl, P.; et al. Molecular-scale simulation of electroluminescence in a multilayer white organic light-emitting diode. Nat. Mater. 2013, 12, 652–658. [Google Scholar] [CrossRef] [PubMed]
- González, D.M.; Körstgens, V.; Yao, Y.; Song, L.; Santoro, G.; Roth, S.V.; Müller-Buschbaum, P. Improved power conversion efficiency of P3HT:PCBM organic solar cells by strong spin–orbit coupling-induced delayed fluorescence. Adv. Energy Mater. 2015, 5, 1401770. [Google Scholar] [CrossRef]
- Luhman, W.A.; Holmes, R.J. Enhanced exciton diffusion in an organic photovoltaic cell by energy transfer using a phosphorescent sensitizer. Appl. Phys. Lett. 2009, 94, 110. [Google Scholar] [CrossRef]
- Yang, C.M.; Wu, C.H.; Liao, H.H.; Lai, K.Y.; Cheng, H.P.; Horng, S.F.; Meng, H.F.; Shy, J.T. Enhanced photovoltaic response of organic solar cell by singlet-to-triplet exciton conversion. Appl. Phys. Lett. 2007, 90, 133509. [Google Scholar] [CrossRef]
- Baranovskii, S. Theoretical description of charge transport in disordered organic semiconductors. Phys. Status Solidi B 2014, 251, 487–525. [Google Scholar] [CrossRef]
- Tessler, N.; Preezant, Y.; Rappaport, N.; Roichman, Y. Charge transport in disordered organic materials and its relevance to thin-film devices: A tutorial review. Adv. Mater. 2009, 21, 2741–2761. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Bortz, A.B.; Kalos, M.H.; Lebowitz, J.L. A new algorithm for Monte Carlo simulation of Ising spin systems. J. Comp. Phys. 1975, 17, 10–18. [Google Scholar] [CrossRef]
- Voter, A.F. Introduction to the kinetic Monte Carlo method. In Radiation Effects in Solids; Springer, NATO Publishing Unit: Dordrecht, The Netherlands, 2007; pp. 1–13. [Google Scholar]
- Schwabl, F. Statistische Physik; Springer: Berlin, Germany, 2006. [Google Scholar]
- Auf der Maur, M.; Albes, T.; Gagliardi, A. Thin-film Solar Cells. In Handbook of Optoelectronic Device Modeling and Simulation: Lasers, Modulators, Photodetectors, Solar Cells, and Numerical Methods—Volume Two, Series: Series in Optics and Optoelectronics, VIII. Solar Cells, 43. 2017-09; Joachim Piprek, NUSOD Institute LLC, N.D.U., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Van Der Holst, J.; Uijttewaal, M.; Ramachandhran, B.; Coehoorn, R.; Bobbert, P.; De Wijs, G.; De Groot, R. Modeling and analysis of the three-dimensional current density in sandwich-type single-carrier devices of disordered organic semiconductors. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Bouhassoune, M.; Van Mensfoort, S.; Bobbert, P.; Coehoorn, R. Carrier-density and field-dependent charge-carrier mobility in organic semiconductors with correlated Gaussian disorder. Org. Electron. 2009, 10, 437–445. [Google Scholar] [CrossRef]
- Szymański, M.Z.; Łuszczyńska, B.; Djurado, D. Modeling the transient space-charge-limited current response of organic semiconductor diodes using the master equation approach. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1–7. [Google Scholar] [CrossRef]
- Groves, C. Developing understanding of organic photovoltaic devices: Kinetic Monte Carlo models of geminate and non-geminate recombination, charge transport and charge extraction. Energy Environ. Sci. 2013, 6, 3202–3217. [Google Scholar] [CrossRef]
- Kaiser, W.; Albes, T.; Gagliardi, A. Charge carrier mobility of disordered organic semiconductors with correlated energetic and spatial disorder. Phys. Chem. Chem. Phys. 2018. [Google Scholar] [CrossRef] [PubMed]
- Troisi, A.; Orlandi, G. Dynamics of the intermolecular transfer integral in crystalline organic semiconductors. J. Phys. Chem. A 2006, 110, 4065–4070. [Google Scholar] [CrossRef] [PubMed]
- Ren, J.; Vukmirović, N.; Wang, L.W. Nonadiabatic molecular dynamics simulation for carrier transport in a pentathiophene butyric acid monolayer. Phys. Rev. B 2013, 87, 205117. [Google Scholar] [CrossRef]
- Vukmirovic, N.; Wang, L.W. Charge carrier motion in disordered conjugated polymers: A multiscale ab-initio study. Nano Lett. 2009, 9, 3996–4000. [Google Scholar] [CrossRef] [PubMed]
- Kordt, P.; Stodtmann, S.; Badinski, A.; Al Helwi, M.; Lennartz, C.; Andrienko, D. Parameter-free continuous drift–diffusion models of amorphous organic semiconductors. Phys. Chem. Chem. Phys. 2015, 17, 22778–22783. [Google Scholar] [CrossRef] [PubMed]
- Mollinger, S.A.; Salleo, A.; Spakowitz, A.J. Anomalous charge transport in conjugated polymers reveals underlying mechanisms of trapping and percolation. ACS Cent. Sci. 2016, 2, 910–915. [Google Scholar] [CrossRef] [PubMed]
- Nenashev, A.; Oelerich, J.; Dvurechenskii, A.; Gebhard, F.; Baranovskii, S. Fundamental characteristic length scale for the field dependence of hopping charge transport in disordered organic semiconductors. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. Journal Für Die Reine und Angewandte Mathematik (Crelles Journal) 1908, 134, 198–287. (In French) [Google Scholar]
- Rycroft, C. Voro++: A three-dimensional Voronoi cell library in C++. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- Kordt, P.; van der Holst, J.J.M.; Al Helwi, M.; Kowalsky, W.; May, F.; Badinski, A.; Lennartz, C.; Andrienko, D. Modeling of Organic Light Emitting Diodes: From Molecular to Device Properties. Adv. Funct. Mater. 2015, 25, 1955–1971. [Google Scholar] [CrossRef]
- Baumeier, B.; Stenzel, O.; Poelking, C.; Andrienko, D.; Schmidt, V. Stochastic modeling of molecular charge transport networks. Phys. Rev. B 2012, 86, 184202. [Google Scholar] [CrossRef]
- Sirringhaus, H.; Wilson, R.; Friend, R.; Inbasekaran, M.; Wu, W.; Woo, E.; Grell, M.; Bradley, D. Mobility enhancement in conjugated polymer field-effect transistors through chain alignment in a liquid-crystalline phase. Appl. Phys. Lett. 2000, 77, 406–408. [Google Scholar] [CrossRef]
- Carbone, P.; Troisi, A. Charge diffusion in semiconducting polymers: Analytical relation between polymer rigidity and time scales for intrachain and inter-chain hopping. J. Phys. Chem. Lett. 2014, 5, 2637–2641. [Google Scholar] [CrossRef] [PubMed]
- Conchuir, B.O.; Tarantini, C.; McNeill, C.R.; Hüttner, S.; Zaccone, A. Chain-assisted charge transport in semicrystalline conjugated polymers. J. Phys. Chem. C 2016, 120, 14539–14548. [Google Scholar] [CrossRef][Green Version]
- Fornari, R.P.; Troisi, A. Theory of charge hopping along a disordered polymer chain. Phys. Chem. Chem. Phys. 2014, 16, 9997–10007. [Google Scholar] [CrossRef] [PubMed]
- Vanlaeke, P.; Swinnen, A.; Haeldermans, I.; Vanhoyland, G.; Aernouts, T.; Cheyns, D.; Deibel, C.; D’Haen, J.; Heremans, P.; Poortmans, J.; et al. P3HT/PCBM bulk heterojunction solar cells: Relation between morphology and electro-optical characteristics. Sol. Energy Mater. Sol. Cells 2006, 90, 2150–2158. [Google Scholar] [CrossRef]
- Singh, C.R.; Gupta, G.; Lohwasser, R.; Engmann, S.; Balko, J.; Thelakkat, M.; Thurn-Albrecht, T.; Hoppe, H. Correlation of charge transport with structural order in highly ordered melt-crystallized poly (3-hexylthiophene) thin films. J. Polym. Sci., Part B: Polym. Phys. 2013, 51, 943–951. [Google Scholar] [CrossRef]
- Sirringhaus, H.; Brown, P.; Friend, R.; Nielsen, M.M.; Bechgaard, K.; Langeveld-Voss, B.; Spiering, A.; Janssen, R.A.; Meijer, E.; Herwig, P.; et al. Two-dimensional charge transport in self-organized, high-mobility conjugated polymers. Nature 1999, 401, 685–688. [Google Scholar] [CrossRef]
- Pröller, S.; Liu, F.; Zhu, C.; Wang, C.; Russell, T.P.; Hexemer, A.; Müller-Buschbaum, P.; Herzig, E.M. Following the morphology formation in situ in printed active layers for organic solar cells. Adv. Energy Mater. 2016, 6. [Google Scholar] [CrossRef]
- Pasveer, W.; Cottaar, J.; Tanase, C.; Coehoorn, R.; Bobbert, P.; Blom, P.; De Leeuw, D.; Michels, M. Unified description of charge-carrier mobilities in disordered semiconducting polymers. Phys. Rev. Lett. 2005, 94, 206601. [Google Scholar] [CrossRef] [PubMed]
- Landau, R.H.; Paez, M.J.; Bordeianu, C.C. Computational Physics: Problem Solving with Python; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015. [Google Scholar]
- Moore, J. Gel permeation chromatography. I. A new method for molecular weight distribution of high polymers. J. Polym. Sci. Part A Polym. Chem. 1964, 2, 835–843. [Google Scholar] [CrossRef]
- Förster, S.; Schmidt, M.; Antonietti, M. Static and dynamic light scattering by aqueous polyelectrolyte solutions: Effect of molecular weight, charge density and added salt. Polymer 1990, 31, 781–792. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer photovoltiac cells: Enhanced efficiencies via a network of internal donor-acceptor heterojunctions. Science 1995, 270, 1789. [Google Scholar] [CrossRef]
- Xu, B.; Holdcroft, S. Phosphorescence and delayed fluorescence of poly (3-hexylthiophene) films. Thin Solid Films 1994, 242, 174–177. [Google Scholar] [CrossRef]
- Köhler, A.; Bässler, H. Triplet states in organic semiconductors. Mater. Sci. Eng. R Rep. 2009, 66, 71–109. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y.; Wang, H.; Xu, C.; Yang, S. Fe3O4 nanoparticles induced magnetic field effect on efficiency enhancement of P3HT: PCBM bulk heterojunction polymer solar cells. Sol. Energy Mater. Sol. Cells 2011, 95, 2880–2885. [Google Scholar] [CrossRef]
- Zhang, W.; Nguyen, N.A.; Murray, R.; Xin, J.; Mackay, M.E. A comparative study on the morphology of P3HT: PCBM solar cells with the addition of Fe3O4 nanoparticles by spin and rod coating methods. J. Nanopart. Res. 2017, 19, 315. [Google Scholar] [CrossRef]
- Baldo, M.A.; O’brien, D.; You, Y.; Shoustikov, A.; Sibley, S.; Thompson, M.; Forrest, S. Highly efficient phosphorescent emission from organic electroluminescent devices. Nature 1998, 395, 151–154. [Google Scholar] [CrossRef]
- Baldo, M.; Thompson, M.; Forrest, S. High-efficiency fluorescent organic light-emitting devices using a phosphorescent sensitizer. Nature 2000, 403, 750–753. [Google Scholar] [CrossRef] [PubMed]
- Sousa, L.; Volpi, R.; da Silva Filho, D.A.; Linares, M. Mobility field and mobility temperature dependence in PC61BM: A kinetic Monte-Carlo study. Chem. Phys. Lett. 2017, 689, 74–81. [Google Scholar] [CrossRef]
- Tanase, C.; Meijer, E.; Blom, P.; De Leeuw, D. Unification of the hole transport in polymeric field-effect transistors and light-emitting diodes. Phys. Rev. Lett. 2003, 91, 216601. [Google Scholar] [CrossRef] [PubMed]
- Gartstein, Y.N.; Conwell, E. High-field hopping mobility in molecular systems with spatially correlated energetic disorder. Chem. Phys. Lett. 1995, 245, 351–358. [Google Scholar] [CrossRef]
- Cordes, H.; Baranovskii, S.; Kohary, K.; Thomas, P.; Yamasaki, S.; Hensel, F.; Wendorff, J.H. One-dimensional hopping transport in disordered organic solids. I. Analytic calculations. Phys. Rev. B 2001, 63, 094201. [Google Scholar] [CrossRef]
- Kordt, P.; Andrienko, D. Modeling of spatially correlated energetic disorder in organic semiconductors. J. Chem. Theory Comput. 2016, 12, 36. [Google Scholar] [CrossRef] [PubMed]
- Miller, A.; Abrahams, E. Impurity conduction at low concentrations. Phys. Rev. 1960, 120, 745. [Google Scholar] [CrossRef]
- Coehoorn, R.; Pasveer, W.; Bobbert, P.; Michels, M. Charge-carrier concentration dependence of the hopping mobility in organic materials with Gaussian disorder. Phys. Rev. B 2005, 72, 155206. [Google Scholar] [CrossRef]
- Coropceanu, V.; Cornil, J.; da Silva Filho, D.A.; Olivier, Y.; Silbey, R.; Brédas, J.L. Charge transport in organic semiconductors. Chem. Rev. 2007, 107, 926–952. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599. [Google Scholar] [CrossRef]
- Ewald, P.P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys. 1921, 369, 253–287. [Google Scholar] [CrossRef]
- Stehr, V.; Pfister, J.; Fink, R.; Engels, B.; Deibel, C. First-principles calculations of anisotropic charge-carrier mobilities in organic semiconductor crystals. Phys. Rev. B 2011, 83, 155208. [Google Scholar] [CrossRef]
- Kirkpatrick, J.; Marcon, V.; Nelson, J.; Kremer, K.; Andrienko, D. Charge mobility of discotic mesophases: A multiscale quantum and classical study. Phys. Rev. Lett. 2007, 98, 227402. [Google Scholar] [CrossRef] [PubMed]
- Scholes, G.D.; Rumbles, G. Excitons in nanoscale systems. Nat. Mater. 2006, 5, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Mikhnenko, O.V.; Blom, P.W.; Nguyen, T.Q. Exciton diffusion in organic semiconductors. Energy Environ. Sci. 2015, 8, 1867–1888. [Google Scholar] [CrossRef]
- Pettersson, L.A.; Roman, L.S.; Inganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Peumans, P.; Yakimov, A.; Forrest, S.R. Small molecular weight organic thin-film photodetectors and solar cells. J. Appl. Phys. 2003, 93, 3693–3723. [Google Scholar] [CrossRef]
- Burkhard, G.F.; Hoke, E.T.; McGehee, M.D. Accounting for interference, scattering, and electrode absorption to make accurate internal quantum efficiency measurements in organic and other thin solar cells. Adv. Mater. 2010, 22, 3293–3297. [Google Scholar] [CrossRef] [PubMed]
- Mikhnenko, O.V.; Lin, J.; Shu, Y.; Anthony, J.E.; Blom, P.W.; Nguyen, T.Q.; Loi, M.A. Effect of thermal annealing on exciton diffusion in a diketopyrrolopyrrole derivative. Phys. Chem. Chem. Phys. 2012, 14, 14196–14201. [Google Scholar] [CrossRef] [PubMed]
- Athanasopoulos, S.; Emelianova, E.V.; Walker, A.B.; Beljonne, D. Exciton diffusion in energetically disordered organic materials. Phys. Rev. B 2009, 80, 195209. [Google Scholar] [CrossRef]
- Hoffmann, S.T.; Athanasopoulos, S.; Beljonne, D.; Bässler, H.; Köhler, A. How do triplets and charges move in disordered organic semiconductors? A Monte Carlo study comprising the equilibrium and nonequilibrium regime. J. Phys. Chem. C 2012, 116, 16371–16383. [Google Scholar] [CrossRef]
- Forster, T. Energiewanderung und Fluoreszenz. Naturwissenschaften 1946, 33, 166–175. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. (In German) [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Ann. Phys. 1906, 326, 756–780. (In German) [Google Scholar] [CrossRef]
- Dexter, D.L. A theory of sensitized luminescence in solids. J. Chem. Phys. 1953, 21, 836–850. [Google Scholar] [CrossRef]
- Hwang, I.W.; Moses, D.; Heeger, A.J. Photoinduced carrier generation in P3HT/PCBM bulk heterojunction materials. J. Phys. Chem. C 2008, 112, 4350–4354. [Google Scholar] [CrossRef]
- Scheidler, M.; Cleve, B.; Bässler, H.; Thomas, P. Monte Carlo simulation of bimolecular exciton annihilation in an energetically random hopping system. Chem. Phys. Lett. 1994, 225, 431–436. [Google Scholar] [CrossRef]
- Murawski, C.; Leo, K.; Gather, M.C. Efficiency roll-off in organic light-emitting diodes. Adv. Mater. 2013, 25, 6801–6827. [Google Scholar] [CrossRef] [PubMed]
- Cheung, D.L.; McMahon, D.P.; Troisi, A. Computational Study of the Structure and Charge-Transfer Parameters in Low-Molecular-Mass P3HT. J. Phys. Chem. B 2009, 113, 9393–9401. [Google Scholar] [CrossRef] [PubMed]
- Kraabel, B.; Moses, D.; Heeger, A. Direct observation of the intersystem crossing in poly (3-octylthiophene). J. Chem. Phys. 1995, 103, 5102–5108. [Google Scholar] [CrossRef]
- Kawamura, Y.; Brooks, J.; Brown, J.J.; Sasabe, H.; Adachi, C. Intermolecular interaction and a concentration-quenching mechanism of phosphorescent Ir (III) complexes in a solid film. Phys. Rev. Lett. 2006, 96. [Google Scholar] [CrossRef] [PubMed]
- Mikhnenko, O.V.; Ruiter, R.; Blom, P.W.; Loi, M.A. Direct measurement of the triplet exciton diffusion length in organic semiconductors. Phys. Rev. Lett. 2012, 108, 137401. [Google Scholar] [CrossRef] [PubMed]



| Description | Parameter | Value |
|---|---|---|
| Gaussian energetic disorder | eV | |
| Attempt-to-escape frequency | 3 × 1012 s−1 | |
| Inverse localization length | 2 nm−1 | |
| Charge density | n | 3.2 × 1016 cm−3 |
| Temperature | T | 298 K |
| Simulation time | 6 μs | |
| Applied field | F | 5 × 105 − 5 × 106 V cm−1 |
| Dielectric constant | 3.5 | |
| Intersite distance | a | 1 nm |
| Description | Parameter | Value | Ref. |
|---|---|---|---|
| Common Parameters | |||
| Phosphorescent dopant concentration | c | % | - |
| Energetic disorder excitons | - | ||
| Inverse localization length | [11,12] | ||
| Simulation time | - | ||
| Exciton parameters | |||
| Optical generation rate | - | ||
| Hopping rate (RW) | [13] | ||
| Singlet decay rate | [12,17,97] | ||
| Singlet binding energy | - | ||
| ISC radius phosphorescent dopant | - | ||
| ISC rate | - | ||
| Förster radius dopant | [98] | ||
| Dexter rate | [22] | ||
| Decay rate dopant | - | ||
| Decay rate host material | [24,63] | ||
| Triplet binding energy | - | ||
| TTA rate Dexter type | [22] | ||
| TTA Förster radius | [98] | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaiser, W.; Popp, J.; Rinderle, M.; Albes, T.; Gagliardi, A. Generalized Kinetic Monte Carlo Framework for Organic Electronics. Algorithms 2018, 11, 37. https://doi.org/10.3390/a11040037
Kaiser W, Popp J, Rinderle M, Albes T, Gagliardi A. Generalized Kinetic Monte Carlo Framework for Organic Electronics. Algorithms. 2018; 11(4):37. https://doi.org/10.3390/a11040037
Chicago/Turabian StyleKaiser, Waldemar, Johannes Popp, Michael Rinderle, Tim Albes, and Alessio Gagliardi. 2018. "Generalized Kinetic Monte Carlo Framework for Organic Electronics" Algorithms 11, no. 4: 37. https://doi.org/10.3390/a11040037
APA StyleKaiser, W., Popp, J., Rinderle, M., Albes, T., & Gagliardi, A. (2018). Generalized Kinetic Monte Carlo Framework for Organic Electronics. Algorithms, 11(4), 37. https://doi.org/10.3390/a11040037






