Design Optimization of Steering Mechanisms for Articulated Off-Road Vehicles Based on Genetic Algorithms

Abstract

Two cylinders arranged symmetrically on a frame have become a major form of steering mechanism for articulated off-road vehicles (AORVs). However, the differences of stroke and arm lead to pressure fluctuation, vibration noise, and a waste of torque. In this paper, the differences of stroke and arm are reduced based on a genetic algorithm (GA). First, the mathematical model of the steering mechanism is put forward. Then, the difference of stroke and arm are optimized using a GA. Finally, a FW50GLwheel loader is used as an example to demonstrate the proposed GA-based optimization method, and its effectiveness is verified by means of automatic dynamic analysis of mechanical systems (ADAMS). The stroke difference of the steering hydraulic cylinders was reduced by 92% and the arm difference reached a decrease of 78% through GA optimization, in comparison with unoptimized structures. The simulation result shows that the steering mechanism optimized by GA behaved better than by previous methods.

1. Introduction

Compared with other steering modes, two hydraulic cylinders arranged symmetrically on a frame has become a major form of steering mechanism for articulated off-road vehicles (AORVs). The frame of an AORV is composed of front frame and rear frame, and the steering of the vehicle is completed by the push and pull of the steering hydraulic cylinders. However, the difference of stroke between two cylinders and the difference arm lead to pressure fluctuation, vibration noise, and a waste of torque during the process of steering [1,2,3,4,5].

As a reaction to the phenomenon above, scholars and researchers have undertaken many discussions and studies on the optimization of the steering mechanism. Fang Jun [1] analyzed the steering geometry based on two medium-sized domestic loaders by means of quasi-discrete methods; he believed that there was much room for steering mechanism optimization. However, the quasi-discrete method-based optimization results of Fang Jun are not the optimal solution; in other words, there is still much room for improvement. Tan Zhuangshi [2] decreased the stroke difference (based on the ZL30 loader) through a sequential unconstrained minimization technique, but the constraints he defined were not clear enough. For example, he put forward that the minimum arm of force depends on the specific structure. Moreover, he did not discuss the impacts of arm difference on steering mechanisms. Zhou Linsong [3] presented that the stroke difference is proportional to the arm difference; an optimized model was put forward through a geometrical analysis method. In his paper, he did not consider the effects of certain essential factors, such as transmission angle and the actual size of the cylinders. A mathematical model of the cylinder’s stroke and arm in the steering process was built by Qiang Wei [4], and the mathematical model was optimized based on a matrix laboratory (MATLAB, 2014) optimization toolbox. Du Lei [5] finished the optimum design for pivot points of steering mechanisms based on the HT25J wheel loader with the optimization toolbox of MATLAB. The parametric design method for the maximum steering torque was obtained by Wang Hegen [6], based on the mathematical analysis of the double-cylinder-driven steering mechanism. However, all of the techniques above were solely based on classical analysis and simple geometric logic, thus making optimization and their results unsatisfactory. To address these shortfalls, a genetic algorithm (GA) is presented in this paper as a new method of AORV steering mechanism optimization which has a stronger global search ability for mechanism design.

As an evolutionary computation method for optimization, GA works by mimicking biological evolution [7]. A new population is generated through competition, multiplication, and mutation among groups from generation to generation during the solution process, and finally the “most environment-adapted” individual is found. Therefore, the global optimal solution is obtained, instead of the local optimal solution [8]. On one hand, the GA method is operated by encoding variables, which ensures that it is not limited by the nature of the variables itself. On the other hand, GA targets groups rather than individuals. Starting with the grouping implies the characteristics of parallel search and global random search, which greatly reduces the possibility of getting an optimal solution. Seyedfakhreddin Nabavi [9] proposed a GA-based design and optimization method for micro-electromechanical systems (MEMS) unimorph piezoelectric energy harvesters, and the GA-based optimization methodology he proposed demonstrated an enhancement of energy harvesting efficiency by 31% in comparison with un-optimized harvesters. This research demonstrated the optimization of micro-electromechanical systems, but only one objective was taken into consideration. In that paper, two objectives—including stroke difference and arm difference—were studied in GA. B. Senthilkumar [10] finished the optimization of flux-cored arc welding process parameters by using GA. Texture shape under unidirectional sliding was optimized by Hui Zhang [11], based on GA. Joanna Ferdyn-Grygierek [12] realized the multi-variable optimization of building thermal design using GA. Junhui Meng [13] put forward the hierarchical optimization of the composite blade of a stratospheric airship propeller by means of GA. The optimization of surface roughness in the cylindrical grinding process was completed by Ravi Kumar Panthangi [14] through GA. This hierarchical optimization method based on GA is very interesting and useful, and can increase the computational efficiency of fitness value in the future. Srikumar Mallik [15] showed how one can optimize the design of a three-phase squirrel cage induction motor, and achieved a more efficient and cost-optimized design of an induction motor based on GA. This study balanced the two objectives (efficiency and cost) to make the best effect, which gives us important guidance on how to achieve a multi-objective optimization. José Humberto S. Almeida, Jr. [16] presented a GA for the optimization of a stacking sequence to improve the strength of a cylindrical shell under internal pressure. Johannes Knust [17] finished the preform optimization for hot forging processes using GA, and his study demonstrated that a GA-based approach could realize the optimization effectively.

In addition, learning approaches consist of stochastic learning automata, payoff-based log-linear learning, learning by trial and error, and no-regret learning [18]. Learning approaches can substitute the proposed genetic algorithm, especially in a real-time environment. Moreover, learning approaches have already been applied in the literature to provide intelligence to the involved parties/entities. Eirini Eleni Tsiropoulou et al. [19] introduced the concept of joint consideration of interest, physical-, and energy-related properties in the clustering and resource management processes in M2M (Machine to Machine) communication networks supporting various IoT (Internet of Things) applications, based on a cluster formation mechanism. P Blasco et al. [20] proposed a learning theoretical approach to energy harvesting communication system optimization, which proved that the transmitter is able to learn the optimal transmission policy that maximizes the expected sum of the data transmitted during the transmitter’s lifetime. R Razavi et al. [21] introduced a solution to enable the self-optimization of coverage and capacity in LTE (Long Term Evolution networks) based on a fuzzy reinforcement-learning approach. However, learning approaches generally have the property of extremely slow convergence when they have a large number of feasible actions [8]. To cope with this problem, a GA is employed to accelerate convergence. Therefore, this paper makes use of a GA to optimize the design of AORV steering mechanisms.

Previous studies have seldom used GA (an evolutionary computation method for optimization problems by mimicking biological evolution [9]) for the design optimization of AORV steering mechanisms. In this paper, a GA is applied to the optimization of the steering mechanism. With a case study, the stroke difference and arm difference are reduced, and an optimized result is obtained.

2. Problem Description

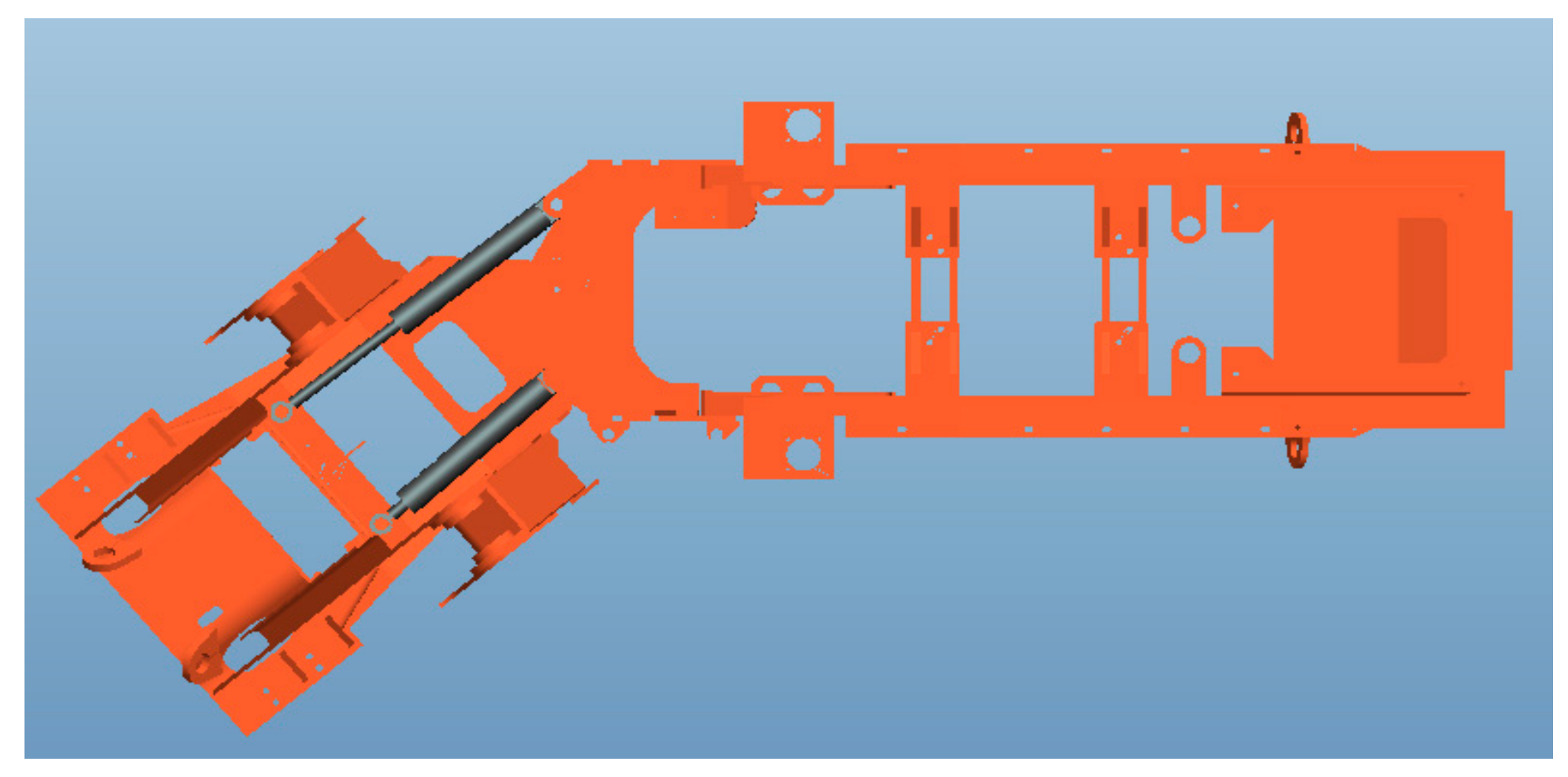
Two cylinders arranged symmetrically on a frame has become a major form of steering mechanisms for AORVs. The steering process of an AORV can be taken as a circular motion with a certain center and radius; the certain center is the hinge-point of the front and rear frames, and the certain radius depends on the installation position of the cylinders. As shown in Figure 1 and Figure 2, one of two cylinders is stretched out, and the other is compressed after turning. However, the stroke of the two cylinders is different.

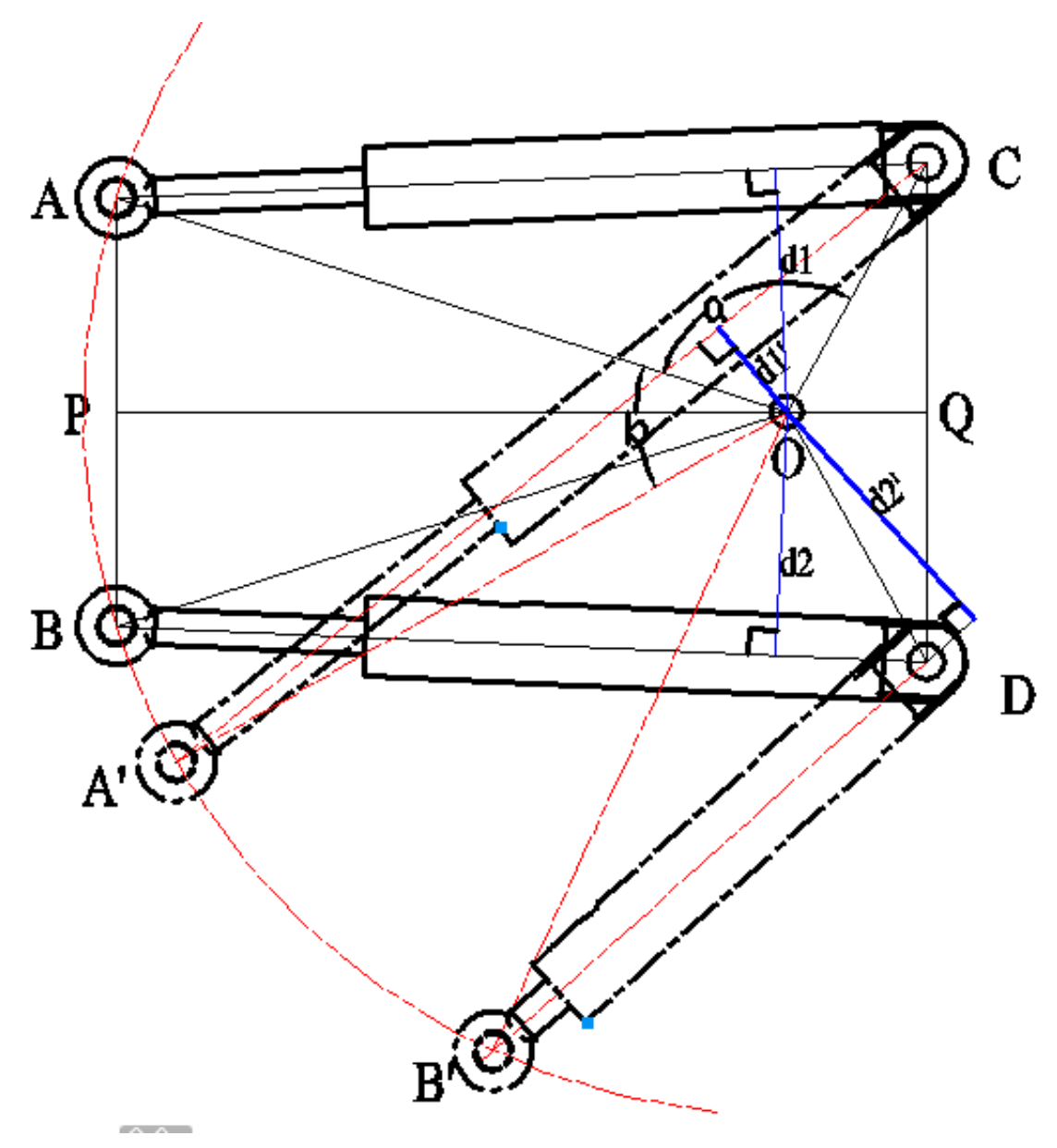
As shown in Figure 3, the stroke difference and arm difference can be analyzed from the perspective of mathematical geometry. To facilitate calculation, $r$ and $h$ are taken as the AO and CO. According to the triangle cosine theorem, it is easy to determine the stroke difference and arm difference. As seen in Figure 3, if the values of AO and CO are $r$ and $h$, then AO = BO = A′O = B′O = $r$, CO = DO = $h$. The geometrical relationship in the picture is shown as follows.

$$\begin{array}{l}AC=BD=\sqrt{r^2+h^2+2r\cdot h\cdot \cos a}\\ A^{\prime }C=\sqrt{r^2+h^2+2r\cdot h\cdot \cos (a+b)}\\ B^{\prime }D=\sqrt{r^2+h^2+2r\cdot h\cdot \cos (a-b)}\end{array}$$

(1)

$$\begin{array}{l}\Delta l=(A^{\prime }C-AC)-(BD-B^{\prime }D)\\ =\sqrt{r^2+h^2+2r\cdot h\cdot \cos (a+b)}+\\ \sqrt{r^2+h^2+2r\cdot h\cdot \cos (a-b)}-\\ 2\sqrt{r^2+h^2+2r\cdot h\cdot \cos a}\end{array}$$

(2)

$$\begin{array}{l}d1=d2=\frac{AO\cdot CO\cdot \sin a}{AC}\\ d{1}^{\prime }=\frac{A^{\prime }O\cdot CO\cdot \sin (a+b)}{A^{\prime }C}\\ d{2}^{\prime }=\frac{B^{\prime }O\cdot DO\cdot \sin (a-b)}{B^{\prime }D}\end{array}$$

(3)

$$\begin{array}{l}\Delta d=(d1-d{1}^{\prime })-(d{2}^{\prime }-d2)\\ =2d1-d{1}^{\prime }-d{2}^{\prime }\\ =\frac{2rh\sin a}{\sqrt{r^2+h^2+2r\cdot h\cdot \cos a}}-\\ \frac{rh\sin (a+b)}{\sqrt{r^2+h^2+2r\cdot h\cdot \cos (a+b)}}\\ -\frac{rh\sin (a-b)}{\sqrt{r^2+h^2+2r\cdot h\cdot \cos (a-b)}}\end{array}$$

(4)

A, B: The installation position of the two cylinders on the front frame;

C, D: The installation position of the two cylinders on the rear frame;

O: The hinge point of the front and rear frame.

$\Delta l$: Stroke difference;

$\Delta d$: Arm difference;

$b$: The steering angle.

From the formula above, as long as the value of $b$ is not equal to 0, it is easy to prove that $\Delta l$ and $\Delta d$ are never equal to 0. In other words, the differences of the stroke and arm are all present. As a result, the stroke difference and arm difference cause the non-constant flow of hydraulic oil, which can lead to a pressure pulsation in the hydraulic system, as well as energy loss [4,11]. Thus, based on GA, it is essential to reduce the two differences.

3. Optimization Based on GA

For the GA method, optimization targets should be proposed first. As demonstrated by Figure 3, both of the $\Delta l$ and $\Delta d$ are determined by the positions of “A”, “B”, “C”, “D”, and “O”; in other words, the joint positions of the hydraulic cylinders are considered as the design variables. Then, a set of constraints are given, including transmission angle, the parameters of the cylinder, triangle conditions, and the steering resistance moment. The stroke difference and the cylinders’ pressure are finally taken as the objective functions. In view of the characteristics of steering mechanism, GA is proposed for the optimization problem.

3.1. Determination of Design Variables

In this paper, the four hinge points of the two cylinders are taken as the design variables. However, as mentioned in Section 2, the two steering cylinders are symmetrically arranged in the same plane. Therefore, we only need to determine the mounting position of the two hinge points of one cylinder. The distances between the hinge point A, C, and the hinging center O in the transverse and longitudinal components were chosen as the design variable.

$$X={\left\{AP,PO,CQ,QO\right\}}^T={\left\{x_1,x_2,x_3,x_4\right\}}^T$$

3.2. Establishment of Constraints

 (1) Constraints of transmission angle

Transmission angle is one of the most important criterions of mechanical transmission efficiency. To ensure the transmission efficiency of the steering cylinder during steering, it is required that the minimum value of the transmission angle be greater than 10 degrees [22]:

$$J(1)=(a+b_{\min })-{170}^{\text{°}}\le 0,$$

(5)

$$J(2)=(a-b_{\max })-{10}^{\text{°}}\ge 0.$$

(6)

 (2) Constraints based on the structure of cylinders

In the design and manufacturing process, it is necessary to fully consider whether the designed structural dimensions meet the actual production requirements and commonality of cylinders. To meet the specification requirements of cylinders, it is essential to make the size and ratio meet the following conditions [2]:

$$J(3)=A^{\prime }{C}_{\max }+\epsilon -(l_{\max }+s)\le 0,$$

(7)

$$J(4)=B^{\prime }{D}_{\min }-(s+\epsilon )\ge 0,$$

(8)

$$1.3\le \frac{l_{\max }+s}{s}\le 1.6,$$

(9)

$l_{\max }$: The maximum stroke of the steering cylinder;

$s$: The minimum installation distance of the steering cylinder;

$\epsilon$: Reserve allowance for stroke, which can prevent the rigid impact between the rod and block of the cylinder.

 (3) Constraints about triangle

It is well-known that the prerequisite for the triangle establishment is that the sum of any two sides is greater than the third:

$$J(5)=CO+A^{\prime }{O}_{\max }-(l_{\max }+s+\epsilon )\ge 0,$$

(10)

$$J(6)=s+\epsilon +O{B}_{\max }^{\prime }-OD\ge 0.$$

(11)

 (4) Constraints on steering resistance moment

The steering resistance moment of pivot steering is usually 2–3 times that of driving. Thus, the pivot steering torque is taken as the calculated load. The following empirical formula comes from the test curve [23]:

$$M_{r_0}=\frac{G{f}^n}{\eta }(0.1L+0.6)(0.3b^2+0.1b+2.6),$$

(12)

$\eta$: Steering mechanism efficiency [1], $\eta =0.9$;

$G$: Vertical load on the tire;

$f$: Friction coefficient, $f=0.1\text{~}0.5$;

$L$: The wheelbase of the vehicle.

The steering torque should satisfy the following relationship:

$$2M_{r_0}-M=0.$$

(13)

 (5) Constraints based on the frame of the AORV

During the actual design process, in order to prevent structural interference and ensure the feasibility of hydraulic cylinders layout, it is important for designers to consider the limits and impact from the structure of the frame, which plays an essential role on the layout of the cylinder position. As a result, there are many boundary constraints related to the frame, which are shown as follows:

$$\begin{array}{l}{c}_1\le CQ\le c_2\\ c_3\le QO\le c_4\\ c_5\le AP\le c_6\\ c_7\le PO\le c_8\end{array}$$

(14)

where $c_1,c_2,c_3,c_4$ are constant values related to the frame structure.

3.3. Objective Function

To summarize, the optimization objective of this paper is to reduce the force arm difference and the stroke difference between the steering cylinders during the steering process by means of optimizing the hinge points of the steering cylinders. The objective function is shown in the following formulas:

$$\min F(x)={\lambda }_1{f}_1(x)+{\lambda }_2{f}_2(x),$$

(15)

$f_1(x)$: Stroke difference function of steering cylinder, $f_1(x)=\left|\Delta l\right|$;

$f_2(x)$: Arm difference function of steering mechanism, $f_2(x)=\left|\Delta d\right|$;

${\lambda }_1,{\lambda }_2$: Weighting factor.

3.4. Penalty Function

The diversity of the population would be affected if the unsatisfied constraint conditions of the individuals were abandoned directly. As a result, the exterior penalty function method (EPFM) was adopted in the aspect of constraints, which simplified the constraint process by means of transforming constrained optimization problems into unconstrained optimization problems [24]. The core of EPFM is to define the penalty function outside the feasible region; that is, to define the newly-generated objective function outside the feasible region. Once the design variable is inside the feasible region, the new objective function is the same as the original one. On the contrary, the new objective function has added a value far greater than the original objective function value, so that the new objective function value can be easily screened out during the selection of the GA. According to the given constraints, the evaluation function can be given as follows:

$$F(x)=\min \left\{{\lambda }_1{f}_1(x)+{\lambda }_2{f}_2(x)+\kappa {\displaystyle \sum _{i=1}^{n}J}{\left\{\max [J(i),0]\right\}}^2\right\},$$

(16)

$\kappa$: Punishment factor;

$n$: The number of constraints.

3.5. Design of Fitness Function

A fitness function is a function used to describe the ability of individuals to adapt to a living environment, and establishes the basis for selection of individuals that will be mated during reproduction. Individuals in the population are selected in order to eliminate those who cannot adapt to the environment based on the fitness function. The greater the value of fitness functions, the greater the individual’s ability to adapt to the environment. At the same time, the individual is less likely to be eliminated.

In the GA-based optimal design process, the fitness function selected is as Equation (17). The larger the objective function value, the smaller the fitness value.

$$S(x)=\frac{1}{F(x)}$$

(17)

To facilitate the calculation, the GA-based optimization was operated through MATLAB, which is often taken as a tool for optimization programs. In the following section, the capability of the GA-based optimization methodology in optimizing the steering mechanism will be discussed and demonstrated.

3.6. GA-Based Optimization

As described in Section 1, GAs are a very popular choice for optimization problems. The GA is an evolutionary computing method for searching and optimizing complex problems, which is motivated by the evolution of animal populations on earth [7,11]. Each possible solution of a problem is considered an “individual” with an encoded “chromosome”. 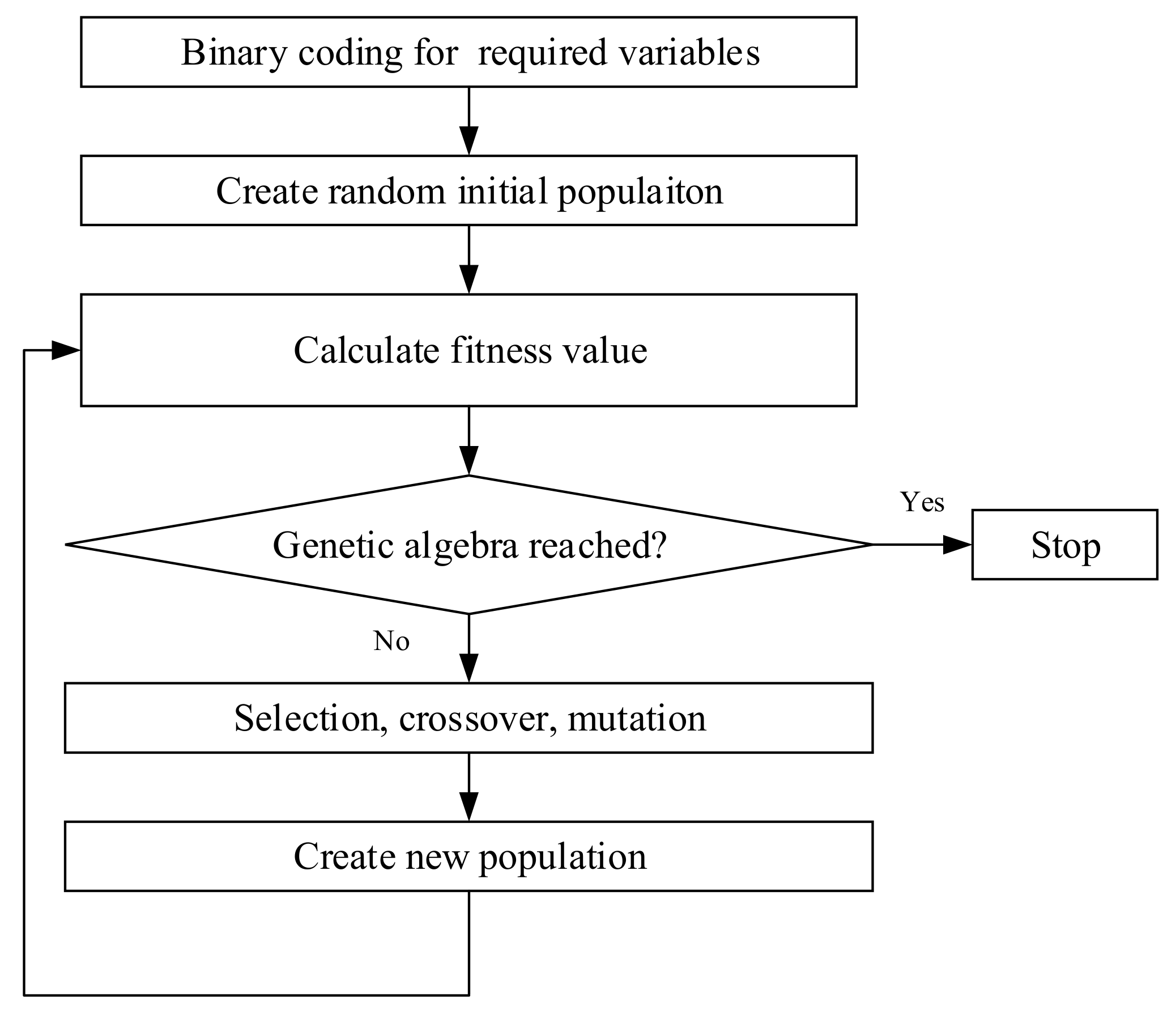During the computation of a GA, different operators can typically be applied to the set of solutions to provide new evolutionary populations [25]. The flowchart of the GA mechanism is illustrated in Figure 4.

• Step 1: Identify design variables and then encode the required variables in the form of a fixed-length binary string. Binary encoding is used because of the following advantages: (a) simple coding and decoding operations; (b) genetic operations such as selection, crossover, and mutation are easy to implement; (c) it complies with the principle of minimum symbol set coding. In this paper, the positions of four hinge points of the two cylinders are taken as the design variables. However, the positions of cylinders will be applied to the actual structure. Given the assembly accuracy, we set the accuracy of the optimization results to four decimal places. Consequently, the length of the binary string is calculated according to Equation (18):

  $$2^{i-1}\le (c_m-c_n)\times {10}^4\le 2^i-1,$$

  (18)
  $i$: The length of the binary string;
  $c_m,c_n$: The top and bottom limits of the design variables.
• Step 2: Create a random initial population. The individuals within the population are digitized codes. Set the evolution algebraic counter and the maximum evolution algebra to 0 and T, respectively.
• Step 3: Calculate their corresponding fitness values by means of the Equation (17) for the populations from Step 2 and those newly-bred populations after selection, crossover, and mutation from the next steps. Then, those individuals with relatively high calculated fitness are selected and kept in the procedure, which will be subsequently taken to reproduce a new generation with better adaptability than themselves in Step 5. As can be seen from Equation (17), the greater the fitness value, the smaller the stroke difference and arm difference. As a result, the optimal value is obtained when the fitness value reaches the maximum.
• Step 4: Check whether the iteration termination criterion for the GA has been reached. If the outputs of the GA do not satisfy the termination criteria, the next steps should be implemented.
• Step 5: Create new population through selection, crossover, and mutation. In GA, a method needs to be constructed to generate new species, in order to keep the objective function close to the optimal value. New species are generated via selection, crossover, and mutation. Selection is related to method and criteria, which are used to choose individuals with high fitness. Then, the selected individuals cross-pair with each other to generate new individuals, and these individuals are inserted into the parent population to generate more highly-adaptive populations, which is the offspring created by crossover. In other words, crossover creates new individuals through the recombination between string pairs of the selected individuals in the mating pool. Mutation refers to a new individual that resulted from a change in a gene of an individual’s chromosome.

4. Case Study

This section takes the steering mechanism of a FW50GL wheel loader as an example to verify the validation of the proposed optimization method in this paper, which is shown in Figure 5.

A wheel loader is a typical articulated steering vehicle. The relevant parameters of the FW50GL steering structure are shown in

Table 1. Parameters of the FW50GL steering mechanism.

Variables	Values
AP	150 mm
CQ	360 mm
PO	1017 mm
QO	13 mm
L	3300 mm
b	40°
$l_{\max }$	1040 mm
$s$	800 mm
G	3.8 t
$\epsilon$	8 mm

.

According to the data listed in the table, the constraints can be obtained from Equations (5)–(13), and Equation (14) can be set as follows based on the frame structure of FW50GL.

$$\begin{array}{l}310\le CQ\le 380\\ 0\le QO\le 40\\ 140\le AP\le 280\\ 980\le PO\le 1050\end{array}$$

In the optimal design presented by this paper, the sus function (random traversal sampling) was used to select individuals with high fitness from the parent population to breed offspring. The probability that each individual is selected is the ratio between the individual fitness value and the sum of all individual fitness values in the population. In other words, the greater the individual fitness value, the greater the probability of being selected. The single-point cross function with a crossover ratio of 0.5 was selected for crossover. Mutant selects must function, and the mutation ratio selected was 0.02. The parameters related to the GA-based optimization algorithm are listed in

Table 2. Parameters related to the GA-based optimization algorithm.

Variables	Values
Population	1000
Mutation ratio	0.02
Crossover ratio	0.5
T (Genetic algebra)	100

.

Based on the method and data proposed above, the steering mechanism of the FW50GL is optimized in MATLAB based on GA. The curve of the fitness function is shown in Figure 6, which indicates that the maximum of the fitness was 1.55, and the maximum emerged in the 58th generation.

Based on the method and data proposed above, the optimized results are compared with the pre-optimization in

Table 3. Data comparison between before and after optimization.

Variables	AP	CQ	PO	QO
Pre-Opt	150 mm	360 mm	1017 mm	13 mm
After-GA-Opt	258 mm	300 mm	1158 mm	0.25 mm

.

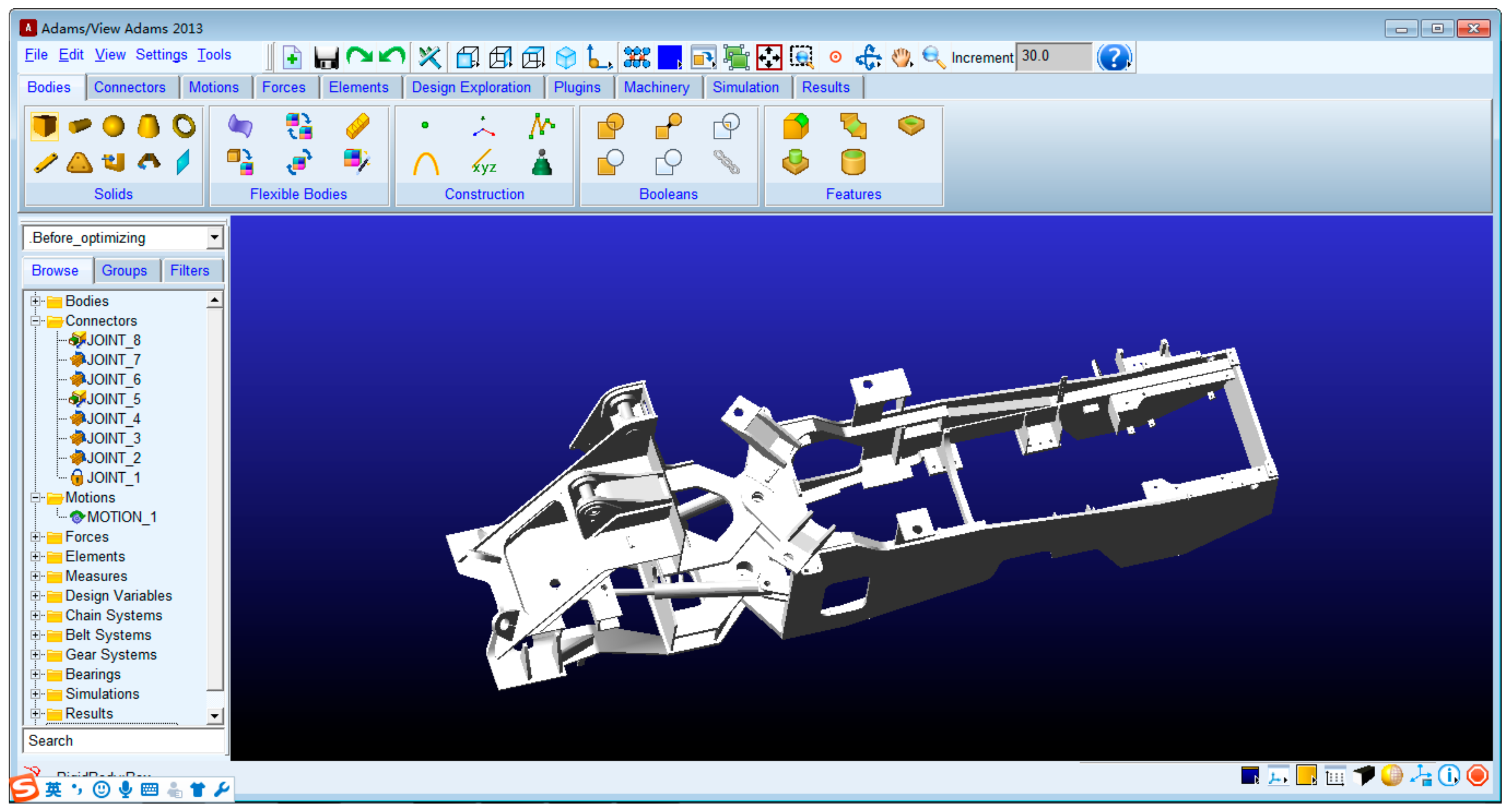
As shown in Figure 7 and Figure 8, the models of the FW50GL-based steering mechanism were built in ADAMS (automatic dynamic analysis of mechanical systems) software according to the data in Table 3. As a result, the simulation curves describing the trend of stroke and arm force varying with the steering angle were obtained, and are shown in Figure 9 and Figure 10.

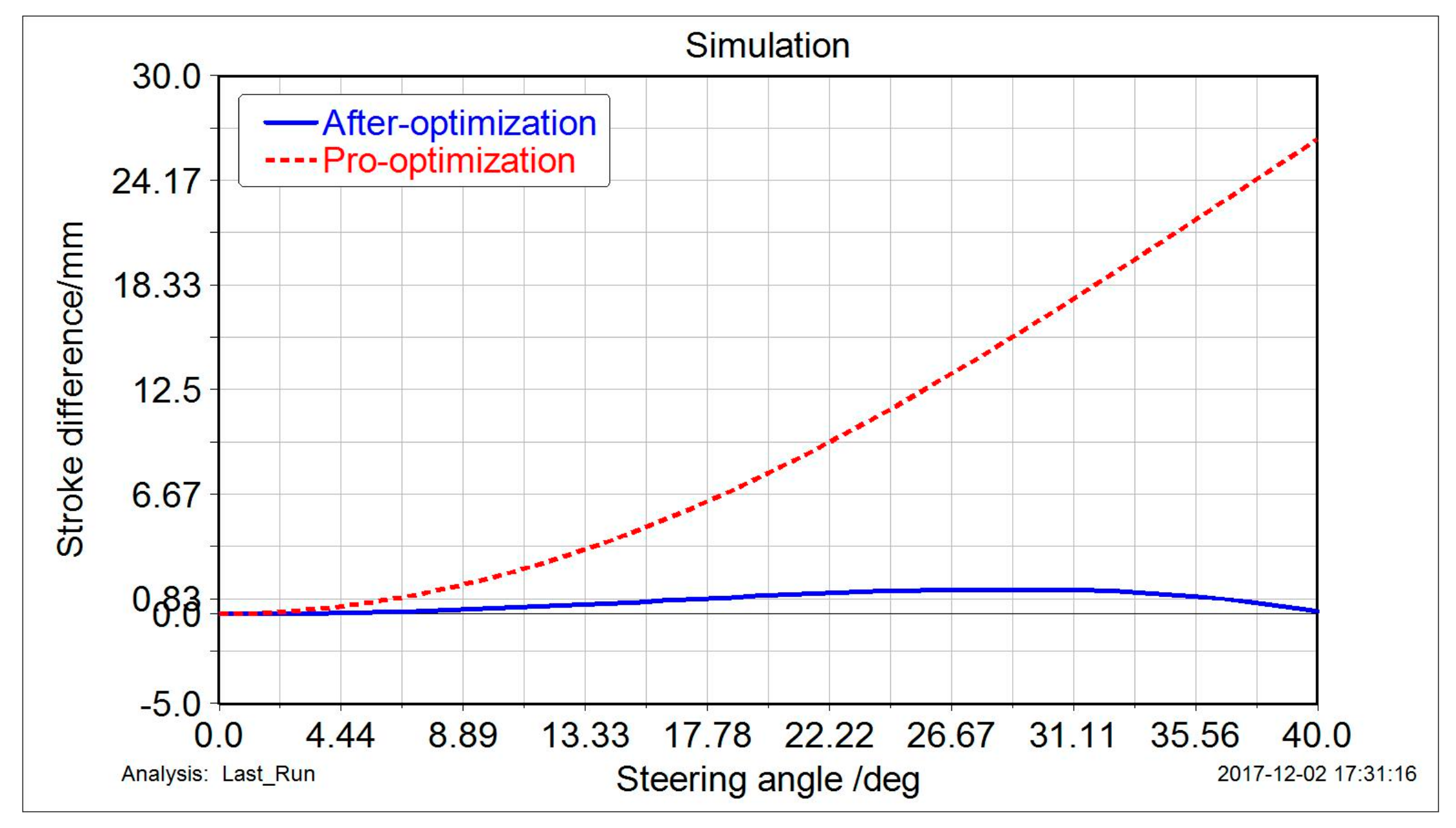
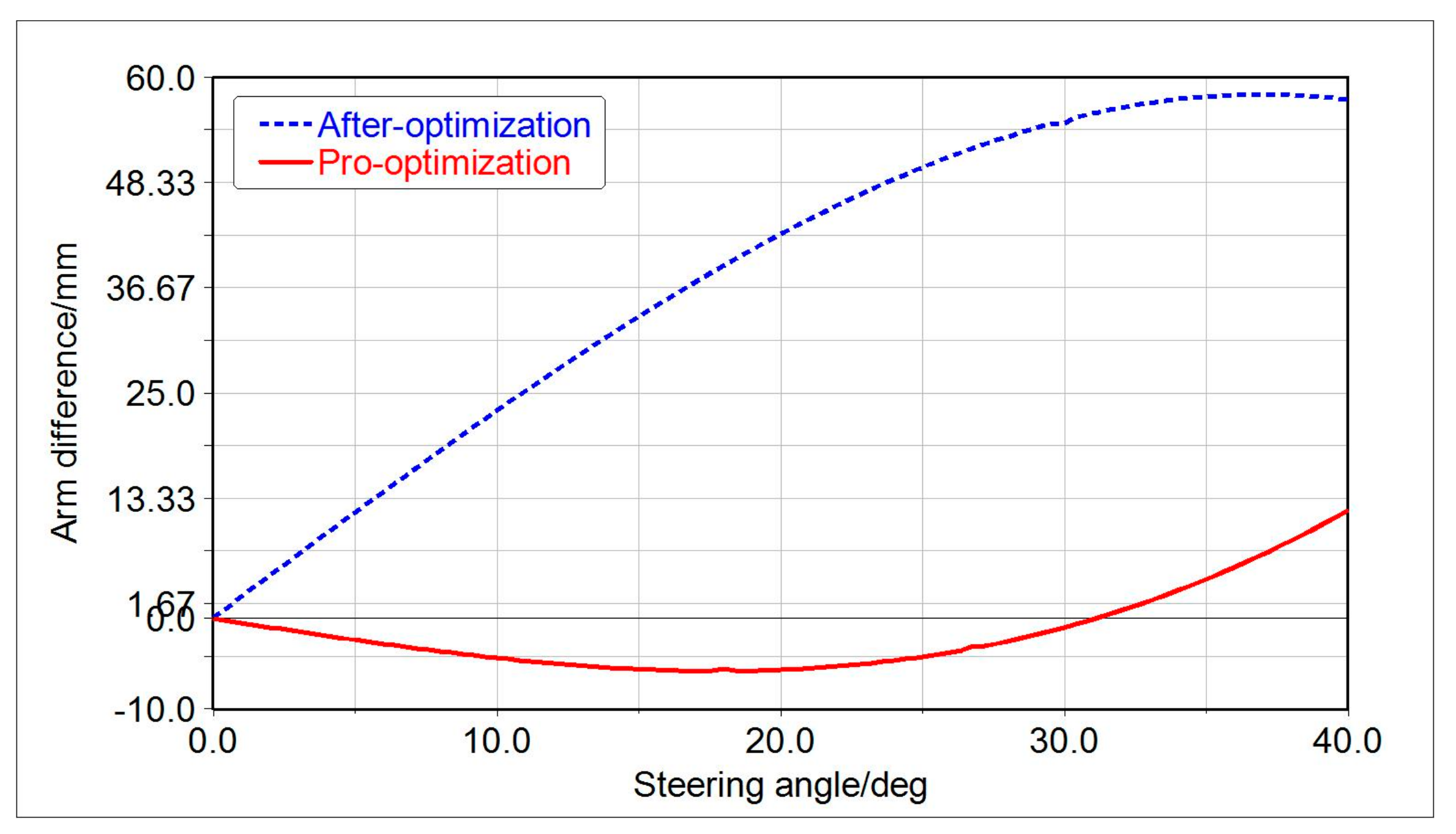
As can be seen from Figure 9, the stroke difference of the two steering hydraulic cylinders reached a maximum of 26 mm when the steering angle reached 40° before optimization. However, the maximum of stroke difference was reduced to 2 mm after optimizing by means of GA, and the maximum appeared at the steering angle of 29°. As shown in Figure 10, the maximum arm difference was reduced from 56 mm to 12 mm after optimizing. Therefore, the stroke difference of steering hydraulic cylinders was reduced by 92%; the arm difference reached a decrease of 78% through GA optimization in comparison with unoptimized structures.

5. Conclusions

In this paper, a GA-based design optimization method for an AORV steering mechanism is proposed. The problems caused by the stroke difference and arm difference for steering mechanisms were first presented and then analyzed by using analytic geometry and ADAMS. To address the problems mentioned above, GA was used to simulate the process of biological evolution for obtaining the best results. Analysis and comparison were made on the obtained results through MATLAB and ADAMS. The proposed GA-based optimization methodology in this study demonstrated an enhancement of stroke difference and arm difference by 92% and 78%, respectively, in comparison with unoptimized structures.

Compared with other studies [9,16], we found that the proposed GA was able to achieve optimization for two objectives: stroke difference and arm difference. Inspired by previous studies [15], the proposed GA gives a specific value of weighting factor ${\lambda }_1$ and ${\lambda }_2$, which has disadvantages in balancing the two objectives to make the best effect. In the next step, we will make joint efforts to combine related methods to design useful and effective weighting factors, in order to balance the stroke difference and arm difference. Moreover, this paper makes full use of hierarchical optimization methods [14] based on GA to improve the computational efficiency of fitness value in the future.