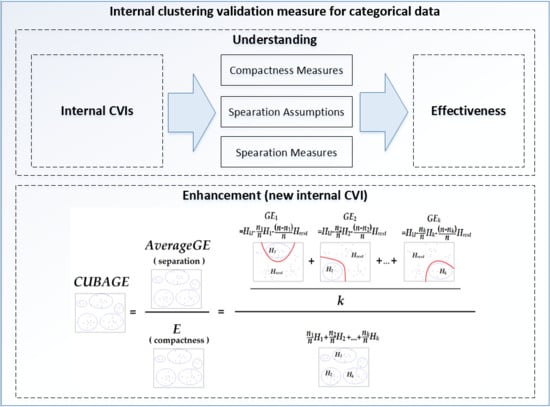
Understanding and Enhancement of Internal Clustering Validation Indexes for Categorical Data
Abstract
:1. Introduction
- Do internal CVIs for categorical data show monotonicity with respect to the number of clusters? One should avoid the monotonicity in validation measurement to prevent the bias towards partitions with more clusters, which would leave the performance of the evaluation to the boundary of the number of clusters in the candidate partitions.
- Do internal CVIs for categorical data which use no separation measures really ignore the separation? A partition of good compactness is not necessarily a good partition, since the objects in one cluster may be similar to the objects in other clusters as well. Some internal CVIs for categorical data use no separation measures based on the attribute distribution between clusters, and have been proven to be effective when the number of clusters is constant in reference [9]. However, if the impact of separation on the clustering validation is ignored, the compactness measure alone may not be effective in evaluating partitions of different sizes due to the first issue.
- What can we offer to enhance performance? After research on the above issues, we wish to offer an alternative internal CVI that has improved performance on categorical data clustering validation measurement.
2. Related Work
2.1. Notations
2.2. Internal Clustering Validation Indexes
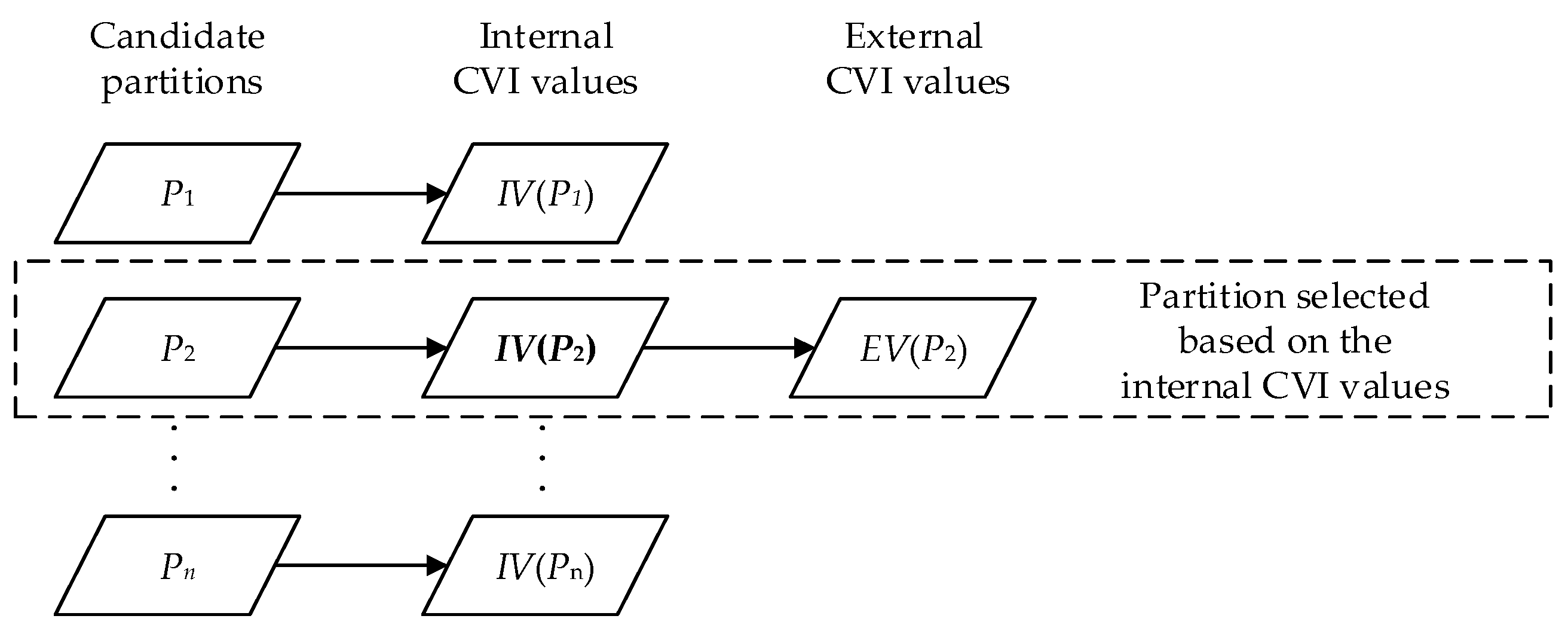
2.3. Comparison of Internal and External Clustering Validation Indexes
3. Understanding of Internal Clustering Validation Indexes
3.1. Generalization and an Example
3.2. Analysis of Indexes E and F
3.3. Analysis of Indexes CU1/k, Cloper, and R
4. Internal Clustering Validation Index: CUBAGE
4.1. Inter-Cluster Separation Measure: AGE
4.2. Upper and Lower Bounds of AGE
4.3. CUBAGE Index
| Algorithm 1 Clustering Utility based on Entropy (CUBAGE) |
| Input: dataset with n objects: U = (Xi); label of a partition with k clusters; Output: CUBAGE value of the partition; Called Function: entropy calculation function: Entropy(objects); Begin: 1. Calculate the entropy of the whole dataset, save as HU: HU = Entropy(U); 2. For each cluster Cl: 3. Calculate the entropy of objects in Cl, save in vector H:H(l) = Entropy(Cl); 4. Calculate the entropy of objects in U − Cl, save in vector HC:HC(l) = Entropy(U − Cl); 5. End for; 6. Generate weight vector: W = 1/n·[|C1|, | C2|, …, | Cl|]; 7. Calculate the dot product E = W·H; 8. Calculate AGE = HU − 1/k·[E + (1 − W)·HC]; Return: 9. CUBAGE = AGE/E; |
| Algorithm 2 Entropy calculation function |
| Input: a set of x objects; Output: Entropy of objects in a single set; Begin: 1. For each attribute Aj: 2. Calculate the entropy of the attribute by Equation (1), save in vector HA; 3. End for; Return: 4. Entropy = sum(HA); |
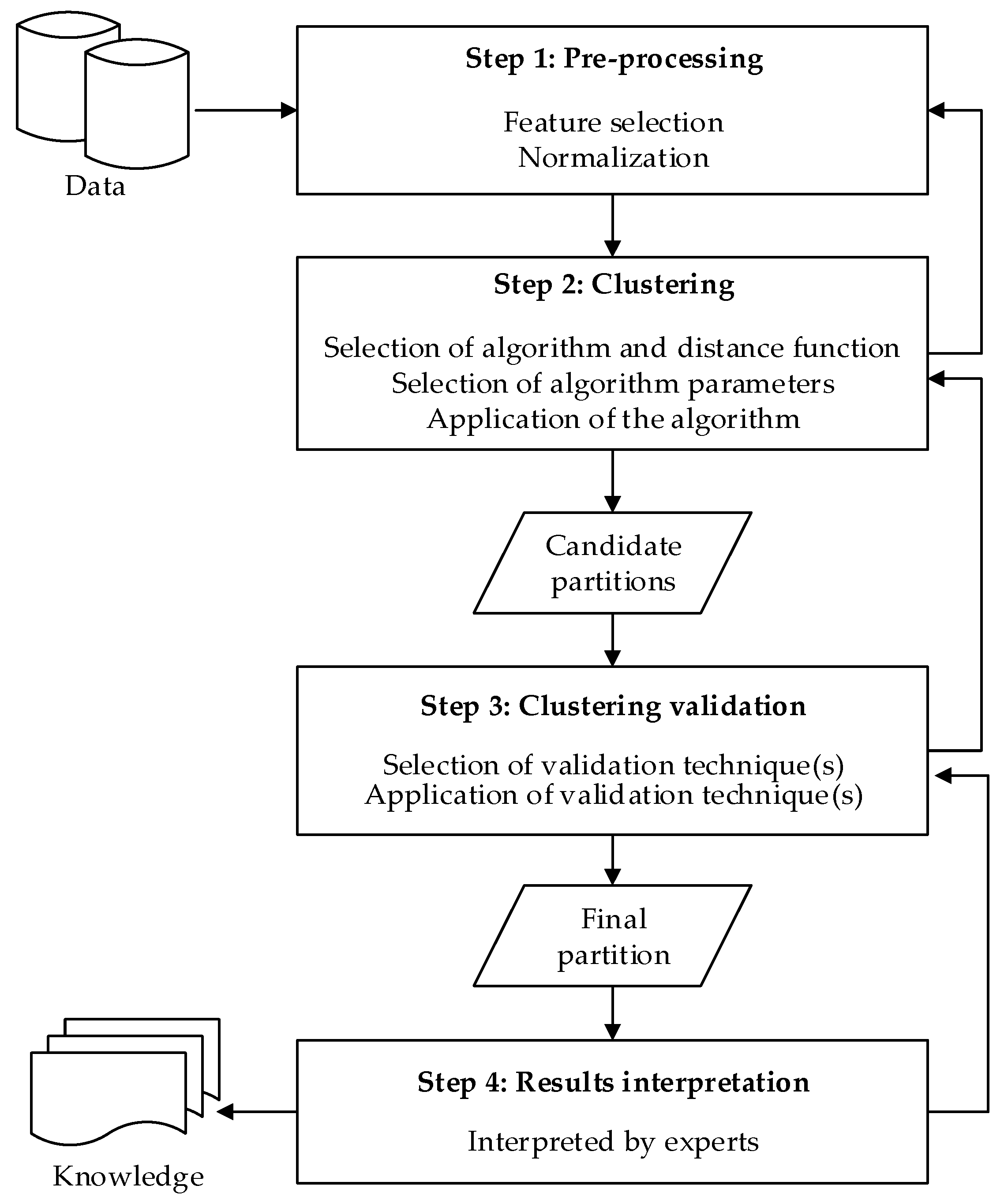
5. Experiments and Discussion
5.1. Experimental Methods
- The adjusted Rand index (ARI)—the corrected-for-chance version of the Rand index—is based on the numbers of objects in common (or not) between the pre-defined classes and the produced clusters [6]. Given two partitions P = {C1, …, Ck} and P’ = {C’1, …, C’k’} ARI is defined as:where nij is the number of common objects in Ci and C’j, nij = | Ci ∩ C’j|, , .
- The normalized mutual information (NMI) calculates the mutual information of two partitions, and normalizes it with the sum of their entropy [16]:
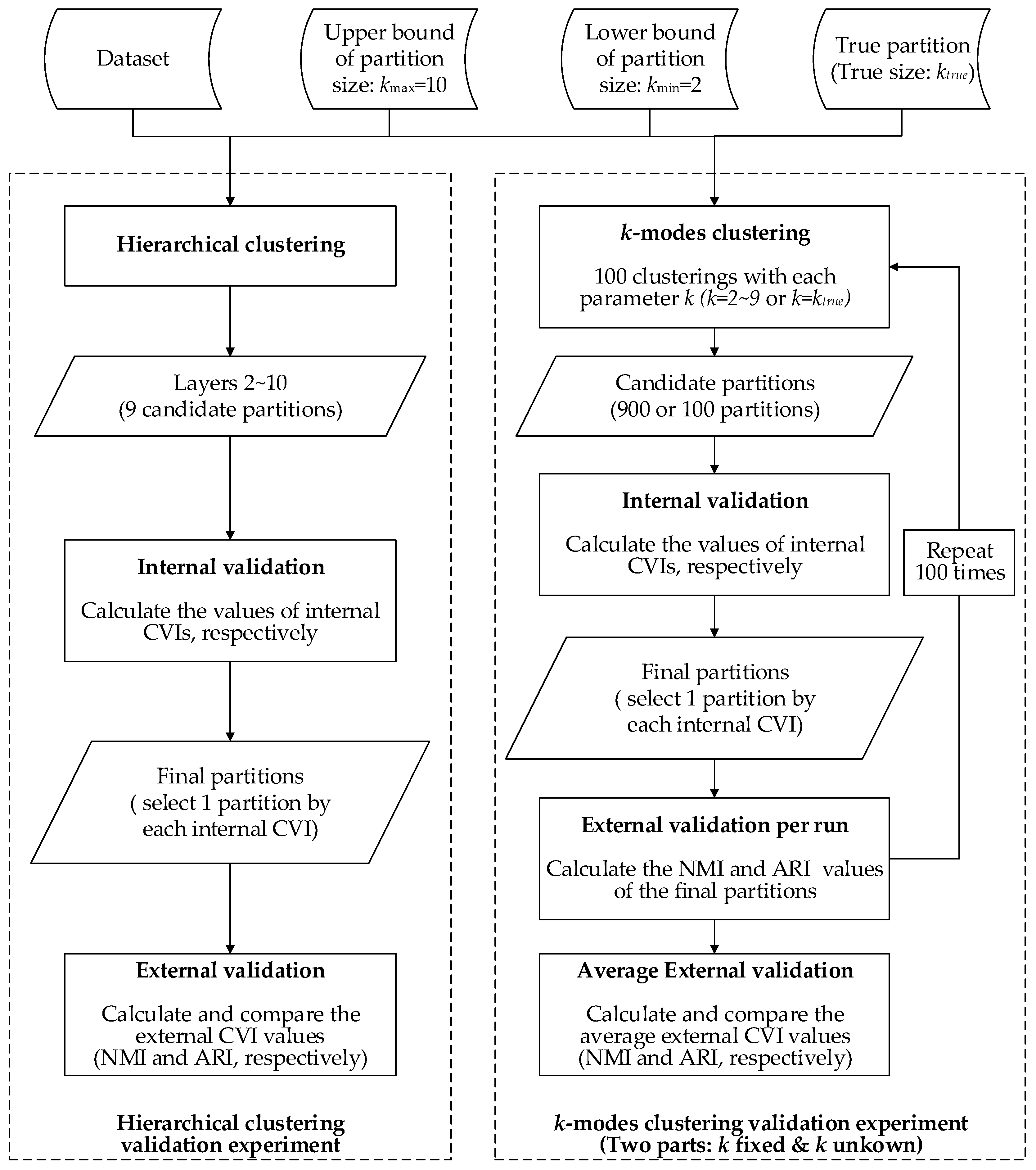
- The agglomerative hierarchical clustering is a ‘bottom-up’ approach; each object is treated as an individual cluster in the beginning. When moving up the hierarchy, pairs of clusters are merged progressively if the dissimilarity of their union is lower than the other pairs in the same layer, until all objects are merged into one cluster eventually. The layers in the hierarchy are different partitions of the dataset. From the generated partitions with the number of clusters ranging from 2–10, we selected one ‘optimal’ partition by each internal CVI, then compared the external CVI values (NMI and ARI, respectively) of the selected partitions.
- The k-modes clustering is a partitioning approach that is similar to the more famous k-means clustering. It starts with k randomly-generated cluster centers (seeds), and each object is assigned to the most appropriate cluster if the dissimilarity of their union is the lowest. In the next iteration, the centers of the clusters are updated by the attribute modes, and the objects are reassigned in the previous manner. The iteration ends if the value of the objective function F stabilizes. The clustering results are inconsistent over different seeds, even if the number of clusters k is fixed. To test the performances when the number of clusters is unknown, we used the internal CVIs to search for the optimal partition from all the partitions produced by k-modes with k ranging from 2–10 (each value of k is conducted 100 times, therefore 900 candidate partitions generated). We further repeated the process 100 times and compared the average external CVI values (ARI and NMI, respectively) of the partitions selected by each internal CVI. Additionally, we tested the internal CVIs with k set to the pre-defined number of clusters to examine the performance when the number of clusters is determined.
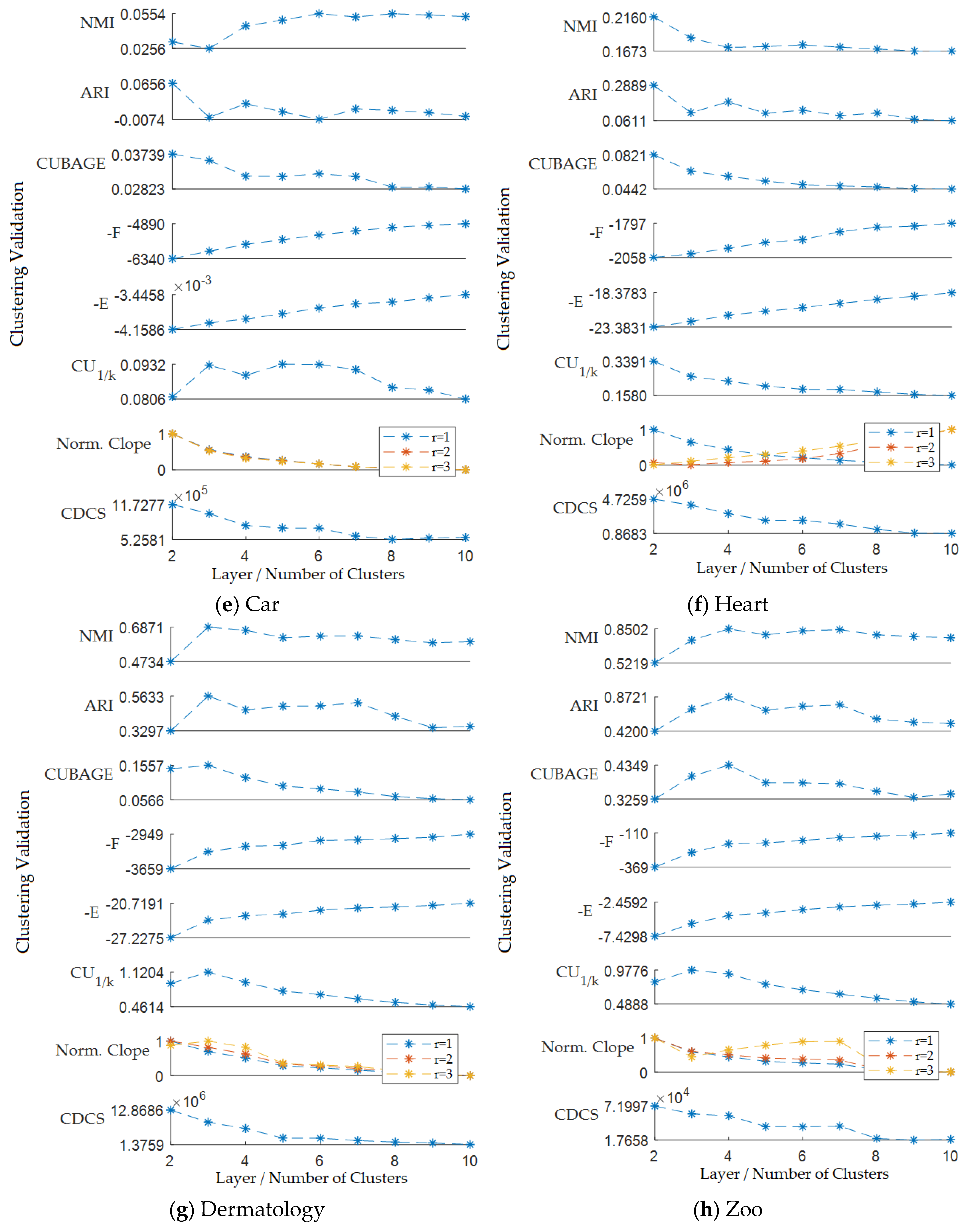
5.2. Results of the Hierarchical Clustering Validation Evaluation
5.3. Results of the k-Modes Clustering Validation Evaluation
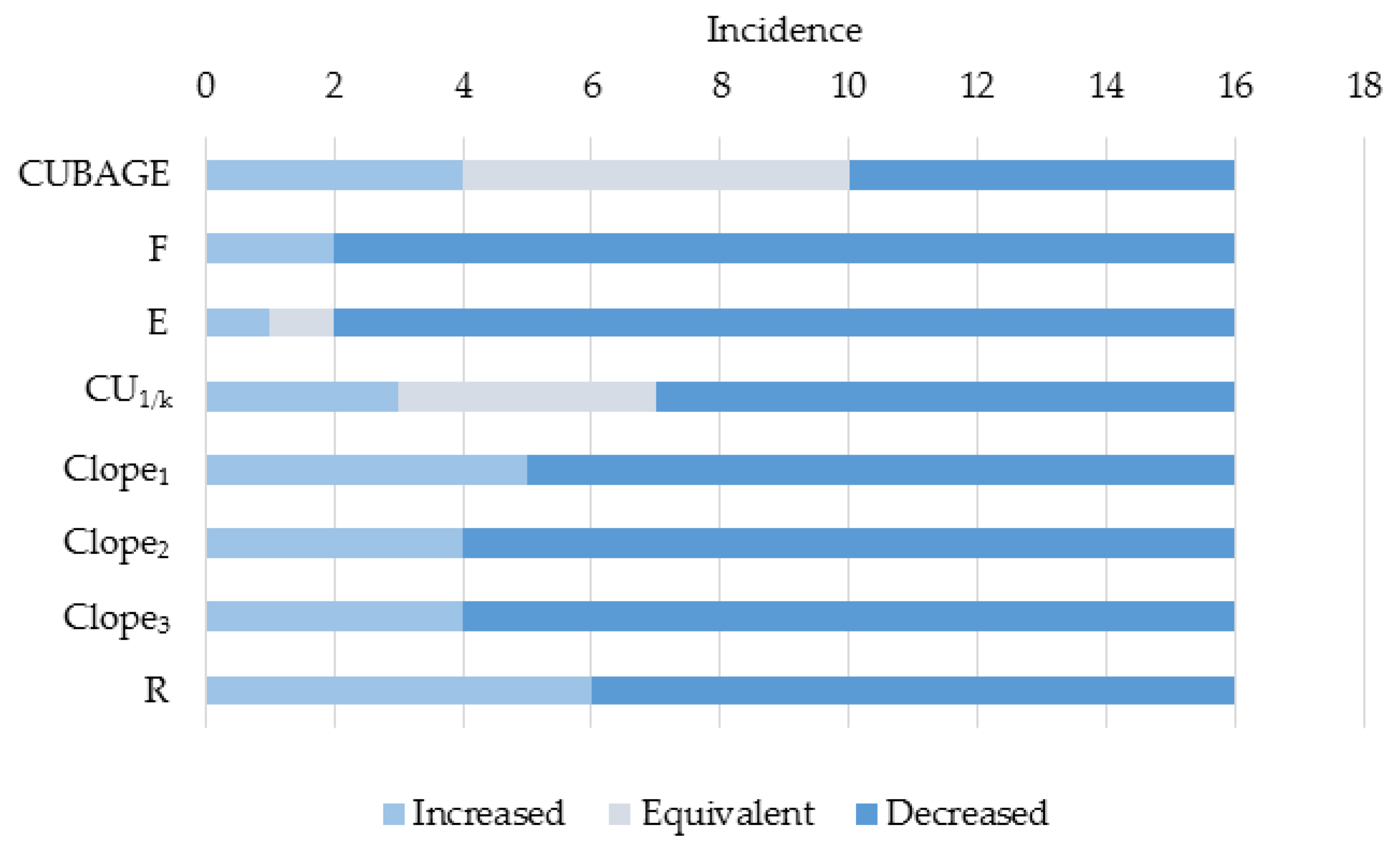
5.4. Discussion
6. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Xu, R.; Ii, D.C.W. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Dubes, R.C. Algorithms for clustering data. Technometrics 1988, 32, 227–229. [Google Scholar]
- Cornuéjols, A.; Wemmert, C.; Gançarski, P.; Bennani, Y. Collaborative Clustering: Why, When, What and How. Inf. Fusion 2017, 39. [Google Scholar] [CrossRef]
- Handl, J.; Knowles, J.; Kell, D.B. Computational cluster validation in post-genomic data analysis. Bioinformatics 2005, 21, 3201–3212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On Clustering Validation Techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Rand, W.M. Objective Criteria for the Evaluation of Clustering Methods. Publ. Am. Stat. Assoc. 1971, 66, 846–850. [Google Scholar] [CrossRef] [Green Version]
- Vinh, N.X.; Epps, J.; Bailey, J. Information theoretic measures for clusterings comparison: Is a correction for chance necessary? In Proceedings of the International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 1073–1080. [Google Scholar]
- Rijsbergen, C.J.V. Information Retrieval; Butterworth-Heinemann: Oxford, UK, 1979; p. 777. [Google Scholar]
- Bai, L.; Liang, J. Cluster validity functions for categorical data: A solution-space perspective. Data Min. Knowl. Discov. 2015, 29, 1560–1597. [Google Scholar] [CrossRef]
- Li, H.; Zhang, S.; Ding, X.; Zhang, C.; Dale, P. Performance evaluation of cluster validity indices (CVIs) on Multi/Hyperspectral remote sensing datasets. Remote Sens. 2016, 8, 295. [Google Scholar] [CrossRef] [Green Version]
- Harimurti, R.; Yamasari, Y.; Ekohariadi; Munoto; Asto, B.I.G.P. Predicting student’s psychomotor domain on the vocational senior high school using linear regression. In Proceedings of the 2018 International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 6–8 March 2018; pp. 448–453. [Google Scholar]
- Luna-Romera, J.M.; García-Gutiérrez, J.; Martínez-Ballesteros, M.; Santos, J.C.R. An approach to validity indices for clustering techniques in Big Data. Prog. Artific. Intell. 2018, 7, 81–94. [Google Scholar] [CrossRef]
- Rizzoli, P.; Loder, E.; Joshi, S. Validity of Cluster Diagnosis in an Electronic Health Record. Headache 2016, 56, 1132–1136. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, C.C.; Procopiuc, C.; Yu, P.S. Finding localized associations in market basket data. IEEE Trans. Knowl. Data Eng. 2002, 14, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Barbará, D.; Jajodia, S. Applications of Data Mining in Computer Security; Kluwer Academic Publishers: Boston, MA, USA, 2002. [Google Scholar]
- Yang, Y. An Evaluation of Statistical Approaches to Text Categorization. Inf. Retr. 1999, 1, 69–90. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J.; Wu, S. Understanding and enhancement of internal clustering validation measures. IEEE Trans. Cybern. 2013, 43, 982–994. [Google Scholar] [PubMed]
- Kremer, H.; Kranen, P.; Jansen, T.; Seidl, T.; Bifet, A.; Holmes, G.; Pfahringer, B. An effective evaluation measure for clustering on evolving data streams. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 868–876. [Google Scholar]
- Song, M.; Zhang, L. Comparison of Cluster Representations from Partial Second- to Full Fourth-Order Cross Moments for Data Stream Clustering. In Proceedings of the Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2009; pp. 560–569. [Google Scholar]
- Xiong, H.; Wu, J.; Chen, J. K-means clustering versus validation measures: A data distribution perspective. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 318–331. [Google Scholar] [CrossRef] [PubMed]
- Brun, M.; Chao, S.; Hua, J.; Lowey, J.; Carroll, B.; Suh, E.; Dougherty, E.R. Model-based evaluation of clustering validation measures. Pattern Recognit. 2007, 40, 807–824. [Google Scholar] [CrossRef] [Green Version]
- Tan, P.N.; Steinbach, M.; Kumar, V. Introduction to Data Mining, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 2005; pp. 86–103. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Cluster validity methods: Part I. ACM SIGMOD Rec. 2002, 31, 40–45. [Google Scholar] [CrossRef]
- Zhang, G.X.; Pan, L.Q. A Survey of Membrane Computing as a New Branch of Natural Computing. Chin. J. Comput. 2010, 33, 208–214. [Google Scholar] [CrossRef]
- Busi, N. Using well-structured transition systems to decide divergence for catalytic P systems. Theor. Comput. Sci. 2007, 372, 125–135. [Google Scholar] [CrossRef]
- An Approximate Algorithm for NP-Complete Optimization Problems Exploiting P-systems. Available online: http://bioinfo.uib.es/~recerca/BUM/nishida.pdf (accessed on 10 November 2004).
- Maulik, U.; Bandyopadhyay, S. Performance Evaluation of Some Clustering Algorithms and Validity Indices; IEEE Computer Society: Washington, WA, USA, 2002; pp. 1650–1654. [Google Scholar]
- Pal, N.R.; Bezdek, J.C. On cluster validity for the fuzzy c-means model. IEEE Trans. Fuzzy Syst. 2002, 3, 370–379. [Google Scholar] [CrossRef]
- Lei, Y.; Bezdek, J.C.; Romano, S.; Vinh, N.X.; Chan, J.; Bailey, J. Ground truth bias in external cluster validity indices. Pattern Recognit. 2017, 65, 58–70. [Google Scholar] [CrossRef] [Green Version]
- Barbará, D.; Li, Y.; Couto, J. COOLCAT: An entropy-based algorithm for categorical clustering. In Proceedings of the Eleventh International Conference on Information and Knowledge Management, McLean, VA, USA, 4–9 November 2002; pp. 582–589. [Google Scholar]
- Huang, Z. A Fast Clustering Algorithm to Cluster Very Large Categorical Data Sets in Data Mining. Res. Issues Data Min. Knowl. Discov. 1997, 1–8. [Google Scholar]
- Gluck, M. Information, Uncertainty and the Utility of Categories. In Proceedings of the Seventh Annual Conference on Cognitive Science Society, Irvine, CA, USA, 15–17 August 1985; pp. 283–287. [Google Scholar]
- Yang, Y.; Guan, X.; You, J. CLOPE:a fast and effective clustering algorithm for transactional data. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–25 July 2002; pp. 682–687. [Google Scholar]
- Chang, C.H.; Ding, Z.K. Categorical Data Visualization and Clustering Using Subjective Factors. Data Knowl. Eng. 2005, 53, 243–262. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Macqueen, J. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965; pp. 281–297. [Google Scholar]
- Fisher, D.H. Knowledge acquisition via incremental conceptual clustering. Mach. Learn. 1987, 2, 139–172. [Google Scholar] [CrossRef] [Green Version]
- Witten, I.; Frank, E.; Hall, M.; Hall, M. Data Mining: Practical Machine Learning Tools and Techniques, Third Edition (The Morgan Kaufmann Series in Data Management Systems). ACM SIGMOD Rec. 2011, 31, 76–77. [Google Scholar] [CrossRef]
- Li, Y.; Le, J.; Wang, M. Improving CLOPE’s profit value and stability with an optimized agglomerative approach. Algorithms 2015, 8, 380–394. [Google Scholar] [CrossRef]
- Campo, D.N.; Stegmayer, G.; Milone, D.H. A new index for clustering validation with overlapped clusters. Expert Syst. Appl. 2016, 64, 549–556. [Google Scholar] [CrossRef]
- Dziopa, T. Clustering Validity Indices Evaluation with Regard to Semantic Homogeneity. In Proceedings of the 2016 Federated Conference on Computer Science and Information Systems, Gdansk, Poland, 11–14 September 2016; pp. 3–9. [Google Scholar]
- Oszust, M.; Kostka, M. Evaluation of Subspace Clustering Using Internal Validity Measures. Adv. Electr. Comput. Eng. 2015, 15, 141–146. [Google Scholar] [CrossRef]
- Desgraupes, B. Clustering Indices; University of Paris Ouest-Lab Modal’X: Nanterre, France, 2013; p. 34. [Google Scholar]
- Baarsch, J.; Celebi, M.E. Investigation of internal validity measures for K-means clustering. In Proceedings of the International Multiconference of Engineers and Computer Scientists, HongKong, China, 14–16 March 2012; pp. 14–16. [Google Scholar]
- Zhao, Q. Cluster Validity in Clustering Methods; University of Eastern Finland: Kuopio, Finland, 2012. [Google Scholar]
- Rendon, E.; Abundez, I.; Arizmendi, A.; Quiroz, E.M. Internal versus external cluster validation indexes. Int. J. Comput. Commun. 2011, 5, 27–34. [Google Scholar]
- Ingaramo, D.; Pinto, D.; Rosso, P.; Errecalde, M. Evaluation of internal validity measures in short-text corpora. In Proceedings of the International Conference on Intelligent Text Processing and Computational Linguistics, Haifa, Israel, 17–23 February 2008; pp. 555–567. [Google Scholar]
- Halkidi, M.; Vazirgiannis, M. Clustering validity assessment: Finding the optimal partitioning of a data set. In Proceedings of the 2001 IEEE International Conference on Data Mining, San Jose, CA, USA, 29 November–2 December 2001; pp. 187–194. [Google Scholar]
- Jiang, D.; Tang, C.; Zhang, A. Cluster analysis for gene expression data: A survey. IEEE Trans. Knowl. Data Eng. 2004, 16, 1370–1386. [Google Scholar] [CrossRef]
- Wu, J.; Chen, J.; Xiong, H.; Xie, M. External validation measures for K-means clustering: A data distribution perspective. Expert Syst. Appl. 2009, 36, 6050–6061. [Google Scholar] [CrossRef]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991; pp. 155–183. [Google Scholar]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]



| CVI | Compactness Core | Objective | |
|---|---|---|---|
| E(P) | |||
| F(P) | * | ||
| Cloper(P) | * | ||
| CU1/k(P) | |||
| R(P) | * |
| Object | A1 | A2 | A3 | Partition 1 | Partition 2 | Partition 3 | Partition 4 | Partition 5 |
|---|---|---|---|---|---|---|---|---|
| X1 | a | d | h | 1 | 1 | 1 | 1 | 1 |
| X2 | a | e | i | 1 | 1 | 1 | 1 | 1 |
| X3 | a | f | h | 1 | 1 | 1 | 2 | 2 |
| X4 | b | g | h | 1 | 2 | 2 | 3 | 3 |
| X5 | b | g | h | 1 | 2 | 2 | 3 | 4 |
| X6 | b | f | h | 1 | 2 | 3 | 4 | 5 |
| X7 | c | d | j | 2 | 3 | 4 | 5 | 6 |
| CVI | Partition 1 | Partition 2 | Partition 3 | Partition 4 | Partition 5 |
| E(P) * | 2.120 | 1.016 | 0.744 | 0.396 | 0.396 |
| F(P) * | 8 | 4 | 3 | 2 | 2 |
| Clope1(P) | 2.071 | 1.750 | 1.500 | 1.343 | 1.057 |
| Clope2(P) | 0.289 | 0.396 | 0.393 | 0.402 | 0.307 |
| Clope3(P) | 0.046 | 0.094 | 0.113 | 0.125 | 0.093 |
| CU1/k(P) | 0.255 | 0.376 | 0.330 | 0.302 | 0.252 |
| R(P) | 47.353 | 29.321 | 20.652 | 14.844 | 8.019 |
| CVI | Partition 1 | Partition 2 | Partition 3 | Partition 4 | Partition 5 |
|---|---|---|---|---|---|
| AGE | 1.032 | 1.191 | 0.912 | 0.769 | 0.601 |
| CUBAGE | 0.487 | 1.172 | 1.226 | 1.941 | 1.518 |
| Dataset | Objects | Attributes | Classes | Object Distribution |
|---|---|---|---|---|
| Voting | 435 | 16 | 2 | 168, 267 |
| Breast Cancer Wisconsin (Original) | 683 | 9 | 2 | 444, 239 |
| Mushroom | 5644 | 22 | 2 | 2156, 3488 |
| Soybean (Small) | 47 | 35 | 4 | 10, 10, 10, 17 |
| Car Evaluation | 1728 | 6 | 4 | 1210, 384, 69, 65 |
| Heart Disease (Cleveland) | 297 | 13 | 5 | 54, 35, 35, 13, 160 |
| Dermatology | 358 | 34 | 6 | 111, 60, 71, 48, 48, 20 |
| Zoo | 101 | 16 | 7 | 41, 20, 5, 13, 4, 8, 10 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.489 | (7) 0.292 | (7) 0.292 | (1) 0.489 | (1) 0.489 | (1) 0.489 | (1) 0.489 | (6) 0.396 |
| Breast | (1) 0.704 | (7) 0.337 | (7) 0.337 | (1) 0.704 | (1) 0.704 | (1) 0.704 | (1) 0.704 | (6) 0.609 |
| Mushroom | (5) 0.362 | (6) 0.339 | (6) 0.339 | (3) 0.368 | (8) 0.256 | (1) 0.412 | (1) 0.412 | (3) 0.368 |
| Soybean | (1) 1 | (4) 0.745 | (4) 0.745 | (1) 1 | (6) 0.669 | (6) 0.669 | (3) 0.878 | (6) 0.669 |
| Car | (4) 0.031 | (1) 0.053 | (1) 0.053 | (3) 0.05 | (4) 0.031 | (4) 0.031 | (4) 0.031 | (4) 0.031 |
| Heart | (1) 0.216 | (5) 0.167 | (5) 0.167 | (1) 0.216 | (1) 0.216 | (5) 0.167 | (5) 0.167 | (1) 0.216 |
| Dermatology | (1) 0.687 | (4) 0.597 | (4) 0.597 | (1) 0.687 | (6) 0.473 | (6) 0.473 | (1) 0.687 | (6) 0.473 |
| Zoo | (1) 0.85 | (2) 0.764 | (2) 0.764 | (4) 0.741 | (5) 0.522 | (5) 0.522 | (5) 0.522 | (5) 0.522 |
| Average NMI * | 0.542 | 0.412 | 0.412 | 0.532 | 0.42 | 0.433 | 0.486 | 0.411 |
| Average Rank * | 1.875 | 4.5 | 4.5 | 1.875 | 4 | 3.625 | 2.625 | 4.625 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.557 | (7) 0.142 | (7) 0.142 | (1) 0.557 | (1) 0.557 | (1) 0.557 | (1) 0.557 | (6) 0.337 |
| Breast | (1) 0.808 | (7) 0.18 | (7) 0.18 | (1) 0.808 | (1) 0.808 | (1) 0.808 | (1) 0.808 | (6) 0.72 |
| Mushroom | (5) 0.288 | (7) 0.161 | (7) 0.161 | (1) 0.375 | (6) 0.286 | (3) 0.318 | (3) 0.318 | (1) 0.375 |
| Soybean | (1) 1 | (7) 0.431 | (7) 0.431 | (1) 1 | (4) 0.501 | (4) 0.501 | (3) 0.781 | (4) 0.501 |
| Car | (1) 0.066 | (7) −0.002 | (7) −0.002 | (6) 0.008 | (1) 0.066 | (1) 0.066 | (1) 0.066 | (1) 0.066 |
| Heart | (1) 0.289 | (5) 0.061 | (5) 0.061 | (1) 0.289 | (1) 0.289 | (5) 0.061 | (5) 0.061 | (1) 0.289 |
| Dermatology | (1) 0.563 | (4) 0.359 | (4) 0.359 | (1) 0.563 | (6) 0.33 | (6) 0.33 | (1) 0.563 | (6) 0.33 |
| Zoo | (1) 0.872 | (3) 0.522 | (3) 0.522 | (2) 0.715 | (5) 0.42 | (5) 0.42 | (5) 0.42 | (5) 0.42 |
| Average ARI * | 0.555 | 0.232 | 0.232 | 0.539 | 0.407 | 0.383 | 0.447 | 0.38 |
| Average Rank * | 1.5 | 5.875 | 5.875 | 1.75 | 3.125 | 3.25 | 2.5 | 3.75 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.443 | (8) 0.312 | (7) 0.324 | (1) 0.443 | (3) 0.418 | (3) 0.418 | (3) 0.418 | (6) 0.397 |
| Breast | (1) 0.674 | (6) 0.363 | (7) 0.358 | (1) 0.674 | (8) 0.016 | (4) 0.48 | (5) 0.407 | (3) 0.491 |
| Mushroom | (1) 0.458 | (5) 0.368 | (4) 0.391 | (3) 0.394 | (8) 0.196 | (2) 0.434 | (6) 0.365 | (7) 0.291 |
| Soybean | (1) 0.838 | (4) 0.746 | (3) 0.752 | (1) 0.838 | (8) 0.492 | (6) 0.553 | (6) 0.553 | (5) 0.572 |
| Car | (5) 0.05 | (2) 0.065 | (1) 0.072 | (3) 0.058 | (6) 0.026 | (6) 0.026 | (6) 0.026 | (4) 0.054 |
| Heart | (1) 0.206 | (3) 0.175 | (4) 0.171 | (2) 0.205 | (8) 0.039 | (7) 0.165 | (6) 0.165 | (5) 0.167 |
| Dermatology | (1) 0.704 | (4) 0.647 | (3) 0.684 | (1) 0.704 | (8) 0.313 | (6) 0.362 | (5) 0.456 | (7) 0.321 |
| Zoo | (2) 0.808 | (3) 0.795 | (4) 0.783 | (5) 0.579 | (8) 0.479 | (7) 0.481 | (1) 0.823 | (6) 0.572 |
| Average NMI * | 0.522 | 0.434 | 0.442 | 0.487 | 0.247 | 0.365 | 0.402 | 0.358 |
| Average Rank * | 1.625 | 4.375 | 4.125 | 2.125 | 7.125 | 5.125 | 4.75 | 5.375 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.53 | (8) 0.174 | (7) 0.191 | (1) 0.53 | (3) 0.503 | (3) 0.503 | (3) 0.503 | (6) 0.428 |
| Breast | (1) 0.787 | (6) 0.217 | (7) 0.195 | (1) 0.787 | (8) −0.001 | (4) 0.551 | (5) 0.337 | (3) 0.639 |
| Mushroom | (1) 0.489 | (7) 0.187 | (6) 0.228 | (3) 0.319 | (8) 0.155 | (2) 0.447 | (5) 0.268 | (4) 0.309 |
| Soybean | (1) 0.654 | (4) 0.442 | (3) 0.461 | (1) 0.654 | (8) 0.26 | (6) 0.297 | (6) 0.297 | (5) 0.352 |
| Car | (2) 0.023 | (4) 0.017 | (3) 0.021 | (1) 0.025 | (6) −0.001 | (6) −0.001 | (6) −0.001 | (5) 0.014 |
| Heart | (2) 0.199 | (4) 0.092 | (5) 0.079 | (3) 0.19 | (6) 0.065 | (8) 0.055 | (7) 0.065 | (1) 0.263 |
| Dermatology | (1) 0.552 | (3) 0.493 | (4) 0.487 | (1) 0.552 | (7) 0.136 | (6) 0.159 | (5) 0.21 | (8) 0.119 |
| Zoo | (1) 0.817 | (3) 0.573 | (4) 0.544 | (5) 0.448 | (7) 0.342 | (8) 0.341 | (2) 0.769 | (6) 0.411 |
| Average ARI * | 0.506 | 0.274 | 0.276 | 0.438 | 0.183 | 0.294 | 0.306 | 0.317 |
| Average Rank * | 1.25 | 4.875 | 4.875 | 2 | 6.625 | 5.375 | 4.875 | 4.75 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.443 | (5) 0.436 | (1) 0.443 | (1) 0.443 | (6) 0.376 | (6) 0.376 | (6) 0.376 | (4) 0.439 |
| Breast | (1) 0.674 | (4) 0.635 | (1) 0.674 | (1) 0.674 | (8) 0.015 | (7) 0.022 | (6) 0.434 | (5) 0.445 |
| Mushroom | (1) 0.458 | (5) 0.451 | (1) 0.458 | (1) 0.458 | (8) 0.037 | (1) 0.458 | (6) 0.435 | (7) 0.136 |
| Soybean | (1) 1 | (4) 0.977 | (1) 1 | (1) 1 | (7) 0.675 | (6) 0.692 | (5) 0.791 | (8) 0.672 |
| Car | (4) 0.048 | (1) 0.057 | (3) 0.05 | (2) 0.055 | (7) 0.038 | (8) 0.037 | (6) 0.042 | (5) 0.048 |
| Heart | (2) 0.181 | (3) 0.18 | (7) 0.171 | (5) 0.175 | (4) 0.177 | (8) 0.167 | (6) 0.173 | (1) 0.187 |
| Dermatology | (3) 0.742 | (4) 0.633 | (1) 0.744 | (2) 0.742 | (7) 0.505 | (6) 0.548 | (5) 0.582 | (8) 0.495 |
| Zoo | (1) 0.852 | (4) 0.818 | (3) 0.836 | (2) 0.838 | (5) 0.811 | (7) 0.804 | (6) 0.809 | (8) 0.781 |
| Average NMI * | 0.55 | 0.523 | 0.547 | 0.548 | 0.329 | 0.388 | 0.455 | 0.4 |
| Average Rank * | 1.75 | 3.75 | 2.25 | 1.875 | 6.5 | 6.125 | 5.75 | 5.75 |
| Dataset | CUBAGE | −F | −E | CU1/k | Clope1 | Clope2 | Clope3 | R |
|---|---|---|---|---|---|---|---|---|
| Voting | (1) 0.53 | (5) 0.511 | (1) 0.53 | (1) 0.53 | (6) 0.451 | (6) 0.451 | (6) 0.451 | (4) 0.53 |
| Breast | (1) 0.787 | (4) 0.738 | (1) 0.787 | (1) 0.787 | (7) 0.008 | (8) 0.001 | (6) 0.488 | (5) 0.513 |
| Mushroom | (1) 0.489 | (5) 0.486 | (1) 0.489 | (1) 0.489 | (8) −0.015 | (1) 0.489 | (6) 0.465 | (7) 0.023 |
| Soybean | (1) 1 | (4) 0.97 | (1) 1 | (1) 1 | (7) 0.474 | (6) 0.489 | (5) 0.598 | (8) 0.469 |
| Car | (1) 0.036 | (4) 0.03 | (2) 0.034 | (3) 0.032 | (8) 0.006 | (7) 0.009 | (5) 0.022 | (6) 0.012 |
| Heart | (3) 0.134 | (7) 0.107 | (5) 0.123 | (6) 0.119 | (2) 0.22 | (4) 0.124 | (8) 0.104 | (1) 0.277 |
| Dermatology | (1) 0.654 | (4) 0.52 | (2) 0.63 | (3) 0.621 | (7) 0.26 | (6) 0.298 | (5) 0.343 | (8) 0.236 |
| Zoo | (3) 0.774 | (8) 0.662 | (6) 0.713 | (7) 0.709 | (2) 0.797 | (5) 0.751 | (4) 0.757 | (1) 0.807 |
| Average ARI * | 0.551 | 0.503 | 0.538 | 0.536 | 0.275 | 0.326 | 0.403 | 0.358 |
| Average Rank * | 1.5 | 5.125 | 2.375 | 2.875 | 5.875 | 5.375 | 5.625 | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Yang, M. Understanding and Enhancement of Internal Clustering Validation Indexes for Categorical Data. Algorithms 2018, 11, 177. https://doi.org/10.3390/a11110177
Gao X, Yang M. Understanding and Enhancement of Internal Clustering Validation Indexes for Categorical Data. Algorithms. 2018; 11(11):177. https://doi.org/10.3390/a11110177
Chicago/Turabian StyleGao, Xuedong, and Minghan Yang. 2018. "Understanding and Enhancement of Internal Clustering Validation Indexes for Categorical Data" Algorithms 11, no. 11: 177. https://doi.org/10.3390/a11110177
APA StyleGao, X., & Yang, M. (2018). Understanding and Enhancement of Internal Clustering Validation Indexes for Categorical Data. Algorithms, 11(11), 177. https://doi.org/10.3390/a11110177