Inapproximability of Rank, Clique, Boolean, and Maximum Induced Matching-Widths under Small Set Expansion Hypothesis
Abstract
:1. Introduction
2. Definitions and Known Results
2.1. Graphs, Expansion, Matrices
2.2. Graph Width Parameters
- T is a subcubic tree with leaves, where a tree is subcubic if every vertex in T has degree 1 or 3;
- is a bijection from of T to V.
- Cut-width:
- For a graph , let be an ordering of V. Let , . Then, .
- Rank-width:
- For a graph , let T be a subcubic tree and be a bijection from to V. Then, .
- Maximum induced matching-width
- For a graph and a subset A of V, we denote the size of a maximum induced matching in the bipartite graph by . Then, .
3. SSE Hypothesis
- Yes
- There exist q disjoint sets such that and holds for all ,
- No
- For every , holds.
4. Method for Showing Inapproximability
- holds if G is a YES instance in Problem 1 (i.e., completeness), and
- holds if G is a NO instance in Problem 1 (i.e., soundness),
| Algorithm 1 DeciInstByAlg |
| Input: a graph G Output: YES/NO  |
5. Hardness Results Derived from Inapproximability of Tree-Width
6. Results
6.1. Simpler Proof of the Inapproximability of {Cut, Path, Tree}-Widths
- , and
6.2. Inapproximability of Rank, Clique, Boolean, and Mim-Widths
7. Future Research
Funding
Acknowledgments
Conflicts of Interest
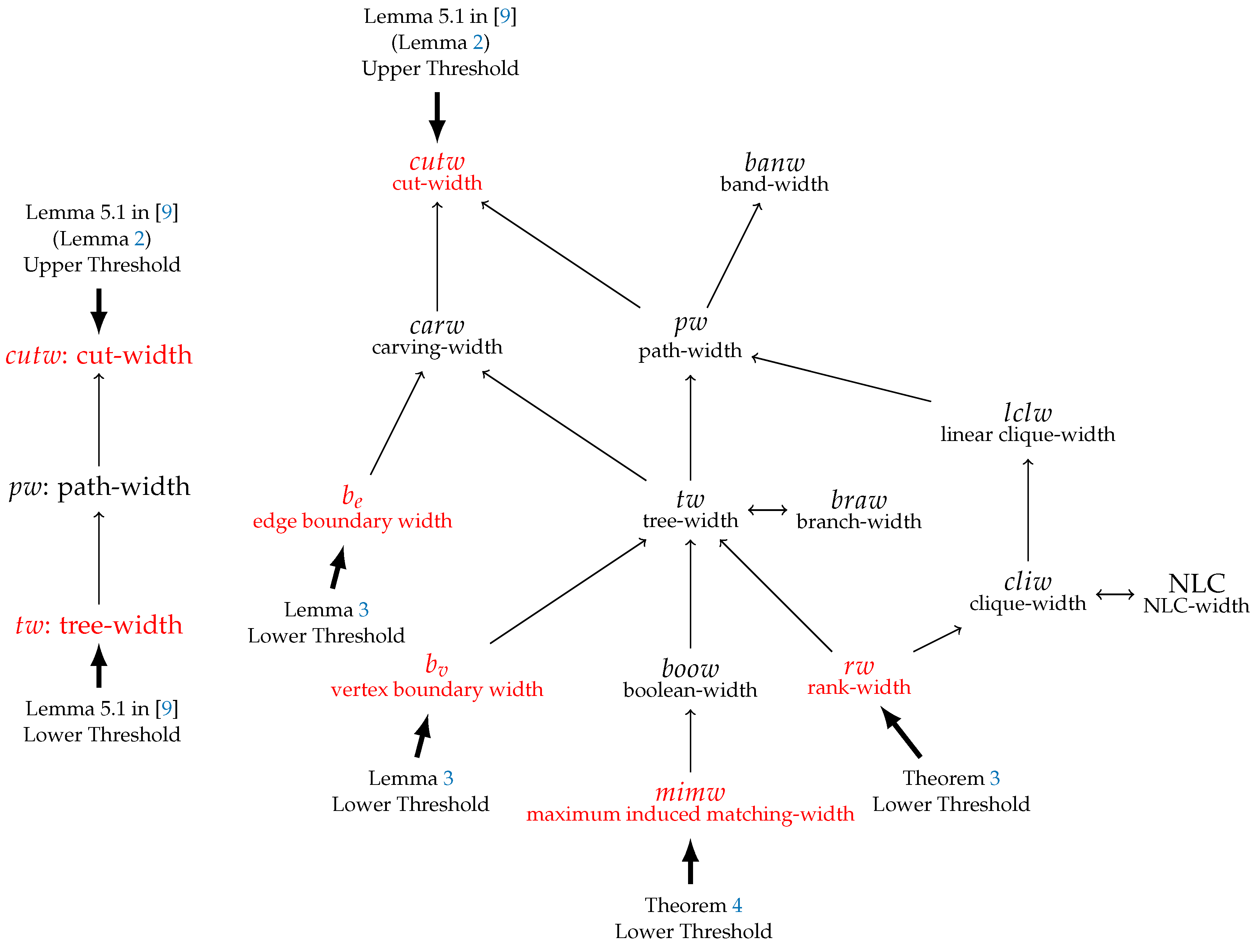
Appendix A. Relations among Graph Parameters
- For each ,
- For each ,
References
- Feige, U.; Hajiaghayi, M.; Lee, J.R. Improved approximation algorithms for minimum weight vertex separators. SIAM J. Comput. 2008, 38, 629–657. [Google Scholar] [CrossRef]
- Bodlaender, H.L.; Gilbert, J.R.; Hafsteinsson, H.; Kloks, T. Approximating treewidth, pathwidth, frontsize, and shortest elimination tree. J. Algorithms 1995, 18, 238–255. [Google Scholar] [CrossRef]
- Oum, S. Approximating rank-width and clique-width quickly. ACM Trans. Algorithms 2008, 5, 10. [Google Scholar] [CrossRef]
- Sæther, S.H.; Vatshelle, M. Hardness of computing width parameters based on branch decompositions over the vertex set. Theor. Comput. Sci. 2016, 615, 120–125. [Google Scholar] [CrossRef]
- Raghavendra, P.; Steurer, D. Graph expansion and the unique games conjecture. In Proceedings of the 42nd ACM Symposium on Theory of Computing, Cambridge, MA, USA, 6–8 June 2010; pp. 755–764. [Google Scholar] [CrossRef]
- Raghavendra, P.; Steurer, D.; Tulsiani, M. Reductions between expansion problems. In Proceedings of the 27th Conference on Computational Complexity, Porto, Portugal, 26–29 June 2012; pp. 64–73. [Google Scholar] [CrossRef]
- Khot, S.A.; Vishnoi, N.K. The unique games conjecture, integrality gap for cut problems and embeddability of negative type metrics into ℓ1. JACM 2015, 62, 8. [Google Scholar] [CrossRef]
- Manurangsi, P. Inapproximability of Maximum Biclique Problems, Minimum k-Cut and Densest At-Least-k-Subgraph from the Small Set Expansion Hypothesis. Algorithms 2018, 11, 10. [Google Scholar] [CrossRef]
- Wu, Y.; Austrin, P.; Pitassi, T.; Liu, D. Inapproximability of Treewidth and Related Problems. J. Artific. Intell. Res. 2014, 49, 569–600. [Google Scholar] [CrossRef]
- Cao, Y.; Sandeep, R. Minimum fill-in: Inapproximability and almost tight lower bounds. In Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, Barcelona, Spain, 16–19 January 2017; pp. 875–880. [Google Scholar]
- Barak, B. Truth vs. Proof in Computational Complexity. EATCS Bull. 2012, 108, 130–142. [Google Scholar]
- Arora, S.; Barak, B.; Steurer, D. Subexponential algorithms for unique games and related problems. In Proceedings of the 51st Annual IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 23–26 October 2010; pp. 563–572. [Google Scholar] [CrossRef]
- Hliněnỳ, P.; Oum, S.i.; Seese, D.; Gottlob, G. Width parameters beyond tree-width and their applications. Comput. J. 2008, 51, 326–362. [Google Scholar] [CrossRef]
- Downey, R.G.; Fellows, M.R. Fundamentals of Parameterized Complexity; Springer: London, UK, 2013. [Google Scholar]
- Cygan, M.; Fomin, F.V.; Kowalik; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer International Publishing: New York, NY, USA, 2015. [Google Scholar]
- Flum, J.; Grohe, M. Parameterized Complexity Theory, Texts in Theoretical Computer Science: An EATCS Series; Springer: Berlin, Germany, 2006. [Google Scholar]
- Lee, C.; Lee, J.; Oum, S. Rank-width of random graphs. J. Graph Theory 2012, 70, 339–347. [Google Scholar] [CrossRef]
- Bodlaender, H.L. A partial k-arboretum of graphs with bounded treewidth. TCS 1998, 209, 1–45. [Google Scholar] [CrossRef]
- Seymour, P.D.; Thomas, R. Call routing and the ratcatcher. Combinatorica 1994, 14, 217–241. [Google Scholar] [CrossRef]
- Courcelle, B.; Olariu, S. Upper bounds to the clique width of graphs. Discret. Appl. Math. 2000, 101, 77–114. [Google Scholar] [CrossRef]
- Bui-Xuan, B.M.; Telle, J.A.; Vatshelle, M. Boolean-width of graphs. Theor. Comput. Sci. 2011, 412, 5187–5204. [Google Scholar] [CrossRef]
- Markov, I.L.; Shi, Y. Constant-degree graph expansions that preserve treewidth. Algorithmica 2011, 59, 461–470. [Google Scholar] [CrossRef]
- Thilikos, D.M.; Serna, M.J.; Bodlaender, H.L. Constructive Linear Time Algorithms for Small Cutwidth and Carving-Width. In Proceedings of the 11th International Symposium on Algorithms and Computation, Taipei, Taiwan, 18–20 December 2000; pp. 192–203. [Google Scholar] [CrossRef]
- Biedl, T.; Vatshelle, M. The point-set embeddability problem for plane graphs. In Proceedings of the 28th Annual Symposium on Computational Geometry, Chapel Hill, NC, USA, 17–20 June 2012; pp. 41–50. [Google Scholar] [CrossRef]
- Nestoridis, N.V.; Thilikos, D.M. Square roots of minor closed graph classes. Discret. Appl. Math. 2014, 168, 34–39. [Google Scholar] [CrossRef] [Green Version]
- Gurski, F.; Wanke, E. Line graphs of bounded clique-width. Discret. Math. 2007, 307, 2734–2754. [Google Scholar] [CrossRef]
- Chandran, L.S.; Subramanian, C. Girth and treewidth. J. Combin. Theory Ser. B 2005, 93, 23–32. [Google Scholar] [CrossRef]
- Chandran, L.S.; Kavitha, T. The carvingwidth of hypercubes. Discret. Math. 2006, 306, 2270–2274. [Google Scholar] [CrossRef]
- Oum, S. Rank-width is less than or equal to branch-width. J. Graph Theory 2008, 57, 239–244. [Google Scholar] [CrossRef] [Green Version]
- Fellows, M.R.; Rosamond, F.A.; Rotics, U.; Szeider, S. Clique-width is NP-complete. SIAM J. Discret. Math. 2009, 23, 909–939. [Google Scholar] [CrossRef]
- Oum, S.; Seymour, P. Approximating clique-width and branch-width. J. Combin. Theory Ser. B 2006, 96, 514–528. [Google Scholar] [CrossRef]
- Vatshelle, M. New width Parameters of Graphs. Ph.D. Thesis, The University of Bergen, Bergen, Norway, 2012. [Google Scholar]
- Adler, I.; Bui-Xuan, B.M.; Rabinovich, Y.; Renault, G.; Telle, J.A.; Vatshelle, M. On the boolean-width of a graph: Structure and applications. In Proceedings of the 36th International Workshop on Graph-Theoretic Concepts in Computer Science, Zarós, Greece, 28–30 June 2010; pp. 159–170. [Google Scholar]
- Yamazaki, K. On approximation intractability of the path–distance–width problem. Discret. Appl. Math. 2001, 110, 317–325. [Google Scholar] [CrossRef]
- Otachi, Y.; Saitoh, T.; Yamanaka, K.; Kijima, S.; Okamoto, Y.; Ono, H.; Uno, Y.; Yamazaki, K. Approximating the path-distance-width for AT-free graphs and graphs in related classes. Discret. Appl. Math. 2014, 168, 69–77. [Google Scholar] [CrossRef]
- Johansson, Ö. Clique-decomposition, NLC-decomposition, and modular decomposition-relationships and results for random graphs. Congr. Numer. 1998, 132, 39–60. [Google Scholar]
- Gurski, F.; Wanke, E. The NLC-width and clique-width for powers of graphs of bounded tree-width. Discrete Appl. Math. 2009, 157, 583–595. [Google Scholar] [CrossRef] [Green Version]
- Wanke, E. k-NLC graphs and polynomial algorithms. Discret. Appl. Math. 1994, 54, 251–266. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamazaki, K. Inapproximability of Rank, Clique, Boolean, and Maximum Induced Matching-Widths under Small Set Expansion Hypothesis. Algorithms 2018, 11, 173. https://doi.org/10.3390/a11110173
Yamazaki K. Inapproximability of Rank, Clique, Boolean, and Maximum Induced Matching-Widths under Small Set Expansion Hypothesis. Algorithms. 2018; 11(11):173. https://doi.org/10.3390/a11110173
Chicago/Turabian StyleYamazaki, Koichi. 2018. "Inapproximability of Rank, Clique, Boolean, and Maximum Induced Matching-Widths under Small Set Expansion Hypothesis" Algorithms 11, no. 11: 173. https://doi.org/10.3390/a11110173




