Online Uniformly Inserting Points on the Sphere †
Abstract
1. Introduction
1.1. Related Works
1.2. Our Contribution
2. Materials and Methods
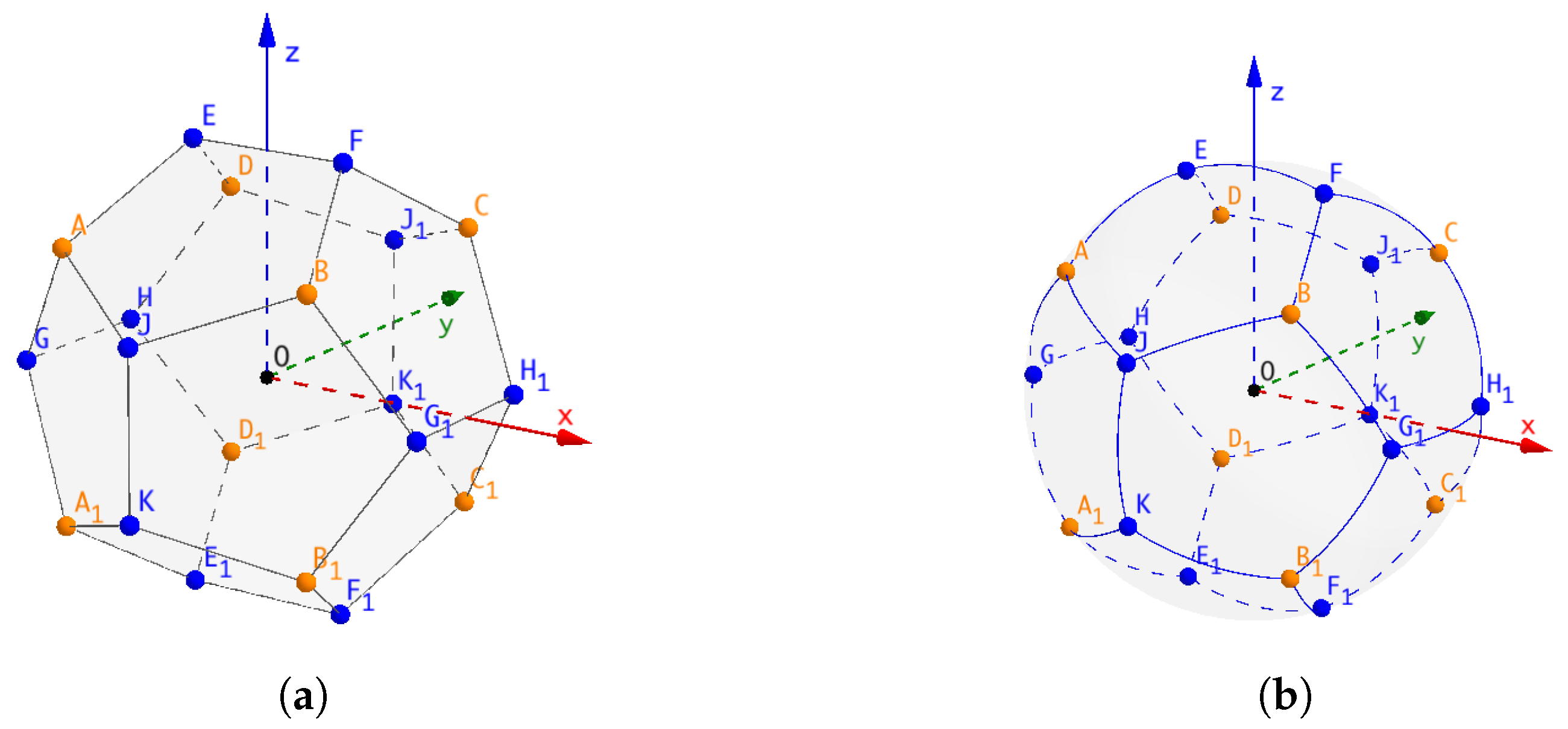
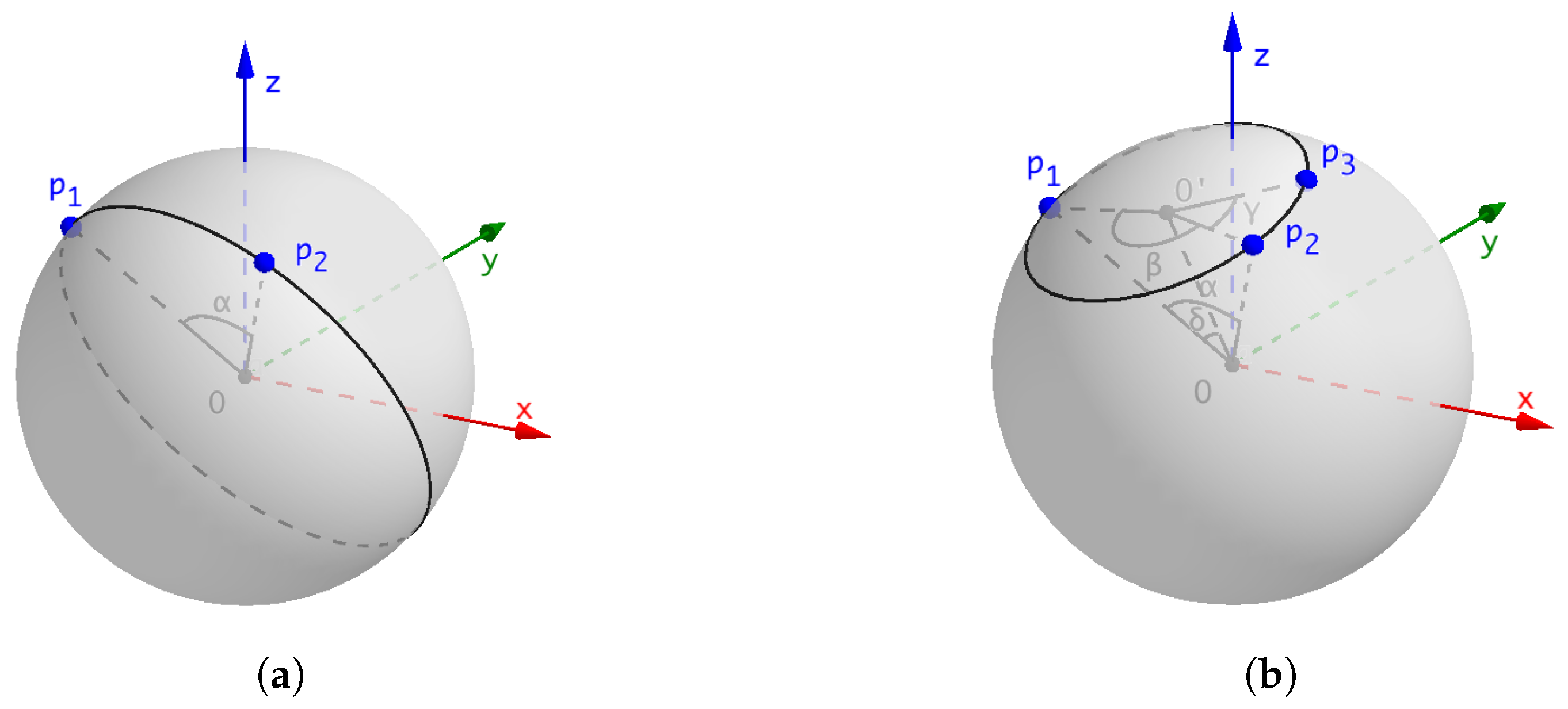
2.1. Problem Description
2.2. The Insertion Strategy
3. Results
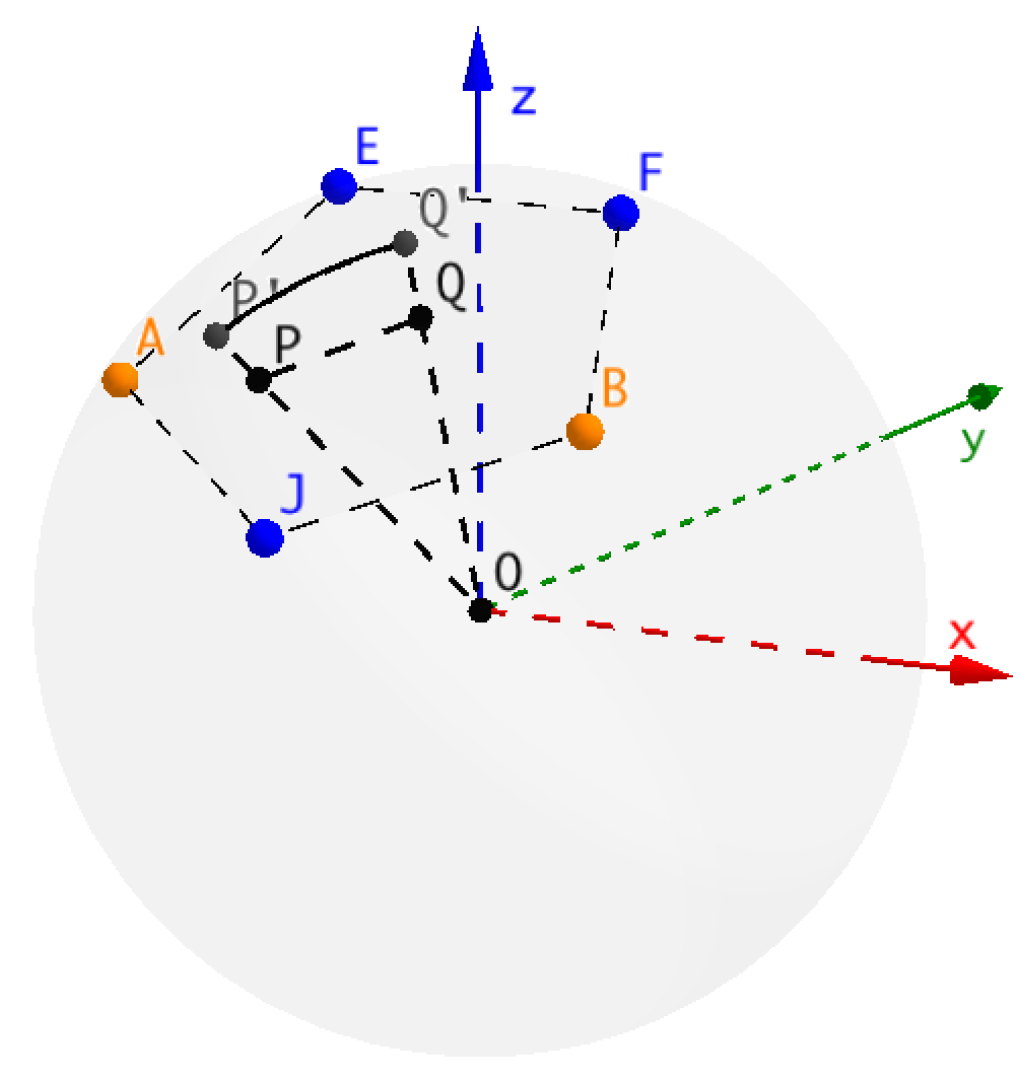
3.1. Analysis of the Upper Bound
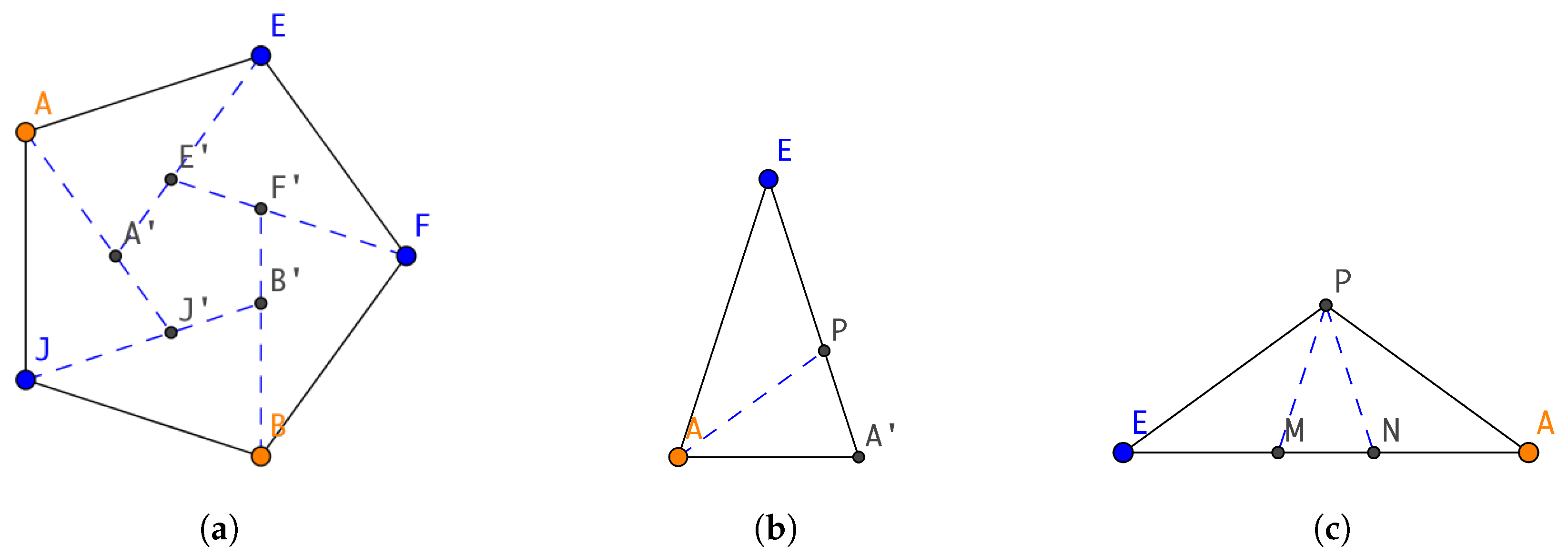
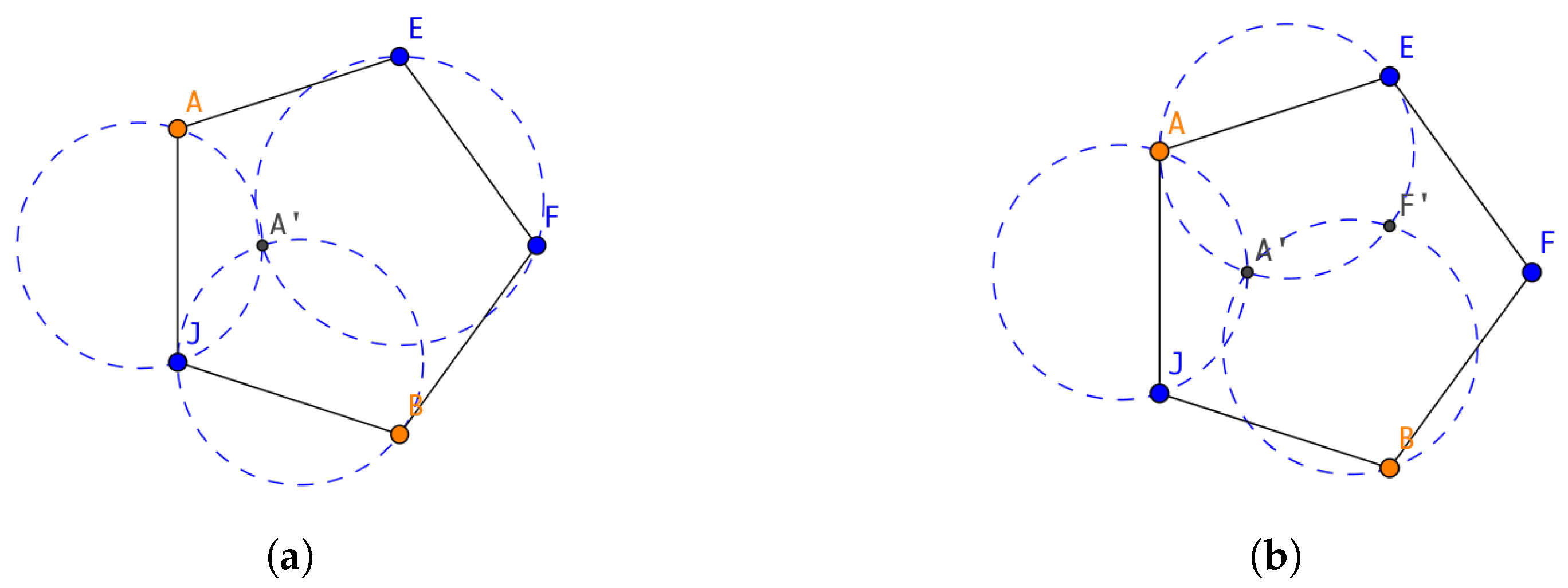
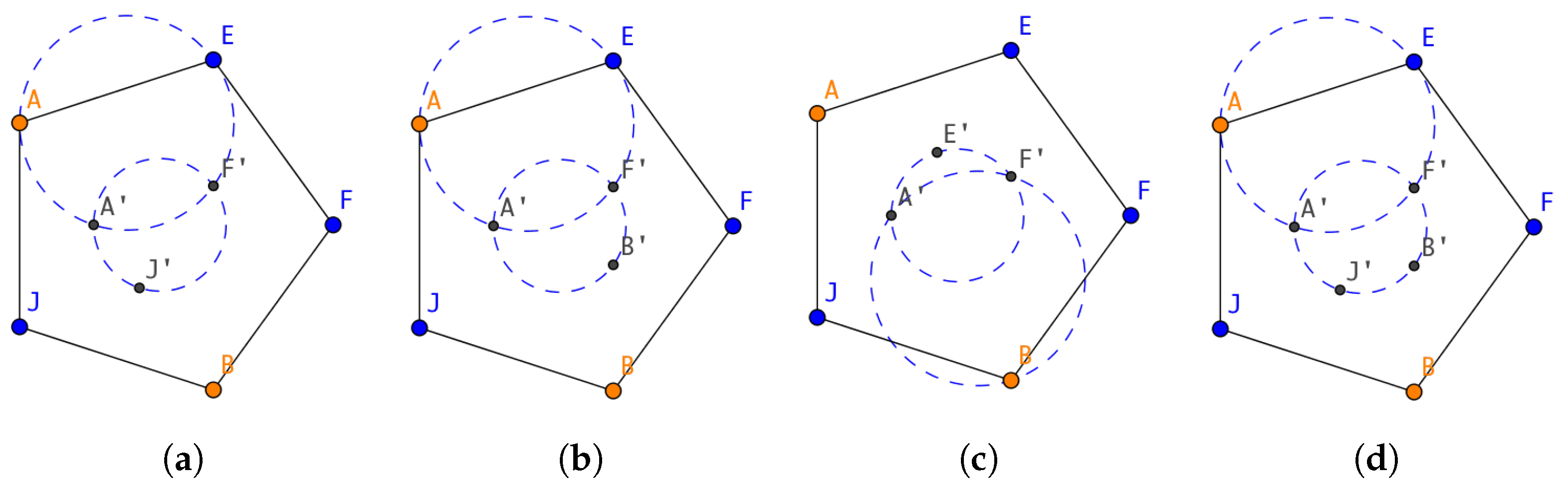
3.1.1. Inserting Points in a Pentagon
3.1.2. Inserting Points in an Acute Isosceles Triangle
3.1.3. Inserting Points in an Obtuse Isosceles Triangle
3.2. Analysis of the Lower Bound
3.2.1. 2-Point Sequence Insertion
3.2.2. 3-Point Sequence Insertion
3.2.3. More Point Sequence Insertion
3.3. Analysis of Computational Complexity
- If the pentagon queue is selected, insertion of 5 points will lead to removing the head of the queue. Meanwhile, a smaller pentagon and five smaller acute triangles will be added to the tail of the corresponding queues respectively.
- If the acute triangle queue is selected, insertion of 1 point will lead to removing the head of the queue. Meanwhile, a smaller acute triangle and a smaller obtuse triangle will be added to the tail of the corresponding queues respectively.
- If the obtuse triangle queue is selected, insertion of 2 points will lead to removing the head of the queue. Meanwhile, a smaller acute triangle and 2 smaller obtuse triangles will be added to the tail of the corresponding queues respectively.
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nurmela, K.J.; Ostergard, P.R.J. More Optimal Packings of Equal Circles in a Square. Discret. Comput. Geom. 1999, 22, 439–457. [Google Scholar] [CrossRef]
- Collins, C.R.; Stephenson, K. A circle packing algorithm. Comput. Geom. Theory Appl. 2003, 25, 233–256. [Google Scholar] [CrossRef]
- García, A.; Saff, E. Asymptotics of greedy energy points. Math. Comput. 2010, 79, 2287–2316. [Google Scholar] [CrossRef]
- Matousek, J. Geometric Discrepancy: An Illustrated Guide; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Chazelle, B. The Discrepancy Method: Randomness and Complexity; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Aistleitner, C.; Brauchart, J.S.; Dick, J. Point sets on the sphere 𝕊2 with small spherical cap discrepancy. Discret. Comput. Geom. 2012, 48, 990–1024. [Google Scholar]
- Grabner, P.J.; Tichy, R.F. Spherical designs, discrepancy and numerical integration. Math. Comput. 1993, 60, 327–336. [Google Scholar] [CrossRef]
- Teramoto, S.; Asano, T.; Katoh, N.; Doerr, B. Inserting points uniformly at every instance. IEICE Trans. Inf. Syst. 2006, 89, 2348–2356. [Google Scholar] [CrossRef]
- Asano, T.; Teramoto, S. On-line uniformity of points. In Proceedings of the Book of Abstracts for 8th Hellenic-European Conference on Computer Mathematics and its Applications, Athens, Greece, 8–11 July 2007; pp. 21–22. [Google Scholar]
- Asano, T. Online uniformity of integer points on a line. Inf. Proc. Lett. 2008. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, Z.; Chin, F.Y.; Ting, H.F.; Tsin, Y.H. Uniformly inserting points on square grid. Inf. Proc. Lett. 2011, 111, 773–779. [Google Scholar] [CrossRef]
- Bishnu, A.; Desai, S.; Ghosh, A.; Goswami, M.; Paul, S. Uniformity of point samples in metric spaces using gap ratio. SIAM J. Discret. Math. 2017, 31, 2138–2171. [Google Scholar] [CrossRef]
- Chen, C.; Lau, F.C.; Poon, S.H.; Zhang, Y.; Zhou, R. Online Inserting Points Uniformly on the Sphere. In Proceedings of the International Workshop on Algorithms and Computation, Hsinchu, Taiwan, 29–31 March 2017; pp. 243–253. [Google Scholar]
- Thomson, J.J. On the structure of the atom: An investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1904, 7, 237–265. [Google Scholar] [CrossRef]
- Hicks, J.S.; Wheeling, R.F. An efficient method for generating uniformly distributed points on the surface of an n-dimensional sphere. Commun. ACM 1959, 2, 17–19. [Google Scholar] [CrossRef]
- Koay, C.G. Analytically exact spiral scheme for generating uniformly distributed points on the unit sphere. J. Comput. Sci. 2011, 2, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Koay, C.G. Distributing points uniformly on the unit sphere under a mirror reflection symmetry constraint. J. Comput. Sci. 2014, 5, 696–700. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Chen, C.; Sun, L.; Lau, F.C.M.; Poon, S.-H.; Zhang, Y. Online Uniformly Inserting Points on the Sphere. Algorithms 2018, 11, 156. https://doi.org/10.3390/a11100156
Zhou R, Chen C, Sun L, Lau FCM, Poon S-H, Zhang Y. Online Uniformly Inserting Points on the Sphere. Algorithms. 2018; 11(10):156. https://doi.org/10.3390/a11100156
Chicago/Turabian StyleZhou, Rong, Chun Chen, Liqun Sun, Francis C. M. Lau, Sheung-Hung Poon, and Yong Zhang. 2018. "Online Uniformly Inserting Points on the Sphere" Algorithms 11, no. 10: 156. https://doi.org/10.3390/a11100156
APA StyleZhou, R., Chen, C., Sun, L., Lau, F. C. M., Poon, S.-H., & Zhang, Y. (2018). Online Uniformly Inserting Points on the Sphere. Algorithms, 11(10), 156. https://doi.org/10.3390/a11100156





