Multi-Branch Deep Residual Network for Single Image Super-Resolution
Abstract
1. Introduction
2. Related Work
2.1. Image Super-Resolution
2.2. Residual Network in Super-Resolution
3. Proposed Methods
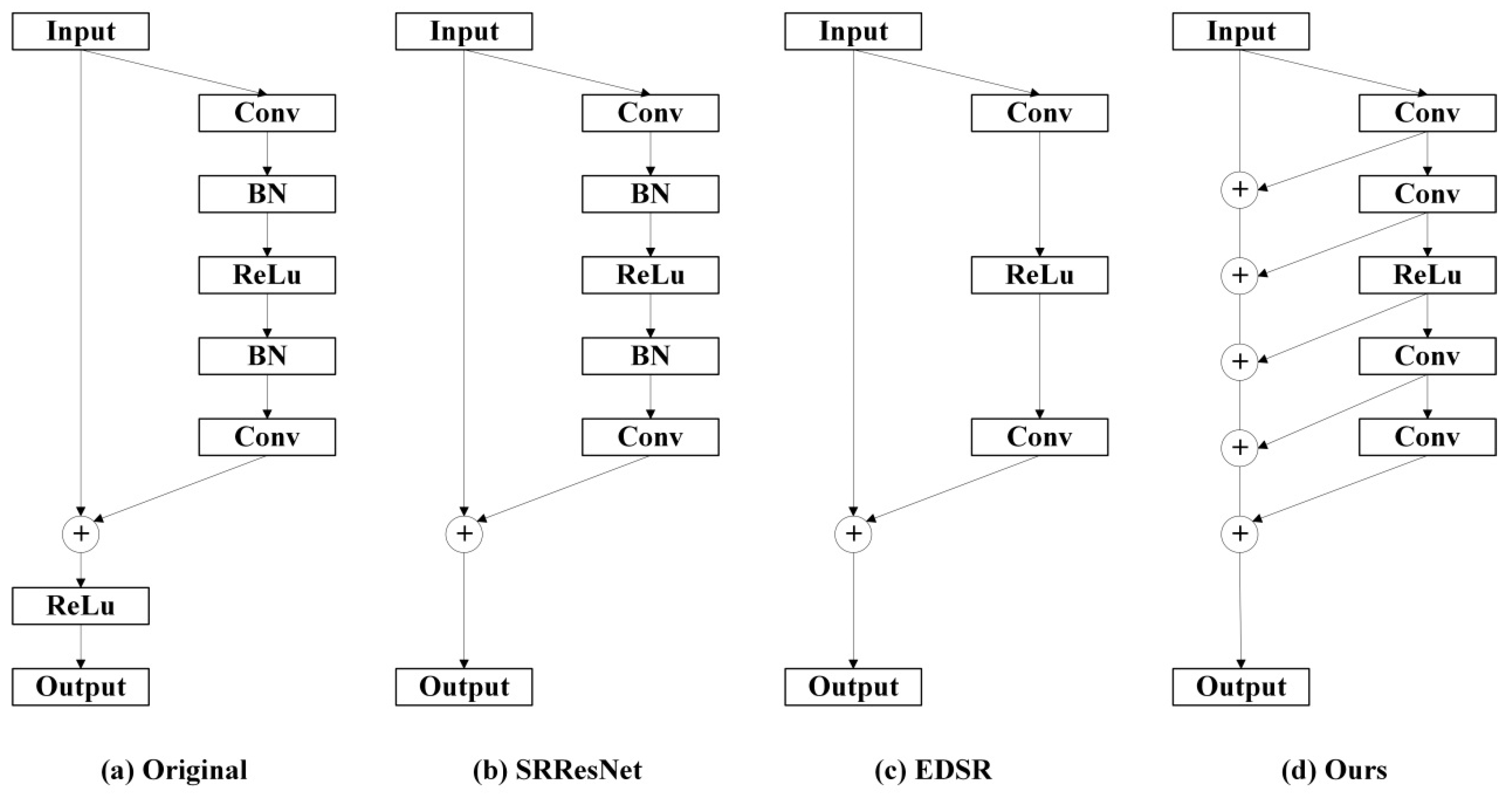
3.1. Residual Blocks
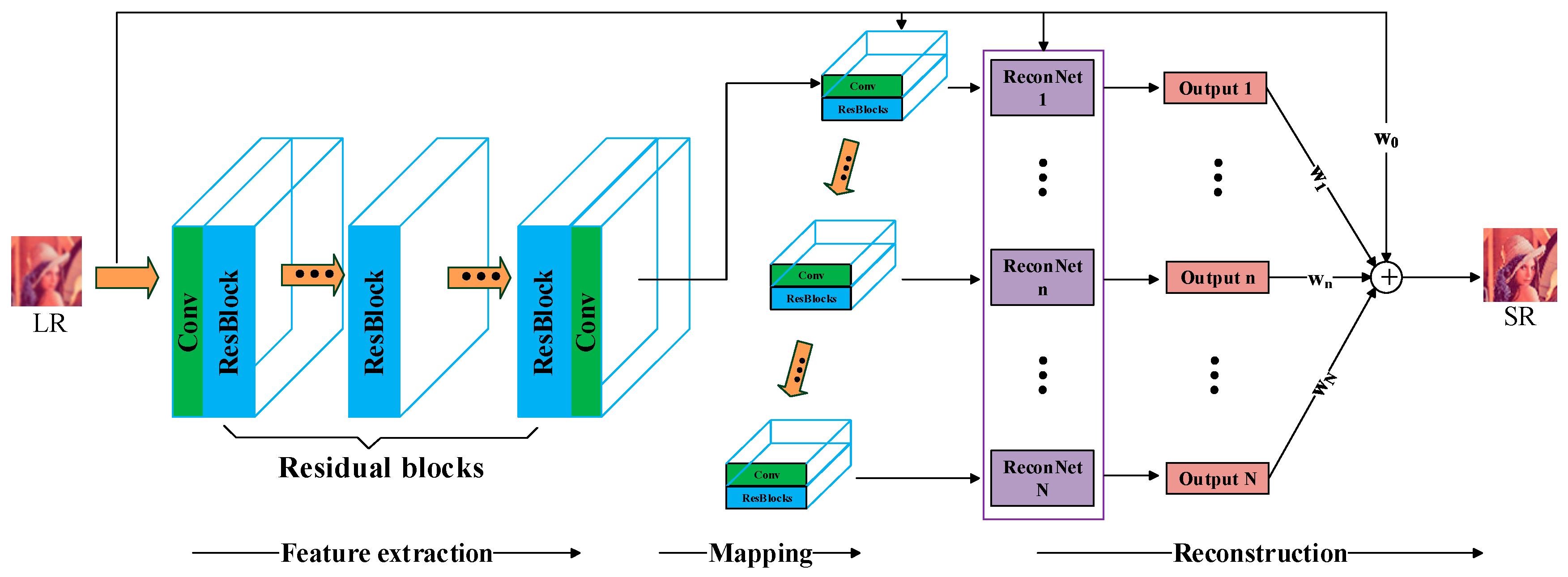
3.2. Model Architecture
3.3. Training
4. Experiments
4.1. Datasets
4.2. Training Details
4.3. Comparisons with State-of-the-Art Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Irani, M.; Peleg, S. Improving resolution by image registration. CVGIP Gr. Models Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Thornton, M.W.; Atkinson, P.M.; Holland, D.A. Sub-pixel mapping of rural land cover objects from fine spatial resolution satellite sensor imagery using super-resolution pixel-swapping. Int. J. Remote Sens. 2006, 27, 473–491. [Google Scholar] [CrossRef]
- Peled, S.; Yeshurun, Y. Superresolution in MRI: Application to human white matter fiber tract visualization by diffusion tensor imaging. Magn. Reson. Med. 2001, 45, 29–35. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Ledig, C.; Zhuang, X.; Bai, W.; Bhatia, K.; de Marvao, A.M.; Dawes, T.; O’Regan, D.; Rueckert, D. Cardiac image super-resolution with global correspondence using multi-atlas patchmatch. Med. Image Comput. Comput. Assist. Interv. 2013, 16, 9–16. [Google Scholar] [PubMed]
- Gunturk, B.K.; Batur, A.U.; Altunbasak, Y.; Hayes, M.H.; Mersereau, R.M. Eigenface-domain super-resolution for face recognition. IEEE Trans. Image Process. 2003, 12, 597–606. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, H.; Shen, H.; Li, P. A super-resolution reconstruction algorithm for surveillance images. Signal Process. 2010, 90, 848–859. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1646–1654. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1637–1645. [Google Scholar]
- Ledig, C.; Wang, Z.; Shi, W.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the Computer Vision and Pattern Recognition, Venice, Italy, 30 October–1 November 2017; pp. 105–114. [Google Scholar]
- Dong, C.; Chen, C.L.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Cun, Y.L.; Boser, B.; Denker, J.S.; Howard, R.E.; Habbard, W.; Jackel, L.D.; Henderson, D. Handwritten digit recognition with a back-propagation network. Adv. Neural Inf. Process. Syst. 1989, 2, 396–404. [Google Scholar]
- Efrat, N.; Glasner, D.; Apartsin, A.; Nadler, B. Accurate Blur Models vs. Image Priors in Single Image Super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Harbour, Sydney, 1–8 December 2013; pp. 2832–2839. [Google Scholar]
- He, H.; Siu, W.C. Single image super-resolution using Gaussian process regression. In Proceedings of the Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 449–456. [Google Scholar]
- Yang, J.; Lin, Z.; Cohen, S. Fast Image Super-Resolution Based on In-Place Example Regression. In Proceedings of the Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1059–1066. [Google Scholar]
- Fernandezgranda, C.; Candes, E.J. Super-resolution via Transform-Invariant Group-Sparse Regularization. In Proceedings of the IEEE International Conference on Computer Vision, Harbour, Sydney, 1–8 December 2013; pp. 3336–3343. [Google Scholar]
- Chang, H.; Yeung, D.Y.; Xiong, Y. Super-resolution through neighbor embedding. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 271, pp. 275–282. [Google Scholar]
- Pan, Q.; Liang, Y.; Zhang, L.; Wang, S. Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis. In Proceedings of the Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2216–2223. [Google Scholar]
- Li, X.; Tao, D.; Gao, X.; Zhang, K. Multi-scale dictionary for single image super-resolution. In Proceedings of the Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1114–1121. [Google Scholar]
- Gao, X.; Zhang, K.; Tao, D.; Li, X. Image super-resolution with sparse neighbor embedding. IEEE Trans. Image Process. 2012, 21, 3194–3205. [Google Scholar] [PubMed]
- Zhu, Y.; Zhang, Y.; Yuille, A.L. Single Image Super-resolution Using Deformable Patches. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2917–2924. [Google Scholar]
- Timofte, R.; Smet, V.D.; Gool, L.V. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; pp. 111–126. [Google Scholar]
- Dai, D.; Timofte, R.; Van Gool, L. Jointly Optimized Regressors for Image Super-resolution. Comput. Graph. Forum 2015, 34, 95–104. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Tai, Y.W.; Liu, S.; Brown, M.S.; Lin, S. Super resolution using edge prior and single image detail synthesis. In Proceedings of the Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 2400–2407. [Google Scholar]
- Timofte, R.; De, V.; Gool, L.V. Anchored Neighborhood Regression for Fast Example-Based Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision, Harbour, Sydney, 1–8 December 2013; pp. 1920–1927. [Google Scholar]
- Allebach, J.; Wong, P.W. Edge-directed interpolation. In Proceedings of the International Conference on Image Processing, Lausanne, Switzerland, 19 September 1996; Volume 703, pp. 707–710. [Google Scholar]
- Li, X.; Orchard, M.T. New edge-directed interpolation. IEEE Trans. Image Process. 2001, 10, 1521–1527. [Google Scholar] [PubMed]
- Glasner, D.; Bagon, S.; Irani, M. Super-resolution from a single image. In Proceedings of the IEEE International Conference on Computer Vision, Lausanne, Switzerland, 19 September 1996; pp. 349–356. [Google Scholar]
- Kim, K.I.; Kwon, Y. Single-Image Super-Resolution Using Sparse Regression and Natural Image Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1127–1133. [Google Scholar] [PubMed]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Yang, J.; Wang, Z.; Lin, Z.; Cohen, S. Couple Dictionary Training for Image Super-resolution. IEEE Trans. Image Process. 2012, 21, 3467–3478. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1874–1883. [Google Scholar]
- Johnson, J.; Alahi, A.; Li, F.F. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 694–711. [Google Scholar]
- Bruna, J.; Sprechmann, P.; Lecun, Y. Super-Resolution with Deep Convolutional Sufficient Statistics. arXiv, 2015; arXiv:1511.05666. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Morel, A. Low-Complexity Single Image Super-Resolution Based on Nonnegative Neighbor Embedding. In Proceedings of the 23rd British Machine Vision Conference (BMVC), Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A Database of Human Segmented Natural Images and its Application to Evaluating Segmentation Algorithms and Measuring Ecological Statistics. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; Volume 412, pp. 416–423. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Timofte, R.; Agustsson, E.; Gool, L.V.; Yang, M.H.; Zhang, L.; Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Ntire 2017 Challenge on Single Image Super-Resolution: Methods and Results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1110–1121. [Google Scholar]
- Cruz, C.; Mehta, R.; Katkovnik, V.; Egiazarian, K. Single Image Super-Resolution based on Wiener Filter in Similarity Domain. IEEE Trans. Image Process. 2017, 27, 1376–1389. [Google Scholar] [CrossRef] [PubMed]





| SRResNet | EDSR | MRSR | |
|---|---|---|---|
| Residual blocks | 16 | 32 | 60 |
| Filters | 64 | 256 | 128 |
| parameters | 1.5 M | 43 M | 12 M |
| Dataset | Scale | Bicubic | A+ | SRCNN | DRCN | SRResNet | EDSR | WSD | MRSR (ours) |
|---|---|---|---|---|---|---|---|---|---|
| Set5 | ×2 | 33.66/0.9299 | 36.54/0.9544 | 36.66/0.9542 | 37.63/0.9588 | -/- | 38.11/0.9601 | 37.21/- | 38.32/0.9610 |
| ×3 | 30.39/0.8682 | 32.58/0.9088 | 32.75/0.9090 | 33.82/0.9226 | -/- | 34.65/0.9282 | 33.50/- | 34.88/0.9305 | |
| ×4 | 28.42/0.8104 | 30.28/0.8603 | 30.48/0.8628 | 31.53/0.8854 | 32.05/0.8910 | 32.46/0.8968 | 31.39/- | 32.97/0.9004 | |
| Set14 | ×2 | 30.24/0.8688 | 32.28/0.9056 | 32.42/0.9063 | 33.04/0.9118 | -/- | 33.92/0.9195 | 32.83/- | 34.25/0.9214 |
| ×3 | 27.55/0.7742 | 29.13/0.8188 | 29.28/0.8209 | 29.76/0.8311 | -/- | 30.52/0.8462 | 29.72/- | 30.83/0.8539 | |
| ×4 | 26.00/0.7027 | 27.32/0.7491 | 27.49/0.7503 | 28.02/0.7670 | 28.53/0.7804 | 28.80/0.7876 | 27.98/- | 29.42/0.7984 | |
| B100 | ×2 | 29.56/0.8431 | 31.21/0.8863 | 31.36/0.8879 | 31.85/0.8942 | -/- | 32.32/0.9013 | 30.29/- | 32.67/0.9081 |
| ×3 | 27.21/0.7385 | 28.29/0.7835 | 28.41/0.7863 | 28.80/0.7963 | -/- | 29.25/0.8093 | 26.95/- | 29.54/0.8112 | |
| ×4 | 25.96/0.6675 | 26.82/0.7087 | 26.90/0.7101 | 27.23/0.7233 | 27.57/0.7354 | 27.71/0.7420 | 25.16/- | 28.23/0.7556 | |
| Urban100 | ×2 | 26.88/0.8403 | 29.20/0.8938 | 29.50/0.8946 | 30.75/0.9133 | -/- | 32.93/0.9351 | -/- | 33.31/0.9384 |
| ×3 | 24.46/0.7349 | 26.03/0.7973 | 26.24/0.7989 | 27.15/0.8076 | -/- | 28.80/0.8653 | -/- | 29.12/0.8705 | |
| ×4 | 23.14/0.6577 | 24.32/0.7183 | 24.52/0.7221 | 25.14/0.7510 | 26.07/0.7839 | 26.64/0.8033 | -/- | 27.17/0.8129 | |
| DIV2K validation | ×2 | 31.01/0.9393 | 32.89/0.9570 | 33.05/0.9581 | -/- | -/- | 35.03/0.9695 | -/- | 35.46/0.9731 |
| ×3 | 28.22/0.8906 | 29.50/0.9116 | 29.64/0.9138 | -/- | -/- | 31.26/0.9304 | -/- | 31.53/0.9382 | |
| ×4 | 26.66/0.8521 | 27.70/0.8736 | 27.78/0.8753 | -/- | -/- | 29.25/0.9017 | -/- | 29.73/0.9076 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Hong, Y.; Liu, Y. Multi-Branch Deep Residual Network for Single Image Super-Resolution. Algorithms 2018, 11, 144. https://doi.org/10.3390/a11100144
Liu P, Hong Y, Liu Y. Multi-Branch Deep Residual Network for Single Image Super-Resolution. Algorithms. 2018; 11(10):144. https://doi.org/10.3390/a11100144
Chicago/Turabian StyleLiu, Peng, Ying Hong, and Yan Liu. 2018. "Multi-Branch Deep Residual Network for Single Image Super-Resolution" Algorithms 11, no. 10: 144. https://doi.org/10.3390/a11100144
APA StyleLiu, P., Hong, Y., & Liu, Y. (2018). Multi-Branch Deep Residual Network for Single Image Super-Resolution. Algorithms, 11(10), 144. https://doi.org/10.3390/a11100144




