Weakly Coupled Distributed Calculation of Lyapunov Exponents for Non-Linear Dynamical Systems
Abstract
:1. Introduction
2. Lyapunov Exponents in Non-Linear Dynamical Systems
2.1. Coupled Oscillations Model
3. Parallel Application Design
- A master node.
- 17 slave nodes with Intel i5-4670 processors (four cores without HT), and 32 GB PC3-12800 of RAM memory each.
- TL-SG1024 24-Port Gigabit Switch.
- Cluster Rocks 6.2 OS.
- Intel FORTRAN 17.0.1.
3.1. MPI Distributed Implementation
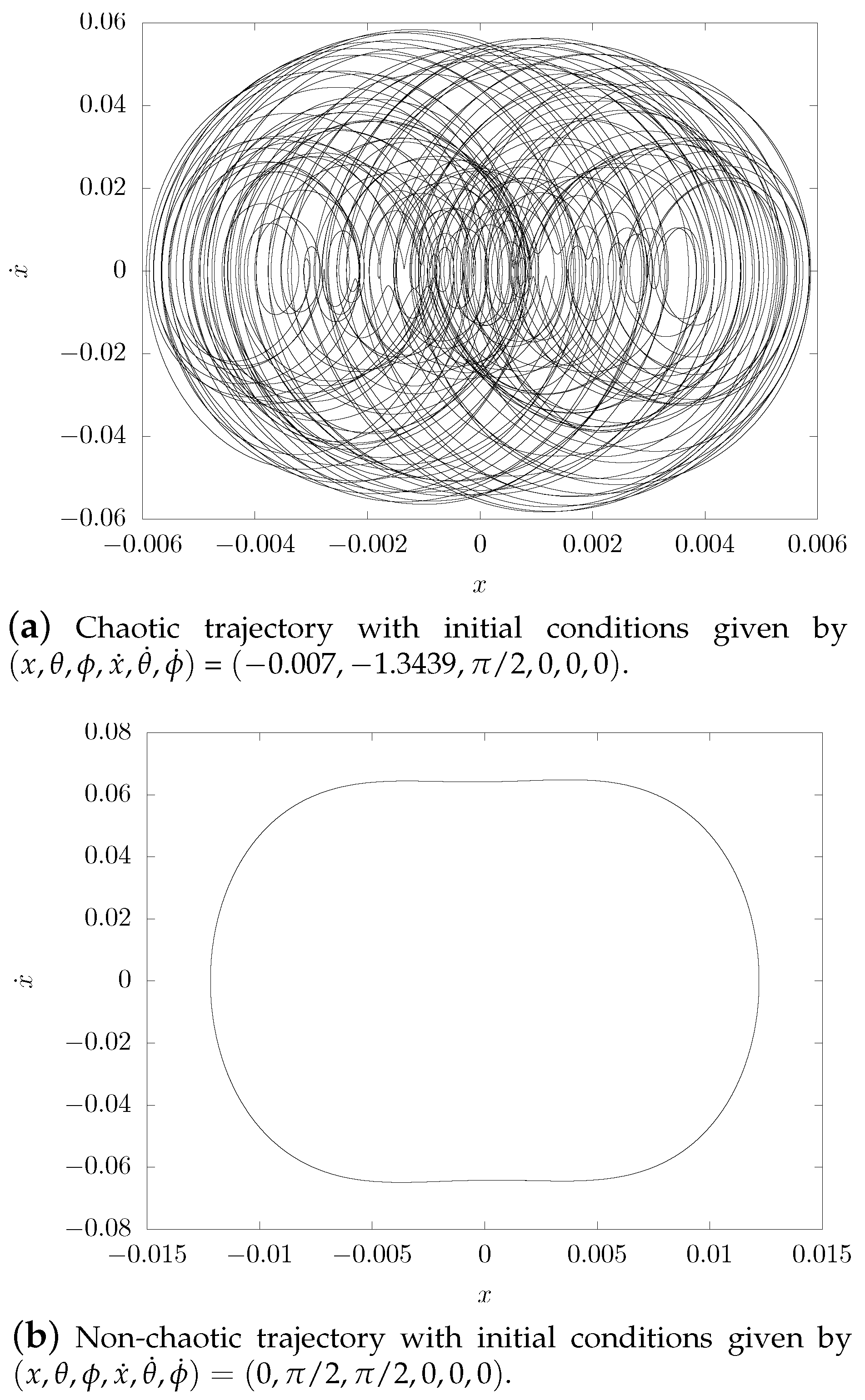
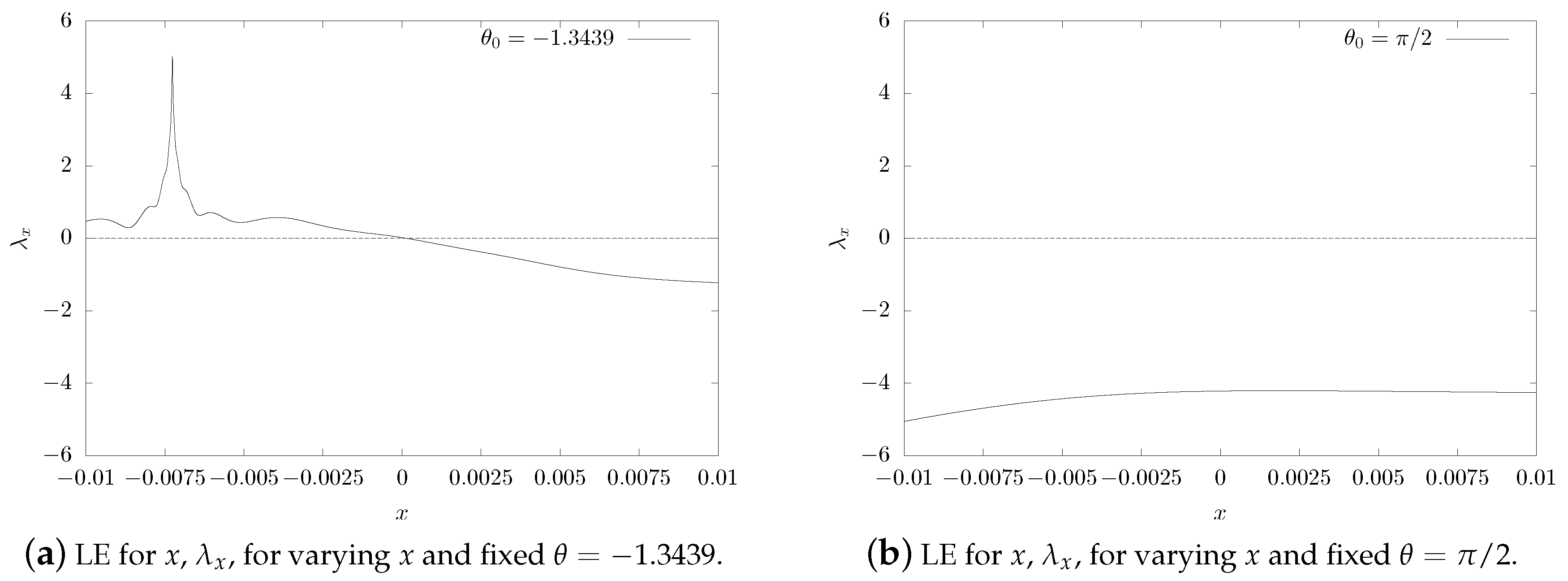
4. Physical Experiments
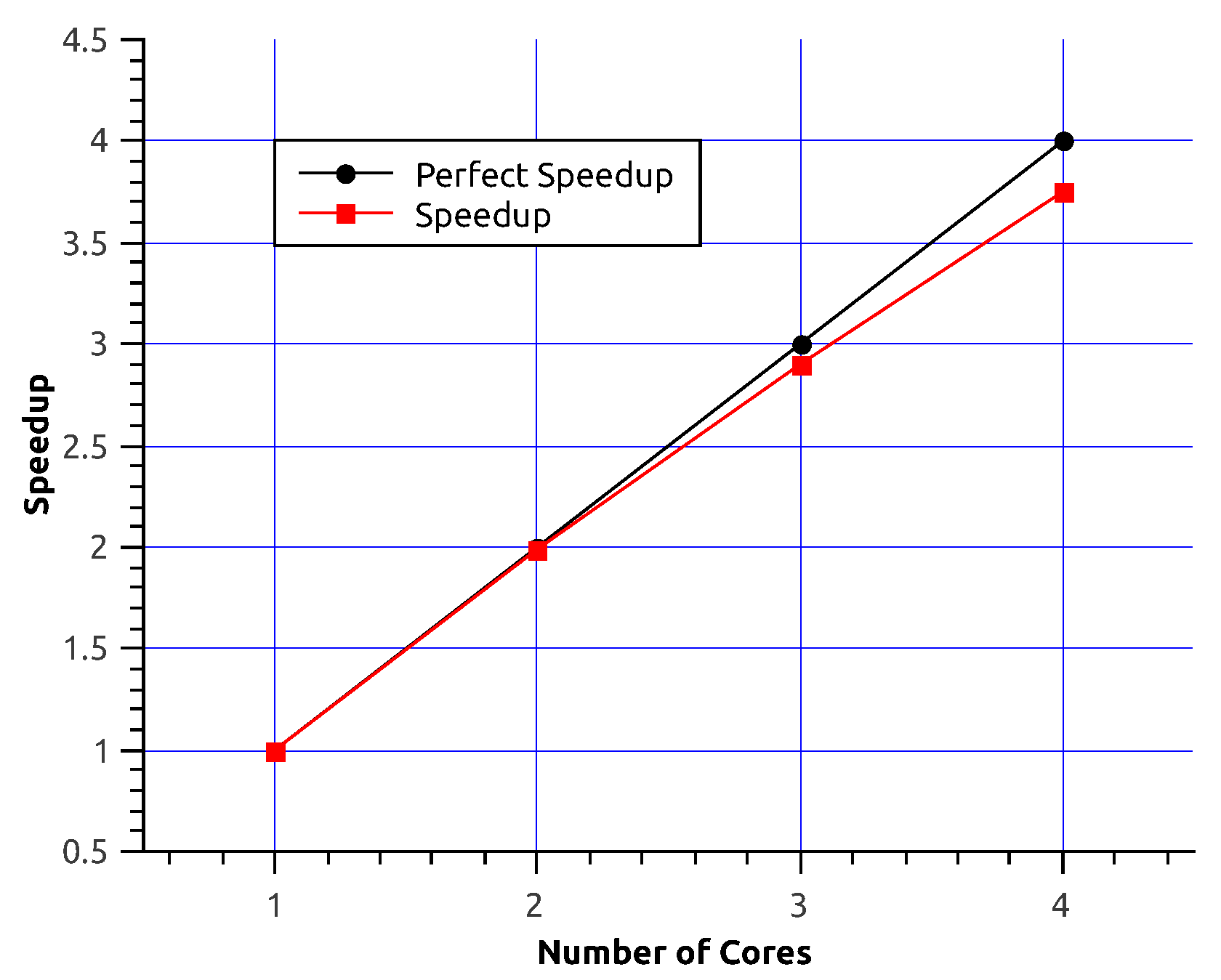
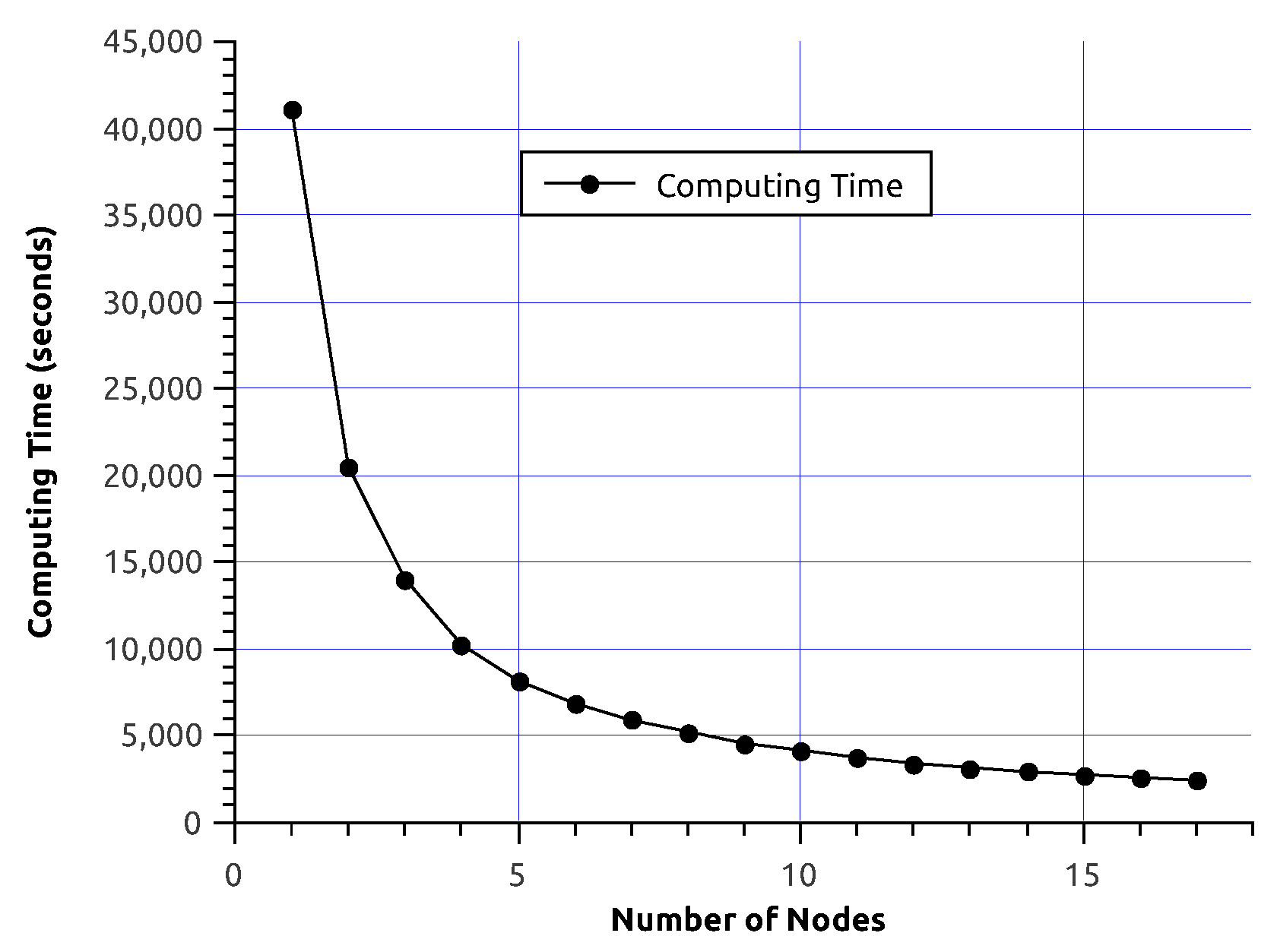
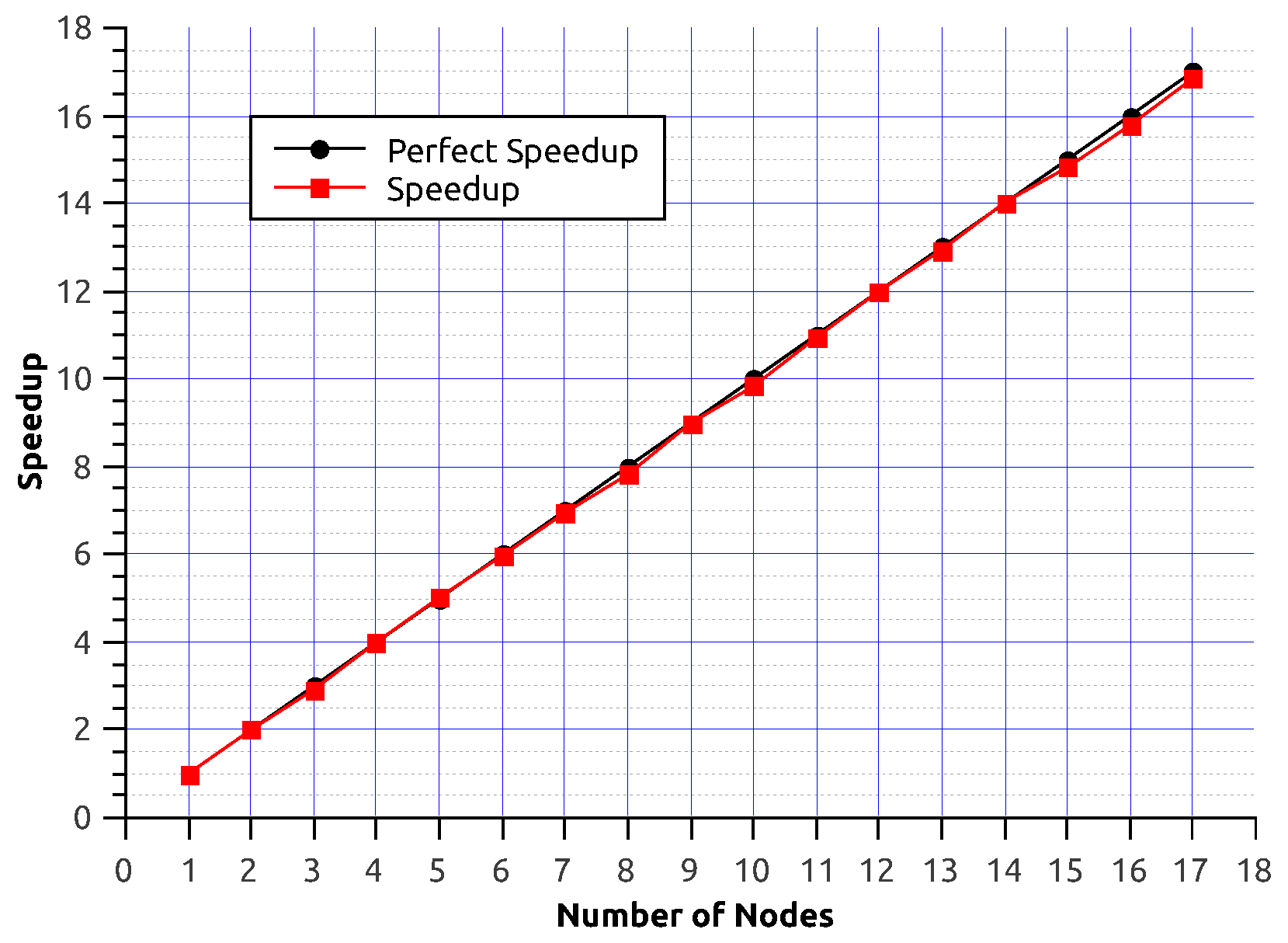
5. Performance Experiments
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Pseudo-Code of the Computation Procedure
| Algorithm A1 Distributed Algorithm for the Calculation of Lyapunov Exponents. |
|
References
- Strogatz, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Studies in Nonlinearity; Avalon Publishing: New York, NY, USA, 2014. [Google Scholar]
- Lyapunov, A.M. The General Problem of the Stability of Motion. Ph.D. Thesis, University of Kharkov, Kharkiv Oblast, Ukraine, 1892. [Google Scholar]
- Benettin, G.; Galgani, L.; Strelcyn, J.M. Kolmogorov entropy and numerical experiments. Phys. Rev. A 1976, 14, 2338. [Google Scholar] [CrossRef]
- Contopoulos, G.; Galgani, L.; Giorgilli, A. On the number of isolating integrals in Hamiltonian systems. Phys. Rev. A 1978, 18, 1183. [Google Scholar] [CrossRef]
- Sato, S.; Sano, M.; Sawada, Y. Practical methods of measuring the generalized dimension and the largest Lyapunov exponent in high dimensional chaotic systems. Prog. Theor. Phys. 1987, 77, 1–5. [Google Scholar] [CrossRef]
- Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 1994, 185, 77–87. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Alexeeva, T.; Leonov, G. Invariance of Lyapunov exponents and Lyapunov dimension for regular and irregular linearizations. Nonlinear Dyn. 2016, 85, 195–201. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Hernández-Gómez, J.J.; Couder-Castañeda, C.; Gómez-Cruz, E.; Solis-Santomé, A.; Ortiz-Alemán, J.C. A simple experimental setup to approach chaos theory. Eur. J. Phys. 2017. under review. [Google Scholar]
- Rauber, T.; Rünger, G. Parallel Programming: For Multicore and Cluster Systems; Springer Science & Business Media: New York, NY, USA, 2013; pp. 1–516. [Google Scholar]
- Couder-Castañeda, C. Simulation of supersonic flow in an ejector diffuser using the JPVM. J. Appl. Math. 2009, 2009, 497013. [Google Scholar] [CrossRef]
- Kshemkalyani, A.; Singhal, M. Distributed Computing: Principles, Algorithms, and Systems; Cambridge University Press: Cambridge, UK, 2008; pp. 1–736. [Google Scholar]
- Iserles, A.; Nørsett, S. On the Theory of Parallel Runge—Kutta Methods. IMA J. Numer. Anal. 1990, 10, 463. [Google Scholar] [CrossRef]
- Bylina, B.; Potiopa, J. Explicit Fourth-Order Runge–Kutta Method on Intel Xeon Phi Coprocessor. Int. J. Parallel Program. 2017, 45, 1073–1090. [Google Scholar] [CrossRef]
- Murray, L. GPU Acceleration of Runge-Kutta Integrators. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 94–101. [Google Scholar] [CrossRef]
- Majid, Z.; Mehrkanoon, S.; Othman, K. Parallel block method for solving large systems of ODEs using MPI. In Proceedings of the 4th International Conference on Applied Mathematics, Simulation, Modelling—Proceedings, Corfu Island, Greece, 22-25 July 2010; pp. 34–38. [Google Scholar]
- Couder-Castañeda, C.; Ortiz-Alemán, J.; Orozco-del Castillo, M.; Nava-Flores, M. Forward modeling of gravitational fields on hybrid multi-threaded cluster. Geofis. Int. 2015, 54, 31–48. [Google Scholar] [CrossRef]
- Arroyo, M.; Couder-Castañeda, C.; Trujillo-Alcantara, A.; Herrera-Diaz, I.E.; Vera-Chavez, N. A performance study of a dual Xeon-Phi cluster for the forward modelling of gravitational fields. Sci. Program. 2015, 2015, 316012. [Google Scholar] [CrossRef]
- Zemlyanaya, E.; Bashashin, M.; Rahmonov, I.; Shukrinov, Y.; Atanasova, P.; Volokhova, A. Model of stacked long Josephson junctions: Parallel algorithm and numerical results in case of weak coupling. In Proceedings of the 8th International Conference for Promoting the Application of Mathematics in Technical and Natural Sciences—AMiTaNS 16, Albena, Bulgaria, 22–27 June 2016; Volume 1773. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Gómez, J.J.; Couder-Castañeda, C.; Herrera-Díaz, I.E.; Flores-Guzmán, N.; Gómez-Cruz, E. Weakly Coupled Distributed Calculation of Lyapunov Exponents for Non-Linear Dynamical Systems. Algorithms 2017, 10, 137. https://doi.org/10.3390/a10040137
Hernández-Gómez JJ, Couder-Castañeda C, Herrera-Díaz IE, Flores-Guzmán N, Gómez-Cruz E. Weakly Coupled Distributed Calculation of Lyapunov Exponents for Non-Linear Dynamical Systems. Algorithms. 2017; 10(4):137. https://doi.org/10.3390/a10040137
Chicago/Turabian StyleHernández-Gómez, Jorge J., Carlos Couder-Castañeda, Israel E. Herrera-Díaz, Norberto Flores-Guzmán, and Enrique Gómez-Cruz. 2017. "Weakly Coupled Distributed Calculation of Lyapunov Exponents for Non-Linear Dynamical Systems" Algorithms 10, no. 4: 137. https://doi.org/10.3390/a10040137
APA StyleHernández-Gómez, J. J., Couder-Castañeda, C., Herrera-Díaz, I. E., Flores-Guzmán, N., & Gómez-Cruz, E. (2017). Weakly Coupled Distributed Calculation of Lyapunov Exponents for Non-Linear Dynamical Systems. Algorithms, 10(4), 137. https://doi.org/10.3390/a10040137





