Hyperspectral Data: Efficient and Secure Transmission

Abstract

Airborne and spaceborne hyperspectral sensors collect information which is derived from the electromagnetic spectrum of an observed area. Hyperspectral data are used in several studies and they are an important aid in different real-life applications (e.g., mining and geology applications, ecology, surveillance, etc.). A hyperspectral image has a three-dimensional structure (a sort of datacube): it can be considered as a sequence of narrow and contiguous spectral channels (bands). The objective of this paper is to present a framework permits the efficient storage/transmission of an input hyperspectral image, and its protection. The proposed framework relies on a reversible invisible watermarking scheme and an efficient lossless compression algorithm. The reversible watermarking scheme is used in conjunction with digital signature techniques in order to permit the verification of the integrity of a hyperspectral image by the receiver.

1. Introduction

Hyperspectral imaging sensors obtain information from the electromagnetic spectrum of an observed area. Spectral imaging techniques cover a significant portion of the electromagnetic spectrum in which the frequencies are in a range that spans from the ultraviolet to the infrared. A hyperspectral sensor subdivides the spectrum into different spectral channels (referred to as “bands”). For such reasons, a hyperspectral image can be considered as a sort of “datacube” [1], since such data can be structured in a three-dimensional manner.

Hyperspectral images are efficiently used in a wide range of real-life and research applications (agriculture, mineralogy, physics, surveillance, etc.). Hyperspectral images are often shared among different entities, sometimes with different purposes (for example different research centres, etc.), in order to carry out conjunct tasks.

Several scenarios can be drawn in which these data are shared/stored/transmitted for sensitive objectives (e.g., military applications [2,3], counter-terrorism [4], forensic applications [5], etc.). Thus, an important concern might be to ensure data protection against tampering, which can occur even in very sensitive cases (e.g., target-detection applications, etc.). Since these images need to be efficiently transmitted to a base as soon as they are acquired, and they need to be efficiently stored, we propose a possible framework for efficient transmission and protection.

The proposed framework relies on two main components: a lossless compression algorithm and a reversible watermarking scheme. Generally, digital watermarking techniques are used for ensuring security, content authentication, and copyright protection (e.g., [6,7,8]). Using watermarking techniques, the input data (i.e., the hyperspectral images) might become a sort of “carrier” of hidden information, which can carry important data (e.g., [9,10]). We highlight the key aspects of the proposed framework, in Section 2, and we outline further details for a possible effective implementation, in Section 2.1. Regarding the implementation, we considered a reversible invisible watermarking scheme (Section 2.1.1), designed specifically for hyperspectral images, and the multiband lossless compression of hyperspectral images (LMBHI) algorithm [11] (reviewed in Section 2.1.2), which is a predictive-based lossless compression algorithm that achieves interesting results.

Finally, we report and discuss the obtained experimental results in Section 3 and Section 4 draws our conclusions.

2. An Efficient and Secure Transmission Framework

Figure 1 shows the architecture of the proposed transmission framework. First, the digest $h(HI)$ of the input hyperspectral image HI is computed, by invoking a cryptographic hash function h(.) (e.g., SHA-3 Keccak [12], etc.). Subsequently, the obtained digest $h(HI)$ is used as a watermark string and is embedded into HI, by using a reversible invisible watermarking scheme. As it is observable from Figure 1, the secret key K, is used for the computation of the digest as well as for the embedding of the obtained digest $h(HI)$ into HI.

After that, the watermarked hyperspectral image HI^W (i.e., the output of the reversible invisible watermarking scheme) is compressed by using an efficient lossless compression algorithm. The output of this compression stage, is denoted as HI^CW and it can be efficiently transmitted.

In the following, we denote as $H{I}^{\prime }$ the hyperspectral image which is reconstructed from HI^W (where HI^W is obtained as the output of the decompression of HI^CW), and as w′ the watermark string which is extracted from HI^W.

The receiver can verify the integrity of HI, in the following manner: if there are no alterations of HI^W, then the value of $h(H{I}^{\prime })$ will be equal to the value of $h(HI)$. Consequently, it is satisfied that w $=h(HI)=h(H{I}^{\prime })=$ w′ and $H{I}^{\prime }$ is exactly equal to HI.

2.1. An Effective Implementation of the Proposed Framework

For an effective implementation of the proposed framework, we considered the reversible watermarking scheme, described in Section 2.1.1, and the multiband lossless compression of hyperspectral images scheme (LMBHI), the compression algorithm is addressed in Section 2.1.2. However, other approaches can be efficiently used for an effective implementation of our proposal.

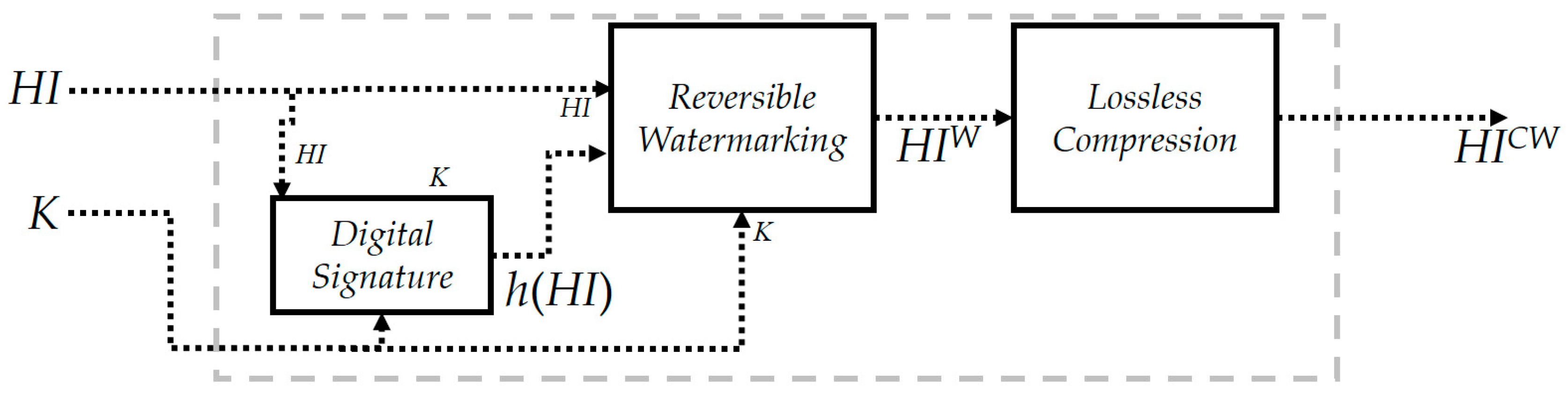
2.1.1. Reversible Invisible Watermarking Scheme for Hyperspectral Images

In [13], we have proposed a preliminary version of a reversible invisible watermarking scheme for hyperspectral images. This scheme relies on the approaches outlined in [9,14], and belongs to the category of additive schemes. In the additive scheme, the watermark signal w (i.e., a watermark string) is directly added to the input signal, namely the pixels of the input hyperspectral image HI. In this way the output produced (i.e., the watermarked hyperspectral image HI^W) contains both the signals (the one that represents the HI and the one that represents the watermark w). A secret key, K, is used to perform the embedding phase.

It is important to note that this scheme is reversible. Therefore, it is possible to restore the original HI and to extract the watermark w. In addition, this scheme is fragile: a simple modification of HI^W might cause the disappearance of the embedded watermark, w.

The basic objective of our scheme is to spread the bits of w among all the bands of HI. More precisely, each bit of w—referred to as b_w—will be embedded into a set of four pixels $S_P=\{x_{(0)}, x_{(0)}, x_{(2)}, x_{(3)}\}$. These pixels are pseudo-randomly selected by means of a pseudo-random number generator (PRNG) based on the secret key, K.

Since it is possible to have a set S_P that cannot be used to carry b_w due to the fact that the extraction algorithm might be unable to extract the hidden bit, it is necessary to classify the sets into two categories: “carrier sets” and “non-carrier sets”. A carrier set is a set in which a bit, b_w, can be embedded, while a non-carrier set is a set in which a bit, b_w, cannot be embedded.

When the algorithm identifies a carrier set S_P, a bit b_w can be embedded by means of the “embedWatermarkBit” procedure, reported in Algorithm 1, which returns as output the set $S_P^w$. $S_P^w$ represents the set S_P in which b_w is embedded. To classify a set S_P, the relationship between S_P and its estimation $S_P^E$ is exploited. This estimation is computed by means of a linear combination of the pixels of S_P, as explained in the “estimate” procedure (see Algorithm 2). By using the estimation, the extraction algorithm can classify, in two steps, a set S_P. Furthermore, the extraction algorithm can restore the original pixel values of the carrier set by manipulating a watermarked carrier set. In this manner, the reversibility property is obtained.

Algorithm 1 The “embedWatermarkBit” procedure (pseudo-code from [13])

procedure embedWatermarkBit ($S_P$, $b_w$)

if $b_w==1$ then  $x_{(0)}^w=x_{(0)}+1$;  $x_{(1)}^w=x_{(1)}-1$;  $x_{(2)}^w=x_{(2)}-1$;  $x_{(3)}^w=x_{(3)}+1$; else  $x_{(0)}^w=x_{(0)}-1$;  $x_{(1)}^w=x_{(1)}+1$;  $x_{(2)}^w=x_{(2)}+1$;  $x_{(3)}^w=x_{(3)}-1$; endif $S_P^w=\{x_{(0)}^w, x_{(1)}^w, x_{(2)}^w, x_{(3)}^w\}$; return $S_P^w$;

end procedure

Algorithm 3 reports the pseudo-code of the “embed” procedure. This procedure embeds the watermark string w into the input hyperspectral image HI by using in the embedding process the secret key K.

In details: the pseudo-random number generator (PRNG) G is initialized by using K as a seed. Subsequently, w is subdivided into M substrings (where M is the number of bands of HI). The ith substring, w_i, will be embedded into the ith band of HI, denoted as HI_(i). Therefore, each band will carry at least $\lfloor N/M\rfloor$ bits, where N denotes the length of w.

The algorithm considers each substring w_i and performs the following steps until all the bits composing w_i are embedded into HI_(i): four pixels (we denote them as $x_{(0)}$, $x_{(1)}$, $x_{(2)}$, and $x_{(3)}$) are randomly selected by using the PRNG G to compose a set $S_P$. Subsequently, the estimation $S_P^E$ (composed by four estimated pixels, that we denote as $x_{(0)}^E$, $x_{(1)}^E$, $x_{(2)}^E$, and $x_{(3)}^E$) of $S_P$ is calculated. This estimation is computed by a linear combination of the pixels of S_P, as it is shown in the estimate procedure of Algorithm 2. In order to classify the set $S_P$, the difference D, in absolute value, between $x_{(0)}$ and $x_{(0)}^E$ is computed. In the case $D$ is less than 1, then the set $S_P$ is classified as a carrier set and, therefore, the “embedWatermarkBit” procedure (Algorithm 1) is performed in order to embed b_w into $S_P$. Thus, the processing of bit b_w is complete. The coordinates of the pixels $x_{(0)}$, $x_{(1)}$, $x_{(2)}$, and $x_{(3)}$ will be no longer selectable and the algorithm proceeds by embedding the next bit of w_i.

Algorithm 2 The “estimate” procedure (pseudo-code from [13])

procedure estimate ($S_P$)

$x_{(0)}^E=\frac{2\times x_{(0)}+x_{(1)}+x_{(2)}}{4}$; $x_{(1)}^E=\frac{2\times x_{(1)}+x_{(0)}+x_{(3)}}{4}$; $x_{(2)}^E=\frac{2\times x_{(2)}+x_{(0)+x_{(3)}}}{4}$; $x_{(3)}^E=\frac{2\times x_{(3)}+x_{(1)}+x_{(2)}}{4}$; $S_P^E=\{x_{(0)}^E, x_{(1)}^E, x_{(2)}^E, x_{(3)}^E\}$; return $S_P^E$;

end procedure

In case S_p is classified, instead, as a non-carrier set, then the value of the pixels of S_p are modelled in order to increase the difference, $D$. In this manner, the extraction algorithm is able to correctly understand that S_p is a non-carrier set. As a consequence, the bit, b_w, cannot be embedded into the set S_p and other four pixels (different from the ones previously selected) will be selected to compose a new set S_p, to try the embedding again.

Algorithm 3 The “embed” procedure (pseudo-code from [13])

procedure embed ($HI$, w, K)

Let $G$ be a PRNG; $N=lengthOf(w)$; Subdivide w into $\{w_1, w_2, \dots , w_M\}$; for i = 1 to M do  $idx=1$;  $N_i=lengthOf(w_i)$  repeat  $b_w=w_i\left[idx\right]$;  By using $G$ along with K, selects $x_{(0)}, x_{(1)}, x_{(2)}, x_{(3)}$ from $H{I}_{(i)}$;  $S_P=\{x_{(0)}, x_{(1)}, x_{(2)}, x_{(3)}\}$;  $S_P^E=estimate(S_P)$;  $D=|x_{(0)}-x_{(0)}^E|$;  if $D<1$ then  $S_P^w=embedWatermarkBit(S_P, b_w)$;  $idx++$;  else  Modifying of $S_P$, by using $S_P=$ embedWatermarkBit($S_P,$ 0) or $S_P=$ embedWatermarkBit($S_P,$ 1), in order to increase the value of $D$;  endif  Setting of the coordinates of $x_{(0)}$, $x_{(1)}$, $x_{(2)}$ and $x_{(3)}$ no longer selectable;  until $idx\le N_i$; end for Copying of all modified and unmodified pixels to $H{I}^W$; return $H{I}^W$;

end procedure

2.1.2. Multiband Lossless Compression of Hyperspectral Images

The predictive-based multiband lossless compression for hyperspectral images (LMBHI) [11] algorithm exploits the inter-band correlation (i.e., the correlation among the neighboring pixels of contiguous bands) as well as the intra-band correlations (i.e., the correlations among the neighboring pixels of the same band), by using a predictive coding model.

Each pixel of the input hyperspectral image HI is predicted by using one of the following predictive structures: the 2-D linearized median predictor (2-D LMP) [15] and the 3-D multiband linear predictor (3D-MBLP).

2-D LMP considers only the intra-band correlation and it is used only for the pixels of the first band for which there are no previous reference bands.

3D-MBLP exploits the intra-band and the inter-band correlations instead and is used to predict the pixels of all the bands except for the first one.

Once the prediction step is performed the prediction error, e, is modelled and coded. In particular, e is obtained by subtracting the value of the prediction of the current pixel from its effective value.

The 3D-MBLP predictor uses a three-dimensional prediction context which is defined by considering two parameters: B and N, where B indicates the number of the previous reference bands and N indicates the number of pixels that will be included in the prediction context that are in the current band and in the previous B reference bands.

In order to permit an efficient and relative indexing of the pixels that form the prediction context of the 3D-MBLP, an enumeration, E, is defined. We denote with $I_{i,j}$ the ith pixel (according to the enumeration E) of the jth band. In addition, we suppose that the current band is the $k$th band. In this manner, $I_{0,j}$ is referred to the pixel that has the same spatial coordinates of the current pixel (denoted as $I_{0,k}$), in the jth band.

The 3D-MBLP predictor is based on the least squares optimization technique and the prediction is computed, as in Equation (1).

$$\widehat{I_{0,k}}={\displaystyle \sum }_{i=1}^B{\alpha }_i\times I_{0,k-i}$$

(1)

It is important to point out that the coefficients ${\alpha }_0={\left[{\alpha }_1, \dots , {\alpha }_B\right]}^T$ are chosen to minimize the energy of the prediction error, as in Equation (2).

$$P={\displaystyle \sum }_{i=1}^N{\left(I_{i,k}-\widehat{I_{i,j}}\right)}^2$$

(2)

It should be observable that Equation (2) can be rewritten (by using the matrix notation), as outlined in the equation

$$P={(C\alpha -X)}^T·(C\alpha -X), \mathrm{where} C=\left[\begin{array}{ccc}{I}_{1,k-1}& \cdots & I_{1,k-B}\\ ⋮& \ddots & ⋮\\ I_{N,k-1}& \dots & I_{N,k-B}\end{array}\right] \mathrm{and} X={\left[I_{1,k}, \dots , I_{N,k}\right]}^T.$$

Subsequently, by computing the derivate of $P$ and by setting it to zero, the optimal coefficients can be obtained

$$(C^{T}C){\alpha }_0=(C^{T}X)$$

(3)

Once the coefficients ${\alpha }_0$, which solve the linear system of Equation (3), are computed, the prediction $\widehat{I_{0,k}}$, of the current pixel $I_{0,k}$, can be calculated.

3. Experimental Results

To validate the proposed framework, we have experimentally tested our proposed algorithms on two datasets, which are composed by airborne visible/infrared imaging spectrometer (AVIRIS) hyperspectral images. Such data is obtained by AVIRIS hyperspectral sensors (NASA Jet Propulsion Laboratory (JPL) [16]), which measure the spectrum in the wavelengths ranging from 380 to 2500 nm (subdivided into 224 spectral bands).

3.1. Description of the Test Datasets

Dataset 1.

The first dataset we used in the testing phase is composed by five AVIRIS hyperspectral images provided by the JPL (Jet Propulsion Laboratory) of NASA. Each hyperspectral image is subdivided into sub-images which are denoted as scenes. In detail, a scene is composed by 614 columns, 512 lines (except for the last scene that might have a lower number of lines), and 224 bands. Each pixel is stored as a signed integer and represented with 16 bits.

In

Table 1. Description of the Dataset 1.

Hyperspectral Image	Number of Scenes
Cuprite	5
Jasper Ridge	6
Low Altitude	8
Lunar Lake	3
Moffett Field	4

, we report for each hyperspectral image (rows) and the number of its scenes (second column).

Dataset 2.

The second dataset is referred to as the “CCSDS Dataset” and it is composed of five calibrated and seven uncalibrated AVIRIS hyperspectral images. This dataset is publicly available, and it is provided by the Consultative Committee for Space Data Systems (CCSDS) Multispectral and Hyperspectral Data Compression [17].

Table 2. Description of the Dataset 2.

Hyperspectral Image	Number of Scenes	Columns
Yellowstone (calibrated)	5	677
Yellowstone (uncalibrated)	5	680
Hawaii (uncalibrated)	1	614
Maine (uncalibrated)	1	680

shortly reports the key information describing Dataset 2 by showing the number of scenes (second column) and the number of columns (third column), concerning the calibrated and the uncalibrated images (first column). We remark that a pixel of the calibrated and the uncalibrated images is stored by using 16 bits (16-bit signed integer, for the calibrated, and 16-bit unsigned integer, for the uncalibrated), except for the Hawaii and Maine hyperspectral images which have pixels stored by using 12 bits (unsigned) [17]. Each of the hyperspectral images in the Dataset 2 is composed of 512 lines.

3.2. Simulation Results Achieved by the Reversible Invisible Watermarking Scheme

This section outlines the experimental results we have achieved by using our reversible invisible watermarking scheme by considering both Dataset 1 and Dataset 2. Analogously to [18], we have considered the peak-signal-to-noise-ratio (PSNR) [19], to evaluate the distortion between the original image HI and the watermarked one (i.e., HI^W). The PSNR metric is computed as in Equation (4).

$$PSNR(HI, H{I}^W)=\frac{1}{M}{\displaystyle \sum }_{i=1}^M\left(10{\log }_{10}\left(\frac{{(2^{15}-1)}^2}{MSE(H{I}_{(i)}, H{I}_{(i)}^W}\right)\right)$$

(4)

The mean squared error (MSE) instead is defined in Equation (5), in which the notation HI_(i)(x, y) is referred to the pixel at the coordinates (x, y) of the ith band.

$$MSE(H{I}_{(i)}, H{I}_{(i)}^W)=\frac{1}{WH}{\displaystyle \sum }_{x=1}^W{\displaystyle \sum }_{y=1}^H{\left(H{I}_{(i)}(x,y)-H{I}_{(i)}^W(x,y)\right)}^2$$

(5)

In all our experiments, we have considered two watermarks:

• w₁—Composed by 1120 bits (pseudo-random generated)
• w₂—Composed by 2240 bits (pseudo-random generated).

3.2.1. Simulation Results on Dataset 1

In

Table 3. Achieved results in terms of PSNR, by embedding w₁ (Dataset 1).

Scenes	Cuprite	Jasper Ridge	Low Altitude	Lunar Lake	Moffett Field
Scene 01	124.45	123.21	123.40	125.21	123.34
Scene 02	123.03	123.28	122.89	125.13	125.32
Scene 03	124.36	122.45	124.11	124.27	127.09
Scene 04	124.58	122.41	123.75	-	123.28
Scene 05	124.83	122.81	123.72	-	-
Scene 06	-	122.60	123.96	-	-
Scene 07	-	-	123.67	-	-
Scene 08	-	-	123.09	-	-
Average	124.25	122.79	123.57	124.87	124.76

we report, in terms of the PSNR metric, the achieved test simulation results by embedding the watermark w₁ into Dataset 1. The PSNR value of the watermarked image with respect to the original image is reported for each scene (first column) of Cuprite (on the second column), Jasper Ridge (on the third column), Low Altitude (on the fourth column), Lunar Lake (on the fifth column), and Moffett Field (on the sixth column) hyperspectral images. In

Table 4. Achieved results in terms of PSNR, by embedding w₂ (Dataset 1). Notice that by “/”, we refer to the fact that the algorithm failed the embedding process (due to the limited dimensions of the hyperspectral image).

Scenes	Cuprite	Jasper Ridge	Low Altitude	Lunar Lake	Moffett Field
Scene 01	121.18	119.88	119.96	121.85	120.12
Scene 02	119.91	120.37	119.72	121.77	122.18
Scene 03	121.23	119.06	120.60	121.26	123.93
Scene 04	121.44	119.09	120.63	-	120.24
Scene 05	121.76	119.54	120.50	-	-
Scene 06	-	/	120.75	-	-
Scene 07	-	-	120.14	-	-
Scene 08	-	-	119.77	-	-
Average	121.10	119.59	120.26	121.63	121.62

, we report the achieved simulation results by embedding the watermark w₂.

Figure 2 synthetizes the average PSNR results we have achieved by embedding the watermark w₁ (columns in red) and the watermark w₂ (columns in blue), by considering Dataset 1.

3.2.2. Simulation Results on the Dataset 2

In

Table 5. Achieved results in terms of PSNR, by embedding w₁ (Dataset 2).

Scenes	Yellowstone (Calibrated)	Yellowstone (Uncalibrated)	Hawaii (Uncalibrated)	Maine (Uncalibrated)
Scene 00	125.75	119.42	-	-
Scene 03	128.84	122.77	130.45	-
Scene 10	132.42	126.63	-	131.92
Scene 11	127.19	120.36	-	-
Scene 18	125.17	118.55	-	-
Average	127.87	121.55	130.45	131.92

and

Table 6. Achieved results in terms of PSNR, by embedding w₂ (Dataset 2).

Scenes	Yellowstone (Calibrated)	Yellowstone (Uncalibrated)	Hawaii (Uncalibrated)	Maine (Uncalibrated)
Scene 00	122.55	116.18	-	-
Scene 03	125.59	119.45	127.28	-
Scene 10	129.44	123.46	-	128.55
Scene 11	123.63	117.30	-	-
Scene 18	122.11	115.15	-	-
Average	124.66	118.31	127.28	128.55

, the achieved simulation results are reported, in terms of the PSNR metric by embedding the watermark w₁ and the watermark w₂, respectively. The value assumed by the PSNR metric is reported for each scene (first column) of the Yellowstone calibrated (on the second column) and uncalibrated (on the third column), Hawaii (on the fourth column), and Maine (on the sixth column) hyperspectral images.

Figure 3 reports the average PSNR results we have achieved by embedding the watermark w₁ (columns in red) and the watermark w₂ (columns in blue), by considering Dataset 2.

3.3. Simulation Results Achieved by the LBMHI Algorithm

In this section, we focus on the simulation results achieved by the LBMHI algorithm, on Dataset 1 and on Dataset 2, which are comparable with the other state-of-the-art predictive-based approaches [11]. Moreover, it is important to note that the parameters of the LBMHI algorithm can be configured.

Table 7. Achieved results in terms of BPP (Dataset 1).

Hyperspectral Image	Average BPP
	N = 8, B = 1	N = 8, B = 2	N = 16, B = 2
Cuprite	5.0165	4.9886	4.8958
Jasper Ridge	5.0722	5.0271	4.9535
Low Altitude	5.3442	5.2995	5.2166
Lunar Lake	5.0207	4.9796	4.8850
Moffett Field	5.1012	5.0313	4.9594

reports the simulations results, in terms of bits per pixel (BPP), achieved by the LMBHI compression algorithm, for each hyperspectral image of the Dataset 1 (rows from the second to the sixth), by considering the following configurations of the parameters: N = 8 and B = 1 (second column), N = 8 and B = 2 (third column), and N = 16 and B = 2 (fourth column). In

Table 8. Achieved results in terms of BPP (Dataset 2).

Hyperspectral Image	Average BPP
	N = 8, B = 1	N = 8, B = 2	N = 16, B = 2
Yellowstone (calibrated)	3.9511	3.8280	3.9511
Yellowstone (uncalibrated)	6.5262	6.2328	6.5262
Hawaii (uncalibrated)	2.9533	2.8748	2.9533
Maine (uncalibrated)	3.0746	2.9528	3.0746

, we report the experimental results achieved with Dataset 2 in the same manner of the ones reported in Table 7.

4. Conclusions and Future Works

Hyperspectral data are involved in real-life and sensitive applications (e.g., geoscience or military applications). In addition, the acquisition of such data is onerous and expensive. By considering such aspects, it is important to protect them by allowing the verification of the inalterability of these data by a receiver (since such data are often exchanged among several entities).

In this paper, we have focused on the protection and the efficient transmission of hyperspectral data by revisiting a framework for the secure and efficient transmission of hyperspectral images. This framework combines a reversible invisible watermarking scheme and the LMBHI algorithm.

In future work, we will consider the possible design of a hybrid approach which provides protection and compression at the same time, as well as the extension of the proposed framework to other typologies of 3-D data: e.g., 3-D medical images [15], etc.