A Selection Process for Genetic Algorithm Using Clustering Analysis
Abstract
1. Introduction
2. Literature Review
3. Problem Definition
| Algorithm 1: Given the function , to minimize |
|
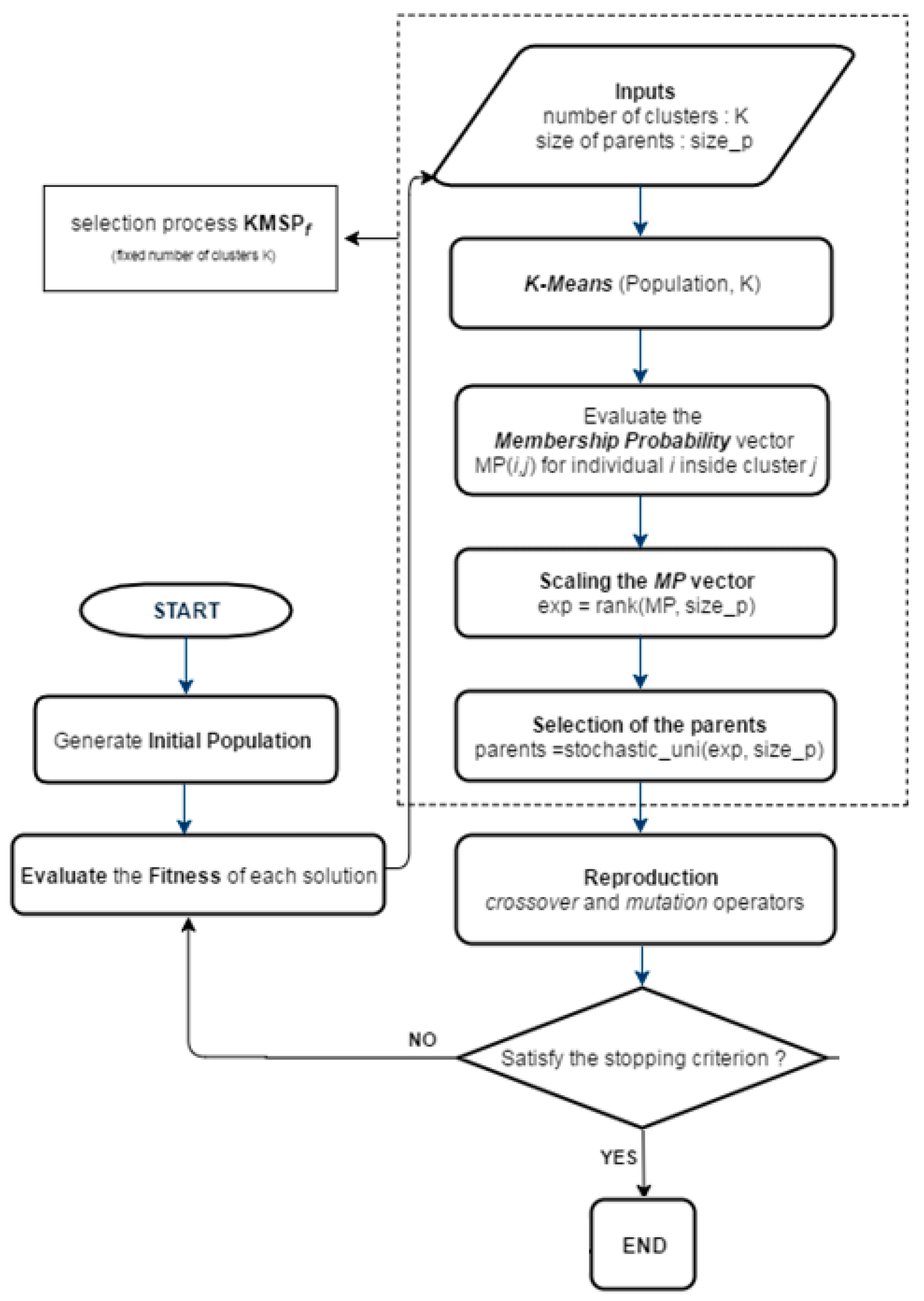
4. The Proposed Algorithm
4.1. KGAf
- 1.
- Choose an initial partition with K clusters.
- 2.
- Generate a new partition by assigning each pattern to its nearest cluster centroid.
- 3.
- Compute new cluster centroids.
- 4.
- If a convergence criterion is not met, repeat steps 2 and 3.
- 5.
- Clustering the population by the k-means algorithm
- 6.
- Computing the membership probability (MP) vector (Equations (2)–(4))
- 7.
- Fitness scaling of MP
- 8.
- Selection of the parents for recombination.
- The sum of the membership probability scores of a given cluster j of size mj is equal to . Consequently, clusters with more individuals will be attributed a larger probability sum.
- An individual with a lower fitness value inside a cluster of size mj is awarded a higher MP score. This is translated in the term, thus allocating fitter solutions a higher probability of selection.
- In order to reduce the probability of recombination between individuals from the same cluster, thus avoiding local optimal traps, fitter individuals in smaller clusters are awarded a higher MP score. This is the direct effect of term.
- The sum of all membership probability scores is equal to one.
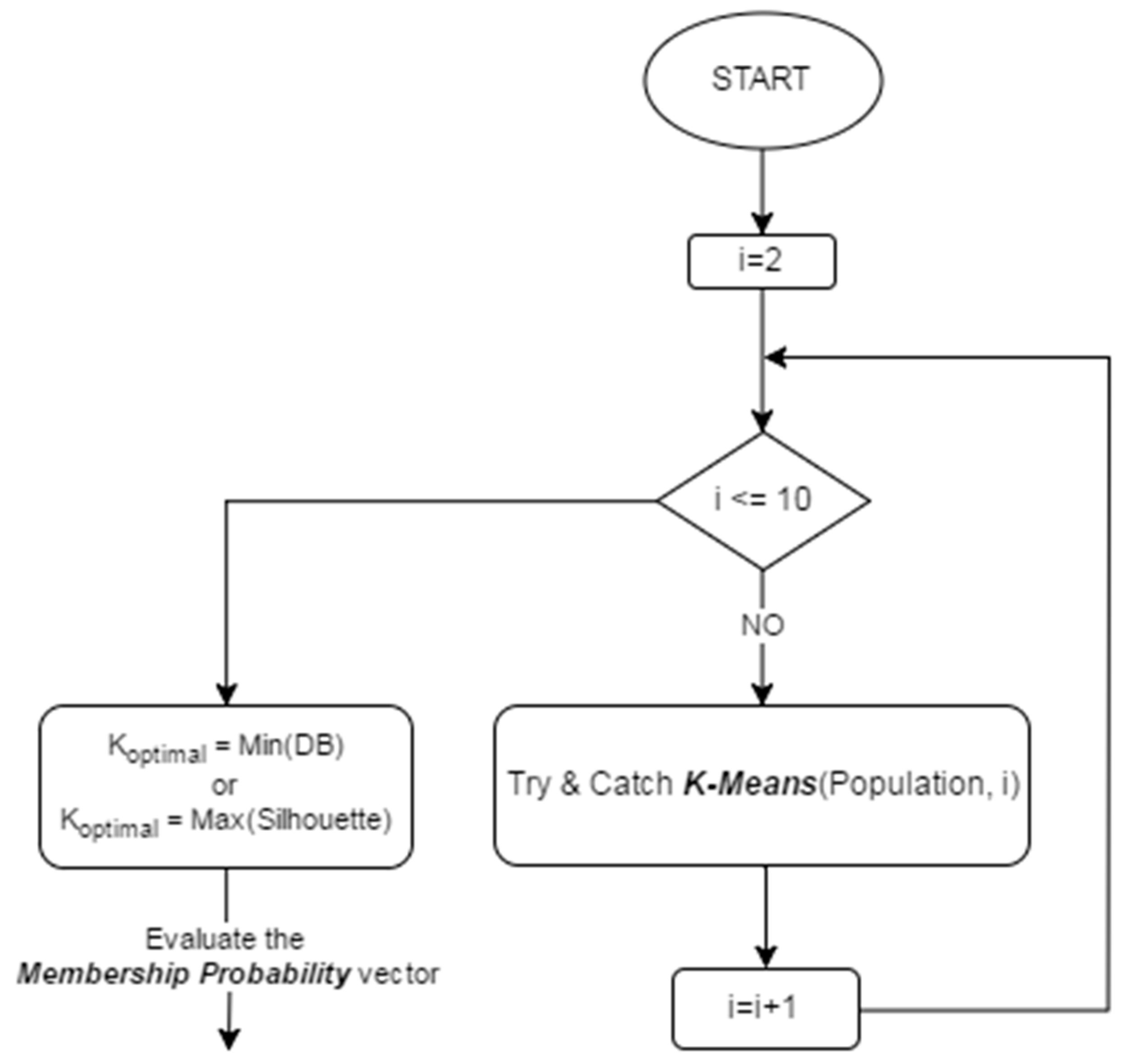
4.2. KGAo
- External criteria: evaluation of the clustering algorithm results is based on previous knowledge about data.
- Internal criteria: clustering results are evaluated using a mechanism that takes into account the vectors of the data set themselves and prior information from the data set is not required.
- Relative criteria: aim to evaluate a clustering structure by comparing it to other clustering schemes.
- In how many clusters can the population be partitioned to?
- Is there a better “optimal” partitioning for our evolving population of chromosomes?
- Compatible Cluster Merging (CCM): starting with a large number of clusters, and successively reducing the number by merging clusters which are similar (compatible) with respect to a similarity criterion.
- Validity Indices (VI’s): clustering the data for different values of K, and using validity measures to assess the obtained partitions.
5. Numerical Simulations
- ;
- ;
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, M.-X.; Zhang, B.; Zheng, Y.-J. Bio-Inspired Meta-Heuristics for Emergency Transportation Problems. Algorithms 2014, 7, 15–31. [Google Scholar] [CrossRef]
- Fister, I.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A brief review of nature-inspired algorithms for optimization. arXiv, 2013; arXiv:1307.4186. [Google Scholar]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yi, J.-H.; Wang, G.-G. A new swarm intelligence approach for clustering based on krill herd with elitism strategy. Algorithms 2015, 8, 951–964. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. B Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Liu, Y.; Xiong, C. An optimization clustering algorithm based on texture feature fusion for color image segmentation. Algorithms 2015, 8, 234–247. [Google Scholar] [CrossRef]
- Sarkar, M.; Yegnanarayana, B.; Khemani, D. A clustering algorithm using an evolutionary programming-based approach. Pattern Recognit. Lett. 1997, 18, 975–986. [Google Scholar] [CrossRef]
- Cura, T. A particle swarm optimization approach to clustering. Expert Syst. Appl. 2012, 39, 1582–1588. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Konar, A. Automatic kernel clustering with a multi-elitist particle swarm optimization algorithm. Pattern Recognit. Lett. 2008, 29, 688–699. [Google Scholar] [CrossRef]
- Yang, F.; Sun, T.; Zhang, C. An efficient hybrid data clustering method based on K-harmonic means and Particle Swarm Optimization. Expert Syst. Appl. 2009, 36, 9847–9852. [Google Scholar] [CrossRef]
- Jiang, H.; Yi, S.; Li, J.; Yang, F.; Hu, X. Ant clustering algorithm with K-harmonic means clustering. Expert Syst. Appl. 2010, 37, 8679–8684. [Google Scholar] [CrossRef]
- Shelokar, P.; Jayaraman, V.K.; Kulkarni, B.D. An ant colony approach for clustering. Anal. Chim. Acta 2004, 509, 187–195. [Google Scholar] [CrossRef]
- Zhang, C.; Ouyang, D.; Ning, J. An artificial bee colony approach for clustering. Expert Syst. Appl. 2010, 37, 4761–4767. [Google Scholar] [CrossRef]
- Maulik, U.; Mukhopadhyay, A. Simulated annealing based automatic fuzzy clustering combined with ANN classification for analyzing microarray data. Comput. Oper. Res. 2010, 37, 1369–1380. [Google Scholar] [CrossRef]
- Selim, S.Z.; Alsultan, K. A simulated annealing algorithm for the clustering problem. Pattern Recognit. 1991, 24, 1003–1008. [Google Scholar] [CrossRef]
- Sung, C.S.; Jin, H.W. A tabu-search-based heuristic for clustering. Pattern Recognit. 2000, 33, 849–858. [Google Scholar] [CrossRef]
- Hall, L.O.; Ozyurt, I.B.; Bezdek, J.C. Clustering with a genetically optimized approach. IEEE Trans. Evolut. Comput. 1999, 3, 103–112. [Google Scholar] [CrossRef]
- Cowgill, M.C.; Harvey, R.J.; Watson, L.T. A genetic algorithm approach to cluster analysis. Comput. Math. Appl. 1999, 37, 99–108. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Genetic algorithm-based clustering technique. Pattern Recognit. 2000, 33, 1455–1465. [Google Scholar] [CrossRef]
- Tseng, L.Y.; Yang, S.B. A genetic approach to the automatic clustering problem. Pattern Recognit. 2001, 34, 415–424. [Google Scholar] [CrossRef]
- Babu, G.P.; Murty, M.N. A near-optimal initial seed value selection in k-means means algorithm using a genetic algorithm. Pattern Recognit. Lett. 1993, 14, 763–769. [Google Scholar] [CrossRef]
- Agustı, L.; Salcedo-Sanz, S.; Jiménez-Fernández, S.; Carro-Calvo, L.; Del Ser, J.; Portilla-Figueras, J.A. A new grouping genetic algorithm for clustering problems. Expert Syst. Appl. 2012, 39, 9695–9703. [Google Scholar] [CrossRef]
- He, H.; Tan, Y. A two-stage genetic algorithm for automatic clustering. Neurocomputing 2012, 81, 49–59. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S.; Mukhopadhyay, A. Multiobjective Genetic Algorithms for Clustering: Applications in Data Mining and Bioinformatics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Razavi, S.H.; Ebadati, E.O.M.; Asadi, S.; Kaur, H. An efficient grouping genetic algorithm for data clustering and big data analysis. In Computational Intelligence for Big Data Analysis; Springer: Berlin, Germany, 2015; pp. 119–142. [Google Scholar]
- Krishnasamy, G.; Kulkarni, A.J.; Paramesran, R. A hybrid approach for data clustering based on modified cohort intelligence and K-means. Expert Syst. Appl. 2014, 41, 6009–6016. [Google Scholar] [CrossRef]
- Popat, S.K.; Emmanuel, M. Review and comparative study of clustering techniques. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 805–812. [Google Scholar]
- Mann, A.K.; Kaur, N. Survey paper on clustering techniques. Int. J. Sci. Eng. Technol. Res. 2013, 2, 803–806. [Google Scholar]
- Jain, A.K.; Maheswari, S. Survey of recent clustering techniques in data mining. Int. J. Comput. Sci. Manag. Res. 2012, 3, 72–78. [Google Scholar]
- Latter, B. The island model of population differentiation: A general solution. Genetics 1973, 73, 147–157. [Google Scholar] [PubMed]
- Qing, L.; Gang, W.; Zaiyue, Y.; Qiuping, W. Crowding clustering genetic algorithm for multimodal function optimization. Appl. Soft Comput. 2008, 8, 88–95. [Google Scholar] [CrossRef]
- Sareni, B.; Krahenbuhl, L. Fitness sharing and niching methods revisited. IEEE Trans. Evolut. Comput. 1998, 2, 97–106. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and their Applications, Nagoya, Japan, 20–22 May 1996; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; pp. 41–49. [Google Scholar]
- Pétrowski, A. A clearing procedure as a niching method for genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 798–803. [Google Scholar]
- Gan, J.; Warwick, K. A genetic algorithm with dynamic niche clustering for multimodal function optimisation. In Artificial Neural Nets and Genetic Algorithms; Springer: Berlin, Germany, 1999; pp. 248–255. [Google Scholar]
- Yang, S.; Li, C. A clustering particle swarm optimizer for locating and tracking multiple optima in dynamic environments. IEEE Trans. Evolut. Comput. 2010, 14, 959–974. [Google Scholar] [CrossRef]
- Blackwell, T.; Branke, J. Multi-swarm optimization in dynamic environments. In Workshops on Applications of Evolutionary Computation; Springer: Berlin, Germany, 2004; pp. 489–500. [Google Scholar]
- Li, C.; Yang, S. A general framework of multipopulation methods with clustering in undetectable dynamic environments. IEEE Trans. Evolut. Comput. 2012, 16, 556–577. [Google Scholar] [CrossRef]
- Li, C.; Yang, S. A clustering particle swarm optimizer for dynamic optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 439–446. [Google Scholar]
- Kennedy, J. Stereotyping: Improving particle swarm performance with cluster analysis. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 1507–1512. [Google Scholar]
- Agrawal, S.; Panigrahi, B.; Tiwari, M.K. Multiobjective particle swarm algorithm with fuzzy clustering for electrical power dispatch. IEEE Trans.Evolut. Comput. 2008, 12, 529–541. [Google Scholar] [CrossRef]
- Zhang, J.; Chung, H.S.-H.; Lo, W.-L. Clustering-based adaptive crossover and mutation probabilities for genetic algorithms. IEEE Trans. Evolut. Comput. 2007, 11, 326–335. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-scale Many-objective Optimization. IEEE Trans. Evolut. Comput. 2016. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, A.; Song, S.; Zhang, Q.; Gao, X.-Z.; Zhang, J. A self-organizing multiobjective evolutionary algorithm. IEEE Trans. Evolut. Comput. 2016, 20, 792–806. [Google Scholar] [CrossRef]
- Vattani, A. The Hardness of K-Means Clustering in the Plane. 2009. Available online: https://cseweb.ucsd.edu/~avattani/papers/kmeans_hardness.pdf (accessed on 1 November 2017).
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; U Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Steinhaus, H. Sur la division des corp materiels en parties. Bull. Acad. Pol. Sci. 1956, 1, 801. [Google Scholar]
- Drineas, P.; Frieze, A.; Kannan, R.; Vempala, S.; Vinay, V. Clustering large graphs via the singular value decomposition. Mach. Learn. 2004, 56, 9–33. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Cluster validity methods: Part I. ACM SIGMM Rec. 2002, 31, 40–45. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Vendramin, L.; Campello, R.J.; Hruschka, E.R. Relative clustering validity criteria: A comparative overview. Stat. Anal. Data Min. 2010, 3, 209–235. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Clustering validity checking methods: Part II. ACM SIGMM Rec. 2002, 31, 19–27. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [PubMed]
- Biswas, S.; Eita, M.A.; Das, S.; Vasilakos, A.V. Evaluating the performance of group counseling optimizer on CEC 2014 problems for computational expensive optimization. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 1076–1083. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Perron, J.; Ilinca, A. A Constraint-Handling Technique for Genetic Algorithms using a Violation Factor. J. Comput. Sci. 2016, 12, 350–362. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 760–766. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
| No. | Functions | Search Ranges | |
|---|---|---|---|
| 1 | shifted sphere | 0 | |
| 2 | shifted ellipsoid | 0 | |
| 3 | shifted and rotated ellipsoid | 0 | |
| 4 | shifted step | 0 | |
| 5 | shifted Ackley | 0 | |
| 6 | shifted Griewank | 0 | |
| 7 | shifted rotated Rosenbrock | 0 |
| Problem | KGAo (S Index) | KGAo (DB Index) | Genetic Algorithm (GA) | KGAf (K = 10) | GCO | |
|---|---|---|---|---|---|---|
| 1 | Best | 8.81 × 10−5 | 1.95 × 10−4 | 2.76 × 10−4 | 5.06 × 10−4 | 3.23 |
| Mean | 2.45 × 10−3 | 5.33 × 10−3 | 8.29 × 10−3 | 2.84 × 10−2 | 1.23 × 101 | |
| Worst | 1.13 × 10−2 | 5.43 × 10−2 | 1.08 × 10−1 | 3.04 × 10−1 | 2.96 × 101 | |
| SD | 2.63 × 10−3 | 8.39 × 10−3 | 1.58 × 10−2 | 5.02 × 10−2 | 6.37 | |
| 2 | Best | 2.91 × 10−4 | 3.34 × 10−4 | 4.60 × 10−4 | 2.08 × 10−3 | 8.46 |
| Mean | 7.12 × 10−3 | 7.12 × 10−3 | 4.75 × 10−2 | 2.09 × 10−1 | 4.14 × 101 | |
| Worst | 6.27 × 10−2 | 4.83 × 10−2 | 7.21 × 10−1 | 3.62 | 2.22 × 102 | |
| SD | 1.07 × 10−2 | 1.06 × 10−2 | 1.17 × 10−1 | 6.13 × 10−1 | 4.61 × 101 | |
| 3 | Best | 5.55 × 10−4 | 2.27 × 10−4 | 5.32 × 10−4 | 3.23 × 10−3 | 1.56 × 101 |
| Mean | 1.01 × 10−2 | 8.24 × 10−3 | 5.01 × 10−2 | 3.12 × 10−1 | 8.85 × 101 | |
| Worst | 5.42 × 10−2 | 7.49 × 10−2 | 2.58 × 10−1 | 2.49 | 2.09 × 102 | |
| SD | 1.25 × 10−2 | 1.46 × 10−2 | 6.73 × 10−2 | 5.63 × 10−1 | 5.54 × 101 | |
| 4 | Best | 4.00 | 2.00 | 1.50 × 10−1 | 3.00 | 3.00 |
| Mean | 9.14 × 101 | 6.48 × 101 | 1.31 × 102 | 6.50 × 101 | 1.00 × 101 | |
| Worst | 3.86 × 102 | 4.19 × 102 | 3.83 × 102 | 2.05 × 102 | 2.70 × 101 | |
| SD | 9.84 × 101 | 8.38 × 101 | 8.88 × 101 | 5.42 × 101 | 6.94 | |
| 5 | Best | 1.48 × 10−3 | 8.42 × 10−3 | 1.21 × 10−2 | 4.01 × 10−2 | 3.92 |
| Mean | 1.50 | 6.55 | 5.15 | 5.62 | 6.36 | |
| Worst | 1.26 × 101 | 1.31 × 101 | 1.24 × 101 | 1.30 × 101 | 9.94 | |
| SD | 2.28 | 4.52 | 3.62 | 4.12 | 1.71 | |
| 6 | Best | 4.94 × 10−2 | 4.97 × 10−2 | 4.95 × 10−2 | 5.04 × 10−2 | 1.24 |
| Mean | 6.41 × 10−2 | 6.32 × 10−2 | 6.38 × 10−2 | 6.96 × 10−2 | 2.11 | |
| Worst | 8.66 × 10−2 | 8.56 × 10−2 | 8.14 × 10−2 | 1.00 × 10−1 | 4.51 | |
| SD | 7.33 × 10−3 | 6.73 × 10−3 | 7.56 × 10−3 | 1.07 × 10−2 | 6.77 × 10−1 | |
| 7 | Best | 2.02 × 10−1 | 3.84 × 10−3 | 1.28 | 1.48 × 10−1 | 4.42 × 101 |
| Mean | 3.77 | 3.65 | 3.22 | 4.60 | 9.28 × 101 | |
| Worst | 7.77 | 8.81 | 5.09 | 1.55 × 101 | 1.80 × 102 | |
| SD | 1.48 | 2.12 | 5.95 × 10−1 | 2.78 | 3.22 × 101 | |
| Problem | KGAo (S Index) | KGAo (DB Index) | Genetic Algorithm (GA) | KGAf (K = 10) | GCO | |
|---|---|---|---|---|---|---|
| 1 | Best | 1.67 × 10−3 | 2.36 × 10−3 | 1.05 | 4.51 × 10−3 | 3.60 × 101 |
| Mean | 1.22 × 10−2 | 1.53 × 10−2 | 1.63 | 1.16 × 10−1 | 1.19 × 101 | |
| Worst | 6.32 × 10−2 | 9.89 × 10−2 | 2.43 | 6.42 × 10−1 | 2.17 × 101 | |
| SD | 1.45 × 10−2 | 1.87 × 10−2 | 3.13 × 10−1 | 1.40 × 10−1 | 5.88 | |
| 2 | Best | 3.76 × 10−3 | 5.68 × 10−3 | 8.99 | 5.01 × 10−2 | 7.79 × 101 |
| Mean | 1.17 × 10−1 | 1.19 × 10−1 | 1.02 × 101 | 4.10 | 9.34 × 101 | |
| Worst | 1.16 | 2.05 | 1.33 × 101 | 2.75 × 101 | 1.79 × 102 | |
| SD | 2.17 × 10−1 | 2.94 × 10−1 | 1.48 | 6.05 | 4.75 × 101 | |
| 3 | Best | 1.96 × 10−1 | 5.50 × 10−3 | 1.49 × 101 | 2.27 × 10−2 | 3.33 |
| Mean | 9.16 × 10−1 | 3.34 × 10−1 | 2.45 × 101 | 2.04 | 1.44 × 102 | |
| Worst | 3.19 | 4.59 | 3.53 × 101 | 1.27 × 101 | 2.62 × 102 | |
| SD | 4.29 × 10−1 | 6.85 × 10−1 | 4.19 | 2.55 | 4.76 × 101 | |
| 4 | Best | 7.00 | 7.00 | 3.19 × 102 | 1.70 × 101 | 3.00 |
| Mean | 7.91 × 101 | 7.52 × 101 | 4.89 × 102 | 8.83 × 101 | 8.48 | |
| Worst | 5.37 × 102 | 3.32 × 102 | 7.23 × 102 | 3.17 × 102 | 1.40 × 101 | |
| SD | 9.23 × 101 | 7.44 × 101 | 9.99 × 101 | 6.41 × 101 | 3.01 | |
| 5 | Best | 1.46 | 1.32 × 10−1 | 9.83 | 1.55 | 1.28 |
| Mean | 6.75 | 5.59 | 1.16 | 5.18 | 4.58 | |
| Worst | 1.26 × 101 | 1.28 × 101 | 1.25 × 101 | 1.20 × 101 | 8.94 | |
| SD | 3.69 | 3.58 | 7.38 × 10−1 | 2.47 | 1.16 | |
| 6 | Best | 1.46 | 1.32 × 10−1 | 9.83 | 1.55 | 1.28 |
| Mean | 6.75 | 5.59 | 1.16 | 5.18 | 4.58 | |
| Worst | 1.26 × 101 | 1.28 × 101 | 1.25 × 101 | 1.20 × 101 | 8.94 | |
| SD | 3.69 | 3.58 | 7.38 × 10−1 | 2.47 | 1.16 | |
| 7 | Best | 1.65 × 10−2 | 1.02 × 10−2 | 7.99 | 5.04 × 10−2 | 3.10 × 101 |
| Mean | 1.87 × 101 | 1.59 × 101 | 2.63 × 101 | 1.96 × 101 | 1.13 × 102 | |
| Worst | 7.54 × 101 | 7.21 × 101 | 6.15 × 101 | 7.85 × 101 | 1.72 × 102 | |
| SD | 2.82 × 101 | 2.75 × 101 | 1.34 × 101 | 2.97 × 101 | 2.67 × 101 | |
| Comparison | R+ | R− | Alpha | z-Score | p-Value |
|---|---|---|---|---|---|
| KGAo (S index)-KGAo (DB index) | 307 | 968 | 0.05 | 3.190 | 1.421 × 10−3 |
| KGAo (S index)-GA | 155 | 1120 | 0.05 | 4.658 | 3.198 × 10−6 |
| KGAo (S index)-KGAf | 74 | 1201 | 0.05 | 5.440 | 5.339 × 10−8 |
| KGAo (DB index)-GA | 451 | 824 | 0.05 | 3.800 | 4.181 × 10−2 |
| KGAo (DB index)-KGAf | 134 | 1141 | 0.05 | 4.860 | 1.170 × 10−6 |
| GA-KGAf | 1275 | 0 | 0.05 | 6.154 | 7.557 × 10−10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chehouri, A.; Younes, R.; Khoder, J.; Perron, J.; Ilinca, A. A Selection Process for Genetic Algorithm Using Clustering Analysis. Algorithms 2017, 10, 123. https://doi.org/10.3390/a10040123
Chehouri A, Younes R, Khoder J, Perron J, Ilinca A. A Selection Process for Genetic Algorithm Using Clustering Analysis. Algorithms. 2017; 10(4):123. https://doi.org/10.3390/a10040123
Chicago/Turabian StyleChehouri, Adam, Rafic Younes, Jihan Khoder, Jean Perron, and Adrian Ilinca. 2017. "A Selection Process for Genetic Algorithm Using Clustering Analysis" Algorithms 10, no. 4: 123. https://doi.org/10.3390/a10040123
APA StyleChehouri, A., Younes, R., Khoder, J., Perron, J., & Ilinca, A. (2017). A Selection Process for Genetic Algorithm Using Clustering Analysis. Algorithms, 10(4), 123. https://doi.org/10.3390/a10040123






