Abstract
This article presents a newly proposed selection process for genetic algorithms on a class of unconstrained optimization problems. The k-means genetic algorithm selection process (KGA) is composed of four essential stages: clustering, membership phase, fitness scaling and selection. Inspired from the hypothesis that clustering the population helps to preserve a selection pressure throughout the evolution of the population, a membership probability index is assigned to each individual following the clustering phase. Fitness scaling converts the membership scores in a range suitable for the selection function which selects the parents of the next generation. Two versions of the KGA process are presented: using a fixed number of clusters K (KGAf) and via an optimal partitioning Kopt (KGAo) determined by two different internal validity indices. The performance of each method is tested on seven benchmark problems.
1. Introduction
The fields of computational intelligence and optimization algorithms have grown rapidly in the past few decades. Classical methods are not efficient in solving current problems in engineering such as energy, transportation and management [1]. The development of these optimization algorithms can be mainly divided into deterministic and stochastic approaches [2].
Most conventional algorithms are deterministic, such as gradient-based algorithms that use the function values and their derivatives. These methods work extremely well for smooth unimodal problems, but in the case of some discontinuities, non-gradient algorithms are preferred [3]. Nelder–Mead downhill simplex [4] and Hooke–Jeeves pattern search technique [5] are a few examples of deterministic gradient-free algorithms. For stochastic algorithms, we have two types: heuristic and meta-heuristic. Although there is no agreed definition of each type in the literature, the aim of stochastic methods is to find feasible solutions in a satisfactory timescale. There is no guarantee that the best solutions can be found; however, it is expected that the algorithm will provide nearly optimal solutions most of the time.
In this paper, we propose a genetic algorithm (GA)-based algorithm that uses clustering analysis to organize the population and select the parents for recombination. Cluster analysis is the study of techniques and algorithms to organize data into sensible groupings (clusters) according to measured or apparent similarities [6]. Clustering has been successfully applied in various engineering and scientific disciplines such as biology, medicine, machine learning, pattern recognition, image analysis and data mining [7,8]. The performance of a newly proposed selection process named the k-means genetic algorithm selection process is investigated on a class of unconstrained optimization problems. The KGA technique is composed of four essential stages: clustering, membership phase, fitness scaling and selection. The authors postulate that clustering the evolving population can help preserve a continuous selection pressure throughout the evolution process. A membership probability index is allocated to each individual following the clustering phase. Fitness scaling alters the membership scores into a range suitable for the selection function, which selects the parents of the succeeding generation. Two versions of the KGA technique are examined: using a fixed number of clusters K (KGAf) and via an optimal number of clusters Kopt (KGAo). The performance of each method is tested on eight benchmark problems. The numerical simulations reveal that the proposed selection process is superior to or competitive with the standard GA for the given problems.
The remainder of the paper is organized as follows: The next section summarizes some relevant studies that have explored clustering analysis in optimization algorithms. Section 3 presents important definitions on genetic algorithm. Section 4 presents the selection processes (KGAf and KGAo) proposed in this paper. Section 5 contains the numerical simulations where the performance of the proposed approaches is demonstrated. Finally, Section 6 concludes with some final remarks and possible future contributions.
2. Literature Review
There are many algorithms that have been proposed in literature to solve the clustering problems. Some relevant studies that have explored the problem of clustering using various approaches include evolutionary algorithms such as evolutionary programing [9], particle swarm optimization [10,11,12], ant colony algorithms [13,14], artificial bee colony [15], simulated annealing [16,17] and tabu search [18]. Conversely, there have been many attempts to use GAs to solve clustering applications [7,19,20,21,22,23,24,25,26,27]. Maulik and Bandyopadhyay [21] proposed a GA approach to clustering. They tested the performance of the algorithm on synthetic and real-life data sets. The GA-k-means algorithm was used to search for the cluster centres which minimize the clustering metric, showing results significantly superior to those of the k-means algorithm. Another genetic algorithm approach, the genetic k-means algorithm, was presented by Krishna and Murty [7]; they defined a mutation operator specific to clustering problems. Recently, a novel optimization algorithm was proposed by Krishnasamy [28] referred to as K-MCI, inspired by the natural and social tendency of cohort individuals to learn from one another.
Since the novelty of the proposed algorithm revolves around the notion of introducing clustering analysis in the selection stage of the genetic algorithm, this section will avoid a survey of clustering techniques. The reader is referred to [29,30,31] for detailed surveys of clustering algorithms. Consequently, in the remainder of this section, we will review the most relevant optimization algorithms that have introduced clustering analysis in one way or another.
In the process of genetic differentiation, the population subdivided was discussed in the literature. For instance, the island model [32] divides the population into discrete finite races, between which some migration occurs. The hypothesis is that multiple subpopulations help preserve a better genetic diversity, since each island can potentially follow a different search trajectory through the search space. Various “islands” conserve some degree of independence and therefore explore different regions of the search space while sharing some information by migration. On the other hand, various niching methods have been introduced into GAs to promote the formation of stable sub-populations in neighborhood of optimal solutions [33]. There are many commonly adopted techniques, such as deterministic crowding [34], sharing [35], clearing [36] and dynamic niche clustering [37]. Standard and deterministic crowding both suffer from genetic drift. In sharing and clearing methods, prior knowledge about the fitness landscape is required to set the niche radius. The set of cluster numbers in dynamic niche clustering will largely affect the quality and quantity of optimal solutions.
Many researchers have investigated evolutionary algorithms for dynamic optimization problems (DOPs) because EAs are fundamentally inspired from biological evolution, which is always subject to an ever-varying environment. From the literature on DOPs, the traditional approaches use the multi-population method to find the optimum solutions for multi-modal functions. The core notion is to divide the search space into different sub-spaces, and then separately search within these sub-spaces. The challenge with these multi-population methods (such as [38,39,40]), is how to choose an appropriate number of sub-populations to cover the entire search space. Three major difficulties arise using multi-population methods: how to guide the particles towards different promising sub-regions, how to define sub-regions and how many sub-populations are required. In order to overcome these questions, a clustering particle swarm optimizer (CPSO) was proposed in [38,41]. In the CPSO algorithm, a proper number of sub-swarms which cover different local regions are created using a clustering method. A hierarchical clustering method is used to locate and track multiple optima and a fast-local search method is employed to find the near optimal solutions in a promising region in the search space. Kennedy [42] originally proposed a PSO algorithm that uses a k-means clustering algorithm to identify the centers of different clusters of particles in the population, and then uses the centers to substitute the personal best or neighborhood best positions. The limitation of this approach lies in that the number of clusters must be predefined. Similarly, a fuzzy clustering-based particle swarm (FCPSO) algorithm was proposed in [43] to solve multiobjective environmental/economic dispatch. The clustering in the FCPSO technique ensures that the obtained Pareto front will have uniform diversity at all stages of the search.
In [44], clustering analysis was applied to adjust the probabilities of crossover px and mutation pm in GAs. By applying the k-means algorithm, the population is clustered in each generation and a fuzzy system is used to adjust the values of the genetic operators. Regulations are based on considering the relative size between the clusters holding the best and worst chromosomes respectively.
Zhang et al. [45] tackled the problem of large-scale many-objective optimization problems based on a decision variable clustering method. The proposed technique divides the decision variables into two clusters based on the features of each variable. The decision variable clustering method adopts the k-means method to divide the decision variables into two types: convergence-related variables and diversity-related variables.
Recently, a self-organizing multiobjective evolutionary algorithm [46] was evaluated on some state-of-the-art multiobjective evolutionary methods. A local PCA partitions the given population into several disjointed clusters, and conducts PCA in each cluster to extract a continuous manifold and build a probabilistic model.
3. Problem Definition
In essence, the basic objective of any clustering algorithm is to find a global or approximate optimal for combinatorial optimization problems which are NP-hard [47]. The k-means algorithm is very likely to converge to a suboptimal partition. The main advantage of stochastic optimization techniques over deterministic-methods is that they are able to avoid convergence to a local optimal solution. Therefore, stochastic approaches have been employed to solve clustering problems; algorithms such as simulated annealing, genetic algorithms, evolution strategies and evolutionary programming. Inspired by the principles of natural selection and biological evolution, evolutionary algorithms seek to optimize a population of individuals by applying a set of evolutionary operators. They are population-based meta-heuristic optimization algorithms that make use of biological evolution operators such as selection, recombination and mutation.
In order to demonstrate the novelty in the use of clustering analysis in the selection process of the genetic algorithm, the performance of the proposed KGA techniques will be compared with existing GA methods. They were originally proposed by Holland [48], inspired by the principle of natural selection of biological systems or ‘Darwinian evolution’. GAs have demonstrated their capability to solve a wide range of optimization problems such as revenue management, optimal engineering system designs, scheduling applications, image processing, quality control etc. John Holland essentially laid the foundation of modern evolutionary computing by fundamentally defining three key genetic operators: crossover, mutation, and selection. These evolutionary operators provide a way to generate offspring from parent solutions.
We summarize the fundamental steps of genetic algorithms in Algorithm 1. In genetic algorithms, each individual (or solution vector) is encoded as either a binary bit string or a real-value vector, both referred to as a chromosome. The standard representation of each individual is a binary array of bits, to facilitate the crossover and mutation operations.
| Algorithm 1: Given the function , to minimize |
|
An initial population is generated according to a heuristic rule or randomly. The population size typically depends on the nature of the optimization problem. Often, the initial population is generated in such a way as to allow a larger range of possible solutions inside the given search space. If the population size is too small, there is not enough evolution going on and consequently there is a risk of premature convergence towards a local optimum and ultimately extinction of the population. However, a larger population will require more computational time and fitness evaluations.
At each successive generation, a percentage of the existing population is ‘selected’ to breed a new generation, thus ensuring the continuity of the population. Thus, a selection function chooses ‘parents’ based on a fitness-based selection process, where ‘fitter’ solutions are more likely to be selected. An individual can be selected more than once, in which case it transfers its genes to more than one offspring.
At each generation, the GA uses the current generation to create the new offspring that will define the next generation. The algorithm will apply a set of genetic operators (crossover and mutation) on the parents selected by the selection function to generate the children. Recombination (or crossover) is the combination of a pair of parents, analogous to biological reproduction. Mutated children are created by a random change (or mutation) of the genes of a single parent. Both genetic operators are essential for the success of the optimization search. Crossover enables the algorithm to preserve the best genes from different individuals and recombine them into possibly fitter children. This allows a better ‘exploitation’ of the search space. Whereas mutation increases the diversity of the population and permits a further ‘exploration’ of the search domain. The crossover probability is usually between 0.7 and 1.0, while the mutation probability is lower 0.001~0.05. Mutation probability is dependent upon the representation type and number of genes. For instance, for an n bit representation, the suggested mutation rate is 1/n. In natural systems, if the mutation rate is too high under a high selection pressure, the population might become extinct. A suitable elitist selection function must be employed to avoid loss of good solutions. Selection, crossover and mutation are iteratively applied to the population until a stopping condition is satisfied.
Introducing the concept of clustering analysis in an evolutionary algorithm is inspired from the notion that clustering the evolving population can help avoid excessive exploitation and therefore escape local optimum (local minimum or local maximum). The role of clustering analysis is to improve the probability of discovering the global optimum by sufficiently covering the solution space (exploration) yet ensuring sufficient pressure to obtain even better solutions from current individuals (exploitation).
Furthermore, in practical multimodal domains problems, it is desirable to evaluate several global optima or some local optima that might be suitable alternatives to the global optima. Traditional genetic algorithms perform well on single optimum problems but fail to provide multiple solutions. By combining the strength of clustering analysis and genetic search, the proposed KGA techniques permit the evaluation of multimodal functions. A detailed explanation of the proposed KGA technique is considered in the next section.
4. The Proposed Algorithm
The following section presents a brief description of the proposed k-means genetic selection processes. We are interested in the unconstrained optimization problems in which we attempt to find which optimizes using GA-based algorithms. Therefore, only the standard GA will be used to test the performance of the proposed KGA algorithms. Below, two distinct selection techniques KGAf and KGAo are presented.
4.1. KGAf
The proposed KGA is different to the standard GA in several ways. Primary, the chromosomes of the population are partitioned into groups in such a way that all individuals inside the same cluster are similar. This offers a novel approach to solve the two important issues in the evolution process of the genetic search: exploitation and exploration. Exploration is responsible for population diversity by exploring the search space, while exploitation attempts to reduce the diversity by focusing on individuals with higher fitness scores. Strong exploitation encourages premature convergence of the genetic search. Recombining individuals inside the same cluster reduces population diversity, and thus clustering the population can allow an enhanced balance between exploitation and exploration.
The aim of clustering is to find a given structure among the series of data and is therefore exploratory in nature [49]. The task of organizing a set of data using cluster analysis requires some dissimilarity measurement among the set of patterns. The dissimilarity metric is defined according to the nature of the data and the purpose of the analysis. Many types of clustering algorithms have been proposed; the reader is referred to [49,50,51,52] for a taxonomy of clustering techniques, discussions on major challenges and key issues and useful surveys of recent advances. The simplest and most popular clustering algorithm is the k-means algorithms (KMA), and was originally published by Steinhaus [53] in 1956. Even though it was first proposed 60 years ago, it is still the most widely used algorithm for clustering.
A general definition of clustering can be stated as follows: given a set of data composed on n objects, find K groups in such a way that the measure of similarities between objects in the same group is low while the similarities between objects in different groups are high.
The k-means algorithm attempts to find a partition such that the squared error between the empirical mean of a cluster and the objects in the cluster is minimized. The goal is to minimize the sum of the squared error J over all K clusters, as follows:
where is the set of N d-dimensional points to be clustered into K clusters, and the mean of cluster .
Minimizing the k-means objective function is an NP-hard problem (even for K = 2) [54], and therefore the algorithm can only converge to local minima. The main steps of the k-means algorithm can be summarized as follows:
- 1.
- Choose an initial partition with K clusters.
- 2.
- Generate a new partition by assigning each pattern to its nearest cluster centroid.
- 3.
- Compute new cluster centroids.
- 4.
- If a convergence criterion is not met, repeat steps 2 and 3.
In the KGAf algorithm, the number of clusters is kept the same throughout the evolution process. The four main stages of KGAf are as follows:
- 5.
- Clustering the population by the k-means algorithm
- 6.
- Computing the membership probability (MP) vector (Equations (2)–(4))
- 7.
- Fitness scaling of MP
- 8.
- Selection of the parents for recombination.
In general, we want to maintain an even selection pressure during the evolution of the genetic search. At the beginning, the search may be bias towards high fitness individuals. Near the end of the search, as the population is converging towards an optimal solution, there may not be much separation among individuals in the population. Neither situation is desirable, thus there is a necessity to scale the fitness in such a manner to keep the selection pressure the same throughout in the population.
The membership probability score of an individual is a measurement of its affiliation with respect to both designated and external clusters (Equation (2)). For a given solution i inside a cluster j of size mj, the membership probability index is calculated as follows:
and
where P is the population size and is the sum of the fitness values inside cluster j.
The key characteristics that are associated with the use of the membership probability function are the following:
- The sum of the membership probability scores of a given cluster j of size mj is equal to . Consequently, clusters with more individuals will be attributed a larger probability sum.
- An individual with a lower fitness value inside a cluster of size mj is awarded a higher MP score. This is translated in the term, thus allocating fitter solutions a higher probability of selection.
- In order to reduce the probability of recombination between individuals from the same cluster, thus avoiding local optimal traps, fitter individuals in smaller clusters are awarded a higher MP score. This is the direct effect of term.
- The sum of all membership probability scores is equal to one.
Fitness scaling converts the membership scores in a range suitable for the selection function which selects the parents of the next generation. The selection function allocates a higher probability of selection to individuals with higher scaled values.
The range of the scaled values can affect the performance of the genetic algorithm. If the scaled values vary too extensively, higher scaled value individuals will reproduce too rapidly and prevent the GA from searching other regions in the search space. In contrast, for lower scaled value variations, all individuals will have an equal chance of reproduction and therefore will result in very slow search progress.
The general framework of the proposed KGAf algorithm is shown in Figure 1 below.
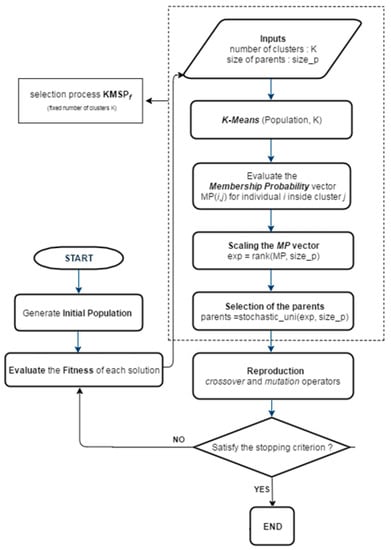
Figure 1.
Flowchart of the proposed KGAf technique.
4.2. KGAo
It is obvious that a problem we face in the KGAf algorithm is to decide the optimal number of clusters. Visual verification of a large multidimensional data set (e.g., more than three) is difficult [55]. In order to find the optimal clustering scheme that best fits the inherent partitions of the data set, the concept of clustering validation has been subject to numerous research efforts. The fundamental concepts, drawbacks and applications of clustering validation techniques were discussed in [55,56,57,58].
In essence, there are three main approaches to examine cluster validity:
- External criteria: evaluation of the clustering algorithm results is based on previous knowledge about data.
- Internal criteria: clustering results are evaluated using a mechanism that takes into account the vectors of the data set themselves and prior information from the data set is not required.
- Relative criteria: aim to evaluate a clustering structure by comparing it to other clustering schemes.
The KGAo attempts to answer the following questions:
- In how many clusters can the population be partitioned to?
- Is there a better “optimal” partitioning for our evolving population of chromosomes?
Two main approaches to determining the suitable number of clusters for a given data set can be distinguished:
- Compatible Cluster Merging (CCM): starting with a large number of clusters, and successively reducing the number by merging clusters which are similar (compatible) with respect to a similarity criterion.
- Validity Indices (VI’s): clustering the data for different values of K, and using validity measures to assess the obtained partitions.
The CCM approach requires more computational operations than the use of a validity index to determine the optimal number of clusters. Moreover, the size of the evolving population is small (less than or equal to 100 chromosomes), therefore there is no need to apply a CCM approach. On the other hand, the validity index is not a clustering algorithm itself, but rather a measurement of the results and thus suggests a scheme that best fits the data set. At each generation in the proposed KGAo technique, the optimal number of clusters is calculated using a validity assessment index. Different validity indices suitable for k-means clustering have been proposed in the literature.
In this paper, two different internal validity indices are applied in the KGAo technique: Silhouette [59] and the Davies–Bouldin index [60] as explained in Figure 2 below.
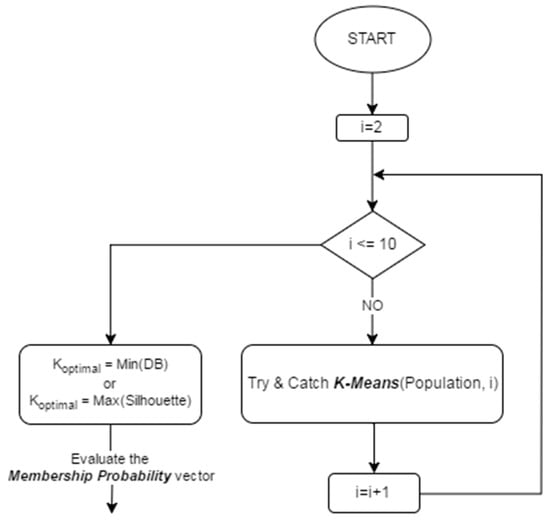
Figure 2.
Search for the optimal number of clusters.
• Silhouette (S) [59]
The silhouette technique assigns to the ith vector of cluster cj (j = 1, …, K), a quality measure known as the silhouette width defined as S:
and
where a(i) is the average distance between the ith vector and the remaining elements inside the same cluster j of size , b(i) is the minimum average distance between vector i and all elements inside clusters ck (k = 1, … K; k ≠ j). The optimal partition is expected to minimize the intra-group distance a while maximizing the inter-group distance b, thus maximizing the silhouette width criterion S.
• Davies–Bouldin (DB) [60]
The DB index aims to evaluate intra-cluster similarity and inter-cluster differences by computing the following:
where and are each the sum of all the distances between the centroid of the cluster and the elements of clusters i and j respectively, is the distance between centroids of cluster and . A good partition composed of compact and separated clusters is represented by a small DB value. The Davies–Bouldin index presents decent results for dissimilar groups. However, it is not intended to handle overlapping clusters [27].
Throughout the KGAo technique, the evaluation of the validity index function is performed within a range of cluster numbers and then an optimal number is chosen. For instance, if the Silhouette index is applied, the number of clusters which maximizes S corresponds to the optimal partition, whereas the minimum DB value determines the optimal number of clusters for the clustering of the population. Since the size of the population is small, the maximum number of partitions is set to ten. Consequently, the search for the optimal partition varies between i = 2 (the minimum number of clusters) and i = 10, as per Figure 2.
5. Numerical Simulations
In this section, the performance of KGA techniques on seven well-known test functions is investigated. In recent years, various kinds of novel computational intelligence methods have been proposed and the field is attracting more and more attention. To promote research on expensive optimization, the CEC 2014 special session competition developed a set of benchmark optimization problems.
All test functions are minimization problems defined as follows:
D dimension of the search space.
Most functions are shifted by , randomly distributed in . Some problems are rotated by a predefined rotation matrix M (Table 1). Each rotation matrix is generated from standard normally distributed entries by Gram–Schmidt ortho-normalization with condition number equal to one or two.

Table 1.
Summary of the test functions.
- ;
- ;
Results of the KGA techniques (KGAo-S, KGAo-DB and KGAf) were taken for D = 10 and 20 and are compared to those of the standard genetic algorithm GA and the Group Counseling Optimizer (GCO) [61] presented at the IEEE Congress on Evolutionary computation (CEC 2014). In all experiments, common parameters such as population number, maximum generation number and stopping criterion were the same for all algorithms. Population sizes of 50 and 100 were selected for dimensions 10 and 20 respectively. Each experiment is repeated 50 times to obtain the statistical features of the algorithms. A system with an Intel core i7 2.9 GHz processor and 4.096 GB RAM is used for implementing the MATLAB code for the proposed KGA techniques. All algorithms run the same number of fitness evaluations equal to 15,000 for D = 10 and 20,000 for D = 20, to ensure a fair comparison.
The statistical results of the test problems are shown in Table 2 and Table 3. The GCO outperformed the proposed techniques in only one data set (test = 4, D = 20). In all other cases, the best solution was obtained with either the KGAo-S or the KGAo-DB. This demonstrates the significant feasibility and efficiency of the proposed techniques over the standard GA. Although the average runtime of each experiment was increased by 10–15%, the KGA techniques ensured a broader and more exhaustive search and prevent premature death of potential solutions.

Table 2.
Comparison of statistical results of four algorithms for test problems 1–7 of dimensions D = 10.

Table 3.
Comparison of statistical results of four algorithms for test problems 1–7 of dimensions D = 20.
The KGA methods implement an efficient partitioning of the population. They extend the diversity by intensifying the scope of the search process and reducing less favourable solutions. The recombination of two similar solutions will more likely generate a descendant with homogenous chromosomes. The evaluation of the membership probability vector inside the proposed selection process guarantees a more fitting parent selection.
In addition, the elitism strategy that results from partitioning the population into a number of clusters ensures that best solutions are always carried forward to the next generation. In fact, rather than obtaining one elite solution, K-strong optimal solutions are generated in each generation. In the long run, this enhances the exploration of future generations and reduces the possibility of premature convergence at local minima. The latter was recorded with the standard GA in problems 4–7 especially. Unlike the KGAf, the KGAo-S and KGAo-DB are designed in such a way that there are no additional parameters to be fine-tuned.
The most frequently used statistical tests to determine significant differences between two computational intelligence algorithms are the t-test and Wilcoxon signed-ranks test [62]. The later is a non-parametric counterpart of the paired t-test, which ranks the differences in performances of two algorithms over each data set. In brief, the test omits the signs, and compares the ranks for the positive and the negative differences. The differences are ranked based on their absolute values and in case of ties average ranks are calculated.
A Wilcoxon test is used for pairwise comparisons between the following pairs of algorithms: KGAo (S index)-KGAo (DB index), KGAo (S index)-GA, KGAo (S index)-KGAf, KGAo (DB index)-GA, KGAo (DB index)-KGAf, GA-KGAf for test function seven (refer to Table 4).

Table 4.
p-Values for the Wilcoxon test in paired comparisons for test number 7.
As we can see, the p-values obtained by the paired Wilcoxon test indicate that the algorithms behave differently, since all p-values are less than the level of significance α = 0.05.
6. Conclusions and Future Work
A k-means Genetic Selection (KGA) is proposed to solve multimodal function optimization problems. Two different versions of the KGA technique were presented: using a fixed number of clusters K (KGAf) and via an optimal number Kopt (KGAo). In the latter, the optimal number of clusters is determined using two validity indexes: Silhouette and Davies–Bouldin. The KGA techniques are composed of four stages: clustering, membership phase, fitness scaling and selection. Clustering the population aids the search algorithm to preserve a selection pressure throughout the evolution. A membership probability number is assigned to each individual following the k-mean clustering phase. Fitness scaling converts the membership scores in a range suitable for the selection function which selects the parents of the next generation. The performance of each KGA technique (KGAo-S, KGAo-DB and KGAf) is tested on seven benchmark problems for two separate dimensions of the search spaces D = 10 and 20. Traditional GAs perform well on single optimum problems but fail to provide multiple solutions. By combining the strength of clustering analysis and genetic search, the proposed KGA techniques permit the evaluation of multimodal functions. The computational results reveal that the proposed selection process is superior to or competitive with the standard genetic algorithm for the problems considered.
In the current study, combining the strengths of evolutionary computation and data mining were limited to single-objective optimization problems. Future research could test the performance of KGA techniques in solving constrained optimization problems and/or multiobjective formulations [63]. The stability of the novel selection processes should also be considered in future work. It would be compelling to integrate the KGA processes in further population-based optimization algorithms such as particle swarm optimization (PSO) [64], ant colony optimization (ACO) [65] and firefly algorithm (FA) [66]. Lastly, larger-scale examples should be tested and further research on the impact of GA parameters (such as population size, probabilities of crossover and mutation) on the KGA process will be examined.
Acknowledgments
The authors greatly acknowledge the Fonds de Recherche Nature et Technologie (FRQNT), Université du Québec à Chicoutimi (UQAC), Anti-Icing Materials International Laboratory (AMIL), Laboratoire de recherche en énergie éolienne (LREE), École Doctorale des Sciences et de la Technologie (EDST), Lebanese University (LU) and the MMC team for their support.
Author Contributions
Adam Chehouri is responsible for the testing, validation and development of the algorithm under the supervision and guidance of Rafic Younes. The initial concept of the algorithm was proposed by Rafic Younes. Jean Perron, Adrian Ilinca and Jihan Khoder were scientific advisors. All of the authors contributed for the publication of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, M.-X.; Zhang, B.; Zheng, Y.-J. Bio-Inspired Meta-Heuristics for Emergency Transportation Problems. Algorithms 2014, 7, 15–31. [Google Scholar] [CrossRef]
- Fister, I.; Yang, X.-S.; Fister, I.; Brest, J.; Fister, D. A brief review of nature-inspired algorithms for optimization. arXiv, 2013; arXiv:1307.4186. [Google Scholar]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yi, J.-H.; Wang, G.-G. A new swarm intelligence approach for clustering based on krill herd with elitism strategy. Algorithms 2015, 8, 951–964. [Google Scholar] [CrossRef]
- Krishna, K.; Murty, M.N. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. B Cybern. 1999, 29, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Liu, Y.; Xiong, C. An optimization clustering algorithm based on texture feature fusion for color image segmentation. Algorithms 2015, 8, 234–247. [Google Scholar] [CrossRef]
- Sarkar, M.; Yegnanarayana, B.; Khemani, D. A clustering algorithm using an evolutionary programming-based approach. Pattern Recognit. Lett. 1997, 18, 975–986. [Google Scholar] [CrossRef]
- Cura, T. A particle swarm optimization approach to clustering. Expert Syst. Appl. 2012, 39, 1582–1588. [Google Scholar] [CrossRef]
- Das, S.; Abraham, A.; Konar, A. Automatic kernel clustering with a multi-elitist particle swarm optimization algorithm. Pattern Recognit. Lett. 2008, 29, 688–699. [Google Scholar] [CrossRef]
- Yang, F.; Sun, T.; Zhang, C. An efficient hybrid data clustering method based on K-harmonic means and Particle Swarm Optimization. Expert Syst. Appl. 2009, 36, 9847–9852. [Google Scholar] [CrossRef]
- Jiang, H.; Yi, S.; Li, J.; Yang, F.; Hu, X. Ant clustering algorithm with K-harmonic means clustering. Expert Syst. Appl. 2010, 37, 8679–8684. [Google Scholar] [CrossRef]
- Shelokar, P.; Jayaraman, V.K.; Kulkarni, B.D. An ant colony approach for clustering. Anal. Chim. Acta 2004, 509, 187–195. [Google Scholar] [CrossRef]
- Zhang, C.; Ouyang, D.; Ning, J. An artificial bee colony approach for clustering. Expert Syst. Appl. 2010, 37, 4761–4767. [Google Scholar] [CrossRef]
- Maulik, U.; Mukhopadhyay, A. Simulated annealing based automatic fuzzy clustering combined with ANN classification for analyzing microarray data. Comput. Oper. Res. 2010, 37, 1369–1380. [Google Scholar] [CrossRef]
- Selim, S.Z.; Alsultan, K. A simulated annealing algorithm for the clustering problem. Pattern Recognit. 1991, 24, 1003–1008. [Google Scholar] [CrossRef]
- Sung, C.S.; Jin, H.W. A tabu-search-based heuristic for clustering. Pattern Recognit. 2000, 33, 849–858. [Google Scholar] [CrossRef]
- Hall, L.O.; Ozyurt, I.B.; Bezdek, J.C. Clustering with a genetically optimized approach. IEEE Trans. Evolut. Comput. 1999, 3, 103–112. [Google Scholar] [CrossRef]
- Cowgill, M.C.; Harvey, R.J.; Watson, L.T. A genetic algorithm approach to cluster analysis. Comput. Math. Appl. 1999, 37, 99–108. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Genetic algorithm-based clustering technique. Pattern Recognit. 2000, 33, 1455–1465. [Google Scholar] [CrossRef]
- Tseng, L.Y.; Yang, S.B. A genetic approach to the automatic clustering problem. Pattern Recognit. 2001, 34, 415–424. [Google Scholar] [CrossRef]
- Babu, G.P.; Murty, M.N. A near-optimal initial seed value selection in k-means means algorithm using a genetic algorithm. Pattern Recognit. Lett. 1993, 14, 763–769. [Google Scholar] [CrossRef]
- Agustı, L.; Salcedo-Sanz, S.; Jiménez-Fernández, S.; Carro-Calvo, L.; Del Ser, J.; Portilla-Figueras, J.A. A new grouping genetic algorithm for clustering problems. Expert Syst. Appl. 2012, 39, 9695–9703. [Google Scholar] [CrossRef]
- He, H.; Tan, Y. A two-stage genetic algorithm for automatic clustering. Neurocomputing 2012, 81, 49–59. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S.; Mukhopadhyay, A. Multiobjective Genetic Algorithms for Clustering: Applications in Data Mining and Bioinformatics; Springer: Berlin, Germany, 2011. [Google Scholar]
- Razavi, S.H.; Ebadati, E.O.M.; Asadi, S.; Kaur, H. An efficient grouping genetic algorithm for data clustering and big data analysis. In Computational Intelligence for Big Data Analysis; Springer: Berlin, Germany, 2015; pp. 119–142. [Google Scholar]
- Krishnasamy, G.; Kulkarni, A.J.; Paramesran, R. A hybrid approach for data clustering based on modified cohort intelligence and K-means. Expert Syst. Appl. 2014, 41, 6009–6016. [Google Scholar] [CrossRef]
- Popat, S.K.; Emmanuel, M. Review and comparative study of clustering techniques. Int. J. Comput. Sci. Inf. Technol. 2014, 5, 805–812. [Google Scholar]
- Mann, A.K.; Kaur, N. Survey paper on clustering techniques. Int. J. Sci. Eng. Technol. Res. 2013, 2, 803–806. [Google Scholar]
- Jain, A.K.; Maheswari, S. Survey of recent clustering techniques in data mining. Int. J. Comput. Sci. Manag. Res. 2012, 3, 72–78. [Google Scholar]
- Latter, B. The island model of population differentiation: A general solution. Genetics 1973, 73, 147–157. [Google Scholar] [PubMed]
- Qing, L.; Gang, W.; Zaiyue, Y.; Qiuping, W. Crowding clustering genetic algorithm for multimodal function optimization. Appl. Soft Comput. 2008, 8, 88–95. [Google Scholar] [CrossRef]
- Sareni, B.; Krahenbuhl, L. Fitness sharing and niching methods revisited. IEEE Trans. Evolut. Comput. 1998, 2, 97–106. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Proceedings of the Second International Conference on Genetic Algorithms on Genetic Algorithms and their Applications, Nagoya, Japan, 20–22 May 1996; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; pp. 41–49. [Google Scholar]
- Pétrowski, A. A clearing procedure as a niching method for genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 798–803. [Google Scholar]
- Gan, J.; Warwick, K. A genetic algorithm with dynamic niche clustering for multimodal function optimisation. In Artificial Neural Nets and Genetic Algorithms; Springer: Berlin, Germany, 1999; pp. 248–255. [Google Scholar]
- Yang, S.; Li, C. A clustering particle swarm optimizer for locating and tracking multiple optima in dynamic environments. IEEE Trans. Evolut. Comput. 2010, 14, 959–974. [Google Scholar] [CrossRef]
- Blackwell, T.; Branke, J. Multi-swarm optimization in dynamic environments. In Workshops on Applications of Evolutionary Computation; Springer: Berlin, Germany, 2004; pp. 489–500. [Google Scholar]
- Li, C.; Yang, S. A general framework of multipopulation methods with clustering in undetectable dynamic environments. IEEE Trans. Evolut. Comput. 2012, 16, 556–577. [Google Scholar] [CrossRef]
- Li, C.; Yang, S. A clustering particle swarm optimizer for dynamic optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 439–446. [Google Scholar]
- Kennedy, J. Stereotyping: Improving particle swarm performance with cluster analysis. In Proceedings of the IEEE Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; pp. 1507–1512. [Google Scholar]
- Agrawal, S.; Panigrahi, B.; Tiwari, M.K. Multiobjective particle swarm algorithm with fuzzy clustering for electrical power dispatch. IEEE Trans.Evolut. Comput. 2008, 12, 529–541. [Google Scholar] [CrossRef]
- Zhang, J.; Chung, H.S.-H.; Lo, W.-L. Clustering-based adaptive crossover and mutation probabilities for genetic algorithms. IEEE Trans. Evolut. Comput. 2007, 11, 326–335. [Google Scholar] [CrossRef]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A Decision Variable Clustering-Based Evolutionary Algorithm for Large-scale Many-objective Optimization. IEEE Trans. Evolut. Comput. 2016. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, A.; Song, S.; Zhang, Q.; Gao, X.-Z.; Zhang, J. A self-organizing multiobjective evolutionary algorithm. IEEE Trans. Evolut. Comput. 2016, 20, 792–806. [Google Scholar] [CrossRef]
- Vattani, A. The Hardness of K-Means Clustering in the Plane. 2009. Available online: https://cseweb.ucsd.edu/~avattani/papers/kmeans_hardness.pdf (accessed on 1 November 2017).
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; U Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. (CSUR) 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Steinhaus, H. Sur la division des corp materiels en parties. Bull. Acad. Pol. Sci. 1956, 1, 801. [Google Scholar]
- Drineas, P.; Frieze, A.; Kannan, R.; Vempala, S.; Vinay, V. Clustering large graphs via the singular value decomposition. Mach. Learn. 2004, 56, 9–33. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Cluster validity methods: Part I. ACM SIGMM Rec. 2002, 31, 40–45. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Vendramin, L.; Campello, R.J.; Hruschka, E.R. Relative clustering validity criteria: A comparative overview. Stat. Anal. Data Min. 2010, 3, 209–235. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Clustering validity checking methods: Part II. ACM SIGMM Rec. 2002, 31, 19–27. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [PubMed]
- Biswas, S.; Eita, M.A.; Das, S.; Vasilakos, A.V. Evaluating the performance of group counseling optimizer on CEC 2014 problems for computational expensive optimization. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 1076–1083. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Perron, J.; Ilinca, A. A Constraint-Handling Technique for Genetic Algorithms using a Violation Factor. J. Comput. Sci. 2016, 12, 350–362. [Google Scholar] [CrossRef]
- Kennedy, J. Particle swarm optimization. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 760–766. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).