Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension
Abstract
:1. Introduction
2. Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension
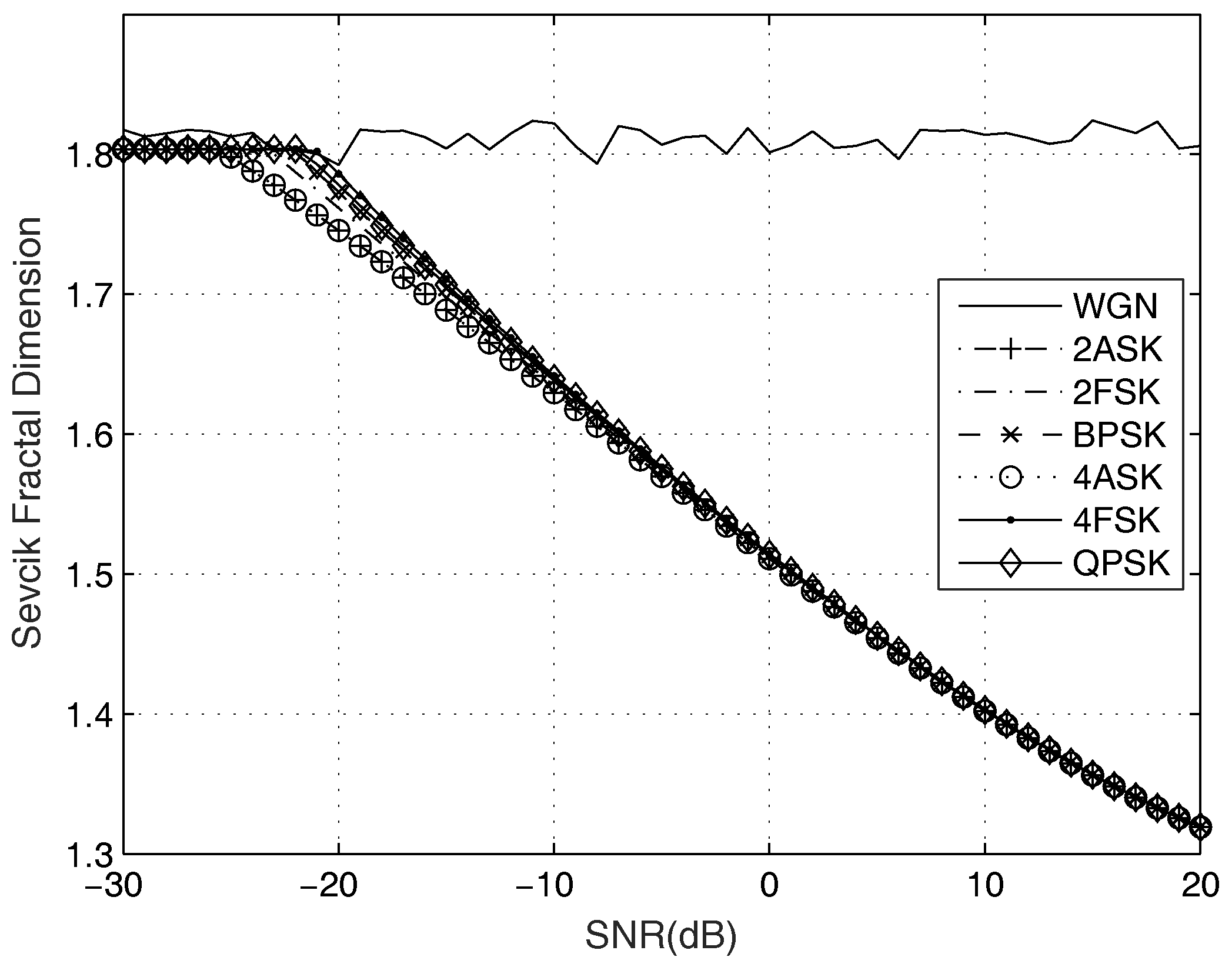
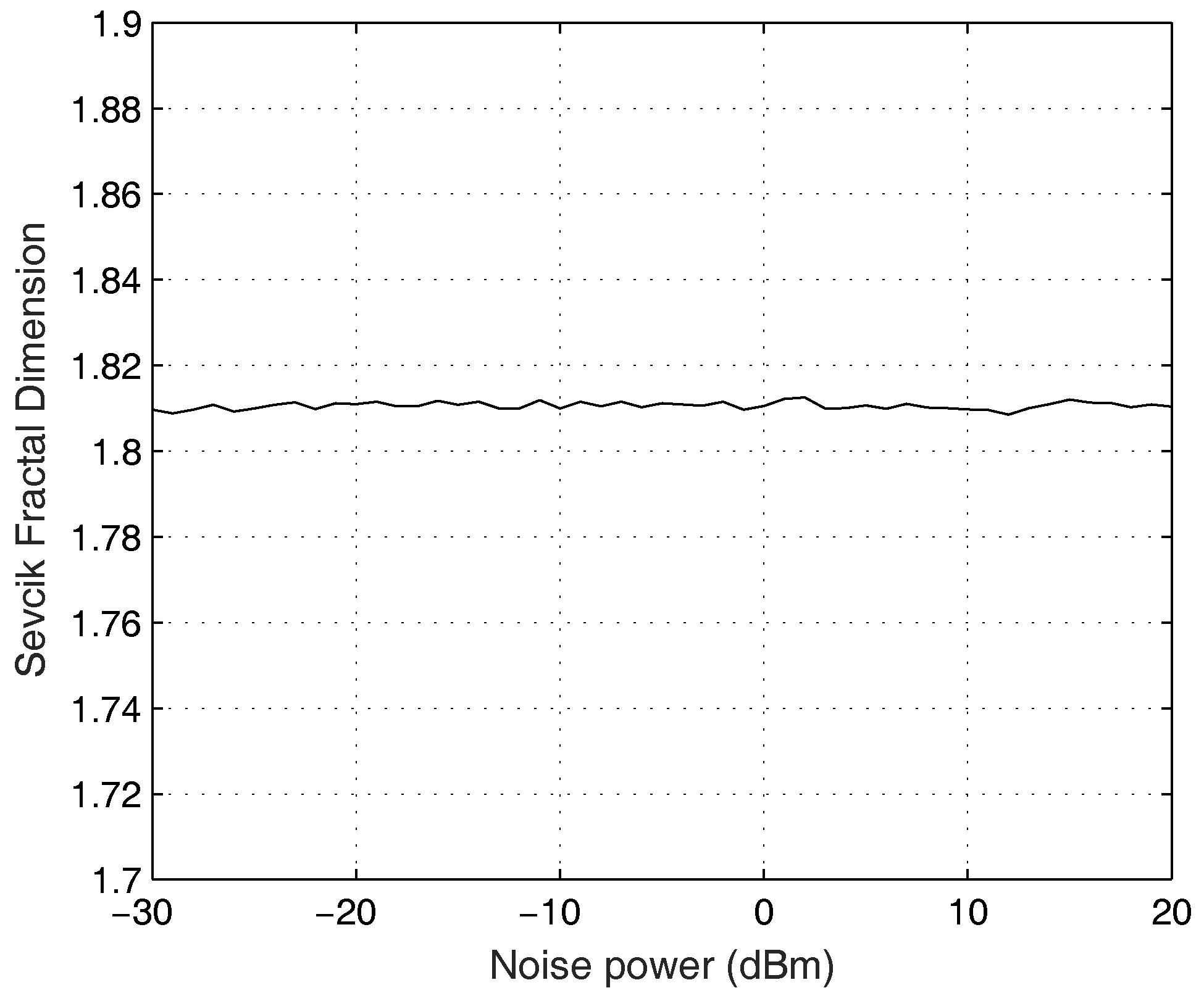
2.1. The Noise Sevcik Fractal Dimension
2.2. System Model of the Proposed Algorithm
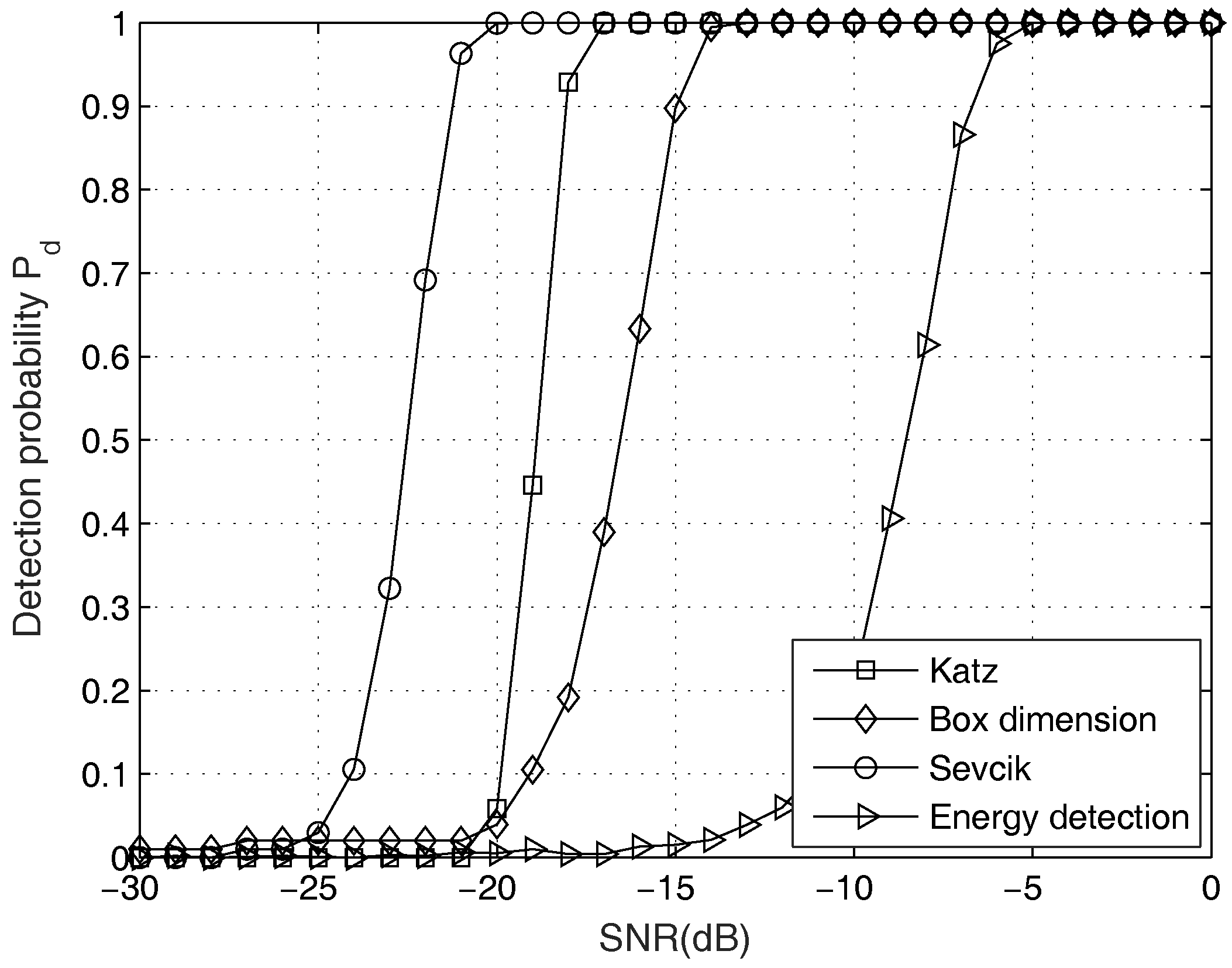
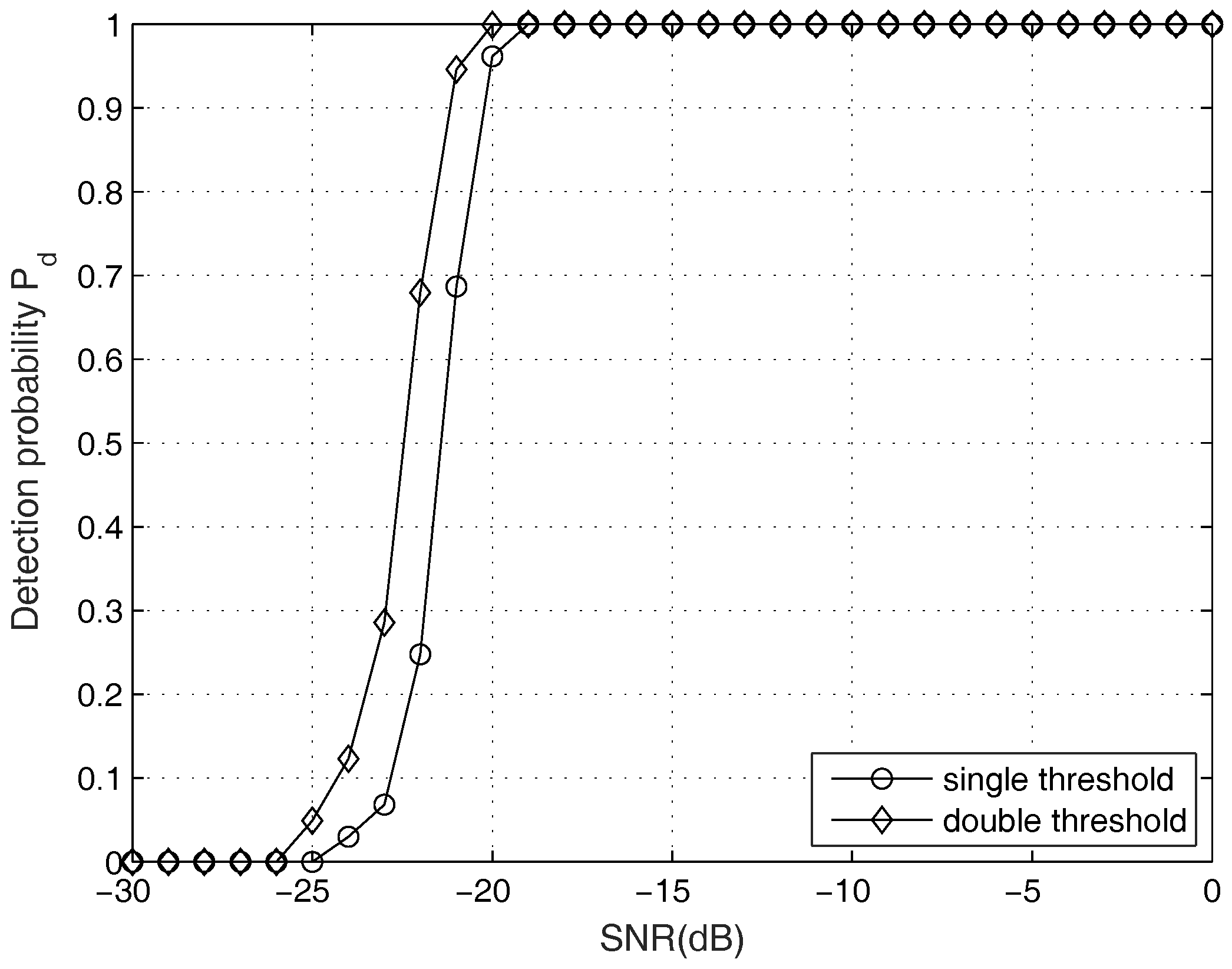
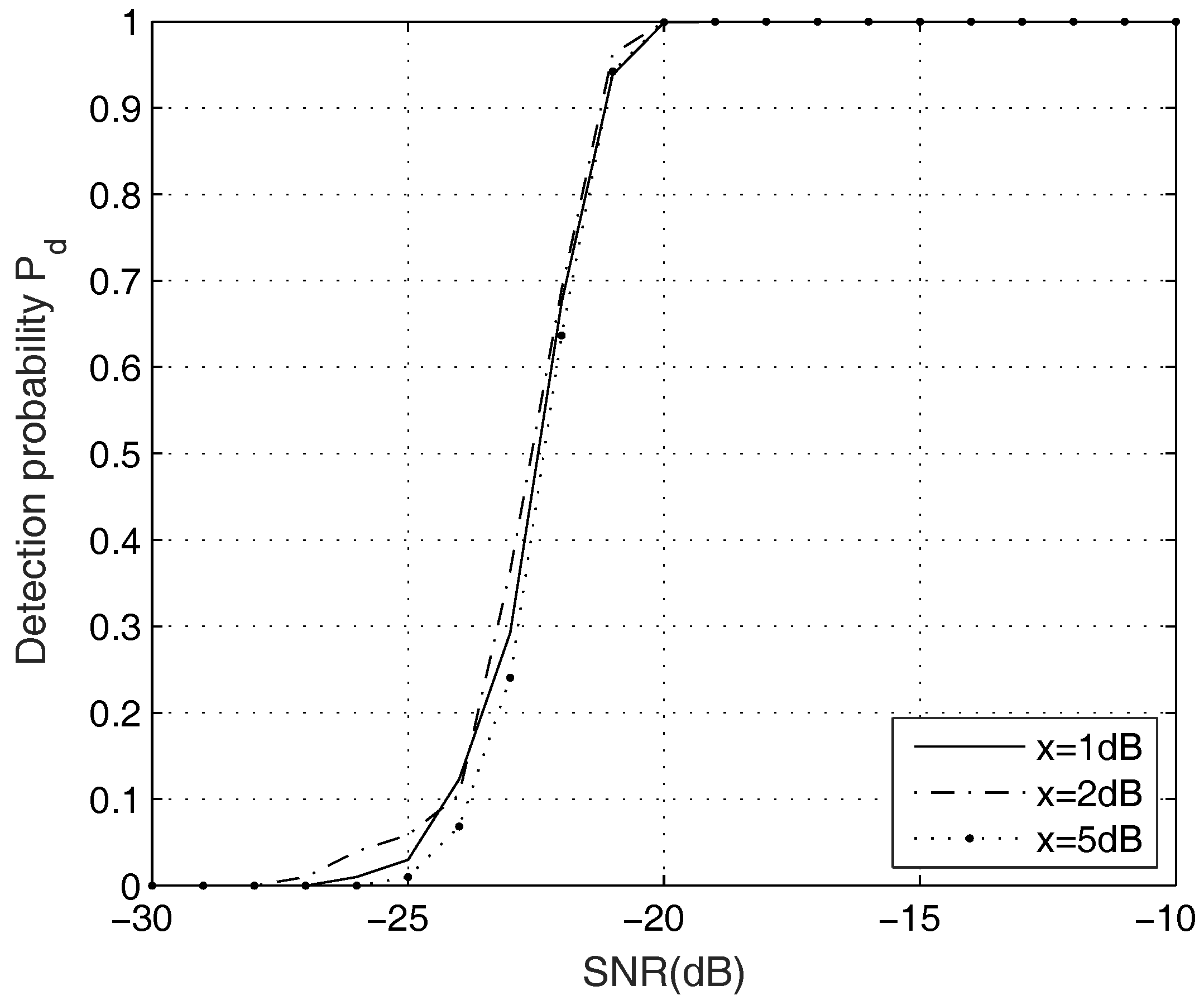
3. Simulation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Visotsky, E.; Kuffner, S.; Peterson, R. On collaborative detection of TV transmissions in support of dynamic spectrum sharing. In Proceedings of the IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 338–345. [Google Scholar]
- Guzzon, E.; Benedetto, F.; Giunta, G. Performance improvements of OFDM signals spectrum sensing in cognitive radio. In Proceedings of the IEEE Vehicular Technology Conference, Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar]
- Sobron, I.; Diniz, P.S.R.; Martins, W.A.; Velez, M. Energy detection technique for adaptive spectrum sensing. IEEE Trans. Commun. 2015, 63, 617–627. [Google Scholar] [CrossRef]
- Matinmikko, M.; Rauma, T.; Mustonen, M.; Del Ser, J. Architecture and Approach for Obtaining Spectrum Availability Information. In Proceedings of the IEEE Vehicular Technology Conference, Yokohama, Japan, 15–18 May 2011; pp. 1–5. [Google Scholar]
- Del Ser, J.; Alonso, A.; Gil-Lopez, S.; Garay, M.; Kretzschmar, U.; Astarloa, A. On the Design of an Heuristically Optimized Multiband Spectrum Sensing Approach for Cognitive Radio Systems. In Proceedings of the IEEE 17th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks, Barcelona, Spain, 17–19 September 2012; pp. 168–169. [Google Scholar]
- Lee, W.Y.; Akyildiz, I.F. Optimal Spectrum Sensing Framework for Cognitive Radio Networks. IEEE Trans. Commun. 2008, 7, 3845–3857. [Google Scholar]
- Benedetto, F.; Giunta, G.; Guzzon, E.; Renfors, M. Detection of hidden users in cognitive radio networks. In Proceedings of the IEEE the International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 8–11 September 2013; pp. 2296–2300. [Google Scholar]
- Benedetto, F.; Tedeschi, A.; Giunta, G. Cooperative spectrum sensing for positioning in cognitive radios. In Proceedings of the 11th International Symposium on Wireless Communications Systems, Barcelona, Spain, 26–29 August 2014; pp. 670–674. [Google Scholar]
- Althunibat, S.; Granelli, F. Energy efficiency analysis of soft and hard cooperative spectrum sensing schemes in cognitive radio networks. In Proceedings of the IEEE Vehicular Technology Conference, Seoul, Korea, 18–21 May 2014; pp. 1–5. [Google Scholar]
- Yang, M.; Li, Y.; Liu, X.; Tang, W. Cyclostationary feature detection based spectrum sensing algorithm under complicated electromagnetic environment in cognitive radio networks. China Commun. 2015, 12, 35–44. [Google Scholar] [CrossRef]
- Sevcik, C. A procedure to Estimate the Fractal Dimension of Waveforms. arXiv 2010, arXiv:1003.5266. Available online: https://arxiv.org/abs/1003.5266 (accessed on 18 August 2017).
- Diaz, M.H.; Cordova, F.M.; Canete, L. Order and Chaos in the Brain: Fractal Time Series Analysis of the EEG Activity During a Cognitive Problem Solving Task. Procedia Comput. Sci. 2015, 55, 1410–1419. [Google Scholar] [CrossRef]
- Esteller, R.; Vachtsevanos, G.; Echauz, J.; Litt, B. A comparison of waveform fractal dimension algorithms. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 177–183. [Google Scholar] [CrossRef]
- Kordan, S.B.; Abolhassani, B. Blind spectrum sensing for cognitive radio based on complexity measurement. In Proceedings of the Iranian Conference on Electrical Engineering, Tehran, Iran, 17–19 May 2011; pp. 1–4. [Google Scholar]
- Wang, R.L.; Huang, Y.; Zhang, J.Z.; Zhang, Y.C. Dynamic Cooperative Sensing Based on Fractal Dimension. Comput. Eng. 2012, 38, 89–92. [Google Scholar]
- Liu, W.T.; Chen, H.; Cai, X.X.; Yuan-Hong, W.U. Step Cooperative Spectrum Sensing Based on Related Box Dimension. Electr. Inf. Warf. Technol. 2014, 6, 97–99. [Google Scholar]
- Chen, X.; Chen, H.; Liu, J.; Cai, X. Cooperative Spectrum Sensing Based on Double Threshold Box Dimension and Information Dimension. J. Detect. Control 2011, 33, 72–76. [Google Scholar]
- Shuang, F.U.; Li, Y.B.; Ye, F.; Gao, Z.G. Fast blind spectrum sensing using Sevcik fractal dimension in frequency domain. J. Jilin Univ. 2014, 44, 854–860. [Google Scholar]



| Fractal Dimension Schemes | Threshold 1 | Threshold 2 | Correction |
|---|---|---|---|
| Sevcik | |||
| Katz | |||
| Box dimension |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diao, X.; Dong, Q.; Yang, Z.; Li, Y. Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension. Algorithms 2017, 10, 96. https://doi.org/10.3390/a10030096
Diao X, Dong Q, Yang Z, Li Y. Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension. Algorithms. 2017; 10(3):96. https://doi.org/10.3390/a10030096
Chicago/Turabian StyleDiao, Xueying, Qianhui Dong, Zijian Yang, and Yibing Li. 2017. "Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension" Algorithms 10, no. 3: 96. https://doi.org/10.3390/a10030096
APA StyleDiao, X., Dong, Q., Yang, Z., & Li, Y. (2017). Double-Threshold Cooperative Spectrum Sensing Algorithm Based on Sevcik Fractal Dimension. Algorithms, 10(3), 96. https://doi.org/10.3390/a10030096




