Abstract
We investigate the efficiency of multi-step Newton method (the classical Newton method in which the first derivative is re-evaluated periodically after m steps) for solving nonlinear equations, . We highlight the following property of multi-step Newton method with respect to some other Newton-type method: for a given n, there exist thresholds of m, that is an interval , such that for m inside of this interval, the efficiency index of multi-step Newton method is better than that of other Newton-type method. We also search for optimal values of m.
1. Introduction
There is currently an increasing interest in developing iterative methods for solving systems of nonlinear equations, , with high order of convergence by using only the first derivative of F and its inverse. We will use the term “Newton-type method” for such an iterative procedure. A typical example of Newton-type method is the multi-step Newton method (other terms, “modified Newton method”, “multi-step frozen Jacobian version of the Newton method” [1], etc.) in which the first derivative of F is re-evaluated periodically after m steps. If x denotes the current iteration, the next iteration is obtained by the following scheme:
The method has high convergence order, equal to , and the computational cost is due by the inner steps for the computation of . This cost can be estimated by the total number d of functional evaluations of F and (in our case ). The efficiency of the method can be then measured by the Ostrowski index of efficiency, given by , where is the convergence order. A more accurate measurement of efficiency is the Traub index of efficiency, given by the same formula, but for which d is now the total number of arithmetical operations (usually products/divisions) necessary to obtain the next iteration (in our case , that is, operations for factorization and operations for solving the triangular systems [2]).
A plethora of high order Newton-type methods also exist, in which the inner steps do not involve any loop calculation, such as, for example, the four order Jarratt method [3], the fifth order “M5” method [2] and sixth order WKG method [4] (these methods will be used in this note as test examples). It is worth mentioning that M5 method has excellent computational properties (convergence order and complexity) and, as a consequence, a high efficiency index.
The particular case was considered by Potra and Ptak [5]. Using non-discrete induction, they proved the order three of convergence and gave sharp a priori and a posteriori error for this particular case. Often it is called “Potra-Ptak” method [6,7]. In the case of a single equation, Potra-Ptak method was considered by Traub [8] (1982). Ortega and Rheinboldt [9] proved order three of convergence for Potra-Ptak method in n-dimensional spaces (Theorem 10.2.4, [9]). Note that Potra-Ptak method is a particular case of a multipoint iterative process with order three of convergence considered by Ezquerro and Hernandez [10].
Numerical experiments show that the Ostrowski/Traub efficiency index of multi-step Newton method has the following property with respect to the other Newton-type method: Under some conditions, for given n, there exists an interval , such that for m inside of this interval, the efficiency index of multi-step Newton method is better than that of considered Newton-type method. We say that are the thresholds of m, inferior and superior, respectively. This property was tested experimentally by the author for several high order Newton-type methods, like classical Newton, Jarratt, M5, WKG.
In this paper, we give a simple condition ensuring that this property holds for some class of Newton-type methods. In particular, this condition is verified by classical Newton method and M5 method.
2. The Threshold
Lemma 1.
Let be the real function in two variables defined by
where is the natural logarithm. Then for any the equation has a unique solution .
Proof.
The proof involves simple elementary calculus, such that some details are omitted.
We have
Suppose that
then . Therefore, there exists such that . The solution of the equation is unique in . Indeed, the derivative of g with respect to m is and the function g is strictly decreasing on . ☐
Remark 1.
Suppose that, for some n and some , the following is true
Then (the proof is elementary). Note that, for given p, (1) is not satisfied for any n, but it is satisfied on some interval of n, usually very large when . For example, if then this interval is ; if then the interval is .
We consider next an iterative method of Newton-type which has as convergence order and which uses only the first derivative and its inverse in inner steps. Jarratt, M5 and WKG methods are examples of such Newton-type method. The main processing consists of the solution of one or several linear systems having the first derivative as matrix. The total number of products/divisions of such a method is given by , where and P is a polynomial of degree 2.
The theorem below gives a comparative analysis of Traub efficiency indexes of multi-step Newton method and this Newton-type method. Recall that the Traub efficiency index of multi-step Newton method, is:
Theorem 1.
Consider a Newton-type method with the convergence order and the number of products/divisions . Suppose that, for a given n, the following condition is satisfied
where is defined in Lemma 1. Then there exist the thresholds such that
Proof.
The derivative of with respect to m is
Thus, for any n, and from Lemma 1 it results that on and on . Therefore is strictly increasing on and strictly decreasing on . For we have
and from (2) we obtain
As
and , for m sufficiently large, we have
From (3) and (4) it results that there exists as superior threshold.
Next we have to consider two cases:
- (1)
- ; in this case for and is the inferior threshold of m.
- (2)
- ; then this inequality and (3) imply that there exists such that for , that is is inferior threshold of m.
☐
The graphs of indexes for the three cases are given in Figure 1.
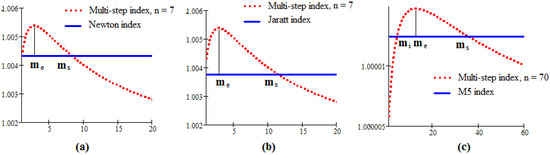
Figure 1.
The Traub efficiency indexes. (a) classical Newton method; (b) Jarratt method; (c) M5 method.
The case is illustrated by classical Newton method (Figure 1a), the case , by Jarratt method (Figure 1b) and the case , by M5 method (Figure 1c).
Remark 2.
It is desirable that condition (2) to be satisfied for a large interval of n, or even for all n. If (1) is satisfied for some n and p, then the condition (2) can be replaced by the following stronger condition
The condition (5) is easier to check, but it gives a more restrictive interval for n.
Particular Cases
We check that the condition (2) is satisfied for classical Newton method and for M5 method and therefore Theorem 1 can be applied.
It is easy to see that in the case of Newton method, the condition (2) is satisfied for all n. The stronger condition (5) gives for n the interval . For example, if then the threshold for m is
In the case of M5 method, the condition (2) is satisfied for all . The stronger condition (5) gives for n the interval . For example, if then the thresholds for m are ,
3. On the Optimal Number of Inner Steps in Multi-Step Newton Method
In [2] M5 method is compared with three high order method, Newton, Jarratt and WKG, and with respect to the both Ostrowski and Traub indexes. It is shown that the M5 method has better efficiency than all these methods. The previous analysis shows that the multi-step Newton method has still better Traub efficiency index, provided that and m belong to the interval . The following two problems arise: 1. Is there an m, independent of n, such that the multi-step Newton index is larger that M5 index? 2. Is there an optimal number of multi-step Newton method for which the difference between the index of the multi-step Newton and the index of M5 method is maxim?
Both problems have affirmative answers.
- Several numerical tests show that the sequence is a decreasing sequence as n increases (the proof is elementary). Therefore we can take for m the larger term of the sequence , which is . Therefore for (Figure 2).
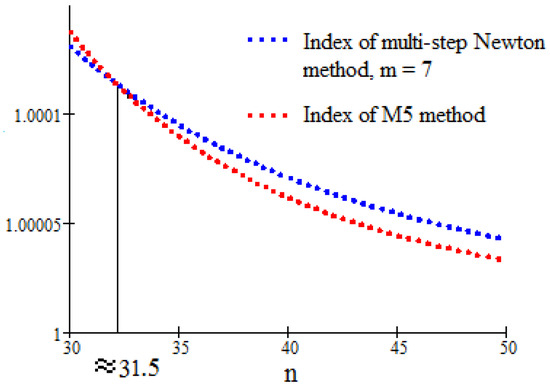 Figure 2. The graphs of indexes of multi-step Newton and M5 methods.
Figure 2. The graphs of indexes of multi-step Newton and M5 methods. - Let I be the efficiency index of some iterative methods of Newton-type. The optimal value of the number of inner steps in multi-step Newton method with respect to some I, is the value of for which is maximum. The properties of functions and I (for all considered cases) show that such optimal value exists and is unique.
For example, if (the Newton method) the value of m for which is maximum, is (Ostrowski index) and (Traub index). Thus . We can conclude that the Potra-Ptak method is the most efficient method with respect to the classical Newton method.
In the case of M5 method the optimal value is (Traub index).
Remark 3.
The efficiency indexes of Newton-type methods tend to value 1 when . Thus, these indexes differ slightly from each other, even for n not very large. For example, if , the thresholds of multi-step Newton method with respect to M5 method are and the maximum of for is obtained by and has the value . The maximum efficiency index of Potra-Ptak method, for the same value of n, is . Therefore, the efficiency index increases very little from Potra-Ptak method to the most efficient Newton-type method, approx in percent.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ullah, M.Z.; Ahmad, F.; Alshomrani, A.S.; Alzahrani, A.K.; Alghamadi, M.S.; Ahmad, S.; Ahmad, S. Frozen Jacobian iterative method for solving systems of nonlinear equations: Application to nonlinear IVPs and BVPs. J. Nonlinear Sci. Appl. 2016, 9, 6021–6033. [Google Scholar]
- Cordero, A.; Hernandez-Veron, M.A.; Romero, N.; Torregrosa, I.R. Semilocal convergence by using recurrence relations for a fifth-order method in Banach spaces. J. Comput. Appl. Math. 2015, 273, 205–213. [Google Scholar] [CrossRef]
- Jarrat, P. Some fourth order multipoint iterative methods for solving equations. Math. Comput. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Wang, X.; Kou, I.; Gu, C. Semilocal convergence for a sixth-order Jarratt method in Banach spaces. Numer. Algorithms 2011, 57, 441–456. [Google Scholar] [CrossRef]
- Potra, F.A.; Ptak, V. Nondiscrete Induction and Iterative Proccesses; Pitman: London, UK, 1984. [Google Scholar]
- Soleymani, F. Optimal eighth-order simple root-finders free from derivative. WSEAS Trans. Inf. Sci. Appl. 2011, 8, 293–299. [Google Scholar]
- Thukral, R. New modification of Newton method with third order of convergence for solving nonlinear equation of type f(0) = 0. Am. J. Comput. Appl. Math. 2016, 6, 14–18. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Chelsea Publishing Company: New York, NY, USA, 1982. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equation in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Ezquerro, J.A.; Hernandez, M.A. An optimization of Chebyshev’s method. J. Complex. 2009, 25, 343–361. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).