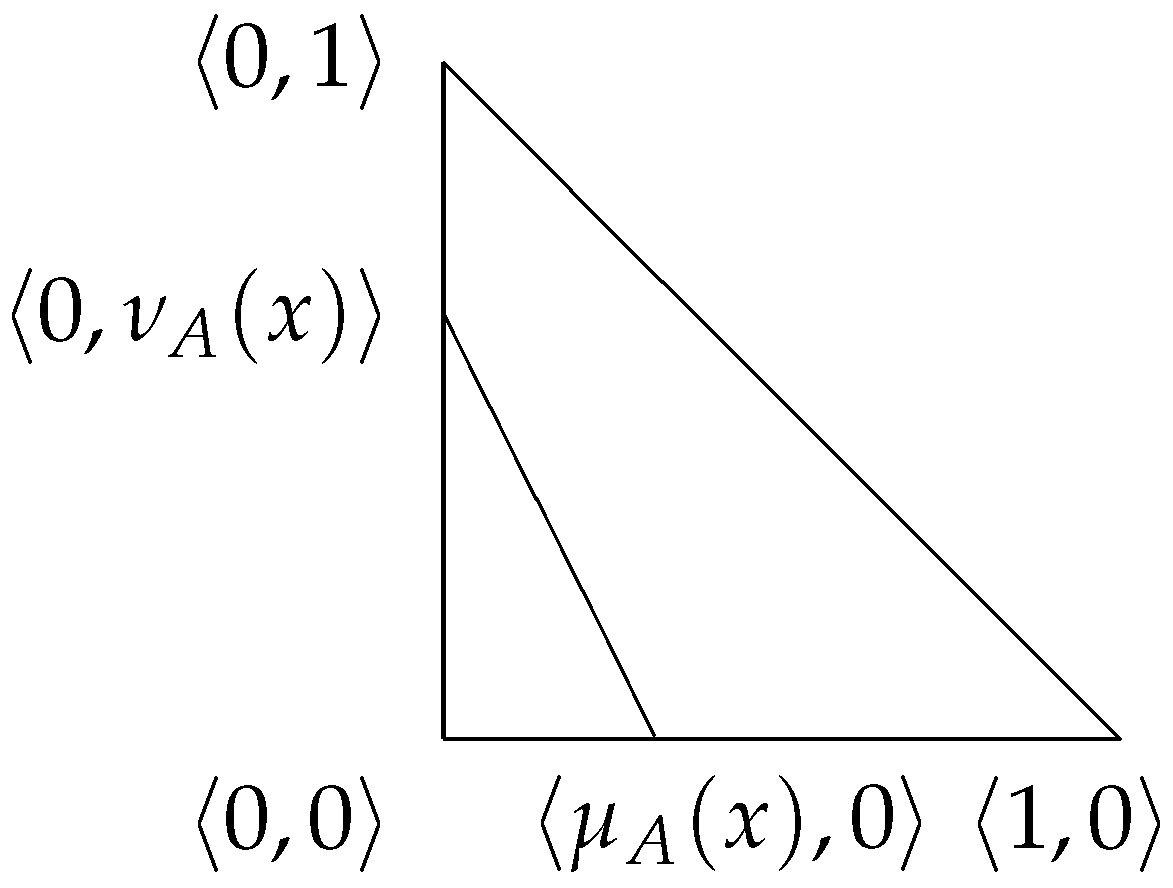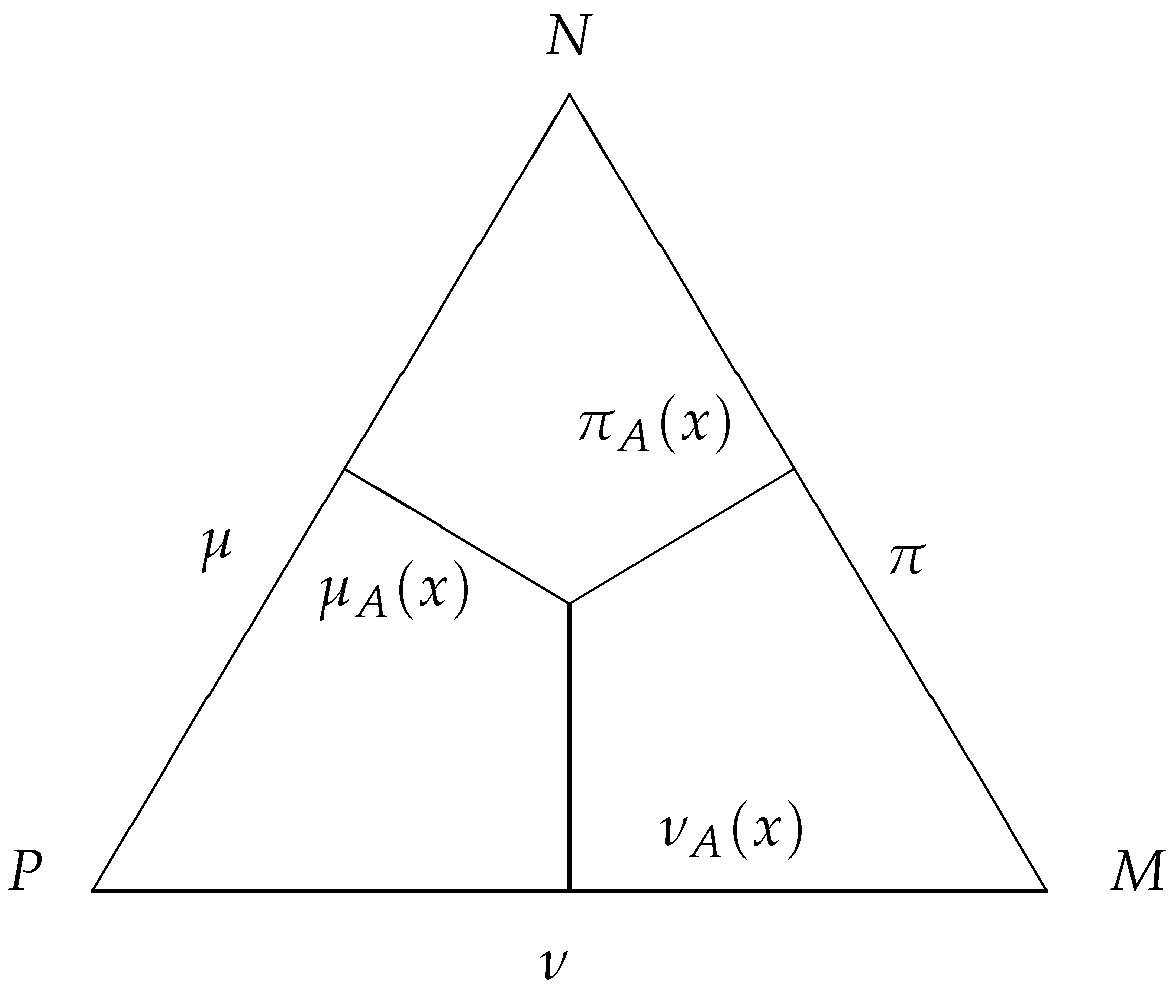1. Introduction
In 1965, Lotfi Zadeh introduced the concept of fuzzy sets [
1]. They are now one of the most serious and prospective directions for the development of Georg Cantor’s set theory. In spite of the concerns and critical remarks against fuzzy sets voiced by some of the most prominent specialists in the area of mathematical logic in the second half of the 1960s, fuzzy sets have been firmly established as a fruitful area of research, as well as of a tool for the evaluation of different objects and processes in nature and society. Soon after their launch, fuzzy sets became an object of extensions by themselves. Chronologically, the first of these extensions,
L-fuzzy sets, were introduced by Goguen in 1969 [
2]. The second extension was from Zadeh [
3], who introduced the idea of interval-valued fuzzy sets. The third extension is the rough sets, which were defined by Z. Pawlak in 1981 [
4,
5]. The fourth was intuitionistic fuzzy sets (IFSs), introduced in 1983 [
6]. In recent years, many other extensions of fuzzy sets have been proposed. It is now clear that a significant part of these are trivial modifications of other existing fuzzy set extensions which have been “re-branded” under new names.
In recent years, some authors have introduced the term “type-1 fuzzy set” (T1FS) as a synonym of Zadeh’s fuzzy set (e.g., [
7,
8,
9]), emphasizing that T1FSs are the basis of the fuzzy sets extensions. Preserving this name, in the present paper, we discuss what is common and what is different between T1FSs and IFSs.
In
Section 2 , we discuss the basic concepts in IFS theory that do not have analogues in T1FS theory and the reasons for this. In
Section 3, we discuss the possibility for the transformation of some concepts from IFSs theory to T1FSs theory. So, we show some new directions for development of T1FS theory. The author is not aware of similar research.
The author would like to mention that his first research in the area of IFS was based on A. Kaufmann’s book [
10], whose Russian translation was the first book on fuzzy sets that appeared in Bulgaria in the early 1980s. For this reason, the theory of IFSs uses the notation of [
10].
2. What Is There in IFS Theory That Has No Analogue in T1FS Theory?
Below, following [
11,
12], we give the definitions of the basic concepts and the basic operations, relations, and operators over IFSs, and discuss which of them do and which do not have analogues in T1FS theory.
Let us have a fixed universe
E and its subset
A. The set
where
is called IFS and functions
and
represent the
degree of membership (validity, etc.) and
non-membership (non-validity, etc.), respectively. In IFSs, we can also define the function
by
which corresponds to the
degree of indeterminacy (uncertainty, etc.).
For brevity, we shall write below A instead of , whenever possible.
Obviously, for every T1FS A: for each , and this set has the form
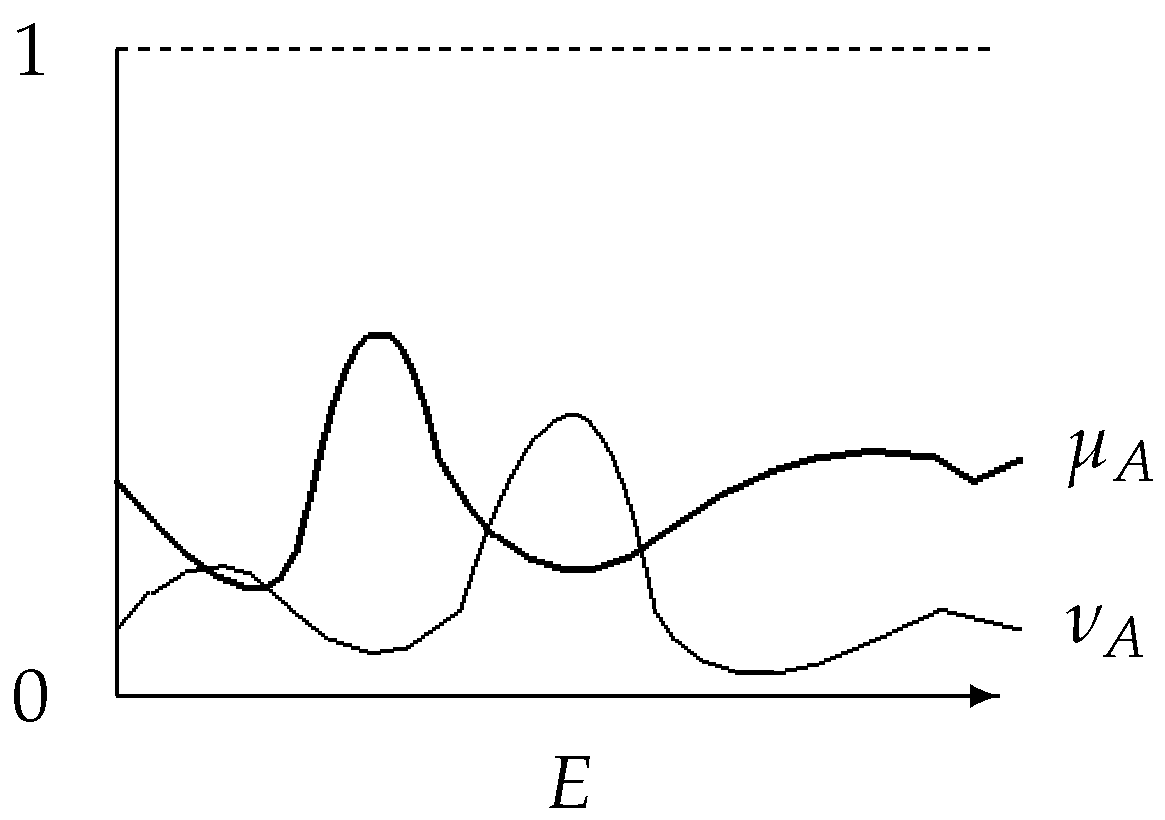
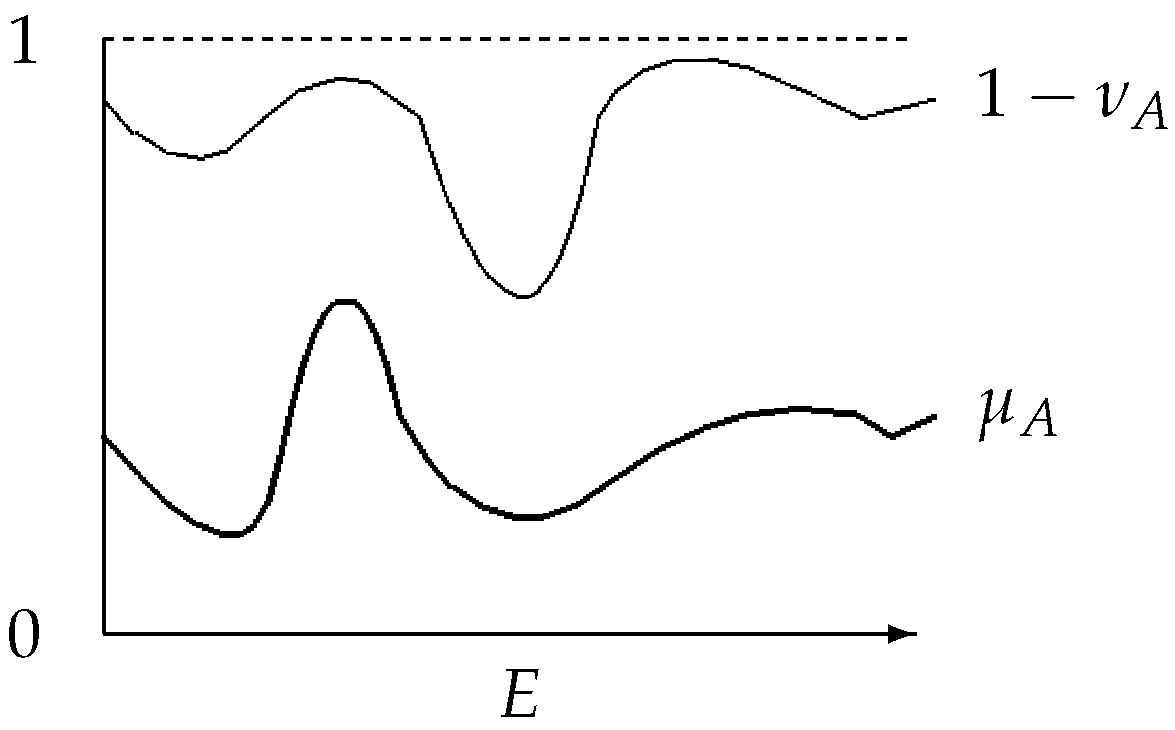
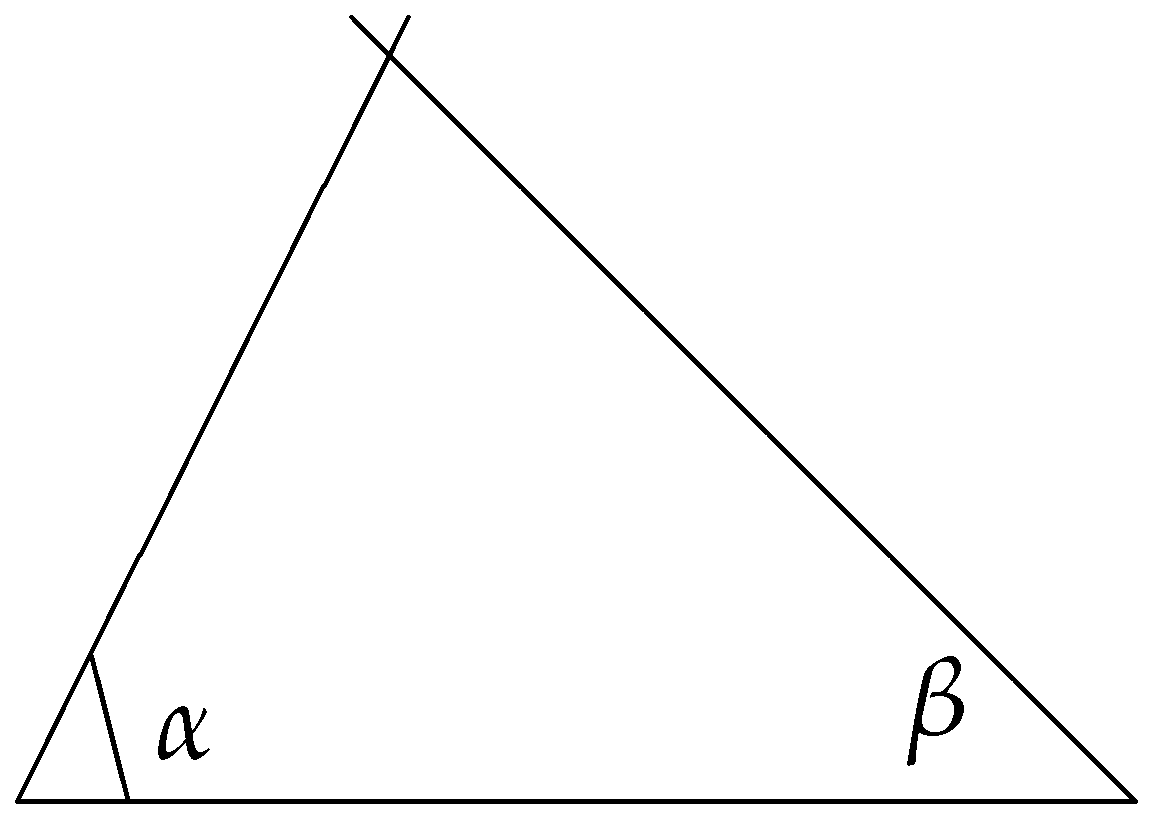
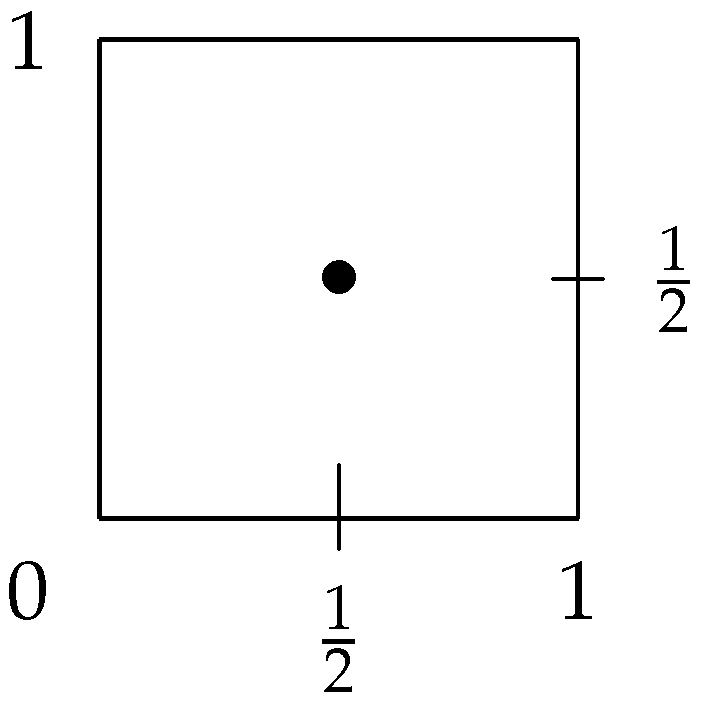
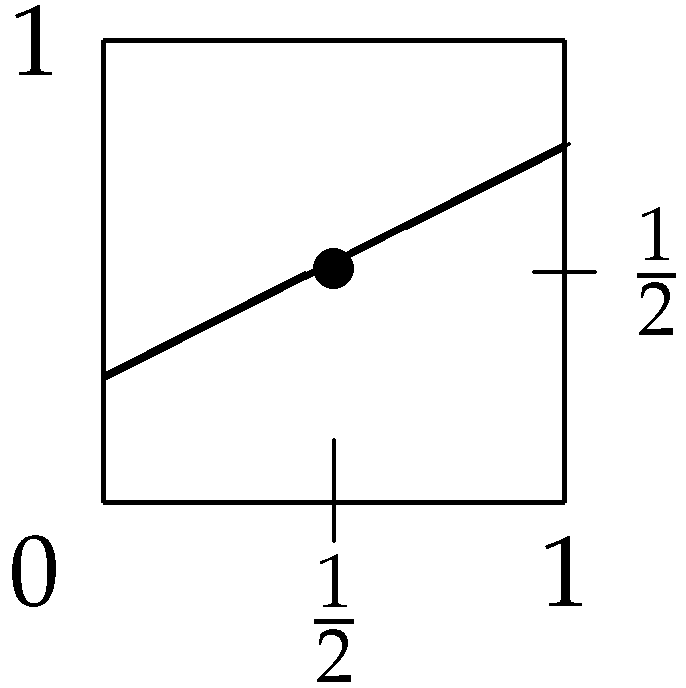
By analogy with the T1FSs, IFSs have the following geometrical interpretation (see
Figure 1 and
Figure 2).
In the T1FS-case, in both figures, the line for is missing and they coincide.
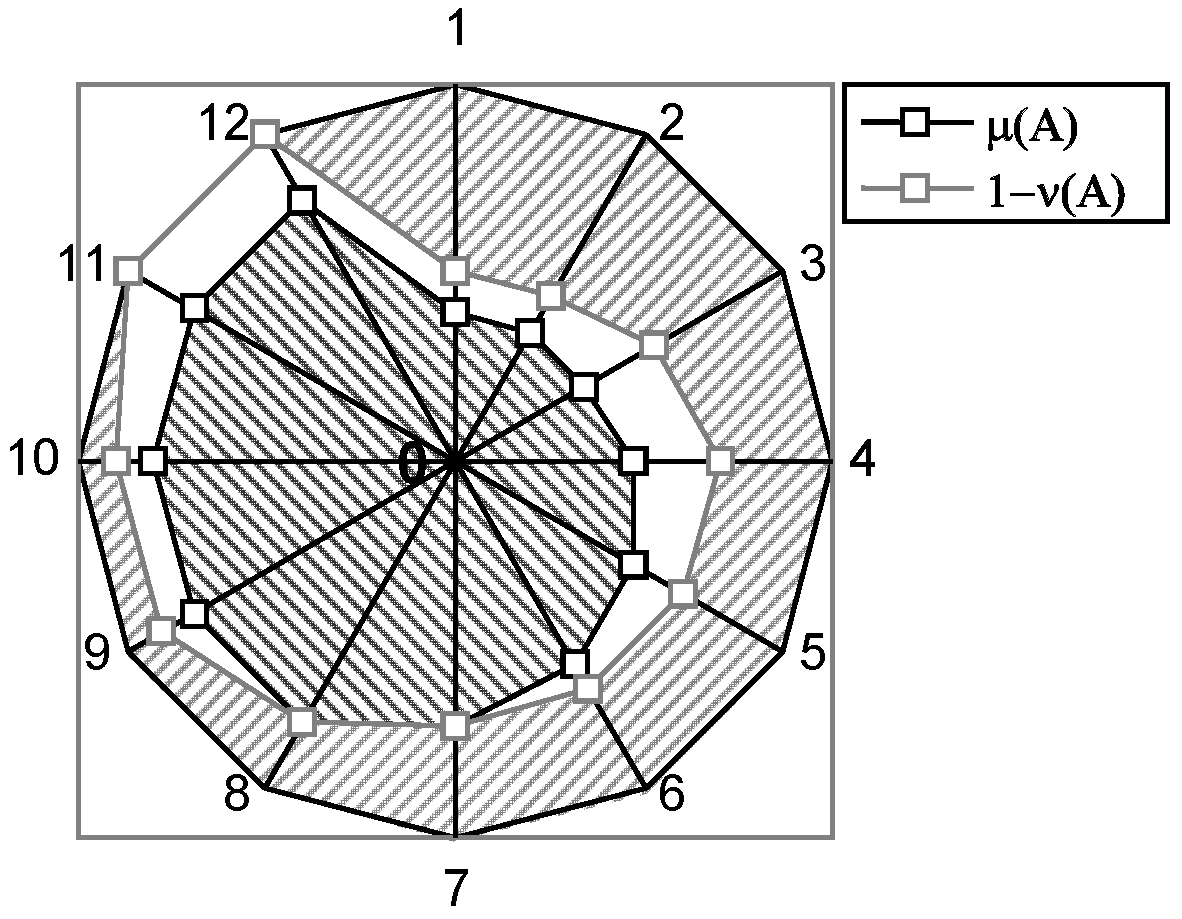
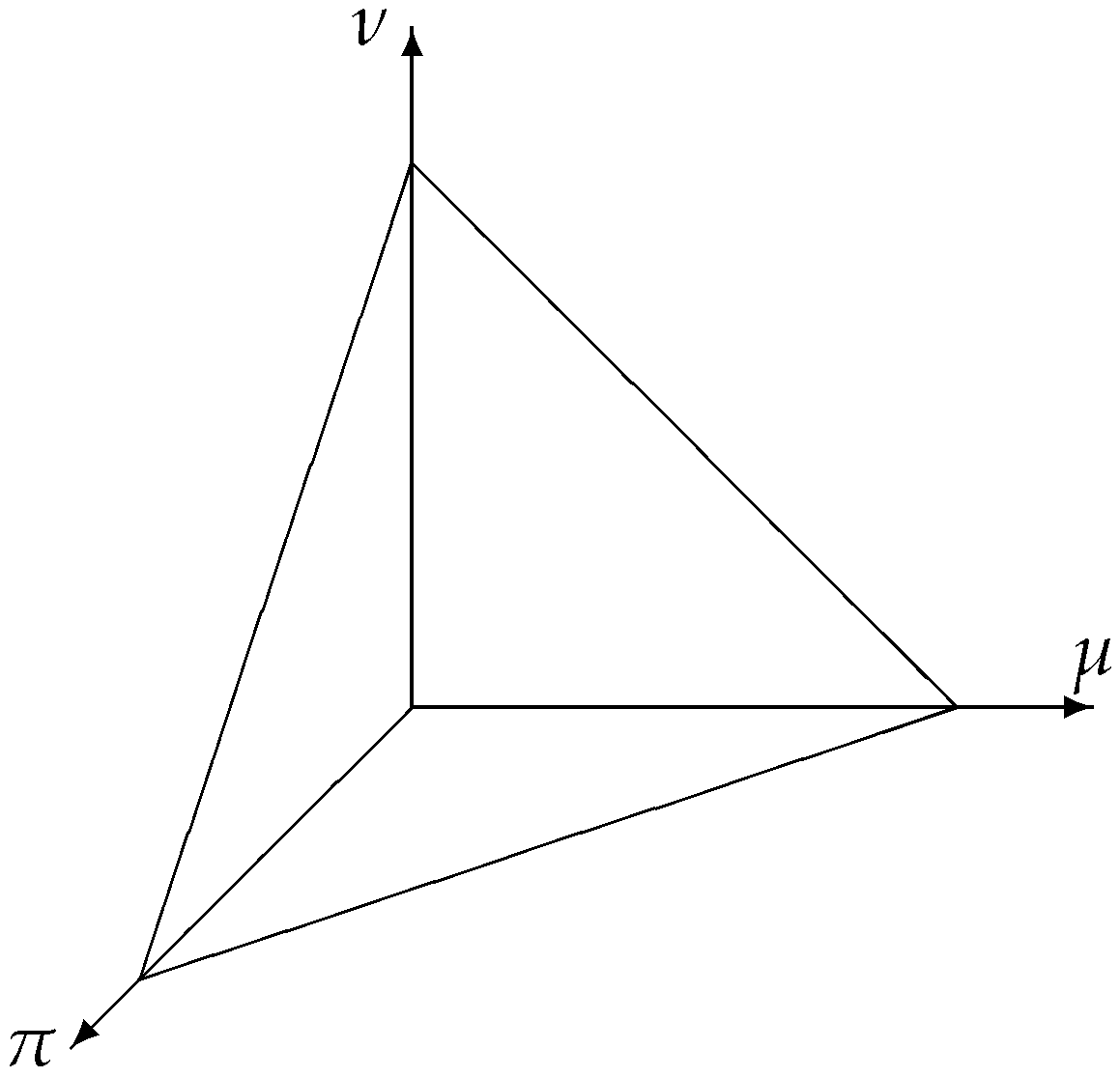
The IFSs have another geometrical interpretation (see
Figure 3) that analogously can be transformed to the T1FS-case with omission of the line for
. It is the first geometrical interpretation in circle.
The most practically useful geometrical interpretation of the IFSs (see
Figure 4) makes no sense for T1FS, since the elements of such a set are only points projected onto the hypotenuse of the intuitionistic fuzzy interpretation triangle.
The situation with the next geometrical interpretation of the IFSs is similar (see
Figure 5,
Figure 6,
Figure 7 and
Figure 8). The interpretation in
Figure 7 was introduced by Danchev in [
13], while Szmidt and Kacprzyk constructed the three-dimensional geometrical interpretation in
Figure 8 in [
14,
15,
16].
In [
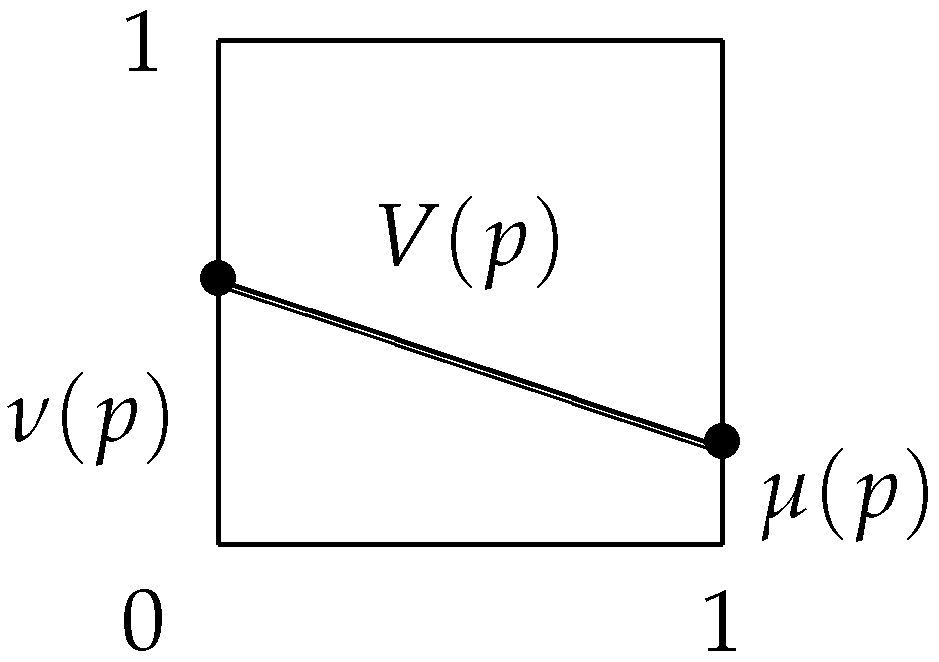
17], the latest geometrical interpretation is introduced (see
Figure 9), where
. In it, the horizontal section and the two vertical sections have length of 1. The section determines the two boundary points that have ordinates with lengths
and
.
In this new interpretation, the central point—marked in
Figure 10 by • with coordinates
—plays an important role. When a section passes through it, then this section corresponds to a T1FS-element (i.e., one, for which
).
It is clear that the basic IFS-operations and relations can be transformed (reduced) to T1FS-operations. Such operations are, e.g.,
defined for every two IFSs
A and
B (see [
11,
12]). The author was is only not aware of an operation over T1FS analogous of operation @ with the form
where
A and
B are T1FSs.
Now, in [
12,
18], 53 different operations of intuitionistic fuzzy negation and 185 different operations of intuitionistic fuzzy implications are described. New 4 implications are given in [
19,
20,
21,
22]. The above implication is one of them. It has a T1FS-analogue, while approximately all the rest do not, but an analogy can be made with the above-mentioned operation @. The situation with the intuitionistic fuzzy negations is similar.
In IFS theory, there are some other operations that we do not discuss here because (at least at the moment) they do not have any practical application.
Now, there are four groups of operators, defined over IFSs. Below, we will shortly describe them and will discuss the possibility for them to obtain T1FS-forms.
As I wrote in [
11,
12], my research in IFSs started in February 1983 as a mathematical game, in which I transformed T1FS-operations to the above-described form of
. However, only when I found analogues of the two standard modal operators for the new type of sets did I understand that these sets are essentially different from the already existing T1FSs. George Gargov (1947–1996) invited me to call the new object an “intuitionistic fuzzy set”, because of its correspondence to Brouwer’s idea for intuitionism (see [
23,
24]). The first two modal operators over IFS
A have the form
When the second geometrical interpretation (
Figure 4) was constructed, it became clear why these two operators lose their sense if we try to define them over T1FS. This is so, because for each IFS
A:
while, if
A is a T1FS
Over the years, the two operators □ and ◊ have been the object of a series of extensions, some of which are mentioned below (see [
12]):
where
are fixed numbers.
Obviously, operator
is an extension of the standard modal operators □ and ◊, because for each IFS
A:
Operator
is an extension of the operator
, because for each IFS
A:
The rest of the operators do not have analogues in modal logic. Operators
are extensions of the operators □ and ◊, but they are objects of further extensions, described in [
12].
It is important to mention that if
, then for each fuzzy set
A and for each
:
Therefore, is not a fuzzy set. Hence, operator cannot be applied over A without changing its status (from fuzzy set to IFS).
The situation with the other extended modal operators is similar.
The second group of modal operators can obtain T1FS-interpretation. They are defined sequentially, so each of the following operators is an extension of the previous ones. These operators are defined for each IFS
A by:
where
;
where
.
where
and
;
where
and
.
where
and
(see [
12]).
In the next section, we discuss the modification of these operators for the T1FS-case.
The rest two groups of modal operators (see [
25,
26]) cannot be transformed for the T1FS-case, and will not be a subject of discussion here.
The basic intuitionistic fuzzy level operators (e.g., [
12]) are:
for
and
.
The degrees of membership and non-membership of the elements of a given universe to its subset can be directly changed by these operators. These operators are a standard extension of the existing operators in T1FS theory.
Following [
12], we introduce two operators that are analogous to the topological operators of closure and interior (e.g., [
27,
28]). They were defined in October 1983 by the author, and their basic properties were studied. Three years later, the relations between the modal and the topological operators over IFSs were studied (see [
11]). These operators are defined for every IFS
A by:
Since the beginning of the new century, these operators have been the objects of certain extensions. Six of these extensions are as follows (see [
12]):
IFSs are extended in some directions (e.g., [
11]): intuitionistic
L-fuzzy sets, interval-valued IFSs, IFSs over different universes, temporal IFSs, multidimensional IFSs, IFSs of
n-type. Now, 30 years after the introduction of this last extension, some authors have incorrectly re-branded them as “Pythagorean fuzzy sets”, repeating the results from [
29].
While the intuitionistic
L-fuzzy sets are a direct extension of
L-fuzzy sets [
2] and the interval-valued IFSs are an extension of interval-values fuzzy sets [
30], the rest extensions are the original ones (i.e., having no fuzzy sets analogues). Moreover, they cannot be transformed to T1FS-forms. For example, the IFSs of
n-type have the form
where
In the T1FS-case, the above inequality is transformed to , which is equivalent to when .
3. What in IFS Theory Can Be Transformed to T1FS Theory?
As we mentioned above, IFS-operations can be transformed to T1FS-operations, but many of them will coincide. For example, if we transform the two IFS-implications, defined for two IFSs
A and
B:
and
to T1FS-forms (i.e., when
A and
B are T1FSs), both sets (
and
) will coincide, obtaining the form
The same is the situation with the IFS-negations. For example, if we transform the three IFS-negations for the IFS
A
to T1FS-forms (i.e., for a T1FS
A), they will coincide, obtaining the form
Obviously, the modal operators from the first group (
) make no sense in the T1FS-case, while some of the operators from the second group can obtain T1FS-forms. Now, they will obtain the following forms:
where
;
where
.
where
and
;
where
and
.
where
and
On the other hand, some of the operator arguments must be omitted. So, in the T1FS-case, these operators will obtain, respectively, the forms:
where
;
where
.
where
and
The topological operators can also be reduced to the T1FS-case, as follows:
where, again,
. Therefore,
is deprecated. The same is the situation with the last three topological operators, because:
Therefore, only the first two topological operators ( and ) make sense in the T1FS-case.