An Improved Brain-Inspired Emotional Learning Algorithm for Fast Classification
Abstract
:1. Introduction
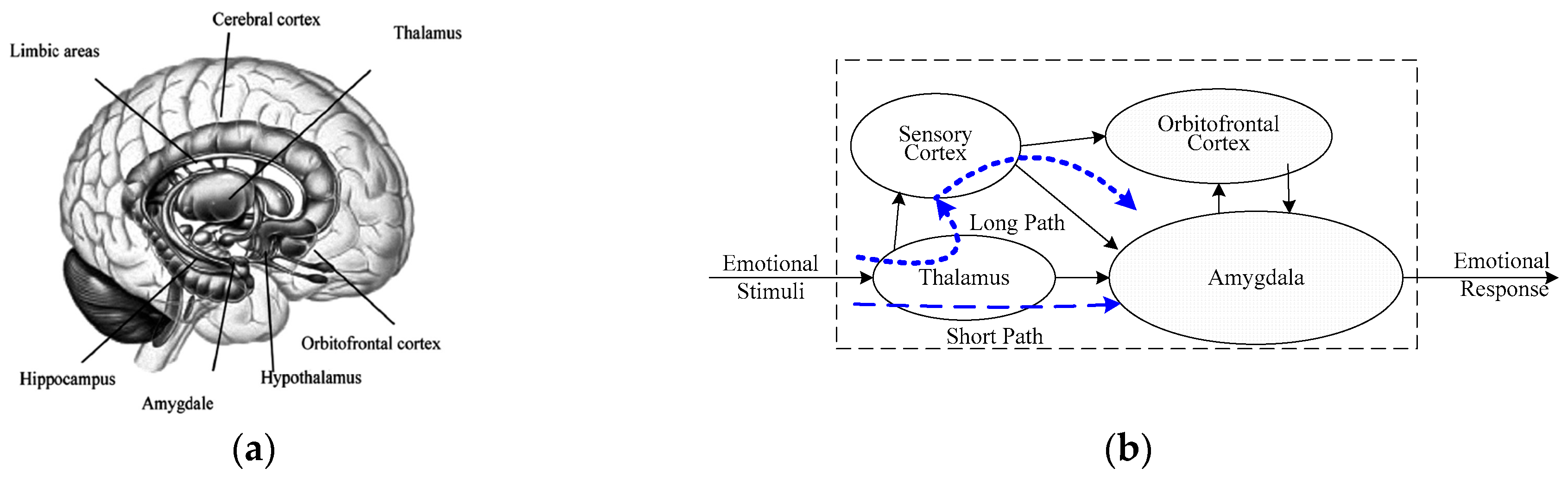
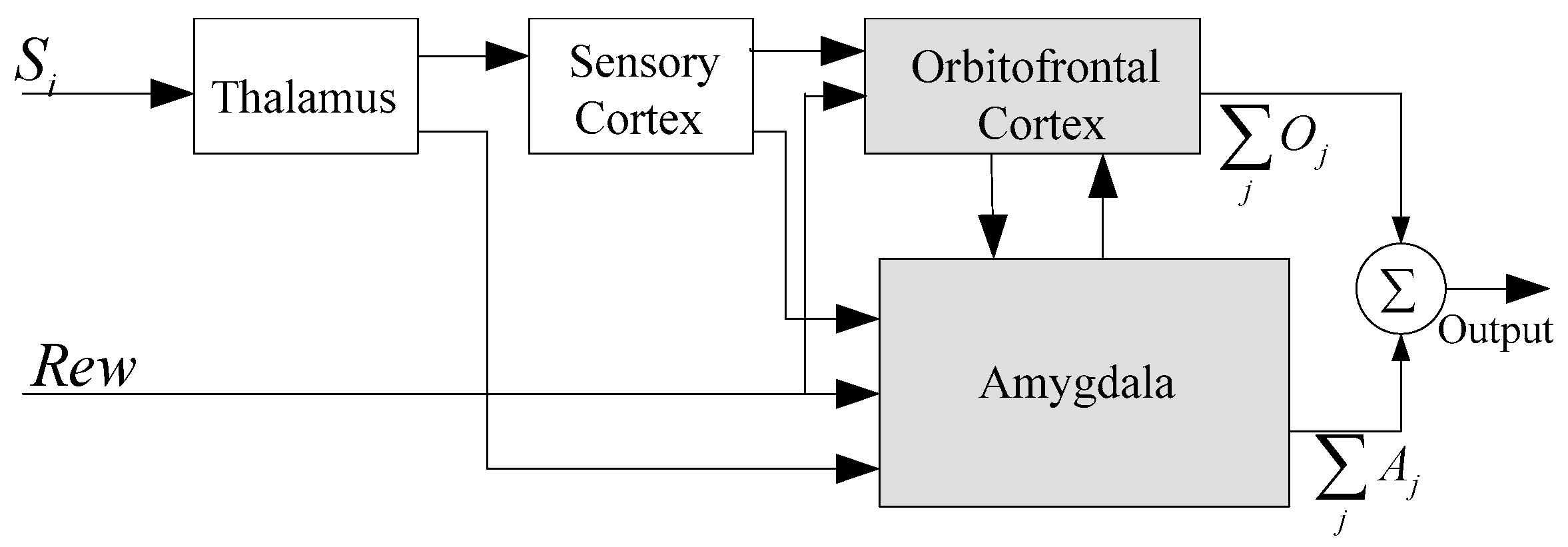
2. Anatomical Foundation and Related Works
3. Implementation
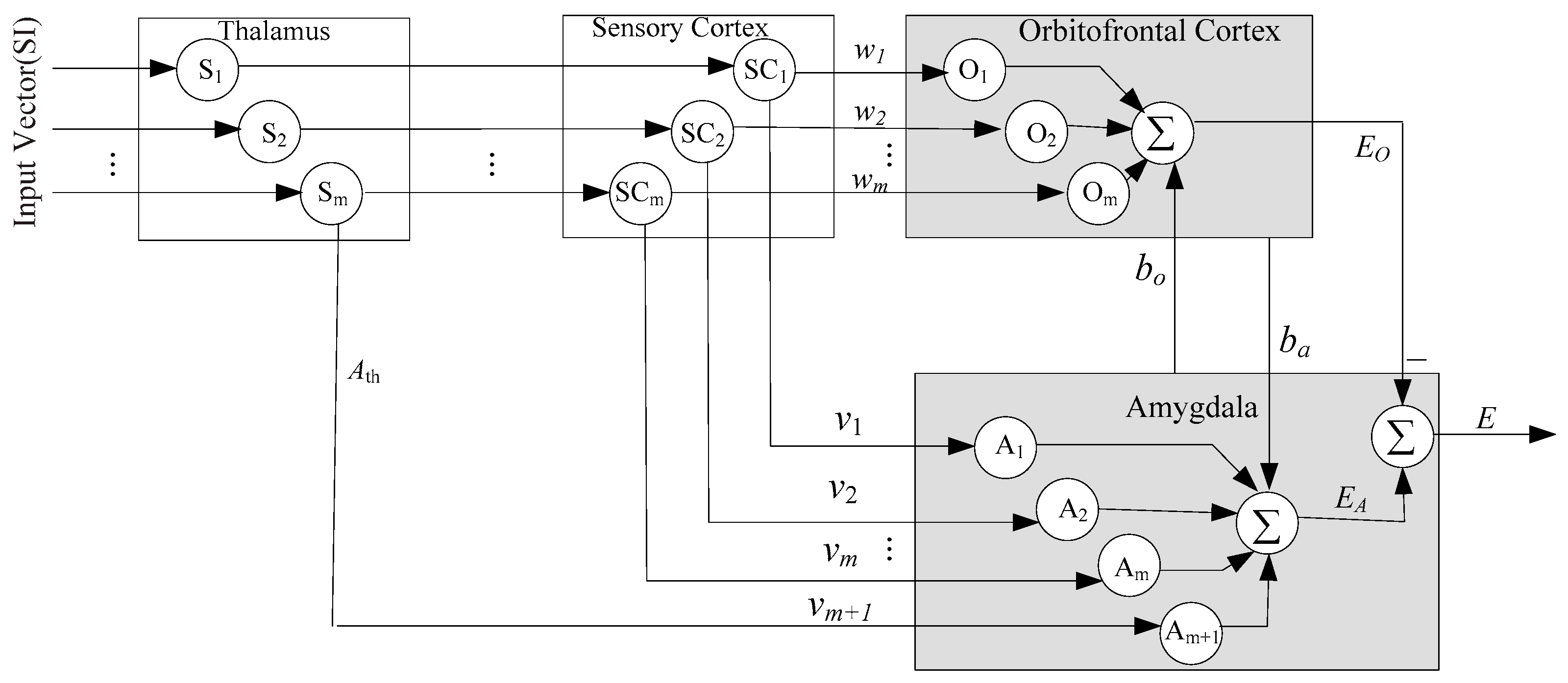
3.1. Improved BEL Neural Network
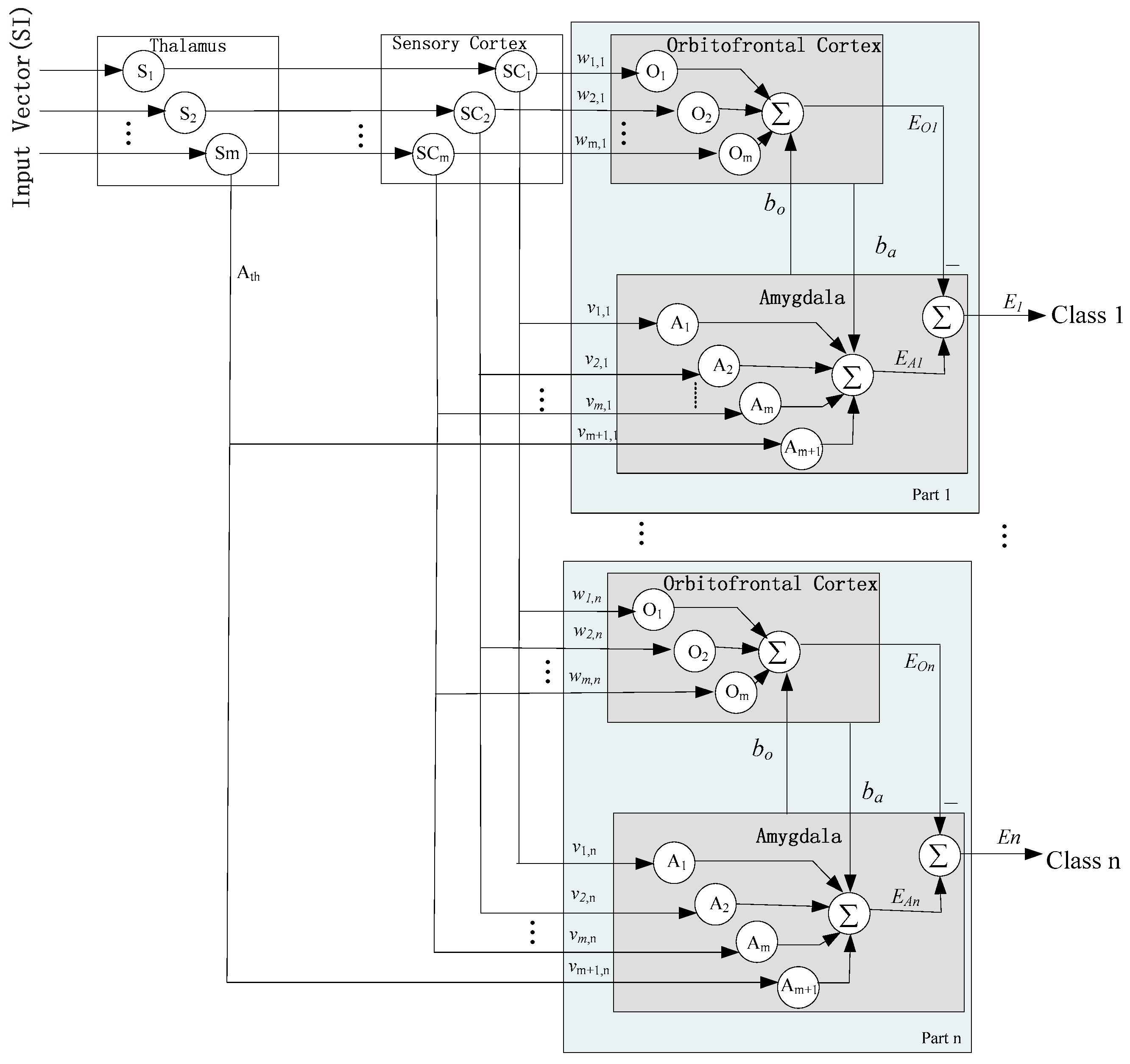
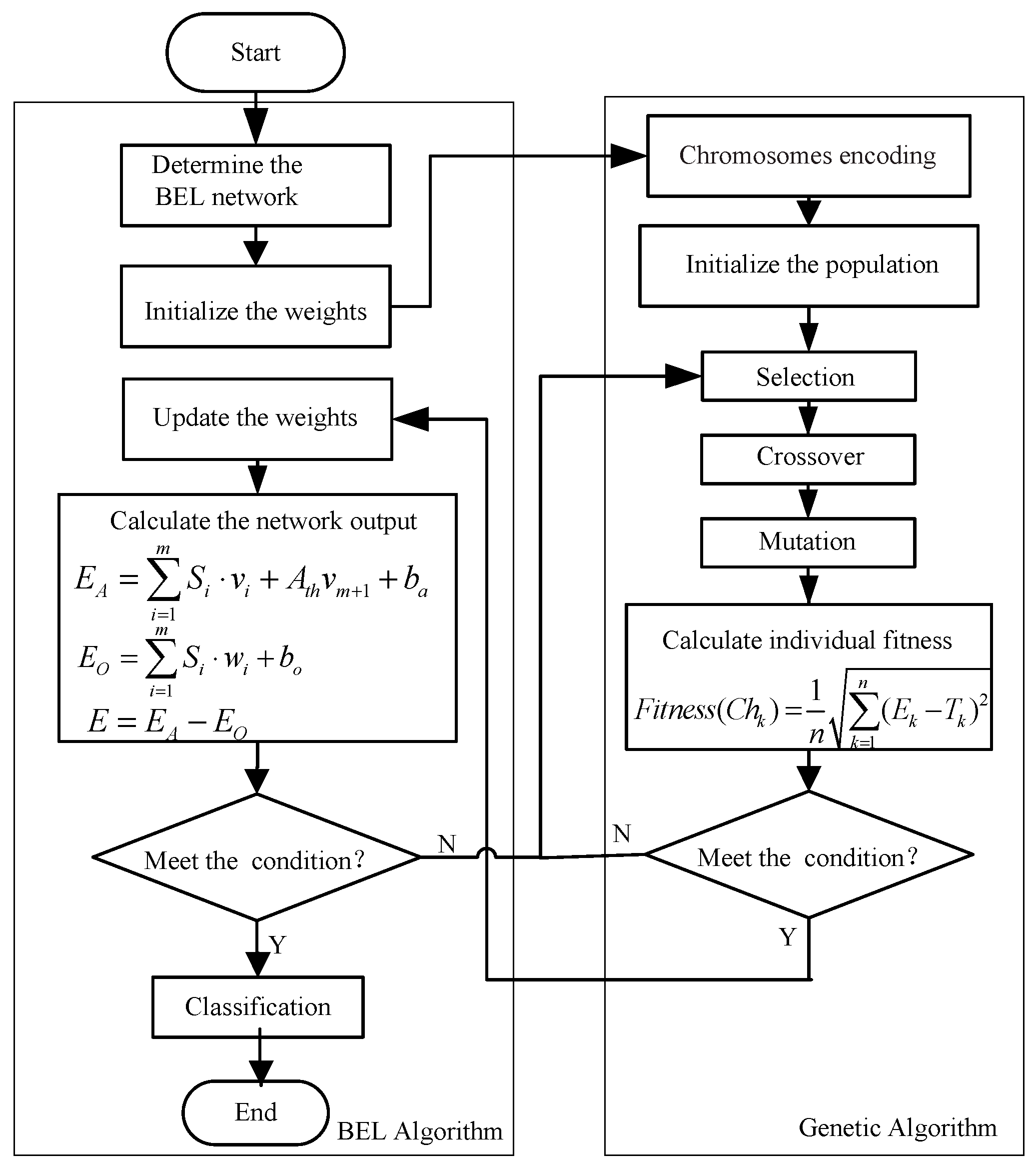
3.2. GA-BEL Algorithm
- /* Matlab code for BEL network simulation */
- function E = sim(net,SI)
- [numSample] = size(SI,2);
- nf = net.numInputs;
- for i = 1:numSample
- EA = sum(net.amygdalaWeights.* SI(1:nf,i)) + net. AthWeights(1,1) * SI(nf + 1,i) + net. biasA;
- EO = sum(net.frontalWeights.* SI(1:nf,i)) + net. biasO;
- E(1,i) = EA - EO;
- end
4. Simulation Results
4.1. Case 1: UCI Datasets’ Classification
4.1.1. Datasets’ Description
4.1.2. Measure for Performance Evaluation
4.1.3. Experimental Results and Discussion
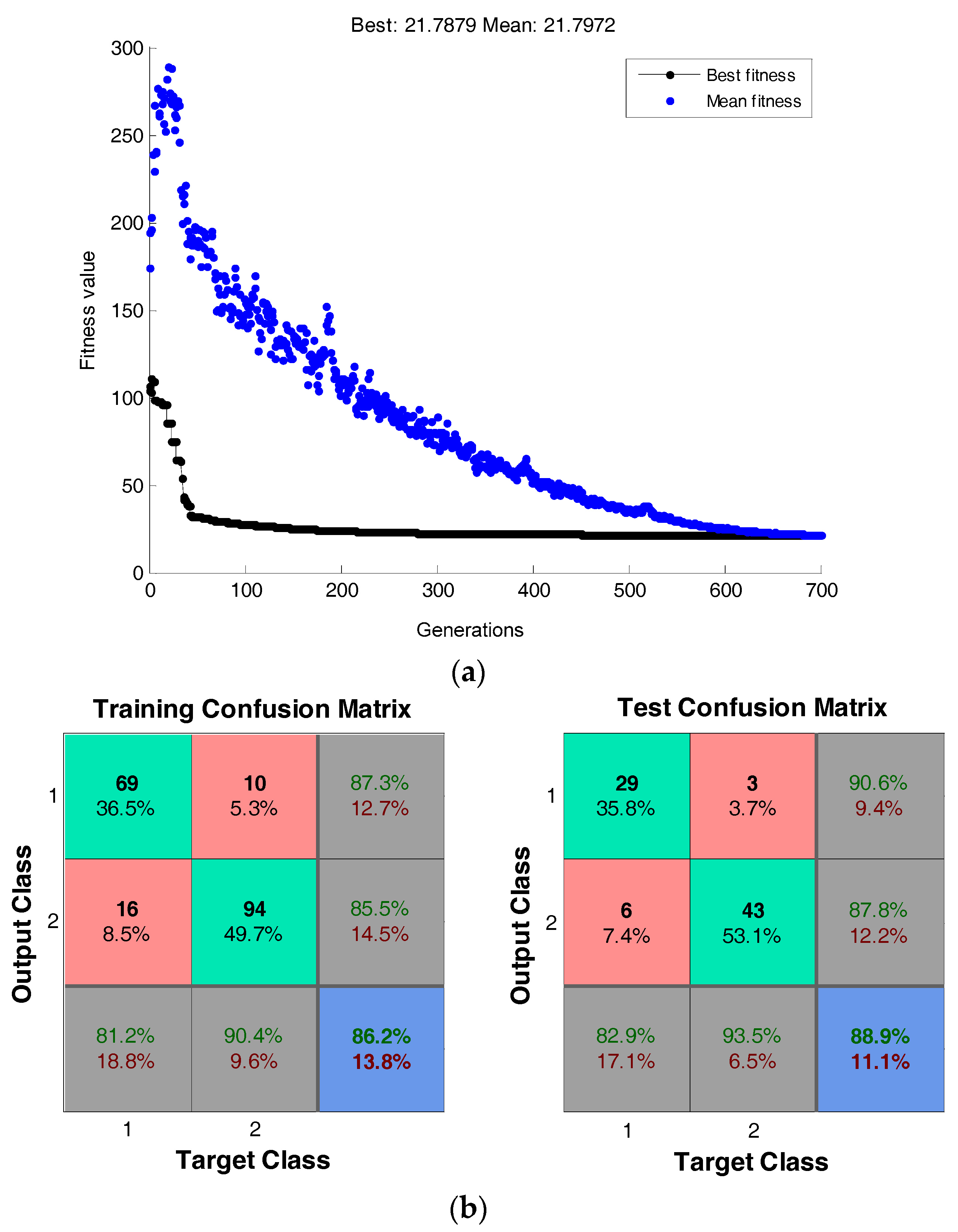
4.1.3.1. Classification on Breast Cancer Dataset
4.1.3.2. Classification on the Heart Dataset
4.1.4. Total Comparison and Discussion
4.2. Case 2: Facial Expression Recognition
4.2.1. Experiments on the JAFFE and Cohn–Kanade Databases
4.2.2. Comparison and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fergus, P.; Idowu, I.; Hussain, A. Advanced artificial neural network classification for detecting preterm births using EHG records. Neural Comput. 2016, 188, 42–49. [Google Scholar] [CrossRef]
- Grbic, D.; Saenko, S.V.; Randriamoria, T.M. Phylogeography and support vector machine classification of colour variation in panther chameleons. Mol. Ecol. 2015, 24, 3455–3466. [Google Scholar] [CrossRef] [PubMed]
- Lajnef, T.; Chaibi, S.; Ruby, P. Learning machines and sleeping brains: Automatic sleep stage classification using decision-tree multi-class support vector machines. J. Neurosci. Math. 2015, 250, 94–105. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.Y.; Qiu, X.; Shi, J.P.; Li, N.; Lu, Z.H.; Chen, P.; Zhang, Y.D. A Pathological Brain Detection System based on Extreme Learning Machine Optimized by Bat Algorithm. CNS Neurol. Disord. Drug Targets 2017, 16, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Du, S.; Zhang, Y.; Phillips, P.; Wu, L.; Zhang, Y.D. Alzheimer’s Disease Detection by Pseudo Zernike Moment and Linear Regression Classification. CNS Neurol. Disord. Drug Targets 2017, 16, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zeng, X.; He, Z. Improved functional link artificial neural network via convex combination for nonlinear active noise control. Appl. Soft Comput. 2016, 42, 351–359. [Google Scholar] [CrossRef]
- Barbey, A.K. Distributed neural system for emotional intelligence revealed by lesion mapping. Soc. Cogn. Affect. Neurosci. 2014, 9, 265. [Google Scholar] [CrossRef] [PubMed]
- Sharbafi, M.A.; Lucas, C.; Daneshvar, R. Motion Control of Omni-Directional Three-Wheel Robots by Brain-Emotional-Learning-Based Intelligent Controller. IEEE Trans. Syst Man Cybern. C 2010, 40, 630–638. [Google Scholar] [CrossRef]
- Sharma, M.K.; Kumar, A. Performance comparison of brain emotional learning-based intelligent controller (BELBIC) and PI controller for continually stirred tank heater (CSTH). Lect. Notes Econ. Math. 2015, 335, 293–301. [Google Scholar]
- Morén, J.; Balkenius, C. A Computational Model of Emotional Learning in the Amygdala. In Proceedings of the 6th International Conference on the Simulation of Adaptive Behaviour; Meyer, J.A., Berthoz, A., Floreano, D., Roitblat, H.L., Wilson, S.W., Eds.; MIT Press: Cambridge, UK, 2000; pp. 115–124. [Google Scholar]
- LeDoux, J.E. Emotion and the limbic system concept. Concept Neurosci. 1991, 2, 169–199. [Google Scholar]
- Pasrapoor, M.; Bilstrup, U. An emotional learning-inspired ensemble classifier (ELiEC). In Proceedings of the 2013 Federated Conference on Computer Science and Information Systems, Krakow, Poland, 8–11 September 2013; pp. 137–141. [Google Scholar]
- Lotfi, E. Wind power forecasting using emotional neural networks. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, San Diego, CA, USA, 5–8 October 2014; pp. 311–316. [Google Scholar]
- Lin, C.M.; Chung, C.C. Fuzzy Brain Emotional Learning Control System Design for Nonlinear Systems. Int. J. Fuzzy Syst. 2015, 17, 117–128. [Google Scholar] [CrossRef]
- Lucas, C. Danial Shahmirzadi, Nima Sheikholeslami. Introducing Belbic: Brain Emotional Learning Based Intelligent Controller. Intell. Autom. Soft Comput. 2013, 10, 11–21. [Google Scholar] [CrossRef]
- Abdi, J.; Moshiri, B.; Abdulhai, B. Forecasting of short-term traffic-flow based on improved neurofuzzy models via emotional temporal difference learning algorithm. Eng. Appl. Artif. Intell. 2012, 25, 1022–1042. [Google Scholar] [CrossRef]
- Parsapoor, M.B. Chaotic Time Series Prediction Using Brain Emotional Learning Based Recurrent Fuzzy System (BELRFS). Intell. Syst. 2013, 2, 113–126. [Google Scholar] [CrossRef]
- Lotfi, E.; Akbarzadeh, T. Brain emotional learning-based pattern recognizer. Cybernet. Syst. 2013, 44, 402–421. [Google Scholar] [CrossRef]
- Shen, Z.Q.; Kong, F.S. Optimizing Weights by Genetic Algorithm for Neural Network Ensemble. Adv. Neural Netw. 2004, 3173, 323–331. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; MIT Press: Cambridge, UK, 1992. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization; Springer: New York, NY, USA, 2011. [Google Scholar]
- Qin, A.K.; Huang, V.L.; Suganthan, P.N. Differential Evolution Algorithm with Strategy Adaptation for Global Numerical Optimization. IEEE Trans. Evolut. Comput. 2009, 13, 398–417. [Google Scholar] [CrossRef]
- LeDoux, J.E. Emotion circuits in the brain. Annu. Rev. Neurosci. 2000, 23, 155–184. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, M.; Pattanaik, L.M. Genetic Algorithms: A survey. IEEE Comput. 1994, 27, 17–27. [Google Scholar] [CrossRef]
- Leng, Z.; Gao, J.; Zhang, B. Short-term traffic flow forecasting model of optimized BP neural network based on genetic algorithm. In Proceedings of the IEEE Control Conference, Xi’an, China, 26–28 July 2013; pp. 8125–8129. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 14 January 2017).
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Assoc. 1952, 47, 583–621. [Google Scholar]
- LIBSVM: A Library for Support Vector Machines. Available online: http://www.csie.ntu.edu.tw/cjlin/libsvm (accessed on 2 February 2017).
- Sengur, A. Multiclass least-squares support vector machines for analog modulation classification. Expert Syst. Appl. 2009, 3, 6681–6685. [Google Scholar] [CrossRef]
- Miche, Y.; Sorjamaa, A.; Bas, P. OP-ELM: Optimally pruned extreme learning machine. IEEE Trans. Neural Netw. 2010, 21, 158–162. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhou, H.; Ding, X. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst Man Cybern. B 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.; Huang, G.B.; Wang, D. Sparse extreme learning machine for classification. IEEE Trans. Cybern. 2014, 44, 1858–1870. [Google Scholar] [CrossRef] [PubMed]
- The Japanese Female Facial Expression (JAFFE) Database. Available online: http://www.kasrl.org/jaffe.html (accessed on 2 March 2017).
- Cohn-Kanade AU-Coded Expression Database. Available online: http://www.pitt.edu/~emotion/ck-spread.htm (accessed on 9 March 2017).
- Happy, S.L.; Routray, A. Automatic Facial Expression Recognition Using Features of Salient Facial Patches. IEEE Trans. Affect. Comput. 2015, 6, 1–12. [Google Scholar] [CrossRef]
- Liu, S.S.; Zhang, Y.; Liu, K.P. Facial expression recognition under random block occlusion based on maximum likelihood estimation sparse representation. Proceeding of International Joint Conference on Neural Networks, Beijing, China, 6–11 July 2014; pp. 1285–1290. [Google Scholar]
- Ar, A.; Demir, Y.; Güzeliş, C. A new facial expression recognition based on curvelet transform and online sequential extreme learning machine initialized with spherical clustering. Neural Comput. Appl. 2016, 27, 131–142. [Google Scholar]
- Saaidia, M.; Zermi, N.; Ramdani, M. Multiple Image Characterization Techniques for Enhanced Facial Expression Recognition. In Intelligent Systems Technologies and Applications; Stefano, B., Sabu, M., Thampi, P.R.S., Eds.; Springer: Brelin, Germany, 2016; Volume 384, pp. 497–509. [Google Scholar]
- Zhang, Y.D.; Yang, Z.J.; Lu, H.M. Facial Emotion Recognition based on Biorthogonal Wavelet Entropy, Fuzzy Support Vector Machine, and Stratified Cross Validation. IEEE Access 2016, 99, 1–11. [Google Scholar] [CrossRef]
- Ouyang, Y.; Sang, N.; Huang, R. Accurate and robust facial expressions recognition by fusing multiple sparse representation based classifiers. Neural Comput. 2015, 149, 71–78. [Google Scholar] [CrossRef]




| Attributes | Datasets | #Samples | #Features | #Classes |
|---|---|---|---|---|
| Low Demensions Small Sizes | Iris | 150 | 4 | 3 |
| Breast Cancer | 699 | 9 | 2 | |
| Low Demensions Large Sizes | Banana | 5300 | 2 | 2 |
| SVMguide1 | 7089 | 4 | 2 | |
| High Demensions Small Sizes | Heart | 270 | 13 | 2 |
| Wine | 178 | 13 | 3 | |
| High Demensions Large Sizes | Satimage | 6435 | 36 | 6 |
| Segment | 2310 | 19 | 7 |
| Performance Metric | BEL | GA-BEL | Paired K-W Test p-Value |
|---|---|---|---|
| Precision (%) | 97.3 | 98.5 | 0.0356 |
| Recall (%) | 94.5 | 95.6 | 0.0202 |
| Accuracy (%) | 94.9 | 97.5 | 0.0183 |
| Time (s) | 8.27 × 10−3 | 7.63 × 10−3 | 0.0316 |
| Performance Metric | BEL | GA-BEL | Paired K-W Test p-Value |
|---|---|---|---|
| Precision (%) | 86.8 | 88.7 | 0.0377 |
| Recall (%) | 85.7 | 87.3 | 0.0313 |
| Accuracy (%) | 85.5 | 87.8 | 0.0258 |
| Time (s) | 5.37 × 10−3 | 6.93 × 10−3 | 0.0329 |
| Data Sets | Algorithms | Precision (%) | Recall (%) | Accuracy (%) | Time(s) |
|---|---|---|---|---|---|
| Breast Cancer | SVM | 97.2 | 95.6 | 96.7 | 5.33 × 10−2 |
| LS-SVM | 98.7 | 96.9 | 97.1 | 2.31 × 10−2 | |
| BEL | 97.3 | 94.5 | 94.9 | 8.27 × 10−3 | |
| GA-BEL | 98.5 | 95.6 | 97.5 | 7.63 × 10−3 | |
| Iris | SVM | 96.3 | 94.4 | 95.1 | 3.01 × 10−2 |
| LS-SVM | 97.9 | 95.3 | 96.7 | 1.64 × 10−2 | |
| BEL | 97.2 | 95.8 | 96.6 | 2.72 × 10−3 | |
| GA-BEL | 99.6 | 97.3 | 97.3 | 2.93 × 10−3 | |
| Banana | SVM | 89.5 | 87.8 | 88.6 | 8.37 × 10−1 |
| LS-SVM | 88.7 | 86.3 | 87.2 | 5.79 × 10−1 | |
| BEL | 91.3 | 88.5 | 88.7 | 3.31 × 10−1 | |
| GA-BEL | 91.7 | 89.2 | 91.3 | 7.75× 10−2 | |
| SVMguide1 | SVM | 97.9 | 95.7 | 96.4 | 5.83 |
| LS-SVM | 96.7 | 94.3 | 95.3 | 4.79 | |
| BEL | 96.2 | 94.5 | 96.5 | 2.43 | |
| GA-BEL | 97.3 | 95.6 | 96.9 | 1.81 | |
| Heart | SVM | 87.3 | 85.5 | 86.1 | 3.71 × 10−2 |
| LS-SVM | 86.2 | 84.8 | 85.7 | 1.26 × 10−2 | |
| BEL | 86.8 | 85.7 | 85.5 | 5.37 × 10−3 | |
| GA-BEL | 88.7 | 87.3 | 87.8 | 6.93 × 10−3 | |
| Wine | SVM | 99.3 | 97.1 | 98.2 | 4.01 × 10−2 |
| LS-SVM | 96.5 | 96.4 | 97.9 | 1.83 × 10−2 | |
| BEL | 98.5 | 96.3 | 97.4 | 2.93 × 10−3 | |
| GA-BEL | 98.6 | 96.5 | 97.1 | 3.51 × 10−3 | |
| Satimage | SVM | 90.7 | 88.5 | 91.1 | 13.7 |
| LS-SVM | 91.6 | 89.9 | 90.6 | 9.43 | |
| BEL | 92.5 | 90.3 | 91.6 | 3.81 | |
| GA-BEL | 94.3 | 92.6 | 93.8 | 2.25 | |
| Segment | SVM | 96.2 | 93.7 | 94.5 | 5.78 |
| LS-SVM | 96.5 | 94.8 | 95.1 | 1.26 | |
| BEL | 96.2 | 94.7 | 94.8 | 3.81 × 10−1 | |
| GA-BEL | 97.1 | 95.7 | 96.6 | 2.73 × 10−1 |
| Data Sets | Study | Algorithms | Accuracy (%) |
|---|---|---|---|
| Breast Cancer | Miche, Y. [31] | Optimally Pruned Extreme Learning Machine | 95.6 |
| This study | GA-BEL | 97.5 | |
| Banana | Huang, G.B. [32] | Extreme Learning Machine | 89.8 |
| This study | GA-BEL | 91.3 | |
| Heart | Lotfi, E. [18] | Brain Emotional Learning | 81.3 |
| This study | GA-BEL | 87.8 | |
| Satimage | Bai, Z. [33] | Sparse Extreme Learning Machine | 90.1 |
| This study | GA-BEL | 93.8 |
| Emotion | Recognition Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|
| Happy | Angry | Sadness | Disgust | Fear | Surprise | Neutral | |
| Happy | 98.47 | 0.0 | 0.43 | 0.0 | 0.0 | 0.68 | 0.25 |
| Angry | 0.0 | 96.69 | 1.79 | 0.0 | 0.0 | 1.52 | 0.0 |
| Sadness | 0.0 | 2.31 | 94.27 | 2.30 | 0.0 | 0.0 | 1.12 |
| Disgust | 0.0 | 2.13 | 2.71 | 94.31 | 0.85 | 0.0 | 0.0 |
| Fear | 0.0 | 0.0 | 2.15 | 2.25 | 94.29 | 1.31 | 0.0 |
| Surprise | 1.37 | 0.53 | 0.0 | 0.0 | 1.73 | 96.37 | 0.0 |
| Neutral | 1.95 | 1.13 | 2.35 | 0.0 | 0.0 | 0.0 | 94.57 |
| Average Accuracy 95.57 | |||||||
| Emotion | Recognition Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| Happy | Angry | Sadness | Disgust | Fear | Surprise | |
| Happy | 98.63 | 0.0 | 0.0 | 0.0 | 0.11 | 1.26 |
| Angry | 0.0 | 96.79 | 1.43 | 1.78 | 0.0 | 0.0 |
| Sadness | 0.0 | 2.01 | 94.21 | 1.43 | 2.35 | 0.0 |
| Disgust | 0.0 | 0.46 | 1.34 | 95.85 | 2.35 | 0.0 |
| Fear | 0.0 | 0.0 | 2.06 | 2.40 | 94.37 | 1.17 |
| Surprise | 1.32 | 0.0 | 0.0 | 0.0 | 1.53 | 97.15 |
| Average Accuracy 96.17 | ||||||
| Databases | Classifiers | Time (s) | Accuracy (%) |
|---|---|---|---|
| JAFFE | SVM | 2.3481 | 93.35 |
| LS-SVM | 1.2872 | 94.56 | |
| BEL | 0.3156 | 94.03 | |
| GA-BEL | 0.2736 | 95.57 | |
| Cohn–Kanade | SVM | 3.6738 | 94.81 |
| LS-SVM | 2.7506 | 95.12 | |
| BEL | 0.5591 | 93.68 | |
| GA-BEL | 0.2958 | 96.17 |
| Data Bases | Study | Classifiers | Measures | Accuracy (%) |
|---|---|---|---|---|
| JAFFE | Liu S.S. [37] | MLESR | 10-fold cross validation | 93.42 |
| Ar A. [38] | OSELM-SC | leave-one-subject-out | 94.65 | |
| Saaidia M. [39] | FFNN | Leave-One-Out | 93.59 | |
| Zhang Y.D. [40] | FSVM | 10-fold cross validation | 95.06 | |
| This study | GA-BEL | 10-fold cross validation | 95.57 | |
| Cohn–Kanade | Liu S.S. [37] | MLESR | 10-fold cross validation | 94.29 |
| Ar A. [38] | OSELM-SC | leave-one-subject-out | 95.15 | |
| Happy S.L. [36] | SVM | 10-fold cross validation | 94.14 | |
| Ouyang Y. [41] | SRC | random selection | 95.64 | |
| This study | GA-BEL | 10-fold cross validation | 96.17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, Y.; Tan, G.; Liu, Z. An Improved Brain-Inspired Emotional Learning Algorithm for Fast Classification. Algorithms 2017, 10, 70. https://doi.org/10.3390/a10020070
Mei Y, Tan G, Liu Z. An Improved Brain-Inspired Emotional Learning Algorithm for Fast Classification. Algorithms. 2017; 10(2):70. https://doi.org/10.3390/a10020070
Chicago/Turabian StyleMei, Ying, Guanzheng Tan, and Zhentao Liu. 2017. "An Improved Brain-Inspired Emotional Learning Algorithm for Fast Classification" Algorithms 10, no. 2: 70. https://doi.org/10.3390/a10020070
APA StyleMei, Y., Tan, G., & Liu, Z. (2017). An Improved Brain-Inspired Emotional Learning Algorithm for Fast Classification. Algorithms, 10(2), 70. https://doi.org/10.3390/a10020070





