1. Introduction
Let
and
be Banach spaces and
D be a non-empty open convex subset of
. Let also
stand for the space of bounded linear operators from
into
. In this study, we are concerned with the problem of approximating a locally unique solution
of the nonlinear equation:
where
is a nonlinear Fréchet-differentiable operator.
Beginning from
, we can consider different third-order iterative methods to solve the scalar equation
, with
and
, [
1,
2].
According to Traub’s classification [
3], these third-order methods are divided into two broad classes. On the one hand, the one-point methods, which require the evaluation of
F,
and
at the current point only. For instance,
The Halley method
where
The family of Newton-like methods:
which includes the well-known iterative methods of the third-order Chebyshev, Halley, Super-Halley, Ostrowski and Euler methods.
Notice that the family (
2) has the inconvenience of reaching order greater than three only for certain equations. For instance, it is known that the family (
2) has fourth order of convergence for quadratic equations, if
.
On the other hand, the second class is the multipoint methods, which cannot require . For instance:
Notice that this iterative method cannot be included in the family (
2). This way, to obtain iterative methods with higher order than three for any function
F and to be able to represent some multipoint methods, as (
3), we can consider a modification of the family (
2) that allow getting this generalization [
4]. Therefore, we consider the following family, which includes all of these methods:
Notice that (
4) is well defined if
for all
p and
and
.
Thus, for instance, for
and
, we obtain the previous family (
2). On the other hand, if we take
, for all
, and:
then we get the two-step method (
3).
In general, the methods (
2) have higher operational cost than the methods (
3) when solving a non-linear system. Another measure that takes into account the operational cost that requires an iterative process
is the computational efficiency given by
where, again,
o is the order of convergence of
and
is the operational cost to apply a step with the iterative process
, that is the number of products needed per iteration and the number of products that appear in the evaluation of the corresponding operator.
Therefore, in order to compare the efficiency of some iterative methods of the new family, we consider the computational efficiency
. Note that the methods selected in the family (
4) as the most efficient have a lower computational efficiency as more terms in the series are considered.
Notice that, for quadratic equations, the Chebyshev method and the two-step method (method in (
7) with
) have the same algorithm:
On the other hand, we note that the family of iterative processes (
7), with
, has the property of having four-order convergence when we consider quadratic equations. Therefore, the iterative process that is more efficient in this family, for quadratic equations, is the known Chebyshev-like method (
and
for
in (
7)). Then, we compare this iterative process with the Chebyshev method.
This fourth-order method for quadratic equations can be written as:
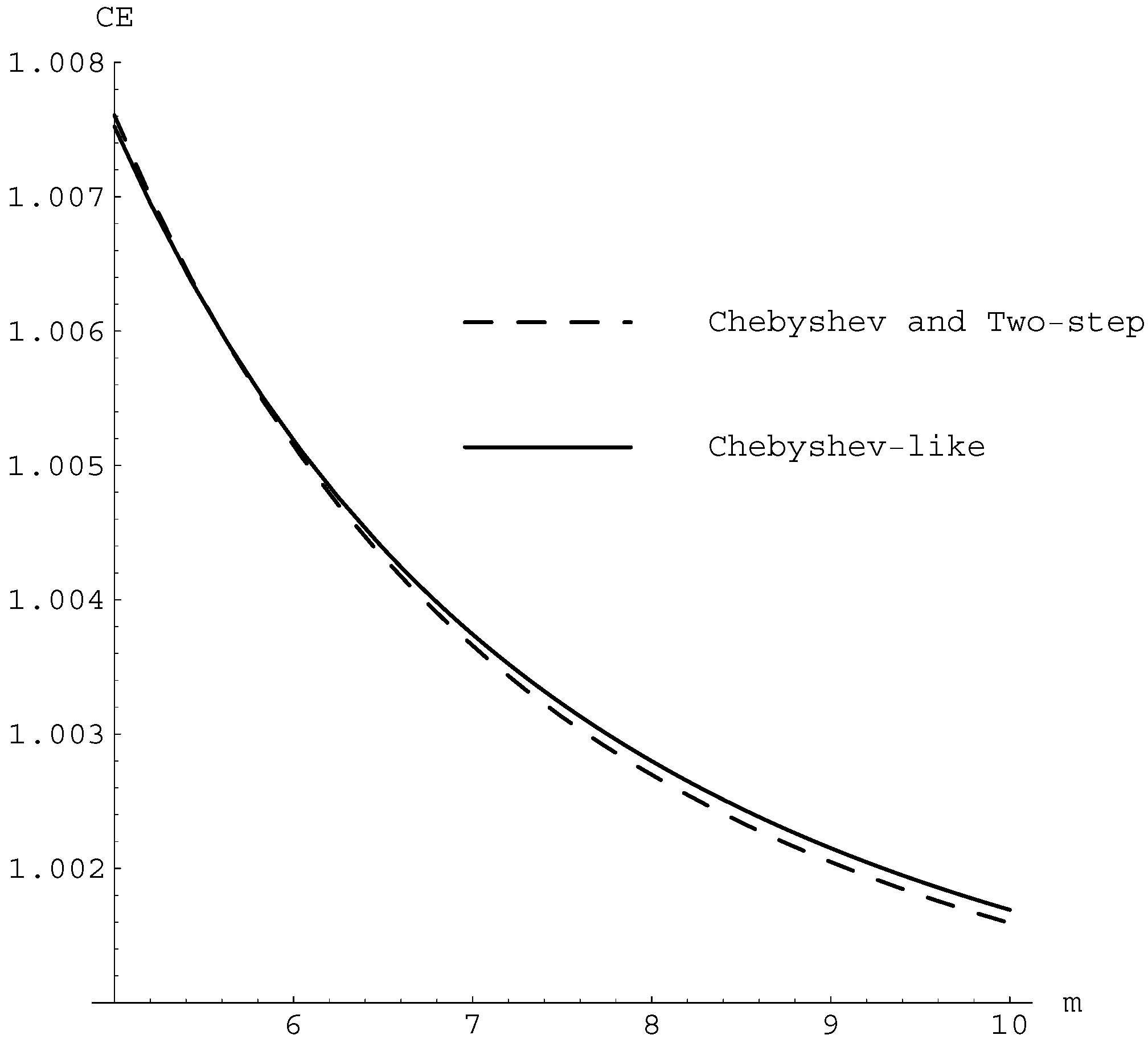
For the quadratic equation, the computational efficiency,
, for the Chebyshev method, (
5) and (
6) methods in the family (
7) is
,
, respectively. As we can observe in
Figure 1, the optimum computational efficiency is for the Chebyshev-like method given in (
6), when the system has at least six equations.
Recently, in the work by Amat et al. [
4], a semilocal convergence analysis was given in a Banach space setting:
where
and the operators
are some particular
k-linear operators.
An interesting application related to image denoising was presented also in [
4]. The approximation, via our family, is of a new nonlinear mathematical model for the denoising of digital images. We are able to find the best method in the family (different of the two-step) for this particular problem. Indeed, the founded method has order four. The denoising model that we propose in this paper permits a good reconstruction of the edges that are the most important visual parts of an image. See also [
5,
6] for more applications.
On the other hand, the semilocal convergence analysis of method (
7) was based on
-type conditions [
7] that constitute an alternative to the classical Kantorovich-type conditions [
8]. The convergence domain for the method (
7) is small in general. In the present study, we use our new idea of restricted convergence domains leading to smaller
-parameters, which in turn lead to the following advantages over the work in [
4] (and under the same computational cost): larger convergence domain; tighter error bounds on the distances involved and an at least as precise information on the location of the solution.
The rest of the paper is organized as follows: the semilocal convergence analysis of the method (
7) is given in
Section 2, whereas the numerical examples are presented in the concluding
Section 3.
2. Semilocal Convergence
We consider Equation (
1), where
F is a nonlinear operator defined in a non-empty open convex subset
D of a Banach space
with values in another Banach space
.
We need the definition of the
-condition given in [
7].
Definition 1. Suppose that is five-times Fréchet-differentiable. Let and . We say that F satisfies the γ-condition, if and for each :where: Then, the following semilocal convergence result for the method defined in (
7) under γ-type conditions was given in [
4], Theorem 1:
Theorem 1. Assume that the operator F satisfies for each :the γ-condition and hypotheses:with f given in (30) and , where . Then, sequences , generated by the method (7) are well defined in , remain in for each and converge to a solution of equation , which is unique in . Moreover, the following estimates hold true for each :where , ,and: Next, we show how to achieve the advantages of our approach as stated in the introduction of this study.
Definition 2. Let be a Fréchet-differentiable operator. Operator F satisfies the center -Lipschitz condition at , if for each : Remark 1. Let . Then, we have that: In view of the Banach lemma on invertible operators [
8],
and:
The corresponding result using the γ-condition given in [
7] is:
for each
. However, if
, then
, so if
, the estimate (
12) is more precise than (
13), leading to more precise majorizing sequences, which in turn lead to the advantages already stated. Indeed, we need the following definition.
Definition 3. Let be a five-times Fréchet-differentiable, which satisfies the center -condition. We say that operator F satisfies the δ-γ-condition at , if for each :Clearly, we have that . Now, we define the scalar sequences , by:where function is defined on the interval by:for some . Moreover, define constants , , and by , , and .
If condition:
holds, then function
has two real roots
and
such that:
Moreover, we have for each
:
,
and:
Notice that:
but not necessarily vice versa, unless, if
.
We need a series of auxiliary results.
Lemma 1. Suppose that , and Then, sequences , generated by (14) are well defined for each and converge monotonically to so that: Proof. Simply replace f, α,
,
,
in the proof of Lemma 2 [
4] by
,
,
,
,
, respectively. ☐
Lemma 2. - (a)
Let be the real function given in (15). Then, the following assertion holds:where:and are real differentiable functions. - (b)
If F has a continuous third-order Fréchet-derivative on D, then the following assertion holds:where:and are some particular k-linear operators. - (c)
.
Proof. - (a)
Simply use function
instead of f in the proof of Lemma 3 in [
4].
- (b)
The same with Lemma 5 in [
4].
- (c)
Use
instead of f in Lemma 5 [
4].
☐
Lemma 3. Suppose F satisfies the -center-condition on D and the δ-γ-condition on . Then, the following items hold:
- (a)
and:where: - (b)
Proof. - (a)
See Remark 1.
- (b)
Simply replace function f by
in Lemma 4 in [
4].
☐
Lemma 4. Suppose F satisfies the γ-condition on D. Then, the following items hold:
- (a)
F satisfies the -condition on D and the δ-γ-condition on ;
- (b)
;
- (c)
;
Moreover, if , then , ,and:Furthermore, (15) supposes that and from (18); we have: Proof. The assertions hold from Lemma 3, (
18), the definition of functions
,
, f and the definition of
, γ and δ-condition. ☐
Theorem 2. Suppose that the operator F satisfies the conditions of Lemma 1, 2, 3, (9), (18), and hold. Then, sequences , , generated by the method (7) are well defined in , remain in for each and converge to a solution of equation . The limit point is the only solution of equation in . Moreover, the following estimates are true for each :where Proof. We shall show the estimates (
19). Using mathematical induction as a consequence of the following recurrence relations:
- ()
;
- ()
;
- ()
;
- ()
;
- ()
.
Items (
),
are true by the initial conditions. Suppose (
) are true for
. Then, we shall show that they hold for
. We have in turn that:
so (
) is true. By Lemma 4 and condition
, we get that
and:
so (
) is true. By Lemma 2, we obtain in turn that
and:
so:
and:
so (
) and (
) are also true, which completes the induction. ☐
Remark 2. We have so far weakened the sufficient semilocal convergence conditions of the method (7) (see (17)) and have also extended the uniqueness of the solution ball from to , since for , we have that . It is worth noticing that these advantages are obtained under the same computational cost, since in practice, the computation of constant γ requires the computation of constants and δ as special cases. Next, it follows by a simple inductive argument and the definition of the majorizing sequences that the error bounds on the distances , , , , and can be improved. In particular, we have:
Proposition 1. Under the hypotheses of Theorem 2 and Lemma 4, further suppose that for each , the following hold:where functions g and are defined by:and: Then, the following estimates hold: Proof. Estimates (
21), (
22) and (
23) follow using a simple inductive argument from conditions given in (
20) Moreover, the estimate (
25) follows by letting
in the estimate (
21). ☐
Remark 3. Clearly, under the hypotheses of Proposition 1, the error bounds on the distances are at least as tight, and the information on the location of the solution is at least as precise with the new technique.
The result of Theorem and Proposition 1 can be improved further, if we use another approach to compute the upper bounds on the norms .
Definition 4. Suppose that there exists such that the center-Lipschitz condition is satisfies:for each holds. Define . Then, we have that:
so
and:
where
Estimate (
27) is more precise than (
12) if:
where
. If
then
is a strict subset of D. This leads to the construction of an at least as tight function
as
.
Definition 5. Let be five-times Fréchet-differentiable, which satisfies the center-Lipschitz condition (26). We say that the operator F satisfies the λ-γ-condition at , if for each :where function is defined on the interval by: Define scalar sequences
,
, points
,
as,
,
, points
,
, respectively, by replacing function
by
, and suppose:
We have by (
29) that:
so:
Then, with above changes, the condition (
28) also replacing the condition in Lemma 3
and the center-Lipschitz condition (
26) replacing the
-center gamma condition, we can recover the results after Definition 4 until Remark 3 in this setting.
3. Concluding Remarks
The results obtained so far in this paper are based on the idea of restricted convergence domains, where the gamma constants (or Lipschitz constants) and consequently the corresponding sufficient semilocal convergence conditions, majorizing functions and sequences are determined by considering the set
(or
), which can be a strict subset of the set
D on which the operator
F is defined. This way, one expects (see also the numerical examples) that the new constants will be at least as small as the ones in [
4] leading to the advantages as already stated before. The smaller the subset of
D is containing the iterates
of the method (
7), the tighter the constants are. When constructing such sets (see, e.g.,
or
), it is desirable if possible not to add hypotheses, but to stay with the same information. Otherwise, the comparison between old and new results will not be fair. Looking in this direction, we can improve our results also, if we simply redefine sets
and
, respectively, as follows:
and:
where:
Notice that
and
. Clearly, the preceding results can be rewritten with
(or
) replacing
(or
). These results will be at least as good as the ones using
(or
), since the constants will be at least as tight. Notice:
- (a)
We are still using the same information, since
is defined by the second sub-step of the method (
7) for
, i.e., it depends on the initial data
- (b)
The iterates lie in (or ), which is an at least as precise a location as (or ). Moreover, the solution (or ), which is a more precise location than (or ).
Finally, the results can be improved further as follows:
Case related to the center
-condition (see Definition 2): Suppose that there exists
such that:
and:
Then, there exists
such that:
Define the set
by:
Then, we clearly have that:
Suppose the conditions of Definition 4 hold, but on the set
. Then, these conditions will hold for some parameter
and function
, which shall be at least as tight as δ,
, respectively. In particular, the sufficient convergence conditions shall be:
and:
The majorizing sequences
,
shall be defined:
and
,
,
as sequences
,
, but with
replacing function
. Then, the conclusions of Theorem 2 will hold in this setting. Notice that the estimate
still uses the initial data as
Case related to the center-Lipschitz condition (
26): Similarly, to the previous case, but:
Then, again, we have that:
An example:
Let us consider , , and the nonlinear operator .
In this case, we can consider
, [
9].