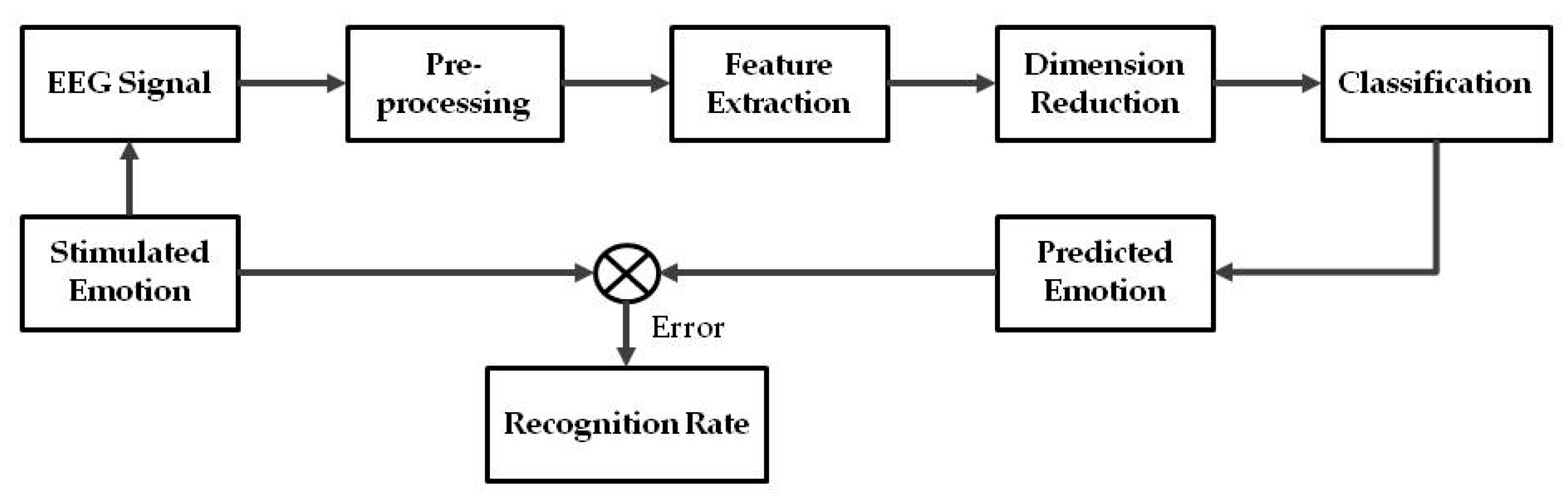
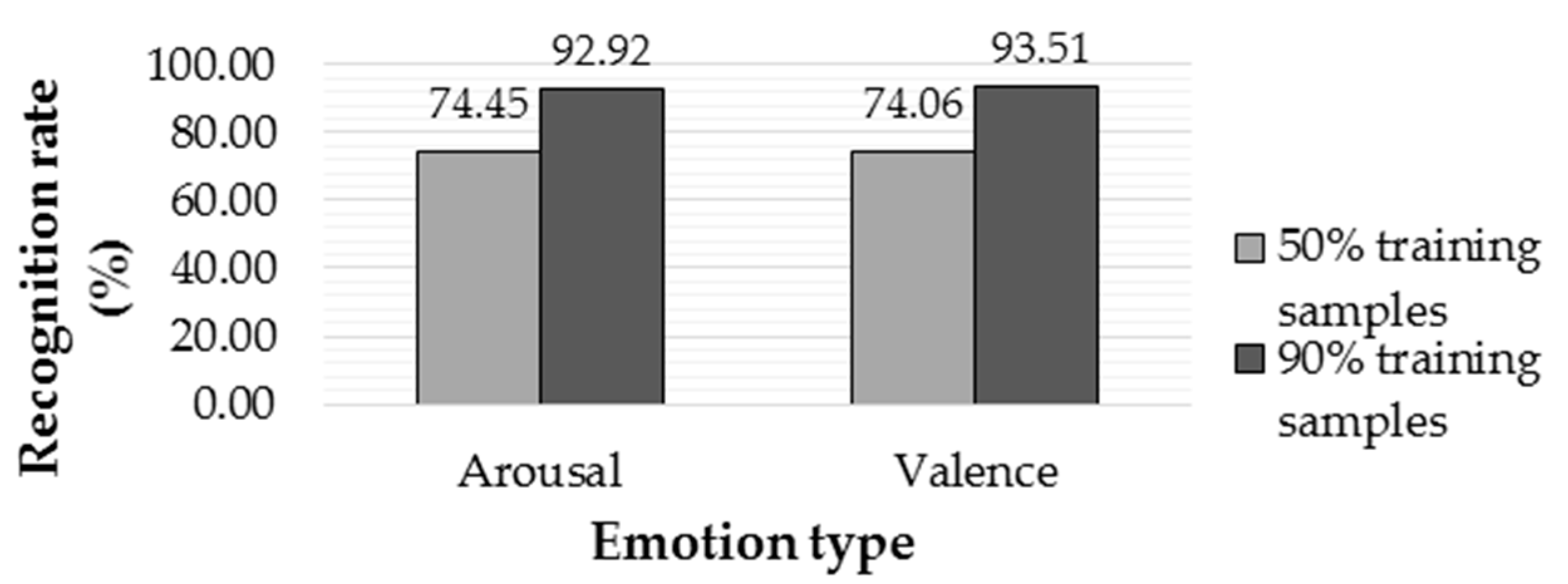
3.4.1. Bispectrum
The power spectrum analysis, which has been widely used in biomedical signal processing, performs power distribution calculation using a function of frequency and pays no attention to the signal phase information. In the power spectral analysis, the signal is assumed to arise from a linear process, thus ignoring any possible interaction between components (phase coupling). However, the brain signal is part of the central nervous system with many nonlinear sources, so it is highly likely to have a phase coupling between signals [
14]. The bispectrum analysis is superior to the power spectrum analysis because in its mathematical formula, there is a correlation calculation between the frequency components [
46]; thus, the phase coupling components of the EEG signals could be revealed. Some characteristics of bispectrum analysis are the ability to extract deviations due to Gaussianity, to suppress the additive colored Gaussian noise of an unknown power spectrum and to detect nonlinearity properties [
47]. Because of its superiority, bispectrum analysis is used in this research as the signal processing technique in the feature extraction step. We expect that by using bispectrum analysis, the recognition rate of the EEG-based automatic emotion recognition system will improve.
For example, suppose there is a signal
S3 that is a combination of two other signals,
S1 and S
2, where the frequencies are
f1 = 20 Hz,
f1 = 10 Hz and
f3 =
f1 +
f2 = 30 Hz, and the phases are φ
1 =
π/6, φ
2 = 5
π/8 and φ
3 = φ
1 + φ
2, respectively. The signals
S1,
S2 and
S3 are then defined as follows:
S1 = 3
cos(2
πf1t +
φ1),
S2 = 5
cos(2
πf2t +
φ2) and
S3 = 8
cos(2
πf3t +
φ3). The resulting signal
X(
t) =
S1 +
S2 +
S3 is then received by a sensor. With the sampling frequency of 100 Hz, signal
X(
t) is processed to reveal its power spectrum and its bispectrum values, and the result can be seen in
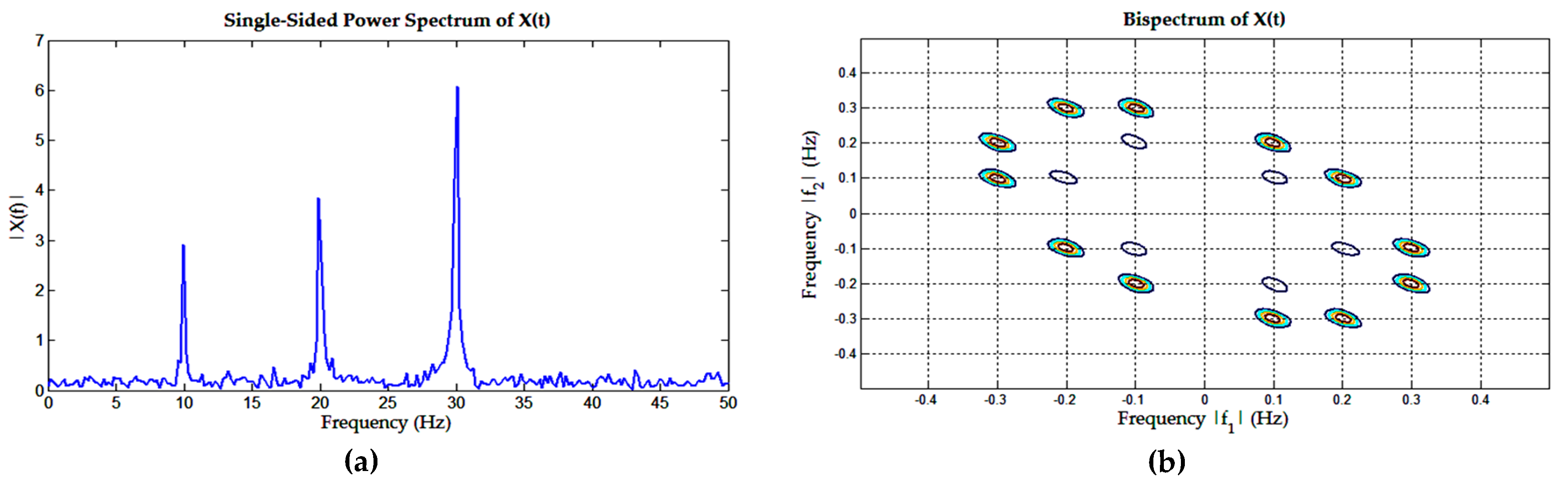
Figure 2. The power spectrum (
Figure 2a) produced using FFT showed that the dominant frequencies are 10, 20 and 30 Hz; however, it does not reveal the fact that the frequency 30 Hz is a resulting combination of frequencies 10 and 20 Hz. On the other hand, in bispectrum (
Figure 2b), the pair of normalized frequencies 0.1 and 0.2 Hz (equal to the original frequencies 10 and 20 Hz), on coordinate (0.1,0.2) and (0.2,0.1), show a high spectrum, which means that they are strongly correlated because they produce the 30-Hz signal. Supposing that the signal
S3 is noise, by using a bispectrum analysis, the noise signal will not be taken into consideration. Thus, we can conclude that through bispectrum analysis, the main frequency components are revealed while the other frequencies are eliminated. Because bispectrum analysis provides more information than the power spectrum analysis, it is expected that the use of bispectrum analysis in the EEG signals’ feature extraction process will increase the recognition rate.
The autocorrelation of a signal is the correlation between the signal and itself at a different time; for example, at time
t and at time
t + m. The autocorrelation function of
x(
n) can be expressed as the expectation of stationary process, defined as:
The higher order moments are a natural generalization of autocorrelation, and the cumulants are a nonlinear combination of moments. The first order cumulant (C1x) from stationary process is the mean, C1x = E {x(t)}, with E{.} an expectation notation. The higher order cumulants have the property invariant to the shift of the mean; therefore, it is practical to describe the cumulants under zero mean assumption, meaning that if the mean of a process is not zero, then as the first step, the mean should be subtracted from each value. The second order polyspectrum, which is the power spectrum, is defined as the Fourier transform of the second order cumulant, while the third order polyspectrum, which is the bispectrum, is defined as the Fourier transform of the third order cumulant.
For the third order cumulant, the autocorrelation of a signal will be calculated until the distance
t + τ1 and
t + τ2, where
τ1 and
τ2 are the lag. The third order cumulant from a zero mean stationary process is defined as [
48]:
Thus, the bispectrum,
, defined as the Fourier transform of the third order cumulant, becomes:
The bispectrum has a specific symmetrical property that is derived from the symmetrical property of the third order cumulant [
46], which results in similarity of the six regions of the bispectrum, shown as follows:
Because the bispectrum matrix has a redundant region as described in (4), it is sufficient to extract features from only one quadrant of the bispectrum matrix, and because the FFT in the calculation of bispectrum value may result in non-imaginary values, then the absolute value of the bispectrum is used. The pseudocode of the bispectrum calculation in the feature extraction process for an EEG signals, derived from (1)−(4), is summarized in Algorithm 1 as follows:
| Algorithm 1: Bispectrum calculation in feature extraction algorithm. |
Define: lag For channel = 1 to C Calculate autocorrelation signal X to the defined lag as (2) Construct symmetrical matrix C3x for the first quadrant Construct cumulant matrix C3x at other quadrant as (4) Calculate bispectrum as (3) Take only 1 quadrant of bispectrum matrix Take the absolute value of the bispectrum matrix End For
|
3.4.2. The 3D Pyramid Filter
The output of the previous step is one quadrant bispectrum matrix, which is a 64 × 64 matrix for each of the 32 EEG channels, equaling a total of 131,072 elements; therefore, the number of elements is too large to be used for calculating the extracted features. To reduce the size of these feature vectors, we have proposed a filtering mechanism by utilizing 3D pyramid shape filters for the bispectrum elements value so that the bispectrum value at the center of the pyramid becomes the most significant value. From the filtered area, one or more statistical properties are derived and calculated as the features-extracted data, which will be described in the next subsection.
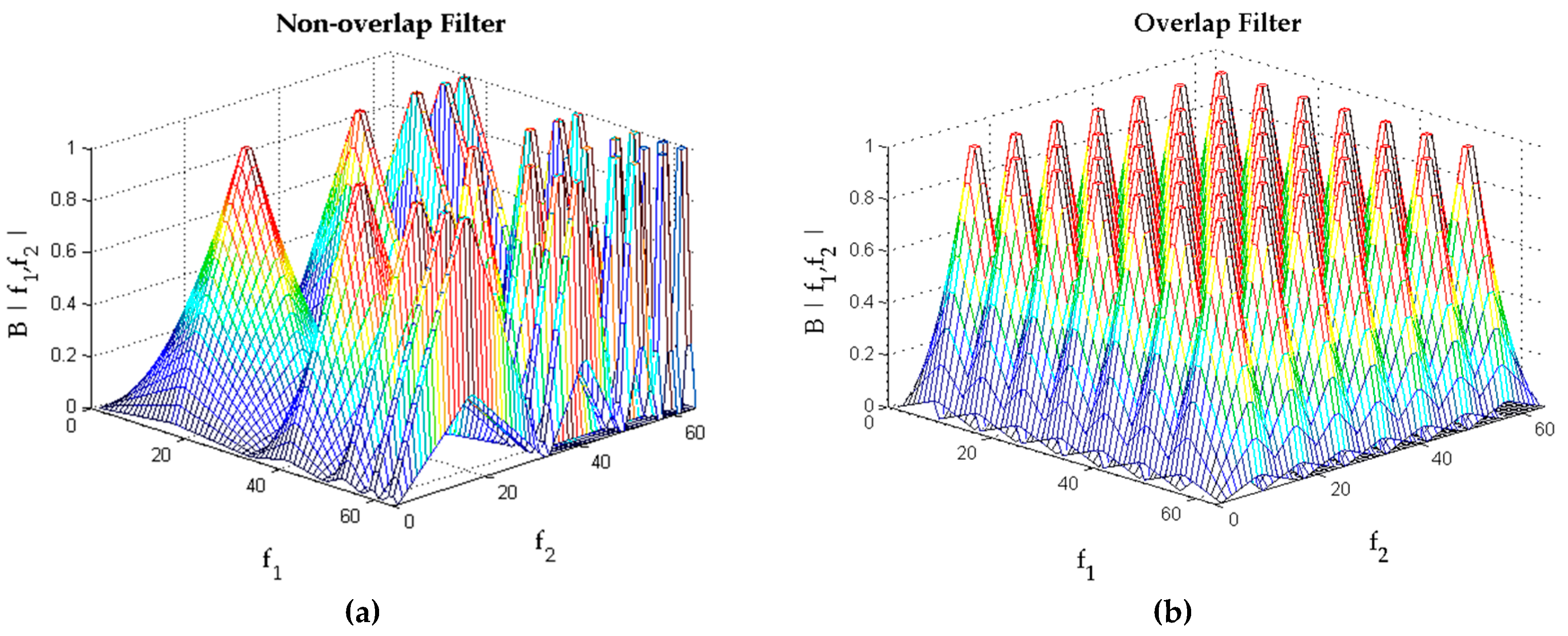
To find the best filtering mechanism, two filter models are proposed, as shown in
Figure 3: the non-overlapping filters with various sizes at the base and the overlapping filters with equal sizes at the base.
Figure 2b shows that the bispectrum usually gathers near the center; thus, in this area, the filters are dense and the bases are small. At the higher frequencies, the bispectrum usually has a very low value, so in this area, the filters are sparse, and the bases are large. Therefore, in the non-overlapping filters, we use 5 × 5 filters (
Figure 3a), with the size of the filter varying (32, 16, 8, 4 and 4) along the
x- and
y-axis.
By increasing the number of filters and overlapping the filters, the quantization process is expected to provide a better approximation; we therefore increased the number of filters up to 7 × 7 and constructed the filters with overlapping areas at the base (
Figure 3b). The size of the bases is 16 × 16 equal elements, and there are 50% overlapping areas with the adjacent filters. However, the complexity and the resulting feature vector’s size of the 7 × 7 filter should be considered as a trade-off.
The height of the overlapping and non-overlapping filters in both pyramid models is equal: in this case, it is one. To filter the bispectrum matrix, each selected area was multiplied by the corresponding filter. The filtering process results in several filtered matrices with their respective bispectrum values, and from these filtered bispectrum matrices, the features are calculated and extracted. The pseudocode of the filtering mechanism for the bispectrum matrices is summarized in Algorithm 2 as follows:
| Algorithm 2: Bispectrum 3D filtering for feature extraction algorithm. |
Define: M = number of column filter N = number of row filter For channel = 1 to C for m = 1 to M for n = 1 to N Calculate length of rectangle base of the filter Calculate width of rectangle base of the filter Construct 2D filter for length side of rectangle with triangle type Construct 2D filter for width side of rectangle with triangle type Construct 3D pyramid filter based on 2D filter Take bispectrum value with the length and width of the rectangle Multiply bispectrum value with the 3D filter Perform calculation for feature Take only half of the triangle (non-redundant) of the feature matrix Transform feature matrix to feature vector end end end
|
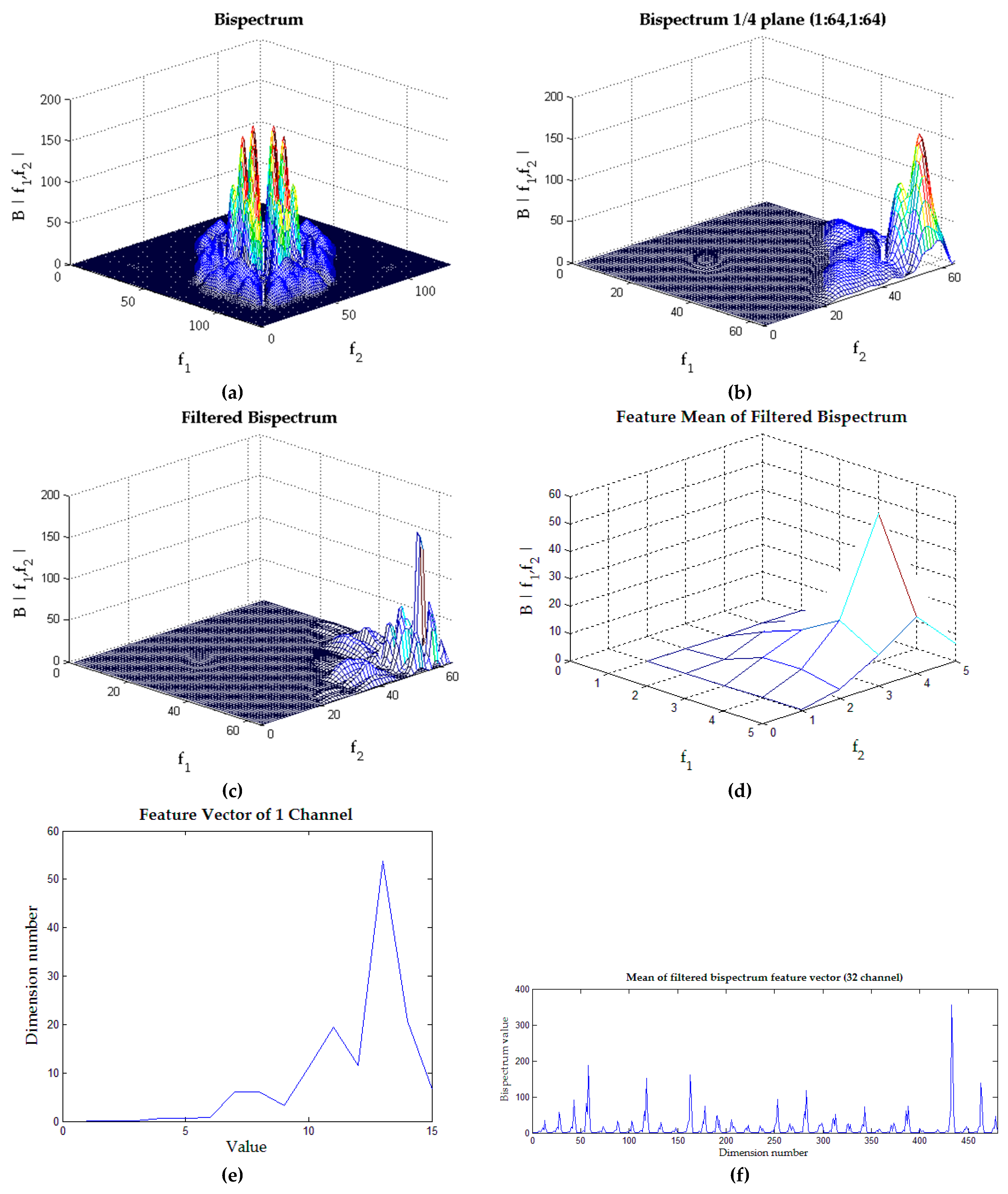
The implementation of the filtering process using the 3D pyramid filters is illustrated in
Figure 4. In this example, the effect of 3D pyramid filtering on the bispectrum matrix from the EEG signal of Person 1-Video 1-Channel 1 is shown. The original bispectrum matrix is shown in
Figure 4a, and then, one-quarter is extracted, resulting in the 64 × 64 matrix shown in
Figure 4b. The filtering process began by multiplying this matrix with the constructed 3D pyramid filters, and for this example, we use the 5 × 5 non-overlapping filters (
Figure 3a). The multiplication process was conducted for each area of the matrix according to the size of the pyramid base; for example, the bispectrum matrix region (0:32,0:32) was multiplied by the filter whose base size is 32 × 32 and whose height is one. Therefore, for 5 × 5 non-overlapping filters, there will be 25 times the filtering process through this multiplication step, and the result is shown in
Figure 4c. The calculation of features from the filtered bispectrum matrix is then conducted; in this example, the features are the mean (average) of each filtered bispectrum matrix, and the result is shown in
Figure 4d.
As the bispectrum matrix shown in
Figure 4b is asymmetrical, then the feature-extracted matrix (such as in
Figure 4d) is also asymmetrical; therefore, it is sufficient to take just half of the whole matrix. For example, in the 5 × 5 filters, the number of non-redundant elements of the matrix equal to the sum of arithmetic sequence
, resulting in 15 dimensions of feature vectors, as shown in
Figure 4e. Thus, for the full 32 EEG channels used, the dimension of feature vectors will be 15 × 32 = 480, as shown in
Figure 4f. Obviously, for the 7 × 7 filters, there will be 28 dimensions of feature vector per channel, resulting in 28 × 32 = 896 dimensions of feature vectors for the whole channel.
3.4.3. Feature Types Based on the Bispectrum
Bispectrum analysis has also been used for an EEG-based emotion recognition system by Kumar [
20], with several entropies, values and moments taken as the features, which we adapted as one of the feature extraction modes in our experiments (Mode #1 feature extraction); however, this feature produces a high dimension of feature vectors and thus requires a high computation cost. In this work, we propose as simpler feature, which is the mean of the bispectrum value, as Mode #3 feature extraction, producing only one feature value for each area of the filter, thereby reducing the dimension of the feature vectors.
In previous work, we have found that the energy percentage performed well as the feature of an EEG signal [
49]; therefore, here, we considered the percentage value as the feature. The percentage value of entropies and moments of Mode #1 becomes the Mode #2 feature extraction, and the percentage of the mean becomes Mode #4 feature extraction. Suppose
Fm is a feature and
M is the number of features per channel; then, the percentage value of the feature
FPm is defined as: