A Flexible Pattern-Matching Algorithm for Network Intrusion Detection Systems Using Multi-Core Processors
Abstract
:1. Introduction
2. Related Work
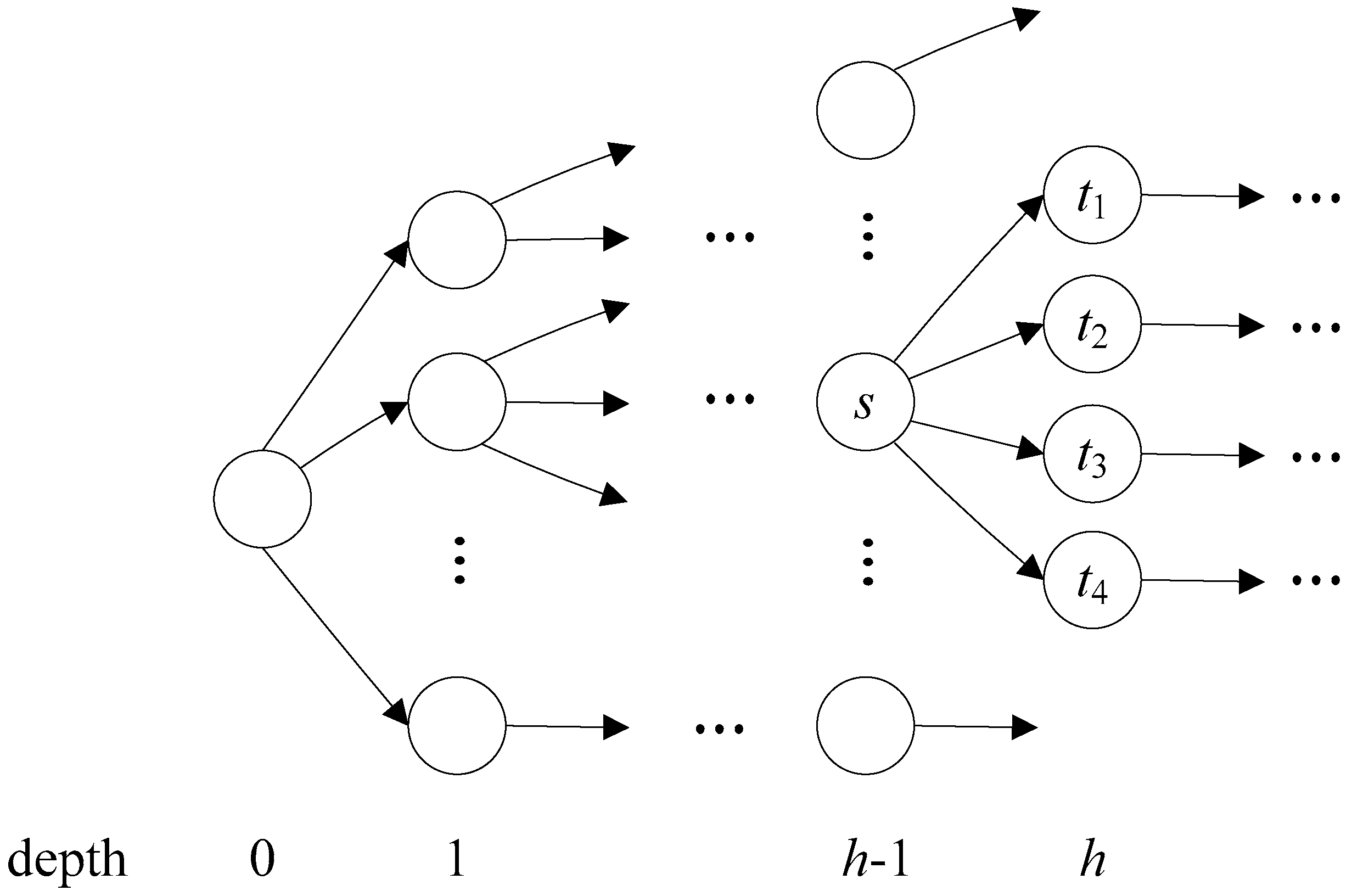
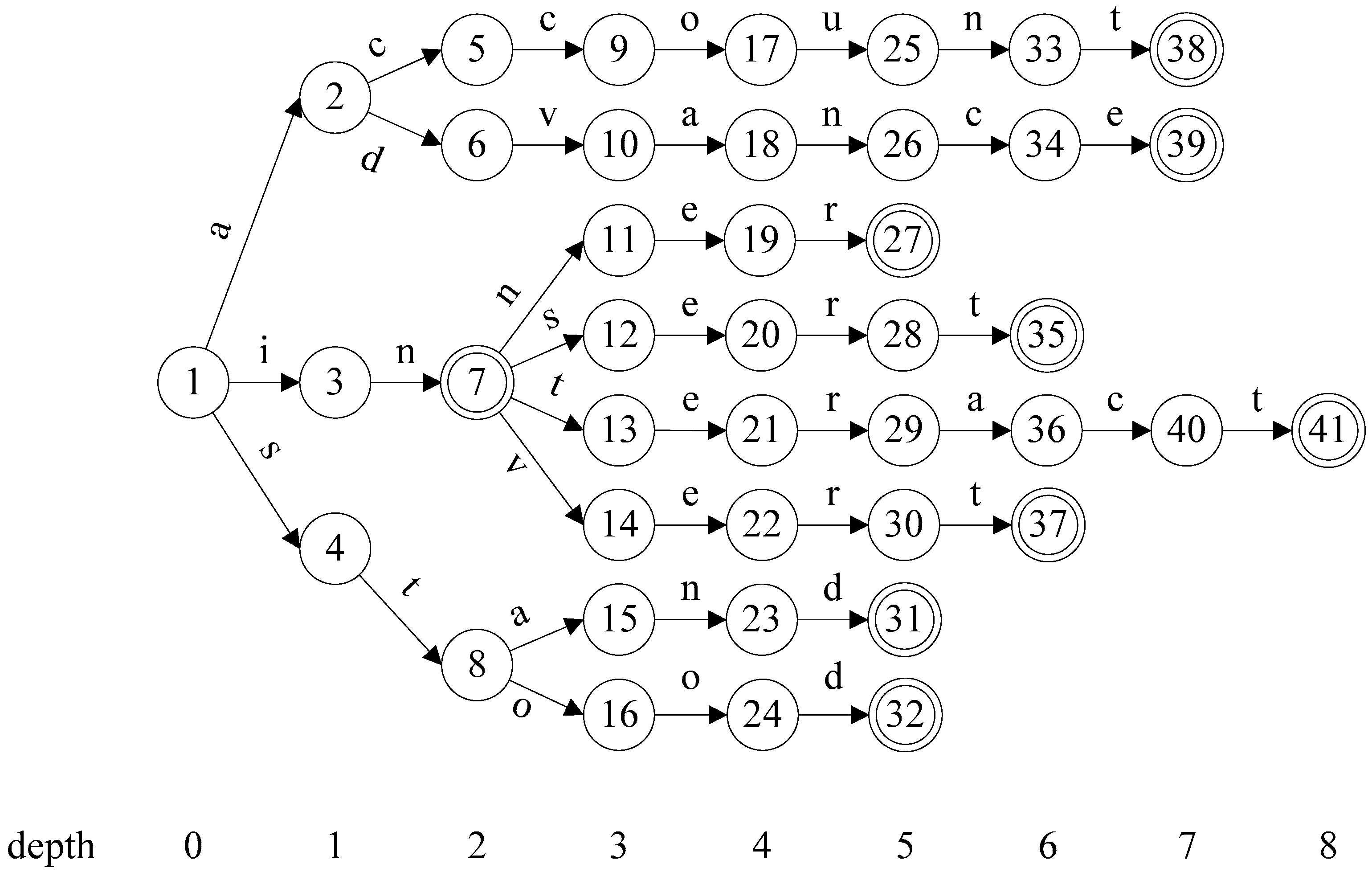
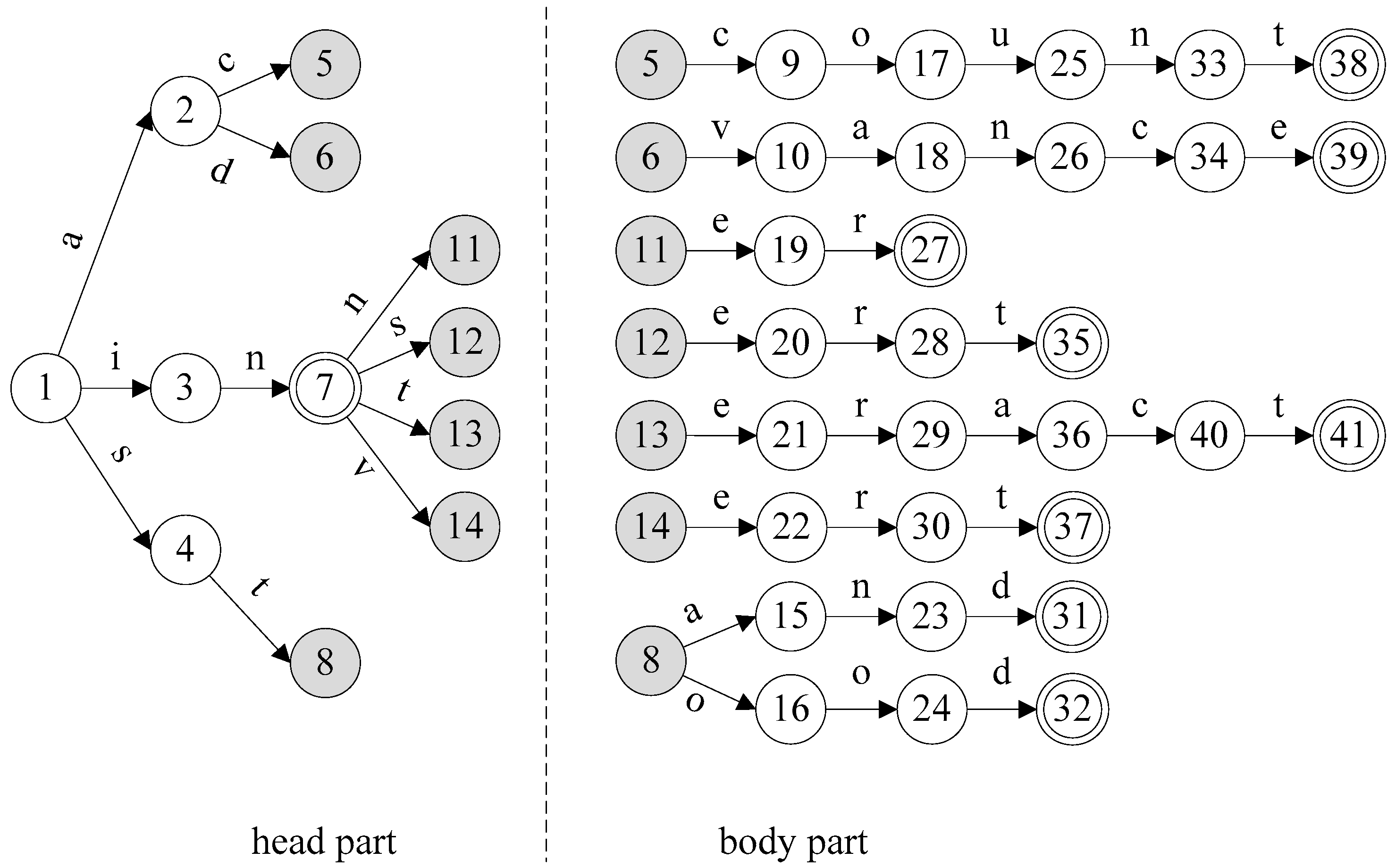
3. Flexible Head-Body Matching Algorithm
| Algorithm 1 Partitioning Algorithm |
| Input: AC_DFA (a DFA constructed with AC algorithm) HSIZE (maximum level of head size) Output: HEAD (set of head states) 1 HEAD ← ; 2 for h ← 0 to AC_DFA.MAX_DEPTH do 3 if HEAD.size() + AC_DFA.depth[h].size() HSIZE then 4 HEAD = HEAD AC_DFA.depth[h]; 5 else 6 T ← ; 7 foreach state p in AC_DFA.level[h-1] do // p.childStates() returns the set of child states of state p. 8 T ← T (p, p.childStates().size()); 9 end 10 Sort T by the second coordinate in descending order; 11 foreach (s,n) in T do 12 if HEAD.size() + n HSIZE then 13 foreach state t in s.childStates() do 14 HEAD ← HEAD t; 15 end 16 if HEAD.size() = HSIZE then 17 return HEAD; 18 end 19 end 20 end 21 break; 22 end 23 end 24 return HEAD; |
4. Experiment Evaluation
4.1. Setup
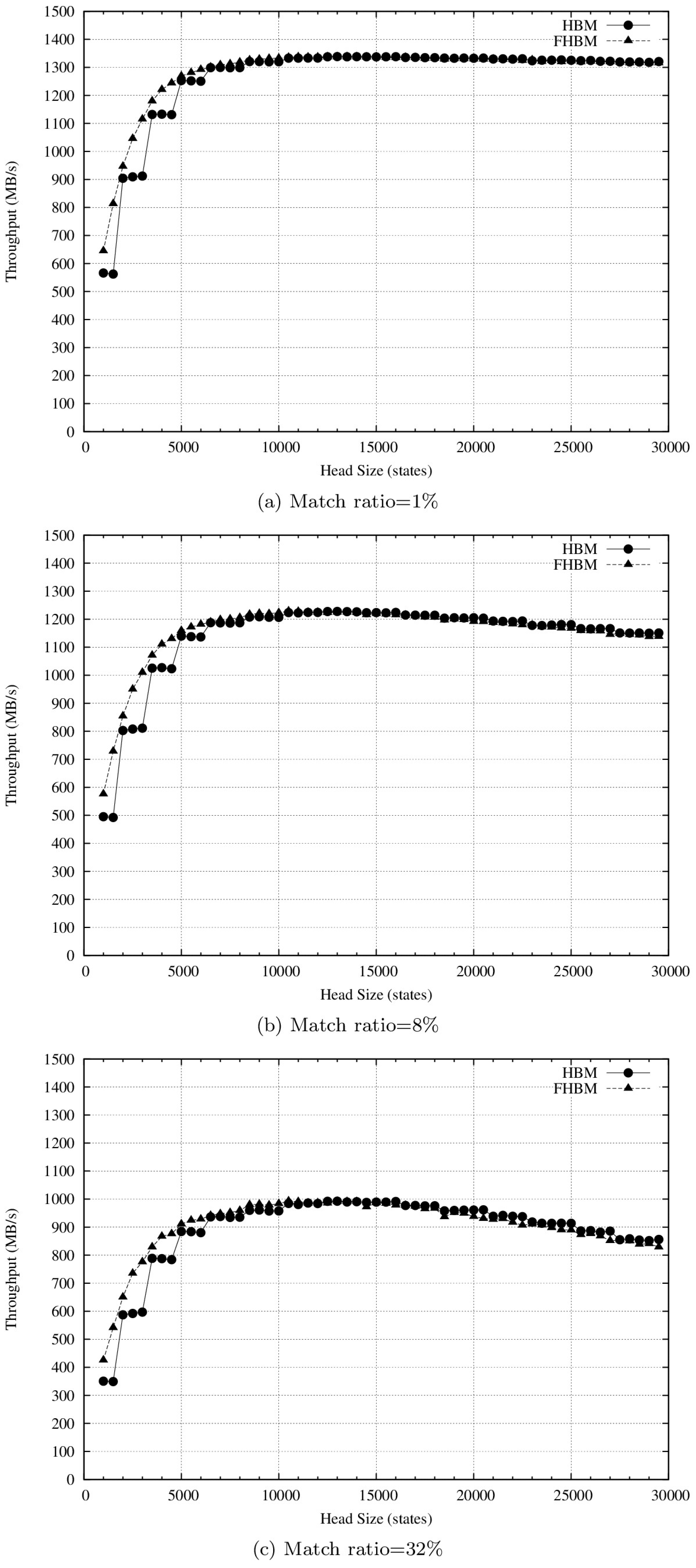
4.2. Results and Discussion
5. Conclusion and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Handley, M.; Paxson, V.; Kreibich, C. Network intrusion detection: Evasion, traffic normalization, and end-to-end protocol semantics. In Proceedings of the Symposium on USENIX Security, Washington, DC, USA, 13–17 August 2001; pp. 115–131. [Google Scholar]
- Kruegel, C.; Valeur, F.; Vigna, G.; Kemmerer, R. Stateful intrusion detection for high-speed networks. In Proceedings of the Symposium on Security and Privacy, Oakland, CA, USA, 12–15 May 2002; pp. 285–293. [Google Scholar]
- Paxson, V. Bro: A system for detecting network intruders in real-time. Comput. Netw. 1999, 31, 2435–2463. [Google Scholar] [CrossRef]
- Tian, D.; Liu, Y.H.; Xiang, Y. Large-scale network intrusion detection based on distributed learning algorithm. Int. J. Inf. Secur. 2009, 8, 25–35. [Google Scholar] [CrossRef]
- Beghdad, R. Critical study of neural networks in detecting intrusions. Comput. Secur. 2009, 27, 168–175. [Google Scholar] [CrossRef]
- Wu, J.; Peng, D.; Li, Z.; Zhao, L.; Ling, H. Network intrusion detection based on a general regression neural network optimized by an improved artificial immune algorithm. PLoS ONE 2015, 10, e0120976. [Google Scholar] [CrossRef] [PubMed]
- Antonatos, S.; Anagnostakis, K.G.; Markatos, E.P. Generating realistic workloads for network intrusion detection systems. In Proceedings of the 4th international workshop on Software and performance (WOSP’04), Redwood Shores, CA, USA, 14–16 January 2004; pp. 207–215. [Google Scholar]
- Cabrera, J.B.; Gosar, J.; Lee, W.; Mehra, R.K. On the statistical distribution of processing times in network intrusion detection. In Proceedings of the Conference on Decision and Control, Woburn, MA, USA, 14–17 December 2004; Volume 1, pp. 75–80. [Google Scholar]
- Erdem, O. Tree-based string pattern matching on FPGAs. Comput. Electr. Eng. 2016, 49, 117–133. [Google Scholar] [CrossRef]
- Kim, H.; Choi, K.-I. A pipelined non-deterministic finite automaton-based string matching scheme using merged state transitions in an FPGA. PLoS ONE 2016, 11, e0163535. [Google Scholar] [CrossRef] [PubMed]
- Kim, H. A failureless pipelined Aho-Corasick algorithm for FPGA-based parallel string matching engine. Lect. Notes Electr. Eng. 2015, 339, 157–164. [Google Scholar]
- Chen, C.C.; Wang, S.D. An efficient multicharacter transition string-matching engine based on the Aho-Corasick algorithm. ACM Trans. Archit. Code Optim. 2013, 10, 1–22. [Google Scholar] [CrossRef]
- Kaneta, Y.; Yoshizawa, S.; Minato, S.I.; Arimura, H.; Miyanaga, Y. A Dynamically Reconfigurable FPGA-Based Pattern Matching Hardware for Subclasses of Regular Expressions. IEICE Trans. Inf. Syst. 2013, E95-D, 1847–1857. [Google Scholar] [CrossRef]
- Tsai, H.J.; Yang, K.H.; Peng, Y.C.; Lin, C.C.; Tsao, Y.H.; Chang, M.F.; Chen, T.F. Energy-efficient TCAM search engine design using priority-decision in memory technology. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 962–973. [Google Scholar] [CrossRef]
- Peng, K.; Tang, S.; Chen, M.; Dong, Q. Chain-based DFA deflation for fast and scalable regular expression matching using TCAM. In Proceedings of the ACM/IEEE Seventh Symposium on Architectures for Networking and Communications Systems, Brooklyn, NY, USA, 3–4 October 2011; pp. 24–35. [Google Scholar]
- Liu, R.T.; Huang, N.F.; Chen, C.H.; Kao, C.N. A fast string-matching algorithm for network processor-based intrusion detection system. ACM Trans. Embedded Comput. Syst. 2004, 3, 614–633. [Google Scholar] [CrossRef]
- Bacon, D.F.; Rabbah, R.; Shukla, S. FPGA programming of the masses. Commun. ACM 2013, 56, 56–63. [Google Scholar] [CrossRef]
- Scarpazza, D.P.; Villa, O.; Petrini, F. Exact multi-pattern string matching on the cell/B.E. processor. In Proceedings of the Conference on Computing Frontiers, Ischia, Italy, 5–7 May 2008; pp. 33–42. [Google Scholar]
- Schuff, D.L.; Choe, Y.R.; Pai, V.S. Conservative vs. optimistic parallelization of stateful network intrusion detection. In Proceedings of the International Symposium on Performance Analysis of Systems and Software, Philadelphia, PA, USA, 20–22 April 2008; pp. 32–43. [Google Scholar]
- Vallentin, M.; Sommer, R.; Lee, J.; Leres, C.; Paxson, V.; Tierney, B. The NIDS cluster: Scalable, stateful network intrusion detection on commodity hardware. In Proceedings of the International workshop on Recent Advances in Intrusion Detection, Queensland, Australia, 5–7 September 2007; pp. 107–126. [Google Scholar]
- Lee, C.L.; Lin, Y.S.; Chen, Y.C. A hybrid CPU/GPU pattern-matching algorithm for deep packet inspection. PLoS ONE 2015, 10, e0139301. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.S.; Lee, C.L.; Chen, Y.C. A capability-based hybrid CPU/GPU pattern matching algorithm for deep packet inspection. Int. J. Comput. Commun. Eng. 2016, 5, 321–330. [Google Scholar] [CrossRef]
- Lin, Y.S.; Lee, C.L.; Chen, Y.C. Length-bounded hybrid CPU/GPU pattern matching algorithm for deep packet inspection. Algorithms 2017, 10. [Google Scholar] [CrossRef]
- Tran, N.P.; Lee, M.; Choi, D.H. Cache locality-centric parallel string matching on many-core accelerator chips. Sci. Program. 2015, 2015, 1–20. [Google Scholar] [CrossRef]
- Zha, X.; Sahni, S. GPU-to-GPU and host-to-host multipattern string matching on a GPU. IEEE Trans. Comput. 2013, 62, 1156–1169. [Google Scholar] [CrossRef]
- Tumeo, A.; Villa, O.; Chavarria-Miranda, D.G. Aho-corasick string matching on shared and distributed-memory parallel architecture. IEEE Trans. Parallel Distrib. Syst. 2012, 23, 436–443. [Google Scholar] [CrossRef]
- Yang, Y.H.; Prasanna, V.K. Robust and scalable string pattern matching for deep packet inspection on multicore processors. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 2283–2292. [Google Scholar] [CrossRef]
- Knuth, D.E.; Morris, J.; Pratt, V. Fast pattern matching in strings. SIAM J. Comput. 1977, 6, 127–146. [Google Scholar] [CrossRef]
- Boyer, R.S.; Moore, J.S. A fast string searching algorithm. Commun. ACM 1977, 20, 762–772. [Google Scholar] [CrossRef]
- Aho, A.V.; Corasick, M.J. Efficient string matching: An aid to bibliographic search. Commun. ACM 1975, 18, 333–340. [Google Scholar] [CrossRef]
- Manber Wu, S.; Manber, U. A Fast Algorithm for Multi-Pattern Searching; Technical Report TR-94-17; Department of Computer Science, University of Arizona: Tucson, AZ, USA, 1994; Available online: http://webglimpse.net/pubs/TR94-17.pdf (accessed on 24 May 2017).
- Tuck, N.; Sherwood, T.; Calder, B.; Varghese, G. Deterministic memory-efficient string matching algorithms for intrusion detection. In Proceedings of the IEEE INFOCOM, Hong Kang, China, 7–11 March 2004; pp. 333–340. [Google Scholar]
- Bremler-Barr, A.; Hay, D.; Koral, Y. CompactDFA: Scalable Pattern Matching Using Longest Prefix Match Solutions. IEEE/ACM Trans. Netw. 2014, 22, 415–428. [Google Scholar] [CrossRef]
- Liu, C.; Pan, Y.; Chen, A.; Wu, J. A DFA with extended character-set for fast deep packet inspection. IEEE Trans. Comput. 2014, 63, 1925–1937. [Google Scholar] [CrossRef]
- Head-body String Matching. Available online: http://sourceforge.net/projects/hbsm (accessed on 23 February 2017).
- Snort.Org. Available online: http://www.snort.org (accessed on 23 February 2017).
- ClamAV. Available online: http://www.clamav.net (accessed on 23 February 2017).


| Component | Specification | |
|---|---|---|
| Main board | Brand/Model | Asus/P8H77-V |
| CPU | Brand/Model | Intel/i7-3770 |
| Number of cores | 4 | |
| Frequency | 3.4 Ghz | |
| L1 cache size | 256 KB | |
| L2 cache size | 1024 KB | |
| L3 cache size | 8 MB | |
| Main memory | Type | DDR3 |
| Size | 8 GB | |
| Frequency | 1600 Mhz | |
| Pattern Set | Number of Patterns | Number of Characters | Number of Depths |
|---|---|---|---|
| Snort | 8673 | 196,967 | 232 |
| ClamAV type 1 | 5248 | 498,014 | 362 |
| ClamAV type 3 | 2899 | 262,256 | 382 |
| Pattern Length | Snort | ClamAV Type 1 | ClamAV Type 3 | |||
|---|---|---|---|---|---|---|
| ≤ 4 | 977 | (11.3%) | 56 | (1.1%) | 7 | (0.2%) |
| 5–8 | 1559 | (18.0%) | 81 | (1.5%) | 29 | (1.0%) |
| 9–12 | 1284 | (14.8%) | 103 | (2.0%) | 53 | (1.8%) |
| 13–16 | 1045 | (12.0%) | 92 | (1.8%) | 62 | (2.1%) |
| > 16 | 3808 | (43.9%) | 4916 | (93.7%) | 2748 | (94.8%) |
| Total count | 8673 | 5248 | 2899 | |||
| Depths | Snort | ClamAV Type 1 | ClamAV Type 3 |
|---|---|---|---|
| ≤2 | 2039 | 3499 | 675 |
| ≤3 | 6204 | 7813 | 1765 |
| ≤4 | 11,100 | 12,349 | 3110 |
| ≤5 | 16,340 | 17,093 | 4652 |
| ≤6 | 21,564 | 21,919 | 6348 |
| ≤7 | 26,785 | 26,779 | 8145 |
| ≤8 | 31,955 | 31,642 | 10,050 |
| Depth | Match Ratio | |||||
|---|---|---|---|---|---|---|
| 1% | 2% | 4% | 8% | 16% | 32% | |
| 1 | 1726 | 1710 | 1680 | 1617 | 1494 | 1244 |
| 2 | 1919 | 1902 | 1868 | 1801 | 1666 | 1393 |
| 3 | 612 | 607 | 599 | 581 | 546 | 475 |
| 4 | 158 | 159 | 159 | 160 | 161 | 164 |
| 5 | 34 | 35 | 38 | 44 | 55 | 78 |
| 6 | 16 | 17 | 20 | 26 | 39 | 63 |
| 7 | 5 | 7 | 10 | 16 | 29 | 53 |
| 8 | 2 | 3 | 6 | 12 | 23 | 46 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-L.; Yang, T.-H. A Flexible Pattern-Matching Algorithm for Network Intrusion Detection Systems Using Multi-Core Processors. Algorithms 2017, 10, 58. https://doi.org/10.3390/a10020058
Lee C-L, Yang T-H. A Flexible Pattern-Matching Algorithm for Network Intrusion Detection Systems Using Multi-Core Processors. Algorithms. 2017; 10(2):58. https://doi.org/10.3390/a10020058
Chicago/Turabian StyleLee, Chun-Liang, and Tzu-Hao Yang. 2017. "A Flexible Pattern-Matching Algorithm for Network Intrusion Detection Systems Using Multi-Core Processors" Algorithms 10, no. 2: 58. https://doi.org/10.3390/a10020058
APA StyleLee, C.-L., & Yang, T.-H. (2017). A Flexible Pattern-Matching Algorithm for Network Intrusion Detection Systems Using Multi-Core Processors. Algorithms, 10(2), 58. https://doi.org/10.3390/a10020058






