1. Introduction
Solving optimization problems using exhaustive search techniques is not always the best way. In fact, in the problems with huge dimensional space search, the classical optimization algorithms do not provide a suitable solution. Many researchers take on the problem to optimize objective functions by designing algorithms inspired by the behaviors of natural phenomena. The issue of tuning some parameters of a search algorithm is one of the most important areas of research in evolutionary computation [
1]. This research line was followed by Montiel et al. [
2] and Castillo et al. [
3], which treated the idea of adjusting an evolutionary algorithm.
Among the intelligent evolutionary optimization methods, the Genetic Algorithms (GA) [
4] are heuristic approaches well suited to solve complex computational problems [
5,
6,
7,
8,
9]. Another evolutionary algorithm is the Particle Swarm Optimization (PSO), which depends on the simulation of social behavior [
10]. This search method has been applied in various optimization problems [
11,
12,
13,
14,
15]. An algorithm that operates through the computational steps of a standard evolutionary algorithm is the Differential Evolution (DE). It employs the difference of the parameter vectors to explore the objective function landscape [
16]. DE algorithms are applied in many fields [
17,
18,
19,
20,
21].
Recently, a new search algorithm based on the law of gravity has been proposed: the Gravitational Search Algorithm (GSA) [
22]. This algorithm is based on Newton’s law of gravity, which states that each particle attracts every other particle with a force called gravitational force [
23]. The speed of the search process of GSA depends on parameters that play the main role in the search process. These parameters can be optimized by using evolutionary algorithms such as PSO and DE. However, they may be tuned through fuzzy systems. Askari and Zahiri [
24,
25] designed fuzzy controllers able to check the search parameters of GSA. In order to improve the performances of GSA, suitable fuzzy logic controllers have been proposed [
26,
27,
28].
Improvements of the original version of GSA have been achieved by using the binary discrete space. In fact, there are many optimization problems [
13,
29,
30,
31,
32,
33,
34], where the solutions are encoded as binary vectors. Rashedi et al. [
35] proposed a binary version of GSA, called BGSA. This work shows the efficiency of BGSA in solving various nonlinear benchmark functions.
This paper aims to improve GSA for certain benchmark functions. The task is to design a fuzzy system able to tune suitable parameters of GSA, taking into account the exploration, the exploitation capabilities and escaping being trapped in local optima. The novelty of the proposed approach is the choice of adjusting, in a fuzzy way, a specific GSA parameter, which may be used both as fuzzy input and output. The fuzzy input is the parameter value in the previous state, whereas the fuzzy output is the GSA parameter value in the current state. In this way, the GSA parameter is tuned depending on the parameter value in the previous state and the remaining fuzzy inputs. Moreover, to assure an intelligent strategy for exploration and exploitation, the fuzzy rules are designed to prevent problems of getting trapped into local optima and premature convergence. The main idea is to design a Fuzzy Gravitational Search Algorithm (FGSA) where the membership functions of the fuzzy controller are optimized by applying evolutionary algorithms such as GA, PSO and DE. The complexity problem is avoided because the fuzzy controller is optimized just one time and than used in GSA. Therefore, FGSA contains the contribution of the optimized fuzzy controller, which does not add considerable complexity with respect to GSA. Finally, the challenge of this work is to improve the average best so far solution of [
22,
26,
27,
28,
35] for certain benchmark functions.
The paper is organized as follows.
Section 2 describes GSA with the same notation of [
22]. The revised GSA optimized through intelligent techniques is described in
Section 3.
Section 4 contains the discussion of the simulation results of the proposed algorithms.
Section 5 concludes the paper.
2. The Gravitational Search Algorithm
The gravitational search algorithm was introduced for the first time by Rashedi et al. in [
22]. Their main idea was to consider the searcher agents as a collection of masses that interact with each other based on Newtonian gravity and the laws of motion.
In nature, there are four fundamental interactions [
36]: the electromagnetic force, the weak nuclear force, the strong nuclear force and the gravitational force. Newton’s law of gravity states that every point mass attracts every single other point mass by a force pointing along the line intersecting both points [
23,
36]. The gravitational force
F is defined by the formula (
1) where
and
are the masses of the particles,
G is the gravitational constant and
R is the distance between the two particles. Note that, the force
F is directly proportional to the product of the masses
and
and inversely proportional to the square of the distance between the particles.
The second law of Newton [
23] states that the ratio between a force
F applied on a particle of mass
M is equal to the acceleration
a of the particle (see (
2)).
In order to describe the gravitational search algorithm, the definitions of active gravitational mass, passive gravitational mass and inertial mass are needed. The active gravitational mass is a measure of the strength of the gravitational field due to a particular object. The passive gravitational mass is a measure of the strength of an object’s interaction with the gravitational field. The inertial mass is a measure of an object resistance of changing its state of motion when a force is applied.
Let
be the position of the
i-th agent for
where
represents the position of the
i-th agent in the
d-th dimension. The force acting on mass
i from mass
j at a specific time
t is denoted with
(see (
3)), where
is the gravitational constant, which depends on time,
is the active gravitational mass related to agent
j,
is the passive gravitational mass related to agent
i,
is a small constant and
is the Euclidean distance between two agents
i and
j as defined in (
4).
In the gravitational search algorithm,
is defined as (
5) [
22], where
is the initial value of
G,
T is the total number of iterations and
is a parameter.
The total force
that acts on agent
i in a dimension
d is a randomly weighted sum of
d-th components of the forces exerted from other agents (see Equation (
6)). In (
6),
is a random number that lies between
.
By the law (
2), it follows that the acceleration of the agent
i at time
t and in direction
d-th,
, is given by (
7), where
is the inertial mass of the
i-th agent.
The velocity of an agent at
time is a fraction of the velocity at
t time added to its acceleration
(see (
8) with
uniform random variable in the interval
). Moreover, the position at
time
is calculated through (
9).
The gravitational and inertial masses are updated by the Equations (
10)–(
12), where
represents the fitness value of the agent
i at time
t, and
and
are defined as in (
13) and (
14) for minimization (maximization) problems.
In order to find a good compromise between exploration and exploitation, the number of agents with a lapse of time has to be reduced. To improve the performance of GSA by controlling exploration and exploitation, only the
agents will attract the others [
22]. Therefore, Equation (
6) can be rewritten as in (
15):
Algorithm 1 describes the gravitational search algorithm.
| Algorithm 1 |
| S1. First of all, the algorithm initializes, in a random way, the position X of the agents in the search space. The initialization procedure depends on the number of agents n, the dimension of the test functions r and the allowable range [up, down] for the search space. The positions X’s are calculated by generating n × r random numbers between 0 and 1 and normalizing them on the range [up, down]. In other terms, the positions are computed by the formula X(i, j) = rand(i, j) * (down − up) + down, with i = 1, ..., n and j = 1, ..., r. |
| S2. Once the positions are generated, the algorithm computes the fitness of the agents for a certain function. In other words, the value of the objective function is computed. Note that the fitness depends on the position of the agents and the dimension of the function. |
| S3. The value of the fitness is necessary to calculate the mass of each agent mi(t) for i = 1, 2, ..., n. (see (11)). On the other hand, mi(t) depends on best(t) and worst(t) (Equations (13) and (14), respectively), which also depend on fitness. Subsequently, the gravitational constant G(t), as defined in (5), is computed. |
| S4. According to G(t), the total force in different directions is calculated. In particular, the algorithm computes the Euclidean distance between two agents Rij(t) and the force acting on mass i from mass j at a specific time t (see (3)). Subsequently, the total force (see (6)) is computed. Therefore, the acceleration of the agents, their velocity and position at t time are calculated by means of (7), (8) and (9), respectively. |
| S5. The steps from S2–S4 are repeated until a certain number of iterations is reached. |
3. The Evolutionary Fuzzy Algorithms
The first task of our study is the choice of the GSA parameter, which must be tuned. Because the gravitational constant
G defined in (
5) has a significant effect on the control of the exploration versus exploitation propensities of the particle swarm [
25], the parameter
of (
5) is chosen. The adjusting of
is accomplished through a fuzzy controller optimized by GA, PSO and DE.
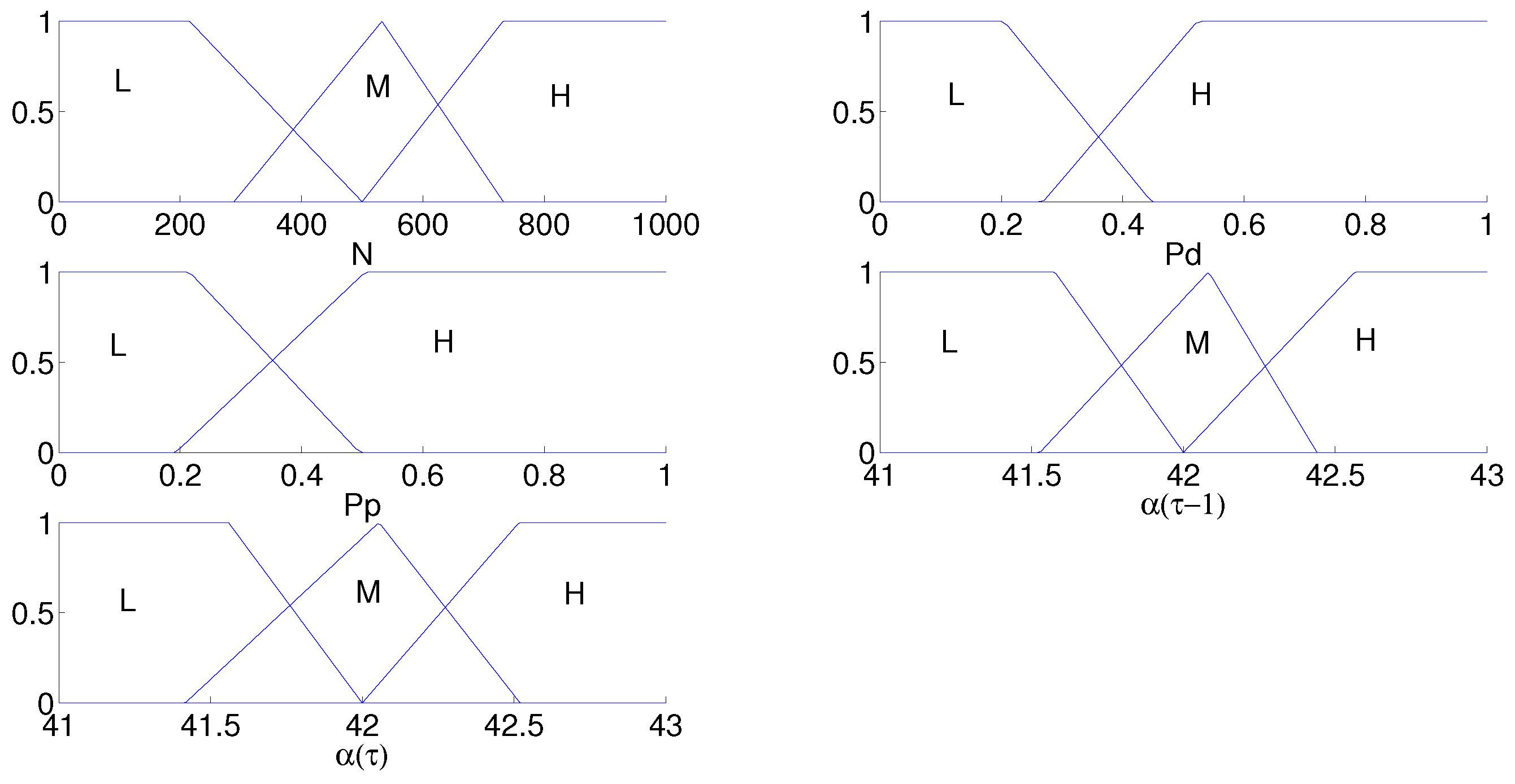
The first step to design a fuzzy controller is the definition of the fuzzy inputs and outputs. The number of fuzzy inputs and outputs depends on the specific problem. In this case, four fuzzy inputs are defined. The first input is the iteration number
. Let
be the population diversity at the
i-th iteration, with
; by considering the (
4), the population diversity is defined as in (
16), where
,
,
are the mean, min and max Euclidean distance between two agents, respectively. The population diversity is the main tool for monitoring the convergence rate of the algorithm, and it represents the second fuzzy input.
Another important parameter for monitoring the convergence rate is the population progress at the
i-th iteration denoted by
. By considering the (
13) and (
14), the definition of
is shown in (
17), where
is the fit mean value at the
i-th iteration.
is the third fuzzy input.
The fourth fuzzy input
is the value of
at the
iteration. Because the parameter
has to be tuned, the fuzzy output is the value
, i.e., the value of
at the
i-th iteration.
The next step is the choice of the number and shape of the membership functions. This choice depends on the specific problem, and sometimes, it is a trial and error procedure. By considering our problem, triangular/trapezoidal membership functions are chosen. The inputs N, and the output have three membership functions: Low (L), Medium (M) and High (H). The other inputs have two membership functions: Low (L) and High (H). The ranges of are defined experimentally for each benchmark function, whereas the ranges of N, and are the same for all of the test functions.
The number of membership functions for each input defines the fuzzy rules number. Therefore, our rule set is composed of
rules (see
Table 1).
The rules shown in
Table 1 are designed to prevent problems of being trapped in local optima and premature convergence. This fact justifies the dependance of the (
16), (
17) and
from the number of iterations; in other terms,
,
and
with
.
All of the rules have been generated through knowledge. The presence of a lack of improvement when the number of iterations is low is a sign of being trapped in the local optimum and premature convergence. If the number of iterations is low and is low, then is set to low. In fact, when is low, the value of the gravitational constant G increases. Therefore, the acceleration and velocity of the agents increase, and the population can escape from being trapped in local optima. In the situations where the population diversity is low and the number of iterations is medium, a reduction of improves the diversity to achieve better solutions.
In order to increase the power of exploitation of the algorithm, when the iteration number is high, the gravitational constant must decrease. Therefore, by increasing , it follows that G decreases.
If the algorithm is at the last iterations, there is a lack of improvement and the diversity is huge, the algorithm has failed the convergence target. In these situations, must be increased. Finally, all of the rules follow the knowledge described before.
Our fuzzy system uses the Mamdani inference system, and the inputs are combined logically using the operator. The centroid is the used defuzzification method.
In the evolutionary fuzzy systems, the membership functions’ shapes can be evolved using a genetic algorithm [
37]. Setnes et al. [
38] proposed a real-coded GA, which simultaneously optimizes the parameters of the antecedent membership functions and the rule consequent. By following this way, we apply a suitable genetic algorithm to establish the best slopes of the triangular/trapezoidal membership functions.
In order to achieve a good optimization, the optimization range for all of the membership functions has to be defined. The ranges are established avoiding possible crossings of more than two membership functions. The inputs N, and have the same ranges for all of the simulations. The whole range of the iteration number N is (i.e., ), whereas the population diversity and population progress are normalized in . On the contrary, the optimization intervals of the membership functions are determined empirically for each benchmark function.
In this work, we consider real-coded GAs [
39] because binary coded or classical GAs [
40] are less efficient when applied to multidimensional, high-precision or continuous problems. In fact, the bit strings can become very long, and the search space blows up.
A serious problem of the genetic algorithms’ design is the definition of the fitness function [
41]. Bad fitness functions can easily make the algorithm get trapped in a local optimum solution and lose the discovery power. Petridis et al. [
42] presented a specific varying fitness function technique that incorporates the problem’s constraints into the fitness function in a dynamic way. However, our evaluation of the fitness functions is based on two features: efficiency and precision. Good fitness functions help the algorithm to explore the search space more effectively and efficiently. In order to assure such features, the fitness function
shown in (
18) is defined.
In Equation (
18), the variable
x represents the best so far solution [
22] to the iteration number
. The genetic algorithm searches the value of
x that maximizes the fitness Function (
18). Such a value of
x will be as small as possible. The slope of the membership functions is adjusted until the optimal value of (
18) is achieved.
The genetic algorithms are characterized by three genetic procedures: selection, crossover and mutation. Among the various selection methods, we choose the roulette wheel selection method [
43]. In roulette wheel selection, the probability that individual
i is selected,
, is computed by Equation (
19), where
l is the population number.
Algorithm 2 implements the roulette wheel selection.
| Algorithm 2 |
| S1. For each individual i, with : |
| S1.1. Generate a random number r between 0 and 1. |
| S1.2. Initialize the variables to 0 and j to 1. |
| S1.3. If go to S.1.4. |
| S1.3.1. Compute , where is defined in (19). |
| S1.3.2. Increment j. |
| S1.3.3. Go to Step S1.3. |
| S1.4. Set , i.e., establish the i-th parent from the -th value of the parameter . |
| S2. Print the values of the parents. |
In order to improve the convergence of the GA, we consider the elitism procedure [
44]. It is an addition to many selection methods that forces the GA to retain some number of the best individuals at each generation. Some studies [
45,
46] show that elitism can increase the performance of GA by preventing the loss of good solutions once they are found.
Another genetic procedure is the crossover. The crossover recombines genetic material of parent chromosomes to produce offspring on the basis of crossover probability [
47]. Given the mutations number
, the number of elitism
, the number of the population
l and the parents
(
), the designed crossover algorithm follows the steps of Algorithm 3.
| Algorithm 3 |
| S1. For all j from 1 to : |
| S1.1. Compute a random number t between and |
| S1.2. Compute the parameters and . |
| S2. Print the parameters p |
The mutation is a genetic operation that occasionally breaks one or more members of a population out of a local minimum/maximum space and potentially discovers a better minimum/maximum space [
44]. Algorithm 4 describes the mutation algorithm, where the mutations number
and the random mutations number
[
41,
43] are given. Moreover, the variable
in Algorithm 4 is calculated through the formula (
20) where
and
are the max and min value of the initial random parameters
.
In our algorithm, the number
l of population
P is set to 100; the number of mutation
m is equal to 20; and number of elitism is equal to two. The designed fuzzy controller is optimized through GA: the steps of the optimization algorithm are described in the Algorithm 5. GA optimizes the slope of the membership functions (four parameters for each membership function), to achieve the optimal membership functions. Because the membership functions number is 13, it follows that
parameters are optimized. Once the fuzzy controller is optimized, it may be used to adjust the parameter
of GSA. The fuzzy gravitational search algorithm optimized by GA is described in Algorithm 6.
| Algorithm 4 |
| S1. For all the i from to : |
| S1.1. Compute a random number between and . |
| S1.2. Compute , where is the inverse error function. |
| S1.3. Compute the parameter p with the formula , where is calculated by (20). |
| S2. Print the parameters p. |
| Algorithm 5 |
| S1. Pass the optimization ranges of the membership functions to GA. |
| S2. Select in a random way the initial optimal values of the parameters in the optimization ranges and calculate the termination criteria of GA. This criteria depends on number of generations and fitness function values. |
| S3. If the termination criteria is achieved, go to S10. |
| S4. For each j-th element of the population P, with , compute the steps from S4.1–S4.4 |
| S4.1. Pass the optimal parameters to the fuzzy inputs/output of the controller. |
| S4.2. Initialize, in a random way, the position X of the agents in the search space. The initialization procedure depends on the number of agents n, the dimension of the test functions r and the allowable range for the search space. The positions X’s are calculated by generating random numbers between 0 and 1, and normalize them on the range . In other terms, the positions are computed by the formula , with and . |
| S4.3. Set the initial value and for each iteration i, with , compute the steps from S4.3.1–S4.3.4 |
| S4.3.1. Compute the fitness of the agents for a certain function. The fitness depends on the position of the agents and the dimension of the function. |
| S4.3.2. The value of the fitness is necessary to calculate the mass of each agent for (see (11)). On the other hand, depends on and (Equations (13) and (14), respectively), which also depend on fitness. The gravitational constant is computed according to at the first iteration, whereas, for the other iterations, is calculated according to the tuned value of . |
| S4.3.3. According to , the total force in different directions is calculated. In particular, the algorithm computes the Euclidean distance between two agents and the force acting on mass i from mass j at a specific time t (see (3)). Subsequently, the total force (see (6)) is computed. Therefore, the acceleration of the agents, their velocity and position at t time are calculated by means of (7), (8) and (9), respectively. |
| S4.3.4. Compute the fuzzy output , i.e., the value of , through the fuzzy controller, which receives the following inputs: iteration number i, population diversity , population progress and . |
| S4.4. Calculate the j-th value of the fitness function defined in (18). |
| S5. Update the termination criteria parameters, which depend on fitness function values. |
| S6. Compute the parents with through the selection method by using the Algorithm 2. |
| S7. Compute the parameters p through the crossover method described in the Algorithm 3. |
| S8. Compute some parameters p with the mutation (Algorithm 4). |
| S9. Go to Step S3. |
| S10. Give to the output the optimal parameters of the membership functions. |
In order to test the algorithms, unimodal and multimodal benchmark functions [
48] are considered.
Table 2 shows the test functions, where
r is the dimension of the function and
S is a subset of
.
The membership functions of the fuzzy controller can be optimized also through evolutionary algorithms such as PSO and DE. The idea is to optimize the parameter
of GSA by PSO and DE. In this case, only the ranges of the
membership functions are optimized. Therefore, 3 × 4 (alpha previous state) + 3 × 4 (alpha current state) = 24 parameters are optimized. In the PSO and DE case, the membership functions ranges of
are defined considering a neighborhood of the optimal value of
that come from PSO [
10] (DE [
16]) optimization. The steps of FGSA-PSO (DE) algorithm are illustrated in Algorithm 7.
| Algorithm 6 |
| S1. Initialize, in a random way, the position X of the agents in the search space. The initialization procedure depends on the number of agents n, the dimension of the test functions r and the allowable range for the search space. The positions X’s are calculated by generating random numbers between 0 and 1, and normalize them on the range . In other terms, the positions are computed by the formula , with and . |
| S2. Set the initial value and for each iteration i, with , compute the steps from S2.1–S2.5. |
| S2.1. Compute the fitness of the agents for a certain function. The fitness depends on the position of the agents and the dimension of the function. |
| S2.2. The value of the fitness is necessary to calculate the mass of each agent for (see (11)). On the other hand, depends on and (Equations (13) and (14), respectively), which also depend on fitness. The gravitational constant is computed according to at the first iteration, whereas, for the other iterations, is calculated according to the adjusted value of (which comes from fuzzy controller). |
| S2.3. According to , the total force in different directions is calculated. In particular, the algorithm computes the Euclidean distance between two agents and the force acting on mass i from mass j at a specific time t (see (3)). Subsequently, the total force (see (6)) is computed. Therefore, the acceleration of the agents, their velocity and position at t time, are calculated by means of (7), (8) and (9), respectively. |
| S2.4. Calculate the population diversity and the population progress as defined in (16) and (17). |
| S2.5. The GA-optimized fuzzy controller receives the inputs: iteration number i, population diversity , population progress and . The controller gives the fuzzy output , i.e., the value of . In this way, the value of is tuned. |
| S3. Give to the output the best-so-far solution. |
| Algorithm 7 |
| S1. Optimize GSA with PSO (DE); in this way, the optimal value is computed. |
| S2. Calculate a suitable neighborhood of with the formulas: and , with . |
| S3. Compute the membership functions ranges of taking into account the neighborhood of . |
| S4. Initialize, in a random way, the position X of the agents in the search space. The initialization procedure depends on the number of agents n, the dimension of the test functions r and the allowable range for the search space. The positions X’s are calculated by generating random numbers between 0 and 1, and normalize them on the range . In other terms, the positions are computed by the formula , with and . |
| S5. Set the initial value and for each iteration i, with , compute the steps from S5.1–S5.5. |
| S5.1. Compute the fitness of the agents for a certain function. The fitness depends on the position of the agents and the dimension of the function. |
| S5.2. The value of the fitness is necessary to calculate the mass of each agent for (see (11)). On the other hand, depends on and (Equations (13) and (14), respectively), which also depend on fitness. The gravitational constant is computed according to at the first iteration, whereas, for the other iterations, is calculated according to the adjusted value of (which comes from fuzzy controller). |
| S5.3. According to , the total force in different directions is calculated. In particular, the algorithm computes the Euclidean distance between two agents and the force acting on mass i from mass j at a specific time t (see (3)). Subsequently, the total force (see (6)) is computed. Therefore, the acceleration of the agents, their velocity and position at t time, are calculated by means of (7), (8) and (9), respectively. |
| S5.4. Calculate the population diversity and the population progress as defined in (16) and (17). |
| S5.5. The PSO (DE)-optimized fuzzy controller receives the inputs: iteration number i, population diversity , population progress and . The controller gives the fuzzy output , i.e. the value of . In this way, the value of is tuned. |
| S6. Give to the output the best-so-far solution. |
4. Simulation and Discussion
The proposed algorithms are tested with MATLAB software on a 2.20-GHz CPU hardware for the benchmark functions of
Table 2. We firstly apply our algorithms to the unimodal functions, i.e., to the test functions from
to
. Subsequently, we take into account the multimodal test functions from
to
. In all of the cases the number
n of agents is set to 50; the dimension of the functions
r is 30; the maximum iteration
k is 1000.
Algorithms 2–5 give the optimal parameters to define the membership functions. For each benchmark function, different membership functions’ slopes are obtained. As an example,
Figure 1 shows the optimal membership functions for the test function
.
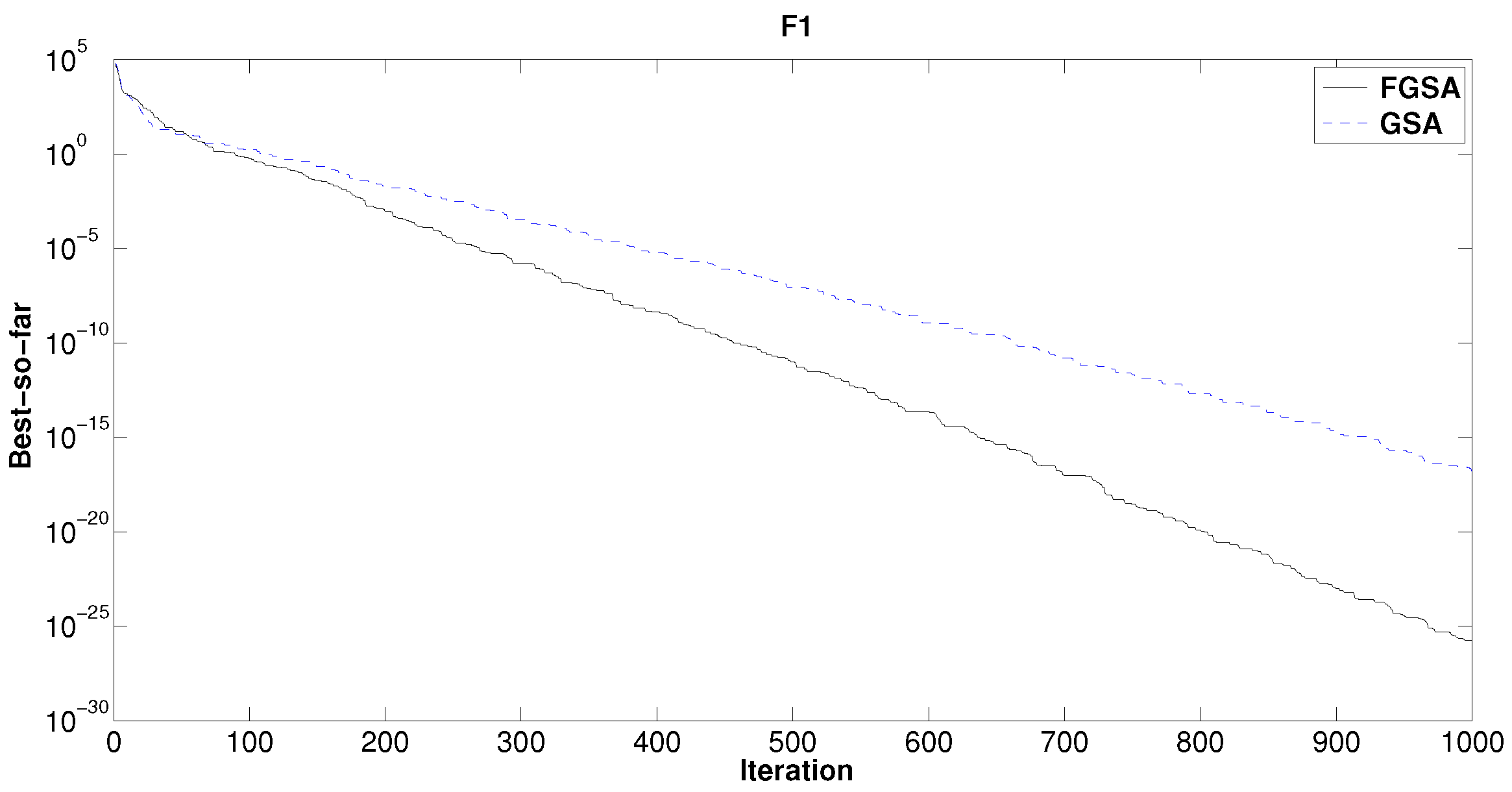
By running Algorithm 6 with the best membership functions, we obtain the solid curve of
Figure 2 for the benchmark function
. The dashed line represents the best so far solution of GSA [
22]. Note that FGSA-GA tends to find the global optimum faster than GSA, and hence, it has a higher convergence rate.
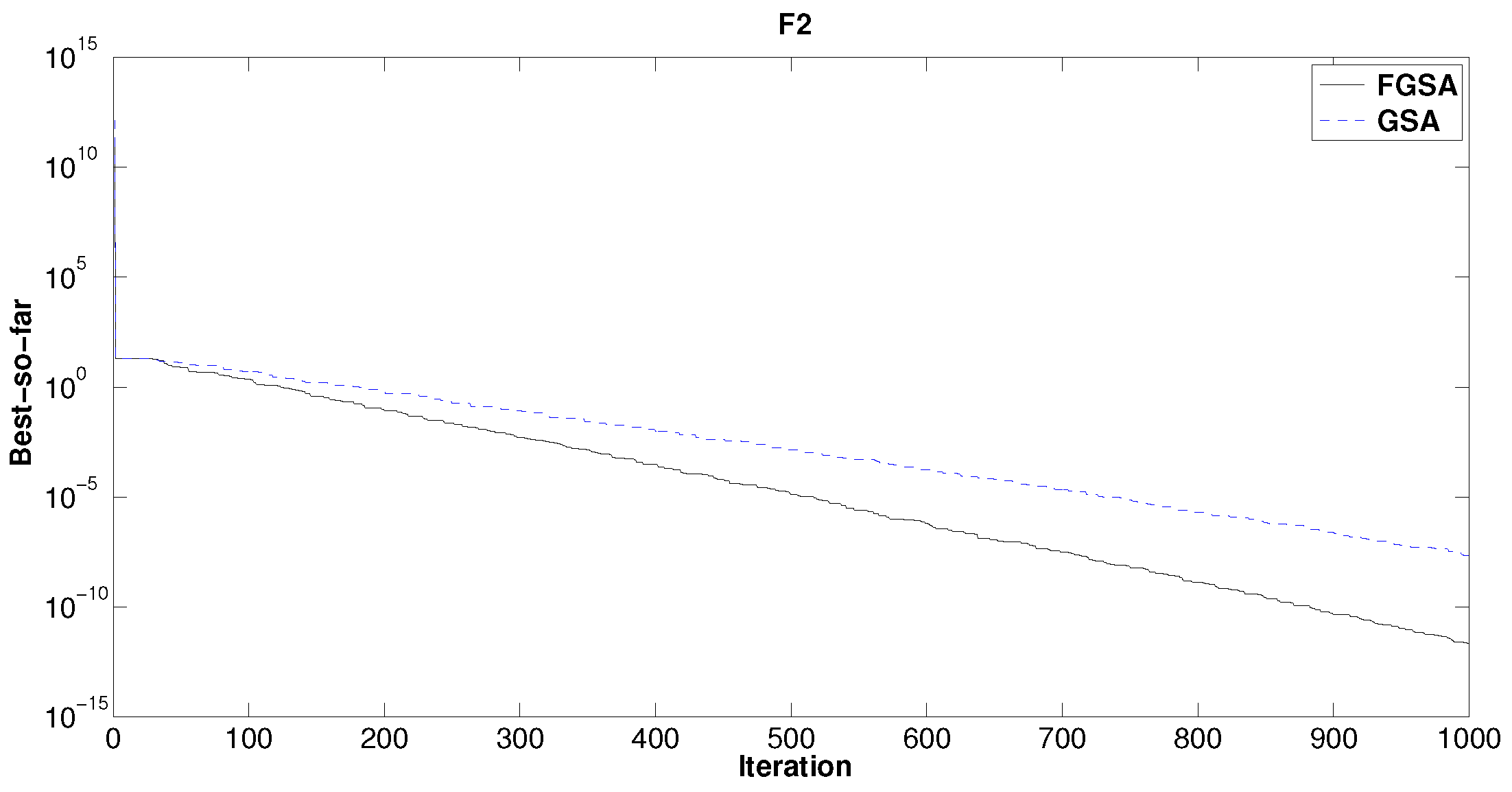
The best so far solutions of GSA and FGSA-GA for
are shown in
Figure 3. Observing
Figure 3, we note that up to the 30th iteration, the trend of GSA and FGSA-GA is about the same. After this value, FGSA-GA is better than GSA. Note that the best so far solution achieved at the last iteration is
.
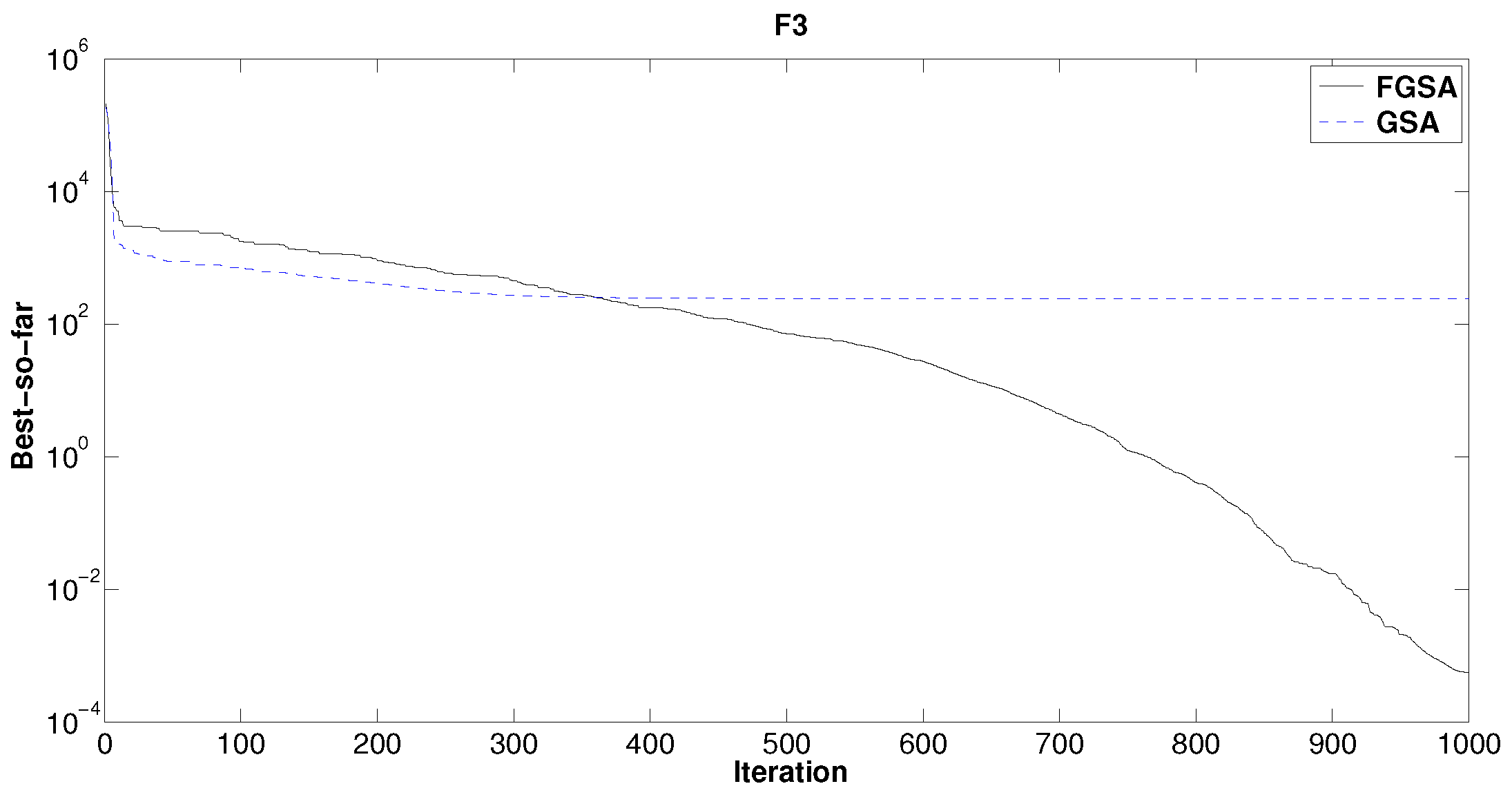
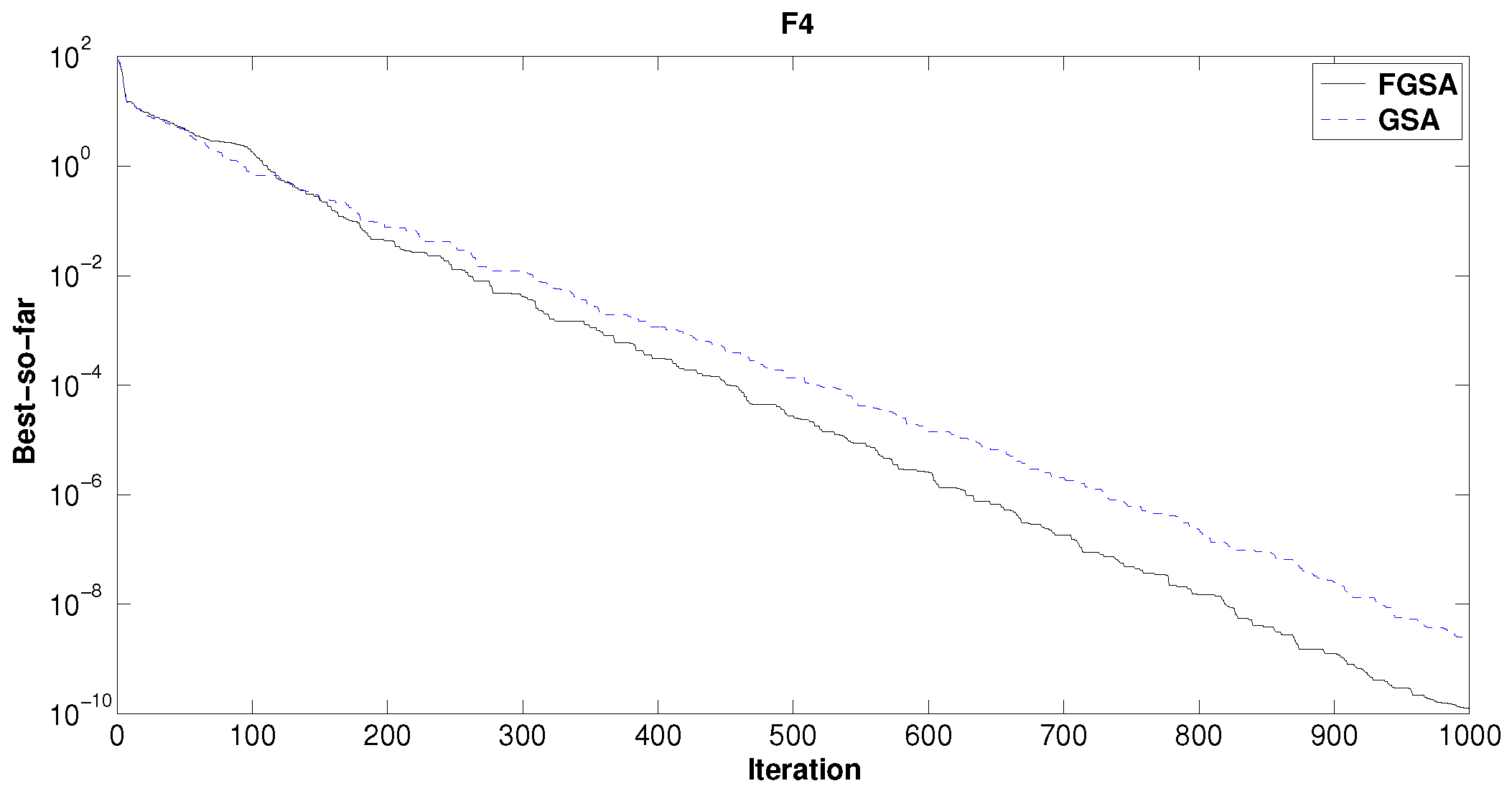
The trend of the GSA and FGSA-GA best so far solution for
is shown in
Figure 4. The improvement of FGSA-GA with respect to GSA is about four orders of magnitude.
From
Figure 5, we observe that the trend of FGSA-GA is close to GSA: a relevant improvement is achieved at the end of the iterations. Quantitatively, for the function
, there is an improvement of two orders of magnitude.
The multimodal functions are most difficult to optimize because they have many local minima. For multimodal functions, the final results are more important, since they reflect the ability of the algorithm to escape from poor local optima and locating a near-global optimum. Using Algorithm 6, significant improvements are achieved with the test functions , and .
For the multimodal function
, FGSA-GA is better than GSA from the beginning to the end of the iterations (see
Figure 6). In particular, the maximum difference is of 10 orders of magnitude.
Observing
Figure 7, we can note that FGSA-GA improves GSA by about eight orders of magnitude: FGSA-GA’s best so far solution is
.
Figure 8 shows the GSA and FGSA-GA trend over iteration number for function
. Note that the trend is about the same up to the 500th iteration. However, there is an improvement of FGSA-GA at the end of the iterations.
Algorithm 5 uses GA to optimize the membership functions of the fuzzy system. However, the parameter of GSA can be optimized with the help of other optimization methods such as PSO and DE. In FGSA, the idea is to define the membership functions range of , taking into account the optimal value of obtained with PSO and DE. The procedure is described in Algorithm 7.
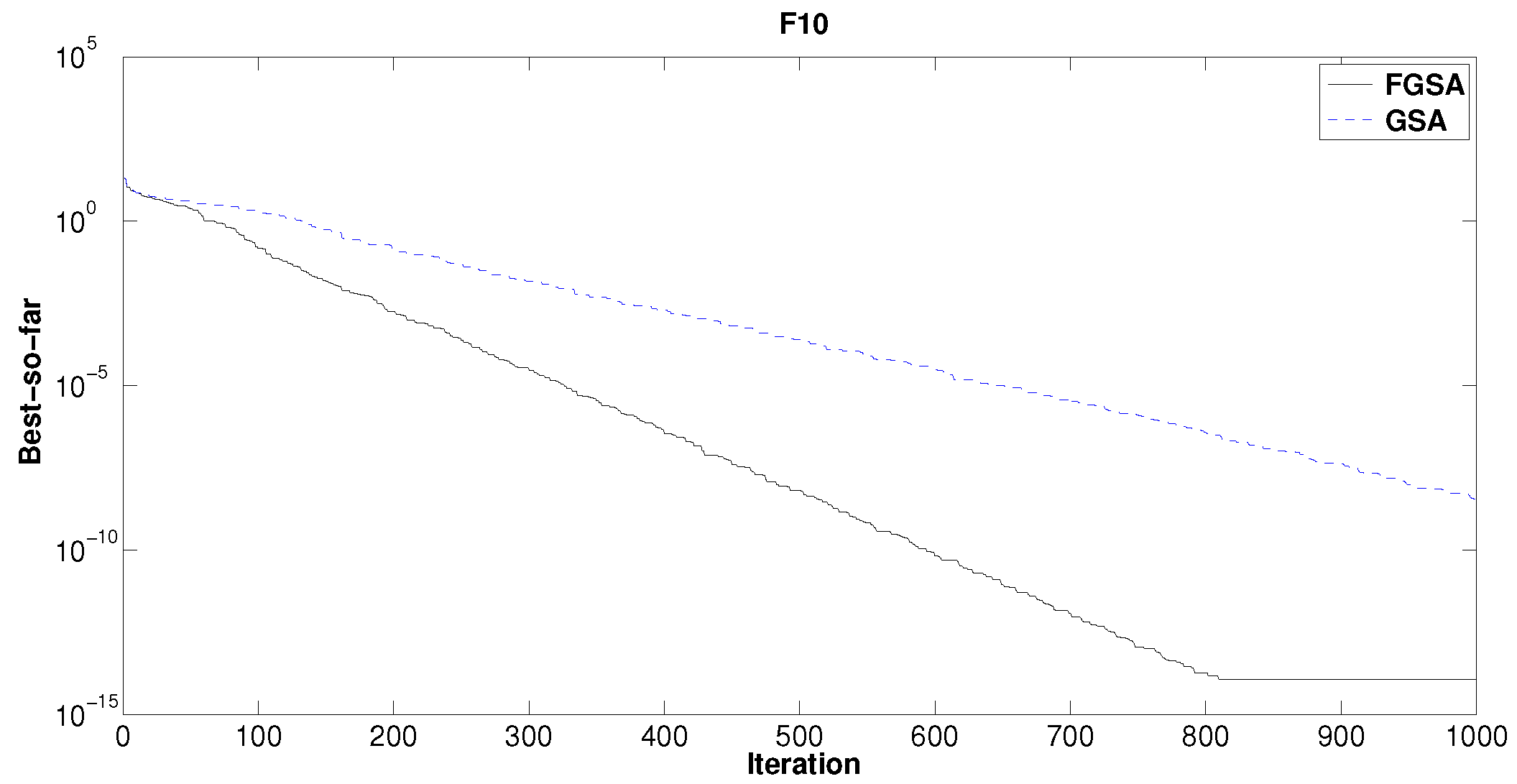
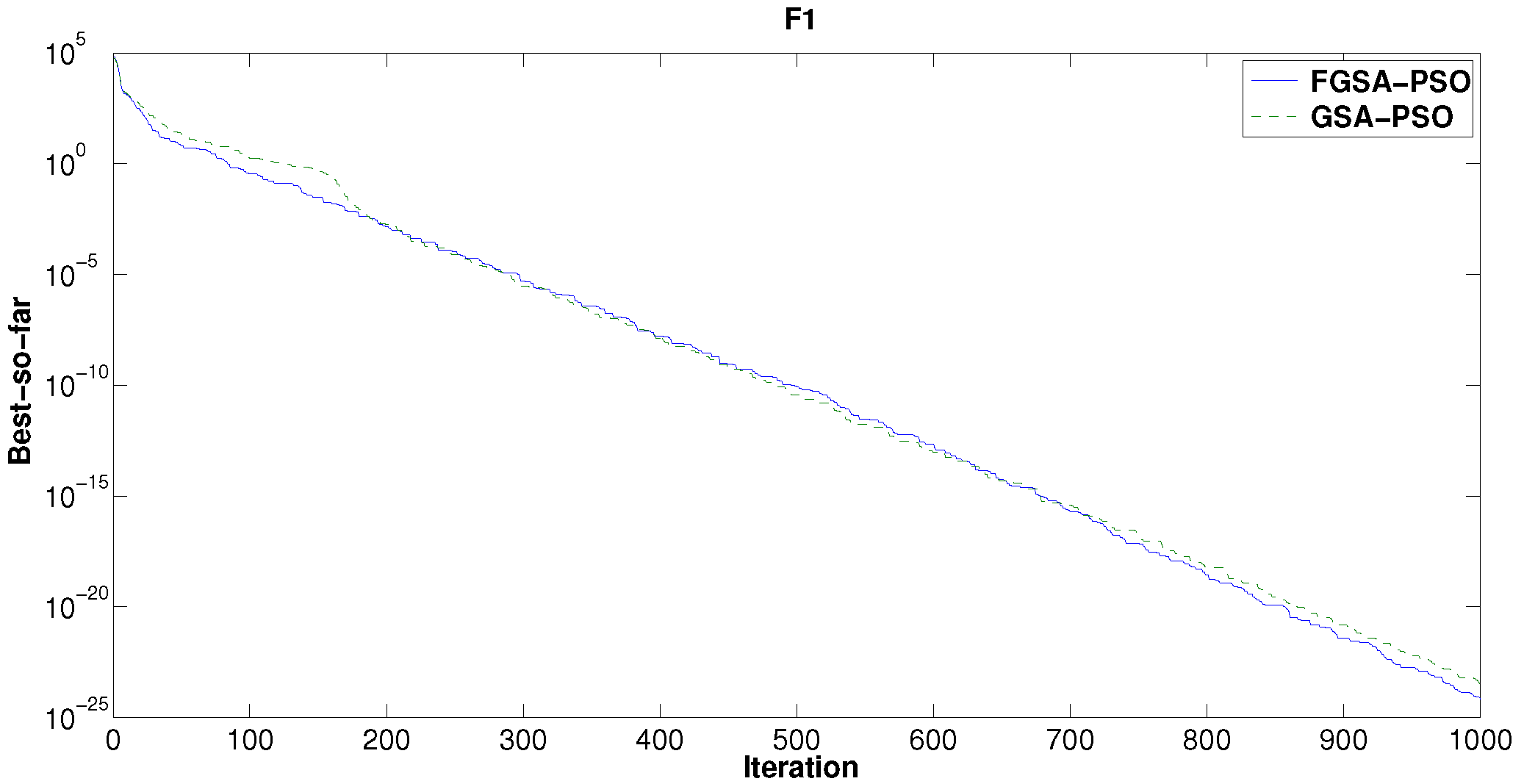
We compare the results of GSA and FGSA optimized by PSO (GSA-PSO and FGSA-PSO, respectively). By observing
Figure 9, we can note that the best-so-far solution of FGSA-PSO is better than GSA-PSO for the test function
. In fact, from Iteration 700–1000, the FGSA curve is below the GSA curve. There is a good improvement for the test function
(see
Figure 10) where FGSA-PSO overcomes the performances of GSA-PSO. For the other test functions, the results are about the sames.
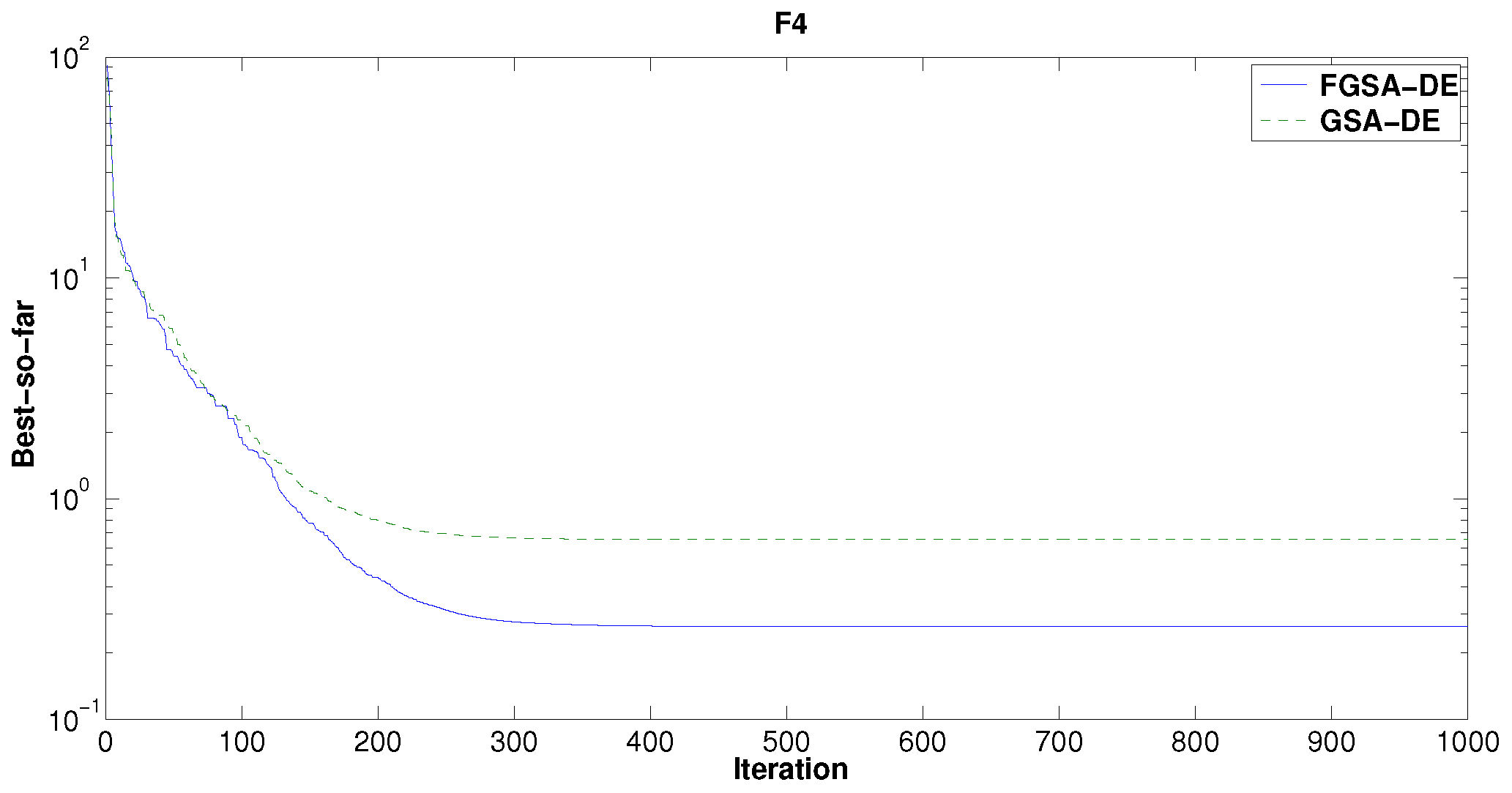
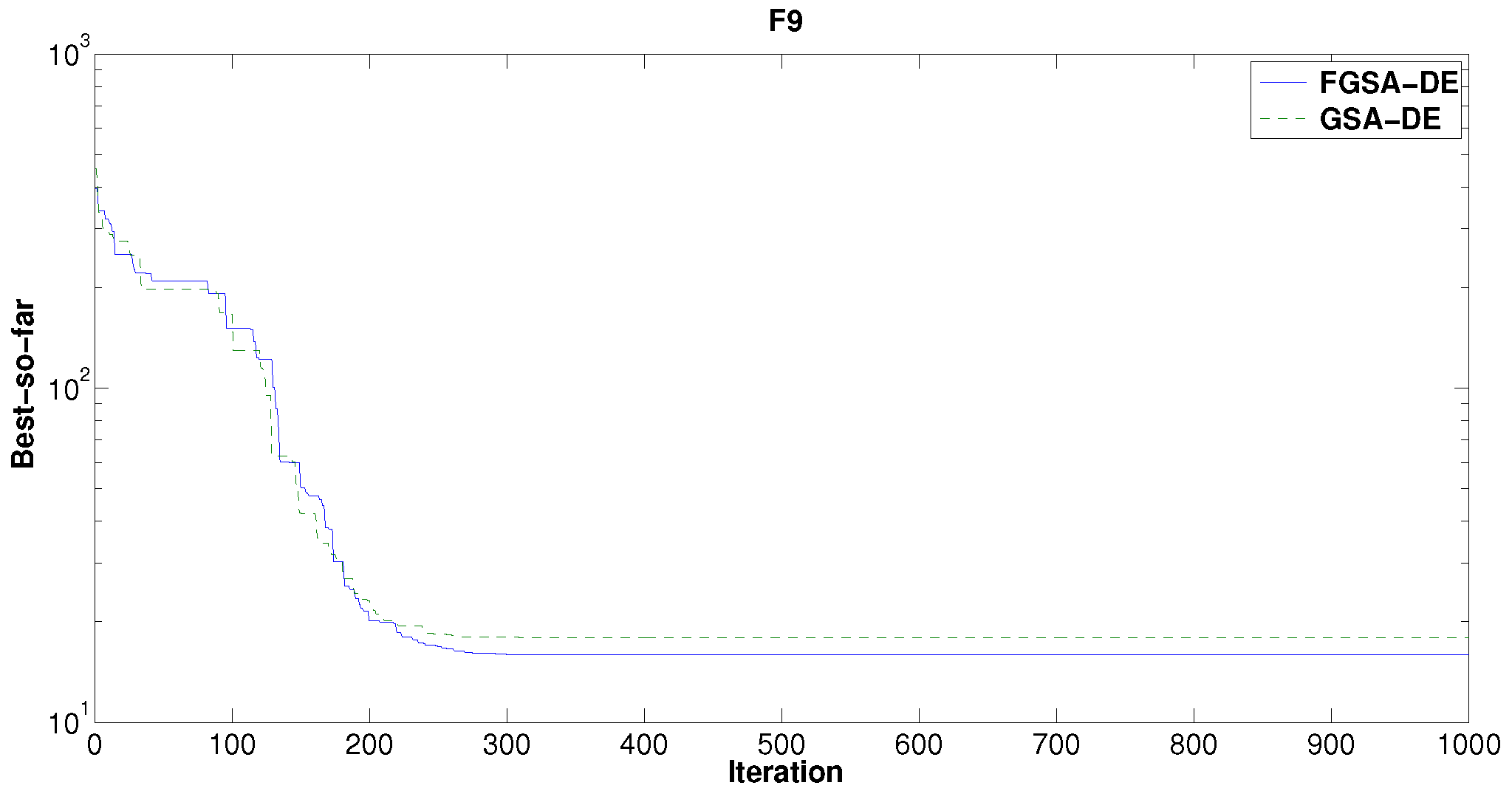
Better results are achieved by FGSA optimized by DE (FGSA-DE) versus GSA optimized by DE (GSA-DE). The results of FGSA-DE come from Algorithm 7.
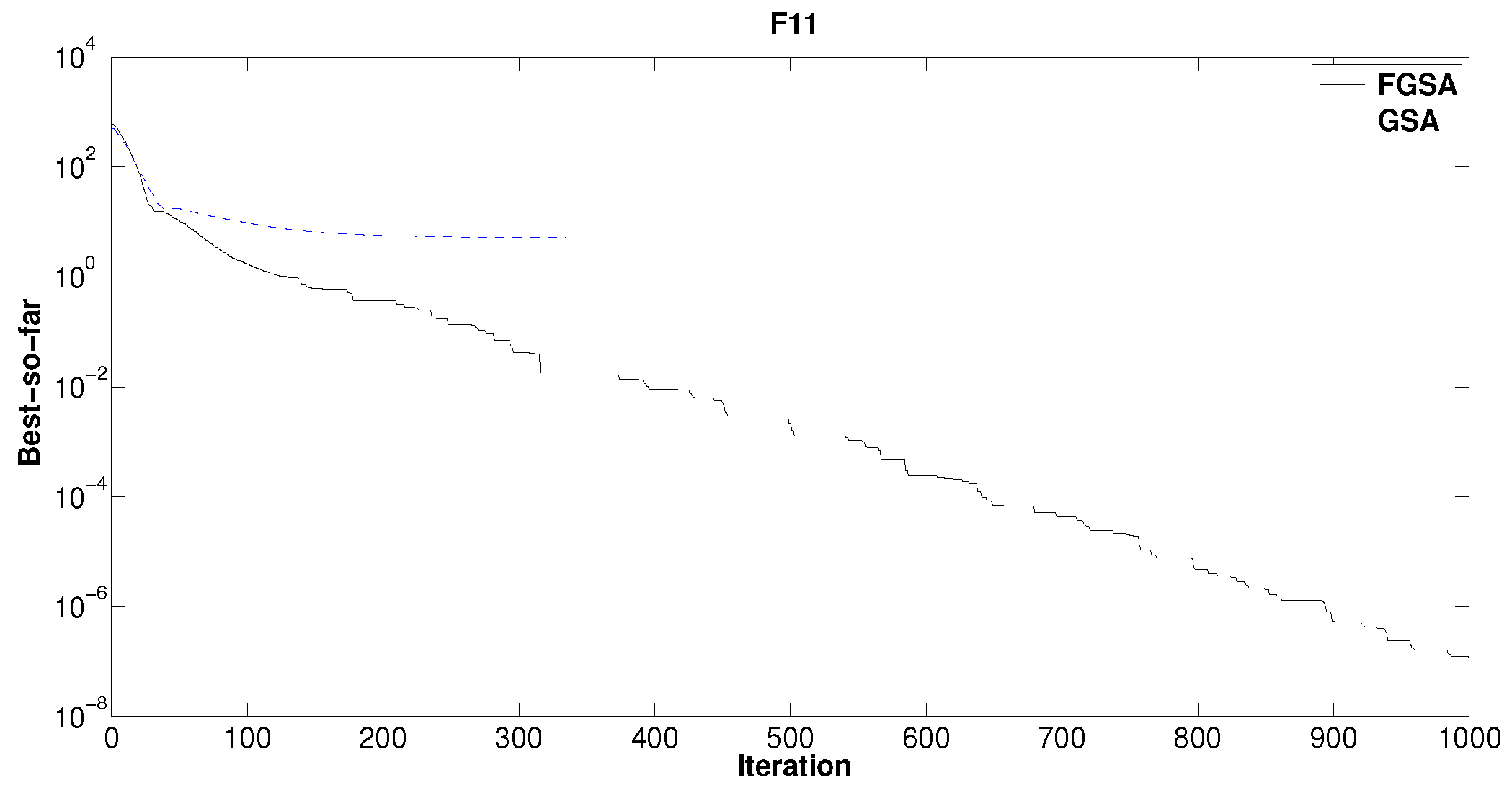
Figure 11 shows the comparison between FGSA-DE and GSA-DE for the minimization of
. Note that the FGSA-DE trend is better than GSA-DE because the FGSA-DE curve is below GSA-DE. A similar situation for the function
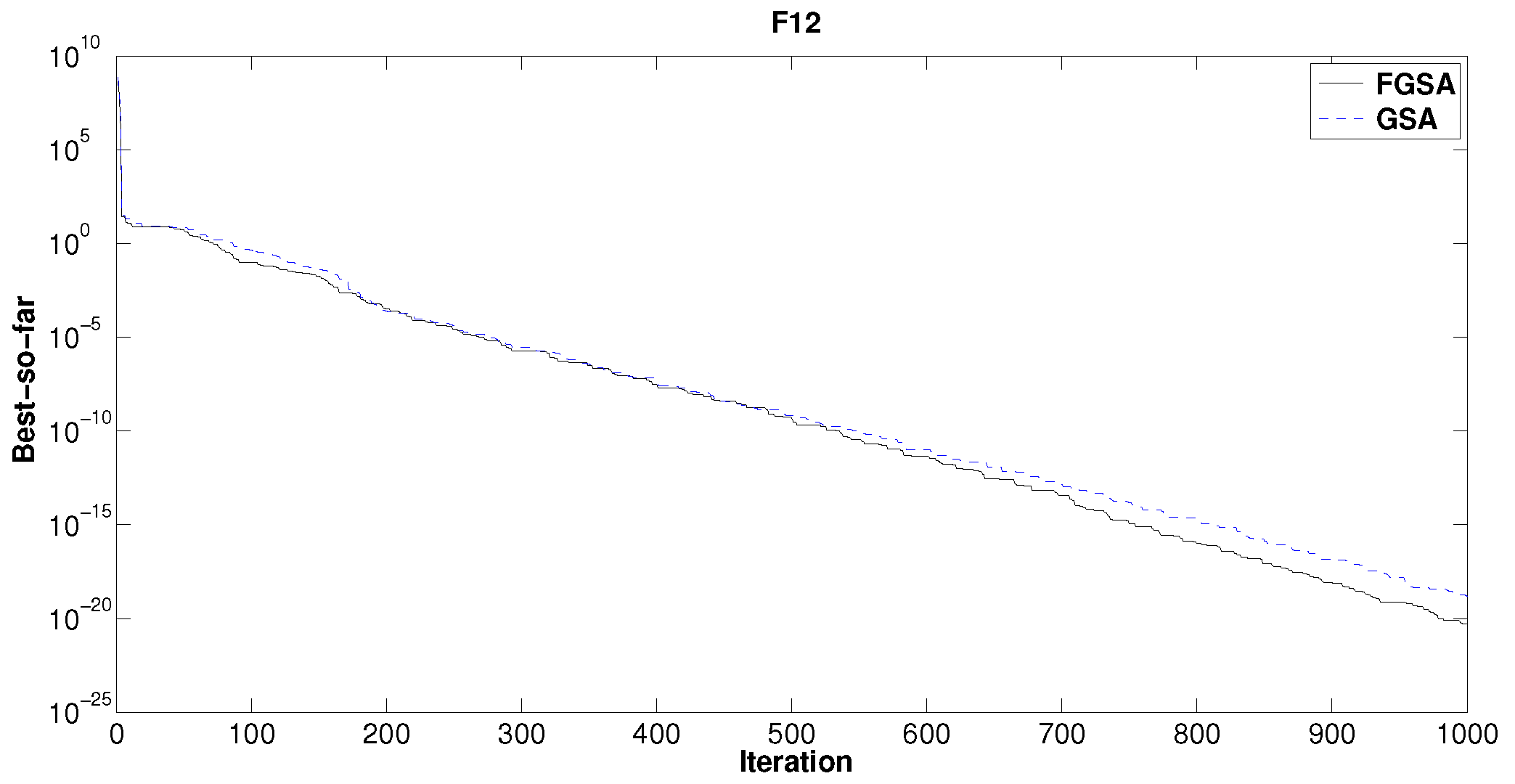
is obtained (see
Figure 12). Moreover, for the test function
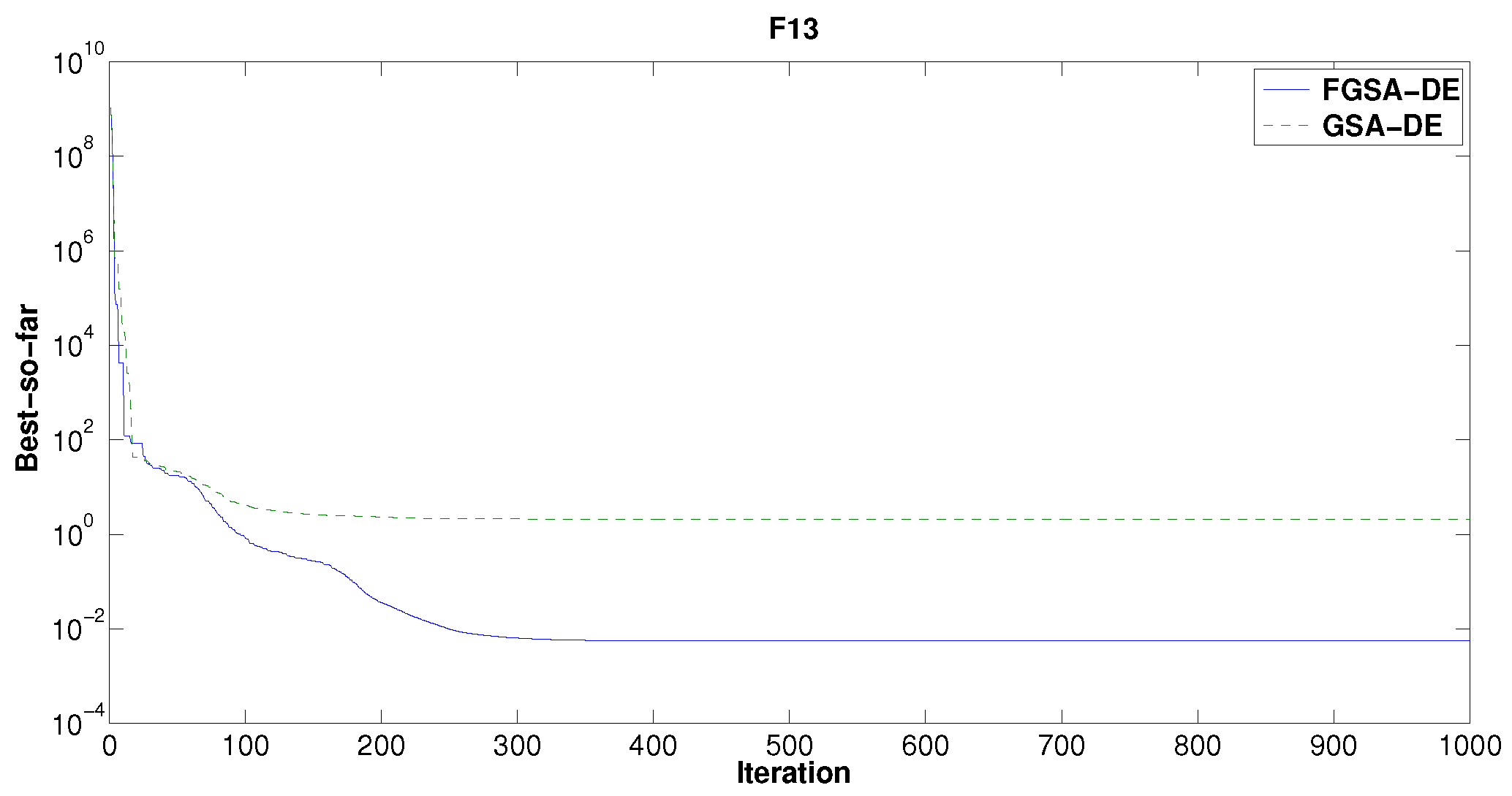
, there is an improvement of about one order of magnitude (see
Figure 13). The simulation results for the function
show that the FGSA-DE curve is always below GSA-DE (see
Figure 14); therefore, FGSA-DE tends to find the global optimum faster than GSA-DE.
The results are averaged over 30 and 16 runs, as in [
22,
26,
27,
35] and [
28], respectively, and the average, standard deviation and median of the best solution in the last iteration are computed.
Table 3,
Table 4,
Table 5 and
Table 6 resume the comparison between the algorithms FGSA-GA, FGSA-PSO and FGSA-DE over 30 and 16 runs. The values shown in the tables are the average, standard deviation and median of the best solution in the last iteration. Note that FGSA-DE is better than FGSA-GA and FGSA-PSO for the functions
and
. On the other hand, FGSA-GA overcomes FGSA-PSO and FGSA-DE for the functions
,
and
. For the test functions
–
, the results are similar: there is not a dominant algorithm.
Table 7 shows the comparison of the results achieved by [
22,
26,
27,
35] with the performances of the algorithms FGSA-GA, FGSA-PSO and FGSA-DE over 30 runs. This table does not contain the results of all 13 test functions, but it resumes the more significant improvements for certain benchmark functions. The last three columns of
Table 7 contain the average of the best solution in the last iteration of Algorithms 6–7. FGSA-GA gives better results than the GSA proposed by [
22] for all of the functions of
Table 7. The maximum improvement is 19 orders of magnitude for the function
. Moreover, FGSA-GA is better than the BGSA proposed in [
35] for all of the functions shown in
Table 7. The best improvement is of 22 orders of magnitude for the function
. FGSA-GA improves the GSA designed in [
27] for the functions
,
,
,
and
. In particular, for the function
, an improvement of 20 orders of magnitude is achieved. The comparison between our FGSA and FGSA proposed by Khabisi [
26] can be accomplished only for the functions
. Except for the function
, our algorithm has better solutions than FGSA in [
26]. FGSA-PSO is better than [
22] for the functions
,
,
,
and
. The best improvement is of 14 orders of magnitude for the function
. Note that, by comparing the FGSA-PSO results with [
35], FGSA-PSO provides better outcomes except for
and
. Only for the function
, FGSA-PSO overcomes the GSA proposed in [
27]. FGSA-DE improves the results of [
22,
26,
27,
35] for all of the functions in
Table 7, except for
of [
26].
Table 8 shows the results of FGSA-GA, FGSA-PSO and FGSA-DE versus GSA of [
28] over 16 runs. FGSA-GA improves the results of [
28] for all of the functions, providing a relevant improvement for
of 20 orders of magnitude. The provided solutions by FGSA-PSO are better than GSA [
28] only for the function
. FGSA-DE is better than GSA [
28] for the functions
and
. In this case, an improvement of 18 orders of magnitude for
is achieved.
Finally, the results show that, both over 30 and 16 runs, FGSA-DE is optimal for unimodal functions, whereas FGSA-GA is good for multimodal functions.
5. Conclusions
The challenge of improving the performances of the search algorithms is an open problem. However, there is no specific algorithm to achieve the best solution of the optimization problems. GSA is a recent search method to find the global optimum. Many researches proposed revised versions of GSA to reduce the time for finding the global optimum. Following this, intelligent techniques have been applied to increase the search performances of GSA. In this paper, some revised FGSA based on the optimization through GA, PSO and DE are proposed. The main idea is to tune the parameter of the gravitational constant G through a fuzzy controller optimized via GA, PSO and DE. The first FGSA uses GA to optimize the membership functions’ slope of the fuzzy variable . In the second and third FGSA, PSO and DE define the best range of the fuzzy input/output membership functions. In both cases, the optimization process of the fuzzy controller is accomplished just one time: once the fuzzy controller is optimized, it is inserted in the steps of GSA to design FGSA.
In order to compare our outcomes to those of [
22,
26,
27,
28,
35], the results are averaged over 30 and 16 runs. The results show that FGSA optimized by GA achieves better results than [
22,
26,
27,
28,
35]. The best improvement with respect to [
22] is of 19 orders of magnitude. Better results have been achieved by comparing our findings with the findings of [
27,
35]: a maximum of 22 and 20 orders of magnitude, respectively, is achieved. The order of magnitude of FGSA-GA is six-times greater than [
26] for the test function
. The results of [
28] are improved for all of the functions achieving a maximum order of magnitude of 10. Moreover, FGSA optimized with PSO achieves better results than GSA-PSO. Significant improvements are achieved for test functions
and
, where FGSA-PSO is better than GSA-PSO. For the function
, FGSA-DE is better than GSA-DE by two orders of magnitude. Comparing the results of FGSA-GA, FGSA-PSO and FGSA-DE, it follows that FGSA-DE is optimal for unimodal functions, whereas FGSA-GA is good for multimodal functions.
Future studies will focus on novel adaptive gravitational search algorithms for fuzzy-controlled servo system.