Modeling Delayed Dynamics in Biological Regulatory Networks from Time Series Data †
Abstract
:1. Introduction
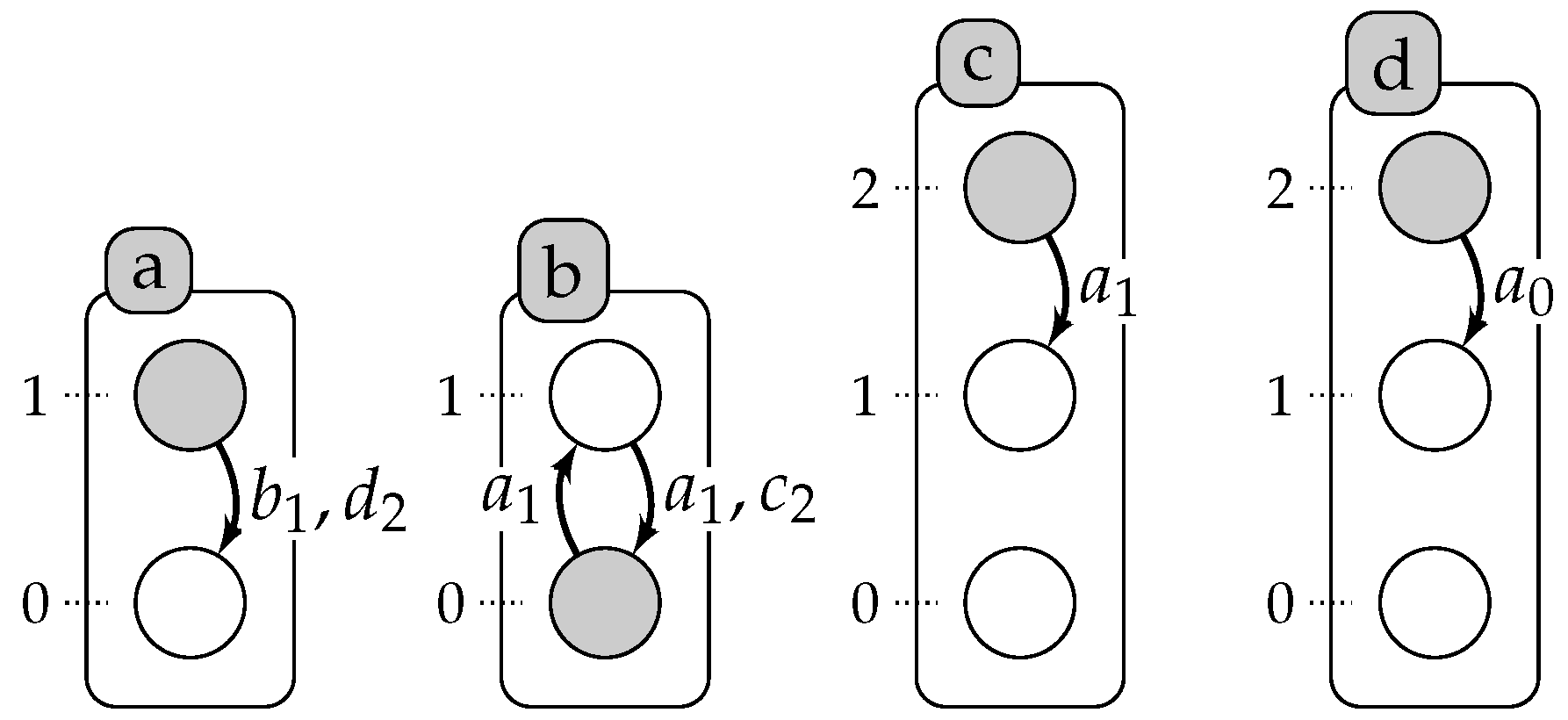
2. Automata Networks
- is the finite set of automata identifiers;
- For each , , is the finite set of local states of automaton a; is the finite set of global states and denotes the set of all of the local states.
- , where with , is the mapping from automata to their finite set of local transitions.
3. Timed Automata Networks
- is the finite set of automata identifiers;
- For each , , is the finite set of local states of automaton a; is the finite set of global states; denotes the set of all of the local states.
- , where with , is the mapping from automata to their finite set of timed local transitions.
4. Learning Timed Automata Networks
Algorithm
| Algorithm 1 MoT-AN: modeling timed automata networks. |
|
5. Refining
5.1. Synchronous Behavior
5.2. More Frequent Timed Automata Networks
5.3. Deterministic Influence
5.4. Several Delays
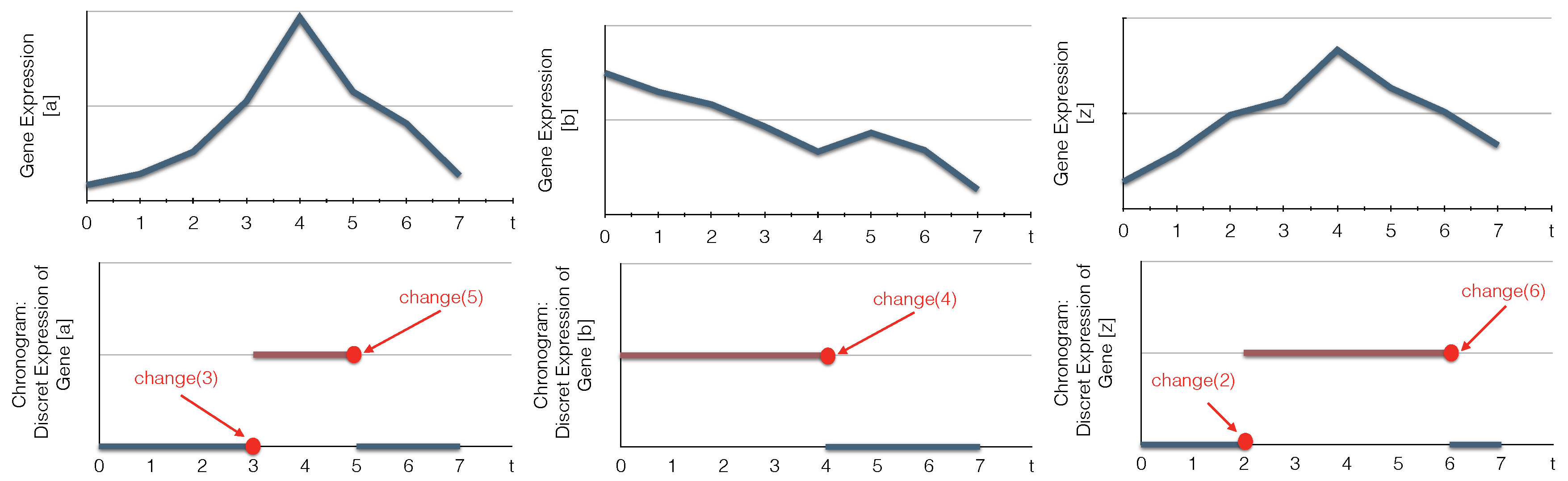
6. Case Study
- -
- Detect biological components’ changes;
- -
- Compute the candidate timed local transitions responsible for the network changes;
- -
- Generate the minimal subset of candidate timed local transitions that can realize all changes;
- -
- Filter the timed candidate actions.
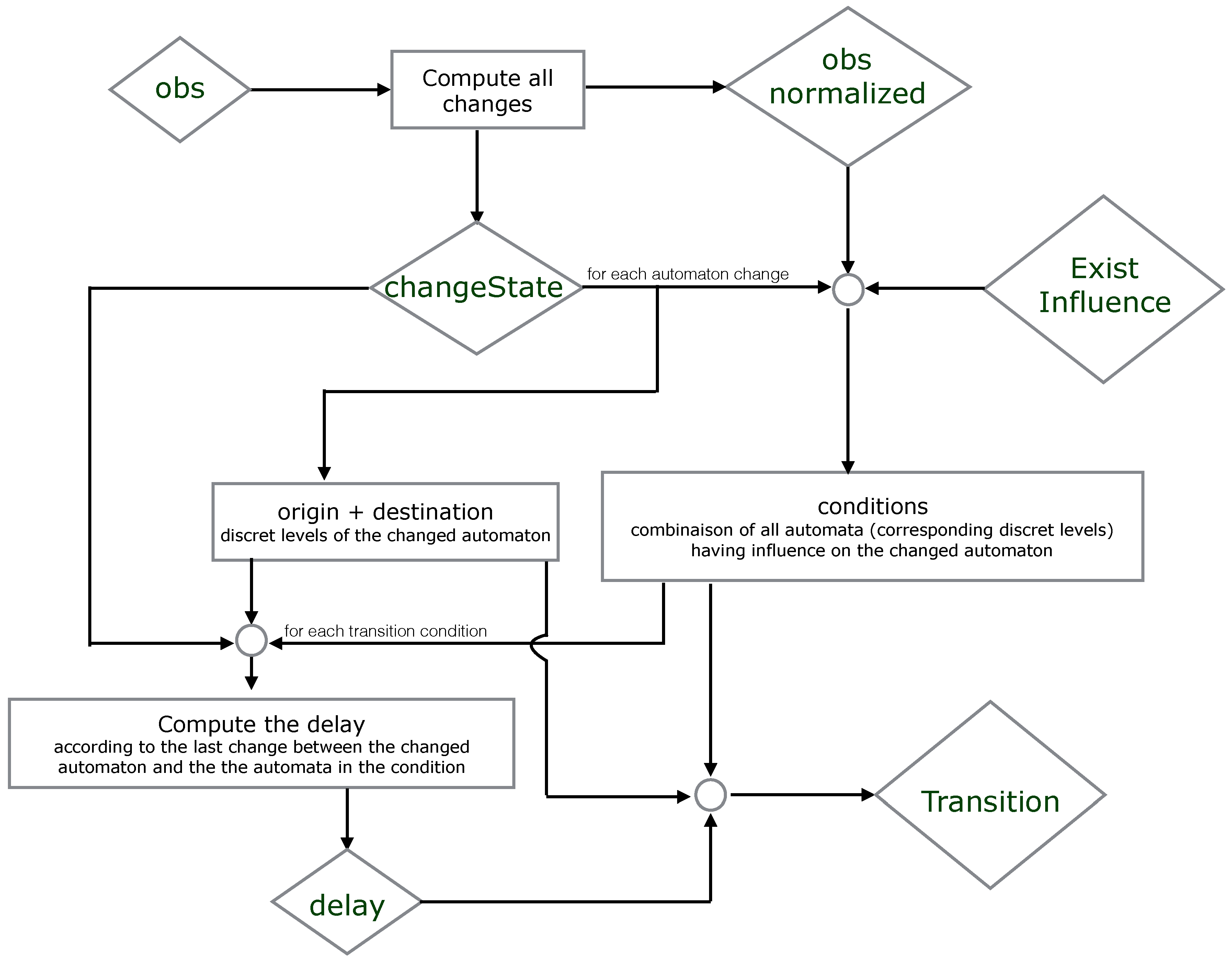
7. ASP Encoding
7.1. ASP Syntax
7.2. All Models
1 % All network components with its levels after discretization 2 automatonLevel("a",0..1). automatonLevel("b",0..1). automatonLevel("c",0..1). 3 % Time series data or the observation of the components 4 obs("a",0,0). obs("a",0,1). obs("a",0,2). obs("a",0,3). obs("a",1,3). obs("a",1,4). obs("a",1,4). 5 obs("a",1,5). obs("a",0,5). obs("a",0,6). obs("a",0,7). obs("b",1,0). obs("b",1,1). obs("b",1,2). 6 obs("b",1,3). obs("b",1,4). obs("b",0,4). obs("b",0,5). obs("b",0,5). obs("b",0,6). obs("b",0,7). 7 obs("c",0,0). obs("c",0,1). obs("c",0,2). obs("c",1,2). obs("c",1,3). obs("c",1,4). obs("c",1,5). 8 obs("c",1,6). obs("c",0,6). obs("c",0,7).
9 % Changes identification 10 % initialization of all changes for each automaton at t=0 (assumption) 11 changeState(X,Val,Val,0) ← obs(X,Val,0). 12 changeState(X,0) ← obs(X,_,0). 13 % Compute all changes of each component according to the observations (chronogram) 14 changeState(X,Val1, Val2, T) ← obs(X, Val1, T), obs(X,Val2,T),obs(X, Val1, T-1), obs(X, Val2, T+1), 15 Val1!=Val2. 16 changeState(X,T) ← changeState(X,_,_,T). 17 % Find all time points where changes occure (reduce complexity) 18 time(T) ← changeState(_,T). 19 delay(D) ← time(T1), time(T2), D=T2-T1, T2>=T1. 20 % Observations processing 21 obs_normalized(X,Val,T1,T2) ← obs(X,Val,T1), obs(X,Val,T2), T1<T2, not existChange(X,Val,T1,T2), 22 time(T1), time(T2). 23 % Verify if X changes its level between two time points T1 and T2 24 existChange(X,Val,T1,T2) ← obs(X,Val,T1), obs(X,Val,T2), obs(X,Val1,T), T>T1, T<T2, Val!=Val1. 25 existChange(X,Val,T1,T2) ← obs(X,Val,T1), obs(X,Val,T2), changeState(X,T), T>T1, T<T2. 26 existChange(X,Val,T1,T2) ← obs(X,Val,T1), obs(X,Val,T2), T1<T2, changeState(X,Val,Val_,T1), Val!=Val_.
27 % Find the time step when the transition has started playing 28 % The last change of X such that W is influencing by X and X is influencing by Y 29 lastchange(X,Y,W,Max,T2) ← Max=#max{ T : changeState(Y,T;X,T;W,T), T<T2}, changeState(X, T2), 30 existInfluence(X,Y), existInfluence(W,X), Max>=0. 31 lastChangeAll(X,Y,Max,T2) ← lastchange(X,Y,W,Max,T2), transition(X,_,W,_,_,D, change(T3)), T3<T2, 32 T2-U>D, lastConditionChange(X,Y,U,T2). 33 % Last change between X and its influencing component Y 34 lastConditionChange(X,Y,H,T2) ← H=#max{ T : changeState(Y,T;X,T) , T<T2}, changeState(X, T2), 35 existInfluence(X,Y), H>=0. 36 % Find the time point of the last change: it is the last change of X, or of the component influenced by X 37 % or of the components involved in the transition condition 38 lastChange(X,Y,Max,T2) ← lastChangeAll(X,Y,Max,T2). 39 lastChange(X,Y,H,T2) ← lastConditionChange(X,Y,H,T2), not lastChangeAll(X,Y,H,T2), H!=H, delay(H).
40 % Compute all models with all candidate timed local transitions 41 {transition(Y,Valy,X,Val1,Val2,D, change(T2))} ← obs_normalized(X,Val1,T1,T2), 42 obs_normalized(Y,Valy,T1,T2), changeState(X,Val1,Val2,T2), existInfluence(X,Y), 43 lastChange(X,Y,T1,T2), T2=T1+D, delay(D). 44 transition(Y,Valy,X,Val1,Val2,D) ← transition(Y,Valy,X,Val1,Val2,D, _). 45 % for each change keep only one transition (xOR) 46 getTransNumber(Tot,X,T)← Tot={transition(_,_,X,_,_,_, change(T))}, changeState(X,T), T!=0. 47 % Exactly one transition by change in a model 48 ← getTransNumber(Tot,X,T), changeState(X,T), Tot=0. 49 ← getTransNumber(Tot,X,T), changeState(X,T), Tot>1.
7.3. Refinement
7.4. Refinement According to the Semantics
50 % A component with the same level inhibits and activates the same component
51 ← transition(Y,Valy,X,Val1,Val2,_), transition(Y,Valy,X,Val3,Val4,_), Val1<Val2, Val3>Val4.
52 % A component with different levels influence another component with the same effect
53 ← transition(Y,Valy,X,Val1,Val2,_), transition(Y,Valy_,X,Val1,Val2,_), Valy_!=Valy.
54 % Last time points in the data 55 timeSeriesSize(Last) ← Last=#max{ T : obs(_,_,T) }. 56 step(0..Last)← timeSeriesSize(Last). 57 % Compute all the obs between all the time points in the data 58 obs_(X,Val,T1,T2) ← obs(X,Val,T1), obs(X,Val,T2), T1<T2, not existsChange(X,Val,T1,T2). 59 existsChange(X,Val,T1,T2) ← obs(X,Val1,T), T>T1, T<T2, Val1!=Val, obs(X,Val,T1), obs(X,Val,T2). 60 % There is a transition with different delays 61 existTransDiffDelays(Y,Valy,X,Val1,Val2,D1,D2) ← transition(Y,Valy,X,Val1,Val2,D1), 62 transition(Y,Valy,X,Val1,Val2,D2), D1!=D2. 63 % There is a transition in conflict with "transition(Y,Valy,X,Val1,Val2,D1)" 64 existTransInConflict(Y,Valy,X,Val1,Val2,D1,T1,T2) ← transition(Y,Valy,X,Val1,Val2,D1), 65 transition(X,Val1,_,_,_,D2,change(T3)), T3>=T2, D2>=D1, T3-D2 <=T2, step(T2), 66 step(T1), T1<T2, D1=T2-T1, obs_(X,Val1,T1,T2), obs_(Y,Valy,T1,T2). 67 % Eliminate all models that do not respect the semantics (Definitions 5–6) 68 ← transition(Y,Valy,X,Val1,Val2,D), obs_(X,Val1,T1,T2), obs_(Y,Valy,T1,T2), step(D), 69 not changeState(X,Val1,Val2,T2), not existTransInConflict(Y,Valy,X,Val1,Val2,D,T1,T2), 70 not existTransDiffDelays(Y,Valy,X,Val1,Val2,D,D2), changeState(X,Val1,Val2,T3), 71 T2!=Max, timeSeriesSize(Max), obs_(X,Val1,T1,T3), T3-T1=D2, delay(D2), D=T2-T1.
7.5. Refinement on the Delays
73 % No different delays for the same transition
74 ← transition(Y,Valy,X,Val1,Val2,D1), transition(Y,Valy,X,Val1,Val2,D2), D1!=D2.
75 % Transitions with the average of delays 76 % Number of the repetition of each transition 77 nbreTotTrans(Y,Valy,X,Val1,Val2,Tot) ← Tot={transition(Y,Valy,X,Val1,Val2,_,_)}, 78 transition(Y,Valy,X,Val1,Val2,_). 79 % The sum of the delays for each transition 80 sumDelays(Y,Valy,X,Val1,Val2,S) ← S=#sum{ D: transition(Y,Valy,X,Val1,Val2,D)}, 81 transition(Y,Valy,X,Val1,Val2,_), S!=0. 82 % Compute the average delay for each transition 83 transAvgDelay(Y,Valy,X,Val1,Val2,Davg) ← nbreTotTrans(Y,Valy,X,Val1,Val2,Tot), 84 sumDelays(Y,Valy,X,Val1,Val2,S), Davg=S/Tot.
85 % Compute the maximum value and the minimum value of the delays of a same transition
86 maxDelay(Y,Valy,X,Val1,Val2,Max) ← Max=#max{ D : transition(Y,Valy,X,Val1,Val2,D)},
87 transition(Y,Valy,X,Val1,Val2,_).
88 minDelay(Y,Valy,X,Val1,Val2,Min) ← Min=#min{ D : transition(Y,Valy,X,Val1,Val2,D)},
89 transition(Y,Valy,X,Val1,Val2,_).
90 transIntervalDelay(Y,Valy,X,Val1,Val2,interval(Min,Max)) ← minDelay(Y,Valy,X,Val1,Val2,Min),
91 maxDelay(Y,Valy,X,Val1,Val2,Max).
8. Evaluation
8.1. DREAM4
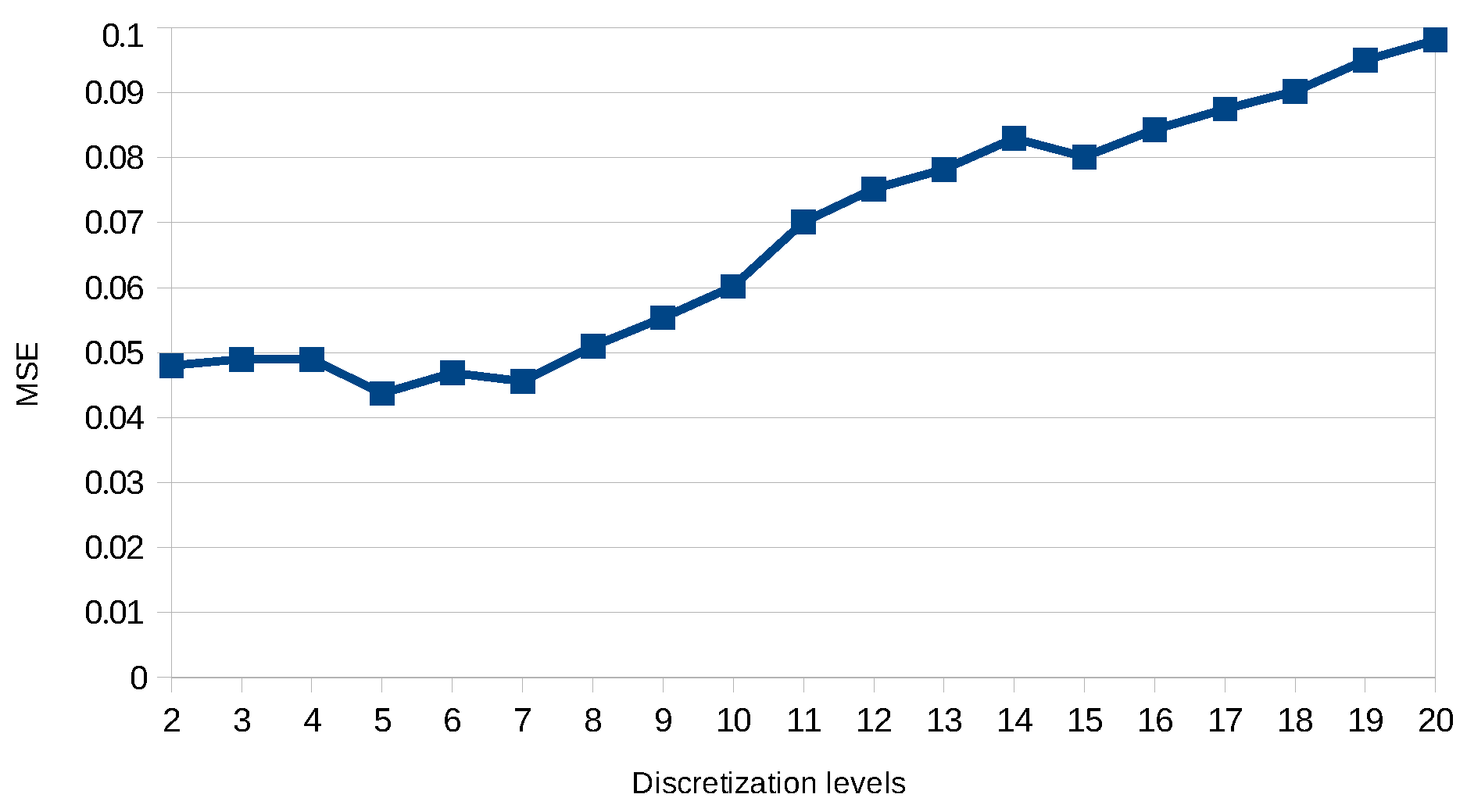
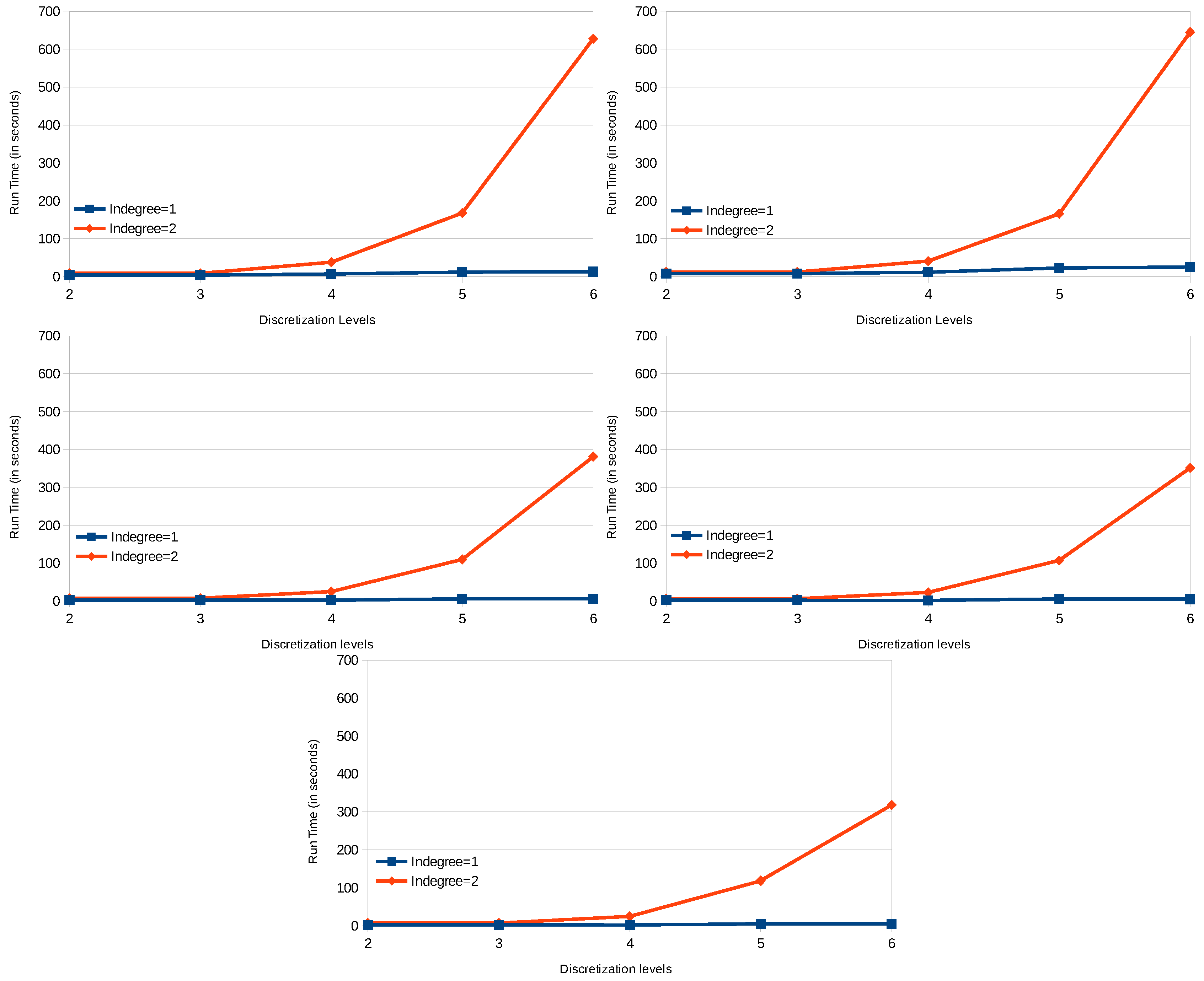
8.2. Results
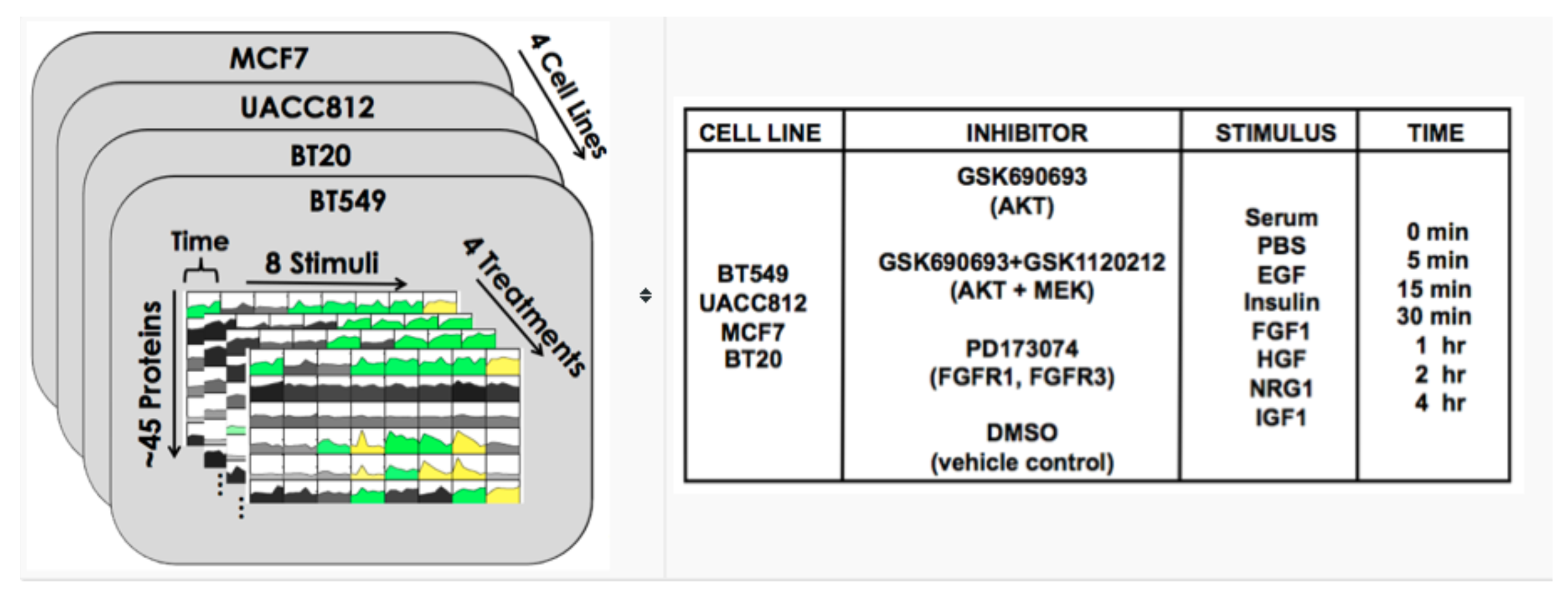
8.3. DREAM8
8.4. Results
8.5. Discussion
9. Conclusions and Perspectives
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AN | Automata Network |
| T-AN | Timed Automata Network |
| ASP | Answer Set Programming |
References
- Marx, V. Biology: The big challenges of big data. Nature 2013, 498, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Callebaut, W. Scientific perspectivism: A philosopher of science’s response to the challenge of big data biology. Stud. Hist. Philos. Sci. Part C 2012, 43, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Akutsu, T.; Kuhara, S.; Maruyama, O.; Miyano, S. Identification of genetic networks by strategic gene disruptions and gene overexpressions under a Boolean model. Theor. Comput. Sci. 2003, 298, 235–251. [Google Scholar] [CrossRef]
- Sima, C.; Hua, J.; Jung, S. Inference of gene regulatory networks using time-series data: A survey. Curr. Genom. 2009, 10, 416–429. [Google Scholar] [CrossRef] [PubMed]
- Koksal, A.S.; Pu, Y.; Srivastava, S.; Bodik, R.; Fisher, J.; Piterman, N. Synthesis of biological models from mutation experiments. In Proceedings of the 40th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Rome, Italy, 23–25 January 2013; Volume 48, pp. 469–482.
- Kim, S.Y.; Imoto, S.; Miyano, S. Inferring gene networks from time series microarray data using dynamic Bayesian networks. Brief. Bioinform. 2003, 4, 228–235. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Serpedin, E.; Dougherty, E.R. Inferring gene regulatory networks from time series data using the minimum description length principle. Bioinformatics 2006, 22, 2129–2135. [Google Scholar] [CrossRef] [PubMed]
- Koh, C.; Wu, F.X.; Selvaraj, G.; Kusalik, A.J. Using a state-space model and location analysis to infer time-delayed regulatory networks. EURASIP J. Bioinform. Syst. Biol. 2009, 2009. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.F.; Sung, W.K.; Mittal, A. Learning multi-time delay gene network using Bayesian network framework. In Proceedings of the 16th IEEE International Conference on Tools with Artificial Intelligence, Boca Raton, FL, USA, 15–17 November 2004; pp. 640–645.
- Silvescu, A.; Honavar, V. Temporal Boolean network models of genetic networks and their inference from gene expression time series. Complex Syst. 2001, 13, 61–78. [Google Scholar]
- Zhang, Z.Y.; Horimoto, K.; Liu, Z. Time Series Segmentation for Gene Regulatory Process with Time-Window-Extension. In Proceedings of the 2nd International Symposium on Optimization and Systems Biology, Lijiang, China, 31 October–3 November 2008; pp. 198–203.
- Akutsu, T.; Tamura, T.; Horimoto, K. Completing networks using observed data. In Algorithmic Learning Theory; Springer: Berlin/Heidelberg, Germany, 2009; pp. 126–140. [Google Scholar]
- Matsuno, H.; Doi, A.; Nagasaki, M.; Miyano, S. Hybrid Petri net representation of gene regulatory network. Pac. Symp. Biocomput. 2000, 5, 341–352. [Google Scholar]
- Siebert, H.; Bockmayr, A. Temporal constraints in the logical analysis of regulatory networks. Theor. Comput. Sci. 2008, 391, 258–275. [Google Scholar] [CrossRef]
- Ahmad, J.; Bernot, G.; Comet, J.P.; Lime, D.; Roux, O. Hybrid modelling and dynamical analysis of gene regulatory networks with delays. ComPlexUs 2006, 3, 231–251. [Google Scholar] [CrossRef]
- Casagrande, A.; Dreossi, T.; Piazza, C. Hybrid Automata and epsilon-Analysis on a Neural Oscillator. In Hybrid Systems Biology: First International Workshop, HSB 2012, Newcastle Upon Tyne, UK; Cinquemani, E., Donzé, A., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2012; pp. 58–72. [Google Scholar]
- Paoletti, N.; Yordanov, B.; Hamadi, Y.; Wintersteiger, C.M.; Kugler, H. Analyzing and synthesizing genomic logic functions. In Computer Aided Verification; Springer: Cham, Switzerland, 2014; pp. 343–357. [Google Scholar]
- Li, R.; Yang, M.; Chu, T. Synchronization of Boolean networks with time delays. Appl. Math. Comput. 2012, 219, 917–927. [Google Scholar] [CrossRef]
- Ribeiro, T.; Magnin, M.; Inoue, K.; Sakama, C. Learning delayed influences of biological systems. Front. Bioeng. Biotechnol. 2014, 2. [Google Scholar] [CrossRef] [PubMed]
- Donnarumma, F.; Murano, A.; Prevete, R.; della Battaglia, V.S.M. Dynamic network functional comparison via approximate-bisimulation. Control Cybern. 2015, 44, 99–127. [Google Scholar]
- Girard, A.; Pappas, G.J. Approximate bisimulations for nonlinear dynamical systems. In Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC 2005), Seville, Spain, 12–15 December 2005; pp. 684–689.
- Comet, J.P.; Fromentin, J.; Bernot, G.; Roux, O. A formal model for gene regulatory networks with time delays. In Computational Systems-Biology and Bioinformatics; Springer: New York, NY, USA, 2010; pp. 1–13. [Google Scholar]
- Merelli, E.; Rucco, M.; Sloot, P.; Tesei, L. Topological characterization of complex systems: Using persistent entropy. Entropy 2015, 17, 6872–6892. [Google Scholar] [CrossRef]
- Merelli, E.; Pettini, M.; Rasetti, M. Topology driven modeling: The IS metaphor. Nat. Comput. 2015, 14, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Ben Abdallah, E.; Ribeiro, T.; Magnin, M.; Roux, O.; Inoue, K. Inference of Delayed Biological Regulatory Networks from Time Series Data. In Computational Methods in Systems Biology, Proceedings of the 14th International Conference, CMSB, Cambridge, UK, 21–23 September 2016; Springer International Publishing AG: Dordrecht, The Netherlands, 2016; pp. 30–48. [Google Scholar]
- Paulevé, L.; Magnin, M.; Roux, O. Refining Dynamics of Gene Regulatory Networks in a Stochastic π-Calculus Framework. In Transactions on Computational Systems Biology XIII; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6575, pp. 171–191. [Google Scholar]
- Paulevé, L.; Chancellor, C.; Folschette, M.; Magnin, M.; Roux, O. Analyzing Large Network Dynamics with Process Hitting. In Logical Modeling of Biological Systems; Wiley: New York, NY, USA, 2014; pp. 125–166. [Google Scholar]
- Paulevé, L. Goal-Oriented Reduction of Automata Networks. In Computational Methods in Systems Biology Proceedings of the 14th International Conference, CMSB, Cambridge, UK, 21–23 September 2016; Springer International Publishing AG: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Goldstein, Y.A.; Bockmayr, A. A lattice-theoretic framework for metabolic pathway analysis. In Computational Methods in Systems Biology; Springer: Berlin/Heidelberg, Germany, 2013; pp. 178–191. [Google Scholar]
- Thomas, R. Regulatory networks seen as asynchronous automata: A logical description. J. Theor. Biol. 1991, 153, 1–23. [Google Scholar] [CrossRef]
- Harvey, I.; Bossomaier, T. Time out of joint: Attractors in asynchronous random Boolean networks. In Fourth European Conference on Artificial Life; MIT Press: Cambridge, MA, USA, 1997; pp. 67–75. [Google Scholar]
- Folschette, M.; Paulevé, L.; Inoue, K.; Magnin, M.; Roux, O. Identification of Biological Regulatory Networks from Process Hitting models. Theor. Comput. Sci. 2015, 568, 49–71. [Google Scholar] [CrossRef]
- Freedman, P. Time, Petri nets, and robotics. IEEE Trans. Robot. Autom. 1991, 7, 417–433. [Google Scholar] [CrossRef]
- Ben Abdallah, E.; Folschette, M.; Roux, O.; Magnin, M. Exhaustive analysis of dynamical properties of Biological Regulatory Networks with Answer Set Programming. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Washington, DC, USA, 9–12 November 2015; pp. 281–285.
- Baral, C. Knowledge Representation, Reasoning and Declarative Problem Solving; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gelfond, M.; Lifschitz, V. The Stable Model Semantics for Logic Programming. In Proceedings of the 5th International Logic Programming Conference and Symposium, Seattle, WA, USA, 15–19 August 1988; pp. 1070–1080.
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Ostrowski, M.; Schaub, T.; Wanko, P. Theory Solving Made Easy with Clingo 5. In Proceedings of the Technical Communications of the 32nd International Conference on Logic Programming (ICLP), New York City, USA, 16–21 October 2016; pp. 1–15.
- Prill, R.J.; Saez-Rodriguez, J.; Alexopoulos, L.G.; Sorger, P.K.; Stolovitzky, G. Crowdsourcing network inference: The DREAM predictive signaling network challenge. Sci. Signal. 2011, 4. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.M.; Heiser, L.M.; Cokelaer, T.; Unger, M.; Nesser, N.K.; Carlin, D.E.; Zhang, Y.; Sokolov, A.; Paull, E.O.; Wong, C.K.; et al. Inferring causal molecular networks: Empirical assessment through a community-based effort. Nature methods 2016, 13, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Schaffter, T.; Marbach, D.; Floreano, D. GeneNetWeaver: In silico benchmark generation and performance profiling of network inference methods. Bioinformatics 2011, 27, 2263–2270. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.M.; Nesser, N.K.; Johnson-Camacho, K.; Jeffress, M.; Johnson, A.; Boniface, C.; Spencer, S.E.F.; Lu, Y.; Heiser, L.M.; Lawrence, Y.; et al. Context Specificity in Causal Signaling Networks Revealed by Phosphoprotein Profiling. Cell Syst. 2016. [Google Scholar] [CrossRef] [PubMed]
- Cokelaer, T.; Bansal, M.; Bare, C.; Bilal, E.; Bot, B.; Chaibub Neto, E.; Eduati, F.; de la Fuente, A.; Gönen, M.; Hill, S.; et al. DREAMTools: A Python package for scoring collaborative challenges. F1000Research 2016, 4. [Google Scholar] [CrossRef] [PubMed]
- Anwar, S.; Baral, C.; Inoue, K. Encoding Higher Level Extensions of Petri Nets in Answer Set Programming. In Logic Programming and Nonmonotonic Reasoning; Springer: New York, NY, USA, 2013; pp. 116–121. [Google Scholar]
- Villaverde, A.F.; Becker, K.; Banga, J.R. PREMER: Parallel Reverse Engineering of Biological Networks with Information Theory. In Computational Methods in Systems Biology, Proceedings of the 14th International Conference, CMSB, Cambridge, UK, 21–23 September 2016; Springer: Berlin, Germany; pp. 323–329.
- Ostrowski, M.; Paulevé, L.; Schaub, T.; Siegel, A.; Guziolowski, C. Boolean Network Identification from Multiplex Time Series Data. In Computational Methods in Systems Biology, Proceedings of the 13th International Conference, CMSB, Nantes, France, September 16–18 2015; Springer: Dordrecht, The Netherlands, 2015; pp. 170–181. [Google Scholar]
- Yu, N.; Seo, J.; Rho, K.; Jang, Y.; Park, J.; Kim, W.K.; Lee, S. hiPathDB: A human-integrated pathway database with facile visualization. Nucleic Acids Res. 2012, 40, D797–D802. [Google Scholar] [CrossRef] [PubMed]
- Talikka, M.; Boue, S.; Schlage, W.K. Causal Biological Network Database: A Comprehensive Platform of Causal Biological Network Models Focused on the Pulmonary and Vascular Systems. In Computational Systems Toxicology; Springer: New York, NY, USA, 2015; pp. 65–93. [Google Scholar]
- Saez-Rodriguez, J.; Alexopoulos, L.G.; Epperlein, J.; Samaga, R.; Lauffenburger, D.A.; Klamt, S.; Sorger, P.K. Discrete logic modelling as a means to link protein signalling networks with functional analysis of mammalian signal transduction. Mol. Syst. Biol. 2009, 5. [Google Scholar] [CrossRef] [PubMed]
- Gallet, E.; Manceny, M.; Le Gall, P.; Ballarini, P. An LTL model checking approach for biological parameter inference. In Formal Methods and Software Engineering, Proceedings of the 16th International Conference on Formal Engineering Methods, ICFEM, Luxembourg, Luxembourg, 3–5 November 2014; Springer: Heidelberg, Germany; pp. 155–170.
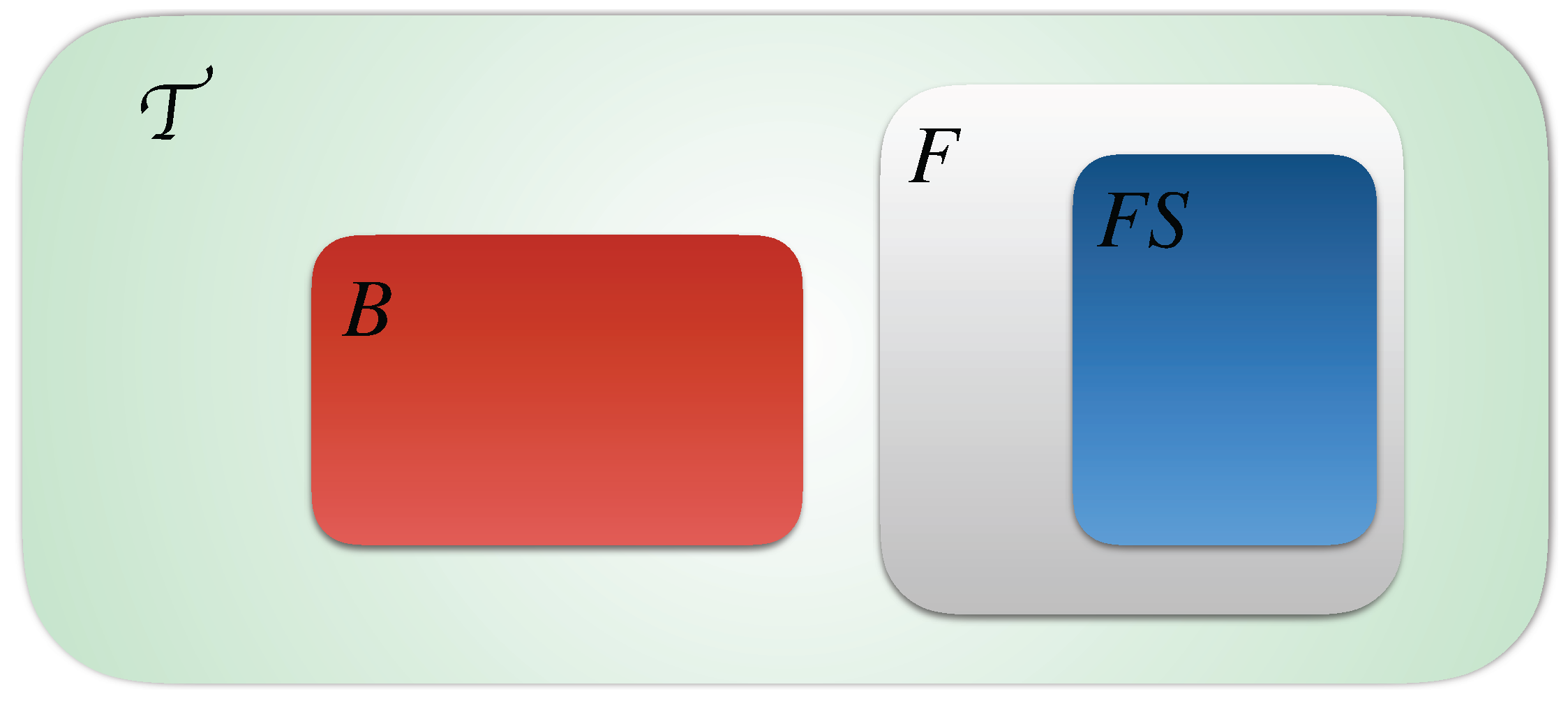
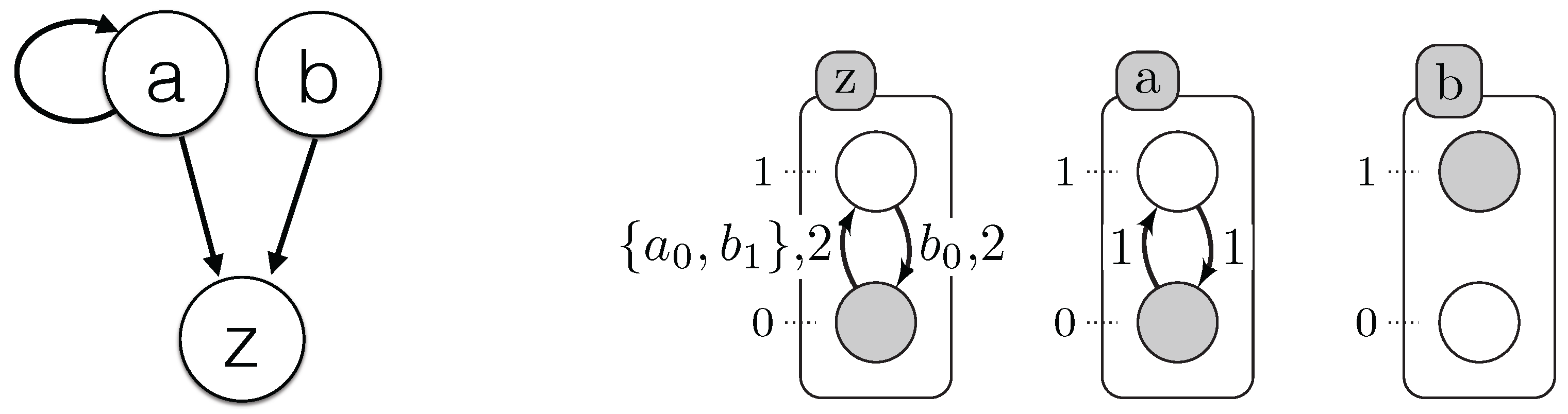
| t | SFS | |||||
|---|---|---|---|---|---|---|
| 0 | ∅ | |||||
| 1 | ∅ | ∅ | ||||
| 2 | ||||||
| 3 | ||||||
| 4 | ∅ | ∅ | ||||
| 5 | ∅ | |||||
| 6 | ∅ | ∅ | ||||
| 10 | ∅ | ∅ | ∅ | ∅ |
| Benchmark | Number of Genes | MSE |
|---|---|---|
| insilico_size10_1 | 10 | 0.086 |
| insilico_size10_2 | 10 | 0.080 |
| insilico_size10_3 | 10 | 0.076 |
| insilico_size10_4 | 10 | 0.039 |
| insilico_size10_5 | 10 | 0.076 |
| insilico_size100_1 | 100 | 0.052 |
| insilico_size100_2 | 100 | 0.042 |
| insilico_size100_3 | 100 | 0.033 |
| insilico_size100_4 | 100 | 0.033 |
| insilico_size100_5 | 100 | 0.052 |
| Discrete Levels | Run Time (s) | Mean RMSE |
|---|---|---|
| 2 | 9775 s | 0.7054 |
| 3 | 7078 s | 0.6419 |
| 4 | 15,941 s | 0.5901 |
| 5 | 14,102 s | 0.5528 |
| 6 | 19,356 s | 0.5667 |
| 7 | 20,963 s | 0.5563 |
| Benchmarks | Mean RMSE | |
|---|---|---|
| 2 Discrete Levels | 5 Discrete Levels | |
| BT20 | 1.712 | 0.458 |
| BT549 | 1.507 | 0.449 |
| MCF7 | 0.713 | 0.310 |
| UACC812 | 12.6 | 3.391 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Abdallah, E.; Ribeiro, T.; Magnin, M.; Roux, O.; Inoue, K. Modeling Delayed Dynamics in Biological Regulatory Networks from Time Series Data. Algorithms 2017, 10, 8. https://doi.org/10.3390/a10010008
Ben Abdallah E, Ribeiro T, Magnin M, Roux O, Inoue K. Modeling Delayed Dynamics in Biological Regulatory Networks from Time Series Data. Algorithms. 2017; 10(1):8. https://doi.org/10.3390/a10010008
Chicago/Turabian StyleBen Abdallah, Emna, Tony Ribeiro, Morgan Magnin, Olivier Roux, and Katsumi Inoue. 2017. "Modeling Delayed Dynamics in Biological Regulatory Networks from Time Series Data" Algorithms 10, no. 1: 8. https://doi.org/10.3390/a10010008
APA StyleBen Abdallah, E., Ribeiro, T., Magnin, M., Roux, O., & Inoue, K. (2017). Modeling Delayed Dynamics in Biological Regulatory Networks from Time Series Data. Algorithms, 10(1), 8. https://doi.org/10.3390/a10010008





