Abstract
Digital image authentication has become a hot topic in the last few years. In this paper, a pixel-based fragile watermarking method is presented for image tamper identification and localization. By analyzing the left and right singular matrices of SVD, it is found that the matrix product between the first column of the left singular matrix and the transposition of the first column in the right singular matrix is closely related to the image texture features. Based on this characteristic, a binary watermark consisting of image texture information is generated and inserted into the least significant bit (LSB) of the original host image. To improve the security of the presented algorithm, the Arnold transform is applied twice in the watermark embedding process. Experimental results indicate that the proposed watermarking algorithm has high security and perceptual invisibility. Moreover, it can detect and locate the tampered region effectively for various malicious attacks.
1. Introduction
Nowadays, digital multimedia like digital images plays an indispensable role in our daily lives. However, with the development of image processing techniques, it has become easier to refine and edit the images. The authenticity and integrity of digital images are suffering from a serious threat. To cope with this problem, the fragile watermarking scheme has recently been proposed. Generally, the fragile watermark used for image authentication can be divided into two types including semi-fragile watermark and complete fragile watermark (also known as fragile watermark). Compared to the semi-fragile watermarking method, the fragile watermarking is more susceptive to various alterations [1]. Therefore, it is more effective for image authentication, especially for the images used in safety-critical applications. According to detection resolution, the fragile watermarking scheme is further split into two categories [2]: the block-wise method and the pixel-wise method. In a block-based watermarking algorithm, the image is firstly partitioned into many sub-blocks. Each image block is inserted with the identification code produced from the block itself. In [3], Walton presented a classical block-wise fragile watermarking algorithm. The least significant bit (LSB) of image sub-block is inserted by the check-sum of the most significant bits (MSBs). However, a false certification arises whereby one can exchange the image block without affecting its authentication information. To resolve this problem, Chang et al. [4] suggested a hash function-based watermarking algorithm. In their scheme, the authentication data of each block is generated via a cryptographic hash function. The binary form of watermarking information is integrated and inserted into the LSB of the center pixel in the corresponding block. They claimed that this method can recognize and locate any manipulation to the watermarked images. However, later research in [5] pointed out that this method is not secure enough for image authentication. In [6], Chen and Wang introduced a fragile watermarking algorithm, where the authentication data was obtained by applying fuzzy c-means (FCM) clustering. To achieve image authentication in JPEG images, Zhang et al. [7] introduced a reversible fragile watermarking method. Experimental results indicate that it can locate the forged blocks when the falsified area is not too large.
From the above analysis, it can be noted that the block-wise fragile watermarking algorithm has achieved great success in tamper identification and localization. However, the detection precision of the block-based watermarking method is limited to the block level [8]. To solve this issue and improve the detection accuracy, many pixel-based fragile watermarking algorithms have been presented in recent years. In [9], Liu et al. presented a simple fragile watermarking algorithm, where a binary authentication watermark was produced by a pixel-value difference between a chaotic image and the host image. Rawat and Raman [10] presented a chaotic map-based method, but this algorithm has a potential security risk since it does not consider the image content in the watermark embedding process [11]. Based on the security analysis, Teng et al. [11] introduced an improved fragile watermarking method. The MSBs of the host image are taken into account in the process of watermark generation, which ensures the safety of the algorithm. The main problem existing in the above pixel-wise fragile watermarking schemes is that an extra binary watermark image is needed on the receiving end for tamper detection and localization. To achieve blind forgery detection, Benrhouma et al. [12] introduced a chaos-based watermarking algorithm. The authentication data is constructed by the local pixel contrast between neighborhood pixels and average pixel value of each block. To achieve image authentication for stereoscopic images, Zhou et al. [13] put forward a binocular visual characteristic-based fragile watermarking method. In their method, the binocular just noticeable difference (BJND) [14] mode is utilized to complete watermark embedding, and a two-stage detection method is performed to increase the detection accuracy.
In this paper, we propose a pixel-based fragile watermarking algorithm for image tamper identification and localization. By analyzing singular value decomposition (SVD), it is found that the matrix product between the first column of the left singular matrix and the transposition of the first column in the right singular matrix has a strong relationship with the image texture information. By setting an appropriate threshold, a binary authentication watermark is generated. After the watermarking message is encrypted via Arnold permutation, it is inserted into the LSB plane of the original image. In tamper detection, the falsified region is revealed by the difference map between the extracted and regenerated watermarks.
The rest of this paper is organized as follows. In Section 2, we describe the SVD in brief and analyze its intrinsic characteristic utilized in this paper. Section 3 introduces the presented fragile watermarking algorithm. Experiments and performance analysis are expatiated in Section 4. The conclusions are given at the end of this paper.
2. Singular Value Decomposition (SVD)
As an effective method of algebraic feature extraction, SVD is widely applied in signal processing [15]. For a matrix A with rank r, SVD can be expressed as
where and are column vectors of singular value matrices and , and and are their matrix elements, respectively. is a diagonal singular matrix made up of singular values , where . The singular values have good stability that it can resist slight disturbances in signal processing. Moreover, the SVD can be implemented to arbitrary matrices without any restriction and the larger singular values contain the most information of an image. Due to these properties, SVD has been gradually applied in digital watermarking schemes [16,17,18].
Taking for example, the SVD can be rewritten as
Because , it is noted from Equation (2) that the first item plays an important role in matrix A. To reveal this relationship, let us consider an exceptional circumstance that all the elements in matrix A are the same. Then, matrix A can be derived as
where is the only singular value in , i.e., . It is generally known that for a matrix with size of , equals in such a circumstance. According to Equation (3), the matrix can be calculated as shown in Equation (4):
From Equation (4), it can be observed that is only related to its matrix size () when the original matrix A has the same matrix elements.
Generally, the local pixel values in each image block change slowly. In other words, they have similar neighboring pixels. Inspired by this, we can promote the conclusion to image processing. To verify this conjecture, the image is firstly partitioned into numerous blocks, for example . For each image block, SVD is applied and is calculated. Figure 1 shows the probability distribution histogram of all the values in , which takes grayscale images Lena and Barbara for example. From Figure 1, we can see that the elements in matrix satisfy the normal distribution approximately. In addition, most of the values are distributed around 0.25 (), which is the reciprocal of the block size. This conclusion is consistent with the above analysis.
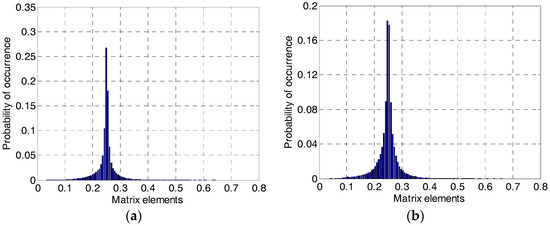
Figure 1.
Probability distribution histogram of the values in : (a) Image Lena; (b) Image Barbara.
For an image, there are two kinds of image blocks including smooth blocks and texture blocks. In smooth blocks, the neighboring pixels have similar pixel values. On the contrary, the probability for similar neighboring pixels in texture blocks becomes much lower than that in the smooth region. In other words, the fluctuation of pixel values in texture blocks is much more serious than the smooth blocks. Based on this characteristic and the above analysis, we can draw the conclusion that the matrix product in the smooth block should be closely associated with its block size, while in the texture block like edge region, this characteristic is severely weakened. According to this conclusion, we can segment an image into the texture region and smooth region by setting an appropriate threshold T. This process can be illustrated in Figure 2. Figure 3 gives the binary segmentation images of image Lena with different thresholds, when the block size . In the figures, the white area refers to the smooth region, while the black area represents the texture region. We can see that the texture features of an image can be well represented, especially when as shown in Figure 3d. This characteristic provides a theoretical basis for the design of the proposed watermarking scheme.
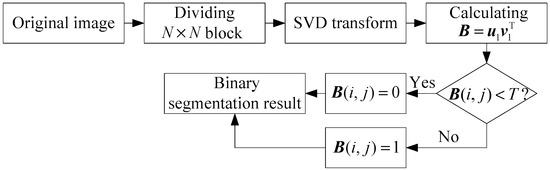
Figure 2.
The process of image segmentation.

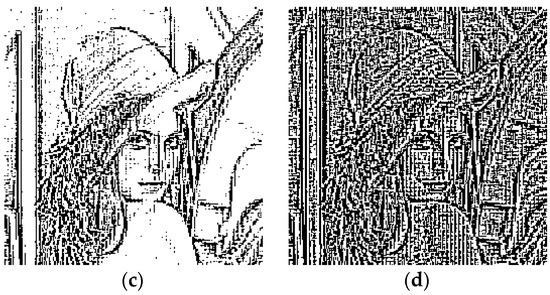
Figure 3.
Image segmentation results for different threshold T: (a) ; (b) ; (c) ; (d) .
3. Proposed Watermarking Scheme
As mentioned above, the matrix product in each image block is closely related to the image texture information. The more similar the pixel values in each block are, the more obvious this characteristic will be. In this section, we make full use of this property to introduce an effective fragile watermarking for image authentication. The binary texture image obtained in Section 2 is served as the authentication information and inserted into the host image. Figure 4 illustrates the flow chart of the presented watermarking algorithm, which consists of two main stages: watermark insertion on the sending side and the authentication process on the receiving side. The concrete procedures of watermark insertion are introduced as follows.
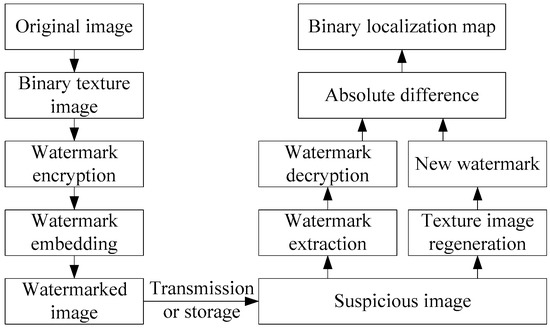
Figure 4.
Block diagram of the presented fragile watermarking algorithm.
Step 1. The LSB plane of the original image is firstly initialized to zeros.
Step 2. The processed image is partitioned into many sub-blocks with a size of . The proposed algorithm is based on the fact that the image block has similar pixel values. However, with the increase of the block size, the probability for similar neighboring pixels is decreased. The characteristic mentioned above will be weakened, which will further affect the image segmentation effect. Generally, an incomplete image feature will lead to a higher false positive ratio in tamper detection. To ensure the effectiveness of the proposed method, we choose in this paper to illustrate the proposed algorithm. The block size is also adopted as an encryption key, which will be used on the receiving end.
Step 3. For each block, the SVD is performed and the matrix is calculated.
Step 4. By setting appropriate threshold T, a binary image consisting of the texture information is obtained. From Figure 3, we can see that the texture feature of the host image is better described than other thresholds when the threshold . Therefore, the threshold is set as 0.25 in this paper.
Step 5. To ensure the security of the proposed algorithm, an encryption algorithm known as Arnold transform [19] is applied twice in the watermark embedding process. The binary texture image is firstly encrypted with a secret key , and the host image is permuted with a secret key ().
Step 6. The embedding process is completed after the permuted LSB plane is replaced by the encrypted watermarking bits.
Step 7. After inverse Arnold transform with secret key , we obtain the watermarked image.
In image transmission or storage, the content of the digital image might be destroyed by malicious attacks, which makes its texture information inconsistent with the original image. We take advantage of this property to realize tamper detection and localization. The watermarked image is firstly permuted by Arnold transform with secret key . Then, the encrypted watermark is extracted from the LSB plane of suspicious image. With the help of secret key , we obtain the decrypted watermark. In addition, a new texture image is regenerated via the same first four steps in the watermark embedding process. By taking the absolute difference between the regenerated texture image and extracted information, a binary localization map is obtained. From this detection map, the tampered region can be determined.
4. Experiments and Performance Analysis
Several experiments are conducted to evaluate the performance of the presented method. In these experiments, we adopt six test images with a size of as the host images, which are shown in Figure 5. In addition, two secret keys and are set as 75 and 32, respectively.

Figure 5.
Test images: (a) Lena; (b) Airplane; (c) Boat; (d) Couple; (e) Lax; (f) Best_cha.
4.1. Invisibility
Perceptual invisibility is one of the most significant indexes in the watermarking scheme. It means that the embedded watermark should not be perceived by human eyes. Figure 6 gives the watermarked images produced by the proposed algorithm. We can see from Figure 6 that the images after watermark embedding are almost the same as unwatermarked images shown in Figure 5. It indicates that the proposed scheme provides satisfactory watermark invisibility.

Figure 6.
Watermarked images: (a) Lena; (b) Airplane; (c) Boat; (d) Couple; (e) Lax; (f) Best_cha.
4.2. Tamper Detection and Localization
Generally, the digital image might be manipulated illegally in the process of transmission or storage. To test the performance of the proposed algorithm under malicious attacks, some classical attacks are performed on the watermarked images such as image cropping, copy–paste attack, and so on. It should be noted that the attacks used in this paper are all finished by Adobe Photoshop CS3. Figure 7 illustrates the watermarked images forged by the corresponding attacks. Without prior knowledge, the tampered images cannot be distinguished from the original host images by human eyes. The tamper localization maps obtained by the proposed watermarking scheme are shown in Figure 8. To remove noise effect and improve the localization accuracy, the median filter is applied to the detection map. From Figure 8, we can see that the falsified areas are clearly identified. It suggests that the proposed algorithm achieves good tamper identification and location results for various malicious attacks.

Figure 7.
Tampered images: (a) Image cropping; (b) Copy–paste attack; (c) Text addition; (d) Collage attack; (e) Content-based attack; (f) Constant-average attack.

Figure 8.
The corresponding tamper localization maps: (a) Image cropping; (b) Copy–paste attack; (c) Text addition; (d) Collage attack; (e) Content-based attack; (f) Constant-average attack.
4.3. Performance under Unintentional Attacks
In addition to the malicious attacks, the host images also suffer from some unintentional attacks in the image processing, such as salt and pepper noise and brightness adjustment. To test the fragility of the proposed watermarking algorithm, three unintentional attacks are performed on the watermarked images, and their corresponding detection results are shown in Figure 9. From the detection results in Figure 8 and Figure 9, we can draw the conclusion that the proposed method is sensitive to any manipulation including malicious attacks and unintentional attacks.

Figure 9.
Tamper detection under unintentional attacks: (a) Salt and pepper noise (0.005); (b) Tamper detection result; (c) Brightness adjustment (+4); (d) Tamper detection result; (e) JPEG compression (Q = 99); (f) Tamper detection result.
4.4. Security Analysis
The security of the watermark is another issue that the watermarking scheme should be considered. Arnold transform also known as cat map is an effective encryption algorithm usually adopted in the watermarking scheme [20]. By Arnold transform, the image pixels are randomly permuted, but after a certain amount of permutations, the original image will reappear. In other words, it has good periodicity. The transform period is decided by the image size. For the image with a size of 256 × 256, the Arnold transform period is 192. By using this feature, we can encrypt the watermark by selecting a scrambling time. At present, most of the watermarking algorithms only apply the Arnold transform to the watermark on the sending side [12]. To further improve the security of the proposed method, in this paper, not only the watermark but also the embedding positions are encrypted by using two different secret keys ( and ). Figure 10 shows the extracted binary texture images, which are obtained by using the correct and incorrect combined keys. We can see that, without correct keys, the embedded watermark shown in Figure 10d cannot be obtained. It proves that the proposed algorithm achieves good security.

Figure 10.
Extracted binary watermarks with different key combinations: (a) ; (b) ; (c) ; (d) .
4.5. Performance Comparisons
In this section, we compare the proposed algorithm with two recently proposed fragile watermarking methods in [10,12]. To compare the sensory effect of the watermarked images, the peak signal-to-noise ratio (PSNR) is utilized to investigate the proximity degree between the original and watermarked images. For an image with size of , the definition of PSNR is formulated as
where is the host image after watermark embedding. Table 1 lists the comparison results among these three methods. As listed in Table 1, the proposed method achieves similar PSNR with the other two methods. This is reasonable since the LSB embedding algorithm is adopted in all three watermarking methods. In addition, the PSNR values of the test images are more than 51 dB, which objectively verify the invisibility of the watermark.

Table 1.
Comparison results of peak signal-to-noise ratio (PSNR/dB).
To further test the precision of tamper localization, two evaluation indexes including the false positive rate (FPR) and false negative rate (FNR) are employed in this paper [21]. The FPR refers to the ratio of authentic pixels that are falsely detected as distorted pixels, and the FNR is the ratio of tampered pixels that are incorrectly detected as authentic pixels. Generally, the lower FPR and FNR mean better localization accuracy. Figure 11 illustrates the FPR and FNR comparisons of the above three methods under different cropping sizes. From Figure 11a, we can observe that the FPR values in Rawat et al.’s method [10] are almost zeros. However, the FNR values in Figure 11b are all greater than 0.5. In addition, a binary reference image in [10] is needed on the receiving end for image authentication, which is impractical in real life. Compared with Benrhouma et al.’s algorithm [12], the proposed scheme achieves lower FPR except in cropping size 192 × 192. Notably, the FNR of the proposed scheme is much lower than that of the methods in [10,12]. From Figure 11, it suggests that the proposed authentication algorithm has lower detection errors and higher detection and localization accuracy.
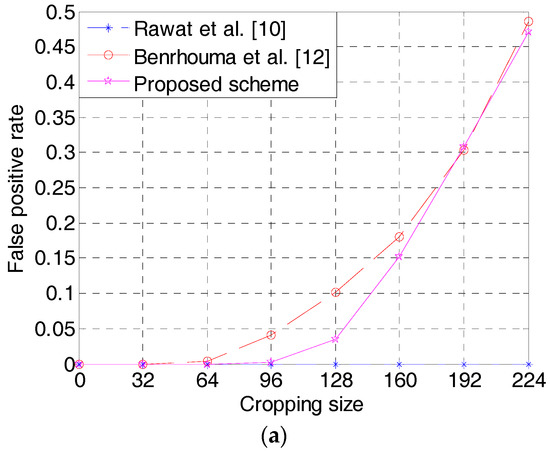
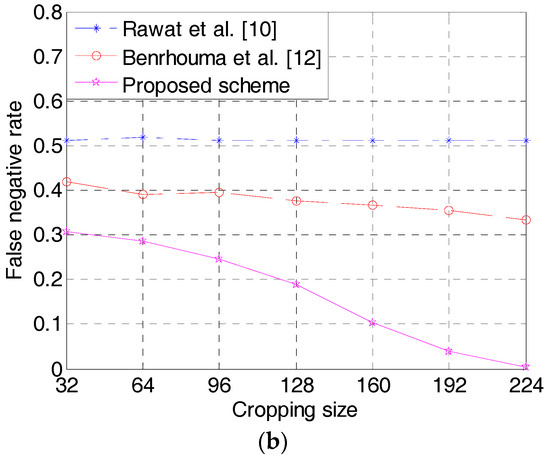
Figure 11.
False positive rate (FPR) and false negative rate (FNR) comparisons under different cropping sizes: (a) FPR; (b) FNR.
Table 2 lists the whole comparisons among the above three algorithms, where the PSNR is the average value of the data in Table 1. From Table 2, it can be observed that, compared with Rawat et al.’s method [10], the proposed algorithm achieves blind tamper detection on the receiving side. In addition, it can detect and locate the falsified region effectively for various malicious attacks, especially for content-based attack and constant-average attack.

Table 2.
All comparisons among the proposed scheme and references [10,12].
5. Conclusions
In this paper, we present a pixel-based fragile watermarking algorithm for image authentication. According to the characteristic of SVD, the binary authentication information is produced and inserted into the host image. Experimental results and analysis demonstrate that the watermarked images obtained via the proposed method have a satisfactory visual effect. In addition, the Arnold transform is used twice in the watermark embedding process, which guarantees the security of the suggested algorithm. Compared with the recently developed watermarking schemes, it not only achieves blind detection but also has higher tamper detection and localization resolution for various attacks. In future work, we hope to further improve detection accuracy and research the effects of different parameters on tamper detection.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (No. 61201371), the Research Award Fund for Outstanding Young and Middle-Aged Scientists of Shandong Province, China (No. BS2013DX022), and the Natural Science Foundation of Shandong Province, China (No. ZR2015PF004).
Author Contributions
Heng Zhang and Chengyou Wang conceived the algorithm and designed the experiments; Heng Zhang performed the experiments; Chengyou Wang and Xiao Zhou analyzed the results; Heng Zhang drafted the manuscript; Xiao Zhou revised the manuscript. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Qi, X.J.; Xin, X. A singular-value-based semi-fragile watermarking scheme for image content authentication with tamper localization. J. Vis. Commun. Image Represent. 2015, 30, 312–327. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wang, S.Z. Statistical fragile watermarking capable of locating individual tampered pixels. IEEE Signal Proc. Lett. 2007, 14, 727–730. [Google Scholar] [CrossRef]
- Walton, S. Image authentication for a slippery new age. Dr Dobb’s J. 1995, 20, 18–26. [Google Scholar]
- Chang, C.C.; Hu, Y.S.; Lu, T.C. A watermarking-based image ownership and tampering authentication scheme. Pattern Recognit. Lett. 2006, 27, 439–446. [Google Scholar] [CrossRef]
- Phan, R.C.W. Tampering with a watermarking-based image authentication scheme. Pattern Recognit. 2008, 41, 3493–3496. [Google Scholar] [CrossRef]
- Chen, W.C.; Wang, M.S. A fuzzy c-means clustering-based fragile watermarking scheme for image authentication. Expert Syst. Appl. 2009, 36, 1300–1307. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wang, S.Z.; Qian, Z.X.; Feng, G.R. Reversible fragile watermarking for locating tampered blocks in JPEG images. Signal Proc. 2010, 90, 3026–3036. [Google Scholar] [CrossRef]
- Zhang, X.P.; Wang, S.Z. Fast communication: Fragile watermarking scheme using a hierarchical mechanism. Signal Proc. 2009, 89, 675–679. [Google Scholar] [CrossRef]
- Liu, S.H.; Yao, H.X.; Gao, W.; Liu, Y.L. An image fragile watermark scheme based on chaotic image pattern and pixel-pairs. Appl. Math. Comput. 2007, 185, 869–882. [Google Scholar] [CrossRef]
- Rawat, S.; Raman, B. A chaotic system based fragile watermarking scheme for image tamper detection. AEU—Int. J. Electron. Commun. 2011, 65, 840–847. [Google Scholar] [CrossRef]
- Teng, L.; Wang, X.Y.; Wang, X.K. Cryptanalysis and improvement of a chaotic system based fragile watermarking scheme. AEU—Int. J. Electron. Commun. 2013, 67, 540–547. [Google Scholar] [CrossRef]
- Benrhouma, O.; Hermassi, H.; El-Latif, A.A.A.; Belghith, S. Chaotic watermark for blind forgery detection in images. Multimed. Tools Appl. 2016, 75, 8695–8718. [Google Scholar] [CrossRef]
- Zhou, W.J.; Yu, L.; Wang, Z.P.; Wu, M.W.; Luo, T.; Sun, L.H. Binocular visual characteristics based fragile watermarking scheme for tamper detection in stereoscopic images. AEU—Int. J. Electron. Commun. 2016, 70, 77–84. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, Z.Z.; Zhu, C.; Tan, Y.P.; Yu, L. Binocular just-noticeable-difference model for stereoscopic images. IEEE Signal Proc. Lett. 2011, 18, 19–22. [Google Scholar] [CrossRef]
- Ranade, A.; Mahabalarao, S.S.; Kale, S. A variation on SVD based image compression. Image Vis. Comput. 2007, 25, 771–777. [Google Scholar] [CrossRef]
- Ansari, I.A.; Pant, M.; Ahn, C.W. Robust and false positive free watermarking in IWT domain using SVD and ABC. Eng. Appl. Artif. Intell. 2016, 49, 114–125. [Google Scholar] [CrossRef]
- Guo, J.M.; Prasetyo, H. False-positive-free SVD-based image watermarking. J. Vis. Commun. Image Represent. 2014, 25, 1149–1163. [Google Scholar] [CrossRef]
- Dadkhah, S.; Manaf, A.A.; Hori, Y.; Hassanien, A.E.; Sadeghi, S. An effective SVD-based image tampering detection and self-recovery using active watermarking. Signal Proc. Image Commun. 2014, 29, 1197–1210. [Google Scholar] [CrossRef]
- Chen, W.; Quan, C.; Tay, C.J. Optical color image encryption based on Arnold transform and interference method. Opt. Commun. 2009, 282, 3680–3685. [Google Scholar] [CrossRef]
- Elayan, M.A.; Ahmad, M.O. Digital watermarking scheme based on Arnold and anti-Arnold transforms. In Proceedings of the International Conference on Image and Signal Processing, Lecture Notes in Computer Science, Trois-Rivières, QC, Canada, 30 May–1 June 2016; Springer: Cham, Germany, 2016; Volume 9680, pp. 317–327. [Google Scholar]
- Solorio, S.B.; Nandi, A.K. Secure fragile watermarking method for image authentication with improved tampering localisation and self-recovery capabilities. Signal Proc. 2011, 91, 728–739. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).