An On-Line Tracker for a Stochastic Chaotic System Using Observer/Kalman Filter Identification Combined with Digital Redesign Method
Abstract
:1. Introduction
2. OKID Formulation
2.1. Basic Observer Equation
2.2. Computation of Markov Parameters
2.2.1. System Markov Parameters
2.2.2. Observer Gain Markov Parameters
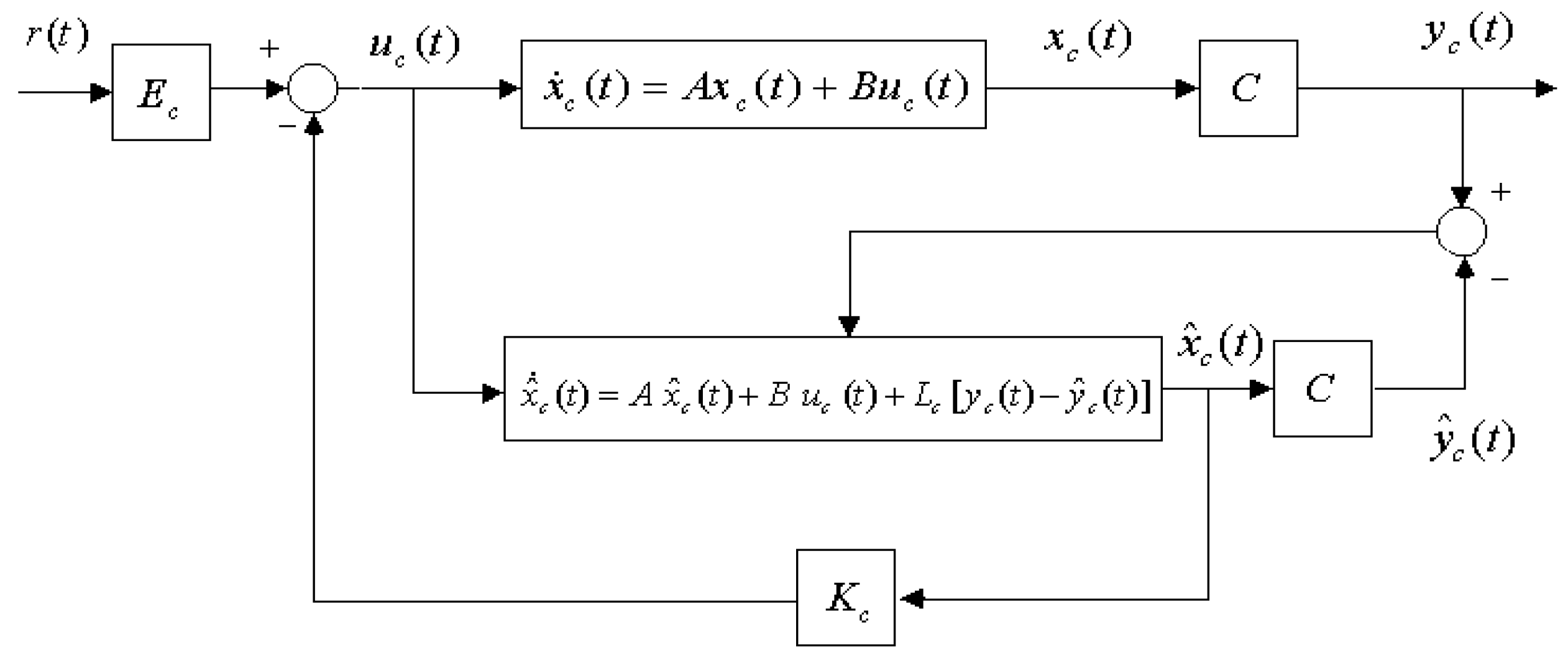
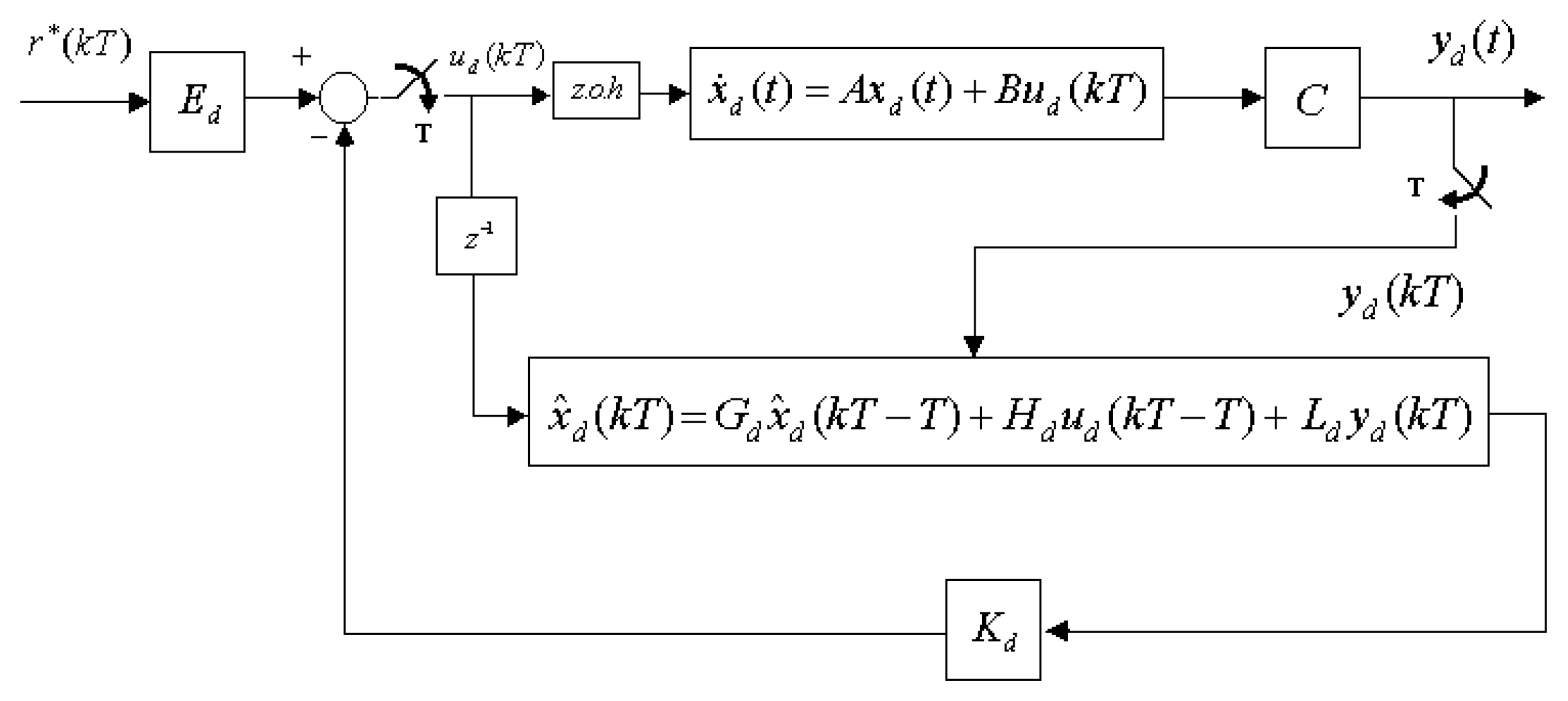
3. Digital Redesign of Full-Order Observer
4. Effective Design Procedures for a Stochastic Chaotic System
- Step 1.
- Perform the off-line system identification scheme to obtain both system and observer-gain Markov parameters of the OKID model.
- (i)
- Compute the observer Markov parameters. Choose a value of that determines the number of observer Markov parameters from the given set of input-output data, and then compute the least-squares solution of the Markov parameter matrix in Equation (10).
- (ii)
- Identify both system and observer-gain Markov parameters. Use the Markov parameters identified in (i) above, and Equations (14) and (18) to determine the combined system and observer-gain Markov parameters. Moreover, set up the Hankel matrix and as shown in Equation (19).
- (iii)
- Realize a state-space model of the system and the corresponding observer gain from the identified sequence of the system and observer-gain Markov parameters by using the ERA method to obtain the desired discrete system realization , and in Equations (21)–(23), where the non-causal term is assumed to be zero.
- Step 2.
- Set the full-order observer-based sampled-data system for the OKID combined with a digital redesign method.
- (i)
- Find the optimal observer gain . Select appropriate weighting matrices in Equation (34).
- (ii)
- By using the new digitally redesigned observer form, obtain the desired discrete system realization , and in Equation (38).
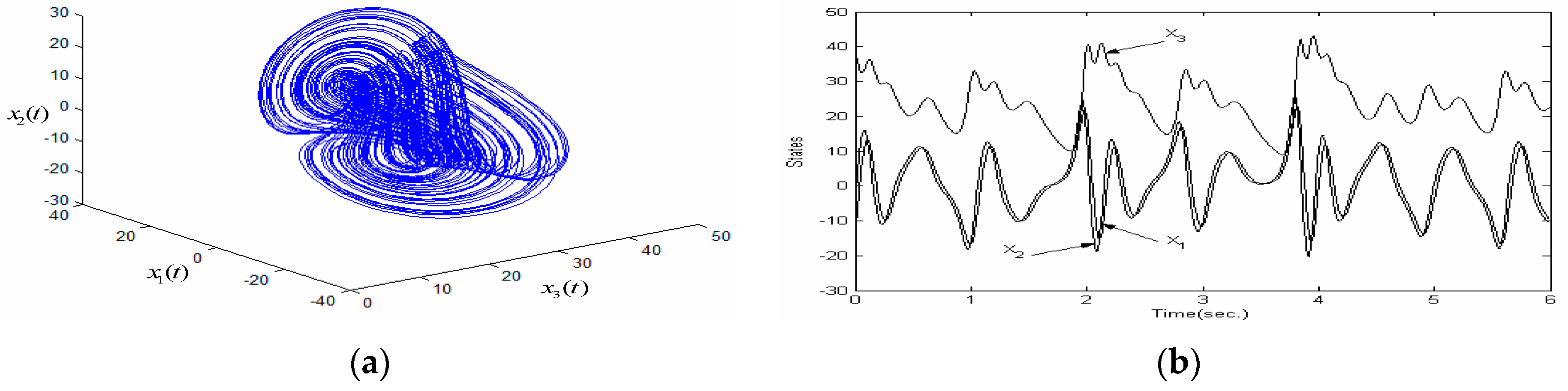
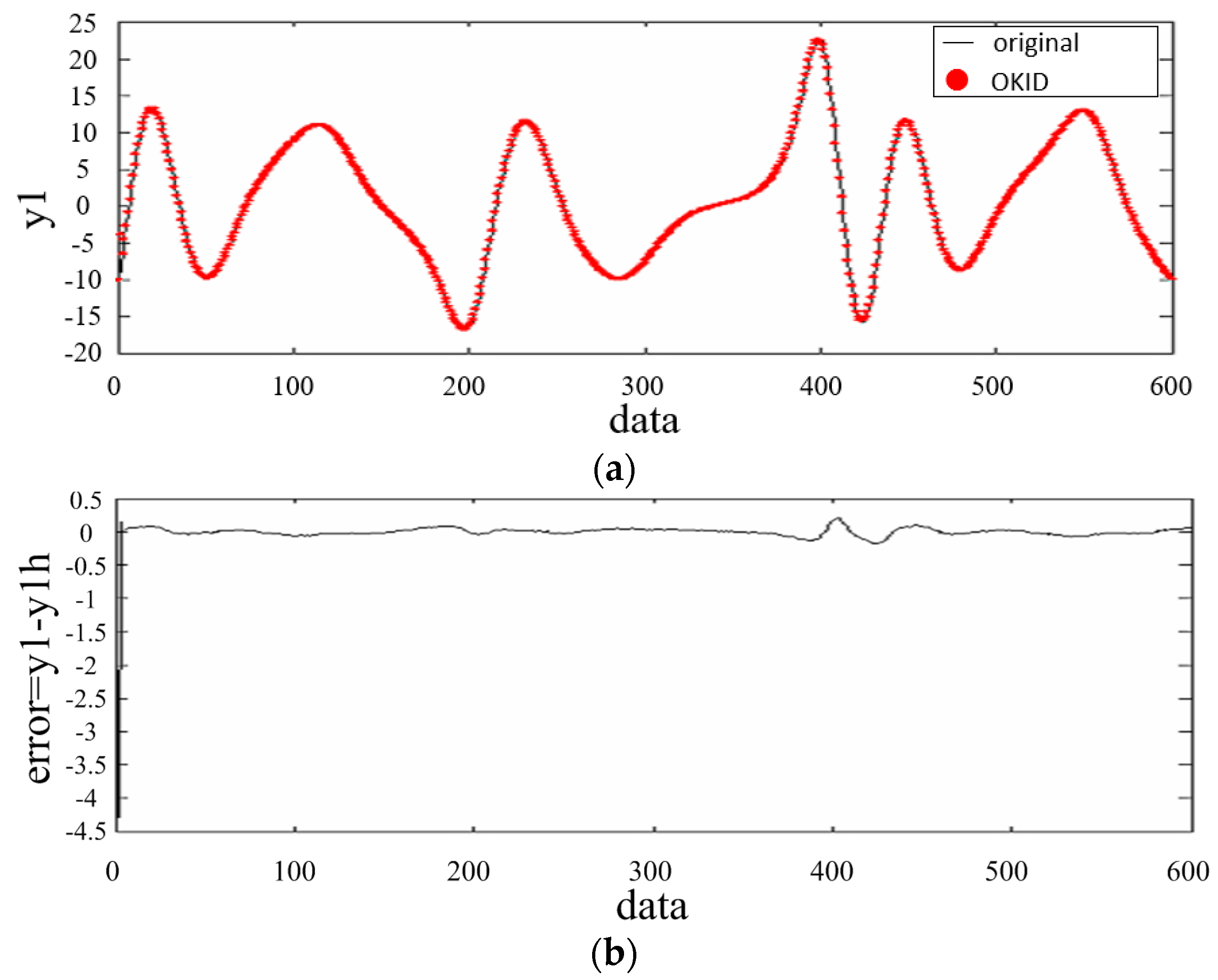
5. An Illustrative Example
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Juang, J.N.; Phan, M.Q.; Horta, L.G.; Longman, R.W. Identification of observer/Kalman filter Markov parameters: Theory and experiments. J. Guid. Control Dyn. 1993, 16, 320–329. [Google Scholar] [CrossRef]
- Ho, B.L.; Kalman, R.E. Effective construction of linear state-variable models from input-output data. In Proceedings of the 3rd Annual Allerton Conference on Circuit and System Theory, Monticello, IL, USA, 20–22 October 1965; pp. 449–459.
- Phan, M.; Horta, L.G.; Juang, J.N.; Longman, R.W. Linear System Identification via an Asymptotically Stable Observer; Technical Report NASA TP 3164; National Research Council, NASA Langley Research Center: Hampton, VA, USA, 1992.
- Juang, J.N.; Pappa, R.S. Effects of noise on modal parameters identified by the eigensystem realization algorithm. J. Guid. Control Dyn. 1986, 3, 294–303. [Google Scholar] [CrossRef]
- Juang, J.N. Applied System Identification; Prentice-Hall: Englewood Cliffs, NJ, USA, 1994; pp. 176–182. [Google Scholar]
- Chien, T.H.; Tsai, J.S.H.; Guo, S.M.; Chen, G. Lower-order state-space self-tuning control for a stochastic chaotic hybrid system. IMA J. Math. Control Inf. 2007, 24, 219–234. [Google Scholar] [CrossRef]
- Guo, S.M.; Shieh, L.S.; Chen, G.; Lin, C.F. Effective chaotic orbit tracker: A prediction-based digital redesign approach. IEEE Trans. Circuits Syst. I Fund. Theory Appl. 2000, 47, 1557–1570. [Google Scholar]
- Wang, H.P.; Tsai, J.S.H.; Yi, Y.I.; Shieh, L.S. Lifted digital redesign of observer-based tracker for a sampled-data system. Int. J. Syst. Sci. 2004, 35, 255–271. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Yu, X.; Xia, Y. Detecting unstable periodic orbits in Chen’s chaotic attractor. Int. J. Bifurc. Chaos 2000, 10, 1987–1991. [Google Scholar] [CrossRef]
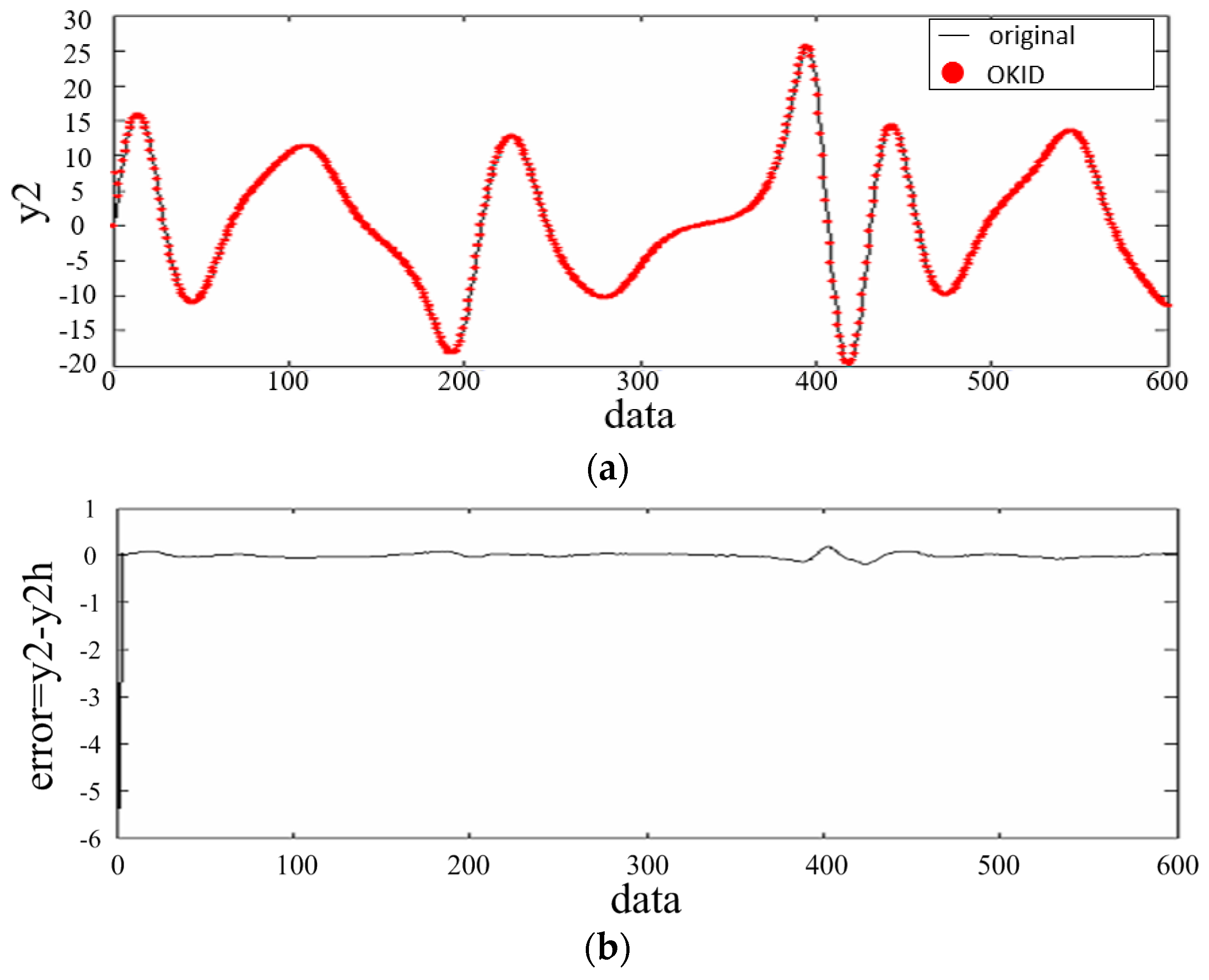

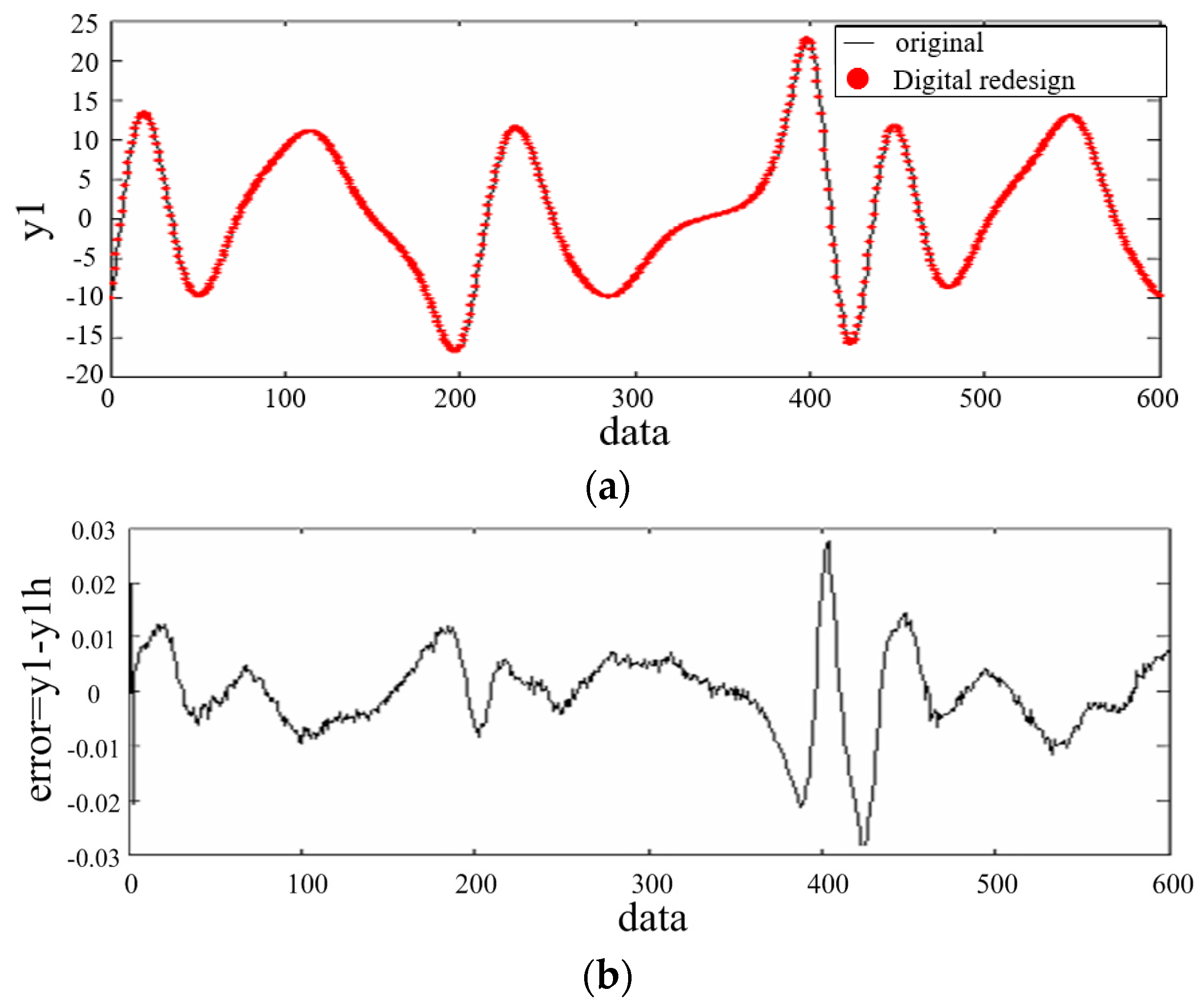
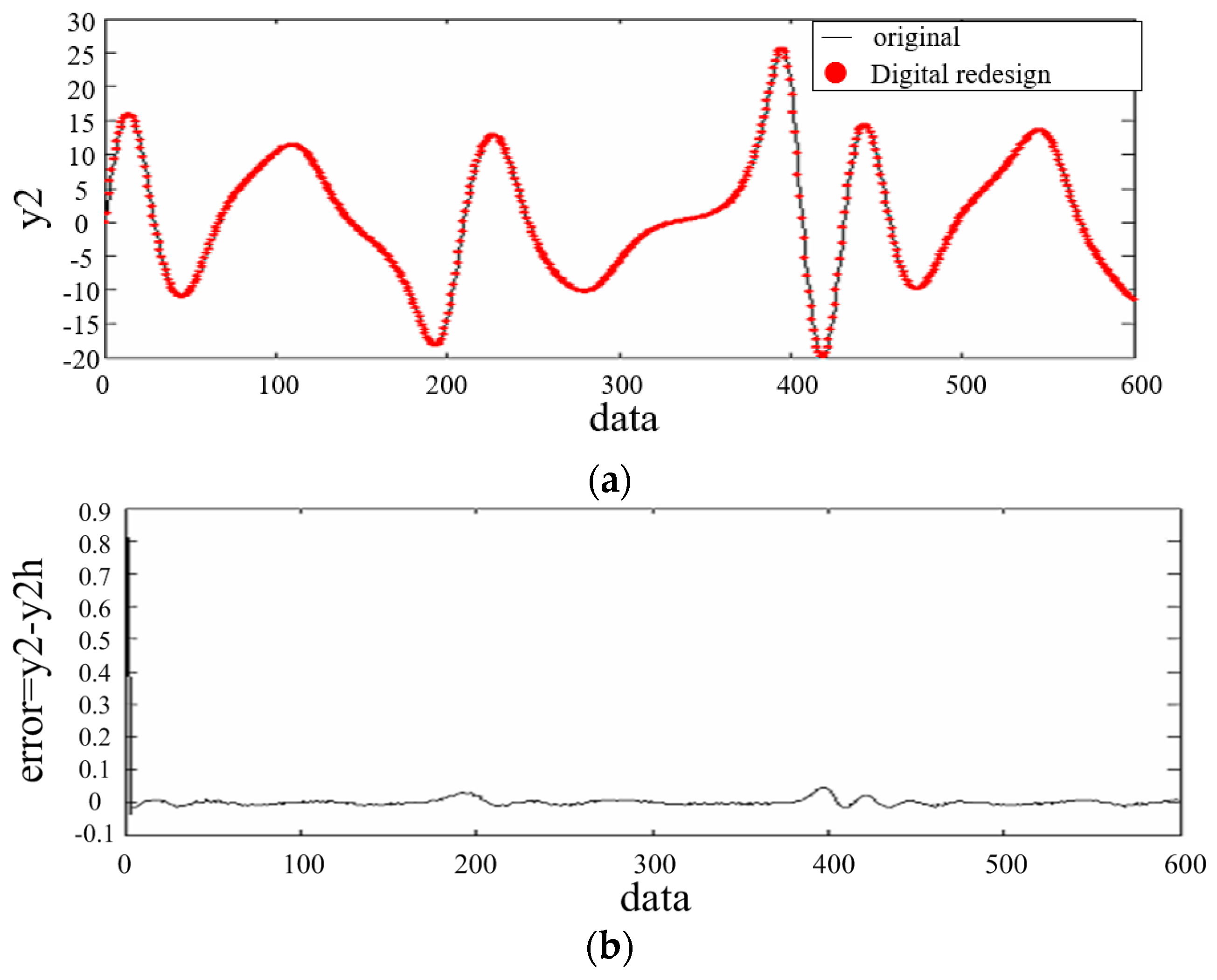
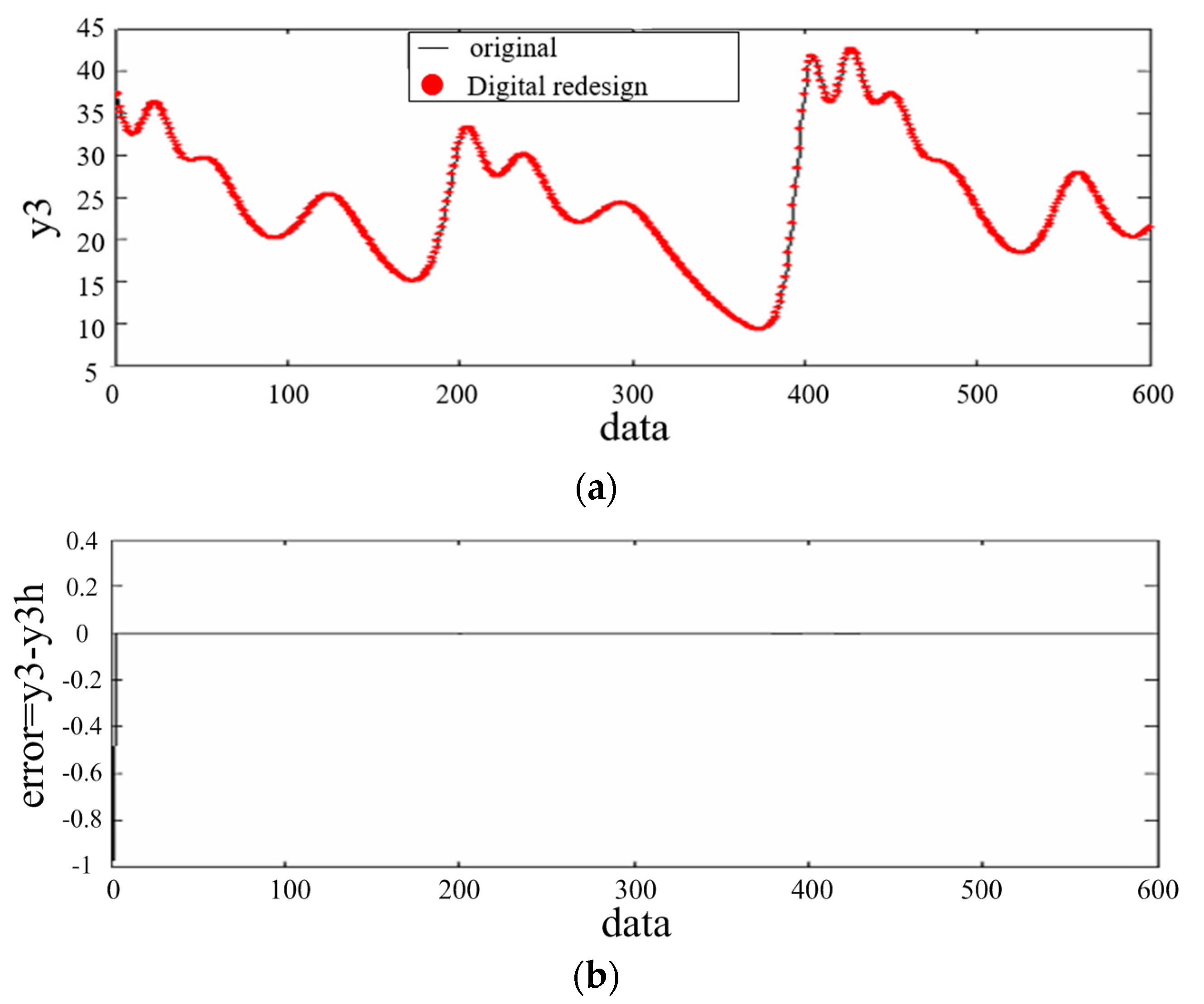
| Method | The Error Range of the Outputs Values | ||
|---|---|---|---|
| OKID | ±0.3 | ±0.5 | ±0.02 |
| OKID combined digital redesign | ±0.03 | ±0.05 | ±0.002 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chien, T.-H.; Chen, Y.-C. An On-Line Tracker for a Stochastic Chaotic System Using Observer/Kalman Filter Identification Combined with Digital Redesign Method. Algorithms 2017, 10, 25. https://doi.org/10.3390/a10010025
Chien T-H, Chen Y-C. An On-Line Tracker for a Stochastic Chaotic System Using Observer/Kalman Filter Identification Combined with Digital Redesign Method. Algorithms. 2017; 10(1):25. https://doi.org/10.3390/a10010025
Chicago/Turabian StyleChien, Tseng-Hsu, and Yeong-Chin Chen. 2017. "An On-Line Tracker for a Stochastic Chaotic System Using Observer/Kalman Filter Identification Combined with Digital Redesign Method" Algorithms 10, no. 1: 25. https://doi.org/10.3390/a10010025
APA StyleChien, T.-H., & Chen, Y.-C. (2017). An On-Line Tracker for a Stochastic Chaotic System Using Observer/Kalman Filter Identification Combined with Digital Redesign Method. Algorithms, 10(1), 25. https://doi.org/10.3390/a10010025





