1. Introduction
Synthetic aperture radar (SAR) is a kind of radar system with the features of all-weather, multi-polarization and penetrability, which played a key role in remote sensing, detection and mapping fields in the past decades [
1,
2,
3]. There are four common observation modes for SAR: Stripmap, Scan, Inverse and Spotlight [
4]. Because the high resolution is conducive to capturing the structure information of the SAR targets, this paper focuses on Spotlight SAR. It is a beamforming-based observation technology, for which the radio beam will always point to the observation scene. The SAR image reconstruction is to acquire the scatter coefficients and to recover spatial distribution of the scatterers from the reflected waves. To obtain a better imaging resolution, a larger aperture will be synthesised by the coherent processing for the motions of targets relative to the antenna, as the pulse compression is usually applied on the range direction. However, in practical applications, traditional SAR imaging methods encounter many problems. Firstly, the receiver needs a higher sampling rate for the wideband waveform because of the Nyquist sampling limit, which leads to a considerable cost for data storing and processing. Secondly, the conventional techniques often suffer from the sidelobe disturbance which may lead to the performance deterioration of reconstruction, such as fuzzy in the SAR target image, etc.
Compressed sensing (CS) [
5,
6,
7], as a novel theoretical framework appearing in literature recently, can obtain necessary information via sub-Nyquist sampling rate for sparse signal, which can reduce storage requirement and simplify the design of hardware system. That is why CS has attracted greater attention in SAR imaging. In 2001, Cetin et al. introduced the sparse constraint into spotlight SAR imaging, and proposed a method to improve the target feature [
8]. CS was first applied in super-resolution radar imaging by Baraniuk et al. in 2007, and a new type of radar system was proposed based on sparse reconstruction [
9]. In 2009, Gurbuz et al. analyzed the application of sparse reconstruction in ground-penetrating radar imaging, and proposed a sparse imaging algorithm based on
-norm minimization [
10]. In the next year, a SAR imaging method based on sparse reconstruction theory was introduced by Potter et al. [
11], which can achieve a higher reconstruction resolution than the traditional imaging methods. In 2011, the effect of parameter selection of SAR imaging based on regularized sparse reconstruction was studied by Batu et al. [
12]. In order to accelerate the speed of SAR imaging algorithm, a sparse regularization technique based on iterative threshold method was proposed by Fang et al. in 2014 [
13]. For moving targets, Zhang et al. proposed an efficient SAR imaging method in 2015 [
14] combining fractional Fourier transform technology with CS framework. However, these studies dealt only with the spatial sparsity of the observation without exploiting the structural characteristics of scatterers in the target scene. In practice, the imaging results show that the scatterers tend to be aggregated together as clumps. The sparse reconstruction schemes have ability to accomplish SAR imaging based on object-level information of scatterers and possess the robustness to noise [
15]. In 2016, Zhao proposed a CS-based SAR imaging algorithm with structured sparsity constraint, in which a hierarchical Bayesian learning framework was applied [
16]. Since hierarchical model is designed, the requirement for model matching of such kind of algorithm is strict, thus the imaging quality may deteriorate once observation data is mismatched with the model.
To solve the above problems, we introduce a tensor decomposition algorithm in this paper both to reap the model robustness and to lower resource requirement. The real-world signal is usually multidimensional and structured. In order to deal with such higher-order data processing problem, tensor decomposition is studied widely. For instance, tensor modeling is utilized in chemometrics to analyse spectroscopy [
17], and is also applied to acquire two-dimensional direction of arrival (DOA) estimation by taking advantage of the Vandermonde structure in array manifold [
18,
19]. For SAR imaging problems, tensor modeling is capable of exploiting the structured sparse distribution of the scatterers to gain more robustness. Because of the
curse of dimensionality in higher-order data processing [
20,
21,
22], making use of the sparsity is becoming a research hotspot in recent years. In 2010, Lim and Comon applied tensor decomposition to propose a sparse reconstruction method, and derived the uniqueness condition of tensor decomposition [
23]. Duarte et al. first introduced the Kronecker constraint into the construction of dictionary in 2011, and proposed the Kronecker-CS model [
24]. In low rank tensor signal processing, Sidiropoulos et al. introduced the CS theorem into a two-step sparse signal reconstruction algorithm in 2012 [
25]. The following year, Caiafa and Cichocki proposed two types of matching pursuit algorithms based on tensor model incorporating with CS method [
26]. Although there has been little public research about combining sparse representation with tensor decomposition in SAR imaging field, potential advantages of this method with robustness and efficiency inspire us to apply it in solving the open problems. The application of higher-order CS in image processing, such as hyperspectral imaging [
24,
27] provides the inspiration of this work, but this is still in the stage of preliminary study. We formulate the SAR echo signal as a Tucker model based on its Kronecker information and then construct a sparse reconstruction algorithm by utilizing the structured sparsity of target scene. Both the theoretical analysis and numerical experiment verifications reveal that the proposed algorithm is superior to the existing methods, such as spatially variant apodization (SVA) [
28,
29] and matching pursuit algorithms [
30,
31,
32].
The following is the organization of other sections in this paper:
Section 2 describes the received signal model of SAR imaging and its tensor modeling;
Section 3 constructs the algorithm based on Kronecker constraint and multiway structured sparsity of the signal model;
Section 4 provides several groups of numerical experiments to verify the proposed method, and compare with the existing methods in performance;
Section 5 concludes this paper.
3. The Proposed Method
3.1. Sparse Reconstruction Based on Kronecker Dictionary
Compressed sensing can reconstruct the source signal from the undersampled measurements. Applying the technique to SAR super-resolution imaging still faces many challenges. The sparse imaging method is mainly to solve an ill-posed linear inverse problem by using the sparsity of radar cross section (RCS). For the large scale data, the classic procedure will be rigorously challenged by many computation problems. For instance, considering a scene with observation points, the classic reconstruction approach will deal with data in length up to 1048576, which leads to a tremendous linear system, consuming computation resource significantly. From the analysis above, it is known that the target scene has the sparsity and the scatterers usually clustered together to blocky areas. Therefore, considering the structured sparse feature, the SAR imaging can be treated as a sparse reconstruction problem with Kronecker dictionary. A multiway structured sparse matching pursuit algorithm can be constructed to estimate the scatter coefficients with much fewer iterations.
Firstly, the SAR echo signal must be decoupled, for which the tensor data , and dictionaries along each mode have to be constructed. Our purpose is reconstructing the nonzero scatter coefficients from , i.e., finding a -structured sparse representation corresponding to . Because of the sparsity of target scene, only a fewer rows need to be randomly extracted from the dictionary.
Let
, and then the Tucker decomposition of the original signal can be rewritten as
where
is the vectorization of all nonzero elements. Consequently, the solution of the problem can be described as
Defining
, the solution of (
14) can be written as
. Efficient calculation steps can be deduced by Cholesky decomposition [
40].
| Algorithm 1 Tucker decomposition based SAR imaging algorithm. |
- Input:
decoupled echo signal ; the number of maximum nonzero entries ; dictionaries along each mode ; the threshold of error ϵ. - Output:
scattering coefficients estimate . - 1:
Initialization: ; ; ; . - 2:
while and , do - 3:
; - 4:
; - 5:
; - 6:
; - 7:
; - 8:
; - 9:
; - 10:
endwhile - 11:
; - 12:
.
|
In iterative process, make sure that the nonzero elements of core tensor are always contained within a small index set. Finally all the nonzero elements and the corresponding index set are obtained and the expected scatter coefficients can be recovered as well. The algorithm flow is represented in Algorithm 1.
3.2. Algorithm Complexity Analysis
The first step of iteration needs to calculate
, and the corresponding computational cost is
. In addition, the absolute maximum optimization should be calculated, which needs
operations. Comparing with this, the classic matching pursuit method, such as orthogonal matching pursuit (OMP) [
30,
32], requires the computation cost
in this step.
With the application of the Cholesky decomposition, the computational complexity of estimating can be reduced efficiently in the iteration. Even if every mode need to be updated, the total computational cost can not exceed . By comparison, the computational cost of OMP algorithm is in this step.
In the residual calculation step, it is needed to compute and subtract it from . The corresponding calculations are . The ones of the OMP algorithm in this step, by contrast, are .
With regard to iterations, for a -structured sparse problem, the maximum iterations is . But OMP algorithm needs times iteration for the same problem.
4. Numerical Simulations and Discussion
This section will demonstrate several experiments to verify the proposed method. The simulations are classified into two parts, one is spotlight SAR imaging realization, including ideal point-scatterer target setting and real data experiments; the other is performance comparisons between the proposed algorithm and the existing methods, including error curves and computational cost. We choose three algorithms as references: SVA [
28], OMP [
30] and compressive sampling MP (CoSaMP) [
31].
The SVA algorithm is a kind of apodization filtering SAR imaging method, which is designed to achieve sidelobe control. However, the performance of such classic algorithm is susceptible by noise, and the resolution is limited, especially for adjacent targets. Both OMP and CoSaMP belong to sparse reconstruction algorithms, which have the advantage of super-resolution due to the robustness to sidelobe disturbance and noise. The hardware configuration for the simulation system is: Intel Core i7-5500U 2.4 GHz, 8 GB RAM, Windows 10.
4.1. Realization of SAR Imaging
In this section, two groups of simulation experiments are presented to verify the effectiveness of the proposed method. One investigates the SAR imaging of ideal point targets and the other considers the practical measured data. The simulation scenario is stated as
Table 1.
4.1.1. SAR Imaging for Ideal Point Targets
This section includes two settings of simulations: The first group investigates the imaging results via modifying the signal-to-noise ratio (SNR) under the condition of fixed number of scatterers. The second one inspects the imaging resolution via changing the the number of scatterers with fixed SNR.
(1) Different SNRs
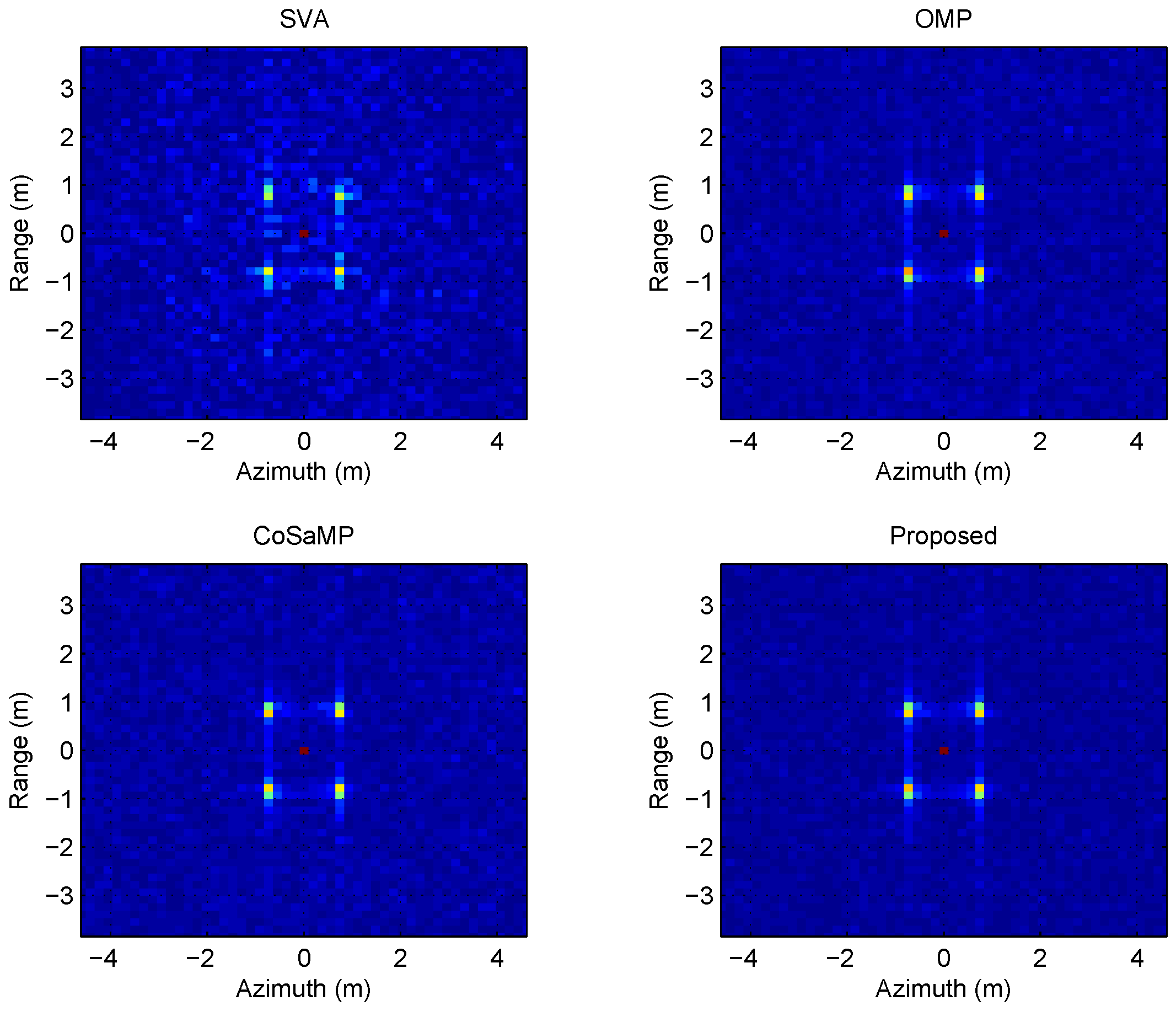
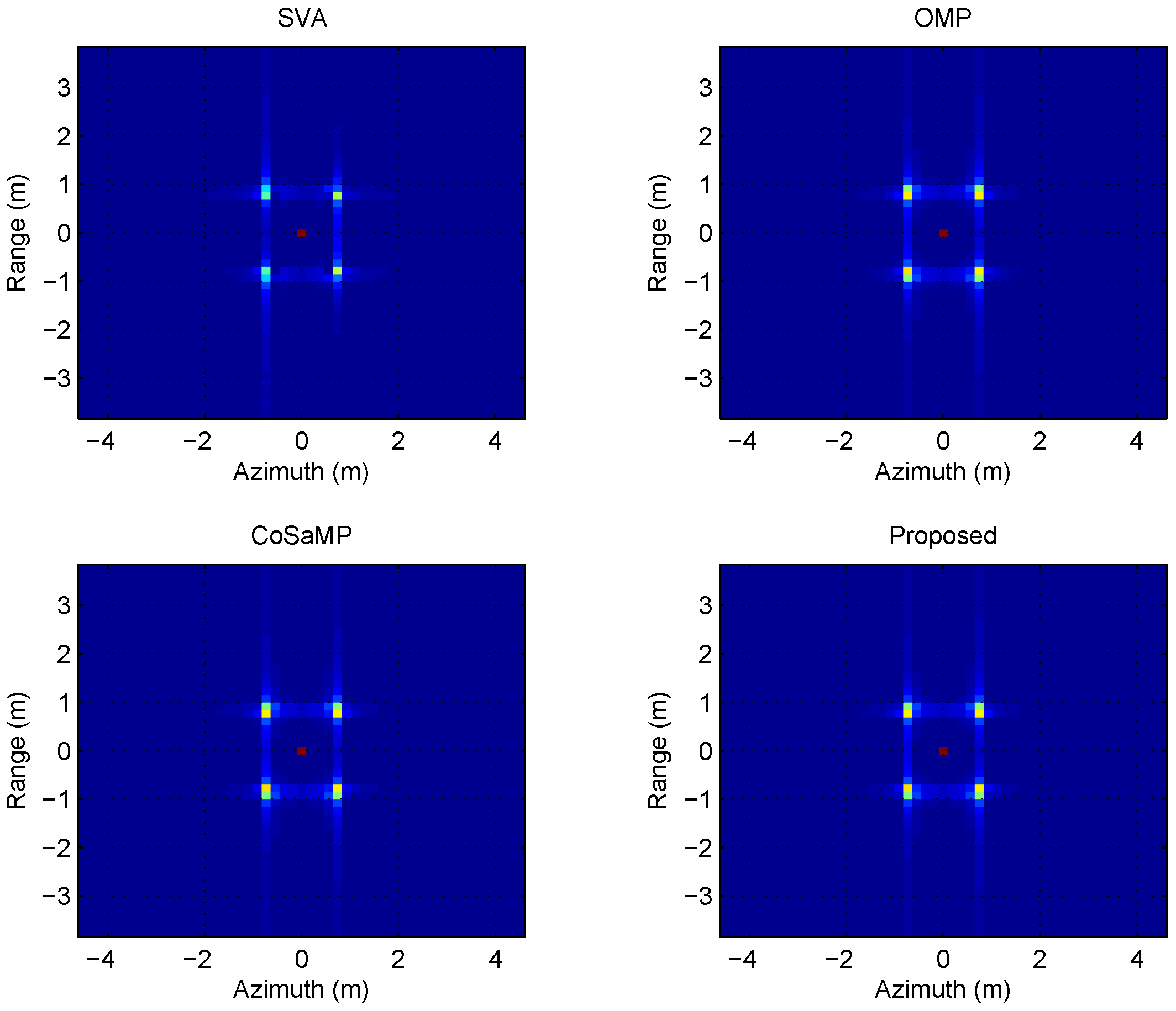
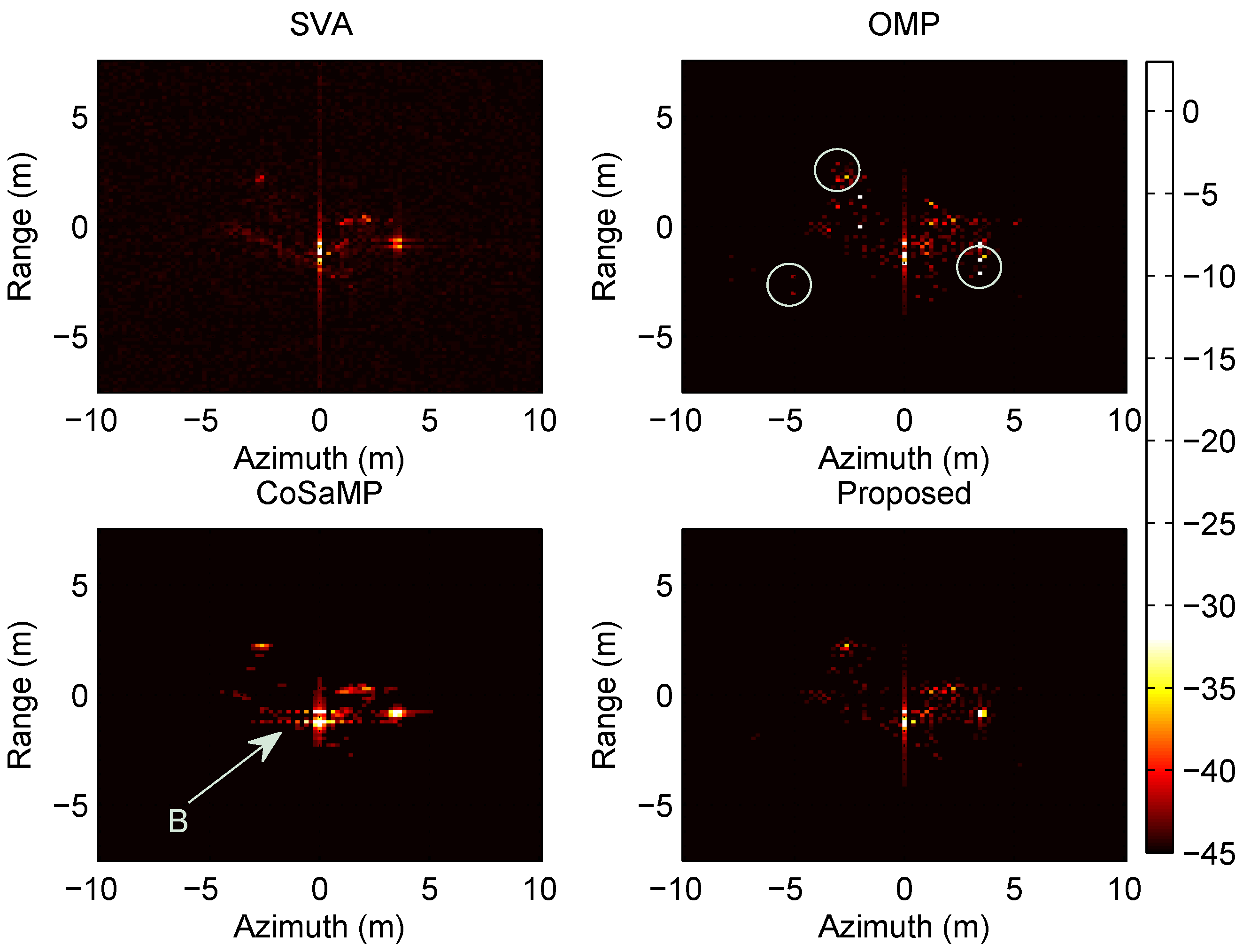
We investigate the effectiveness of the proposed method according to different noise conditions, from the low to the high SNR configurations. Five ideal point scatterers are placed around the centre of target scene in this simulation scenario.
The
Figure 2 and
Figure 3 show the SAR imaging realizations at the situation of the 3 dB and 30 dB SNR, respectively.
These two simulations demonstrate the imaging quality of the proposed method. For the low SNR, the imaging result of SVA shows severe ambiguity owing to the noise instability of this procedure. In comparison, the proposed algorithm performs much better, and the two matching pursuit algorithms also show good results. For the highest SNR, the imaging quality of all algorithms approach to the same.
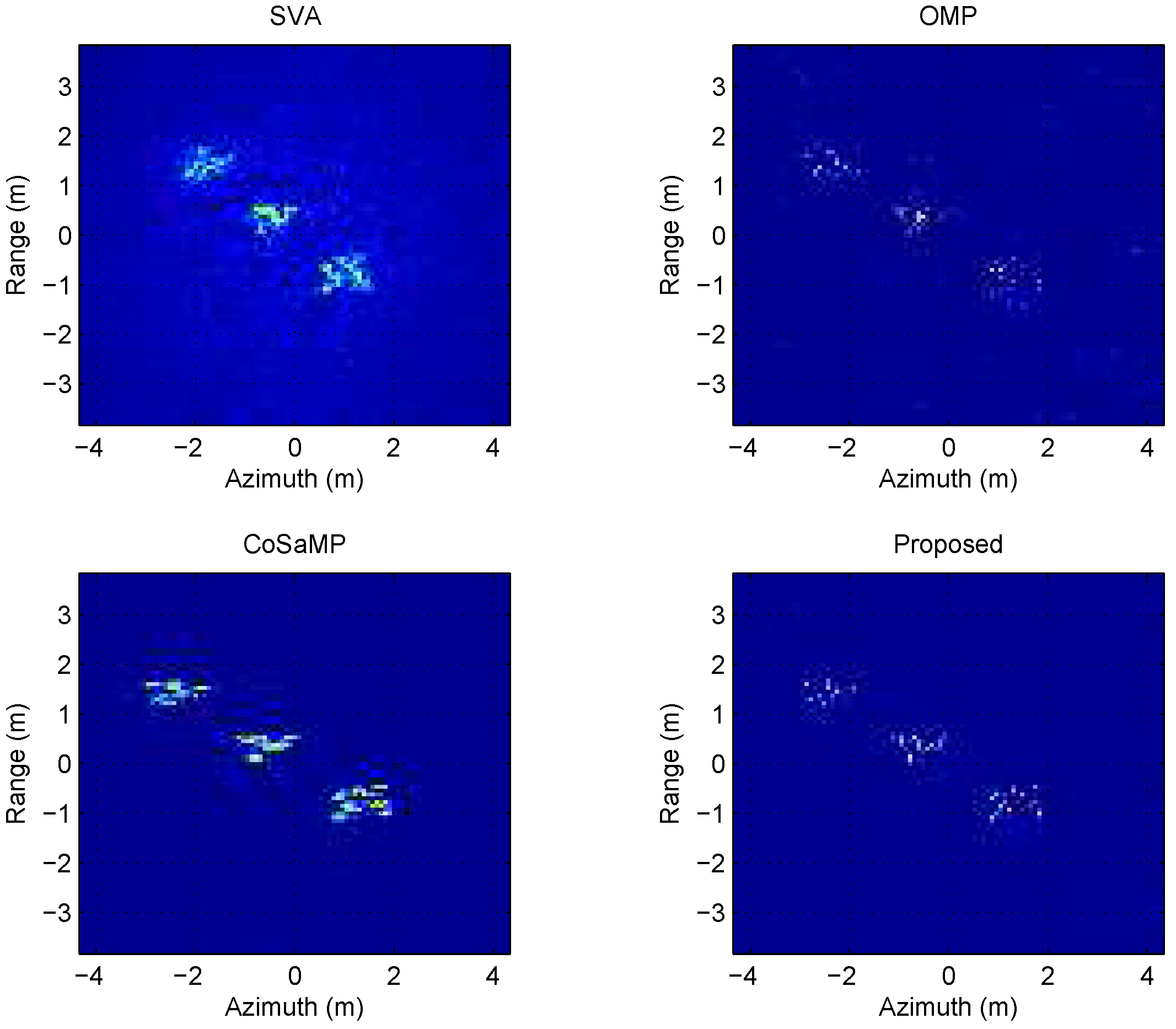
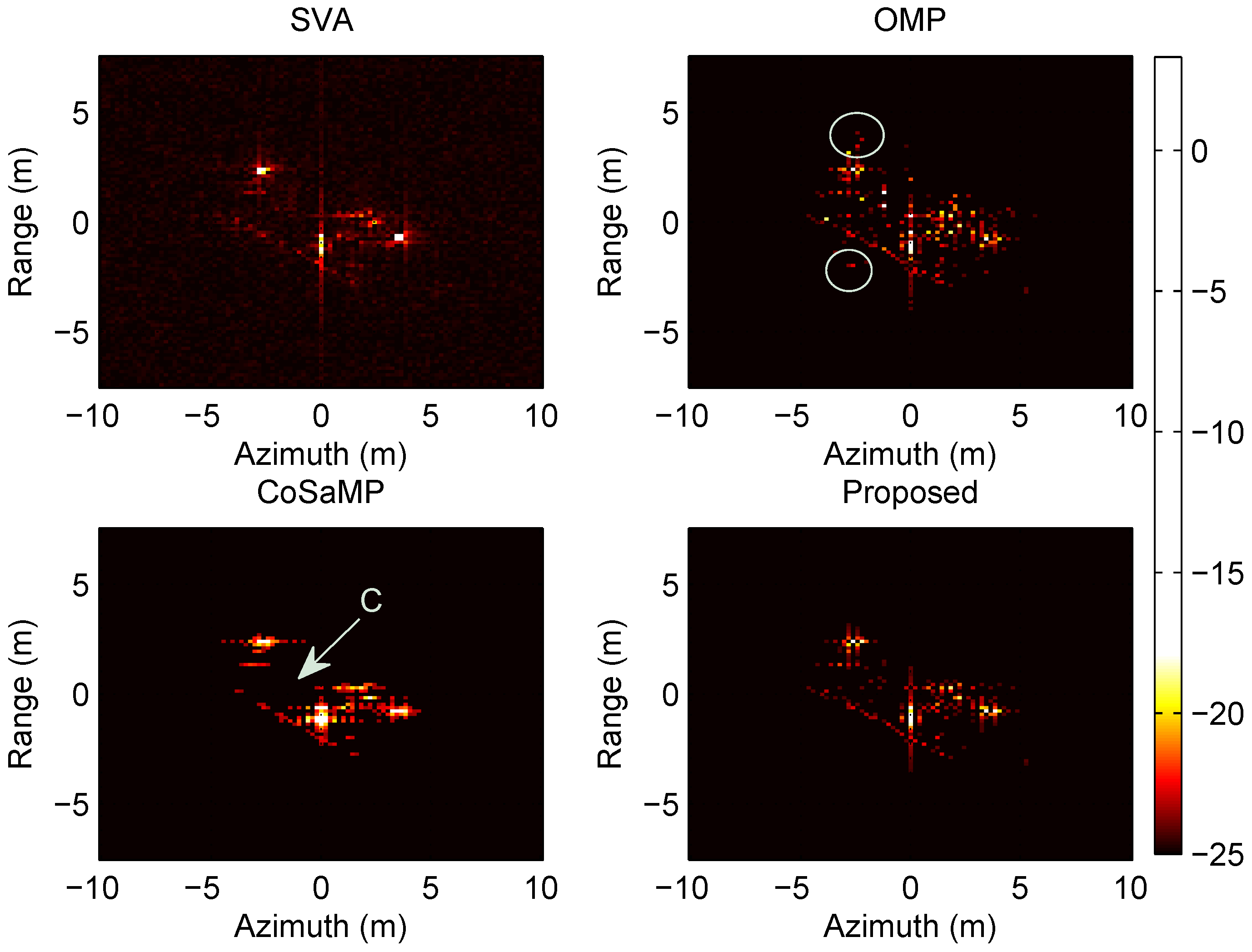
(2) Different number of scatterers
In this simulation scenario, the SNR is fixed at 5 dB. All the scatterers are gathered around three target clumps and such scatter centers are distributed along the diagonal line of the scene.
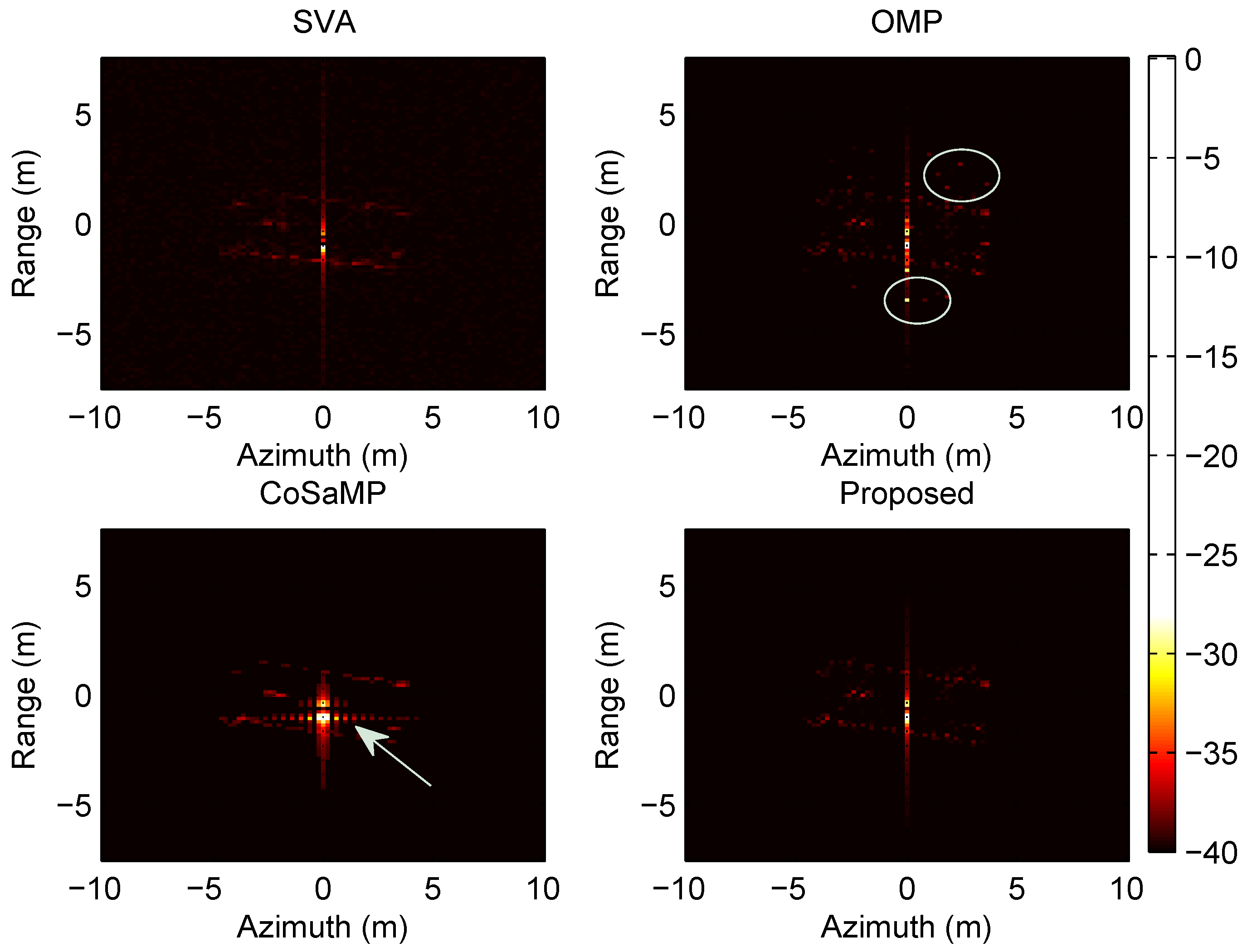
At the situation of scatterer number being 30, the SAR imaging realizations are shown in
Figure 4. When the number of scatterers is set to 150, the SAR imaging realizations are shown in
Figure 5.
From the two groups of simulations above, it is indicated that for the small number of scatterers, all the methods are able to reconstruct target scene well. Compared with SVA, the sparse-reconstruction-based methods obtain more explicit images. It is worth noting that simulation results of the proposed method contain few noisy points. As the scatterer number increases, the scatterers imaging results appear fuzzy. Under the same scenario, the reconstructed scene of the proposed method achieve the most accurate images.
4.1.2. SAR Imaging for Practical Measured Data
This group of experiments deal with real data, measured by a spotlight SAR. The observed target is a crawler-type vehicle. The radar data are obtained from different azimuth and pitch angles. The angle aperture is . The center frequency is 9 GHz and the bandwidth is 1 GHz. The number of observation angle samples and frequency samples are both set to 101, thus the number of total pixels of image is .
The matrix
is constructed as the indication of the Equation (
3), and
rows are extracted from it to form a projection matrix. Here,
is taken. Note that the number of observations
, where
K is the sparsity. Therefore, the sparsity can be expressed as
.
K is designed as 200 in this experiment.
In the following, we investigate the results at different azimuth angles under the condition at a fixed pitch angle firstly, and observe the results at different pitch angles under the condition at a fixed azimuth angle secondly.
(1) Different azimuth angles
The pitch angle is fixed at
. The observation data are acquired from three azimuth central angles,
,
and
, respectively. And the corresponding SAR imaging realizations are shown in
Figure 6,
Figure 7 and
Figure 8, respectively.
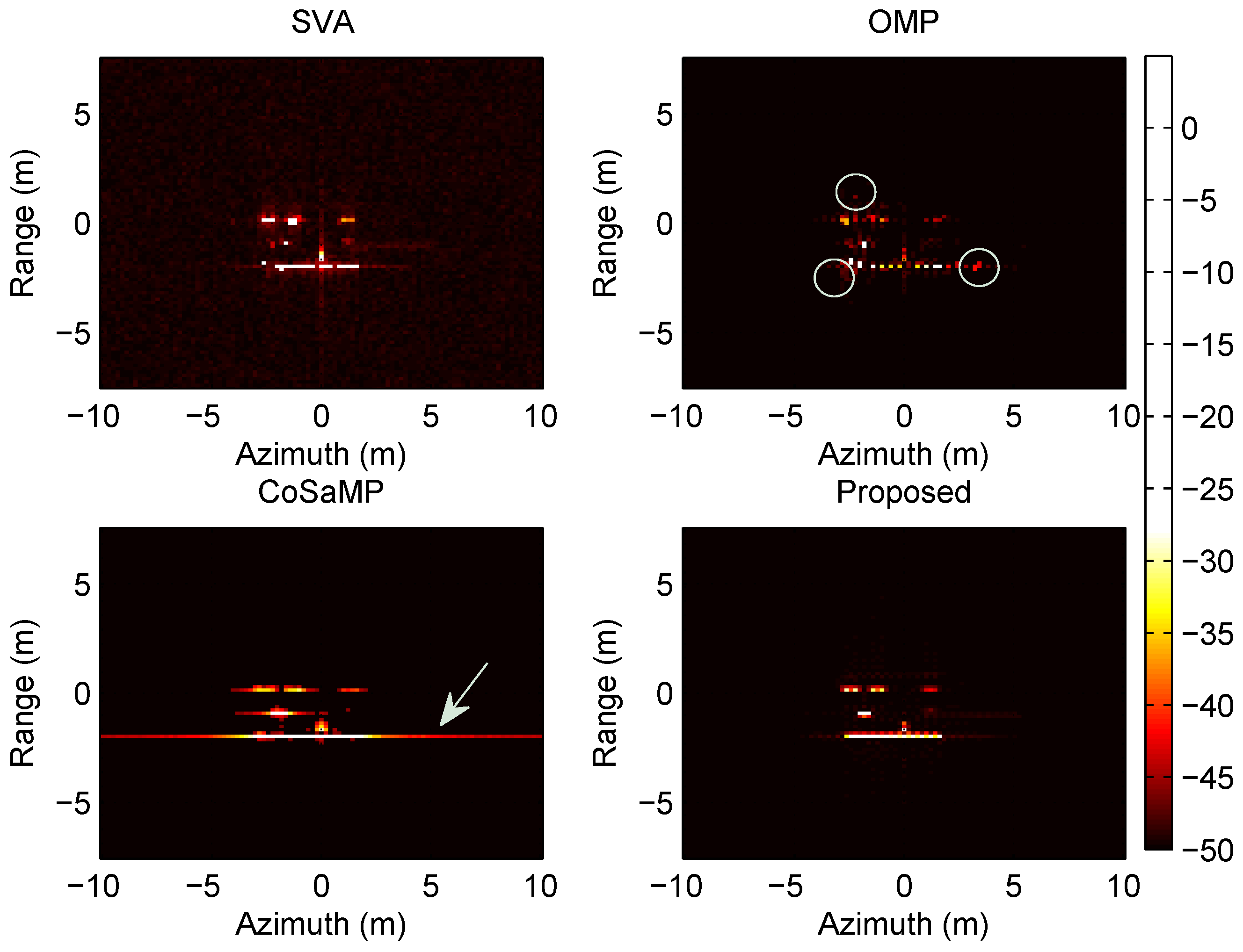
The above experiments demonstrate the effectiveness of the proposed method in practical implementation. With the comparison between the selected algorithms, the proposed method obtains the better imaging results. When the azimuth central angle is
, the imaging result of SVA is dim and blurred, but the vehicle contour is clearly visible with the proposed method. For the experiments of different azimuth angles, although the classic matching pursuit approaches, i.e., OMP and CoSaMP, perform much better than SVA, the problem of imaging target ambiguity still exists. For instance, the CoSaMP imaging result has a remarkable bright streak at
of the azimuth central angle, as shown in
Figure 7. Besides, as indicated by the arrows in
Figure 6 and
Figure 8, CoSaMP shows raster lines over the target image at the central region, which will disturb the recognition of targets significantly. Under the same scenario, there exist incorrect scattering points on the sides of the target in the OMP imaging results, which are circled in white for each images. By contrast, the proposed method does not have such problems in all the experimental tests.
(2) Different pitch angles
The azimuth angle is fixed at
. The observation data is obtained from three pitch angles,
,
and
, respectively. And the corresponding SAR imaging realizations are shown in
Figure 9,
Figure 10 and
Figure 11, respectively.
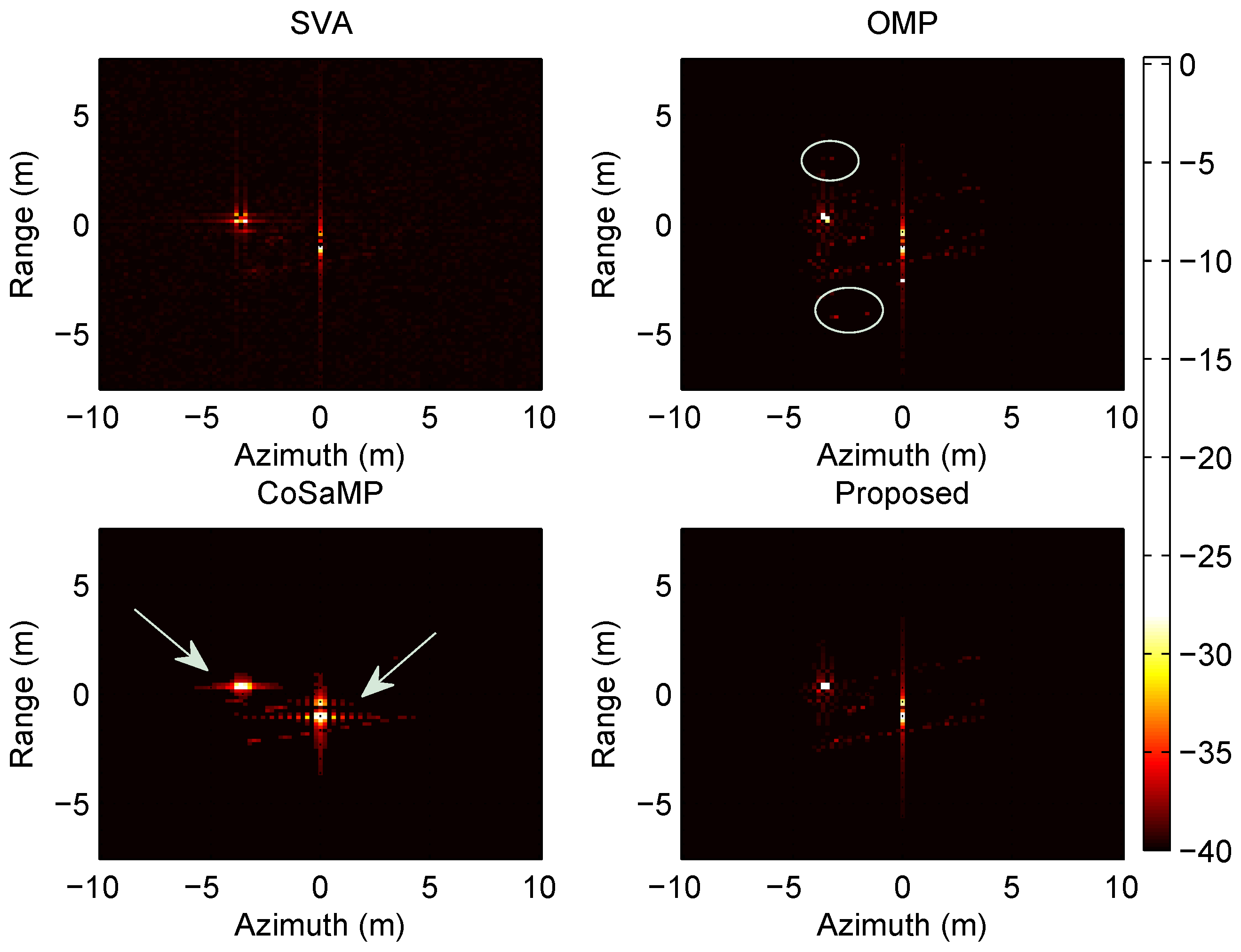
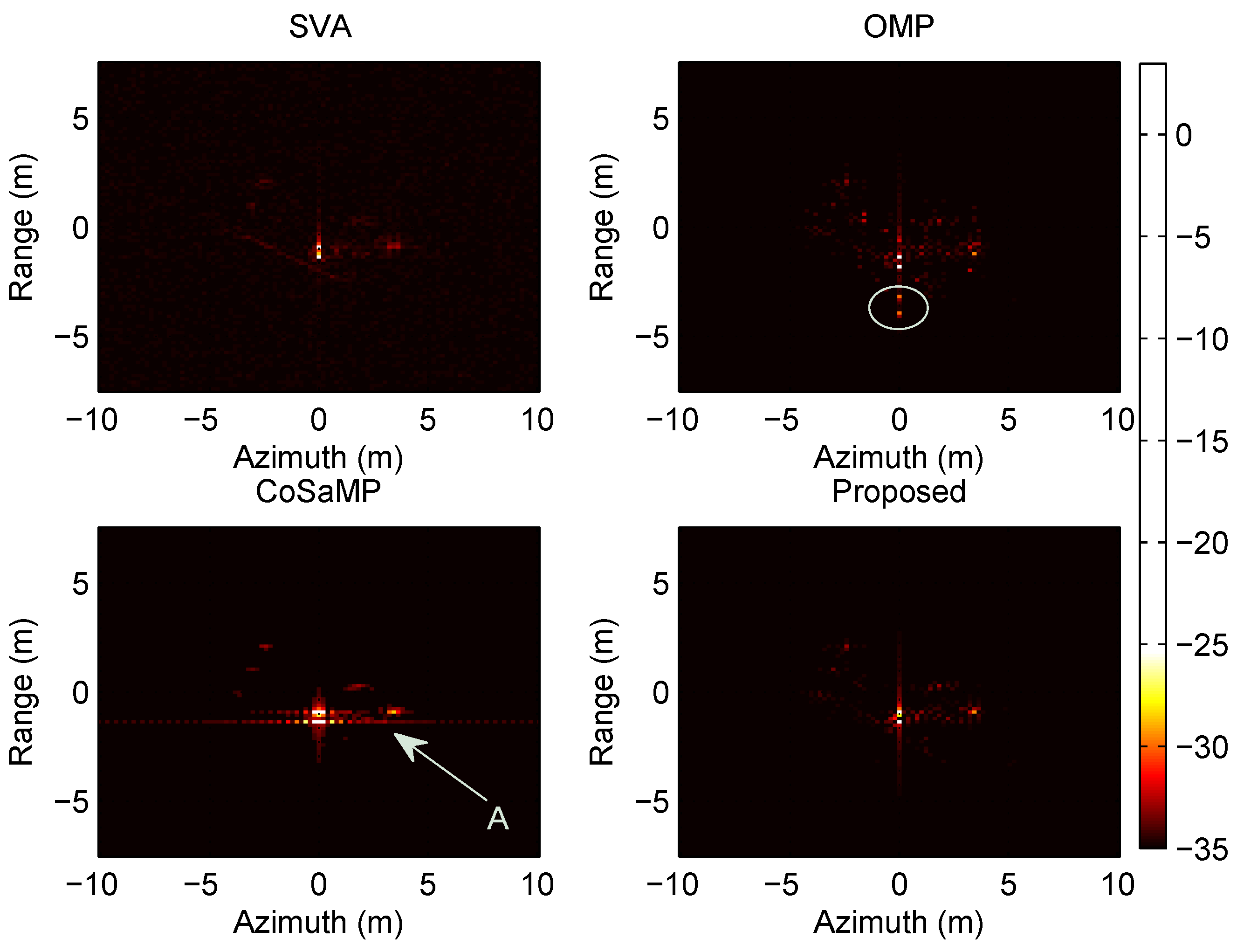
With the comparison between the experiments of different pitch angles, the superiority of the proposed method is demonstrated. As shown in
Figure 11, the imaging result of SVA contains many noisy points appearing blurred; OMP outputs several outliers which are marked by white circles; for CoSaMP, a part of the scatter points in the central are lost, which is indicated by arrow C; but the proposed method obtains the clear and accurate imaging result. As shown in
Figure 9 and
Figure 10, the imaging results of CoSaMP contain raster lines over the targets which are indicated by arrow A and B, respectively; the other three methods achieve the similar performance as demonstrated above. Although the two classic matching pursuit methods can obtain clearer images than SVA, but both of them result in errors of the estimation beyond tolerance. By contrast, the proposed method can achieve the better imaging results. This is true especially as the pitch angle increases.
4.2. Performance Comparison
This section focuses on two performance indicators of the proposed method and the reference methods, one is the root mean square error (RMSE) curve, the other is the computational resource requirements.
4.2.1. RMSE
The RMSE of SAR imaging model is defined as follows:
where
is the estimate of scatter coefficients in the
lth Monte-Carlo independent trial.
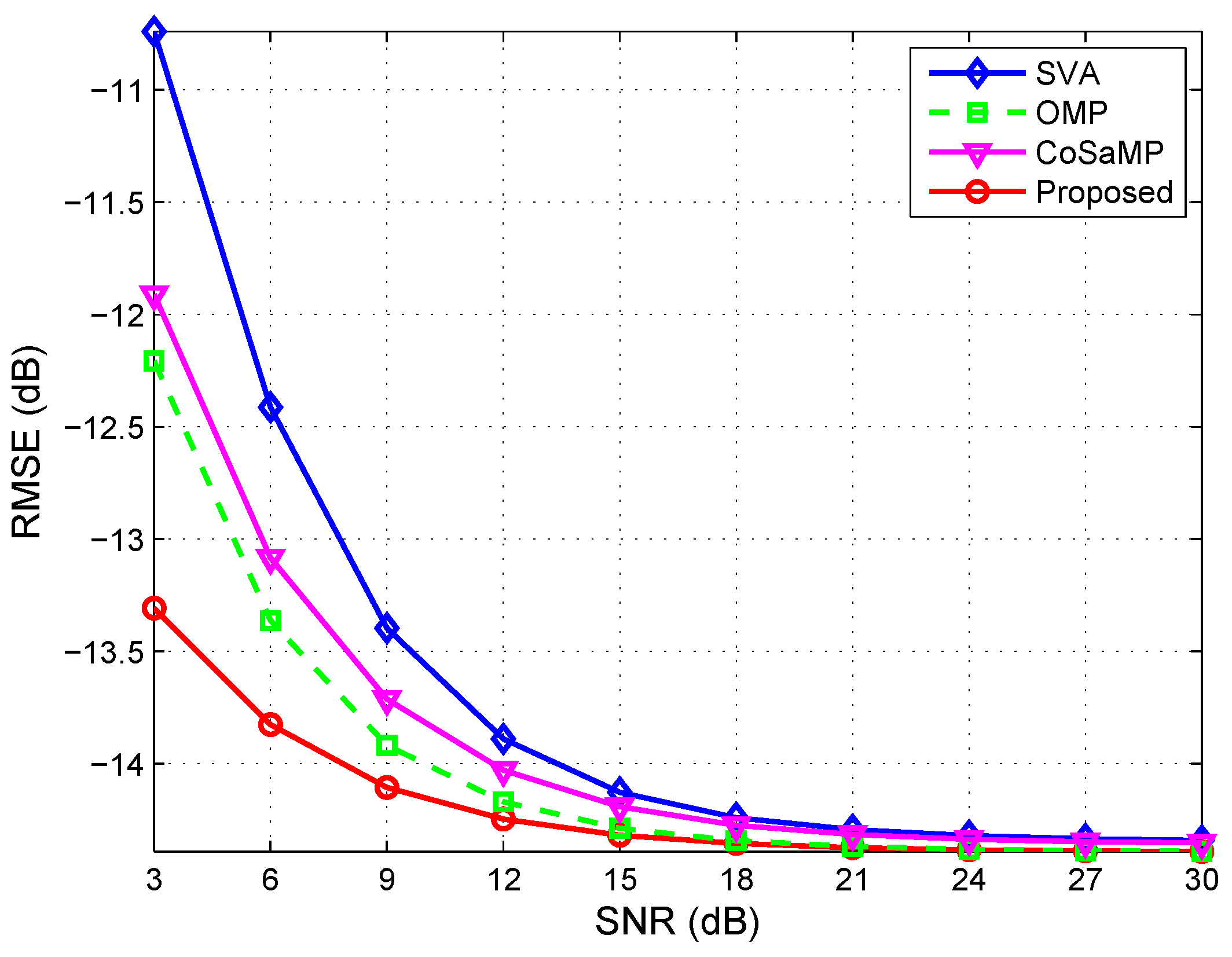
(1) Different SNRs
The configuration of this experiment is the same as
Section 4.1.1. The SNR range is 3∼30 dB, and
L, the number of independent trials, is set to 500. The RMSE curves are shown in
Figure 12.
It is demonstrated from the RMSE curves that the performance of the proposed method is better than the others under the condition with low SNR. As the SNR increasing, the RMSE curves of the reference methods are approximately approaching to the one of the proposed method. Because of the sensitivity to noise, the reconstruction error of SVA algorithm is considerable in low SNR. In this respect, the sparse-reconstruction-based methods are robust to noise. The simulation results show that the performance of CoSaMP is slightly worse than that of OMP. The reason is that CoSaMP only chooses atoms at each iteration, which can help to improve the efficiency of the algorithm, but may reduce the success rate of reconstruction. In comparison, the proposed method performs much better, even if the noise interference is serious. This is because the Kronecker information of the echo signal is fully utilized.
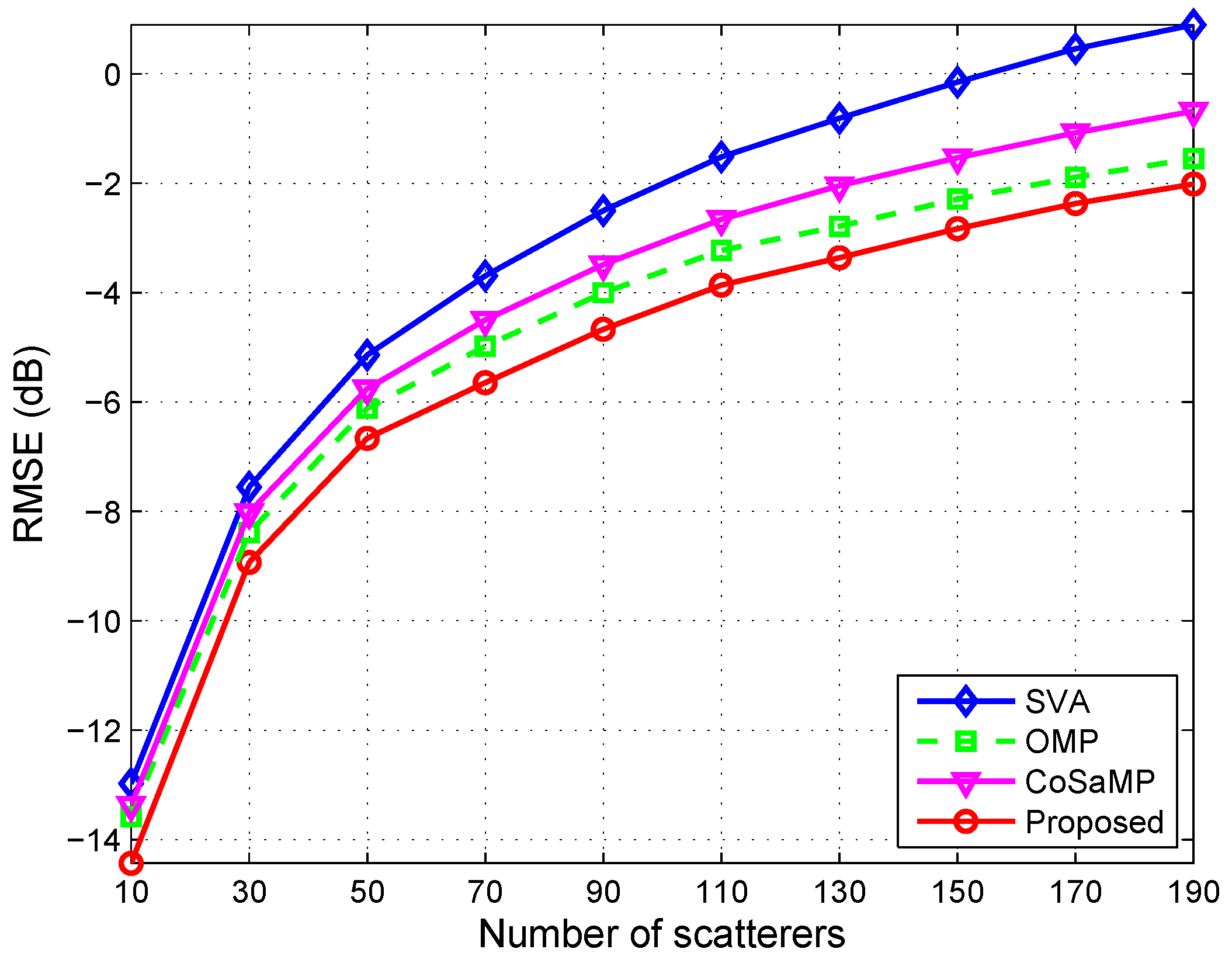
(2) Different number of scatterers
The number of scattering points in the target area will directly affect the imaging quality. In the following experiment, the performance of the proposed method versus different number of scatterers will be investigated. The configuration of this simulation is the same as
Section 4.1.1. The SNR is set to 5 dB, and the RMSE curves are shown in
Figure 13.
The simulation result indicates that the performance of proposed method is superior to the reference methods with all the test scenarios. When the numbers of scatterers is less than 30, the performance of all reference methods seems to be close. With the number of scatterers increasing, the performance of SVA, limited by the resolution of itself, becomes worse. The sparse-reconstruction-based methods with super-resolution maintain better robustness even as the scatterers become dense. Exploiting the structured feature of target, the proposed method provides the advantage for imaging, and achieves effective sidelobe control. Of all the curves of RMSE versus scatterer quantity, the one of the proposed method grows most slowly and always has the lowest RMSE value, according to the curves shown in
Figure 13. Even the number of scatterers is larger than 90, the RMSE of the proposed method is still lower 3 dB than that of the SVA method.
4.2.2. Computational Resource Requirement
This group of experiments investigate the requirements for computing resources of different methods. The evaluation indicator is CPU time. The configuration of this experiment is the same as in
Section 4.2.1. The statistical results for the case of different SNRs are shown in
Table 2.
The last experiment considers the case of different number of scatter points. Setting the configuration be the same as in
Section 4.2.1, the statistical results are shown in
Table 3.
From the statistical results in
Table 2 and
Table 3, it is shown that the fastest algorithm is SVA, the second fastest one is the proposed method, followed by CoSaMP and OMP in sequence. Although SVA is the fastest algorithm, its performance is the worst among all these methods, especially in the low SNR case, which is shown in
Figure 12. Compared with this, OMP and CoSaMP perform better, but both the two algorithms require a large amount of system resources. Since OMP algorithm needs to match every atom at each iteration step, it runs extremely time-consuming, which means it unsuitable for the real-time applications. So far as that is concerned, the proposed method of this paper could not only run faster one order of magnitude than CoSaMP, but also ensure the better performance than the latter, which determines its prominent advantages in practical applications.
5. Conclusions
In this paper, a tensor decomposition algorithm for the spotlight SAR imaging is developed based on Tucker model which formulizes SAR echo signal with Kronecker constraint. Under the common scenario in SAR imaging, the scatterers usually cluster together and the targets are sparsely located. This structured sparse feature provides a prerequisite for the proposed method. Not only has this method better robustness for signal reconstruction, but also produces less algorithm complexity and requires smaller computation resource as well, due to exploiting the Kronecker information in each mode sufficiently.
In comparison with the existing SAR imaging methods, such as the SVA and classic matching pursuit algorithms, the proposed method performs much better with respect to robustness about noise and sidelobe disturbance. Numerical analysis has demonstrated that the recovery upper bound of the multiway sparse reconstruction based on structured sparsity is larger than that of the classic matching pursuit methods. Both the theoretical analysis and simulation results also indicate that the proposed algorithm requires much less computational resources than the reference methods, which is by far the most important in practical applications.