Imperfection Sensitivity of Nonlinear Vibration of Curved Single-Walled Carbon Nanotubes Based on Nonlocal Timoshenko Beam Theory
Abstract
:1. Introduction
2. Problem Formulation
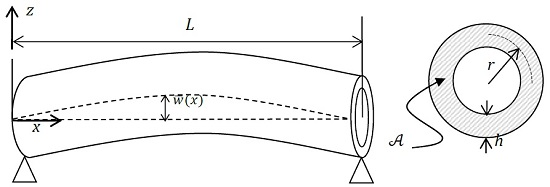
2.1. Timoshenko Beam Model for Vibration of Curved Single-Walled Carbon Nanotubes (SWCNTs)
2.2. Nonlocal Theory of Nano-Beams
2.3. Derivation of Nonlocal Governing Equations of Motion
2.4. Differential Quadrature Solution Procedure
3. Numerical Results and Discussions
3.1. Results Verification
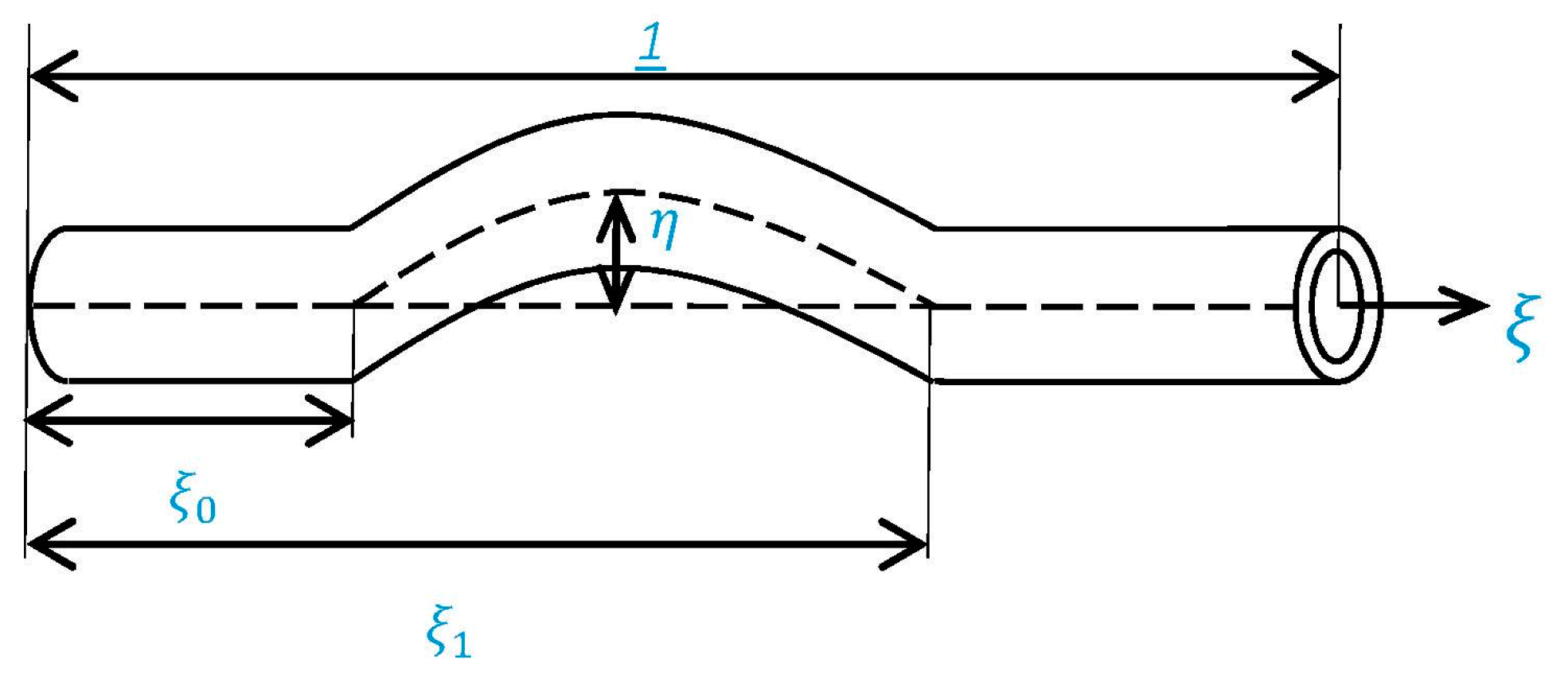
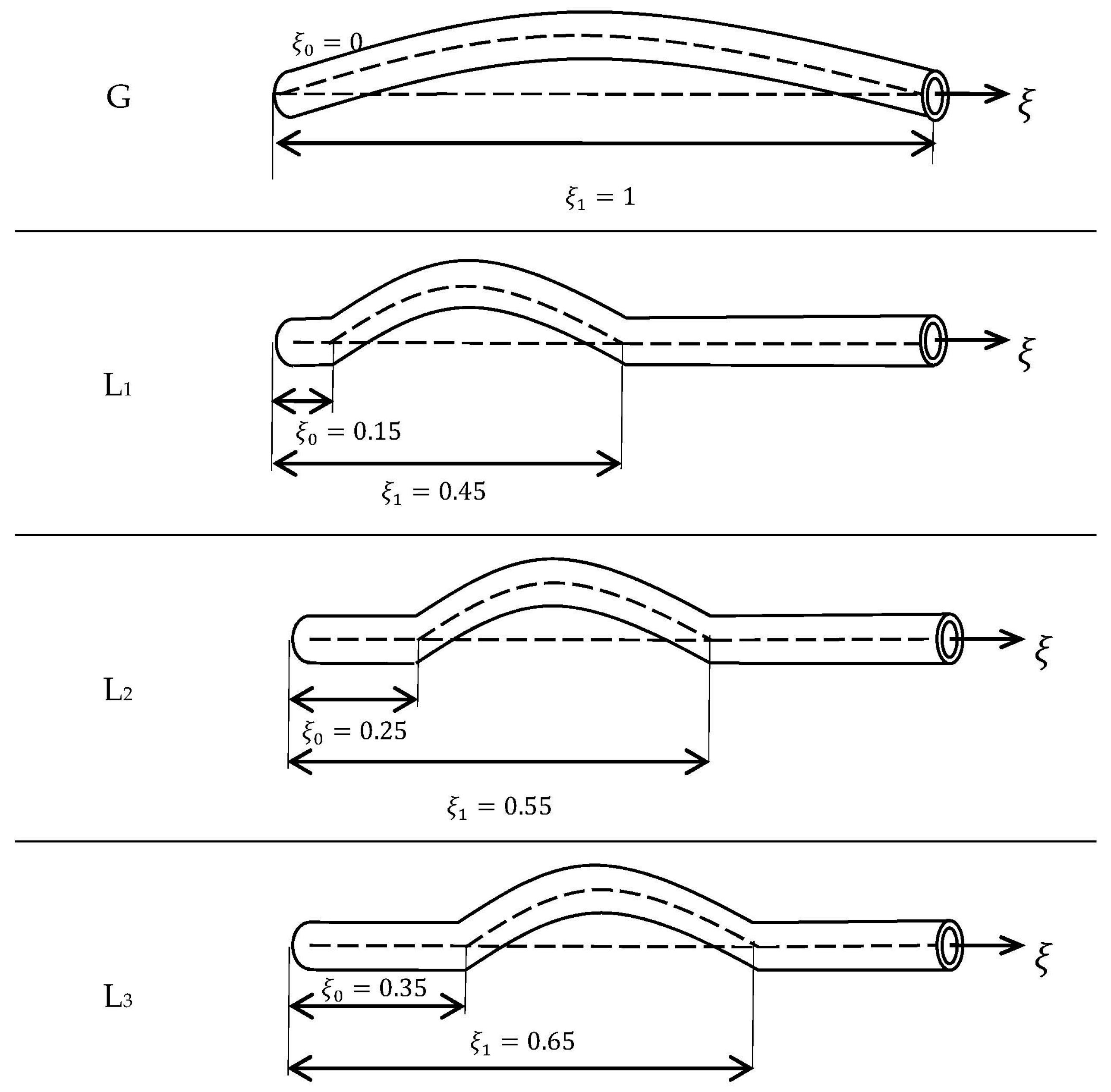
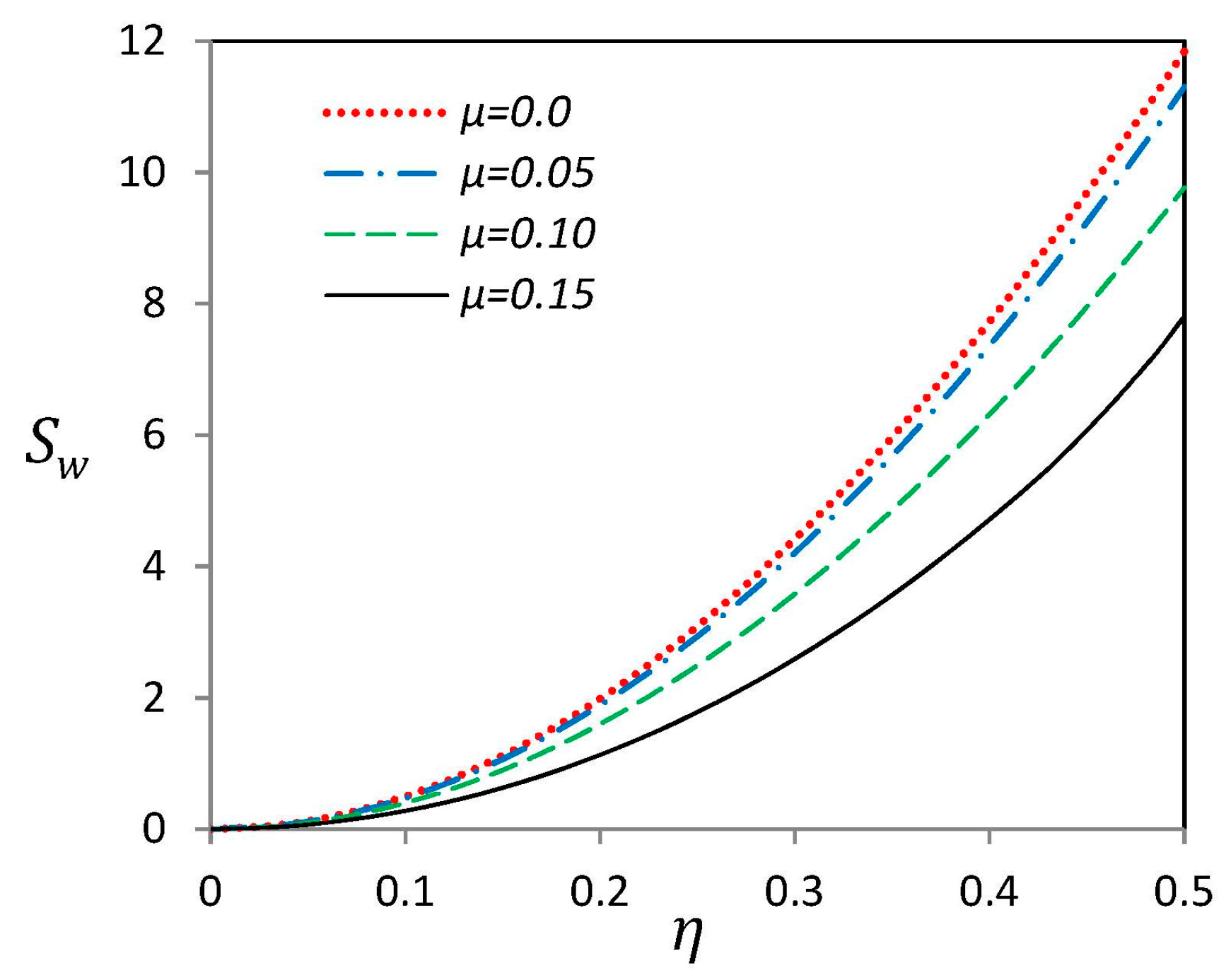
3.2. Geometric Imperfection Function
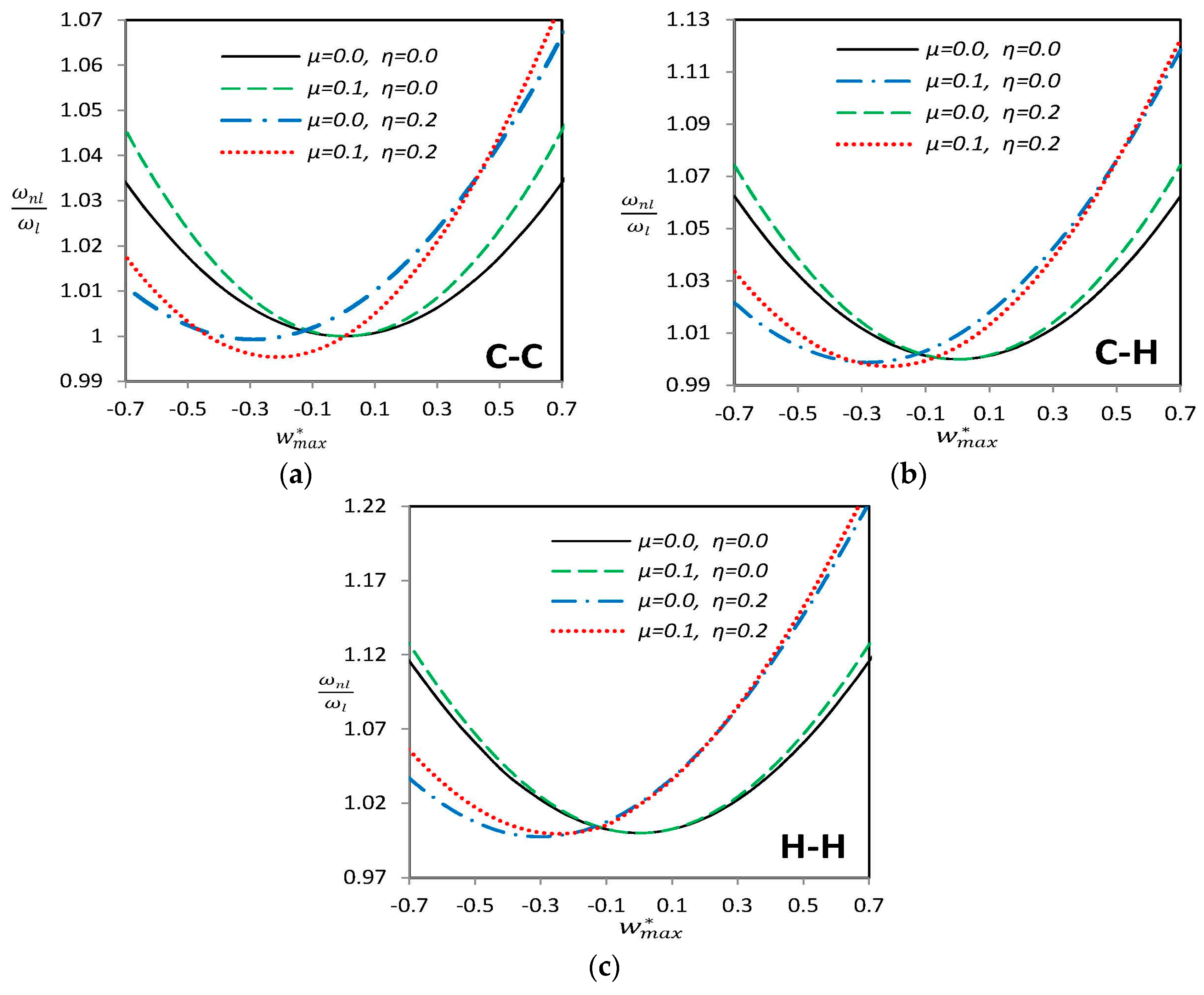
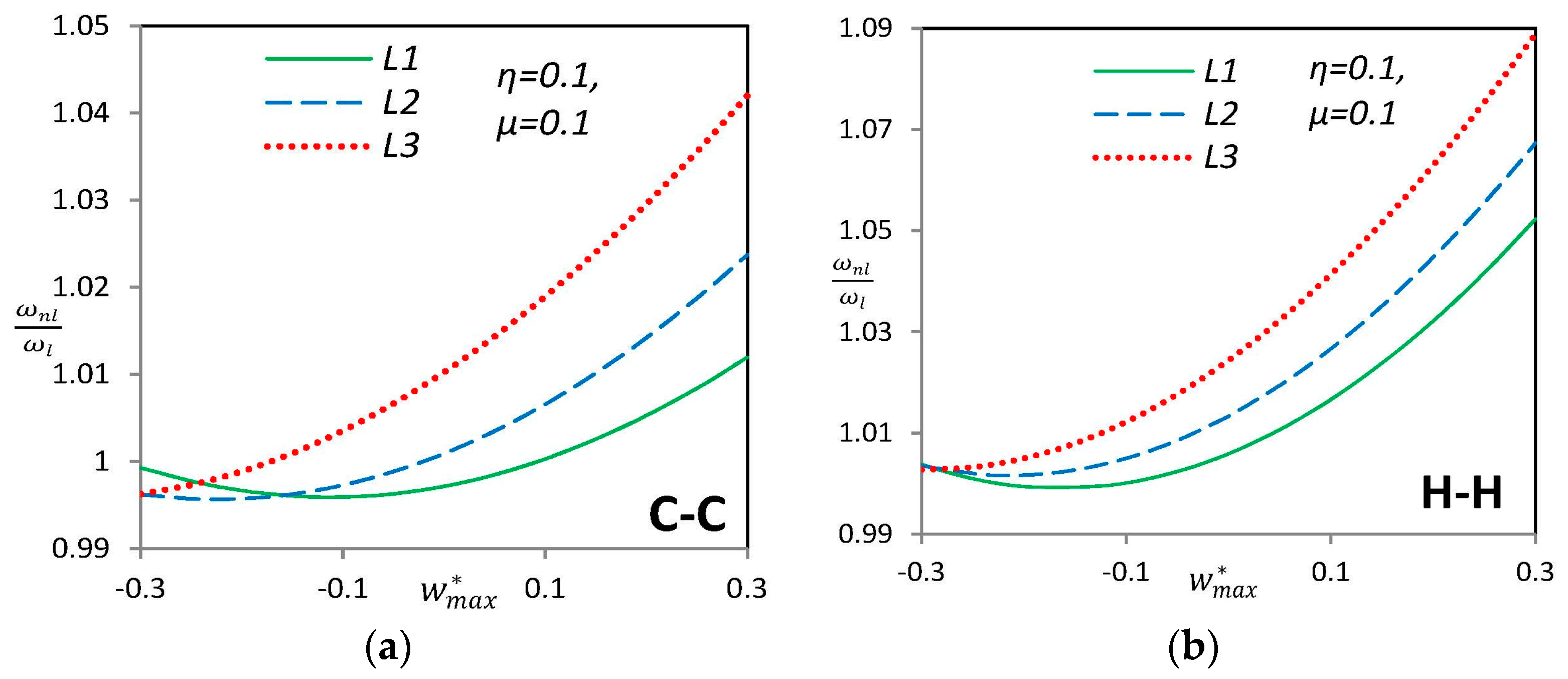
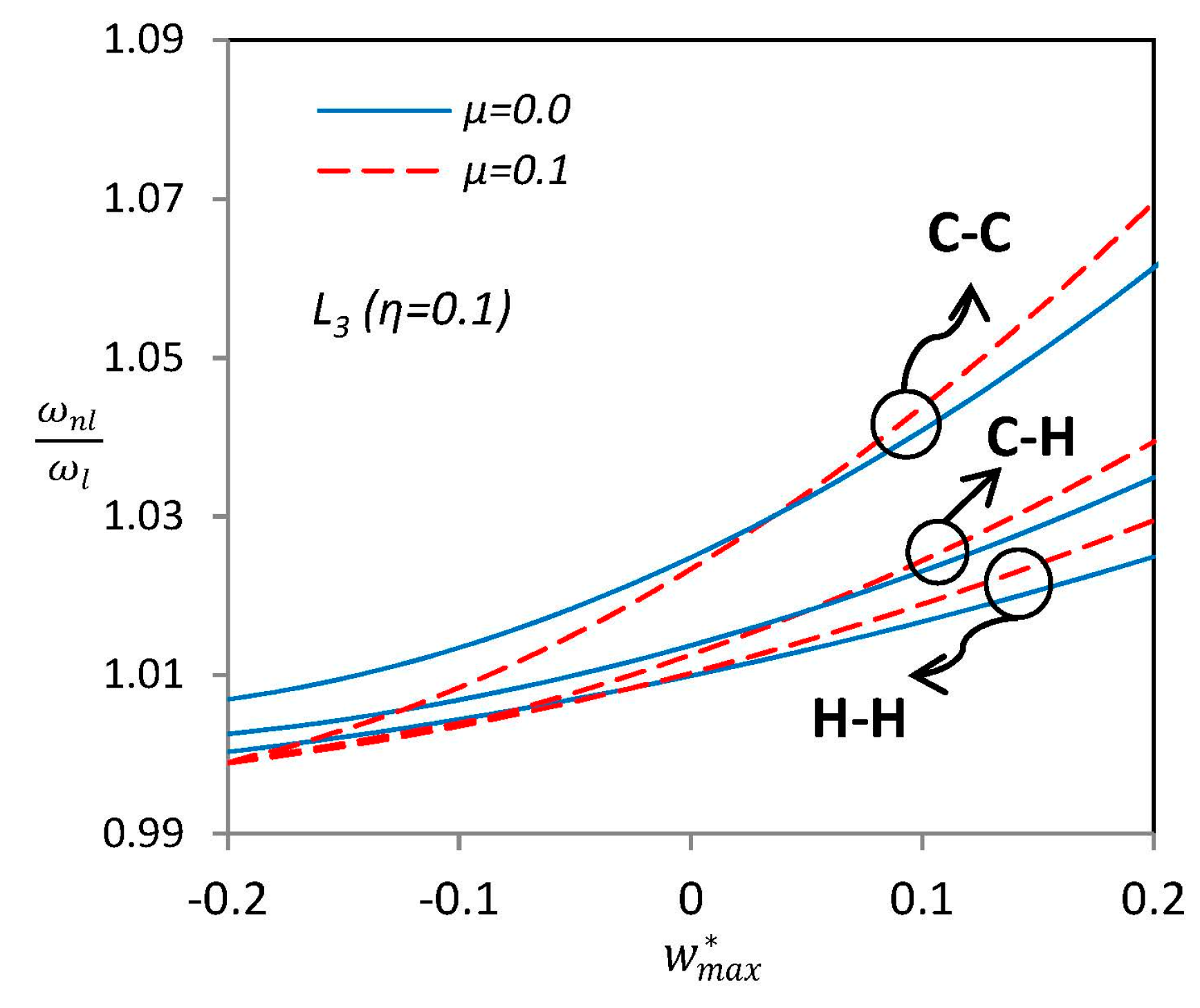
3.3. Nonlinear Vibration of Curved SWCNTs
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CNTs | Carbon Nano Tubes |
| DQ | Differential Quadrature |
| MD | Molecular Dynamics |
| NEMS | Nano Electro Mechanical System |
| SWCNTs | Single-Walled Carbon Nano Tubes |
References
- Bosia, F.; Lepore, E.; Alvarez, N.T.; Miller, P.; Shanov, V.; Pugno, N. Knotted synthetic polymer or carbon nanotube microfibres with enhanced toughness, up to 1400 J/g. Carbon 2016, 102, 116–125. [Google Scholar] [CrossRef]
- Ke, C.H.; Pugno, N.; Peng, B.; Espinosa, H.D. Experiments and modeling of carbon nanotube-based NEMS devices. J. Mech. Phys. Solids 2005, 53, 1314–1333. [Google Scholar] [CrossRef]
- Ke, C.H.; Espinosa, H.D.; Pugno, N. Numerical analysis of nanotubes based NEMS devices—Part II: Role of finite kinematics, stretching and charge concentrations. J. Appl. Mech. 2005, 72, 519–526. [Google Scholar] [CrossRef]
- Hierold, C.H.; Jungen, A.; Stampfer, C.H.; Helbling, T.H. Nano electromechanical sensors based on carbon nanotubes. Sens. Actuators A Phys. 2007, 136, 51–61. [Google Scholar] [CrossRef]
- Liew, K.M.; Wang, Q. Analysis of wave propagation in carbon nanotubes via elastic shell theories. Int. J. Eng. Sci. 2007, 45, 227–241. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Milani, M.; Pellicano, F. Nonlinear vibrations and energy exchange of single-walled carbon nanotubes. Circumferential flexural modes. J. Sound Vib. 2016, 381, 156–178. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ru, C.Q.; Mioduchowski, A. Applicability and limitations of simplified elastic shell equations for carbon nanotubes. J. Appl. Mech. 2004, 71, 622–631. [Google Scholar] [CrossRef]
- Smirnov, V.V.; Manevitch, L.I.; Strozzi, M.; Pellicano, F. Nonlinear optical vibrations of single-walled carbon nanotubes, Energy exchange and localization of low-frequency oscillations. Physica D 2016, 325, 113–125. [Google Scholar] [CrossRef]
- Silvestre, N.; Wang, C.M.; Zhang, Y.Y.; Xiang, Y. Sanders shell model for buckling of single-walled carbon nanotubes with small aspect ratio. Compos. Struct. 2011, 93, 1683–1691. [Google Scholar] [CrossRef]
- Amabili, M. A comparison of shell theories for large-amplitude vibration of circular cylindrical shells: Lagrangian approach. J. Sound Vib. 2003, 264, 1091–1125. [Google Scholar] [CrossRef]
- Gibson, R.F.; Ayorinde, O.E.; Wen, Y.F. Vibration of carbon nanotubes and there composites: A review. Compos. Sci. Technol. 2007, 67, 1–28. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F. An Eringen-like model for Timoshenko nanobeams. Compos. Struct. 2016, 139, 104–110. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Functionally graded Timoshenko nanobeams: A novel nonlocal gradient formulation. Compos. B 2016, 100, 208–219. [Google Scholar] [CrossRef]
- Čanadija, M.; Barretta, R.; Marotti de Sciarra, F. On functionally graded Timoshenko nonisothermal nanobeams. Compos. Struct. 2016, 135, 286–296. [Google Scholar] [CrossRef]
- Wang, Q.; Varadan, V.K. Wave characteristics of carbon nanotubes. Int. J. Solids Struct. 2006, 43, 254–265. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C.; Zhang, P.Q. Application of nonlocal beam models for carbon nanotubes. Int. J. Solids Struct. 2007, 44, 5289–5300. [Google Scholar] [CrossRef]
- Murmu, T.; Pradhan, S.C. Thermo-mechanical vibration of a single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Comput. Mater. Sci. 2009, 46, 854–859. [Google Scholar] [CrossRef]
- Ansari, R.; Sahmani, S. Small scale effect on vibrational response of single-walled carbon nanotubes with different boundary conditions based on nonlocal beam models. Commun. Nonlinear Sci. 2012, 17, 1965–1979. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. Int. J. Eng. Sci. 2010, 48, 1507–1518. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling, and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Yang, J.; Ke, L.L.; Kitipornchai, S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E 2010, 42, 1727–1735. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.; Zhang, C.; Tang, Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Appl. Math. Model. 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Yang, J.; Liew, K.M. Semi-analytical solution for nonlinear vibration of laminated FGM plates with geometric imperfections. Int. J. Solids Struct. 2004, 41, 2235–2257. [Google Scholar] [CrossRef]
- Yamaki, N.; Otomo, K.; Chiba, M. Nonlinear vibrations of a clamped rectangular plate with initial deflection and initial edge displacement-Part 2: Experiment. Thin. Walled Struct. 1983, 1, 101–109. [Google Scholar] [CrossRef]
- Calabri, L.; Pugno, N.; Ding, W.; Ruoff, R. Resonance of curved nanowires. J. Phys. Condens. Matter 2006, 18, S2175–S2183. [Google Scholar] [CrossRef]
- Farshidianfar, A.; Soltani, P. Nonlinear flow-induced vibration of a SWCNT with a geometrical imperfection. Comput. Mater. Sci. 2012, 53, 105–116. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. Natural frequencies and mode shapes of initially curved carbon nanotube resonators under electric excitation. J. Sound Vib. 2011, 330, 3182–3195. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear vibrations of rectangular plates with different boundary conditions: Theory and experiments. Comput. Struct. 2004, 82, 2587–2605. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Jalali, S.K.; Rastgoo, A.; Eshraghi, I. Large amplitude vibration of imperfect shear deformable nano-plates using non-local theory. J. Solid Mech. 2011, 3, 64–73. [Google Scholar]
- Pradhan, S.C.; Murmu, T. Small Scale Effect on the Buckling of Single-Layered Graphene Sheets under Bi-axial Compression via Nonlocal Continuum Mechanics. Comput. Mater. Sci. 2009, 47, 268–274. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: London, UK, 2000. [Google Scholar]
- Malekzadeh, P.; Vosoughi, A.R. DQM large amplitude vibration of composite beams on nonlinear elastic foundations with restrained edges. Commun. Nonlinear Sci. 2009, 14, 906–915. [Google Scholar] [CrossRef]
- Bhasyam, G.R.; Prathap, G. Galerkin finite element method for non-linear beam vibrations. J. Sound Vib. 1980, 72, 191–203. [Google Scholar] [CrossRef]
- Marur, S.R.; Prathap, G. Non-linear beam vibration problems and simplifications in finite element models. Comput. Mech. 2005, 35, 352–360. [Google Scholar] [CrossRef]
- Wang, C.M.; Zhang, Y.Y.; He, X.Q. Vibration of nonlocal Timoshenko beams. Nanotechnology 2007, 18, 105401. [Google Scholar] [CrossRef]
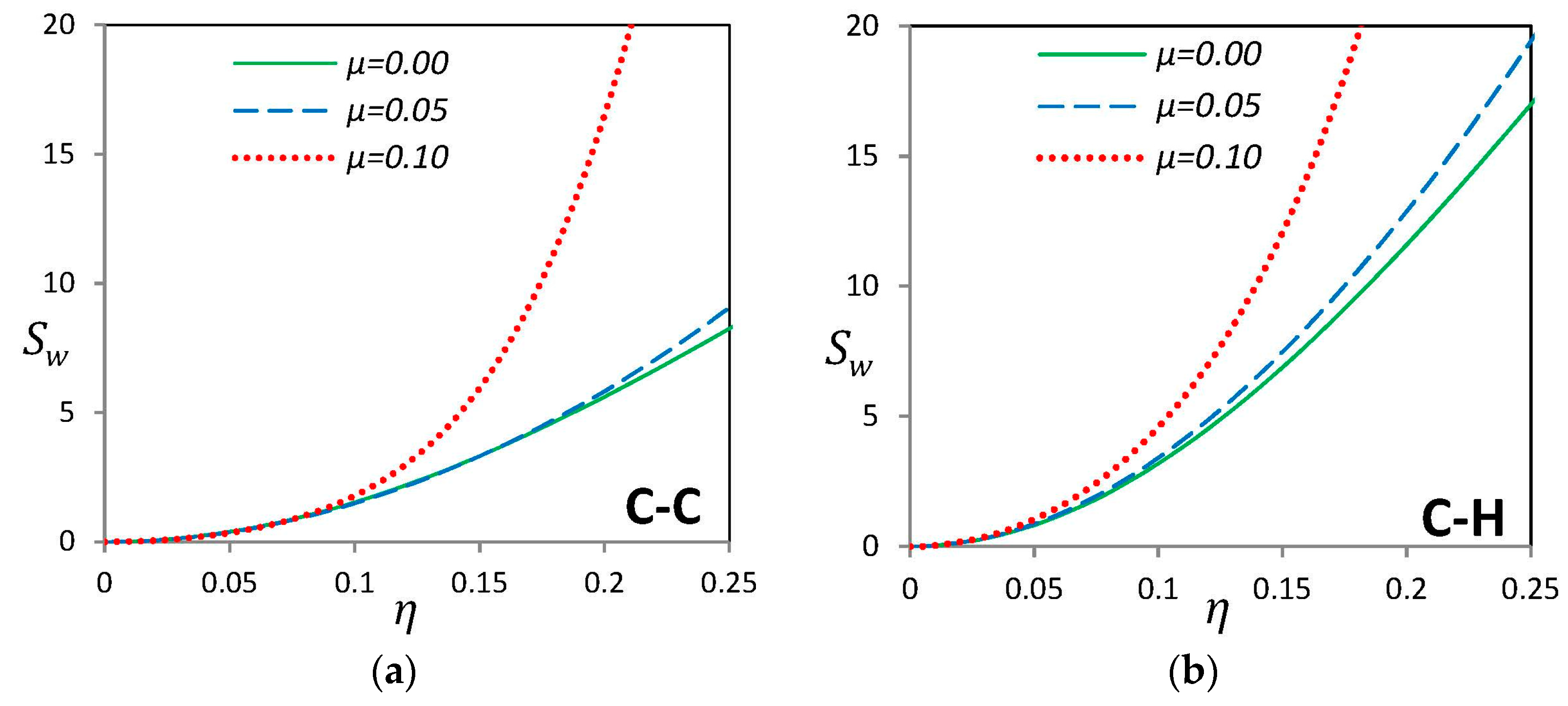
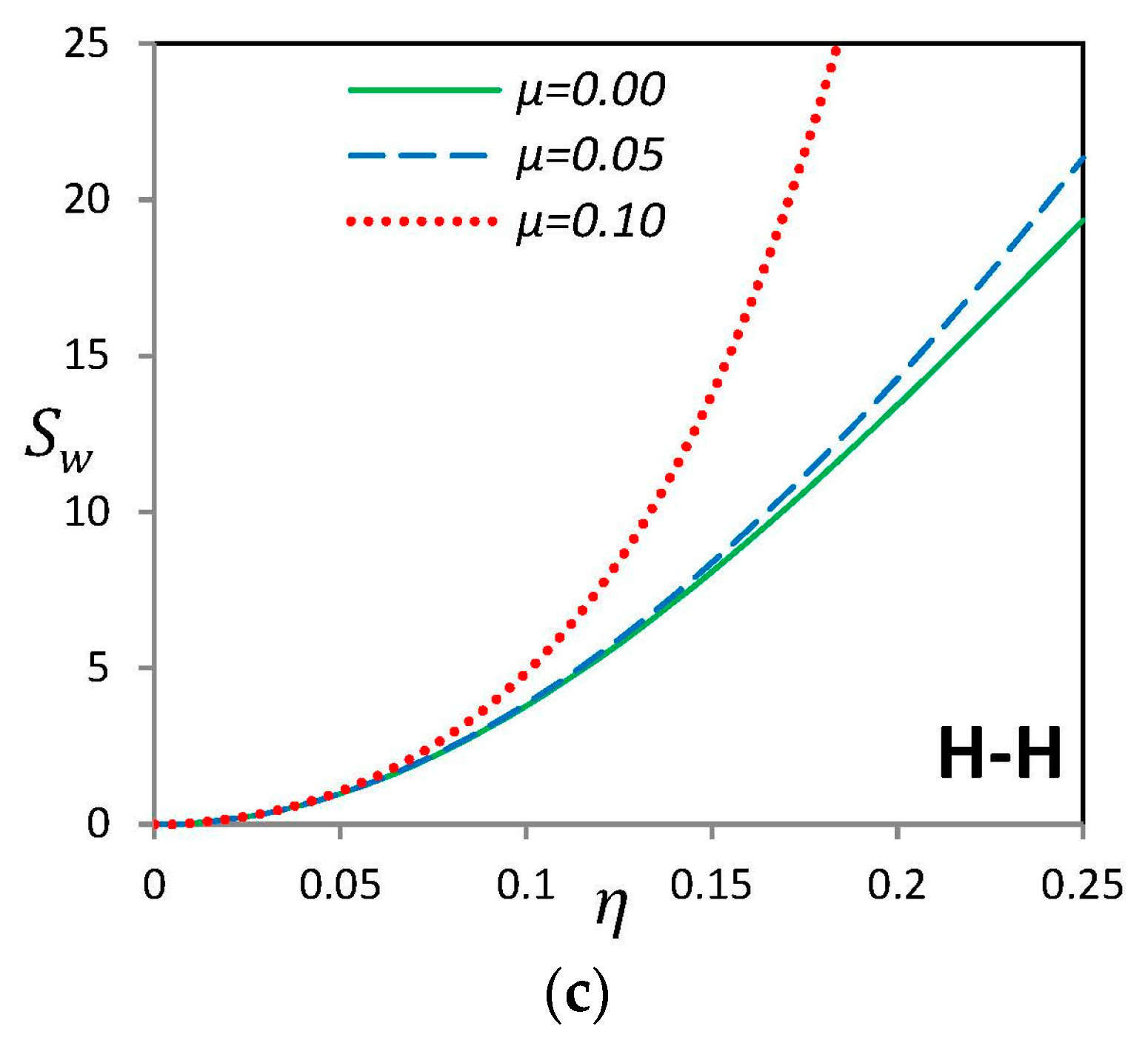
| H–H | C–C | C–H | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | Ref. [35] | Ref. [36] | Present | |
| 1.0 | 1.118 | 1.118 | 1.1181 | 1.0295 | 1.0283 | 1.0295 | 1.0641 | 1.0582 | 1.0593 |
| 2.0 | 1.4141 | 1.4135 | 1.4143 | 1.1127 | 1.1105 | 1.1128 | 1.2318 | 1.215 | 1.2182 |
| 3.0 | 1.8026 | 1.8027 | 1.8029 | 1.2377 | 1.2336 | 1.2378 | 1.4603 | 1.4368 | 1.4416 |
| 4.0 | 2.2359 | 2.2361 | 2.2363 | 1.3920 | 1.3856 | 1.3921 | 1.7210 | 1.6822 | 1.7026 |
| 5.0 | 2.6923 | 2.6925 | 2.6928 | 1.5659 | 1.5574 | 1.5660 | 1.9995 | 1.9180 | 1.9862 |
| μ | H–H | C–C | C–H | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ref. [37] | Ref. [22] | Present | Ref. [37] | Ref. [22] | Present | Ref. [37] | Ref. [22] | Present | |
| 0.0 | 3.0929 | – | 3.0929 | 4.4491 | – | 4.4491 | 3.7845 | – | 3.7844 |
| 0.1 | 3.0243 | 3.0210 | 3.0210 | 4.3471 | 4.3269 | 4.3269 | 3.6939 | 3.6849 | 3.6849 |
| 0.3 | 2.6538 | 2.6385 | 2.6385 | 3.7895 | 3.7032 | 3.7032 | 3.2115 | 3.1724 | 3.1724 |
| 0.5 | 2.2867 | 2.2665 | 2.2665 | 3.2420 | 3.1372 | 3.1371 | 2.7471 | 2.6982 | 2.6980 |
| 0.7 | 2.0106 | – | 1.9899 | 2.8383 | – | 2.7327 | 2.4059 | – | 2.3569 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eshraghi, I.; Jalali, S.K.; Pugno, N.M. Imperfection Sensitivity of Nonlinear Vibration of Curved Single-Walled Carbon Nanotubes Based on Nonlocal Timoshenko Beam Theory. Materials 2016, 9, 786. https://doi.org/10.3390/ma9090786
Eshraghi I, Jalali SK, Pugno NM. Imperfection Sensitivity of Nonlinear Vibration of Curved Single-Walled Carbon Nanotubes Based on Nonlocal Timoshenko Beam Theory. Materials. 2016; 9(9):786. https://doi.org/10.3390/ma9090786
Chicago/Turabian StyleEshraghi, Iman, Seyed K. Jalali, and Nicola Maria Pugno. 2016. "Imperfection Sensitivity of Nonlinear Vibration of Curved Single-Walled Carbon Nanotubes Based on Nonlocal Timoshenko Beam Theory" Materials 9, no. 9: 786. https://doi.org/10.3390/ma9090786