Effects of the CO2 Guest Molecule on the sI Clathrate Hydrate Structure
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
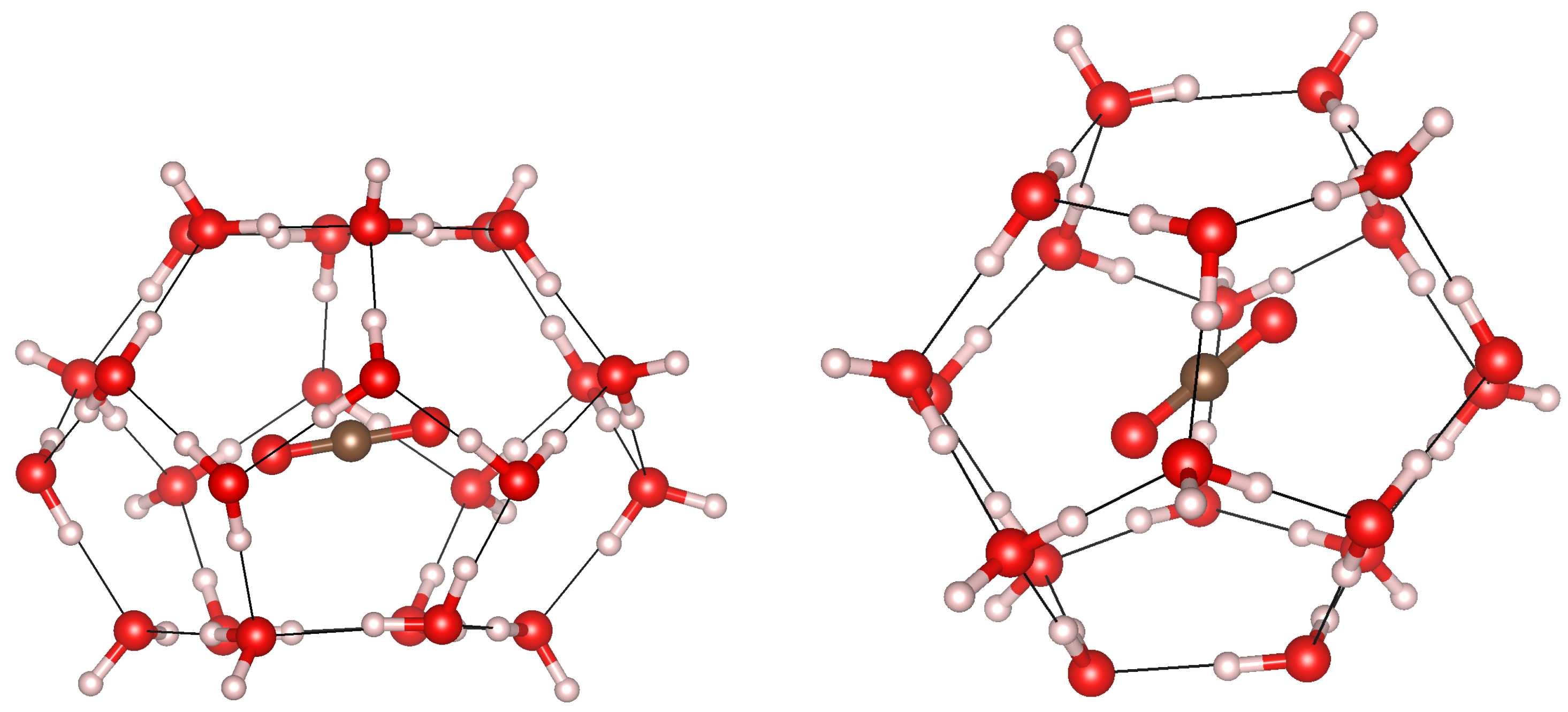
3.1. Geometry Optimization and Structural Properties at Zero Pressure
3.2. Equation of State. Microscopic Partition
3.3. Cage Deformation
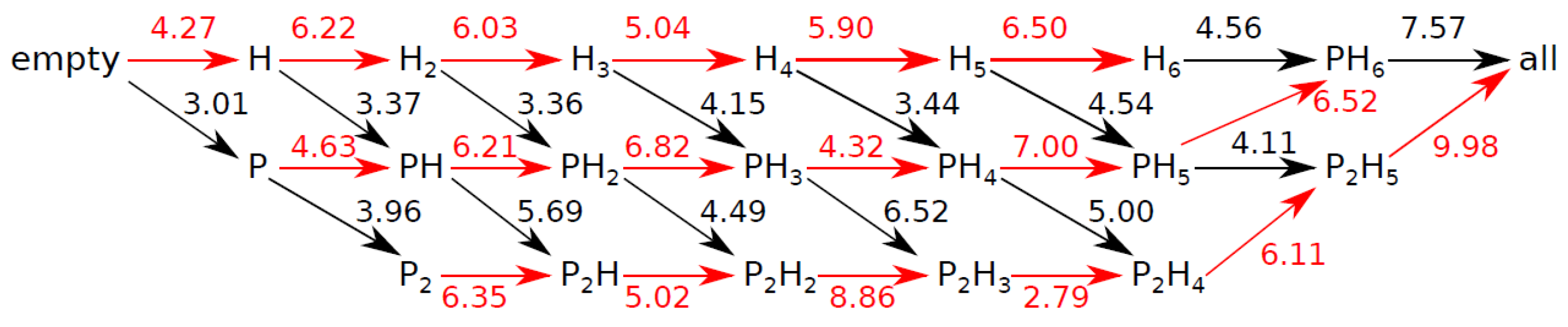
3.4. Internal Rotations, Conformations
3.5. Cage Occupation
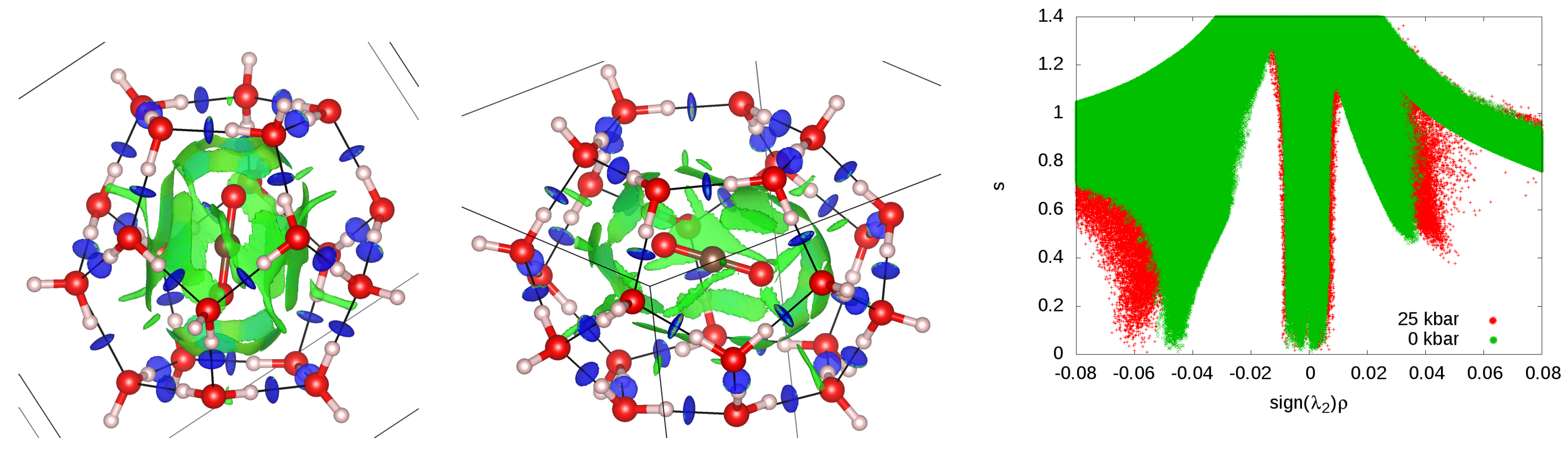
3.6. Guest–Host Interactions
3.7. Vibrations
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saji, A.; Yoshida, H.; Sakai, M.; Tanii, T.; Kamata, T.; Kitamura, H. Fixation of carbon dioxide by clathrate-hydrate. Energy Convers. Manag. 1992, 33, 643–649. [Google Scholar] [CrossRef]
- Jadhawar, P.; Mohammadi, A.H.; Yang, J.; Tohidi, B. Subsurface carbon dioxide storage through clathrate hydrate formation. In Advances in the Geological Storage of Carbon Dioxide; Springer: Dordrecht, The Netherlands, 2006; pp. 111–126. [Google Scholar]
- Hussmann, H.; Sohl, F.; Spohn, T. Subsurface oceans and deep interiors of medium-sized outer planet satellites and large trans-neptunian objects. Icarus 2006, 185, 258–273. [Google Scholar] [CrossRef]
- Fortes, A.D. Titan’s internal structure and the evolutionary consequences. Planet. Space Sci. 2012, 60, 10–17. [Google Scholar] [CrossRef]
- Izquierdo-Ruiz, F.; Méndez, A.S.J.; Prieto-Ballesteros, O.; Recio, J.M. Study of high pressure carbon dioxide clathrates hydrates on Ganymede. In Proceedings of the European Planetary Science Congress, EPSC2015-849, Nantes, France, 27 September–2 October 2015.
- Bollengier, O.; Choukrounb, M.; Grasseta, O.; le Menna, E.; Bellinoa, G.; Morizeta, Y.; Bezaciera, L.; Oanceaa, A.; Taffina, C.; Tobie, G. Phase equilibria in the H2O–CO2 system between 250–330 K and 0–1.7 GPa: Stability of the CO2 hydrates and H2O-ice VI at CO2 saturation. Geochim. Cosmochim. Acta 2013, 119, 322–339. [Google Scholar] [CrossRef]
- Henning, R.W.; Schultz, A.J.; Thieu, V.; Halpern, Y. Neutron diffraction studies of CO2 clathrate hydrate: Formation from deuterated ice. J. Phys. Chem. A 2000, 104, 5066–5071. [Google Scholar] [CrossRef]
- Udachin, K.A.; Ratcliffe, C.I.; Ripmeester, J.A. Structure, composition, and thermal expansion of CO2 hydrate from single crystal X-ray Diffraction measurements. J. Phys. Chem. B 2001, 105, 4200–4204. [Google Scholar] [CrossRef]
- Loveday, J.S.; Nelmes, R.J. High-pressure gas hydrates. Phys. Chem. Chem. Phys. 2008, 10, 937–950. [Google Scholar] [CrossRef] [PubMed]
- Tulk, C.A.; Machida, S.; Klug, D.D.; Lu, H.; Guthrie, M.; Molaison, J.J. The structure of CO2 hydrate between 0.7 and 1.0 GPa. J. Chem. Phys. 2014, 141, 174503. [Google Scholar] [CrossRef] [PubMed]
- Falenty, A.; Salamatin, A.N.; Kuhs, W.F. Kinetics of CO2-hydrate formation from ice powders: Data summary and modeling extended to low temperatures. J. Phys. Chem. C 2013, 117, 8443–8457. [Google Scholar] [CrossRef]
- Ambuehl, D.; Madden, M.E. CO2 hydrate formation and dissociation rates: Application to Mars. Icarus 2014, 234, 45–52. [Google Scholar] [CrossRef]
- Srivastava, H.K.; Sastry, G.N. Viability of clathrate hydrates as CO2 capturing agents: A theoretical study. J. Phys. Chem. A 2011, 115, 7633–7637. [Google Scholar] [CrossRef] [PubMed]
- Bernal, J.D.; Fowler, R.H. A theory of water and ionic solution, with particular reference to hydrogen and hydroxyl ions. J. Chem. Phys. 1933, 1, 515–514. [Google Scholar] [CrossRef]
- Takeuchi, F.; Hiratsuka, M.; Ohmura, R.; Alavi, S.; Sum, A.K.; Yasuoka, K. Water proton configurations in structures I, II, and H clathrate hydrate unit cells. J. Chem. Phys. 2013, 138, 124504. [Google Scholar] [CrossRef] [PubMed]
- Raza, Z.; Alfe, D.; Salzmann, C.G.; Klimeš, J.; Michaelides, A.; Slater, B. Proton ordering in cubic ice and hexagonal ice; A potential new ice phase—XIc. Phys. Chem. Chem. Phys. 2011, 13, 19788–19795. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800–8802. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Lacks, D.J.; Gordon, R.G. Pair interactions of rare-gas atoms as a test of exchange-energy-density functionals in regions of large density gradients. Phys. Rev. A 1993, 47, 4681–4690. [Google Scholar] [CrossRef] [PubMed]
- Kannemann, F.O.; Becke, A.D. Van der Waals interactions in density-functional theory: Rare-gas diatomics. J. Chem. Theory Comput. 2009, 5, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. Exchange-hole dipole moment and the dispersion interaction revisited. J. Chem. Phys. 2007, 127, 154108. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la-Roza, A.; Johnson, E.R. Van der Waals interactions in solids using the exchange-hole dipole moment model. J. Chem. Phys. 2012, 136, 174109. [Google Scholar] [CrossRef] [PubMed]
- Arabi, A.A.; Becke, A.D. Assessment of the PW86 + PBE + XDM density functional on van der Waals complexes at non-equilibrium geometries. J. Chem. Phys. 2012, 137, 014104. [Google Scholar] [CrossRef] [PubMed]
- Otero-De-La-Roza, A.; Johnson, E.R. A benchmark for non-covalent interactions in solids. J. Chem. Phys. 2012, 137, 054103. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la-Roza, A.; Johnson, E.R. Non-covalent interactions and thermochemistry using XDM-corrected hybrid and range-separated hybrid density functionals. J. Chem. Phys. 2013, 138, 204109. [Google Scholar] [CrossRef] [PubMed]
- Otero-De-La-Roza, A.; Johnson, E.R.; DiLabio, G.A. Halogen bonding from dispersion-corrected density-functional theory: The role of delocalization error. J. Chem. Theory Comput. 2014, 10, 5436–5447. [Google Scholar] [CrossRef] [PubMed]
- Otero-De-La-Roza, A.; Johnson, E.R. Predicting energetics of supramolecular systems using the XDM dispersion model. J. Chem. Theory Comput. 2015, 11, 4033–4040. [Google Scholar] [CrossRef] [PubMed]
- Vinet, P.; Smith, J.R.; Ferrante, J.; Rose, J.H. Temperature effects on the universal equation of state of solids. Phys. Rev. B 1987, 35, 1945–1953. [Google Scholar] [CrossRef]
- Recio, J.M.; Franco, R.; Martín Pendás, A.; Blanco, M.A.; Pueyo, L.; Pandey, R. Theoretical explanation of the uniform compressibility behavior observed in oxide spinels. Phys. Rev. B 2001, 63, 184101. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. JACS 2010, 132, 6498. [Google Scholar] [CrossRef] [PubMed]
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting noncovalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625. [Google Scholar] [CrossRef] [PubMed]
- Otero-de-la-Roza, A.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B. 01; Gaussian Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the colle–salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1998, 37, 785–789. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Herzberg, G. Electronic Spectra and Electronic Structure of Polyatomic Molecules; Van Nostrand: New York, NY, USA, 1966. [Google Scholar]
- Kuhs, W.F.; Lehmann, M.S. The structure of the ice Ih by neutron diffraction. J. Phys. Chem. 1983, 87, 4312–4313. [Google Scholar] [CrossRef]
- Jendi, Z.M.; Rey, A.D.; Servio, P. Ab initio DFT study of structural and mechanical properties of methane and carbon dioxide hydrates. Mol. Simul. 2015, 41, 572–579. [Google Scholar] [CrossRef]
- Shimizu, H.; Kumazaki, T.; Kume, T.; Sasaki, S. Elasticity of single-crystal methane hydrate at high pressure. Phys. Rev. B 2002, 65, 212102. [Google Scholar] [CrossRef]
- Falenty, A.; Hansen, T.C.; Kuhs, W.F. Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate. Nature 2014, 516, 231–233. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo-Ruiz, F.; Otero-de-la-Roza, A.; Contreras-García, J.; Menéndez, J.M.; Prieto-Ballesteros, O.; Recio, J.M. Guest–host interactions in gas clathrate hydrates under pressure. High Press. Res. 2015, 35, 49–56. [Google Scholar] [CrossRef]
- Izquierdo-Ruiz, F.; Méndez, A.S.J.; Recio, J.M.; Prieto-Ballesteros, O. High Pressure phases of gas clathrate hydrates and their Impact to the habitability of the icy moons. In Proceedings of the Astrobiology Science Conference, Chicago, IL, USA, 15–19 June 2015; p. 7565.
- Takeya, S.; Udachin, K.A.; Moudrakovski, I.L.; Susilo, R.; Ripmeester, J.A. Direct space methods for powder X-ray diffraction for guest–host materials: Applications to cage occupancies and guest distributions in clathrate hydrates. J. Am. Chem. Sci. 2010, 132, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Vance, S.; Bouffardc, M.; Choukrouna, M.; Sotina, C. Ganymede’s internal structure including thermodynamics of magnesium sulfate oceans in contact with ice. Planet. Space Sci. 2014, 96, 62–70. [Google Scholar] [CrossRef]
- Contreras-Garcia, J.; Boto, R.A.; Izquierdo-Ruiz, F.; Reva, I.; Woller, T.; Alonso, M. A benchmark for the Non-Covalent Interaction index (NCI) or...is it really all in the geometry? Theor. Chem. Acc. 2016, in press. [Google Scholar]
- Ikeda, T.; Mae, S.; Uchida, T. Effect of guest–host interaction on Raman spectrum of a CO2 clathrate hydrate single crystal. J. Chem. Phys. 1998, 108, 1352–1359. [Google Scholar] [CrossRef]
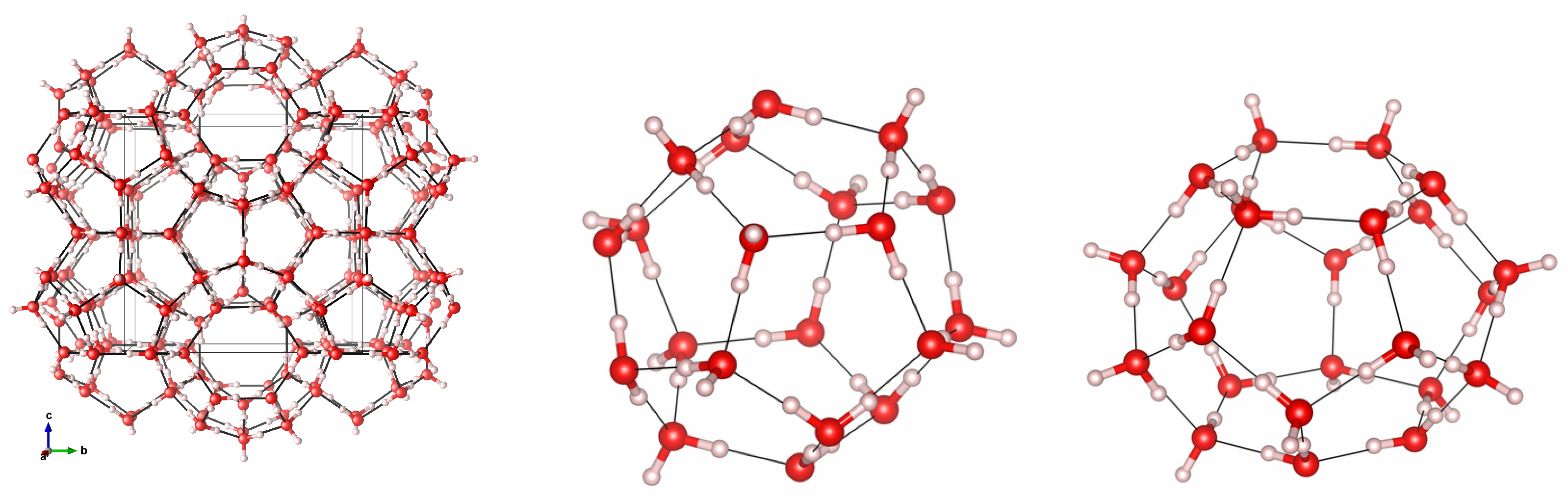
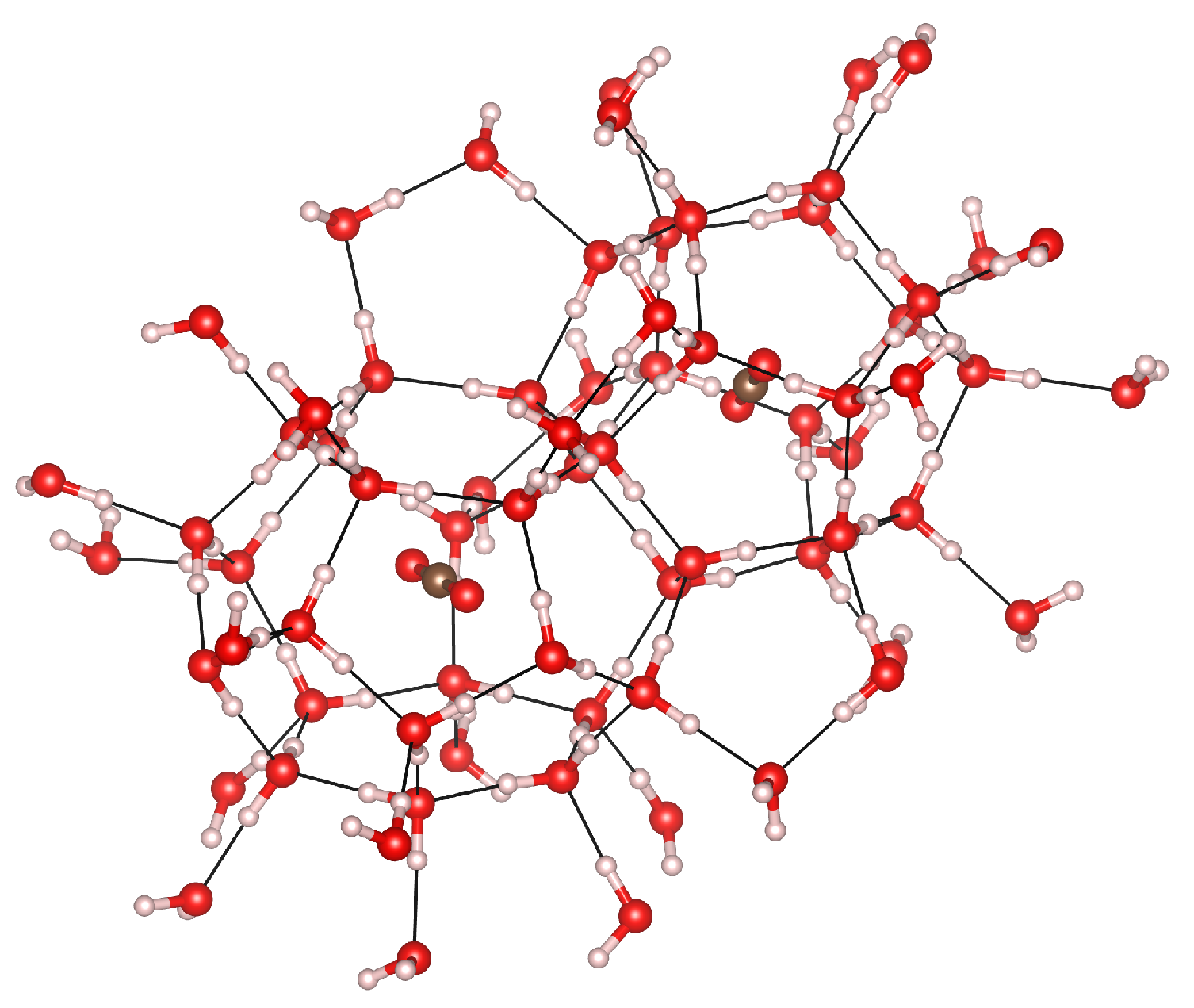
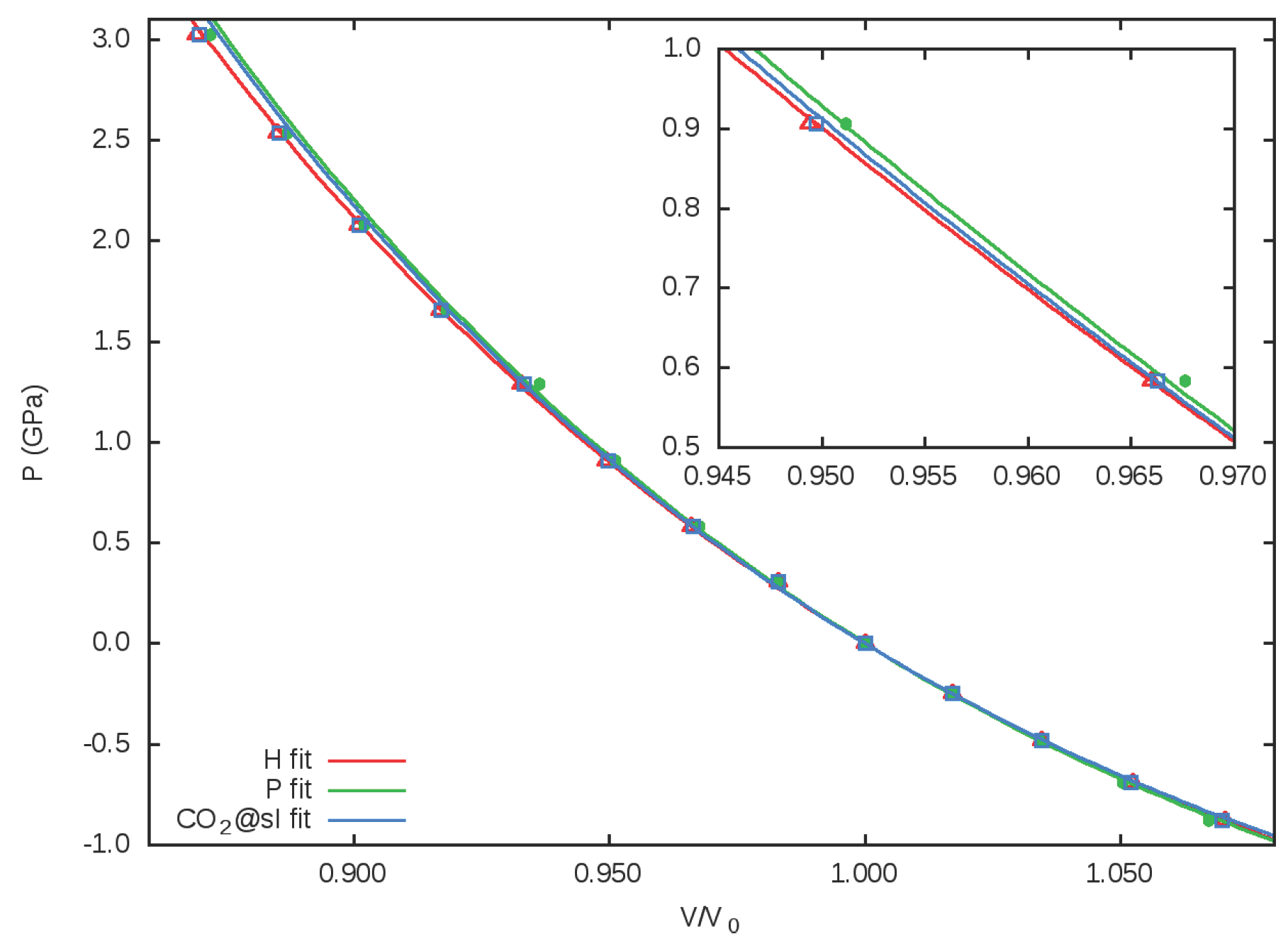
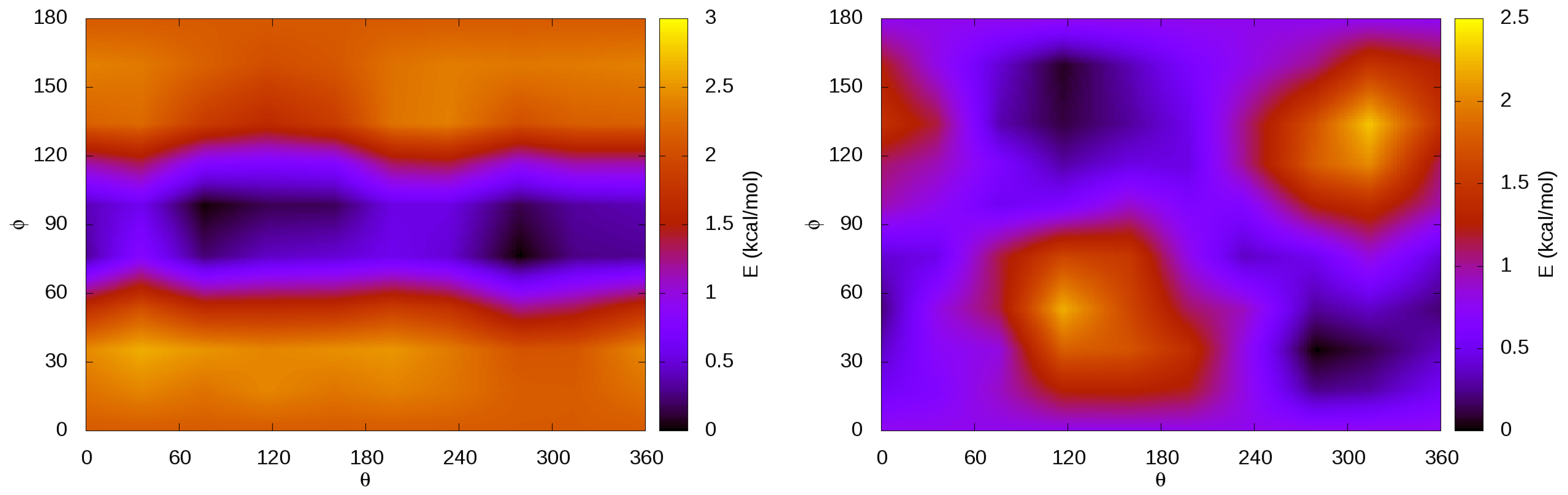
| V0 (Å3) | B0 (GPa) | ||
|---|---|---|---|
| CO2@H2O | 1577.87 | 15.42 | 5.59 |
| P cage | 151.54 | 15.75 | 5.46 |
| H cage | 212.46 | 15.41 | 5.09 |
| Empty | Full | ||||||
|---|---|---|---|---|---|---|---|
| p (GPa) | Dp | DH | IH | p (GPa) | Dp | DH | IH |
| 3.60 | 0.0106 | 0.0663 | 0.8193 | 3.37 | 0.4035 | 0.3081 | 0.8184 |
| 3.01 | 0.0100 | 0.0679 | 0.8194 | 3.04 | 0.3688 | 0.2174 | 0.8188 |
| 2.53 | 0.0098 | 0.0675 | 0.8193 | 2.56 | 0.3457 | 0.1945 | 0.8188 |
| 2.07 | 0.0094 | 0.0671 | 0.8193 | 2.10 | 0.3366 | 0.1863 | 0.8188 |
| 1.73 | 0.0092 | 0.0634 | 0.8189 | 1.68 | 0.3172 | 0.1788 | 0.8188 |
| 1.33 | 0.0096 | 0.0633 | 0.8188 | 1.31 | 0.2561 | 0.1590 | 0.8191 |
| 0.97 | 0.0107 | 0.0633 | 0.8188 | 0.93 | 0.2543 | 0.1531 | 0.8190 |
| 0.65 | 0.0118 | 0.0635 | 0.8188 | 0.61 | 0.2297 | 0.1471 | 0.8190 |
| 0.36 | 0.0131 | 0.0639 | 0.8188 | 0.33 | 0.2061 | 0.1367 | 0.8189 |
| 0.10 | 0.0141 | 0.0640 | 0.8187 | 0.02 | 0.1936 | 0.1314 | 0.8189 |
| −0.14 | 0.0152 | 0.0642 | 0.8187 | −0.22 | 0.1815 | 0.1256 | 0.8189 |
| −0.35 | 0.0164 | 0.0645 | 0.8187 | −0.46 | 0.1708 | 0.1216 | 0.8189 |
| −0.52 | 0.0167 | 0.0627 | 0.8185 | −0.67 | 0.1626 | 0.1155 | 0.8188 |
| −0.68 | 0.0150 | 0.0604 | 0.8183 | −0.86 | 0.1536 | 0.1112 | 0.8187 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izquierdo-Ruiz, F.; Otero-de-la-Roza, A.; Contreras-García, J.; Prieto-Ballesteros, O.; Recio, J.M. Effects of the CO2 Guest Molecule on the sI Clathrate Hydrate Structure. Materials 2016, 9, 777. https://doi.org/10.3390/ma9090777
Izquierdo-Ruiz F, Otero-de-la-Roza A, Contreras-García J, Prieto-Ballesteros O, Recio JM. Effects of the CO2 Guest Molecule on the sI Clathrate Hydrate Structure. Materials. 2016; 9(9):777. https://doi.org/10.3390/ma9090777
Chicago/Turabian StyleIzquierdo-Ruiz, Fernando, Alberto Otero-de-la-Roza, Julia Contreras-García, Olga Prieto-Ballesteros, and Jose Manuel Recio. 2016. "Effects of the CO2 Guest Molecule on the sI Clathrate Hydrate Structure" Materials 9, no. 9: 777. https://doi.org/10.3390/ma9090777
APA StyleIzquierdo-Ruiz, F., Otero-de-la-Roza, A., Contreras-García, J., Prieto-Ballesteros, O., & Recio, J. M. (2016). Effects of the CO2 Guest Molecule on the sI Clathrate Hydrate Structure. Materials, 9(9), 777. https://doi.org/10.3390/ma9090777







