Microstructure Design of Tempered Martensite by Atomistically Informed Full-Field Simulation: From Quenching to Fracture
Abstract
:1. Introduction
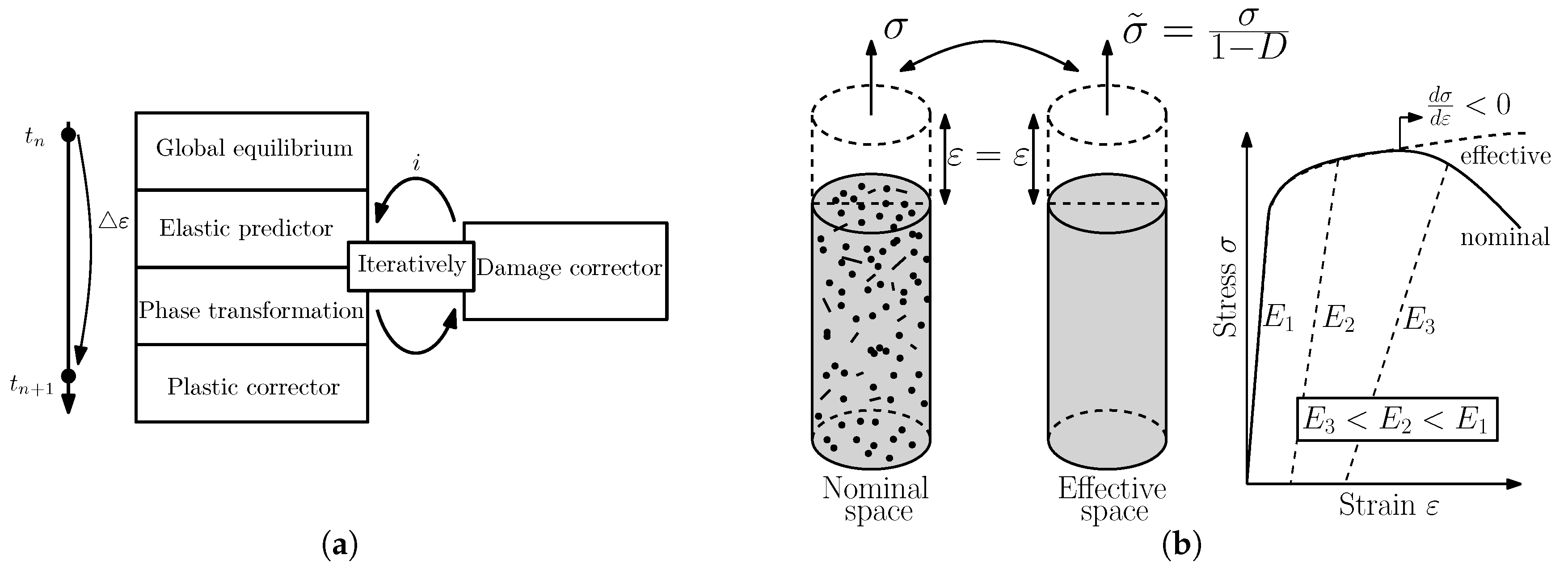
2. Multi-Phase Field Method
3. Mechanics
3.1. Linear Limit
3.2. Large Deformation Framework
3.3. Crystal Plasticity Model
3.4. Damage Model
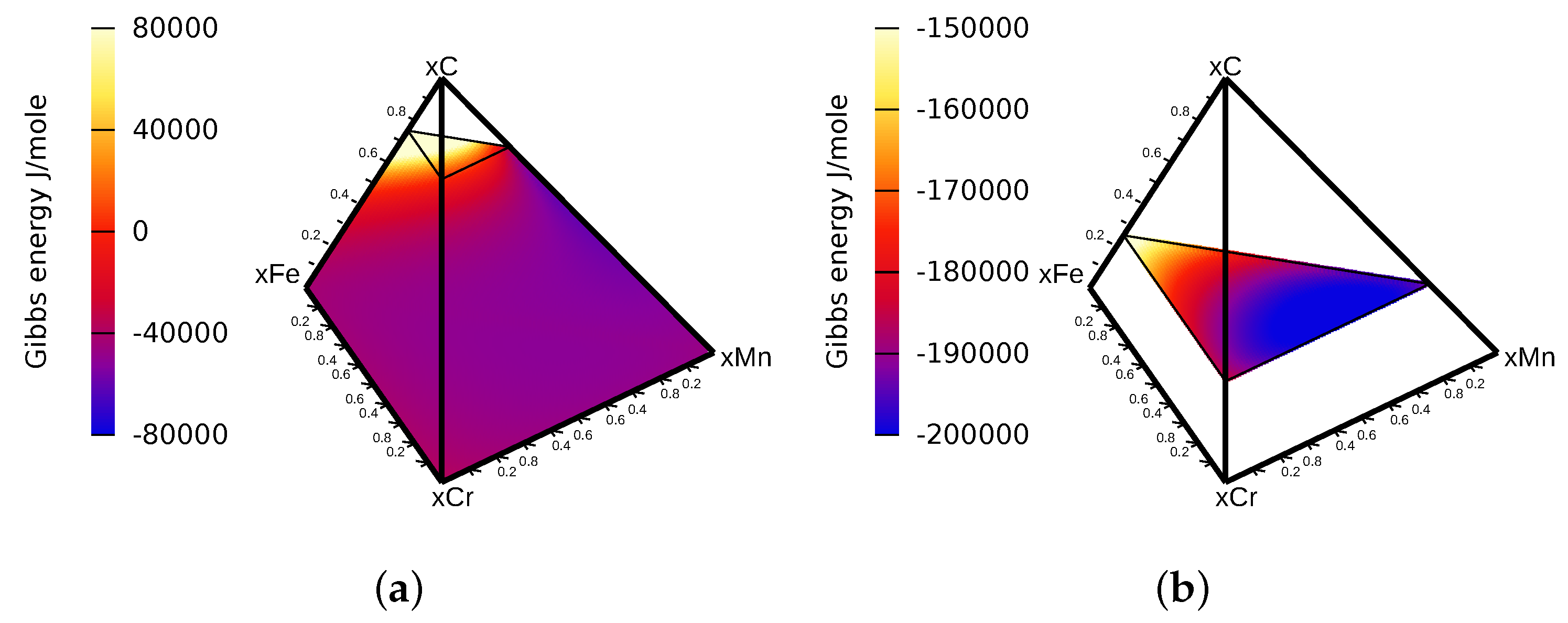
4. Thermodynamics and Diffusion
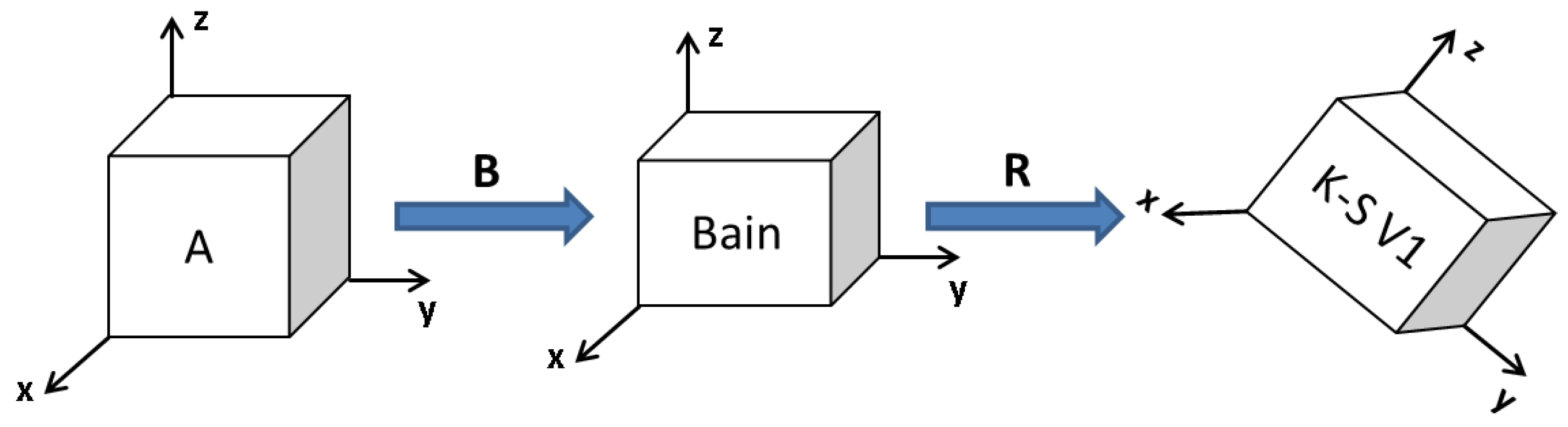
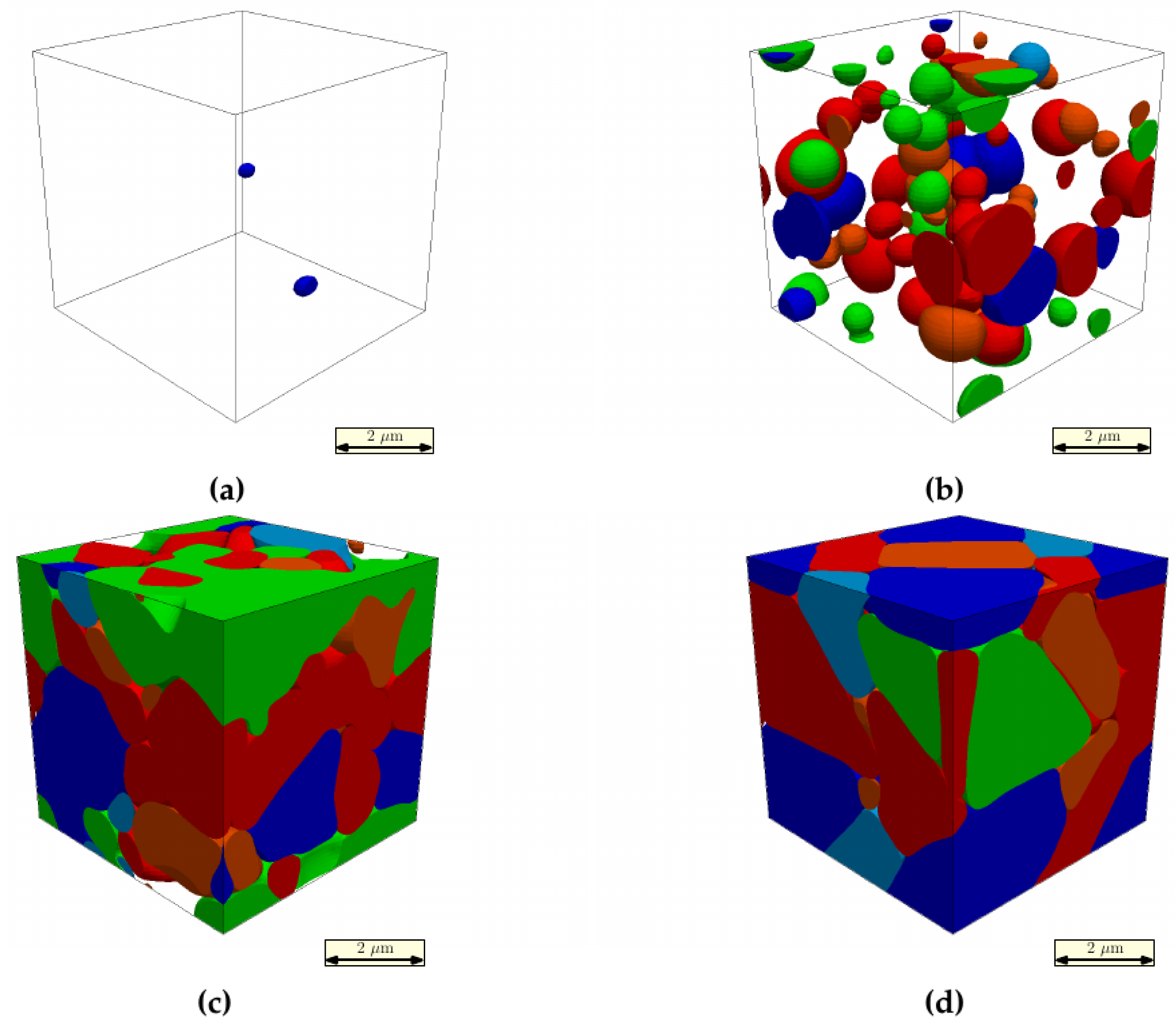
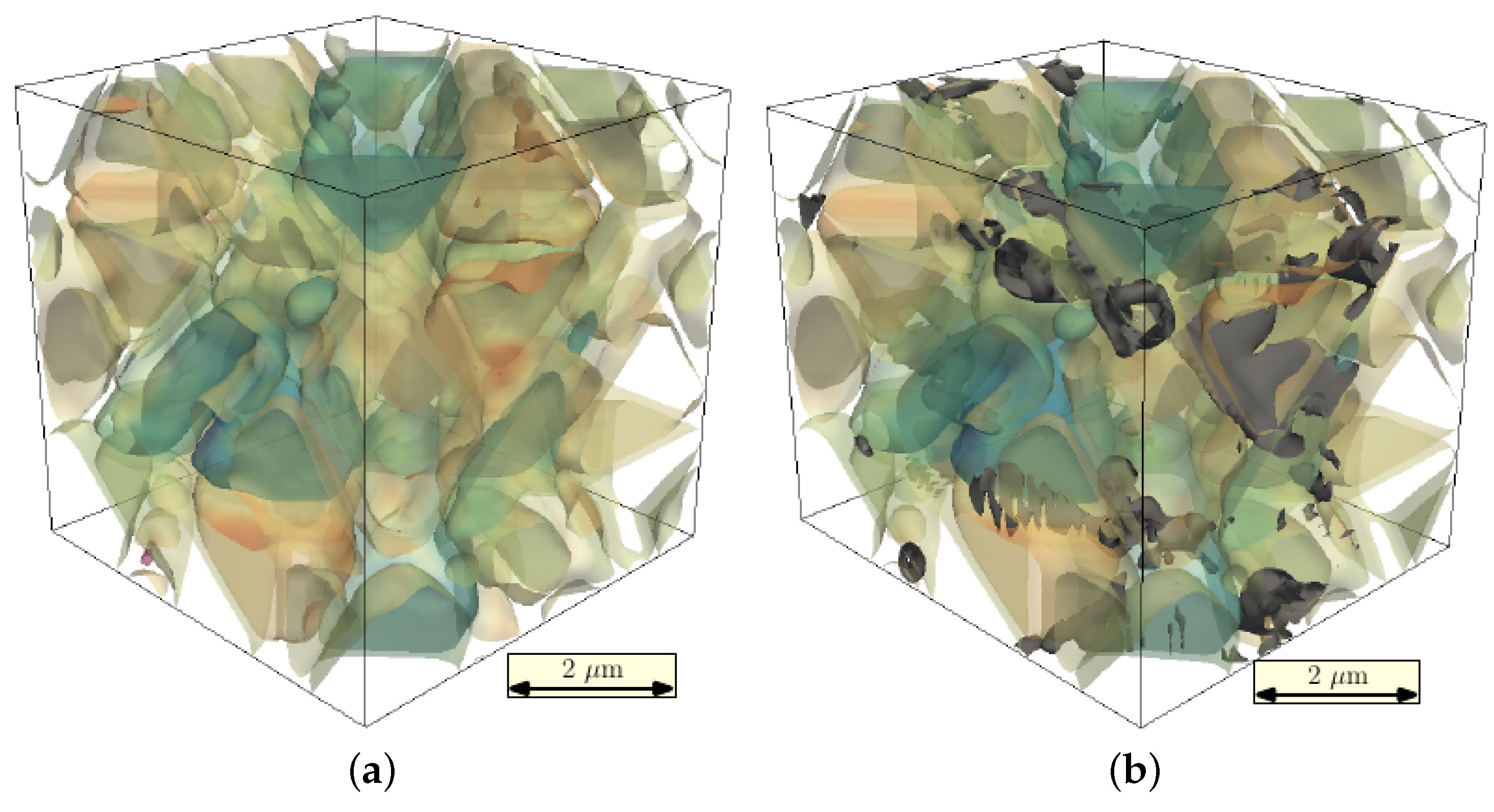
5. Results: Martensite Microstructure
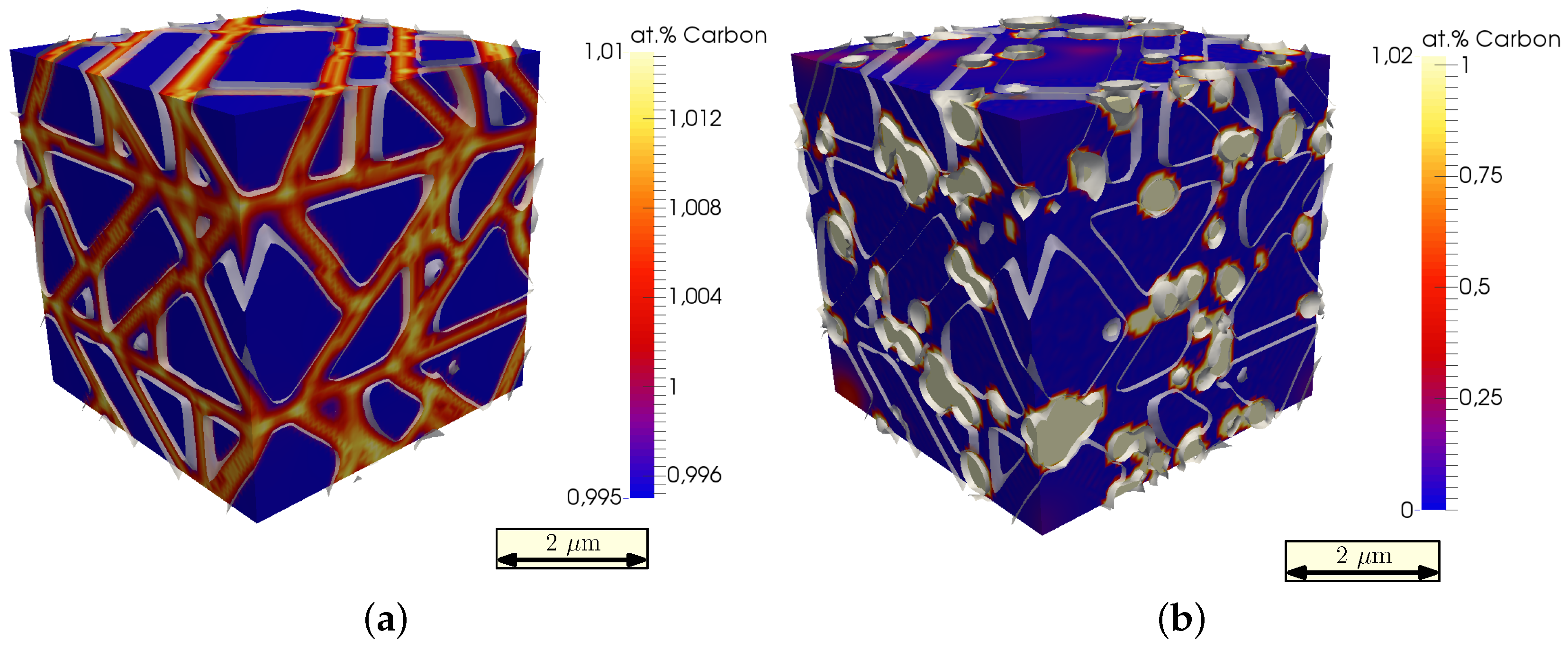
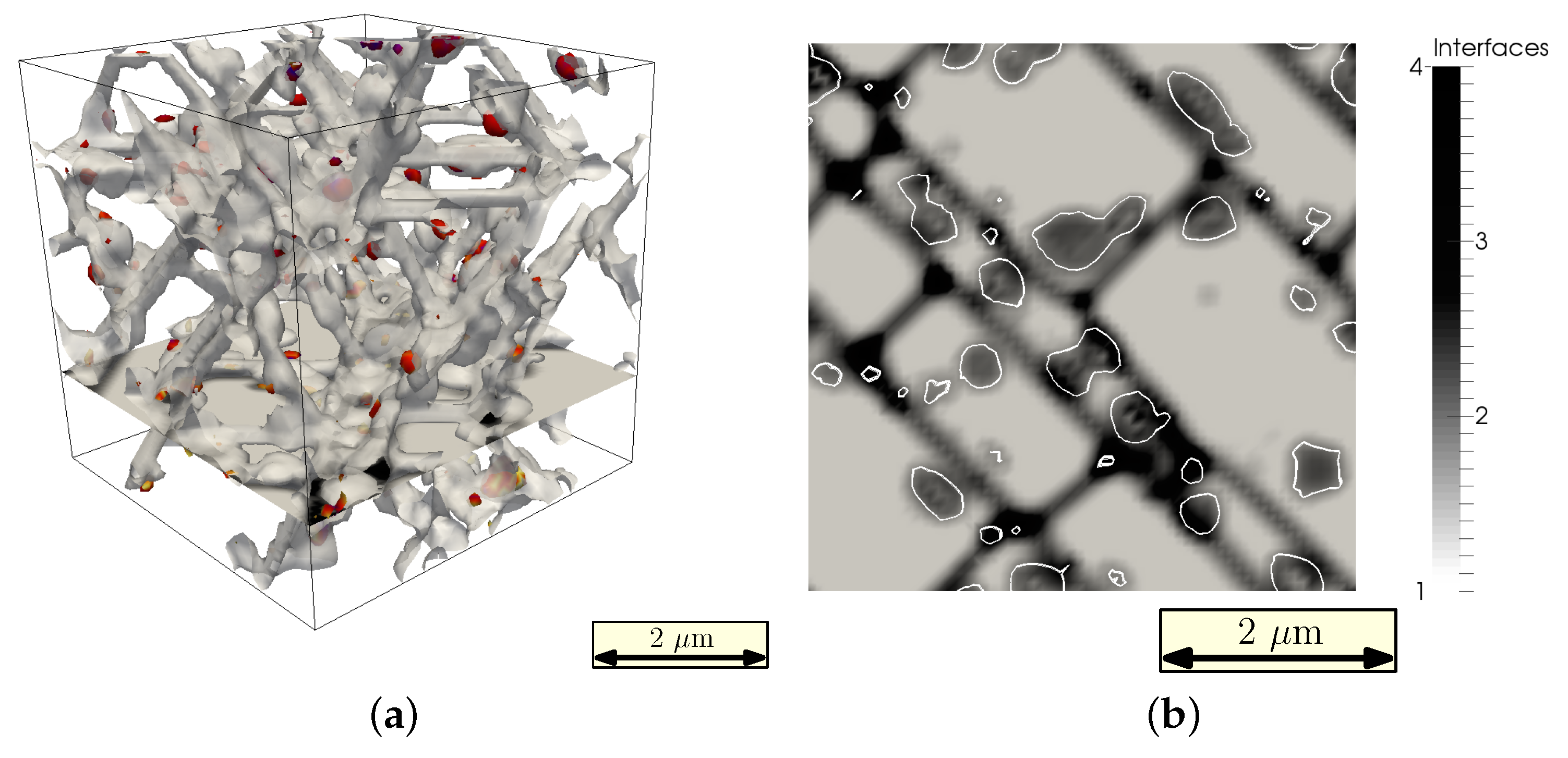
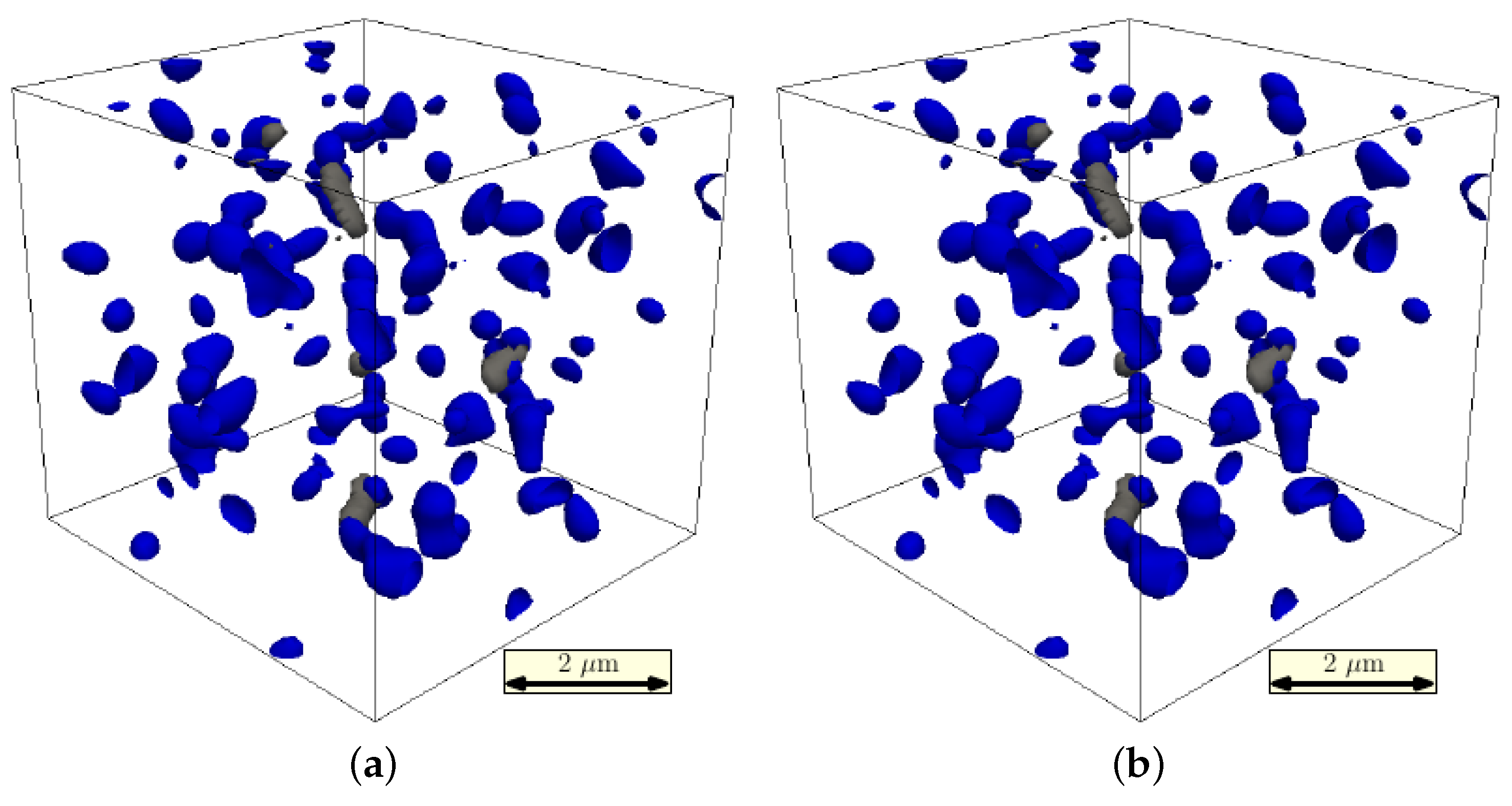
6. Results: Precipitation
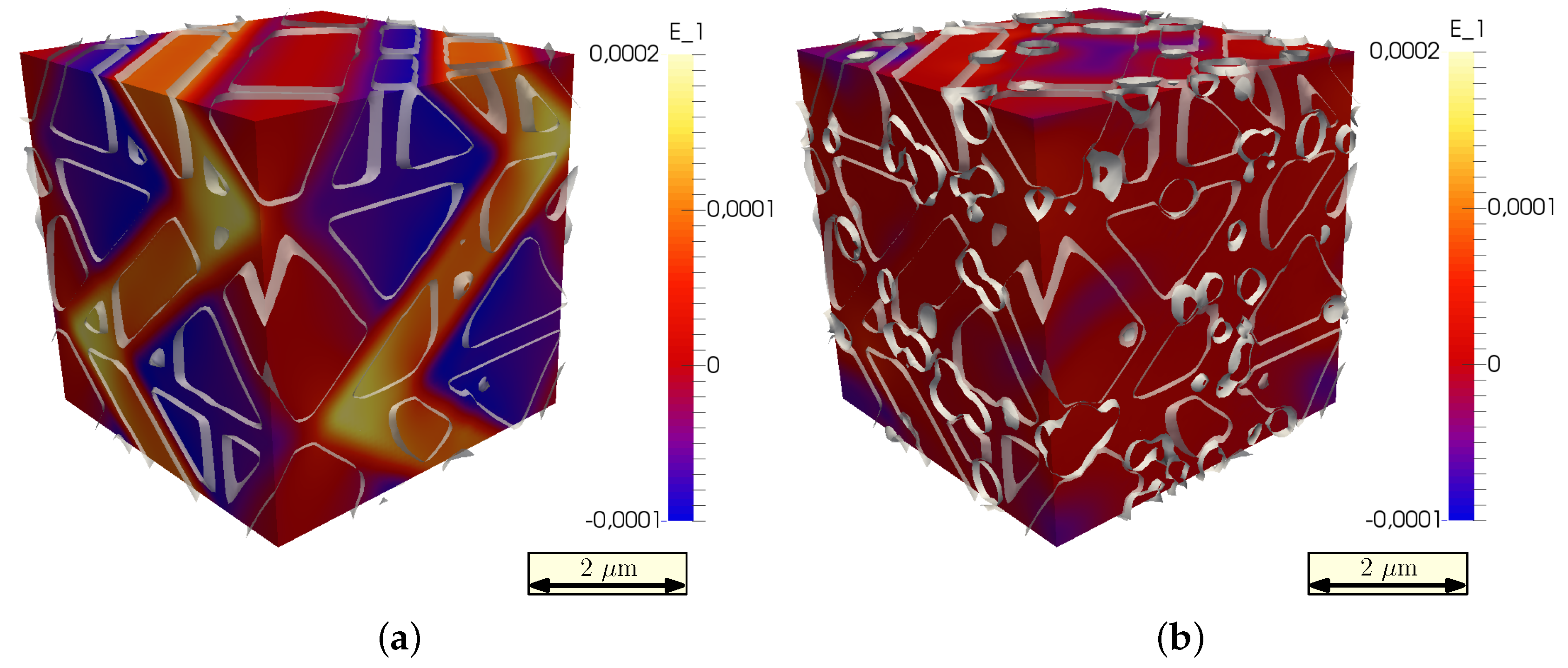
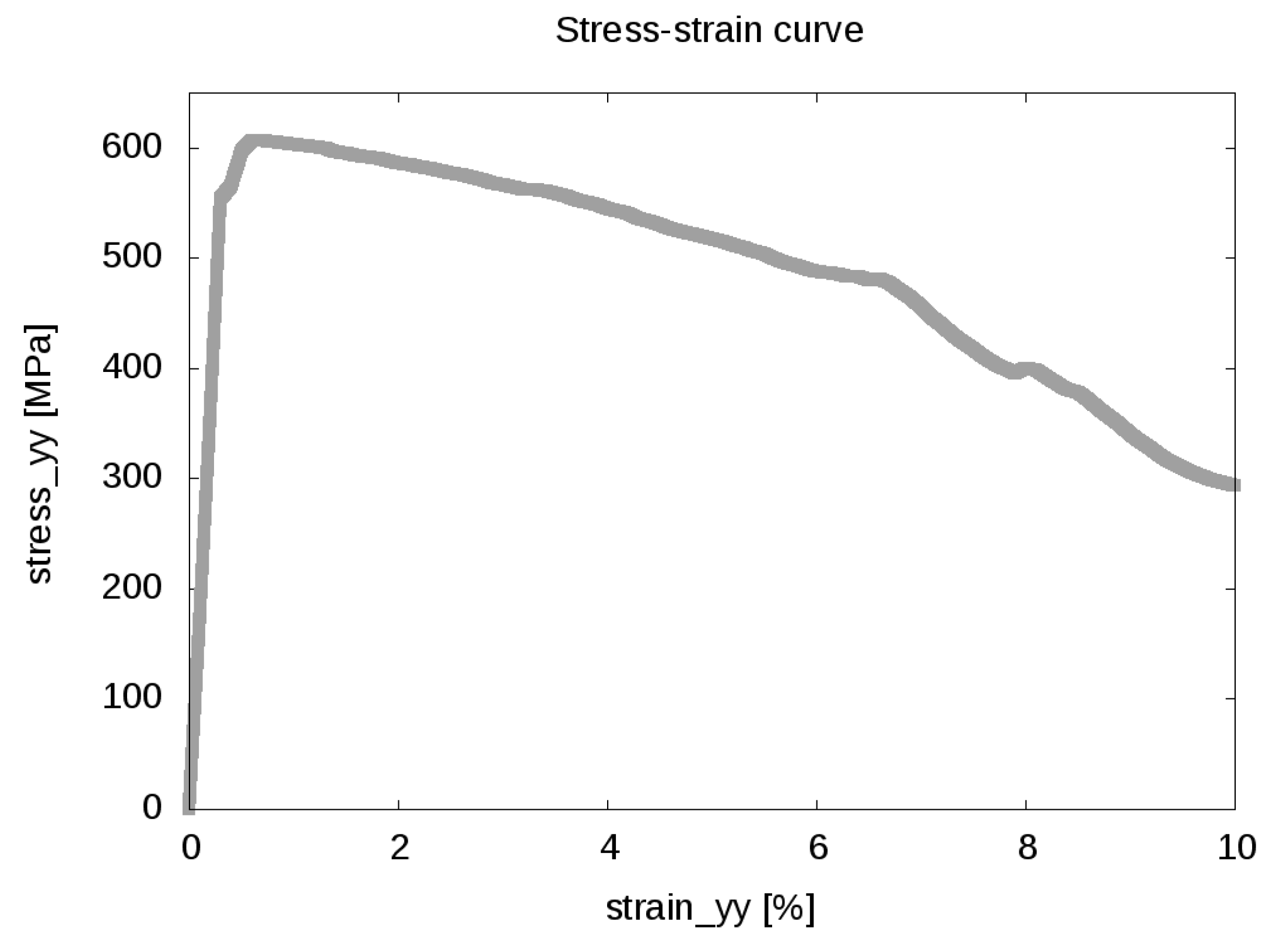
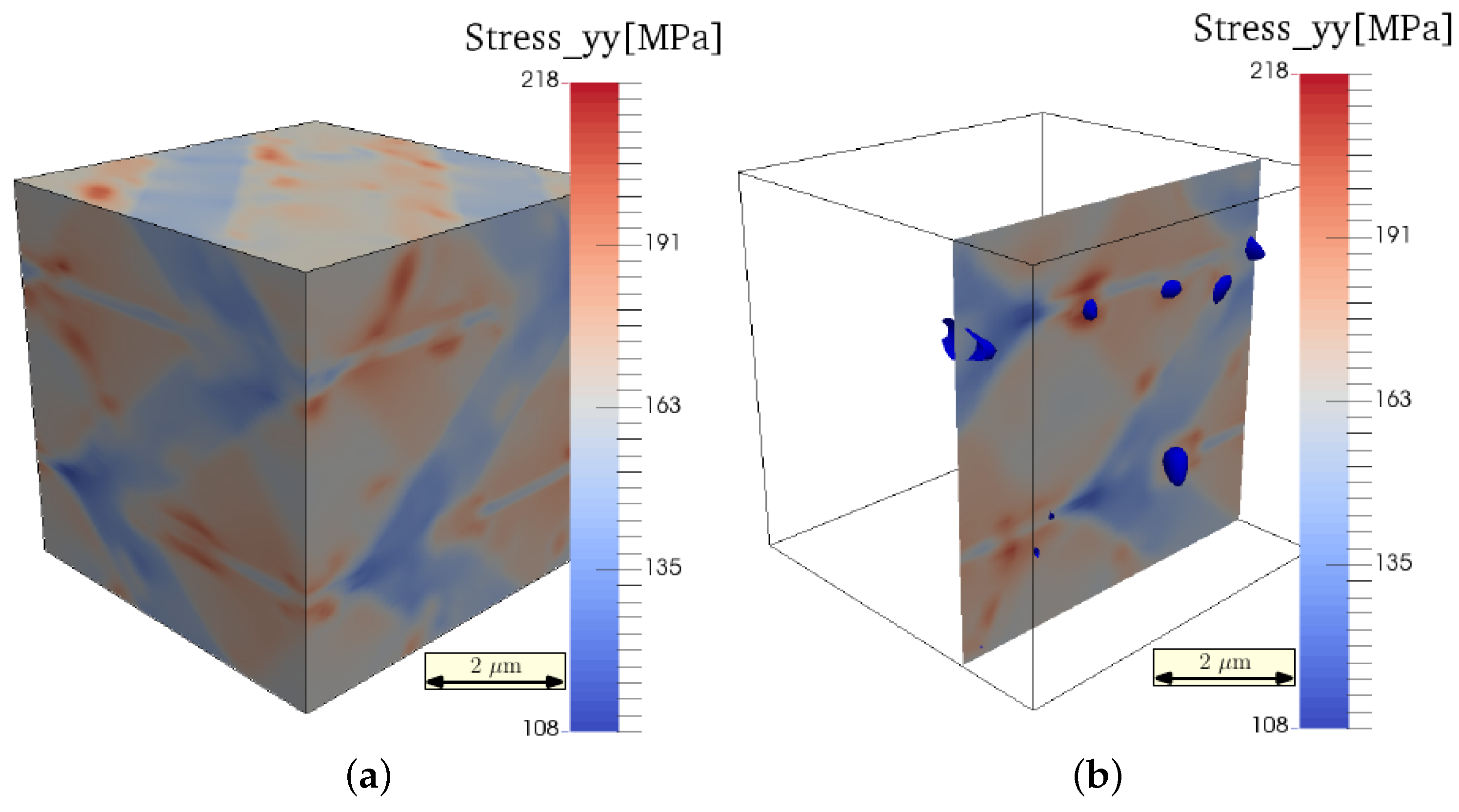
7. Results: Mechanical Testing Simulation
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Li, D.F.; Golden, B.J.; O’Dowd, N.P. Multiscale modeling of mechanical response in a martensitic steel: A micromechanical and length-scale-dependent framework for precipitate hardening. Acta Mater. 2014, 80, 445–456. [Google Scholar] [CrossRef]
- Shchyglo, O.; Borukhovich, E.; Engels, P.; Kamachali, R.D.; Boeff, M.; Medvedev, D.; Gladkov, S.; Spatschek, R.; Zeng, M.; Steinbach, I. OpenPhase. Available online: http://www.openphase.de (accessed on 1 June 2016).
- Steinbach, I.; Pezzolla, F.; Nestler, B.; Seeßelberg, M.; Prieler, R.; Schmitz, G.J.; Rezende, J.L.L. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135–147. [Google Scholar] [CrossRef]
- Tiaden, J.; Nestler, B.; Diepers, H.J.; Steinbach, I. The multiphase-field model with an integrated concept for modeling solute diffusion. Phys. D Nonlinear Phenom. 1998, 115, 73–86. [Google Scholar] [CrossRef]
- Steinbach, I.; Pezzolla, F. A generalized field method for multiphase transformations using interface fields. Phys. D Nonlinear Phenom. 1999, 134, 385–393. [Google Scholar] [CrossRef]
- Hu, S.; Chen, L. A phase-field model for evolving microstructures with strong elastic Inhomogeneity. Acta Mater. 2001, 49, 1879–1890. [Google Scholar] [CrossRef]
- Borukhovich, E.; Engels, P.S.; Böhlke, T.; Shchyglo, O.; Steinbach, I. Large strain elasto-plasticity for diffuse interface models. Model. Simul. Mater. Sci. Eng. 2014, 22, 34008. [Google Scholar] [CrossRef]
- Borukhovich, E.; Engels, P.S.; Mosler, J.; Shchyglo, O.; Steinbach, I. Large deformation framework for phase-field simulations at the mesoscale. Comput. Mater. Sci. 2015, 108, 367–373. [Google Scholar] [CrossRef]
- Steinbach, I.; Zhang, L.; Plapp, M. Phase-field model with finite interface dissipation. Acta Mater. 2012, 60, 2689–2701. [Google Scholar] [CrossRef]
- Zhang, L.; Steinbach, I. Phase-field model with finite interface dissipation: Extension to multi-component multi-phase alloys. Acta Mater. 2012, 60, 2702–2710. [Google Scholar] [CrossRef]
- Kamachali, R.D.; Borukhovich, E.; Shchyglo, O.; Steinbach, I. Solutal gradients in strained equilibrium. Philos. Mag. Lett. 2013, 93. [Google Scholar] [CrossRef]
- Shchyglo, O.; Hammerschmidt, T.; Cak, M.; Drautz, R.; Steinbach, I. Atomistically informed extended Gibbs energy description for phase-field simulation of tempering martensitic steel. Materials 2016, in press. [Google Scholar]
- Steinbach, I.; Apel, M. Multi phase field model for solid state transformation with elastic strain. Phys. D Nonlinear Phenom. 2006, 217, 153–160. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater.s Sci. Eng. 2009, 17, 73001. [Google Scholar] [CrossRef]
- Steinbach, I. Phase-field model for microstructure evolution at the mesoscopic scale. Annu. Rev. Mater. Res. 2013, 43, 89–107. [Google Scholar] [CrossRef]
- Ammar, K.; Appoloire, B.; Cailletaud, G.; Forest, S. Combining phase field approach and homogenization methods for modeling phase transformation in elastoplastic media. Eur. J. Comput. Mech. 2009, 18, 485–523. [Google Scholar]
- Lin, R. Numerical study of consistency of rate constitutive equations with elasticity at finite deformation. Int. J. Numer. Methods Eng. 2002, 55, 1053–1077. [Google Scholar] [CrossRef]
- Borukhovich, E. Consistent Coupling of Geometrically Non-Linear Finite Deformation with Alloy Chemistry and Diffusion within the Phase-Field Framework. Ph.D. Thesis, Ruhr-University Bochum, Bochum, Germany, 1 March 2016. [Google Scholar]
- Abaqus, Corp., D.S.S.: Johnston, RI, USA, 2011.
- Boeff, M.; Engels, P.S.; Ma, A.; Hartmaier, A. Formulation of nonlocal damage models based on spectral methods for application to complex microstructures. Eng. Fract. Mech. 2015, 147, 373–387. [Google Scholar] [CrossRef]
- Peerlings, R. Enhanced damage modeling for fracture and fatigue. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 23 March 1999. [Google Scholar]
- Simo, J.; Ju, J. Strain-and stress-based continuum damage models—I. Formulation. Int. J. Solids Struct. 1987, 23, 821–840. [Google Scholar] [CrossRef]
- Nedjar, B. Elastoplastic-damage modeling including the gradient of damage: Formulation and computational aspects. Int. J. Solids Struct. 2001, 38, 5421–5451. [Google Scholar] [CrossRef]
- Addessi, D.; Marfia, S.; Sacco, E. A plastic nonlocal damage model. Comput. Methods Appl. Mech. Eng. 2002, 191, 1291–1310. [Google Scholar] [CrossRef]
- Boers, S.; Schreurs, P.; Geers, M. Operator-split damage-plasticity applied to groove forming in food can lids. Int. J. Solids Struct. 2005, 42, 4154–4178. [Google Scholar] [CrossRef]
- Lee, B.J. A thermodynamic evaluation of the Fe-Cr-Mn-C system. Metall. Trans. A 1993, 24, 1017–1025. [Google Scholar] [CrossRef]
- Lukas, H.L.; Fries, S.G.; Sundman, B. Computational Thermodynamics–The Calphad Method; Cambradge University Press: Cambridge, UK, 2007. [Google Scholar]
- Sundman, B.; Ågren, J. A regular solution model for phases with several components and sublattices, suitable for computer applications. J. Phys. Chem. Solids 1987, 42, 297–301. [Google Scholar] [CrossRef]
- Zhang, L.; Stratmann, M.; Du, Y.; Sundman, B.; Steinbach, I. Incorporating the CALPHAD sublattice approach of ordering into the phase-field model with finite interface dissipation. Acta Mater. 2015, 88, 156–169. [Google Scholar] [CrossRef]
- Okamoto, H. The C-Fe (carbon-iron) system. J. Phase Equilib. 1992, 13, 543–565. [Google Scholar] [CrossRef]
- Wang, J.; Janisch, R.; Madsen, G.K.H.; Drautz, R. First-principles study of carbon segregation in bcc iron symmetrical tilt grain boundaries. Acta Mater. 2016, 115, 259–268. [Google Scholar] [CrossRef]
- Cool, T.; Bhadeshia, H.K.D.H. Prediction of martensite start temperature of power plant steels. Mater. Sci. Technol. 1996, 12, 40–44. [Google Scholar] [CrossRef]
- Moyer, J.M.; Ansell, G.S. The volume expansion accompanying the martensite transformation in iron-carbon alloys. Metall. Trans. A 1975, 6, 1785–1791. [Google Scholar] [CrossRef]
- Laptev, A.; Baufeld, B.; Swarnakar, A.K.; Zakharchuk, S.; van der Biest, O. High temperature thermal expansion and elastic modulus of steels used in mill rolls. J. Mater. Eng. Perform. 2012, 21, 271–279. [Google Scholar] [CrossRef]
- Sauzay, M. Cubic elasticity and stress distribution at the free surface of polycrystals. Acta Mater. 2007, 55, 1193–1202. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Ledbetter, H.; Urbassek, H.M. Experimental and atomistic study of the elastic properties of α′ Fe-C martensite. Acta Mater. 2012, 60, 4901–4907. [Google Scholar] [CrossRef]
- Jiang, C.; Srinivasan, S.G.; Caro, A.; Maloy, S.A. Structural, elastic, and electronic properties of Fe3C from first principles. J. Appl. Phys. 2008, 103, 043502. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic features of lath martensite in low-carbon steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borukhovich, E.; Du, G.; Stratmann, M.; Boeff, M.; Shchyglo, O.; Hartmaier, A.; Steinbach, I. Microstructure Design of Tempered Martensite by Atomistically Informed Full-Field Simulation: From Quenching to Fracture. Materials 2016, 9, 673. https://doi.org/10.3390/ma9080673
Borukhovich E, Du G, Stratmann M, Boeff M, Shchyglo O, Hartmaier A, Steinbach I. Microstructure Design of Tempered Martensite by Atomistically Informed Full-Field Simulation: From Quenching to Fracture. Materials. 2016; 9(8):673. https://doi.org/10.3390/ma9080673
Chicago/Turabian StyleBorukhovich, Efim, Guanxing Du, Matthias Stratmann, Martin Boeff, Oleg Shchyglo, Alexander Hartmaier, and Ingo Steinbach. 2016. "Microstructure Design of Tempered Martensite by Atomistically Informed Full-Field Simulation: From Quenching to Fracture" Materials 9, no. 8: 673. https://doi.org/10.3390/ma9080673
APA StyleBorukhovich, E., Du, G., Stratmann, M., Boeff, M., Shchyglo, O., Hartmaier, A., & Steinbach, I. (2016). Microstructure Design of Tempered Martensite by Atomistically Informed Full-Field Simulation: From Quenching to Fracture. Materials, 9(8), 673. https://doi.org/10.3390/ma9080673








