The Resistive Switching Characteristics in ZrO2 and Its Filamentary Conduction Behavior
Abstract
:1. Introduction
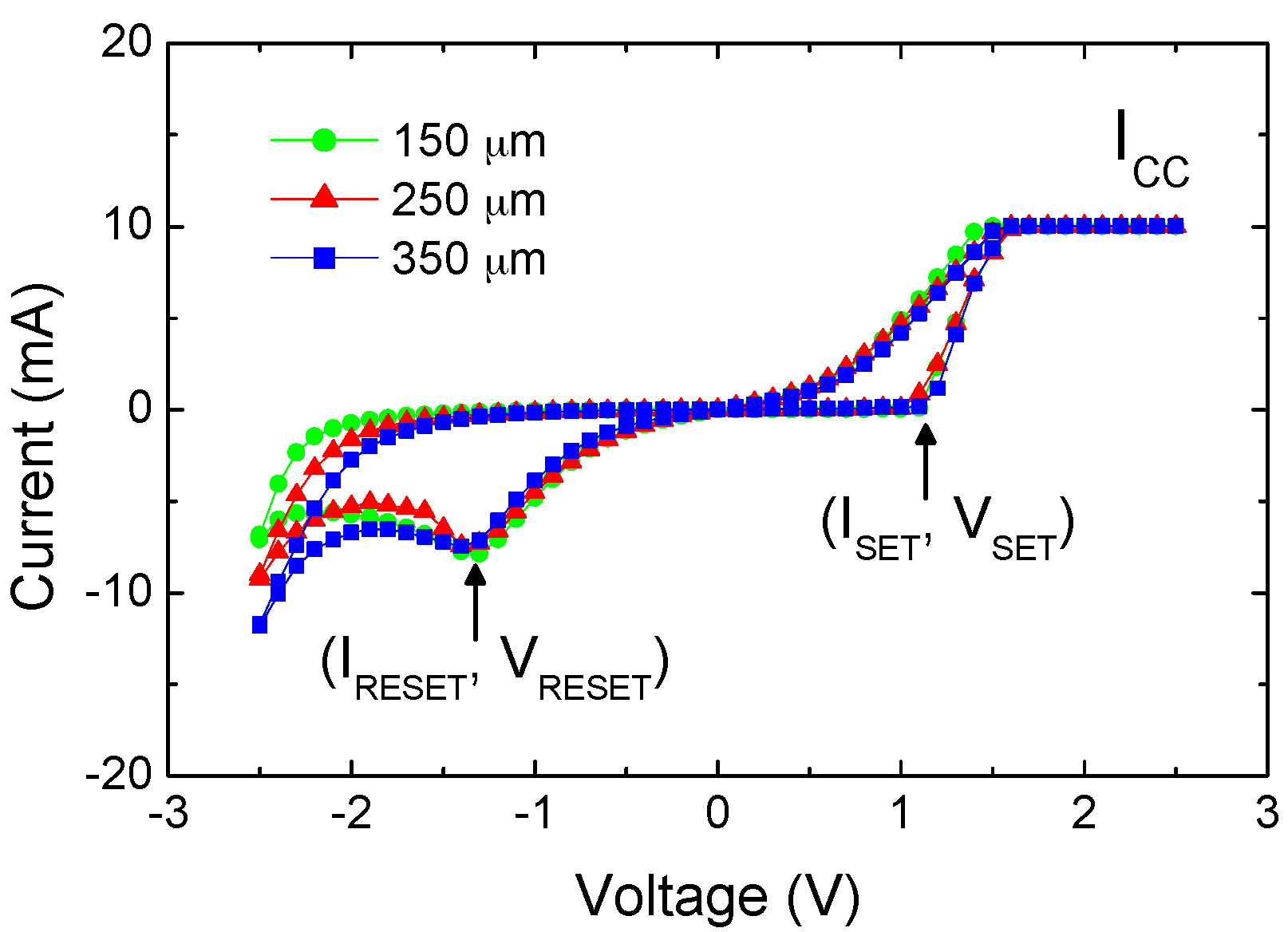
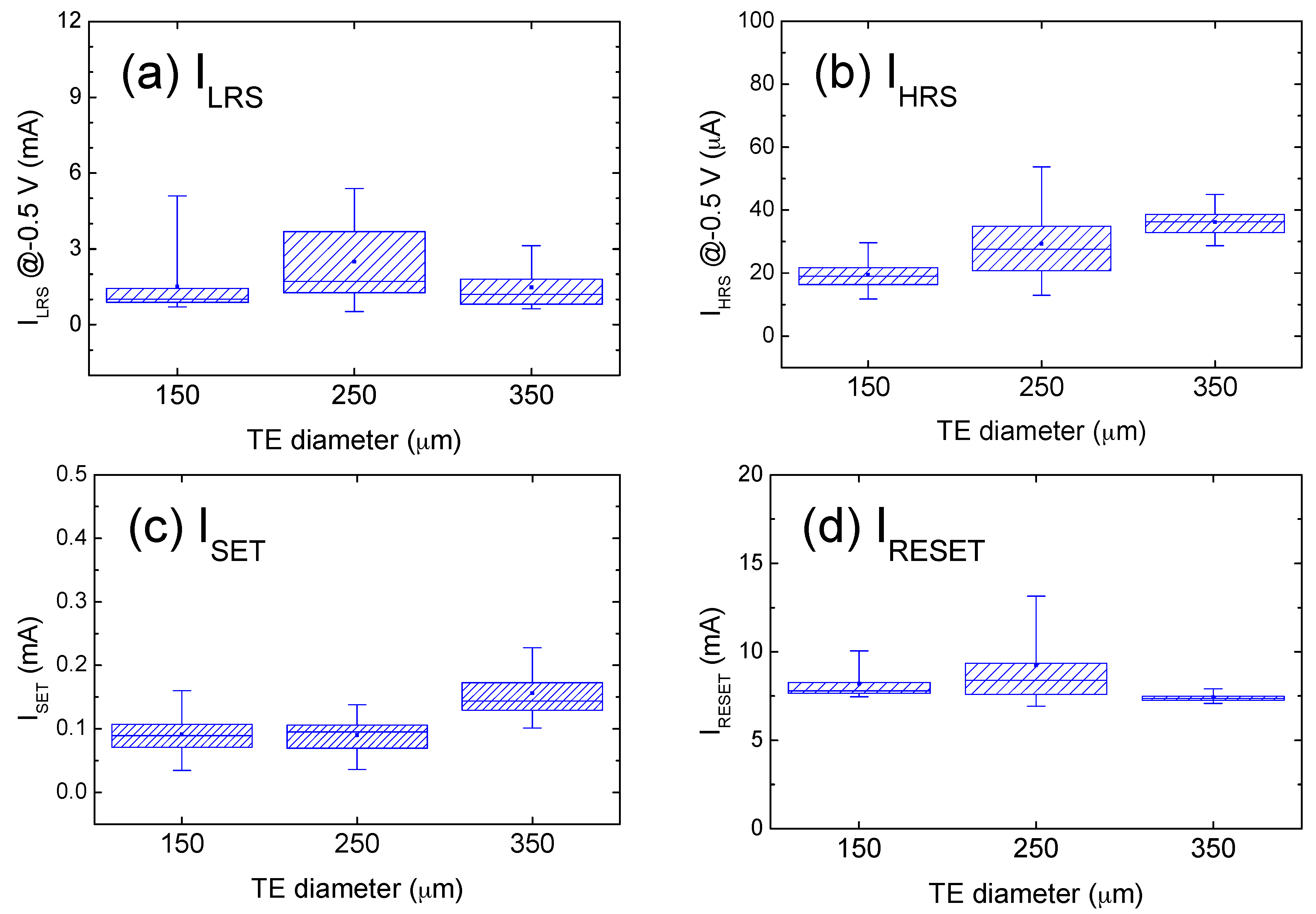
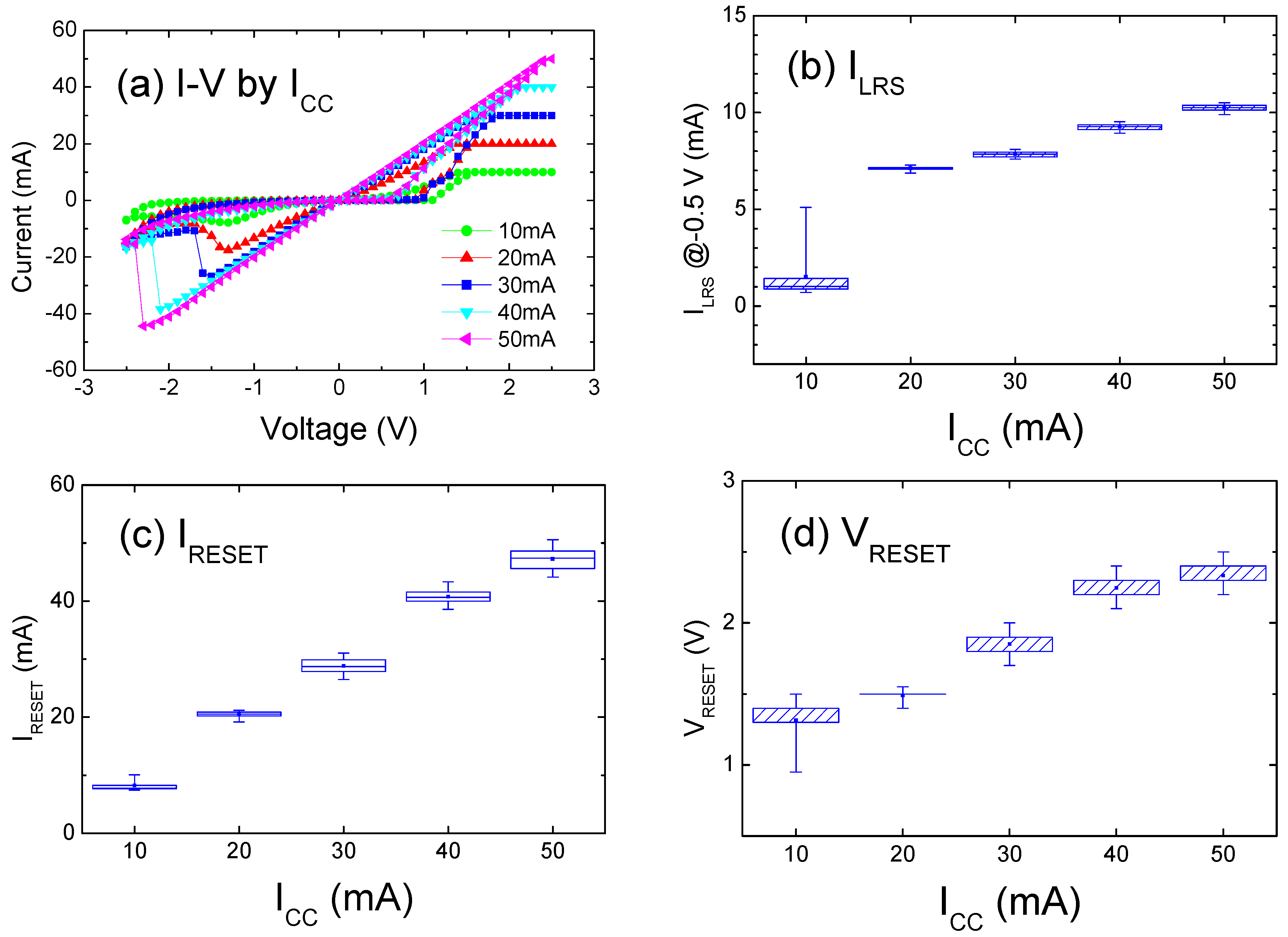
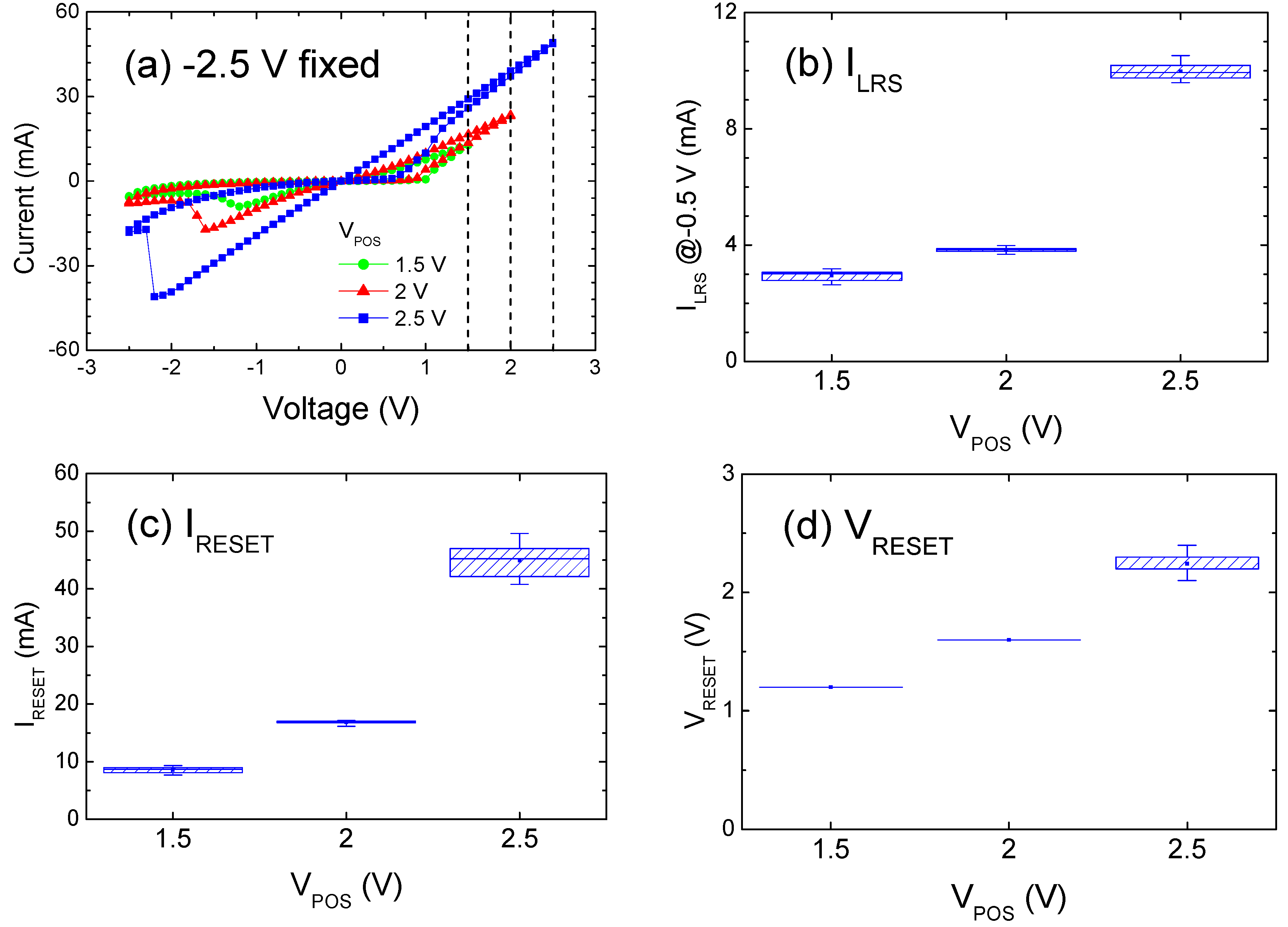
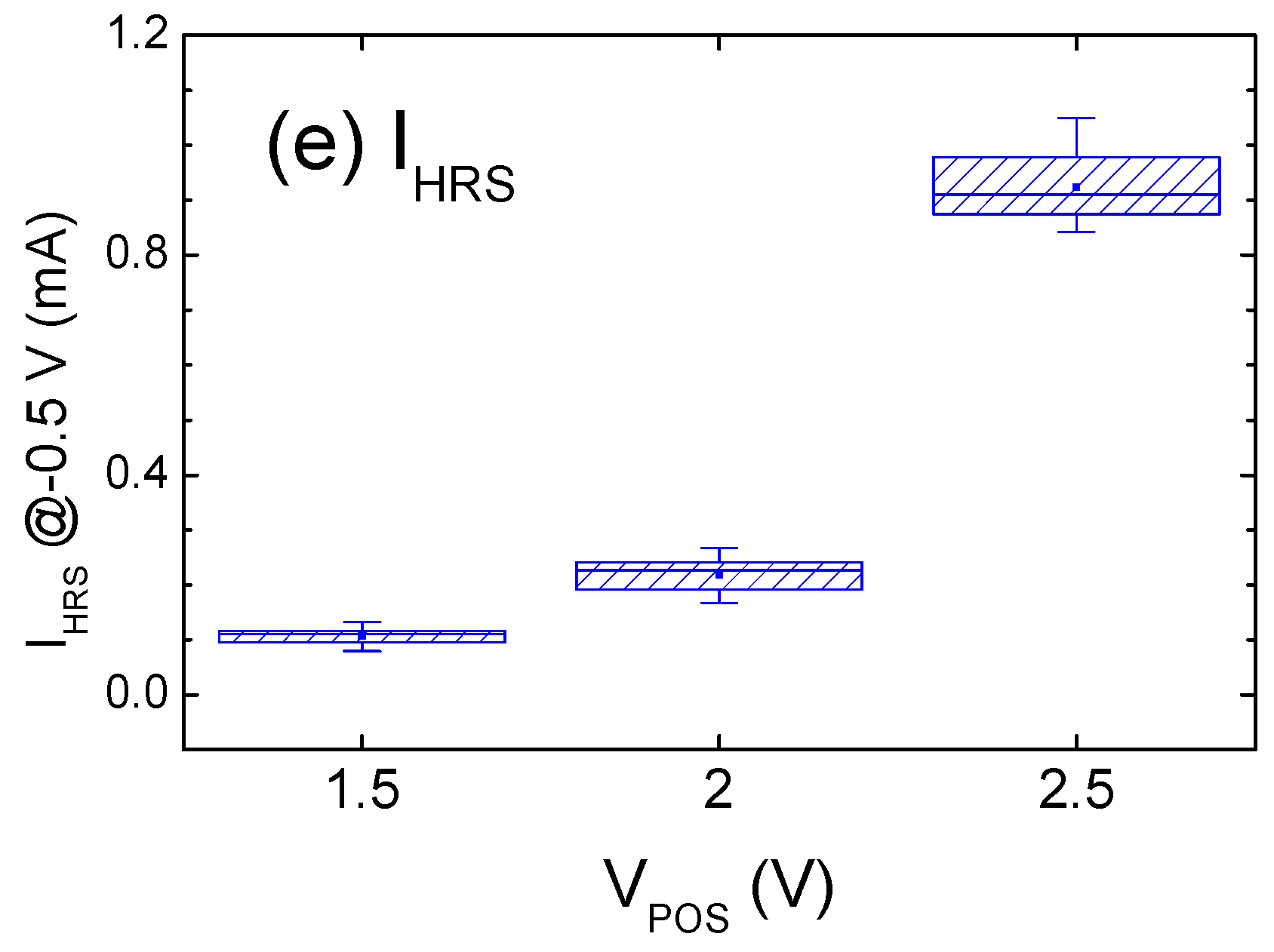
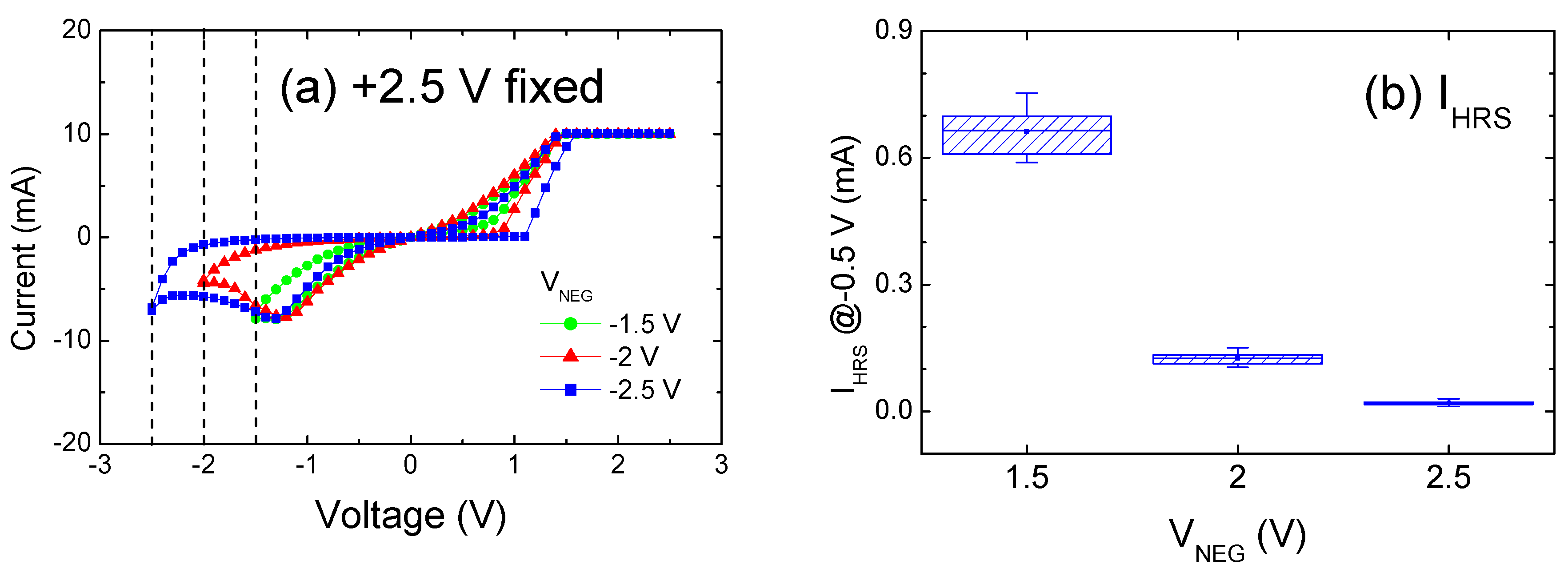
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, C.Y.; Wu, P.H.; Wang, A.; Jang, W.Y.; Young, J.C.; Chiu, K.Y.; Tseng, T.Y. Bistable resistive switching of a sputter-deposited Cr-doped SrZrO3 memory film. IEEE Electron Device Lett. 2005, 26, 351–353. [Google Scholar] [CrossRef]
- Jeong, D.S.; Schroeder, H.; Waser, R. Coexistence of bipolar and unipolar resistive switching behaviors in a Pt/TiO2/Pt stack. Electrochem. Solid State Lett. 2007, 10, G51–G53. [Google Scholar] [CrossRef]
- Goux, L.; Lisoni, J.G.; Jurczak, M.; Wouters, D.J.; Courtade, L.; Muller, Ch. Coexistence of the bipolar and unipolar resistive-switching modes in NiO cells made by thermal oxidation of Ni layers. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Park, J.; Yong, K. Coexistence of unipolar and bipolar resistive switching characteristics in ZnO thin films. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Lin, C.Y.; Wu, C.Y.; Wu, C.Y.; Tseng, T.Y. Modified resistive switching behavior of ZrO2 memory films based on the interface layer formed by using Ti top electrode. J. Appl. Phys. 2007, 102. [Google Scholar] [CrossRef]
- Govoreanu, B.; Kar, G.S.; Chen, Y.; Paraschiv, V.; Kubicek, S.; Fantini, A.; Radu, I.P.; Goux, L.; Clima, S.; Degraeve, R.; et al. 10 × 10 nm2 Hf/HfOX crossbar resistive RAM with excellent performance, reliability and low-energy operation. IEDM Tech. Dig. 2011, 31.6.1–31.6.4. [Google Scholar]
- Lee, M.-J.; Lee, C. B.; Lee, D.; Lee, S.R.; Chang, M.; Hur, J. H.; Kim, Y.-B.; Kim, C.-J.; Seo, D.H.; Seo, S.; et al. A fast, high-endurance and scalable non-volatile memory device made from asymmetric Ta2O5-X/TaO2-X bilayer structures. Nat. Mater. 2011, 10, 625–630. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.; Seo, H.; Kim, Y.; Im, H.; Hong, J.; Park, J.W.; Lee, J.K. Temperature dependence of high- and low-resistance bistable states in polycrystalline NiO films. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
- Chen, X.; Wu, N.J.; Strozier, J.; Ignatiev, A. Synthesis and magnetic properties of Fe3Pt nanowire arrays fabricated by electrodeposition. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Q.; Xie, H.; Wu, X.; Xu, F. In situ observation of nickel as an xxidizable electrode material for the solid-electrolyte-based resistive random access memory. Appl. Phys. Lett. 2013, 102. [Google Scholar] [CrossRef]
- Liu, C.Y.; Lin, X.J.; Wang, H.Y.; Lai, C.H. Improved resistive switching dispersion of NiOX thin film by Cu-doping method. Jap. J. Appl. Phys. 2010, 49. [Google Scholar] [CrossRef]
- Yoon, J.H.; Han, J.H.; Jung, J.S. Highly improved uniformity in the resistive switching parameters of TiO2 thin films by inserting Ru nanodots. Adv. Mater. 2013, 25, 1987–1992. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Fujita, S.; Wong, S.S. Reset mechanism of TiOX resistance-change memory device. IEEE Electron Device Lett. 2009, 30, 733–735. [Google Scholar] [CrossRef]
- Celano, U.; Goux, L.; Belmonte, A.; Giammaria, G.; Opsomer, K.; Detavernier, C.; Richard, O.; Bender, H.; Irrera, F.; Jurczak, M.; et al. Progressive vs. abrupt reset behavior in conductive bridging devices: A C-AFM tomography study. IEDM Tech. Dig. 2014, 14.1.1–14.1.4. [Google Scholar]
- Clima, S.; Sankaran, K.; Chen, Y.Y.; Fantini, A.; Celano, U.; Belmonte, A.; Zhang, L.; Goux, L.; Govoreanu, B.; Degraeve, R.; et al. RRAMs based on anionic and cationic switching: A short overview. Phys. Status Solid Rapid Res. Lett. 2014, 8, 501–511. [Google Scholar] [CrossRef]
- Jeong, D.S.; Schroeder, H.; Waser, R. Mechanism for bipolar switching in a Pt/TiO2/Pt resistive switching cell. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Rahaman, S.Z.; Maikap, S.; Chen, W.S.; Lee, H.Y.; Chen, F.T.; Tien, T.C.; Tsai, M.J. Impact of TaOX nanolayer at the GeSeX/W interface on resistive switching memory performance and investigation of Cu nanofilament. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Guan, W.; Long, S.; Liu, Q.; Liu, M.; Wang, W. Nonpolar nonvolatile resistive switching in Cu doped ZrO2. IEEE Electron Device Lett. 2008, 29, 434–437. [Google Scholar] [CrossRef]
- Rohde, C.; Choi, B.J.; Jeong, D.S.; Choi, S.; Zhao, J.S.; Hwang, C.S. Identification of a determining parameter for resistive switching of TiO2 thin films. Appl. Phys. Lett. 2005, 86. [Google Scholar] [CrossRef]
- Noh, J.; Jo, M.; Kang, C.Y.; Gilmer, D.; Kirsch, P.; Lee, J.C.; Lee, B.H. Development of a semiempirical compact model for DC/AC cell operation of HfOX-based ReRAMs. IEEE Electron Device Lett. 2013, 34, 1133–1135. [Google Scholar] [CrossRef]
- Wang, S.Y.; Huang, C.W.; Lee, D.Y.; Tseng, T.Y.; Chang, T.C. Multilevel resistive switching in Ti/CuXO/Pt memory devices. J. Appl. Phys. 2010, 108. [Google Scholar] [CrossRef]
- Wedig, A.; Luebben, M.; Cho, D.Y.; Moors, M.; Skaja, K.; Rana, V.; Hasegawa, T.; Adepalli, K.K.; Yildiz, B.; Waser, R.; et al. Nanoscale cation motion in TaOX, HfOX and TiOX memristive systems. Nat. Nanotechnol. 2016, 11, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Chen, C.; Zhai, Z.; Liu, H.Y.; Lin, Y.S.; Li, S.Z.; Lu, S.H.; Wang, G.Y.; Song, C.; Zeng, F.; et al. Resistive switching and conductance quantization in Ag/SiO2/indium tin oxide resistive memories. Appl. Phys. Lett. 2014, 105. [Google Scholar] [CrossRef]
- Tsuruoka, T.; Valov, I.; Tappertzhofen, S.; Hurk, J.; Hasegawa, T.; Waser, R.; Aono, M. Redox reactions at Cu,Ag/Ta2O5 interfaces and the effects of Ta2O5 film density on the forming process in atomic switch structures. Adv. Funct. Mater. 2015, 25, 6374–6381. [Google Scholar] [CrossRef]
- Choi, S.J.; Kim, K.H.; Park, G.S.; Bae, H.J.; Yang, W.Y.; Cho, S. Multibit operation of Cu/Cu-GeTe/W resistive memory device controlled by pulse voltage magnitude and width. IEEE Electron Device Lett. 2011, 32, 375–377. [Google Scholar] [CrossRef]
- Puglisi, F.M.; Larcher, L.; Bersuker, G.; Padovani, A.; Pavan, P. An empirical model for RRAM resistance in low- and high-resistance states. IEEE Electron Device Lett. 2013, 34, 387–389. [Google Scholar] [CrossRef]
- McWilliams, C.R.; Celinska, J.; Araujo, C.A.; Xue, K.H. Device characterization of correlated electron random access memories. J. Appl. Phys. 2011, 109. [Google Scholar] [CrossRef]
- Hu, W.; Chen, X.; Wu, G.; Lin, Y.; Qin, N.; Bao, D. Bipolar and tri-state unipolar resistive switching behaviors in Ag/ZnFe2O4/Pt memory devices. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Kumar, S.; Graves, C.E.; Strachan, J.P.; Grafals, E.M.; Kilcoyne, A.L.D.; Tyliszczak, T.; Weker, J.N.; Nishi, Y.; Williams, R.S. Direct observation of localized radial oxygen migration in functioning tantalum oxide memristors. Adv. Mater. 2016, 28, 2772–2776. [Google Scholar] [CrossRef] [PubMed]
- Celano, U.; Goux, L.; Degraeve, R.; Fantini, A.; Richard, O.; Bender, H.; Jurczak, M.; Vandervorst, W. Imaging the three-dimensional conductive channel in filamentary-based oxide resistive switching memory. Nano Lett. 2015, 15, 7970–7975. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Q.; Li, X.H.; Xu, H.Y.; Wang, W.; Yu, H.; Zhang, X.T.; Liu, Y.X.; Liu, Y.C. Effects of compliance currents on the formation and rupture of conducting filaments in unipolar resistive switching of CoO film. J. Phys. D Appl. Phys. 2010, 43. [Google Scholar] [CrossRef]
- Park, J.; Jo, M.; Lee, J.; Jung, S.; Kim, S.; Lee, W.; Shin, J.; Hwang, H. Improved switching uniformity and speed in filament-type RRAM using lightning rod effect. IEEE Electron Device Lett. 2011, 32, 63–65. [Google Scholar] [CrossRef]
- Long, S.; Lian, X.; Ye, T.; Cagli, C.; Perniola, L.; Miranda, E.; Liu, M.; Suñé, J. Cycle-to-cycle intrinsic reset satistics in HfO2-based unipolar RRAM devices. IEEE Electron Device Lett. 2013, 34, 623–625. [Google Scholar] [CrossRef]
- Liu, Q.; Long, S.; Lv, H.; Wang, W.; Niu, J.; Huo, Z.; Chen, J.; Liu, M. Controllable growth of nanoscale conductive filaments in solid-electrolyte-based ReRAM by using a metal nanocrystal covered bottom electrode. ACS Nano 2010, 4, 6162–6168. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Biju, K.P.; Jung, S.; Lee, W.; Lee, J.; Kim, S.; Park, S.; Shin, J.; Hwang, H. Multibit operation of TiOX-based ReRAM by schottky barrier height engineering. IEEE Electron Device Lett. 2011, 32, 476–478. [Google Scholar] [CrossRef]
- Yu, S.; Jeyasingh, R.; Wu, Y.; Wong, H.-S.P. AC conductance measurement and analysis of the conduction processes in HfOX based resistive switching memory. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
- Chen, M.C.; Chang, T.C.; Chiu, Y.C.; Chen, S.C.; Huang, S.Y.; Chang, K.C.; Tsai, T.M.; Yang, K.H.; Sze, S.M.; Tsai, M.J. The resistive switching characteristics in TaON films for nonvolatile memory applications. Thin Solid Films 2013, 528, 224–228. [Google Scholar] [CrossRef]
- Messerschmitt, F.; Kubicek, M.; Rupp, J.L.M. How does moisture affect the physical property of memristance for anionic–electronic resistive switching memories? Adv. Funct. Mater. 2015, 25, 5117–5125. [Google Scholar] [CrossRef]
- Lübben, M.; Karakolis, P.; Ioannou-Sougleridis, V.; Normand, P.; Dimitrakis, P.; Valov, I. Graphene-modified interface controls transition from VCM to ECM switching modes in Ta/TaOX based memristive devices. Adv. Mat. 2015, 27, 6202–6207. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, C.-H.; Chen, H.-W.; Liu, C.-Y. The Resistive Switching Characteristics in ZrO2 and Its Filamentary Conduction Behavior. Materials 2016, 9, 551. https://doi.org/10.3390/ma9070551
Lai C-H, Chen H-W, Liu C-Y. The Resistive Switching Characteristics in ZrO2 and Its Filamentary Conduction Behavior. Materials. 2016; 9(7):551. https://doi.org/10.3390/ma9070551
Chicago/Turabian StyleLai, Chun-Hung, Hung-Wei Chen, and Chih-Yi Liu. 2016. "The Resistive Switching Characteristics in ZrO2 and Its Filamentary Conduction Behavior" Materials 9, no. 7: 551. https://doi.org/10.3390/ma9070551
APA StyleLai, C.-H., Chen, H.-W., & Liu, C.-Y. (2016). The Resistive Switching Characteristics in ZrO2 and Its Filamentary Conduction Behavior. Materials, 9(7), 551. https://doi.org/10.3390/ma9070551





