A Reinvestigation of a Superhard Tetragonal sp3 Carbon Allotrope
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Structural Properties
3.2. Mechanical Properties
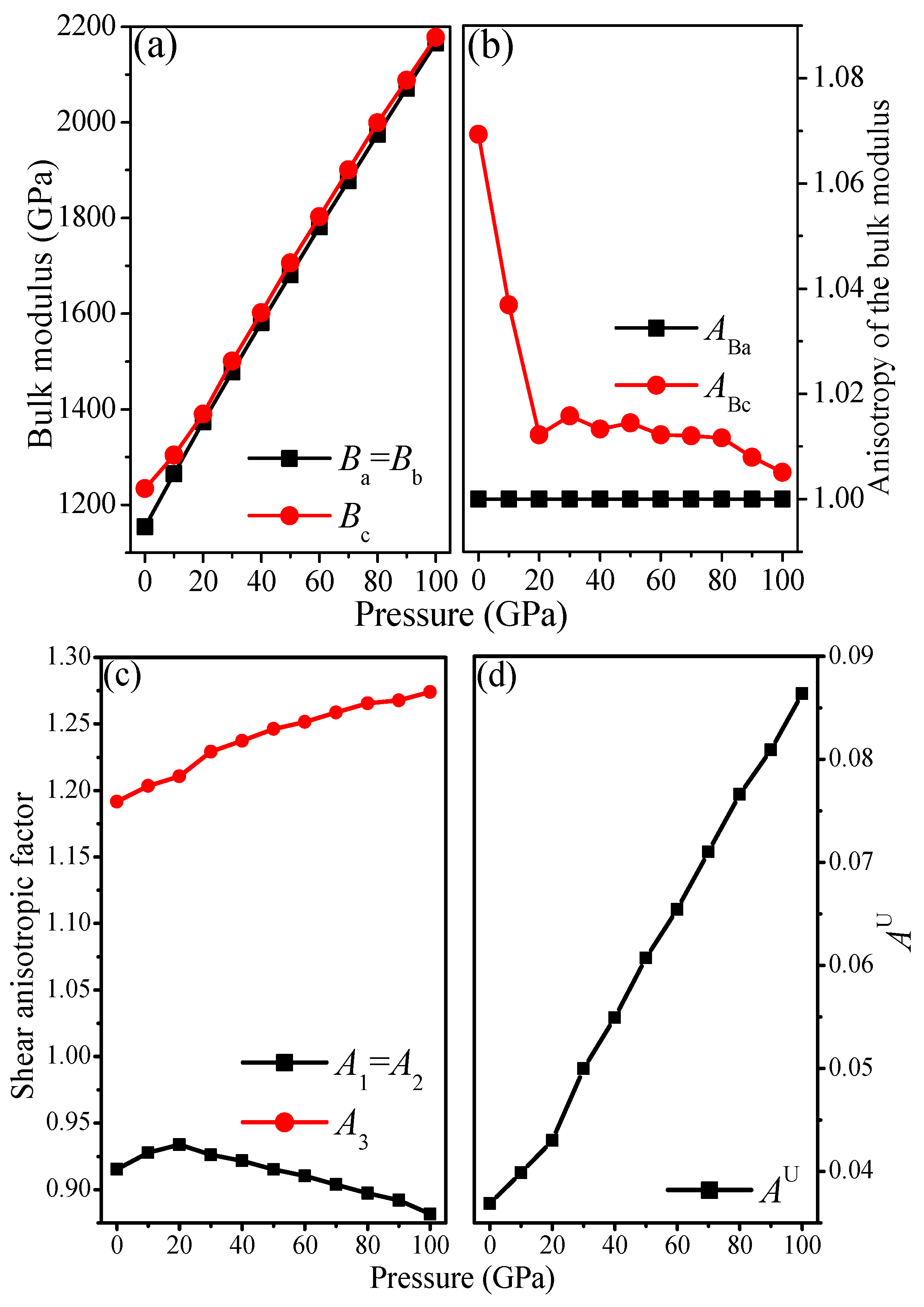
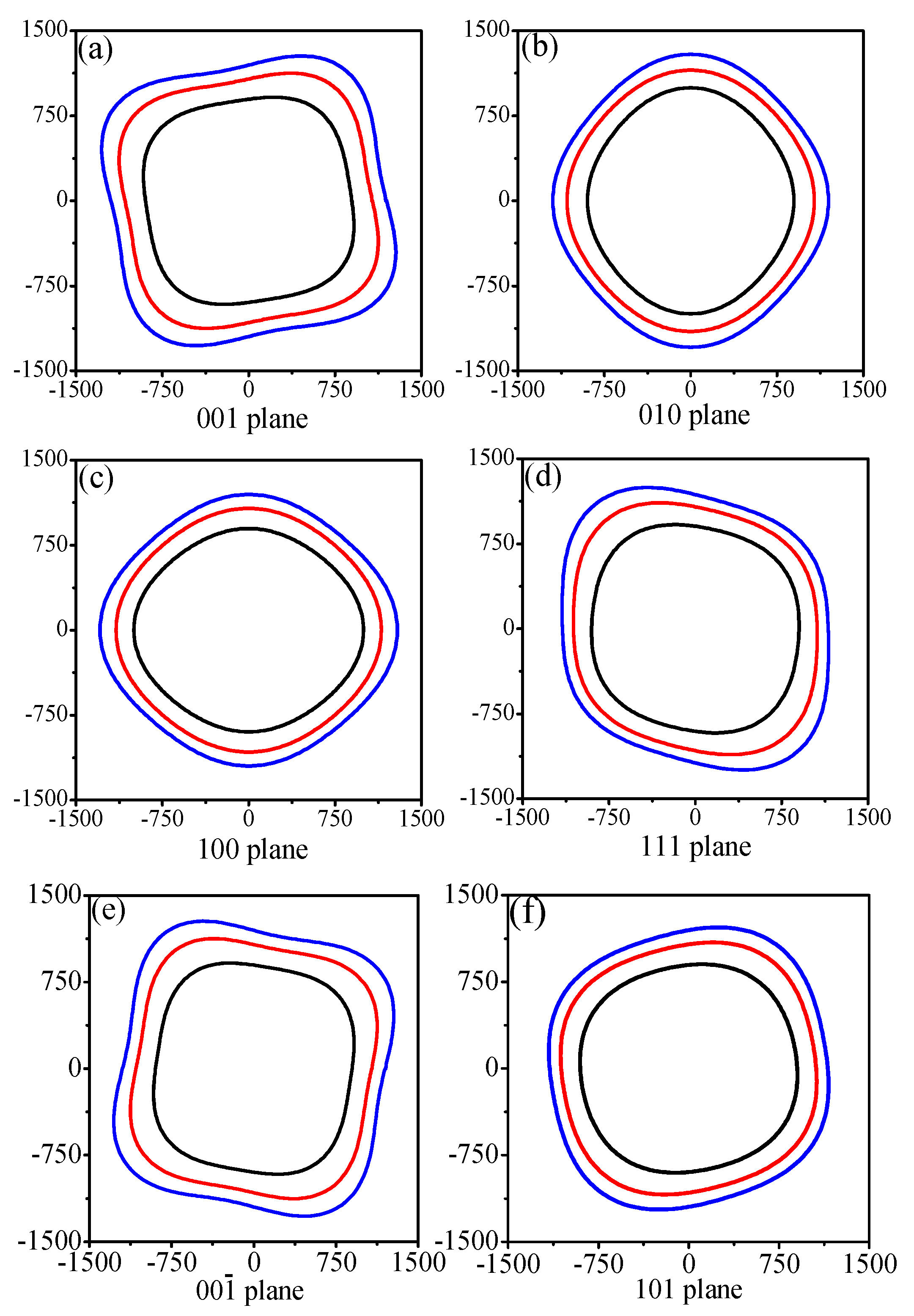
3.3. Anisotropic Properties
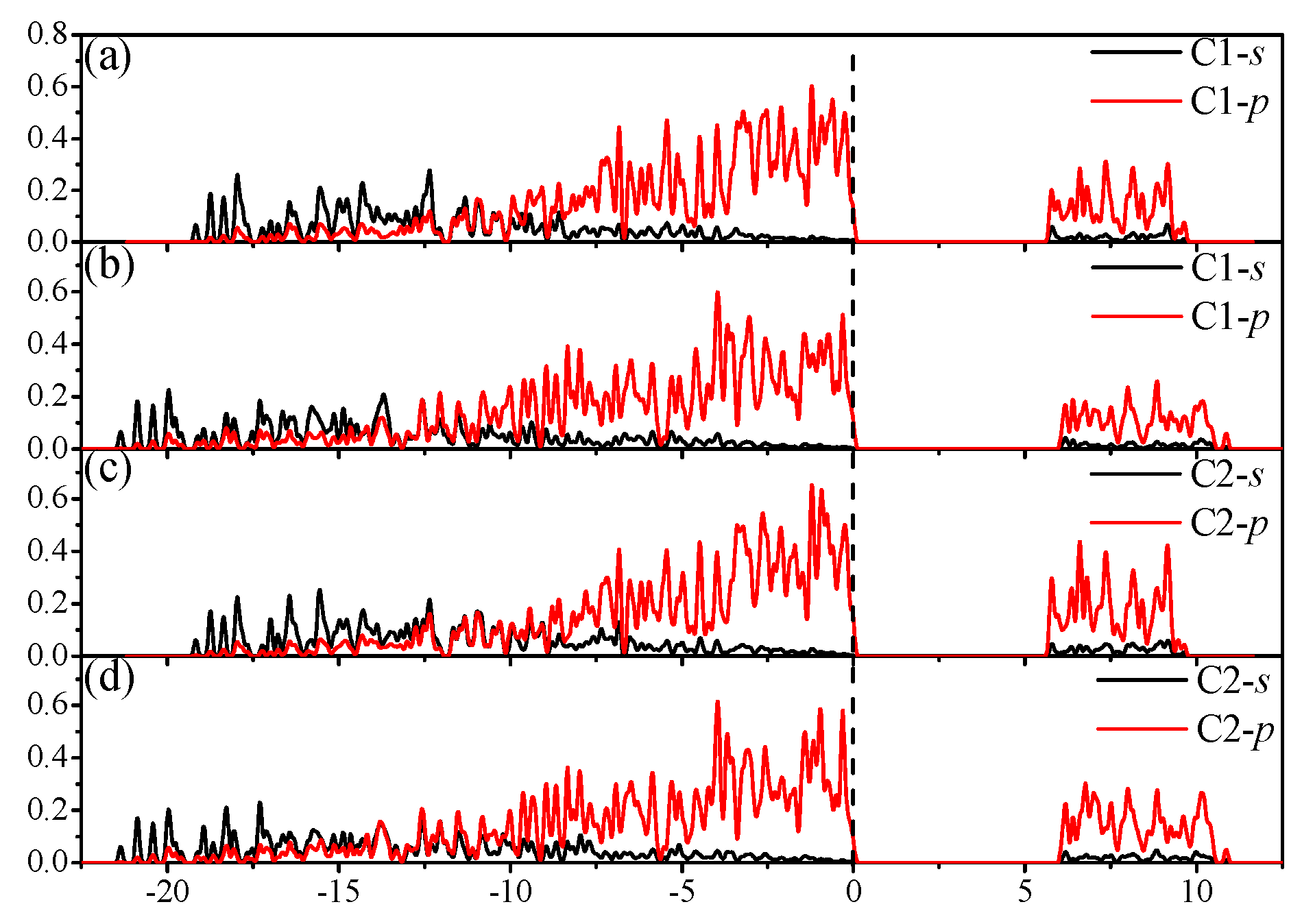
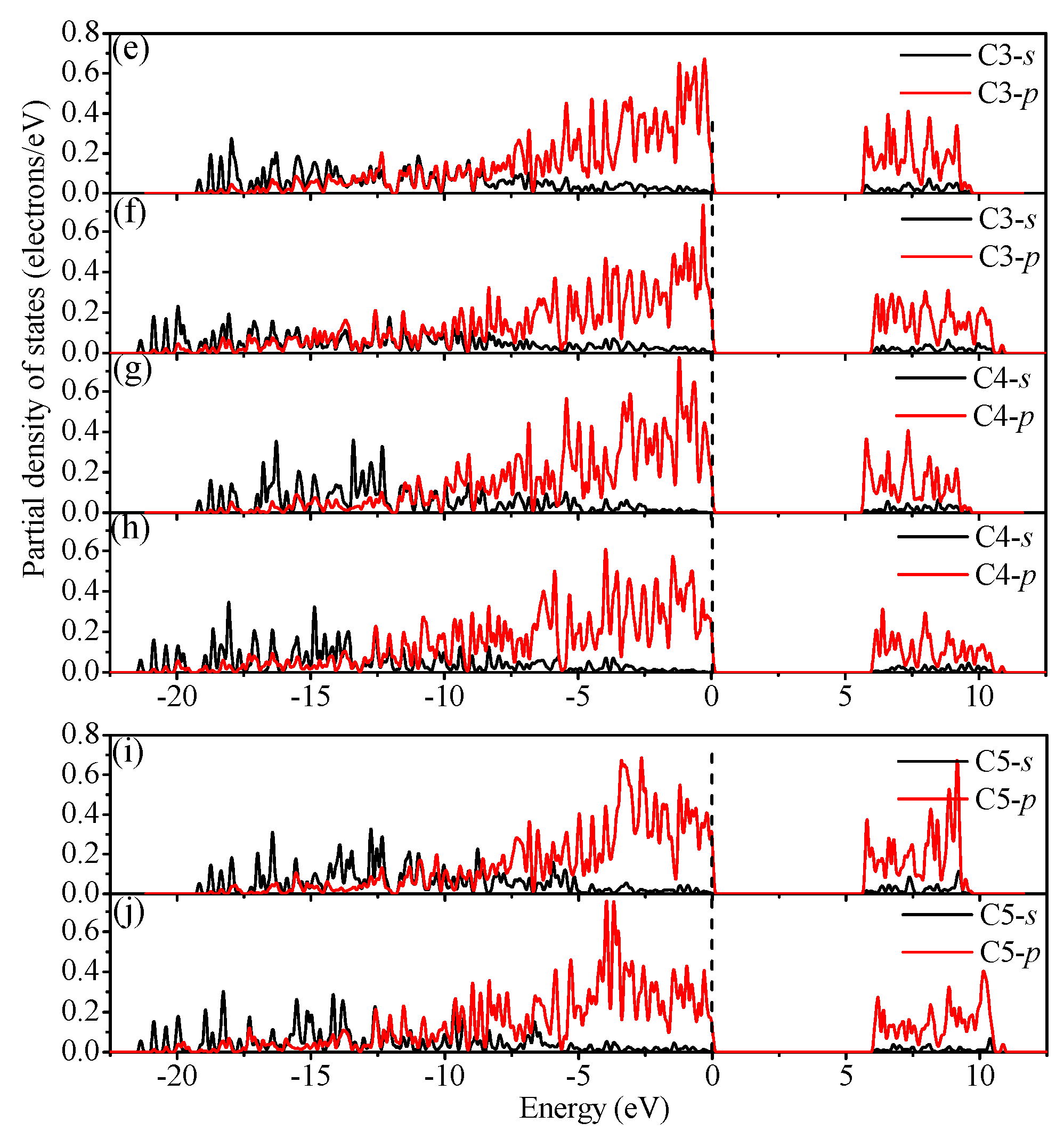
3.4. Electronic Properties
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Oganov, A.R.; Glass, C.W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 2006, 124, 244704. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Ma, Y.M.; Oganov, A.R.; Wang, H.B.; Wang, H.; Xu, Y.; Cui, T.; Mao, H.K.; Zou, G.T. Superhard Monoclinic Polymorph of Carbon. Phys. Rev. Lett. 2009, 102, 175506. [Google Scholar] [CrossRef] [PubMed]
- Tian, F.; Dong, X.; Zhao, Z.S.; He, J.L.; Wang, H.T. Superhard F-carbon predicted by ab initio particle-swarm optimization methodology. J. Phys. Condens. Matter 2012, 24, 165504. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.; Kawazoe, Y. Low-Temperature Phase Transformation from Graphite to sp3 Orthorhombic Carbon. Phys. Rev. Lett. 2011, 106, 075501. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.P.; Gao, F.M.; Xu, Z.M. Strength, hardness, and lattice vibrations of Z-carbon and W-carbon: First-principles calculations. Phys. Rev. B 2012, 85, 144115. [Google Scholar] [CrossRef]
- He, C.Y.; Sun, L.Z.; Zhang, C.X.; Peng, X.Y.; Zhang, K.W.; Zhong, J.X. New superhard carbon phases between graphite and diamond. Solid State Commun. 2012, 152, 1560–1563. [Google Scholar] [CrossRef]
- Li, D.; Bao, K.; Tian, F.B.; Zeng, Z.W.; He, Z.; Liu, B.B.; Cui, T. Lowest enthalpy polymorph of cold-compressed graphite phase. Phys. Chem. Chem. Phys. 2012, 14, 4347–4350. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Zhang, M.G.; Yan, H.Y.; Lin, Z.Z.; Zhu, X.M. Structural, electronic and mechanical properties of Imma-carbon. EPL 2014, 107, 27007. [Google Scholar] [CrossRef]
- Liu, Y.M.; Lu, M.C.; Zhang, M. First-principles study of a novel superhard sp3 carbon allotrope. Phys. Lett. A 2014, 378, 3326. [Google Scholar] [CrossRef]
- He, C.Y.; Zhong, J.X. M585, a low energy superhard monoclinic carbon phase. Solid State Commun. 2014, 181, 24–27. [Google Scholar] [CrossRef]
- Zhao, Z.S.; Tian, F.; Dong, X.; Li, Q.; Wang, Q.Q.; Wang, H.; Zhong, X.; Xu, B.; Yu, D.L.; He, J.L.; et al. Tetragonal Allotrope of Group 14 Elements. J. Am. Chem. Soc. 2012, 134, 12362–12365. [Google Scholar] [CrossRef] [PubMed]
- Xing, M.J.; Li, B.H.; Yu, Z.T.; Chen, Q. C2/m-carbon: Structural, mechanical, and electronic properties. J. Mater. Sci. 2015, 50, 7104–7114. [Google Scholar] [CrossRef]
- Xing, M.J.; Li, B.H.; Yu, Z.T.; Chen, Q. Structural, Elastic, and Electronic Properties of a New Phase of Carbon. Commun. Theor. Phys. 2015, 64, 237–243. [Google Scholar] [CrossRef]
- Zhao, Z.S.; Xu, B.; Zhou, X.F.; Wang, L.M.; Wen, B.; He, J.L.; Liu, Z.Y.; Wang, H.T.; Tian, Y.J. Novel Superhard Carbon: C-Centered Orthorhombic C8. Phys. Rev. Lett. 2011, 107, 215502. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.G.; Wang, Q.; Kawazoe, Y.; Jena, P. A New Silicon Phase with Direct Band Gap and Novel Optoelectronic Properties. Sci. Rep. 2015, 5, 14342. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yan, H.Y.; Zhao, Y.B.; Yang, Y.T.; Yu, X.H.; Liu, Y.; Xing, M.J.; Zhang, J.Q.; et al. Novel silicon allotropes: Stability, mechanical, and electronic properties. J. Appl. Phys. 2015, 118, 185704. [Google Scholar] [CrossRef]
- Lee, I.H.; Lee, J.Y.; Oh, Y.J.; Kim, S.; Chang, K.J. Computational search for direct band gap silicon crystals. Phys. Rev. B 2014, 90, 115209. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Chai, C.C.; Wei, Q.; Yang, Y.T.; Yang, Q.; Chen, P.Y.; Xing, M.J.; Zhang, J.Q.; Yao, R.H. Prediction of novel phase of silicon and Si–Ge alloys. J. Solid State Chem. 2016, 233, 471–483. [Google Scholar] [CrossRef]
- De, A.; Pryor, C.E. Electronic structure and optical properties of Si, Ge and diamond in the lonsdaleite phase. J. Phys. Condens. Matter 2014, 26, 045801. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.Q.; Xu, B.; Sun, J.; Liu, H.Y.; Zhao, Z.S.; Yu, D.L.; Fan, C.Z.; He, J.L. Direct Band Gap Silicon Allotropes. J. Am. Chem. Soc. 2014, 136, 9826–9829. [Google Scholar] [CrossRef] [PubMed]
- Sheng, X.L.; Yan, Q.B.; Ye, F.; Zheng, Q.R.; Su, G. T-Carbon: A Novel Carbon Allotrope. Phys. Rev. Lett. 2011, 106, 155703. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.Y.; Kim, B.G. Carbon allotropes with triple bond predicted by first-principle calculation: Triple bond modified diamond and T-carbon. Phys. Rev. B 2012, 86, 075151. [Google Scholar] [CrossRef]
- Srinivasu, K.; Ghosh, S.K. Electronic Structure, Optical Properties, and Hydrogen Adsorption Characteristics of Supercubane-Based Three-Dimensional Porous Carbon. J. Phys. Chem. C 2012, 116, 25015. [Google Scholar] [CrossRef]
- Li, D.; Tian, F.B.; Duan, D.F.; Zhao, Z.L.; Liu, Y.X.; Chu, B.H.; Sha, X.J.; Wang, L.; Liu, B.B.; Cui, T. Modulated T carbon-like carbon allotropes: An ab initio study. RSC Adv. 2014, 4, 17364–17369. [Google Scholar] [CrossRef]
- Martoňák, R.; Oganov, A.R.; Glass, C.W. Crystal structure prediction and simulations of structural transformations: Metadynamics and evolutionary algorithms. Phase Transit. 2007, 80, 277–298. [Google Scholar] [CrossRef]
- Zhu, Q.; Oganov, A.R.; Lyakhov, A.O. Evolutionary metadynamics: A novel method to predict crystal structures. Crystengcomm 2012, 14, 3596–3601. [Google Scholar] [CrossRef]
- Boulfelfel, S.E.; Zhu, Q.; Oganov, A.R. Novel sp3 forms of carbon predicted by evolutionary metadynamics and analysis of their synthesizability using transition path sampling. J. Superhard Mater. 2012, 34, 350–359. [Google Scholar] [CrossRef]
- Finkelstein, G.J.; Dera, P.K.; Jahn, S.; Oganov, A.R.; Holl, C.M.; Meng, Y.; Duffy, T.S. Phase transitions and equation of state of forsterite to 90 GPa from single-crystal X-ray diffraction and molecular modelling. Am. Mineral. 2014, 99, 35–43. [Google Scholar] [CrossRef]
- Oganov, A.R.; Glass, C.W. Evolutionary crystal structure prediction as a tool in materials design. J. Phys. Condens. Matter 2008, 20, 064210. [Google Scholar] [CrossRef] [PubMed]
- Oganov, A.R.; Ma, Y.M.; Lyakhov, A.O.; Valle, M.; Gatti, C. Evolutionary Crystal Structure Prediction as a Method for the Discovery of Minerals and Materials. Theor. Comput. Methods Miner. Phys. Geophys. Appl. Rev. Miner. Geochem. 2010, 71, 271–298. [Google Scholar] [CrossRef]
- Oganov, A.R.; Lyakhov, A.O.; Valle, M. How Evolutionary Crystal Structure Prediction Works—And Why. Accounts Chem. Res. 2011, 44, 227–237. [Google Scholar] [CrossRef] [PubMed]
- Lyakhov, A.O.; Oganov, A.R.; Stokes, H.T.; Zhu, Q. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 2013, 184, 1172–1182. [Google Scholar] [CrossRef]
- Selli, D.; Baburin, I.A.; Martonák, R.; Leoni, S. Superhard sp3 carbon allotropes with odd and even ring topologies. Phys. Rev. B 2011, 84, 161411. [Google Scholar] [CrossRef]
- Amsler, M.; Flores-Livas, J.A.; Lehtovaara, L.; Balima, F.; Ghasemi, S.A.; Machon, D.; Pailhès, S.; Willand, A.; Caliste, D.; Botti, S.; et al. Crystal Structure of Cold Compressed Graphite. Phys. Rev. Lett. 2012, 108, 065501. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.; Kawazoe, Y. Orthorhombic carbon allotrope of compressed graphite: Ab initio calculations. Phys. Rev. B 2012, 85, 033410. [Google Scholar] [CrossRef]
- He, C.Y.; Sun, L.Z.; Zhang, C.X.; Zhong, J.X. Two viable three-dimensional carbon semiconductors with an entirely sp2 configuration. Phys. Chem. Chem. Phys. 2013, 15, 680–684. [Google Scholar] [CrossRef] [PubMed]
- He, C.Y.; Sun, L.Z.; Zhang, C.X.; Peng, X.Y.; Zhang, K.W.; Zhong, J.X. Four superhard carbon allotropes: A first-principles study. Phys. Chem. Chem. Phys. 2012, 14, 8410–8414. [Google Scholar] [CrossRef] [PubMed]
- Kvashnina, Y.A.; Kvashnin, A.G.; Sorokin, P.B. Investigation of new superhard carbon allotropes with promising electronic properties. J. Appl. Phys. 2013, 114, 183708. [Google Scholar] [CrossRef]
- Xie, H.X.; Yin, F.X.; Yu, T. Mechanism for direct graphite-to-diamond phase transition. Sci. Rep. 2014, 4, 5930. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.T.; Chen, C.F.; Kawazoe, Y. Phase conversion from graphite toward a simple monoclinic sp3-carbon allotrope. J. Chem. Phys. 2012, 137, 024502. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Zeng, X.C. Polymorphic Phases of sp3-hybridized carbon under cold compression. J. Am. Chem. Soc. 2012, 134, 7530–7538. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Tian, F.B.; Chu, B.H.; Duan, D.F.; Wei, S.L.; Lv, Y.Z.; Zhang, H.D.; Wang, L.; Lu, N.; Liu, B.B.; et al. Cubic C96: A novel carbon allotrope with a porous nanocube network. J. Mater. Chem. A 2015, 3, 10448–10452. [Google Scholar] [CrossRef]
- Fitzgibbons, T.C.; Guthrie, M.; Xu, E.S.; Crespi, V.H.; Davidowski, S.K.; Cody, G.D.; Alem, N.; Badding, J.V. Benzene-derived carbon nanothreads. Nat. Mater. 2015, 14, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Zhan, H.F.; Zhang, G.; Tan, V.B.C.; Cheng, Y.; Bell, J.M.; Zhang, Y.W.; Gu, Y.T. From Brittle to Ductile: A Structure Dependent Ductility of Diamond Nanothread. Nanoscale 2016, 8, 11177–11184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.X.; Wang, Y.C.; Lv, J.; Zhu, C.Y.; Li, Q.; Zhang, M.; Li, Q.; Ma, Y.M. First-principles structural design of superhard materials. J. Chem. Phys. 2013, 138, 114101. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892R. [Google Scholar] [CrossRef]
- Pfrommer, B.G.; Côté, M.; Louie, S.G.; Cohen, M.L. Relaxation of crystals with the quasi-newton method. J. Comput. Phys. 1997, 131, 233–240. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Lyakhov, A.O.; Oganov, A.R. Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 2011, 84, 092103. [Google Scholar] [CrossRef]
- Wu, Z.J.; Zhao, E.J.; Xiang, H.P.; Hao, X.F.; Liu, X.J.; Meng, J. Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 2007, 76, 054115. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. Ser. 7 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Wang, W.H.; Greer, A.L. Intrinsic plasticity or brittleness of metallic glasses. Philos. Mag. Lett. 2005, 85, 77–87. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Panda, K.B.; Ravi, K.S. Determination of elastic constants of titanium diboride (TiB2) from first principles using FLAPW implementation of the density functional theory. Comput. Mater. Sci. 2006, 35, 134–150. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Yan, H.Y.; Zhang, M.G.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Elastic and electronic properties of Pbca-BN: First-principles calculations. Comput. Mater. Sci. 2014, 85, 80–87. [Google Scholar] [CrossRef]
- Connetable, D.; Thomas, O. First-principles study of the structural, electronic, vibrational, and elastic properties of orthorhombic NiSi. Phys. Rev. B 2009, 79, 094101. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.D.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Wei, Q.; Chai, C.C.; Yan, H.Y.; Zhang, M.G.; Lin, Z.Z.; Zhang, Z.X.; Zhang, J.Q.; Zhang, D.Y. Structural, mechanical, and electronic properties of P3m1-BCN. J. Phys. Chem. Solids 2015, 79, 89–96. [Google Scholar] [CrossRef]
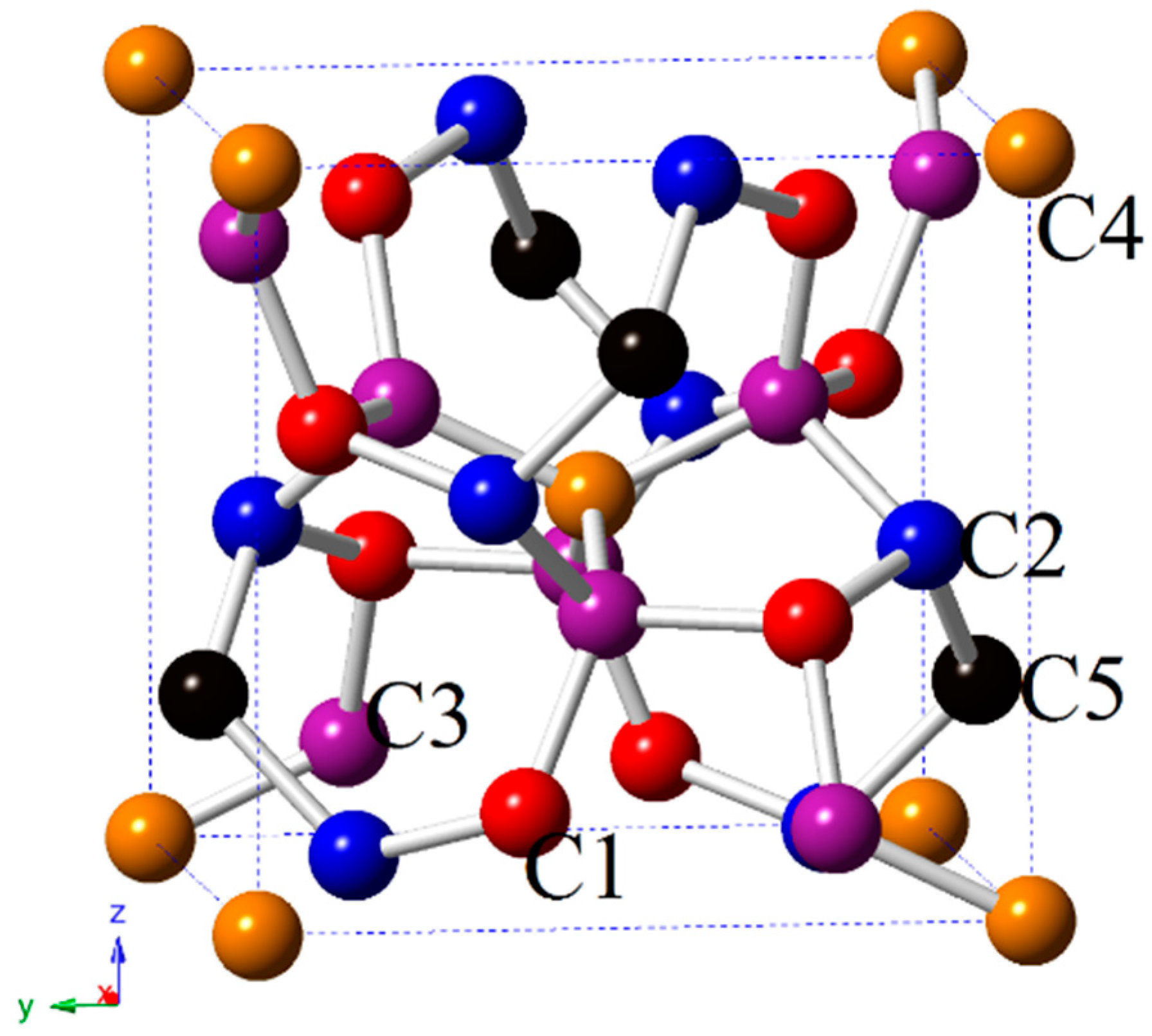
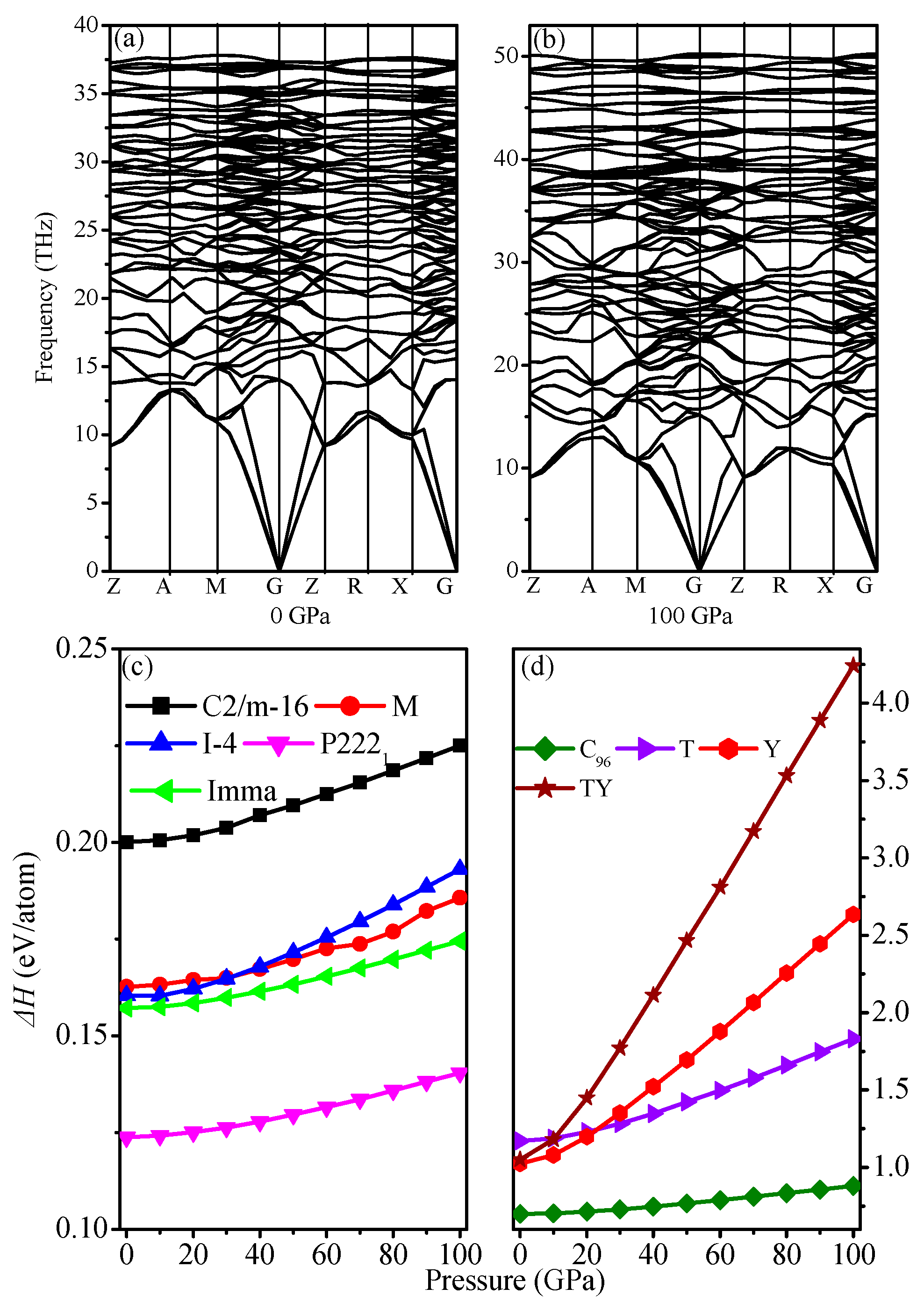
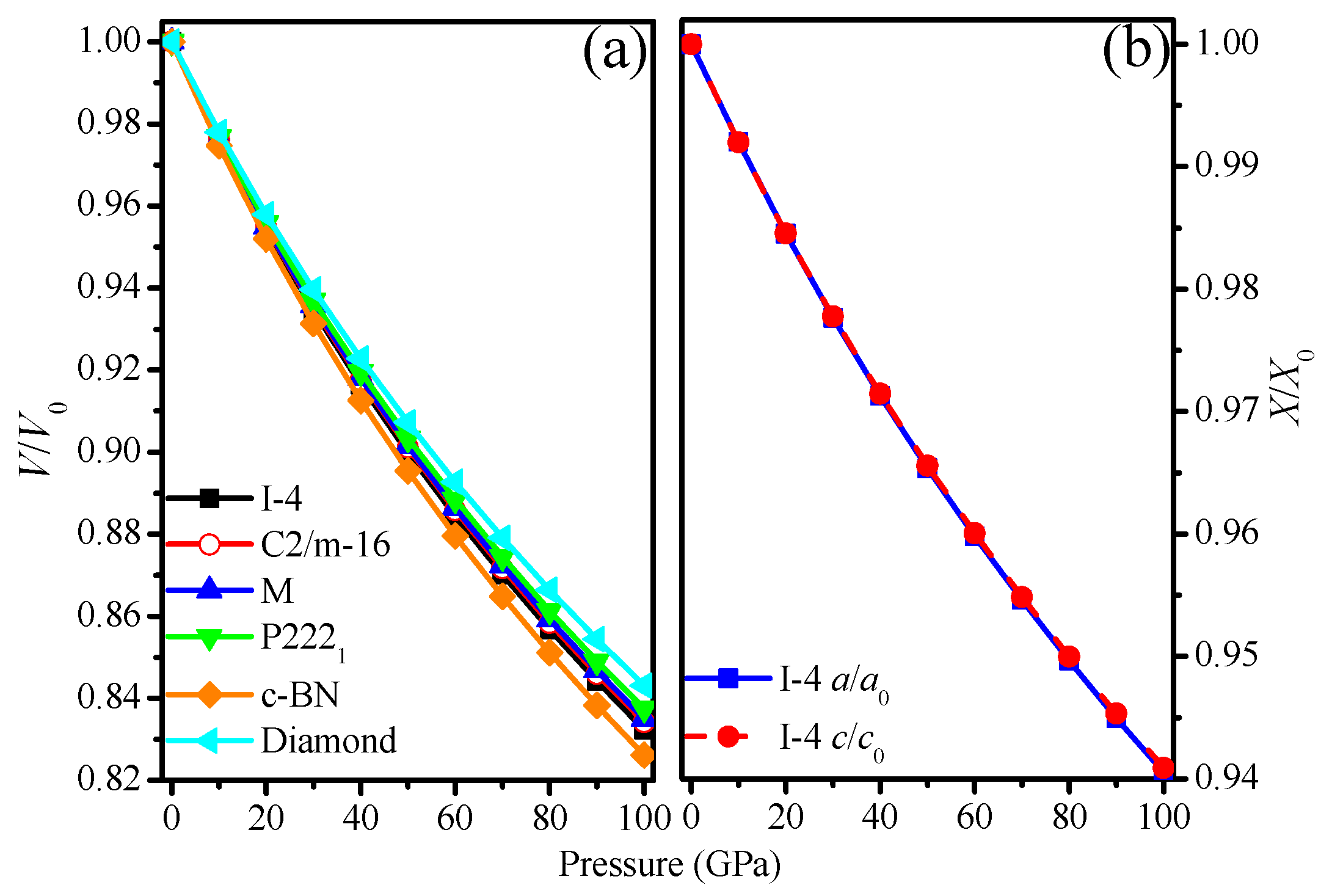

| Methods | a | c | dC1-C2 | dC1-C3 | dC2-C3 | dC2-C5 | dC3-C4 |
|---|---|---|---|---|---|---|---|
| GGA | 5.5628 | 5.5082 | 1.5586 | 1.5555 | 1.5694 | 1.5871 | 1.5430 |
| 1.5224 | 1.5207 | ||||||
| LDA | 5.5017 | 5.4471 | 1.5435 | 1.5408 | 1.5531 | 1.5683 | 1.5253 |
| 1.5036 | 1.5039 |
| P | C11 | C12 | C13 | C16 | C33 | C44 | C66 | B | G |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 926 | 133 | 101 | −28 | 1017 | 398 | 472 | 393 | 421 |
| 10 | 1015 | 175 | 142 | −35 | 1028 | 408 | 493 | 441 | 434 |
| 20 | 1034 | 189 | 153 | −40 | 1081 | 422 | 511 | 460 | 446 |
| 30 | 1079 | 220 | 182 | −43 | 1132 | 428 | 528 | 495 | 455 |
| 40 | 1128 | 248 | 208 | −46 | 1181 | 436 | 544 | 529 | 466 |
| 50 | 1174 | 274 | 235 | −49 | 1229 | 442 | 559 | 563 | 475 |
| 60 | 1220 | 304 | 261 | −53 | 1275 | 449 | 573 | 596 | 484 |
| 70 | 1263 | 332 | 287 | −56 | 1320 | 454 | 586 | 629 | 491 |
| 80 | 1306 | 360 | 303 | −59 | 1364 | 458 | 598 | 661 | 499 |
| 90 | 1347 | 387 | 340 | −62 | 1403 | 462 | 608 | 692 | 504 |
| 100 | 1383 | 419 | 366 | −63 | 1441 | 461 | 614 | 723 | 507 |
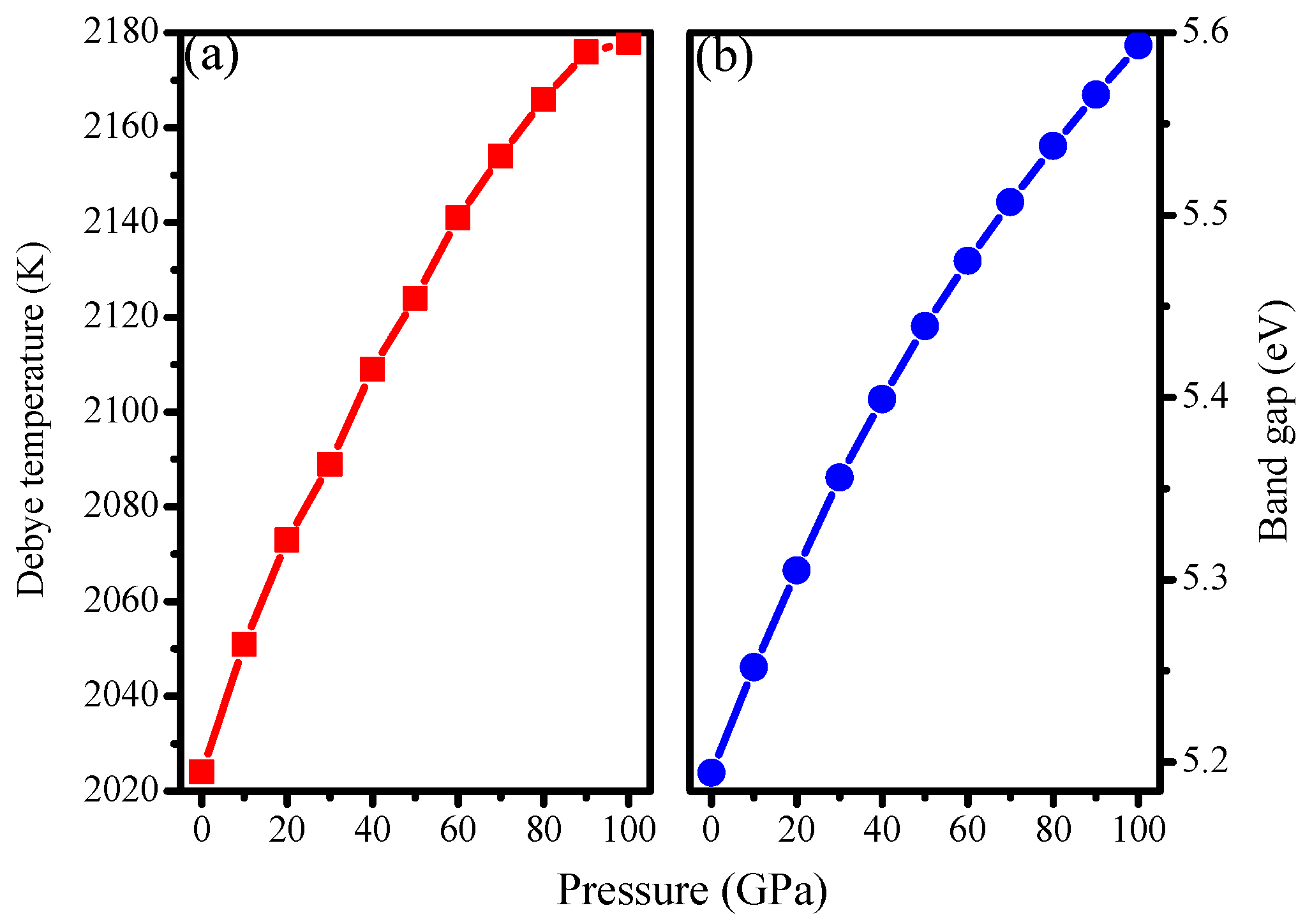
| P | ρ | vl | vt | vm | ΘD |
|---|---|---|---|---|---|
| 0 | 3.2764 | 17,069 | 11,336 | 12,398 | 2024 |
| 10 | 3.3564 | 17,434 | 11,373 | 12,467 | 2051 |
| 20 | 3.4332 | 17,529 | 11,402 | 12,503 | 2073 |
| 30 | 3.5059 | 17,730 | 11,395 | 12,513 | 2089 |
| 40 | 3.5750 | 17,939 | 11,415 | 12,549 | 2109 |
| 50 | 3.6412 | 18124 | 11417 | 12566 | 2124 |
| 60 | 3.7045 | 18303 | 11427 | 12589 | 2141 |
| 70 | 3.7654 | 18465 | 11424 | 12598 | 2154 |
| 80 | 3.8243 | 18617 | 11417 | 12602 | 2166 |
| 90 | 3.8814 | 18751 | 11400 | 12594 | 2176 |
| 100 | 3.9365 | 18852 | 11345 | 12547 | 2178 |
| Plane | P | Maximum | Minimum | Emax/Emin |
|---|---|---|---|---|
| (001) | 0 | 999 | 887 | 1.126 |
| 50 | 1250 | 1054 | 1.186 | |
| 100 | 1427 | 1168 | 1.222 | |
| (010) | 0 | 998 | 889 | 1.123 |
| 50 | 1153 | 1053 | 1.095 | |
| 100 | 1292 | 1150 | 1.123 | |
| (100) | 0 | 998 | 889 | 1.123 |
| 50 | 1153 | 1053 | 1.095 | |
| 100 | 1292 | 1150 | 1.123 | |
| (111) | 0 | 992 | 888 | 1.117 |
| 50 | 1233 | 1045 | 1.180 | |
| 100 | 1402 | 1139 | 1.231 | |
| () | 0 | 999 | 887 | 1.126 |
| 50 | 1250 | 1054 | 1.186 | |
| 100 | 1427 | 1168 | 1.222 | |
| (101) | 0 | 949 | 885 | 1.072 |
| 50 | 1160 | 1050 | 1.105 | |
| 100 | 1298 | 1147 | 1.132 | |
| All | 0 | 999 | 882 | 1.133 |
| 50 | 1250 | 1042 | 1.200 | |
| 100 | 1427 | 1138 | 1.254 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, M.; Li, B.; Yu, Z.; Chen, Q. A Reinvestigation of a Superhard Tetragonal sp3 Carbon Allotrope. Materials 2016, 9, 484. https://doi.org/10.3390/ma9060484
Xing M, Li B, Yu Z, Chen Q. A Reinvestigation of a Superhard Tetragonal sp3 Carbon Allotrope. Materials. 2016; 9(6):484. https://doi.org/10.3390/ma9060484
Chicago/Turabian StyleXing, Mengjiang, Binhua Li, Zhengtao Yu, and Qi Chen. 2016. "A Reinvestigation of a Superhard Tetragonal sp3 Carbon Allotrope" Materials 9, no. 6: 484. https://doi.org/10.3390/ma9060484
APA StyleXing, M., Li, B., Yu, Z., & Chen, Q. (2016). A Reinvestigation of a Superhard Tetragonal sp3 Carbon Allotrope. Materials, 9(6), 484. https://doi.org/10.3390/ma9060484





