Contrastive Numerical Investigations on Thermo-Structural Behaviors in Mass Concrete with Various Cements
Abstract
:1. Introduction
2. Thermo-Chemical-Mechanical Coupled Model
2.1. Conventional Method for Concrete Hydration Heat and Elastic Modulus Estimation
2.2. Long-Term Hydration Model
2.3. Transient Heat Transfer Process
2.4. Thermal-Creep Stress Calculation
2.4.1. Shrinkage
2.4.2. Creep
2.4.3. Thermal Strain
2.5. Thermal and Mechanical Characteristics
2.5.1. Heat Capacity
2.5.2. Thermal Conductivity
2.5.3. Aging Degree
2.5.4. Compressive and Tensile Strength
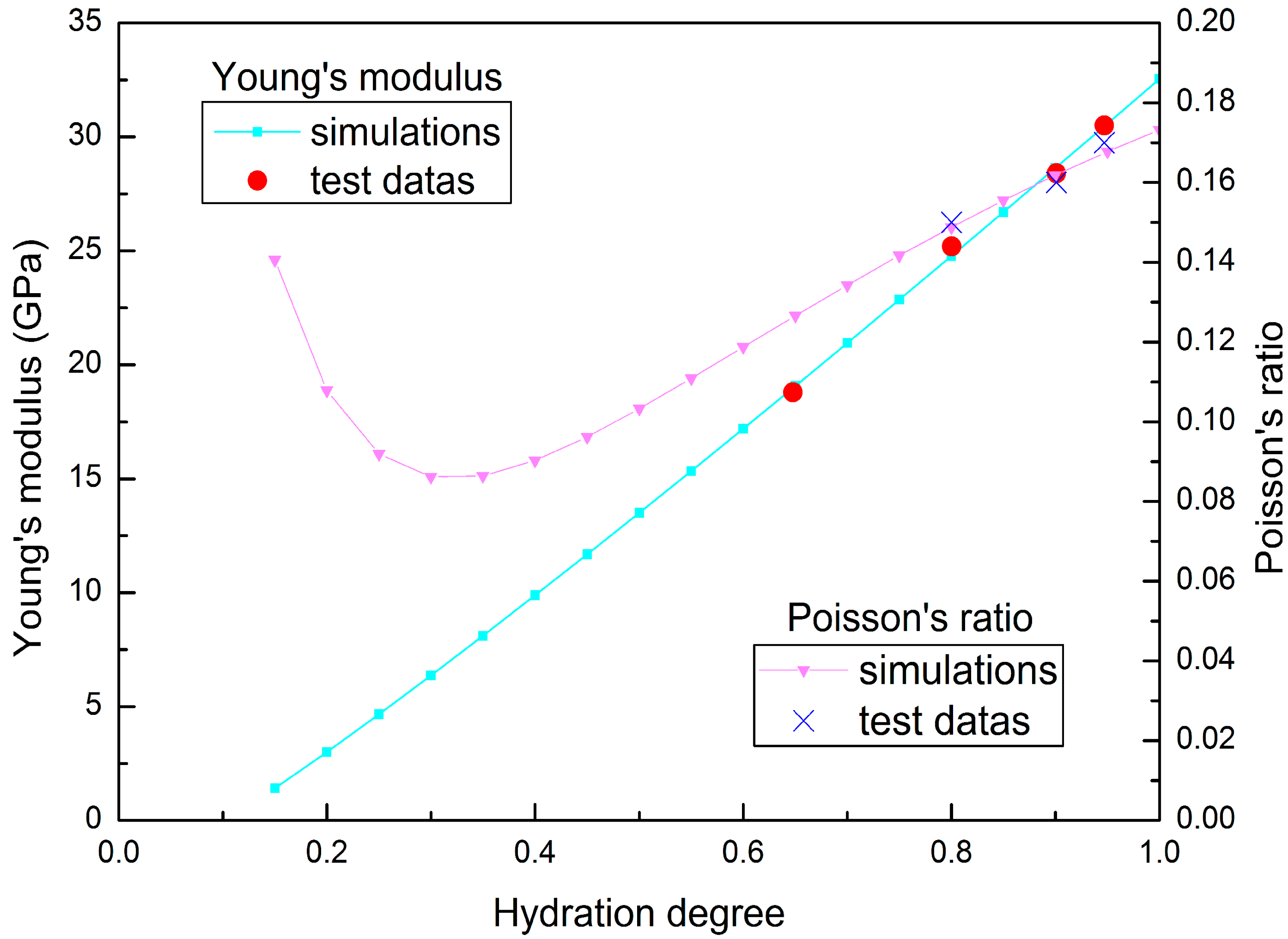
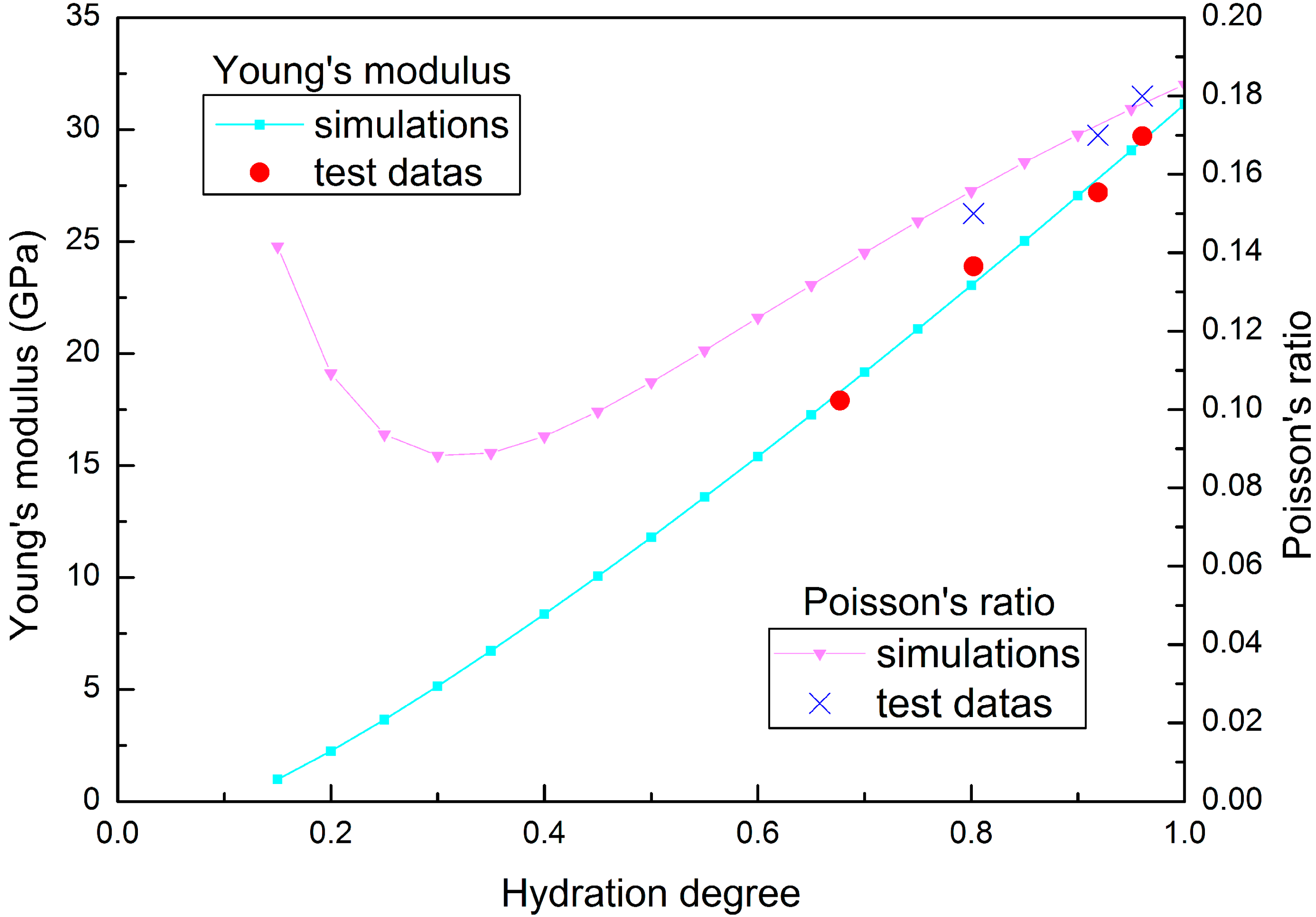
2.5.5. Young’s Modulus
2.5.6. Poisson’s Ratio
3. Validation
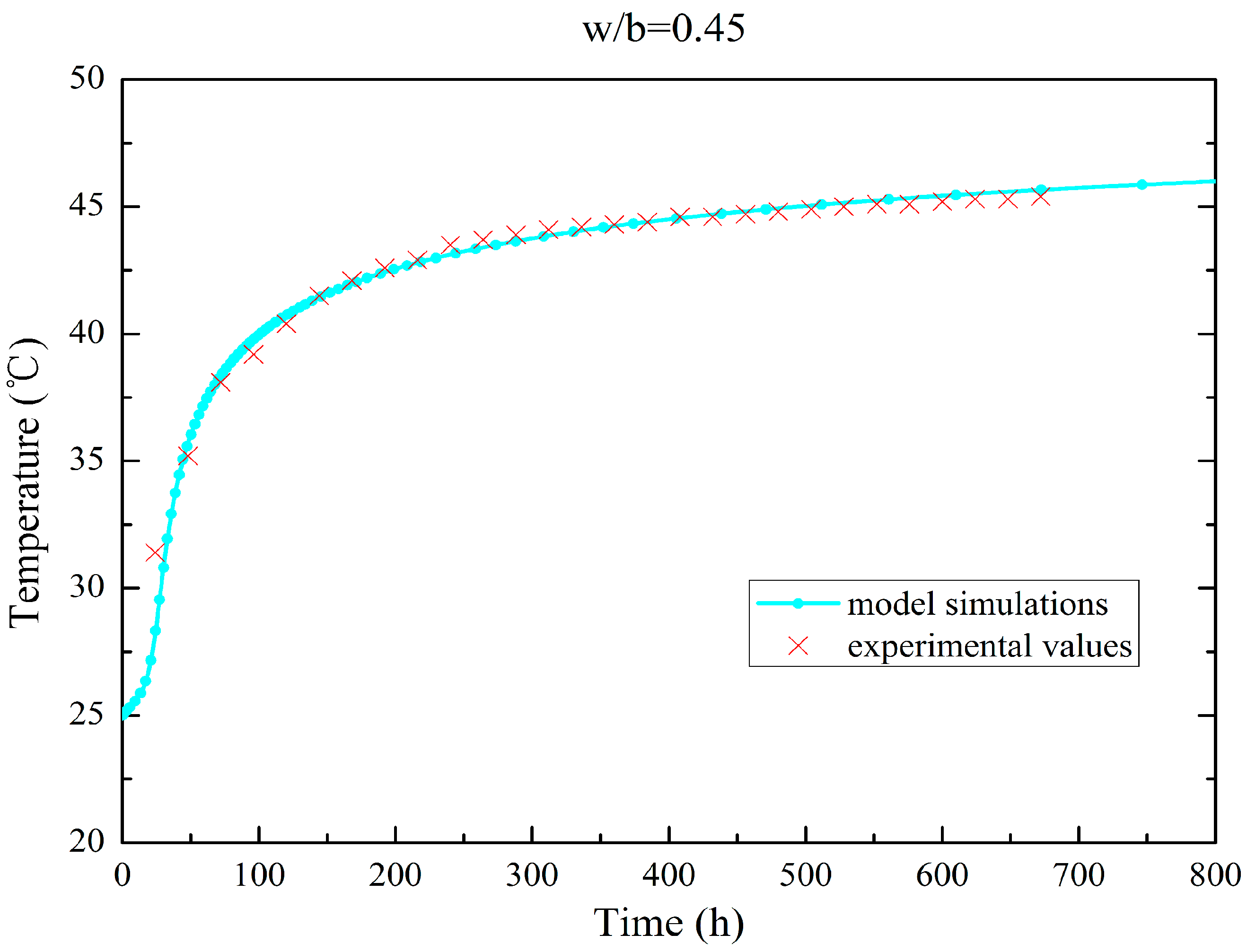
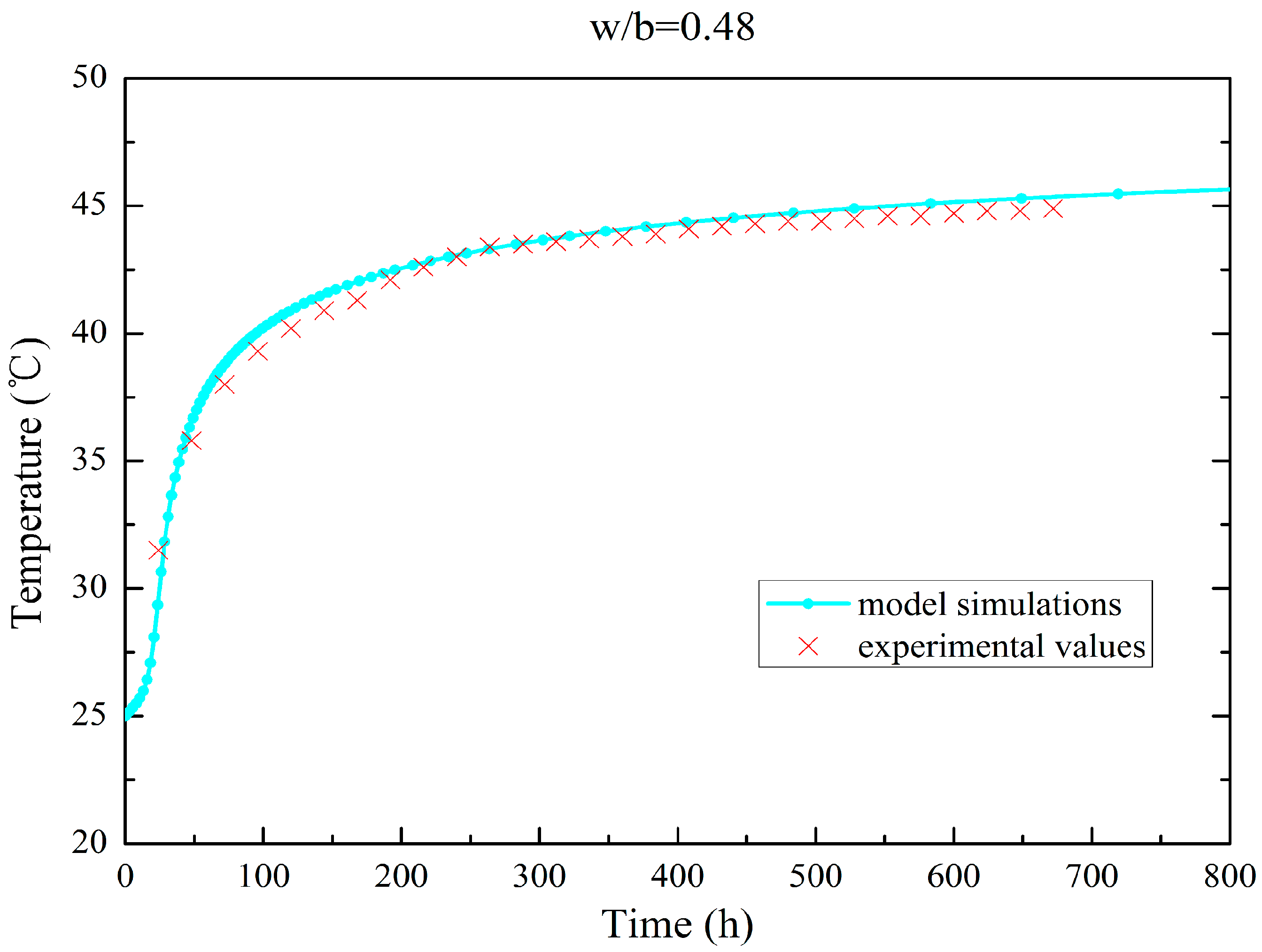
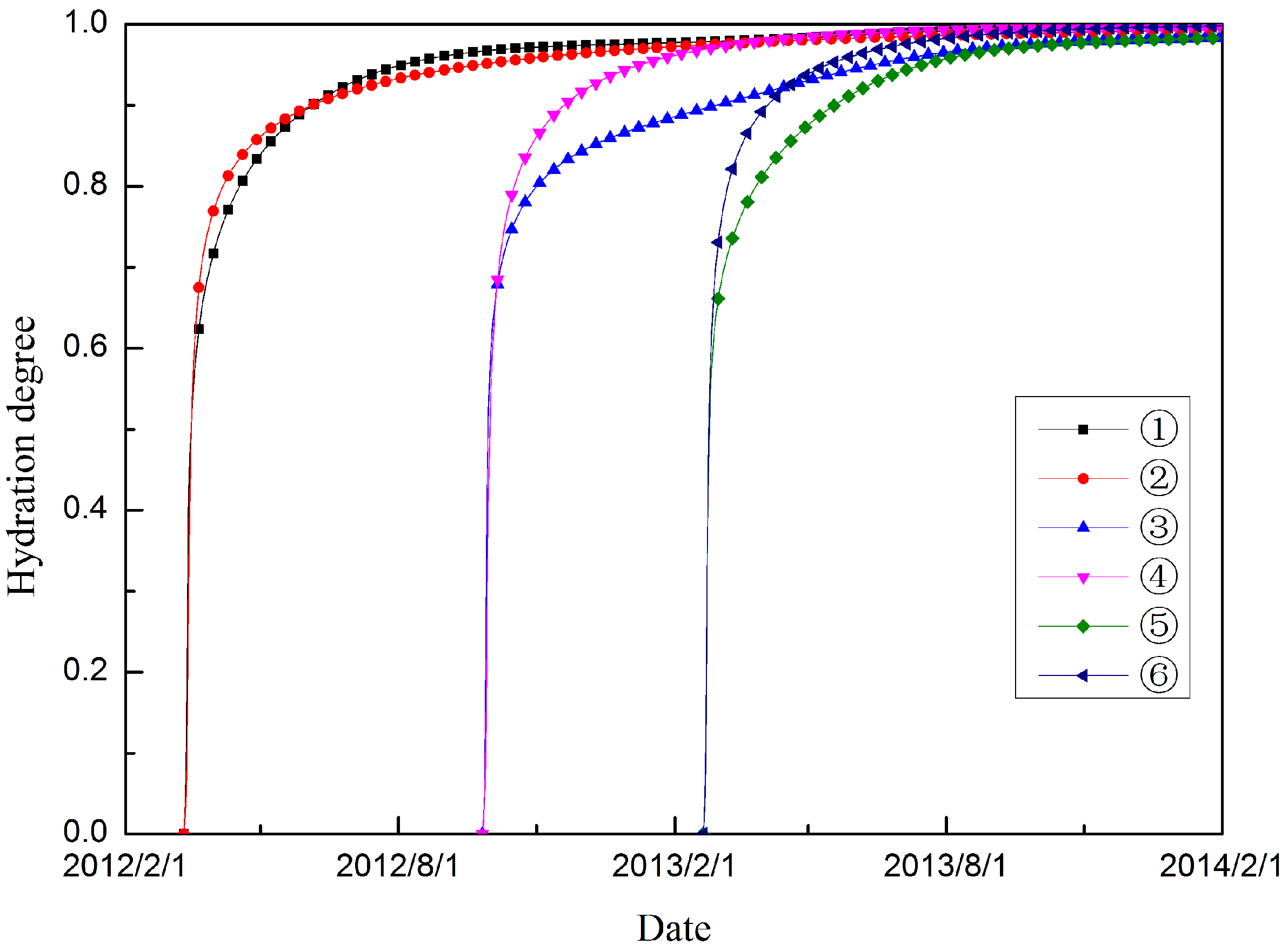
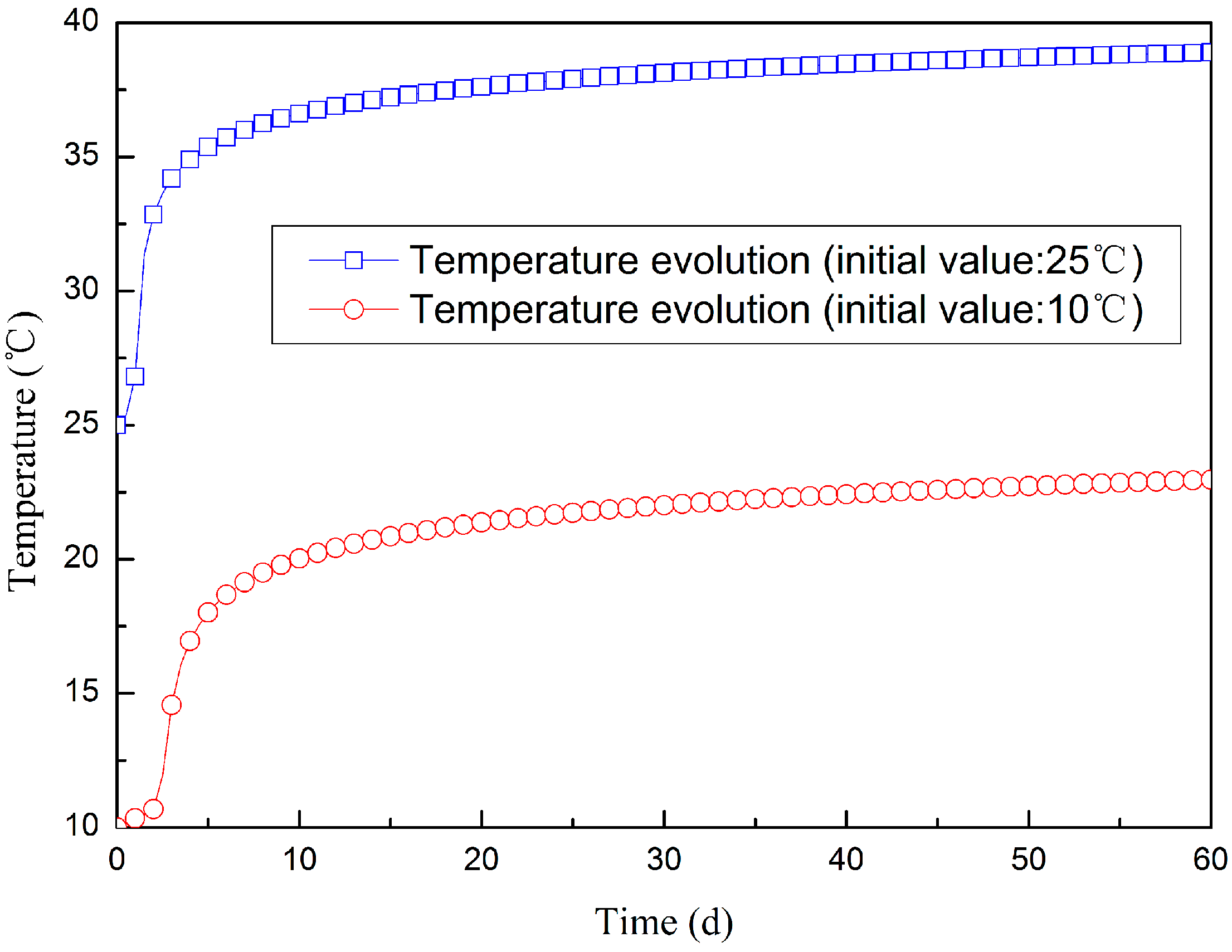
3.1. Calibration Method of the Hydration Model
3.2. Fly Ash Concrete
3.3. SSC Concrete
4. Engineering Application
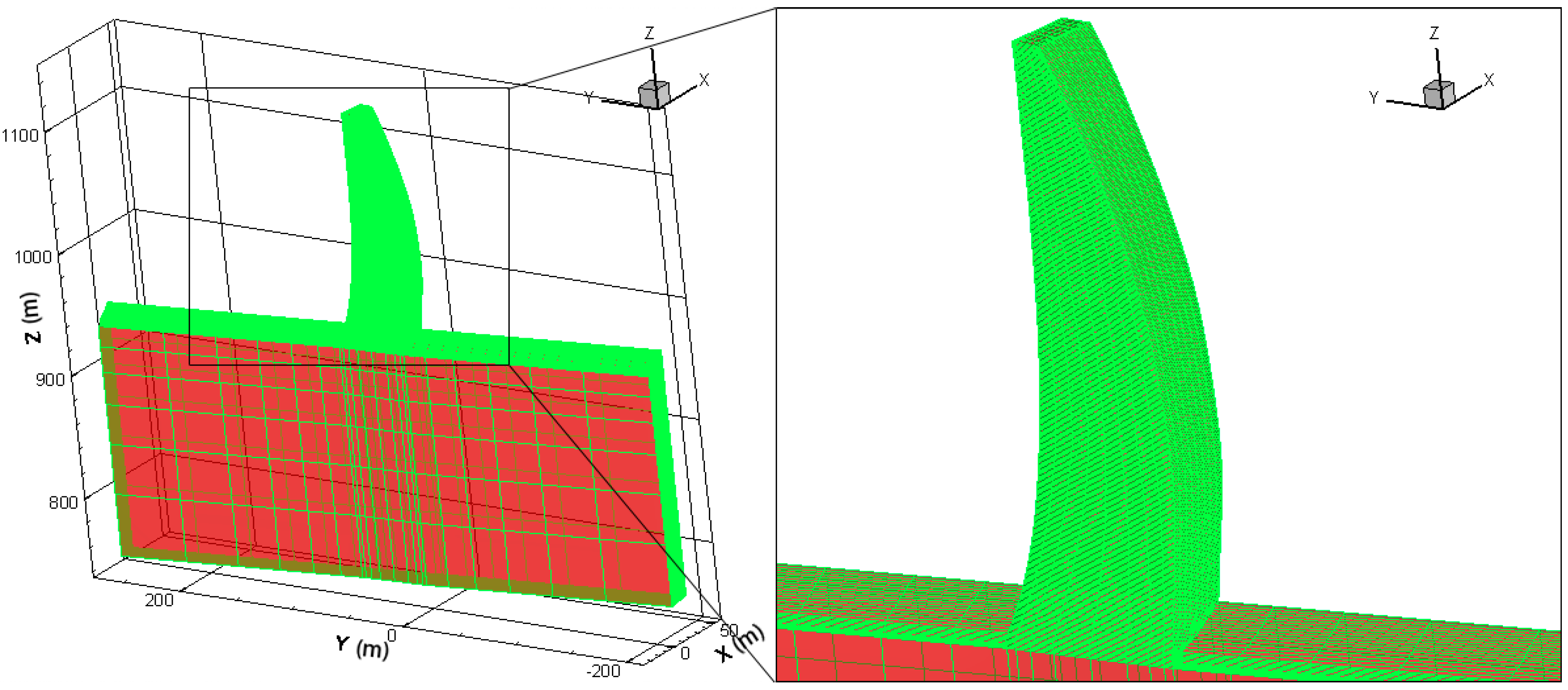
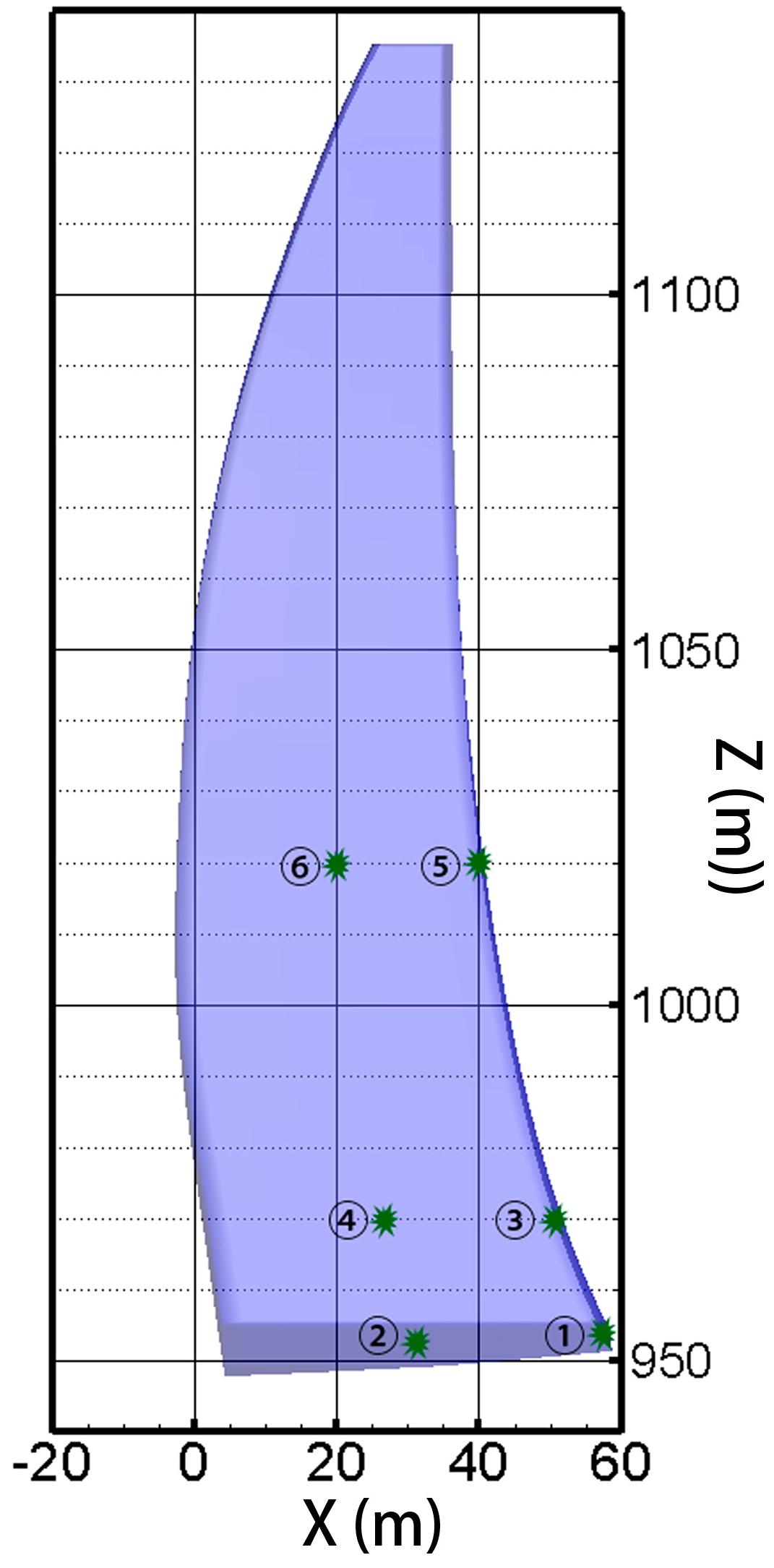
4.1. Project Background and Assumptions
4.2. FE Model Description and Initial Conditions
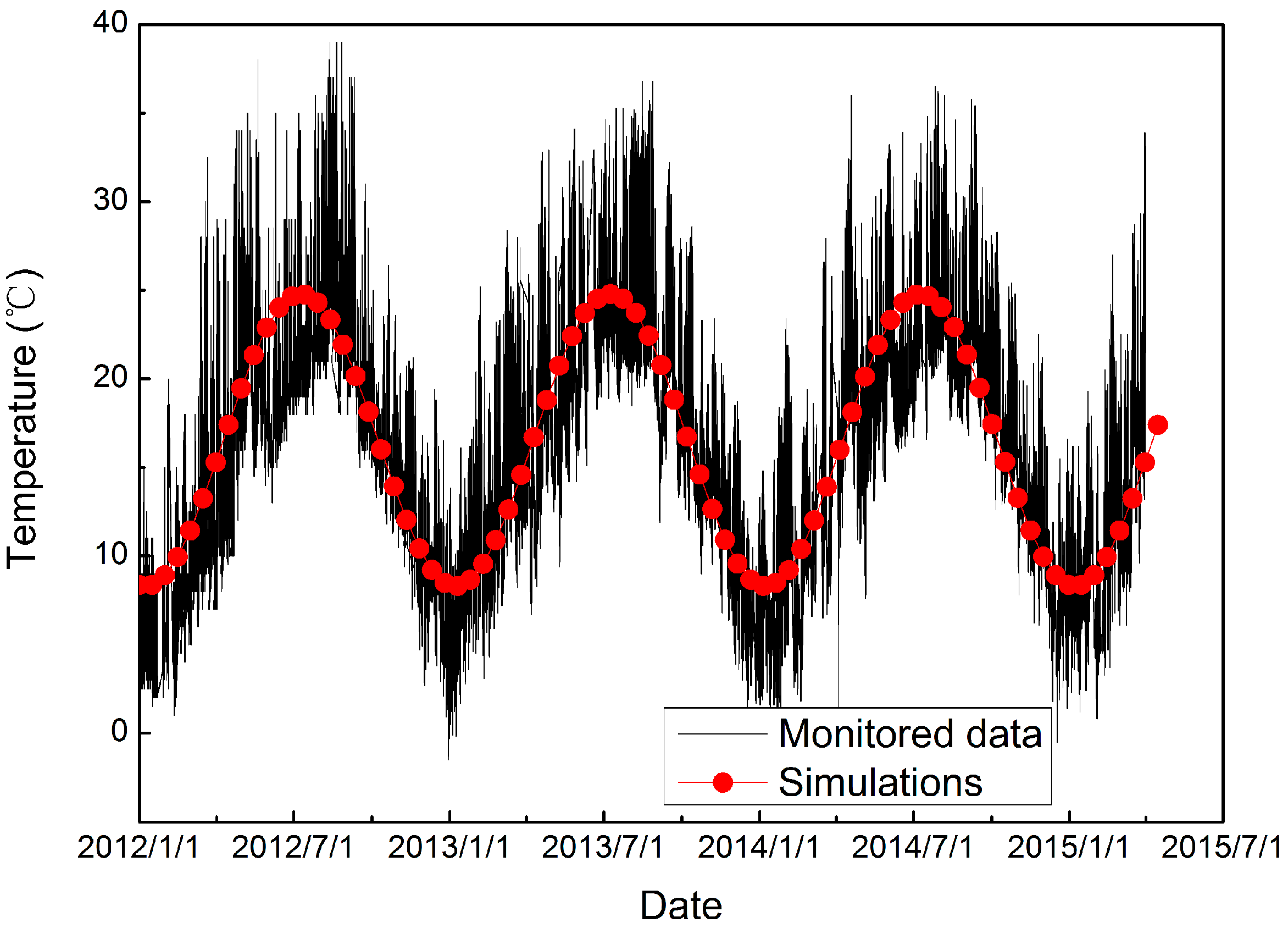
4.3. Boundary Conditions
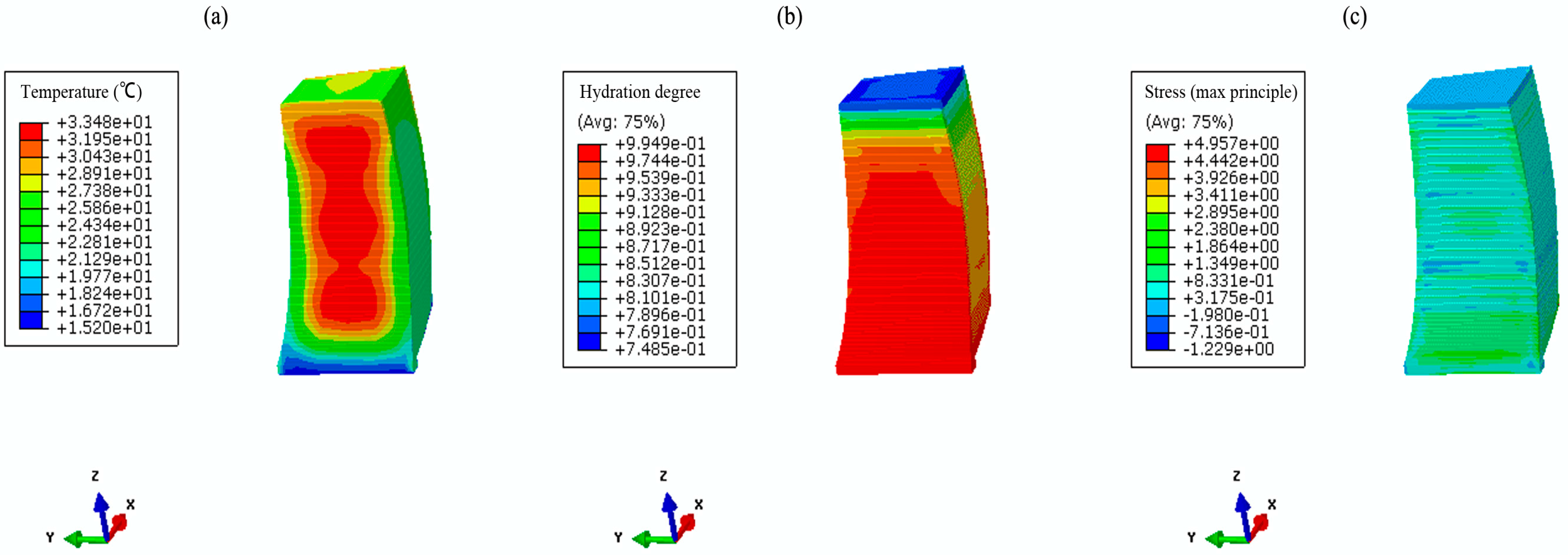
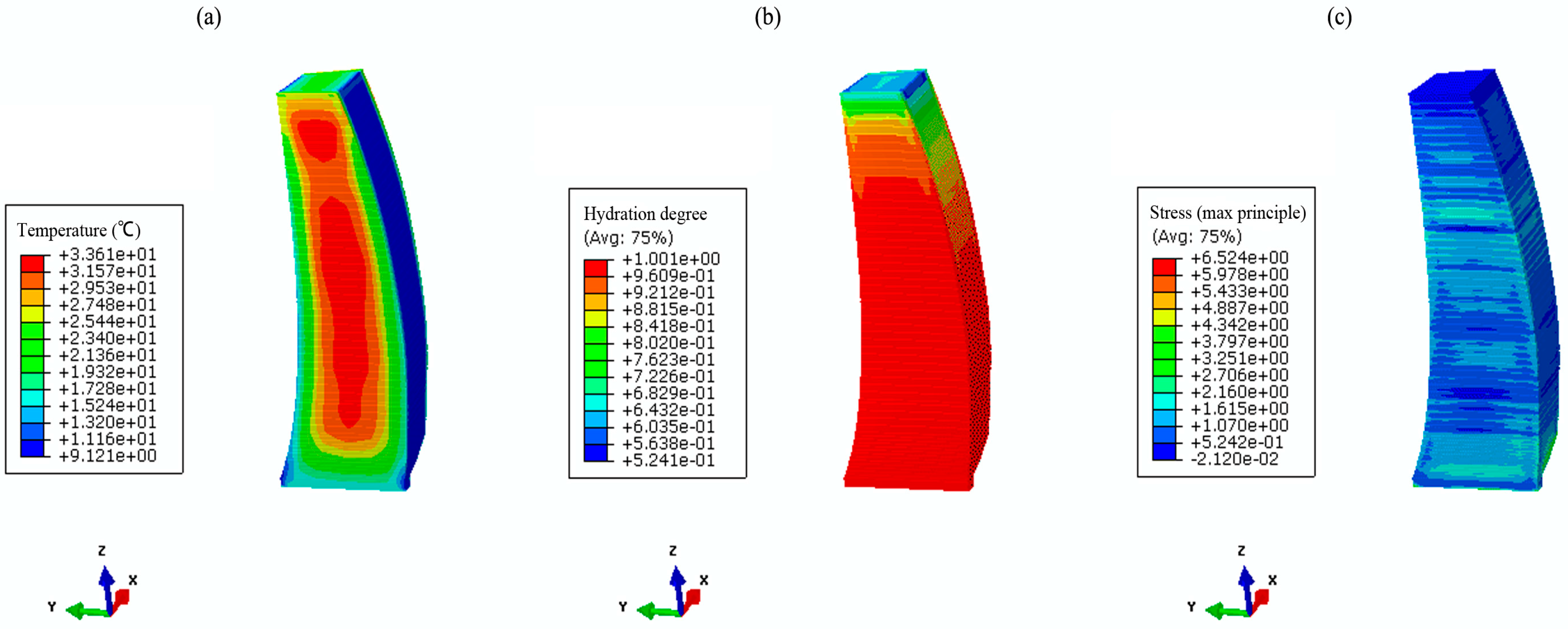
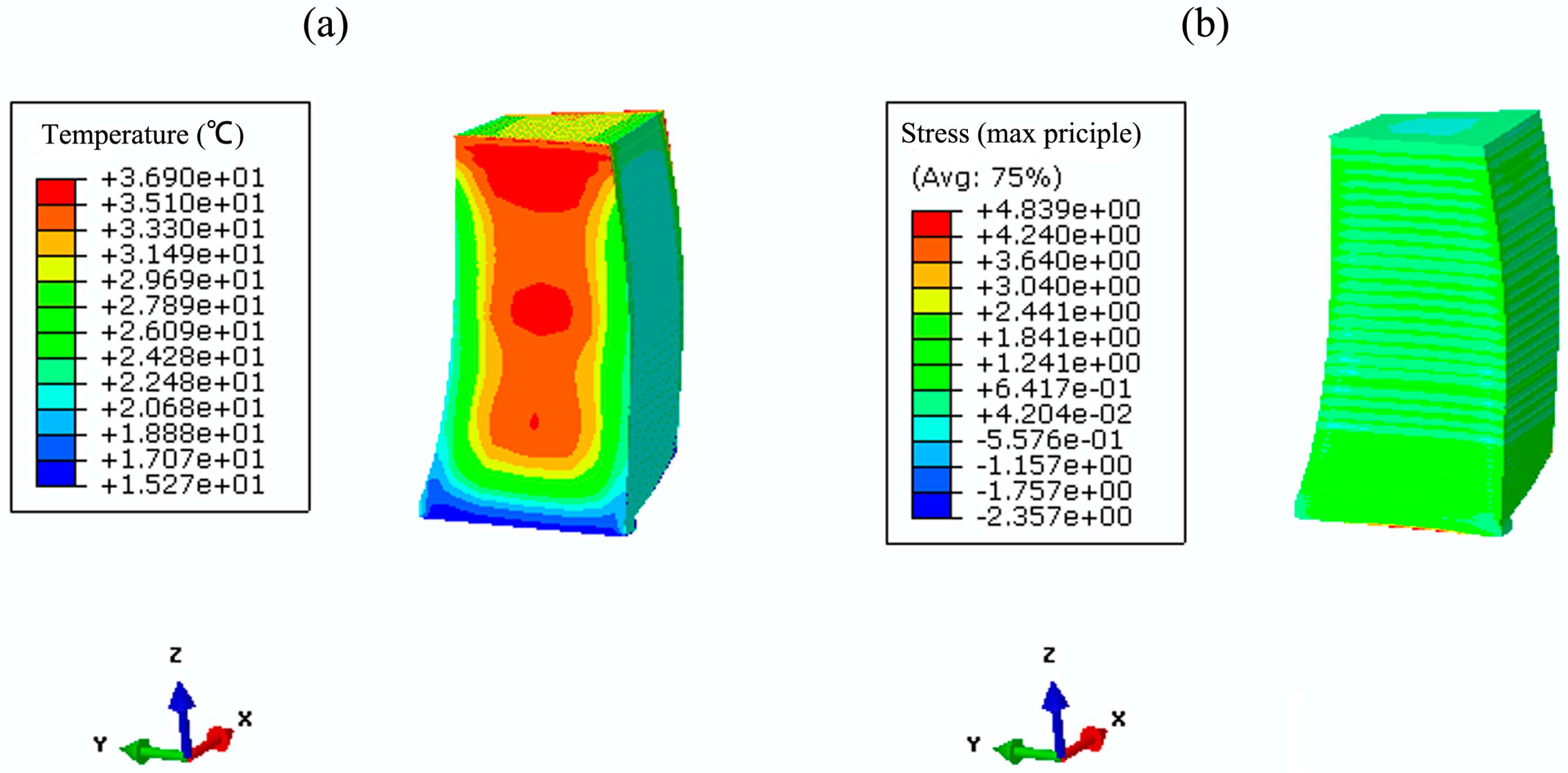
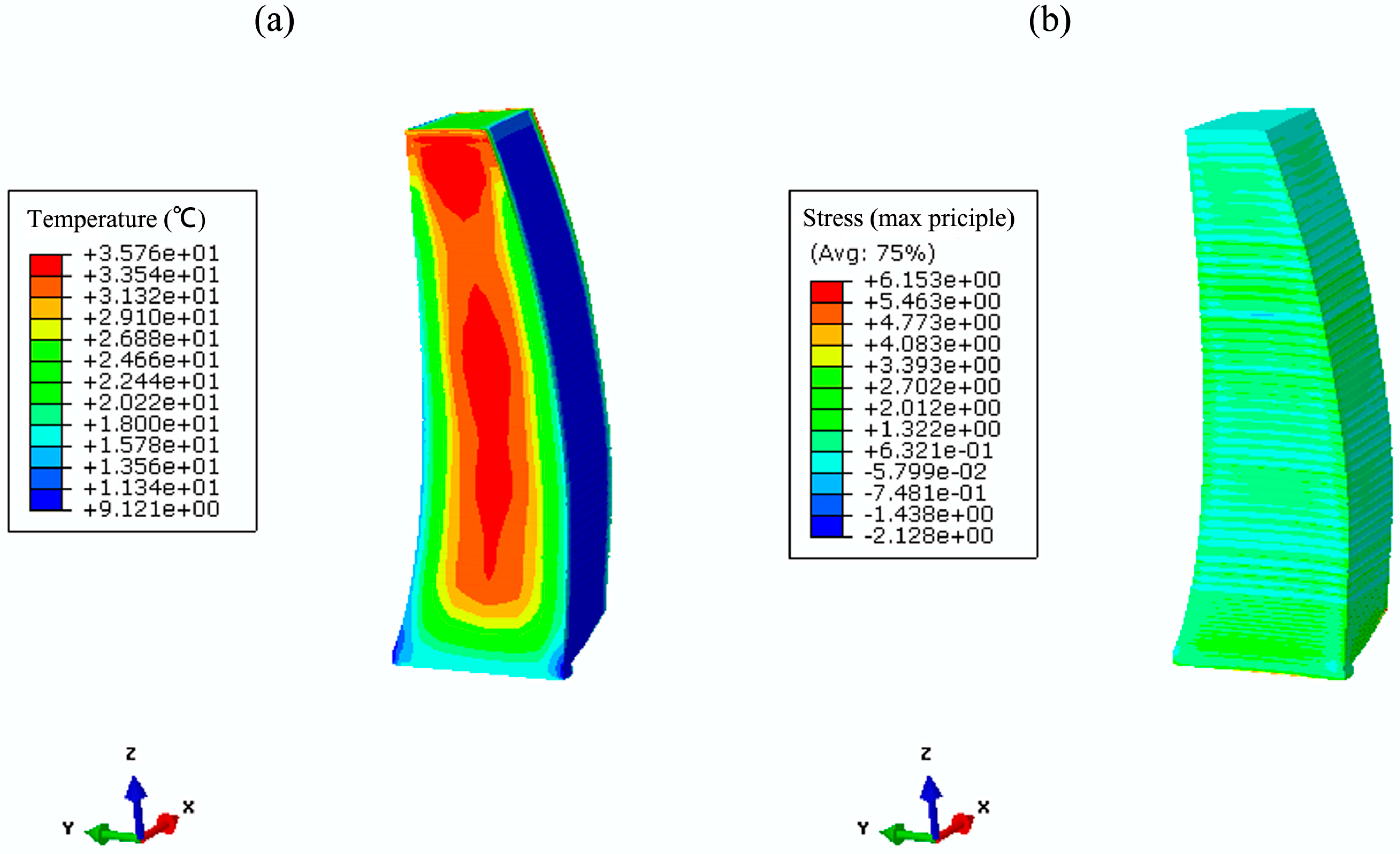
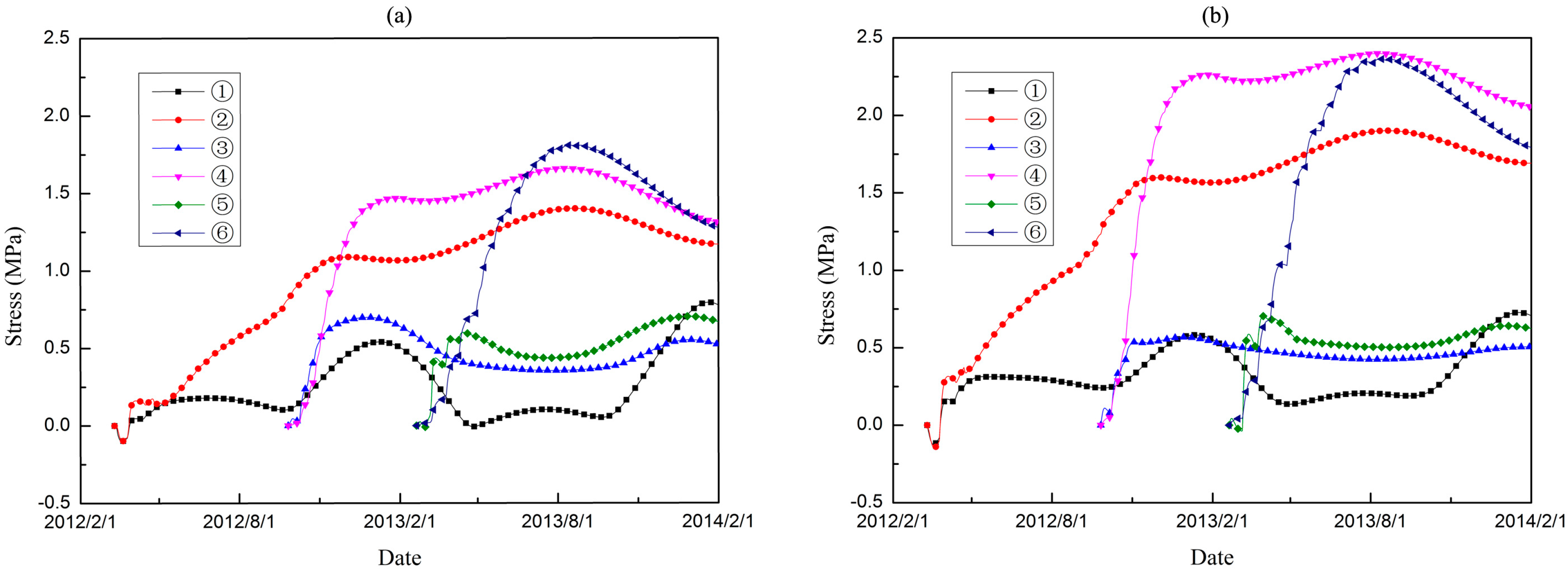
4.4. Results and Discussion
5. Conclusions
- The conventional heat release model of mass concrete only relates the heat liberation rate to time, which ignores the effect of real-time temperature on the hydration process. To overcome the problem, a chemical-physical coupled model is introduced.
- Based on the chemical-physical coupled model, the hydration properties of fly ash concrete and SSC concrete are studied.
- A multi-scale framework is employed to obtain the nonlinear thermal characteristics. Using a homogenization scheme that is well suited for heterogeneous materials, the hydration process of mass concrete structures can be estimated.
- Contrastive analysis of the coupled model and the conventional model are conducted, based on an engineering project.
- Temperature prediction values of the conventional model and the coupled hydration model show a difference, especially at an early age when cracking is prone to occur within mass concrete structures.
- The cooling effect of the cooling pipes used inside the mass concrete was neglected. Thus, the chemical-physical responses under actual working conditions should be scrutinized in future research.
- When using proper materials such as super sulfated slag concrete, water cooling is likely to be abrogated, which can induce cost-savings.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Juenger, M.C.G.; Winnefeld, F.; Provis, J.L.; Ideker, J.H. Advances in alternative cementitious binders. Cem. Concr. Res. 2011, 41, 1232–1243. [Google Scholar] [CrossRef]
- Damtoft, J.S.; Lukasik, J.; Herfort, D.; Sorrentino, D.; Gartner, E.M. Sustainable development and climate change initiatives. Cem. Concr. Res. 2008, 38, 115–127. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Gao, Y.; Yu, B.; Tang, W. Influence of fineness on hydration kinetics of supersulfated cement. Thermochim. Acta 2015, 605, 37–42. [Google Scholar] [CrossRef]
- Gartner, E. Industrially interesting approaches to “low-CO2” cements. Cem. Concr. Res. 2004, 34, 1489–1498. [Google Scholar] [CrossRef]
- Stevens, J.E. Hoover Dam: An American Adventure; University of Oklahoma Press: Norman, OK, USA, 1990. [Google Scholar]
- Chu, I.; Lee, Y.; Amin, M.N.; Jang, B.; Kim, J. Application of a thermal stress device for the prediction of stresses due to hydration heat in mass concrete structure. Constr. Build. Mater. 2013, 45, 192–198. [Google Scholar] [CrossRef]
- Scerrato, D.; Giorgio, I.; Della Corte, A.; Madeo, A.; Dowling, N.E.; Darve, F. Towards the design of an enriched concrete with enhanced dissipation performances. Cem. Concr. Res. 2016, 84, 48–61. [Google Scholar] [CrossRef]
- Giorgio, I.; Scerrato, D. Multi-scale concrete model with rate-dependent internal friction. Eur. J. Environ. Civ. Eng. 2016. [Google Scholar] [CrossRef]
- Waller, V.; D’Aloïa, L.; Cussigh, F.; Lecrux, S. Using the maturity method in concrete cracking control at early ages. Cem. Concr. Compos. 2004, 26, 589–599. [Google Scholar] [CrossRef]
- Benboudjema, F.; Torrenti, J.M. Early-age behaviour of concrete nuclear containments. Nucl. Eng. Des. 2008, 238, 2495–2506. [Google Scholar] [CrossRef]
- Zreiki, J.; Bouchelaghem, F.; Chaouche, M. Early-age behaviour of concrete in massive structures, experimentation and modelling. Nucl. Eng. Des. 2010, 240, 2643–2654. [Google Scholar] [CrossRef]
- Wang, X.; Cho, H.; Lee, H. Prediction of temperature distribution in concrete incorporating fly ash or slag using a hydration model. Compos. Part B Eng. 2011, 42, 27–40. [Google Scholar] [CrossRef]
- Thomas, J.J.; Biernacki, J.J.; Bullard, J.W.; Bishnoi, S.; Dolado, J.S.; Scherer, G.W.; Luttge, A. Modeling and simulation of cement hydration kinetics and microstructure development. Cem. Concr. Res. 2011, 41, 1257–1278. [Google Scholar] [CrossRef]
- Martinelli, E.; Koenders, E.A.B.; Caggiano, A. A numerical recipe for modelling hydration and heat flow in hardening concrete. Cem. Concr. Compos. 2013, 40, 48–58. [Google Scholar] [CrossRef]
- De Freitas, J.A.T.; Cuong, P.T.; Faria, R.; Azenha, M. Modelling of cement hydration in concrete structures with hybrid finite elements. Finite Elem. Anal. Des. 2013, 77, 16–30. [Google Scholar] [CrossRef]
- Cervera, M.; Faria, R.; Oliver, J.; Prato, T. Numerical modelling of concrete curing, regarding hydration and temperature phenomena. Comput. Struct. 2002, 80, 1511–1521. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete. I: Hydration and aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Bentz, D.P.; Waller, V.; de Larrard, F. Prediction of Adiabatic Temperature Rise in Conventional and High-Performance Concretes Using a 3-D Microstructural Model. Cem. Concr. Res. 1998, 28, 285–297. [Google Scholar] [CrossRef]
- Lackner, R.; Mang, H.A. Chemoplastic material model for the simulation of early-age cracking: From the constitutive law to numerical analyses of massive concrete structures. Cem. Concr. Compos. 2004, 26, 551–562. [Google Scholar] [CrossRef]
- Gawin, D.; Pesavento, F.; Schrefler, B.A. Hygro-thermo-chemo-mechanical modelling of concrete at early ages and beyond. Part I: Hydration and hygro-thermal phenomena. Int. J. Numer. Methods Eng. 2006, 67, 299–331. [Google Scholar] [CrossRef]
- Di Luzio, G.; Cusatis, G. Hygro-thermo-chemical modeling of high performance concrete. I: Theory. Cem. Concr. Compos. 2009, 31, 301–308. [Google Scholar] [CrossRef]
- Di Luzio, G.; Cusatis, G. Hygro-thermo-chemical modeling of high-performance concrete. II: Numerical implementation, calibration, and validation. Cem. Concr. Compos. 2009, 31, 309–324. [Google Scholar] [CrossRef]
- Zhu, B.F. Thermal Stresses and Temperature Control of Mass Concrete; Tsinghua University Press: Beijing, China, 2014. [Google Scholar]
- Yang, J.; Hu, Y.; Zuo, Z.; Jin, F.; Li, Q. Thermal analysis of mass concrete embedded with double-layer staggered heterogeneous cooling water pipes. Appl. Therm. Eng. 2012, 35, 145–156. [Google Scholar] [CrossRef]
- De Schutter, G.; Taerwe, L. General hydration model for Portland cement and blast furnace slag cement. Cem. Concr. Res. 1995, 25, 593–604. [Google Scholar] [CrossRef]
- Zhou, W.; Feng, C.; Liu, X.; Liu, S.; Zhang, C. A macro–meso chemo-physical analysis of early-age concrete based on a fixed hydration model. Mag. Concr. Res. 2016. [Google Scholar] [CrossRef]
- Di Luzio, G.; Cusatis, G. Solidification-microprestress-microplane (SMM) theory for concrete at early age: Theory, validation and application. Int. J. Solids Struct. 2013, 50, 957–975. [Google Scholar] [CrossRef]
- Di Luzio, G. Numerical Model for Time-Dependent Fracturing of Concrete. J. Eng. Mech. 2009, 135, 632–640. [Google Scholar] [CrossRef]
- Bažant, Z.P.; L’Hermite, R. Mathematical Modeling of Creep and Shrinkage of Concrete; Wiley: Chichester, UK, 1988. [Google Scholar]
- Ulm, F.; Coussy, O. Couplings in early-age concrete: From material modeling to structural design. Int. J. Solids Struct. 1998, 35, 4295–4311. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Cusatis, G.; Cedolin, L. Temperature Effect on Concrete Creep Modeled by Microprestress-Solidification Theory. J. Eng. Mech. 2004, 130, 691–699. [Google Scholar] [CrossRef]
- Bentz, D.P. Transient plane source measurements of the thermal properties of hydrating cement pastes. Mater. Struct. 2007, 40, 1073–1080. [Google Scholar] [CrossRef]
- Zhang, Y.; Pichler, C.; Yuan, Y.; Zeiml, M.; Lackner, R. Micromechanics-based multifield framework for early-age concrete. Eng. Struct. 2013, 47, 16–24. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-chemo-mechanical model for concrete. II: Damage and creep. J. Eng. Mech. 1999, 125, 1028–1039. [Google Scholar] [CrossRef]
- Schutter, G.D.; Taerwe, L. Degree of hydration-based description of mechanical properties of early age concrete. Mater. Struct. 1996, 29, 335–344. [Google Scholar] [CrossRef]
- Sciumè, G.; Benboudjema, F.; De Sa, C.; Pesavento, F.; Berthaud, Y.; Schrefler, B.A. A multiphysics model for concrete at early age applied to repairs problems. Eng. Struct. 2013, 57, 374–387. [Google Scholar] [CrossRef]
- De Schutter, G. Degree of hydration based Kelvin model for the basic creep of early age concrete. Mater. Struct. 1999, 32, 260–265. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Gao, Y.; Yu, B.; Bai, Y. Comparing study on hydration properties of various cementitious systems. J. Therm. Anal. Calorim. 2014, 118, 1483–1492. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Chang, X.; Zhou, W.; Cheng, Y.; Duan, Y. Precise simulation analysis of the thermal field in mass concrete with a pipe water cooling system. Appl. Therm. Eng. 2015, 78, 449–459. [Google Scholar] [CrossRef]
- Liu, X.; Duan, Y.; Zhou, W.; Chang, X. Modeling the Piped Water Cooling of a Concrete Dam Using the Heat-Fluid Coupling Method. J. Eng. Mech. 2015, 139, 1278–1289. [Google Scholar] [CrossRef]
- Zhu, B.F. Equivalent equation of heat conduction in mass concrete considering the effect of pipe cooling. J. Hydraul. Eng. 1991, 3, 28–34. [Google Scholar]
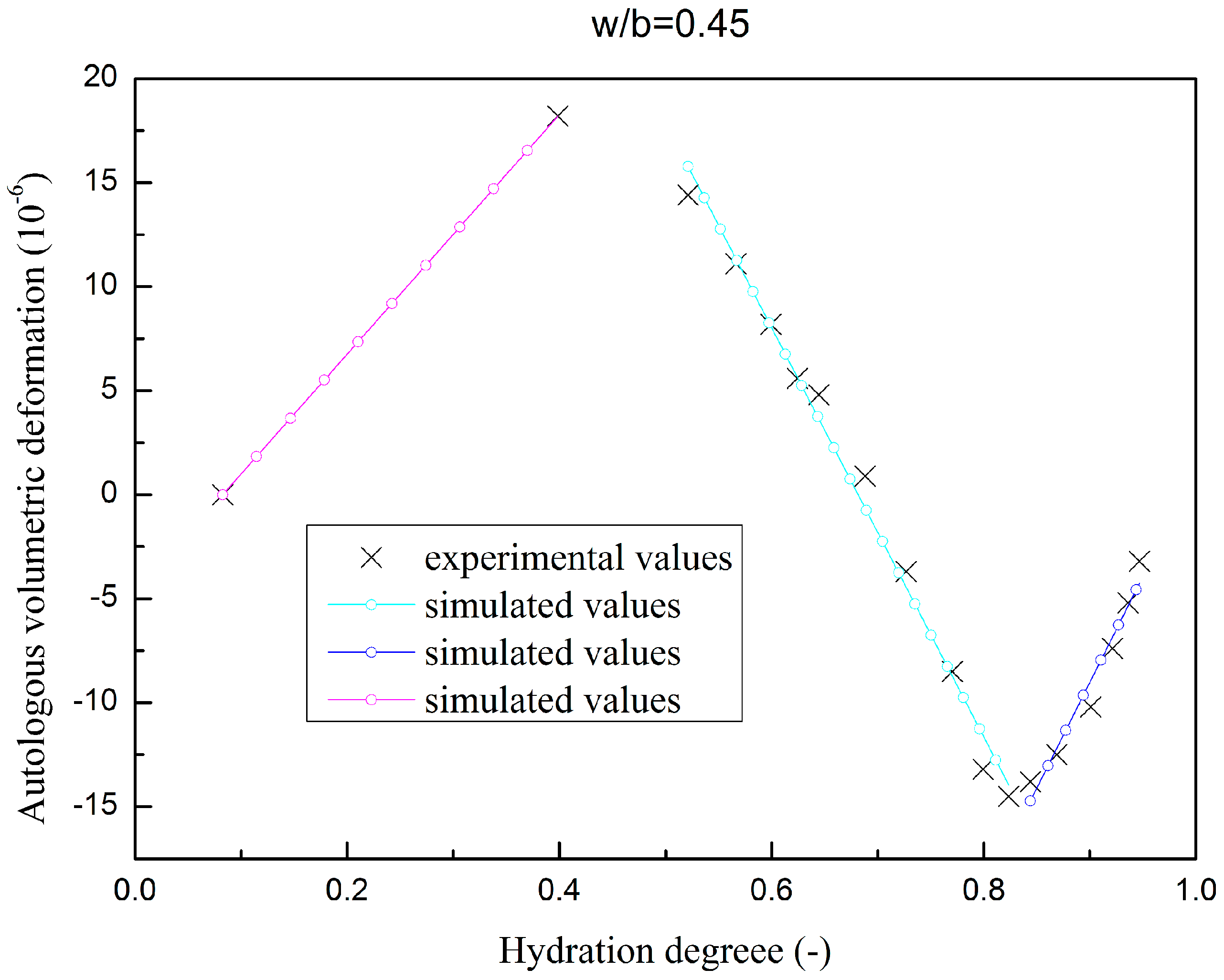
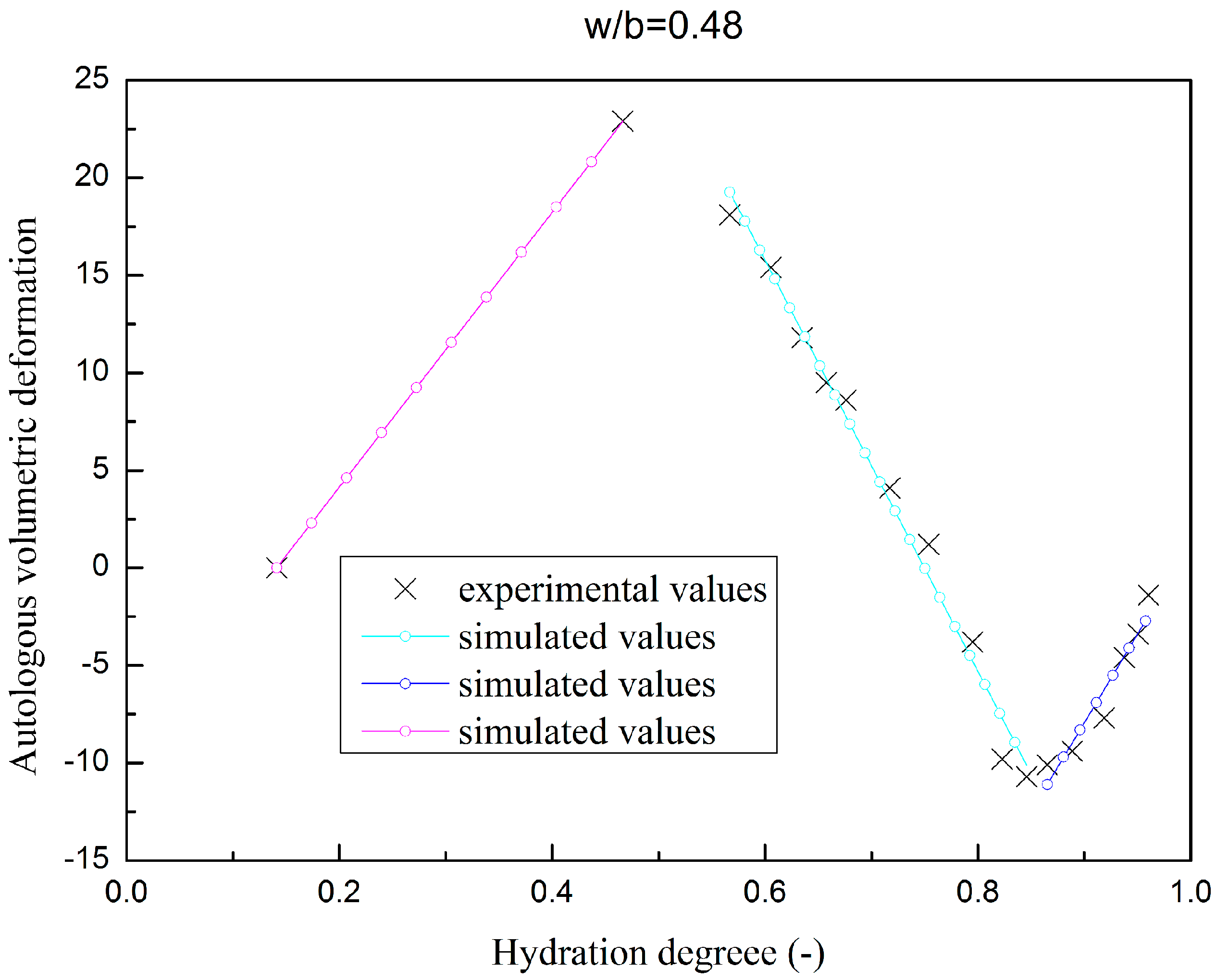
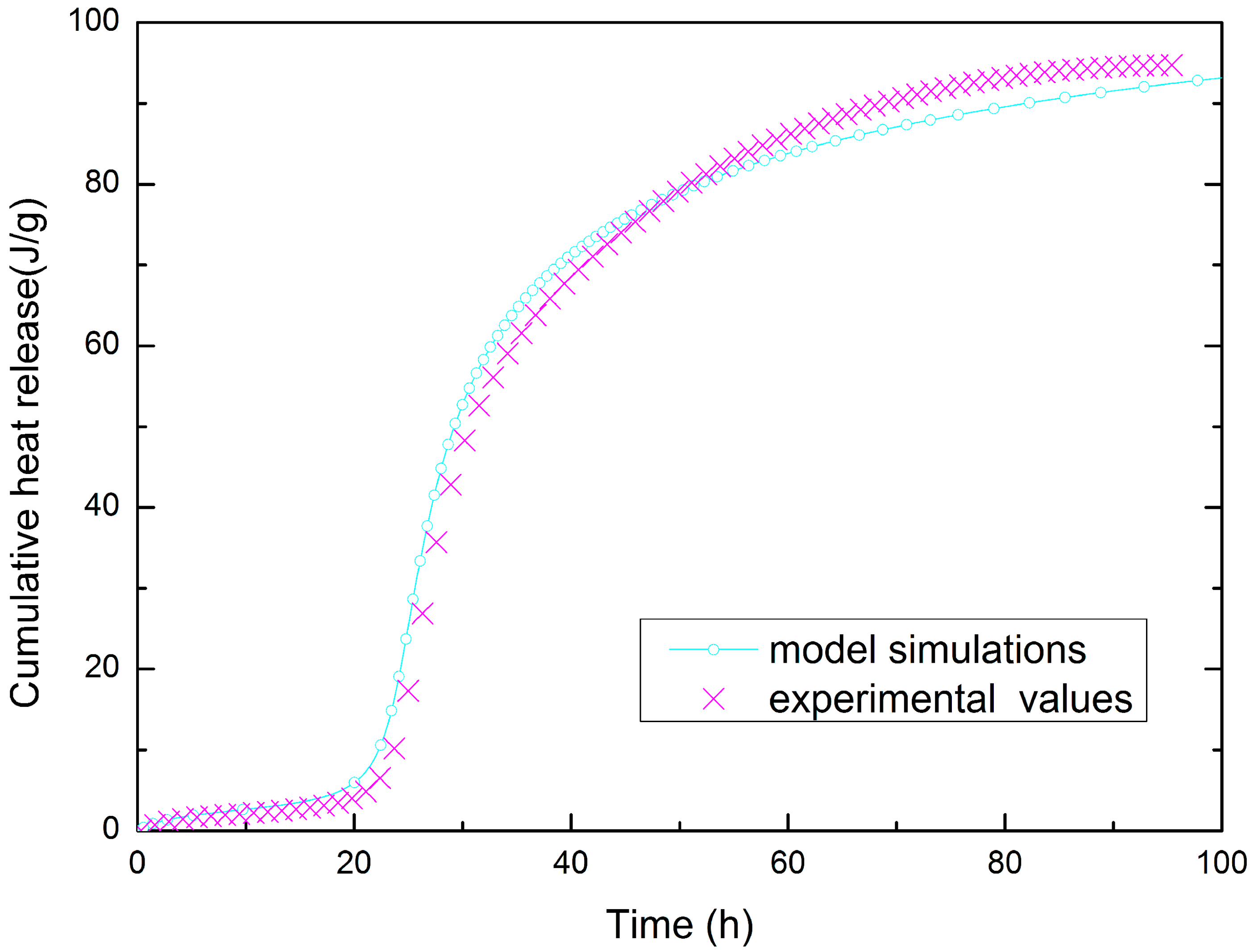
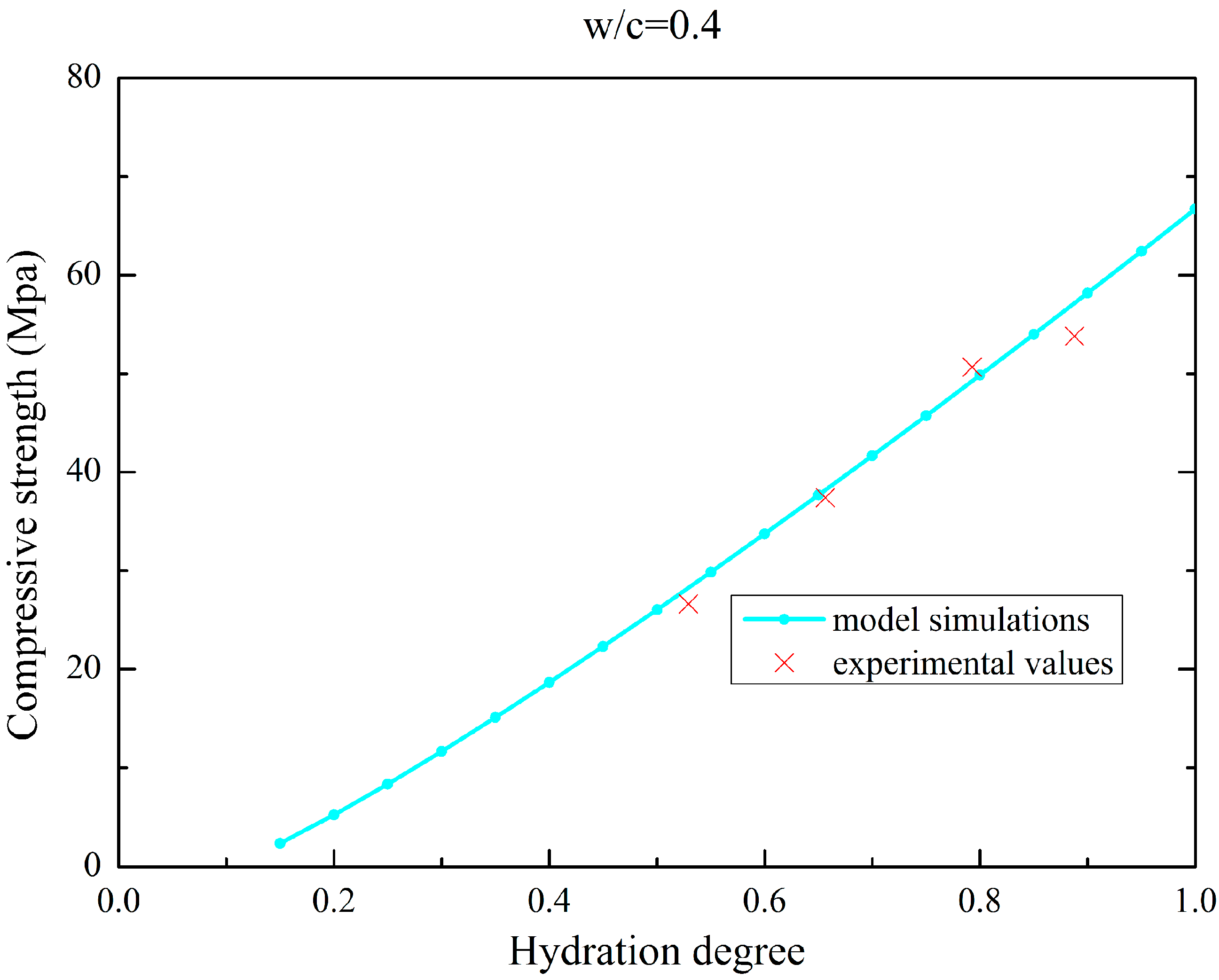

| w/b | Composition of Concrete (kg/m3) | Set-Retarding Superplasticizer | Air Entraining Agent | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Water | Cement | Fly Ash | Sand | Stone Small | Stone Middle | Stone Large | Stone Extra | |||
| 0.45 | 85 | 123 | 66 | 558 | 318 | 318 | 477 | 477 | 0.7% | 0.02% |
| 0.48 | 85 | 115 | 62 | 572 | 317 | 317 | 476 | 476 | 0.7% | 0.02% |
| (kg·m−3) | (kg·m−3) | (kg·m−3) | (kg·m−3) | (kg·m−3) |
|---|---|---|---|---|
| 1040 | 1000 | 3240 | 2380 | 2620 |
| (kJ·m−3·K−1) | (kJ·m−3·K−1) | (kJ·m−3·K−1) | (kJ·m−3·K−1) | (kJ·m−3·K−1) |
| 980 | 4180 | 2415 | 2190 | 1886 |
| (J·h−1·m−1·K−1) | (J·h−1·m−1·K−1) | (J·h−1·m−1·K−1) | (J·h−1·m−1·K−1) | (J·h−1·m−1·K−1) |
| 2160 | 2174 | 5580 | 840 | 8800 |
| Parameters | (107 h−1) | (10−4) | (-) | (-) | (-) | (J·kg−1) | (K) |
|---|---|---|---|---|---|---|---|
| w/b = 0.45 | 6.4 | 9.2 | −0.016 | 1 | 9.6 | 19,200 | 5000 |
| w/b = 0.48 | 7.5 | 8 | −0.012 | 1 | 9.5 | 18,550 | 5000 |
| Parameters | (108 h−1) | (10−4) | (-) | (-) | (-) | (-) | (-) |
|---|---|---|---|---|---|---|---|
| w/c = 0.40 | 2.4 | 6.6 | −0.046 | 1 | 11.5 | 108,700 | 5000 |
| w/c | Composition of Concrete (kg/m3) | Set-Retarding Superplasticizer | Air Entraining Agent | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Water | Cement | Sand | Stone Small | Stone Middle | Stone Large | Stone Extra | |||
| 0.40 | 78 | 195 | 558 | 318 | 318 | 477 | 477 | 0.7% | 0.02% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Feng, C.; Liu, X.; Liu, S.; Zhang, C.; Yuan, W. Contrastive Numerical Investigations on Thermo-Structural Behaviors in Mass Concrete with Various Cements. Materials 2016, 9, 378. https://doi.org/10.3390/ma9050378
Zhou W, Feng C, Liu X, Liu S, Zhang C, Yuan W. Contrastive Numerical Investigations on Thermo-Structural Behaviors in Mass Concrete with Various Cements. Materials. 2016; 9(5):378. https://doi.org/10.3390/ma9050378
Chicago/Turabian StyleZhou, Wei, Chuqiao Feng, Xinghong Liu, Shuhua Liu, Chao Zhang, and Wei Yuan. 2016. "Contrastive Numerical Investigations on Thermo-Structural Behaviors in Mass Concrete with Various Cements" Materials 9, no. 5: 378. https://doi.org/10.3390/ma9050378
APA StyleZhou, W., Feng, C., Liu, X., Liu, S., Zhang, C., & Yuan, W. (2016). Contrastive Numerical Investigations on Thermo-Structural Behaviors in Mass Concrete with Various Cements. Materials, 9(5), 378. https://doi.org/10.3390/ma9050378





