Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling
Abstract
:1. Introduction
2. Experimental
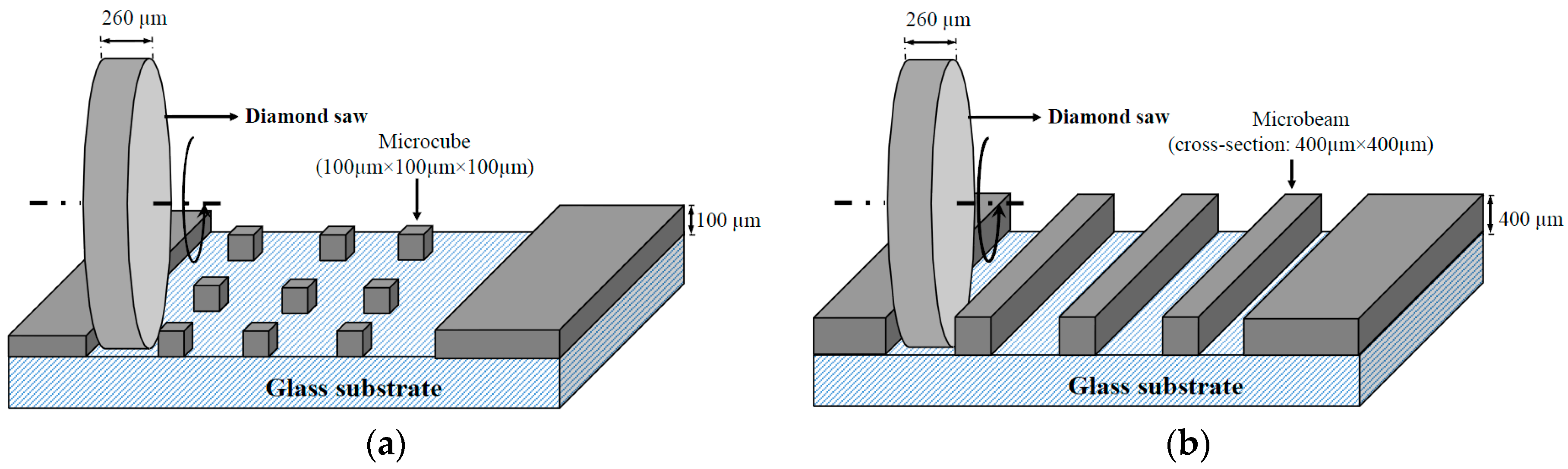
2.1. Sample Preparation
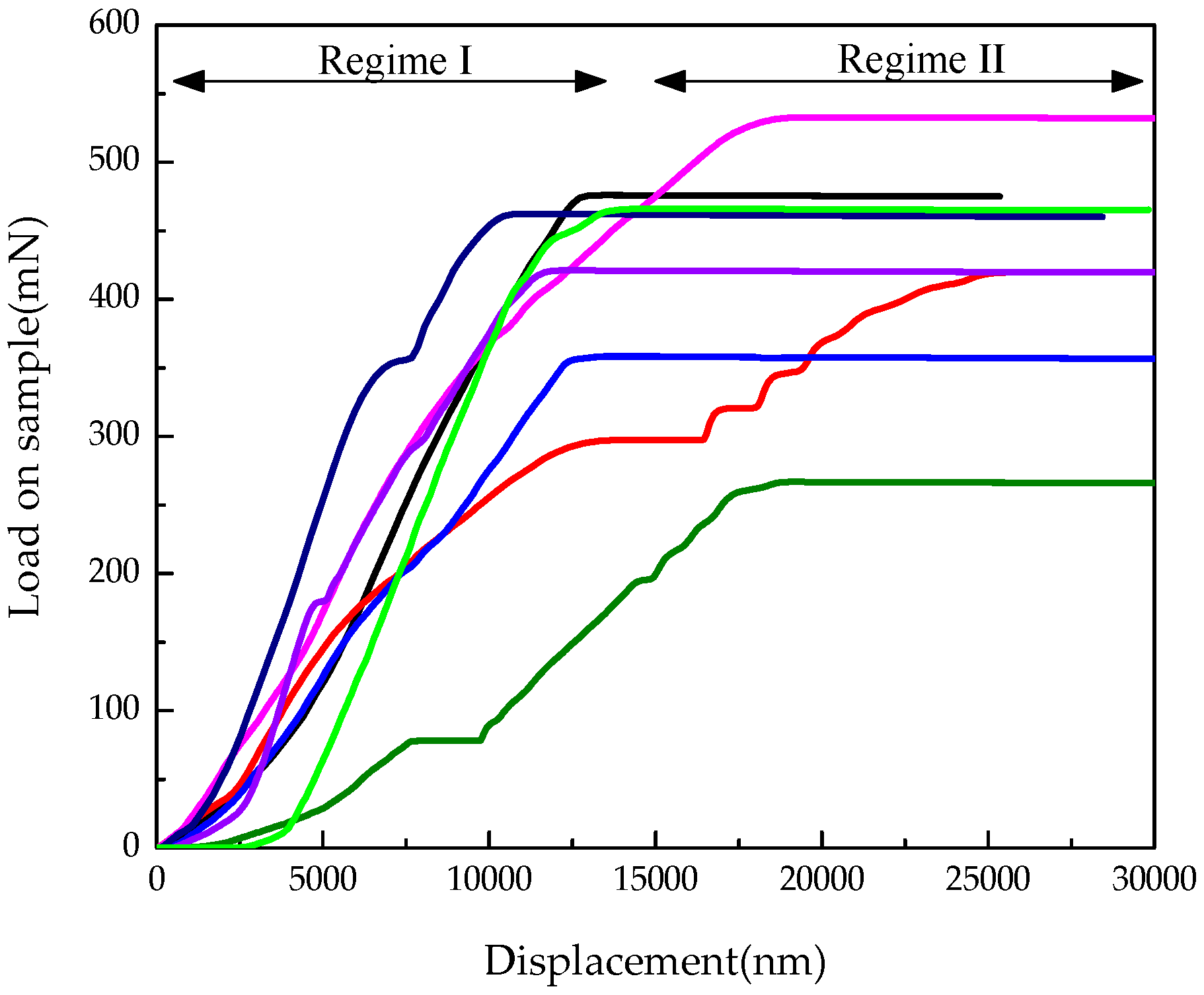
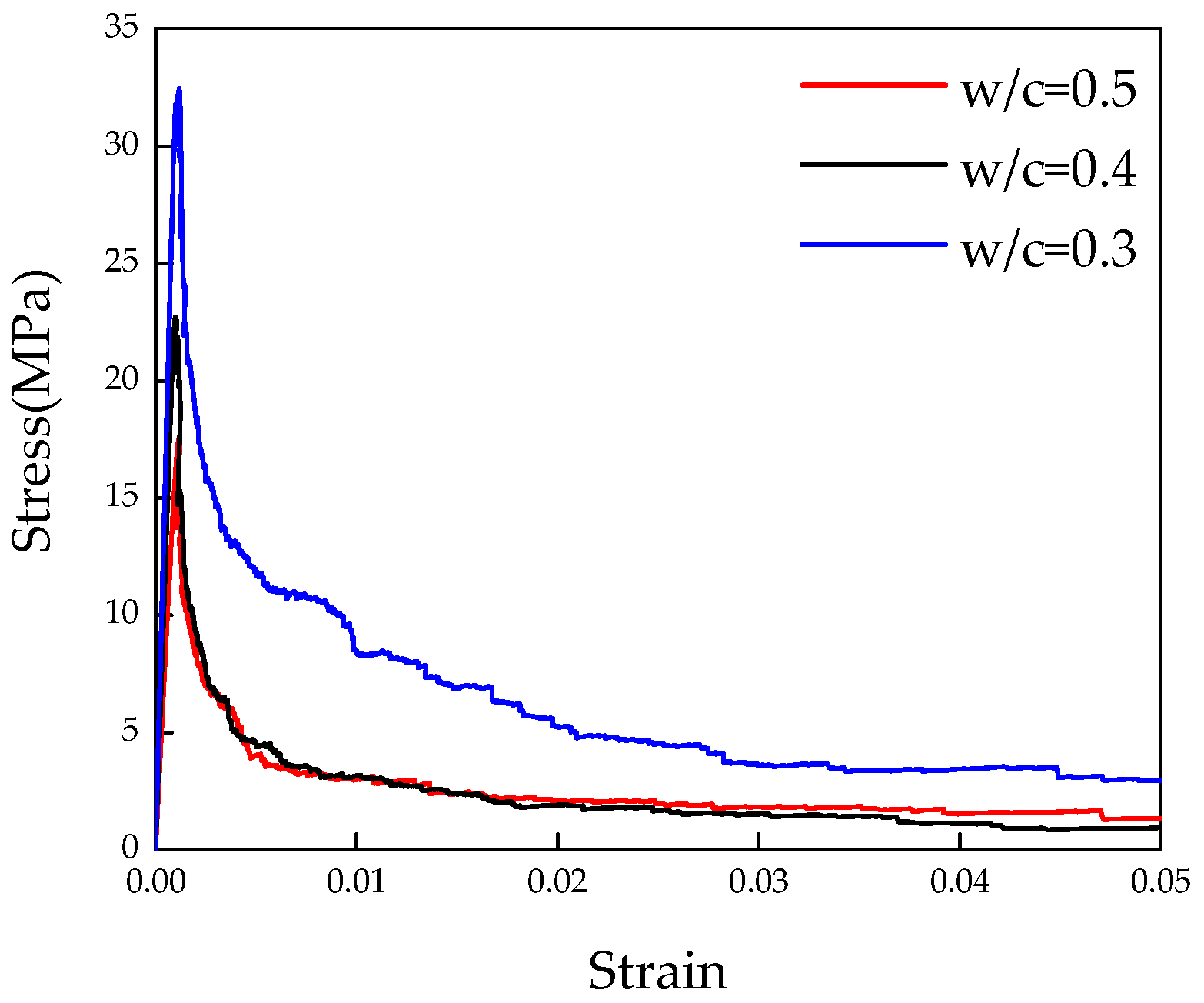
2.2. Global Micro-Mechanical Performance Using Microcube Indentation
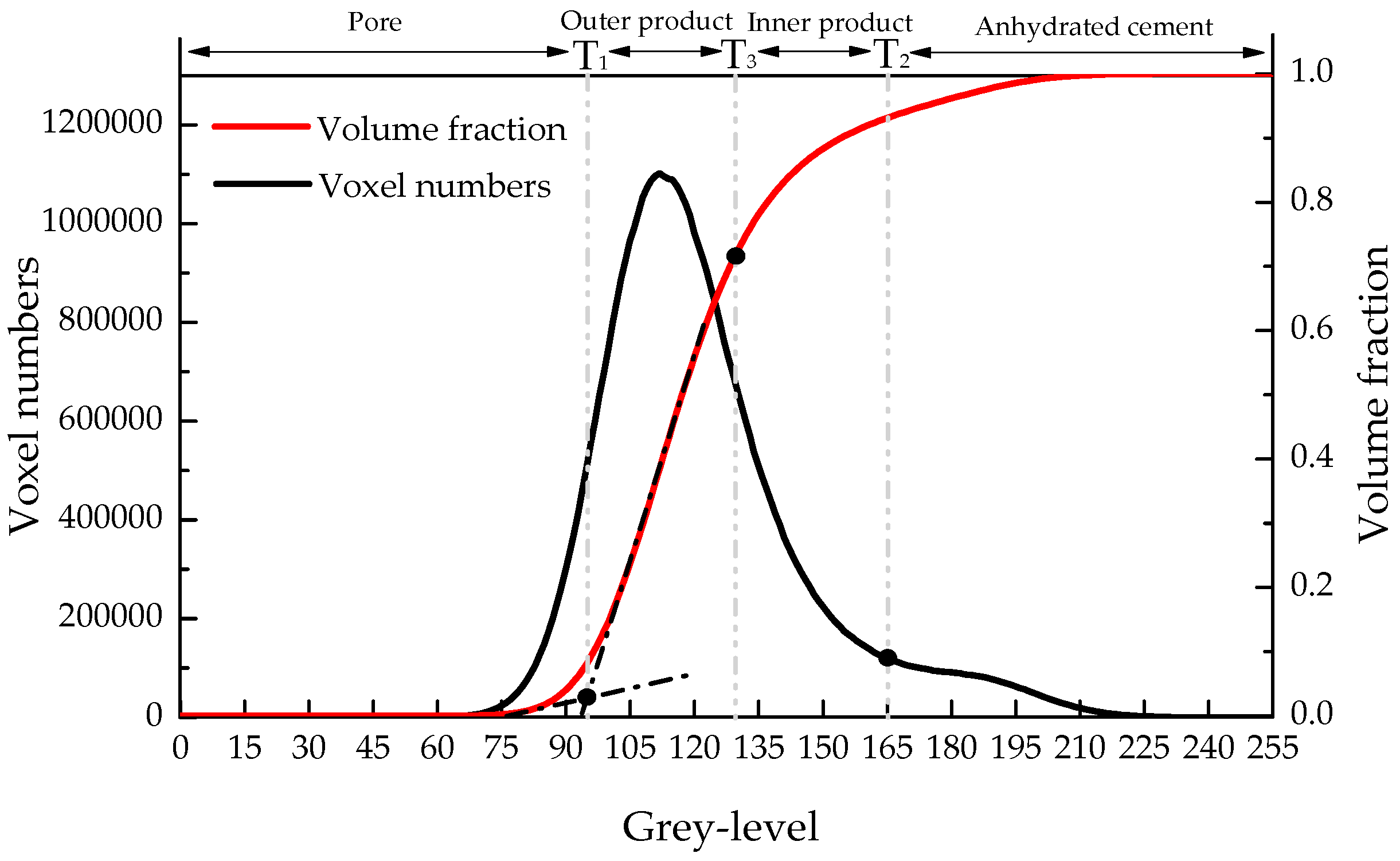
2.3. Microstructure Characterization Using of Micro-CT
3. Modelling
3.1. Modelling Approach
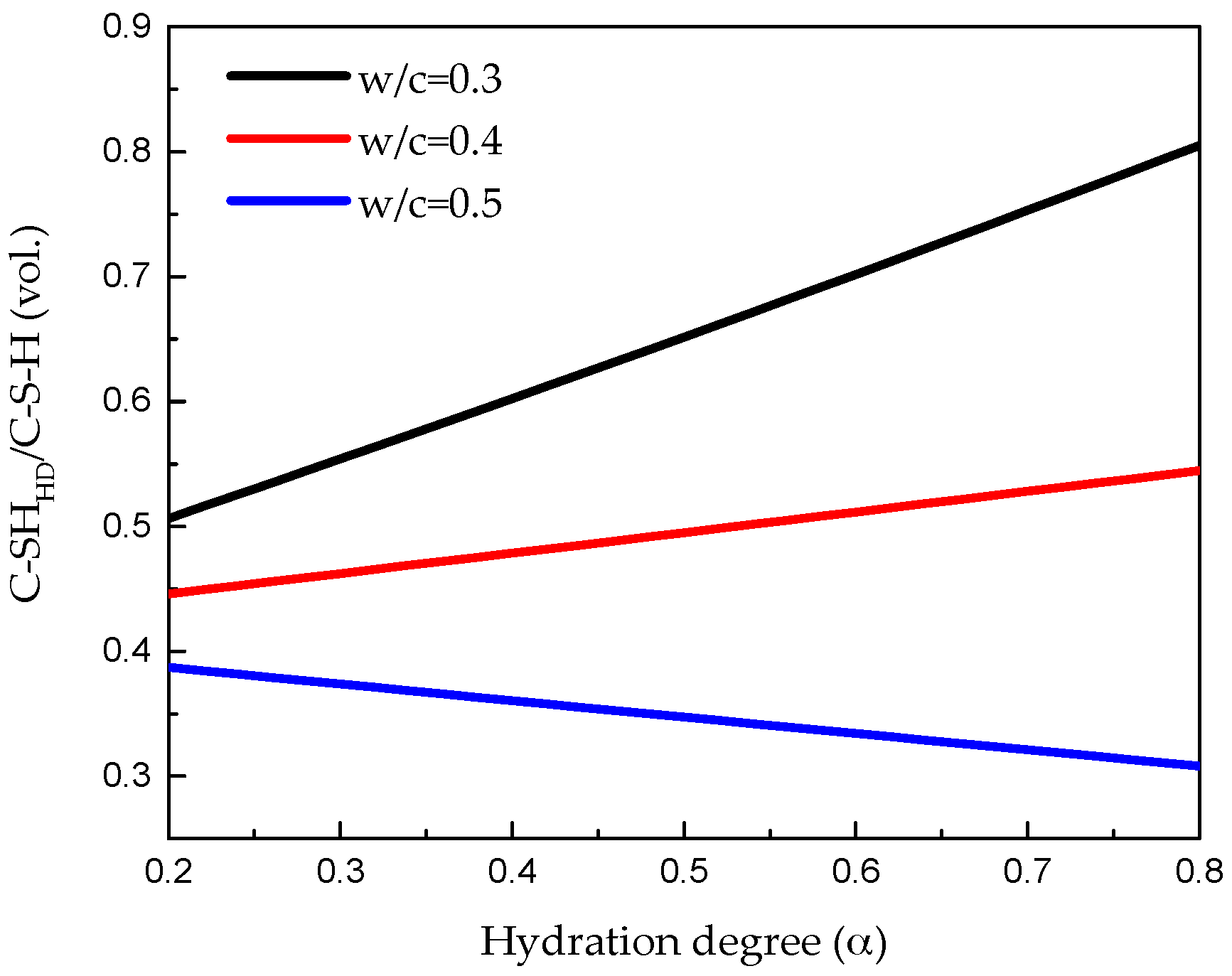
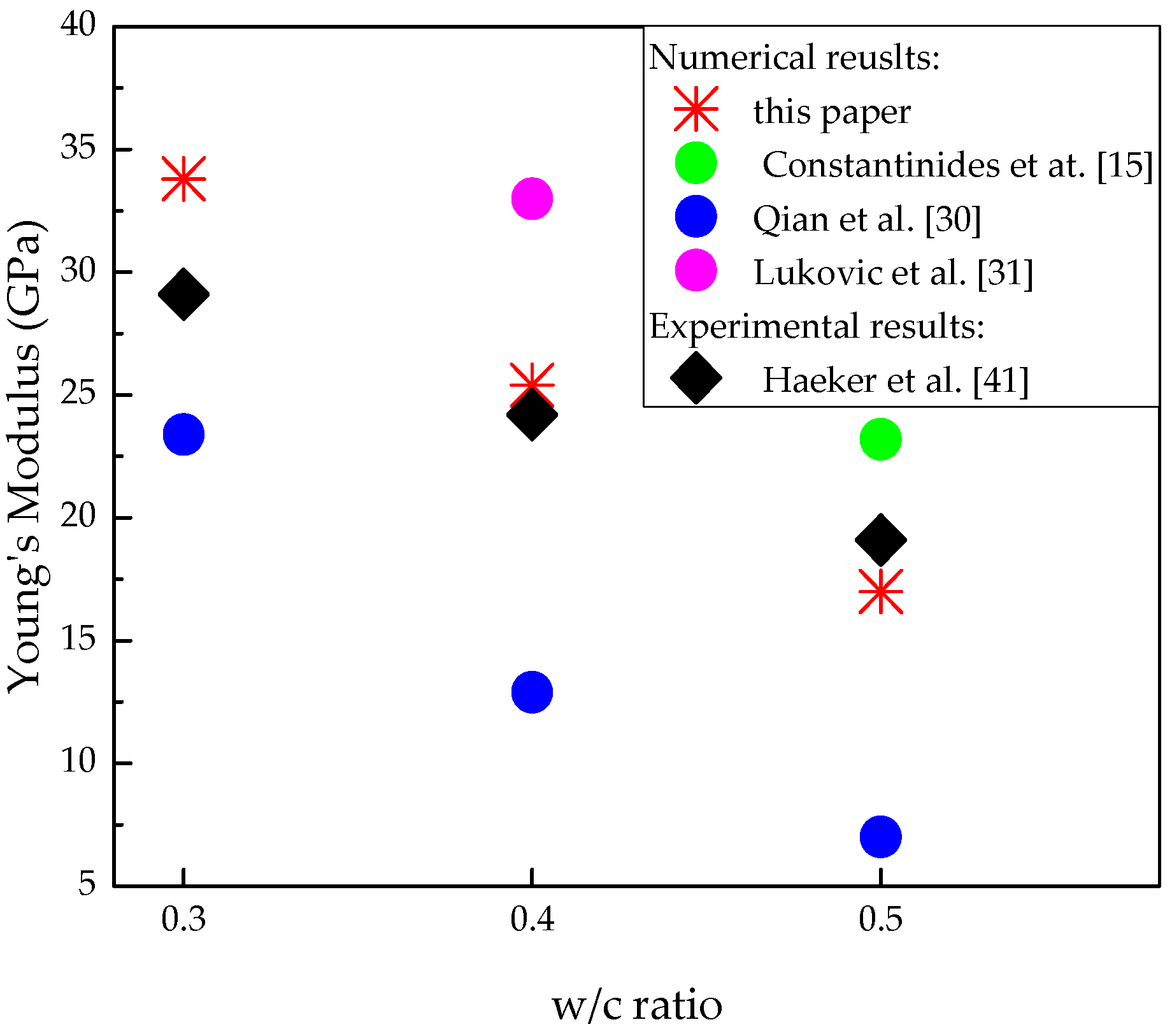
3.2. Calibration and Discussion
3.3. Tensile Strength Prediction and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mehta, P.K.; Monteiro, P.J. Concrete Structures, Properties and Materials; McGraw-Hill Education: Englewood Cliffs, NJ, USA, 1993; Volume 9. [Google Scholar]
- Van Mier, J.G. Concrete Fracture: A Multiscale Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials: (II) applications. Cem. Concr. Res. 1995, 25, 522–530. [Google Scholar] [CrossRef]
- Ye, G.; Van Breugel, K.; Fraaij, A. Three-dimensional microstructure analysis of numerically simulated cementitious materials. Cem. Concr. Res. 2003, 33, 215–222. [Google Scholar] [CrossRef]
- Bishnoi, S.; Scrivener, K.L. µic: A new platform for modelling the hydration of cements. Cem. Concr. Res. 2009, 39, 266–274. [Google Scholar] [CrossRef]
- Bullard, J.W.; Garboczi, E.J. A model investigation of the influence of particle shape on portland cement hydration. Cem. Concr. Res. 2006, 36, 1007–1015. [Google Scholar] [CrossRef]
- Scrivener, K.L. Backscattered electron imaging of cementitious microstructures: Understanding and quantification. Cem. Concr. Compos. 2004, 26, 935–945. [Google Scholar] [CrossRef]
- Hall, C.; Colston, S.L.; Jupe, A.C.; Jacques, S.D.; Livingston, R.; Ramadan, A.O.; Amde, A.W.; Barnes, P. Non-destructive tomographic energy-dispersive diffraction imaging of the interior of bulk concrete. Cem. Concr. Res. 2000, 30, 491–495. [Google Scholar] [CrossRef]
- Gallucci, E.; Scrivener, K.; Groso, A.; Stampanoni, M.; Margaritondo, G. 3D experimental investigation of the microstructure of cement pastes using synchrotron X-ray microtomography (μct). Cem. Concr. Res. 2007, 37, 360–368. [Google Scholar] [CrossRef]
- Chotard, T.; Boncoeur-Martel, M.; Smith, A.; Dupuy, J.; Gault, C. Application of X-ray computed tomography to characterise the early hydration of calcium aluminate cement. Cem. Concr. Compos. 2003, 25, 145–152. [Google Scholar] [CrossRef]
- Bentz, D.; Quenard, D.; Kunzel, H.; Baruchel, J.; Peyrin, F.; Martys, N.; Garboczi, E. Microstructure and transport properties of porous building materials. II: Three-dimensional X-ray tomographic studies. Mater. Struct. 2000, 33, 147–153. [Google Scholar] [CrossRef]
- Promentilla, M.A.B.; Sugiyama, T.; Hitomi, T.; Takeda, N. Quantification of tortuosity in hardened cement pastes using synchrotron-based x-ray computed microtomography. Cem. Concr. Res. 2009, 39, 548–557. [Google Scholar] [CrossRef]
- Zhang, M.; He, Y.; Ye, G.; Lange, D.A.; van Breugel, K. Computational investigation on mass diffusivity in portland cement paste based on X-ray computed microtomography (μct) image. Constr. Build. Mater. 2012, 27, 472–481. [Google Scholar] [CrossRef]
- Hu, C.; Li, Z. Micromechanical investigation of portland cement paste. Constr. Build. Mater. 2014, 71, 44–52. [Google Scholar] [CrossRef]
- Constantinides, G.; Ulm, F.J. The effect of two types of csh on the elasticity of cement-based materials: Results from nanoindentation and micromechanical modeling. Cem. Concr. Res. 2004, 34, 67–80. [Google Scholar] [CrossRef]
- Jennings, H.M.; Thomas, J.J.; Gevrenov, J.S.; Constantinides, G.; Ulm, F.J. A multi-technique investigation of the nanoporosity of cement paste. Cem. Concr. Res. 2007, 37, 329–336. [Google Scholar] [CrossRef]
- Hughes, J.J.; Trtik, P. Micro-mechanical properties of cement paste measured by depth-sensing nanoindentation: A preliminary correlation of physical properties with phase type. Mater. Charact. 2004, 53, 223–231. [Google Scholar] [CrossRef]
- Manzano, H.; Dolado, J.; Guerrero, A.; Ayuela, A. Mechanical properties of crystalline calcium-silicate-hydrates: Comparison with cementitious c-s-h gels. Phys. Status Solidi A 2007, 204, 1775–1780. [Google Scholar] [CrossRef]
- Manzano, H.; Dolado, J.S.; Ayuela, A. Structural, mechanical, and reactivity properties of tricalcium aluminate using first-principles calculations. J. Am. Ceram. Soc. 2009, 92, 897–902. [Google Scholar] [CrossRef]
- Bentz, D.P. Three-dimensional computer simulation of portland cement hydration and microstructure development. J. Am. Ceram. Soc. 1997, 80, 3–21. [Google Scholar] [CrossRef]
- Bittnar, Z. Microstructure-based micromechanical prediction of elastic properties in hydrating cement paste. Cem. Concr. Res. 2006, 36, 1708–1718. [Google Scholar]
- Hain, M.; Wriggers, P. Numerical homogenization of hardened cement paste. Comput. Mech. 2008, 42, 197–212. [Google Scholar] [CrossRef]
- Valentini, L.; Parisatto, M.; Russo, V.; Ferrari, G.; Bullard, J.W.; Angel, R.J.; Dalconi, M.C.; Artioli, G. Simulation of the hydration kinetics and elastic moduli of cement mortars by microstructural modelling. Cem. Concr. Compos. 2014, 52, 54–63. [Google Scholar] [CrossRef]
- Schlangen, E.; Qian, Z. 3D modeling of fracture in cement-based materials. J. Multiscale Model. 2009, 1, 245–261. [Google Scholar] [CrossRef]
- Asahina, D.; Landis, E.; Bolander, J. Modeling of phase interfaces during pre-critical crack growth in concrete. Cem. Concr. Compos. 2011, 33, 966–977. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Meso-scale approach to modelling the fracture process zone of concrete subjected to uniaxial tension. Int. J. Solids Struct. 2010, 47, 957–968. [Google Scholar] [CrossRef]
- Mohammadipour, A.; Willam, K. Lattice approach in continuum and fracture mechanics. J. Appl. Mech. 2016, 83, 071003. [Google Scholar] [CrossRef]
- Asahina, D.; Aoyagi, K.; Kim, K.; Birkholzer, J.T.; Bolander, J.E. Elastically-homogeneous lattice models of damage in geomaterials. Comput. Geotech. 2017, 81, 195–206. [Google Scholar] [CrossRef]
- Schlangen, E. Experimental and Numerical Analysis of Fracture Processes in Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1993. [Google Scholar]
- Qian, Z. Multiscale Modeling of Fracture Processes in Cementitious Materials. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2012. [Google Scholar]
- Luković, M.; Schlangen, E.; Ye, G. Combined experimental and numerical study of fracture behaviour of cement paste at the microlevel. Cem. Concr. Res. 2015, 73, 123–135. [Google Scholar] [CrossRef]
- Schlangen, E.; Lukovic, M.; Šavija, B.; Copuroglu, O. Nano-indentation testing and modelling of cement paste. In Proceedings of the 10th International Conference on Mechanics and Physics of Creep, Shrinkage, and Durability of Concrete and Concrete Structures, Vienna, Austria, 21–23 September 2015.
- Zhang, J.; Scherer, G.W. Comparison of methods for arresting hydration of cement. Cem. Concr. Res. 2011, 41, 1024–1036. [Google Scholar] [CrossRef]
- Poelma, R.H.; Morana, B.; Vollebregt, S.; Schlangen, E.; van Zeijl, H.W.; Fan, X.; Zhang, G.Q. Tailoring the mechanical properties of high-aspect-ratio carbon nanotube arrays using amorphous silicon carbide coatings. Adv. Funct. Mater. 2014, 24, 5737–5744. [Google Scholar] [CrossRef]
- Zhang, M.; Jivkov, A.P. Microstructure-informed modelling of damage evolution in cement paste. Constr. Build. Mater. 2014, 66, 731–742. [Google Scholar] [CrossRef]
- Tennis, P.D.; Jennings, H.M. A model for two types of calcium silicate hydrate in the microstructure of portland cement pastes. Cem. Concr. Res. 2000, 30, 855–863. [Google Scholar] [CrossRef]
- Van Breugel, K. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1991. [Google Scholar]
- Schlangen, E.; Garboczi, E. Fracture simulations of concrete using lattice models: Computational aspects. Eng. Fract. Mech. 1997, 57, 319–332. [Google Scholar] [CrossRef]
- Hlobil, M.; Šmilauer, V.; Chanvillard, G. Micromechanical multiscale fracture model for compressive strength of blended cement pastes. Cem. Concr. Res. 2016, 83, 188–202. [Google Scholar] [CrossRef]
- Němeček, J.; Králík, V.; Šmilauer, V.; Polívka, L.; Jäger, A. Tensile strength of hydrated cement paste phases assessed by micro-bending tests and nanoindentation. Cem. Concr. Compos. 2016, 73, 164–173. [Google Scholar] [CrossRef]
- Haecker, C.-J.; Garboczi, E.; Bullard, J.; Bohn, R.; Sun, Z.; Shah, S.; Voigt, T. Modeling the linear elastic properties of portland cement paste. Cem. Concr. Res. 2005, 35, 1948–1960. [Google Scholar] [CrossRef]
- Schlangen, E. Crack Development in Concrete, Part 1: Fracture Experiments and CT-Scan Observations; Key Eng. Mater.; Trans Tech Publications: Stafa-Zurich, Switzerland, 2008; pp. 69–72. [Google Scholar]
- Schlangen, E. Crack Development in Concrete, Part 2: Modelling of Fracture Process; Key Eng. Mater.; Trans Trans Tech Publications: Stafa-Zurich, Switzerland, 2008; pp. 73–76. [Google Scholar]




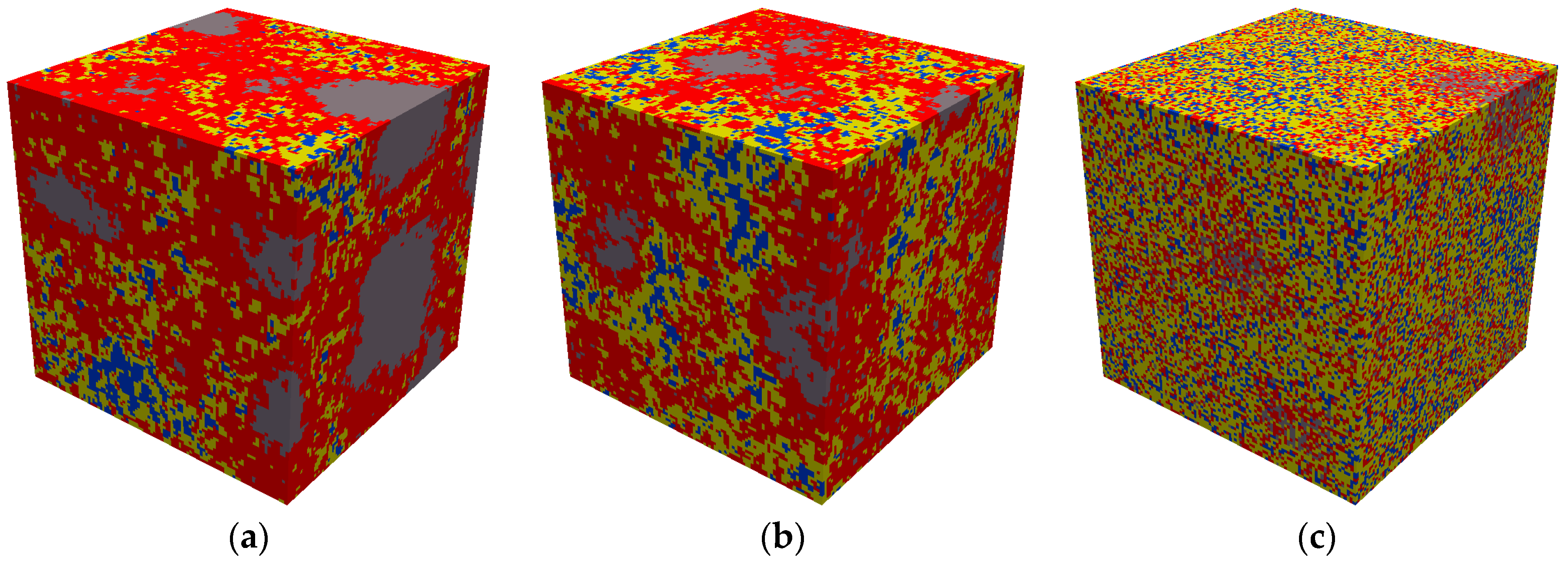
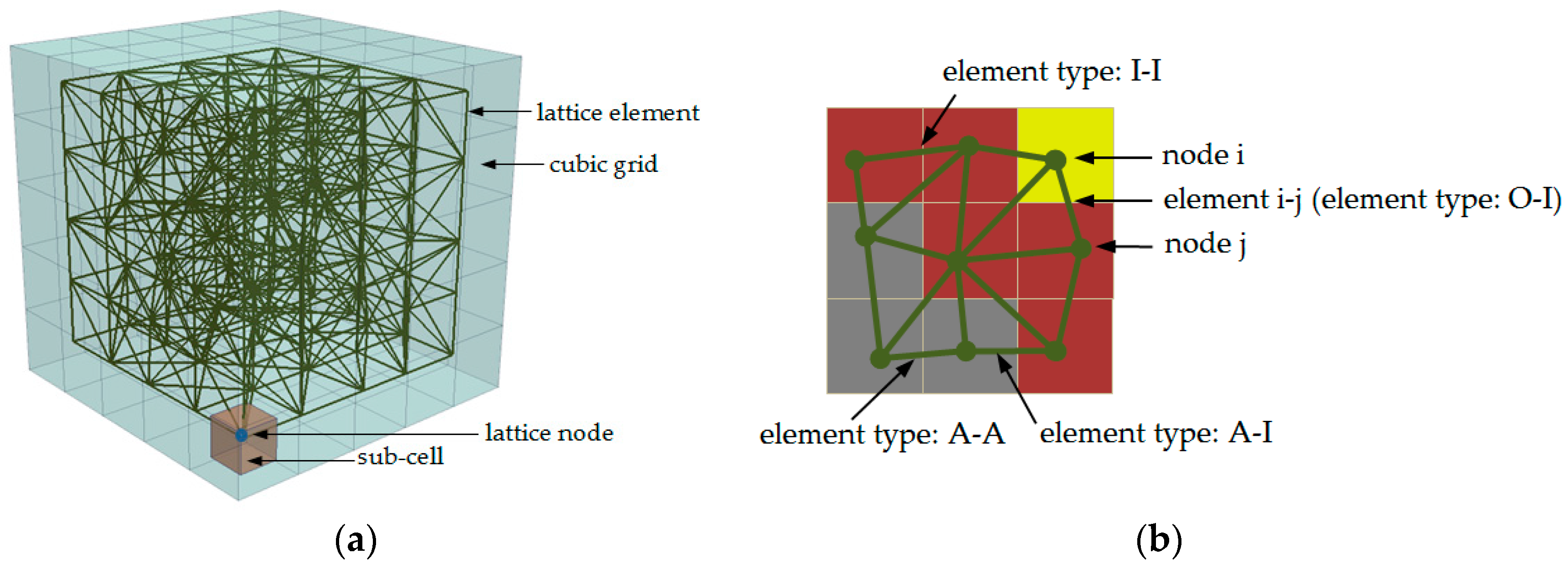

| Element Type | Phase 1 | Phase 2 |
|---|---|---|
| A–A | Anhydrous cement | Anhydrous cement |
| I–I | Inner product | Inner product |
| O–O | Outer product | Outer product |
| A–I | Anhydrous cement | Inner product |
| I–O | Inner product | Outer product |
| A–O | Anhydrous cement | Outer product |
| Phases | Modulus of Elasticity (GPa) | Hardness (GPa) |
|---|---|---|
| Anhydrous cement | 99.2 | 8.24 |
| Inner product | 31.6 | 1.14 |
| Outer product | 25.2 | 0.75 |
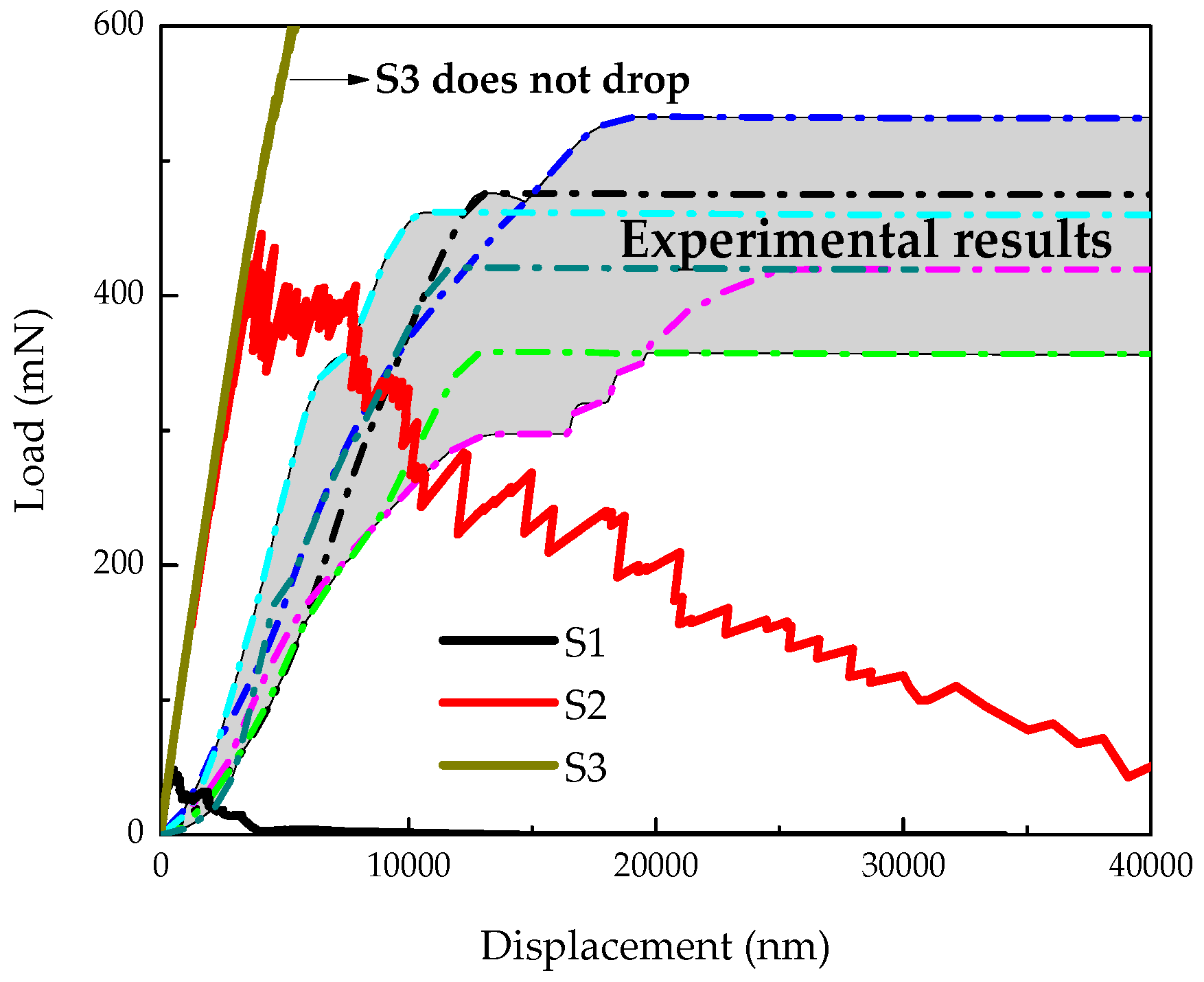
| Set | Anhydrous Cement | Inner Product | Outer Product | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E (GPa) | ft (GPa) | fc (GPa) | E (GPa) | ft (GPa) | fc (GPa) | E (GPa) | ft (GPa) | fc (GPa) | |
| S1 | 99.2 | 0.683 | 6.830 | 31.6 | 0.092 | 0.92 | 25.2 | 0.0583 | 0.58 |
| S2 | 99.2 | 0.683 | 68.3 | 31.6 | 0.092 | 9.2 | 25.2 | 0.0583 | 5.8 |
| S3 | 99.2 | 0.683 | ∞ | 31.6 | 0.092 | ∞ | 25.2 | 0.058 | ∞ |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Šavija, B.; Chaves Figueiredo, S.; Lukovic, M.; Schlangen, E. Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling. Materials 2016, 9, 907. https://doi.org/10.3390/ma9110907
Zhang H, Šavija B, Chaves Figueiredo S, Lukovic M, Schlangen E. Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling. Materials. 2016; 9(11):907. https://doi.org/10.3390/ma9110907
Chicago/Turabian StyleZhang, Hongzhi, Branko Šavija, Stefan Chaves Figueiredo, Mladena Lukovic, and Erik Schlangen. 2016. "Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling" Materials 9, no. 11: 907. https://doi.org/10.3390/ma9110907
APA StyleZhang, H., Šavija, B., Chaves Figueiredo, S., Lukovic, M., & Schlangen, E. (2016). Microscale Testing and Modelling of Cement Paste as Basis for Multi-Scale Modelling. Materials, 9(11), 907. https://doi.org/10.3390/ma9110907









