Room Temperature Electroluminescence from Tensile-Strained Si0.13Ge0.87/Ge Multiple Quantum Wells on a Ge Virtual Substrate
Abstract
:1. Introduction
2. Experiments
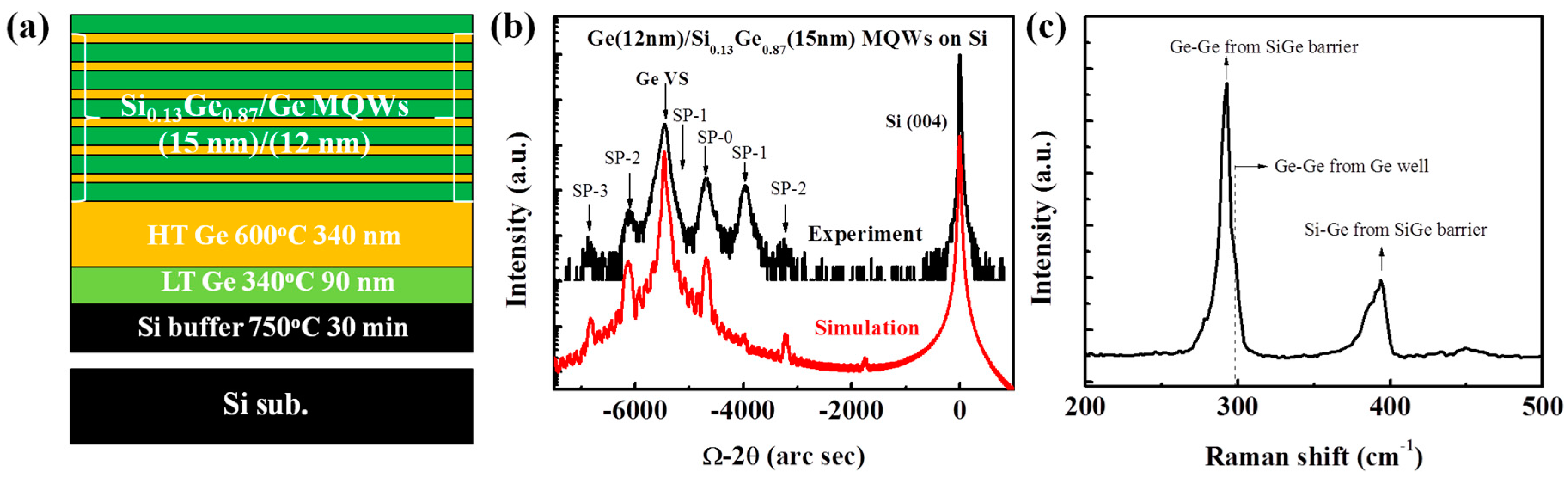
2.1. Material Growth
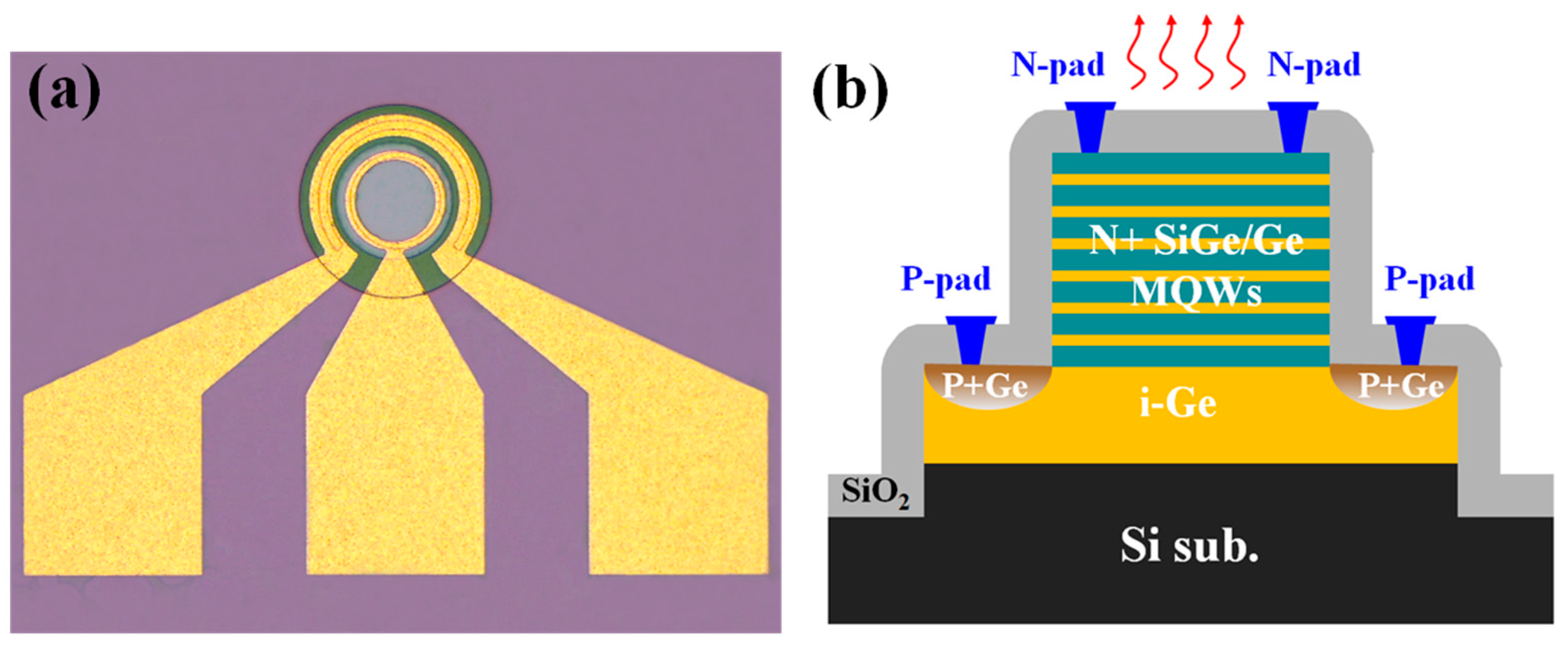
2.2. Device Fabrication
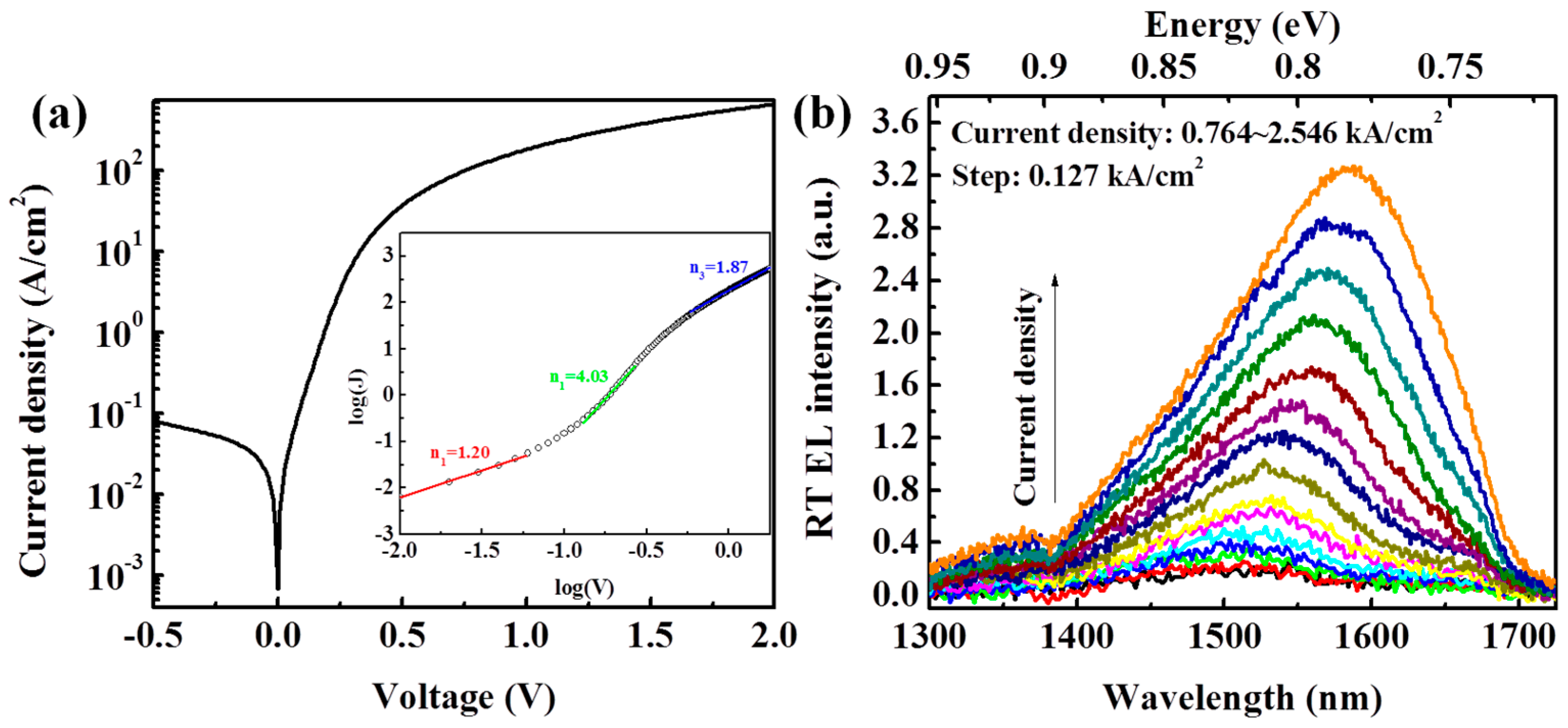
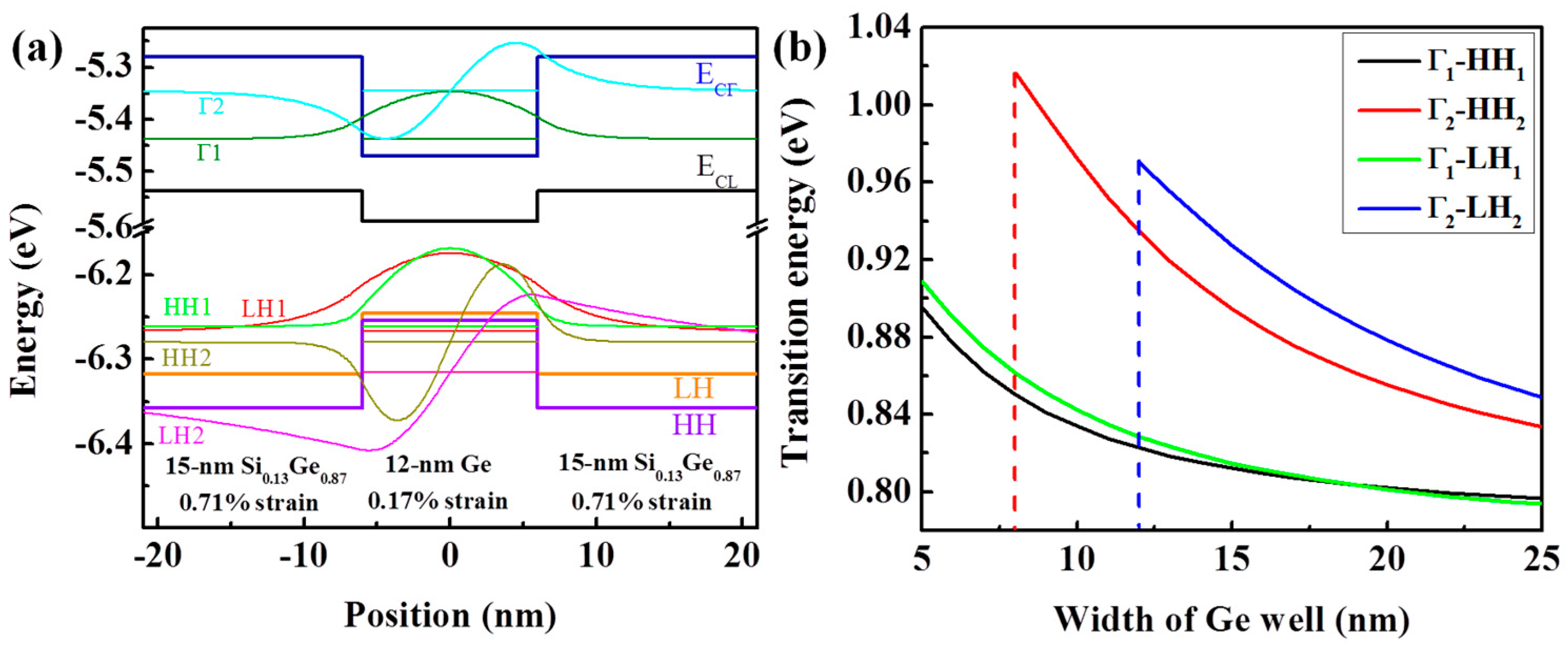
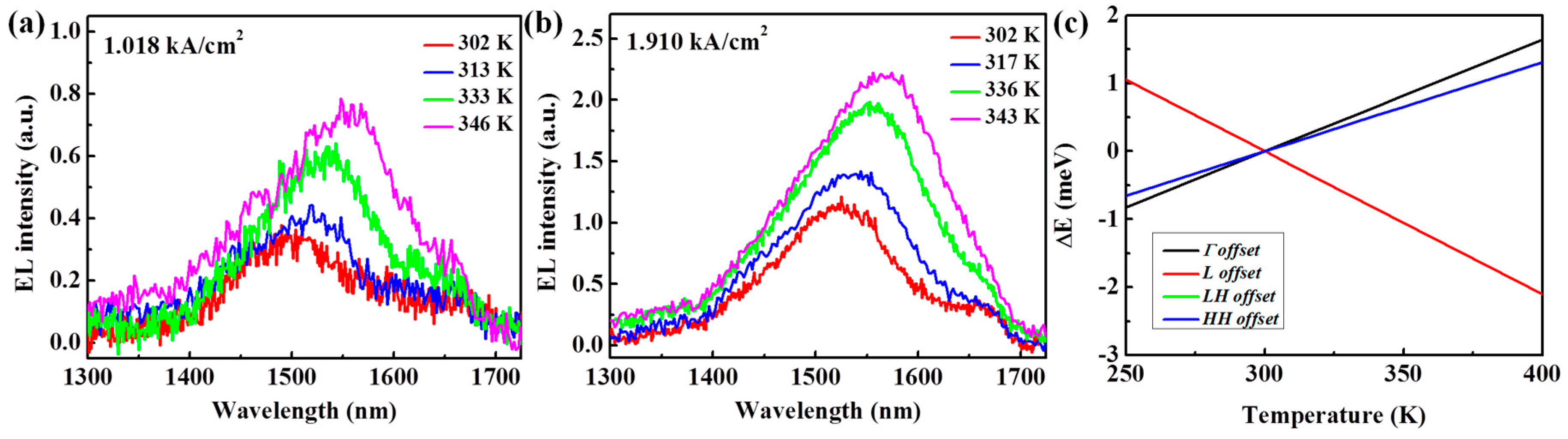
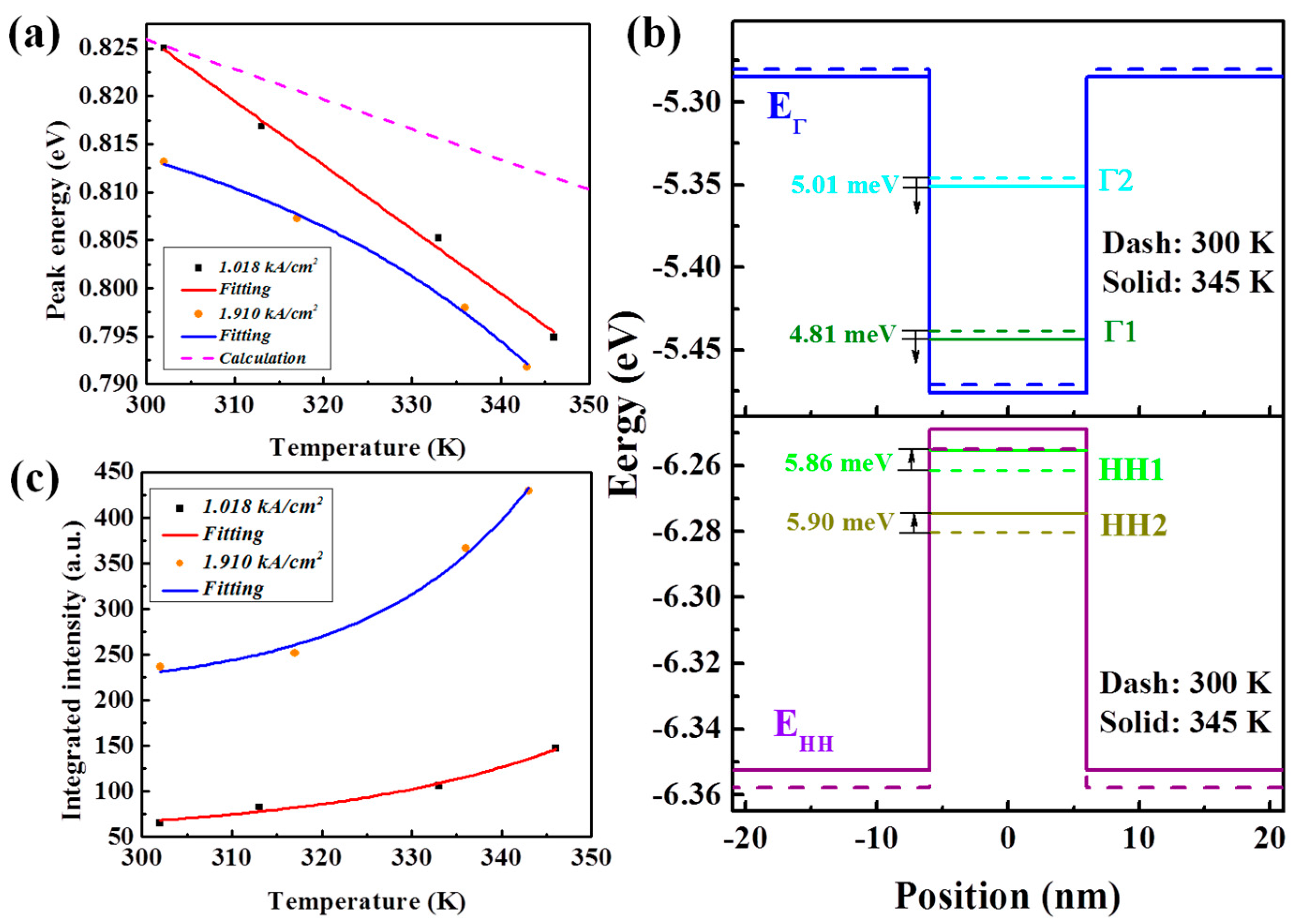
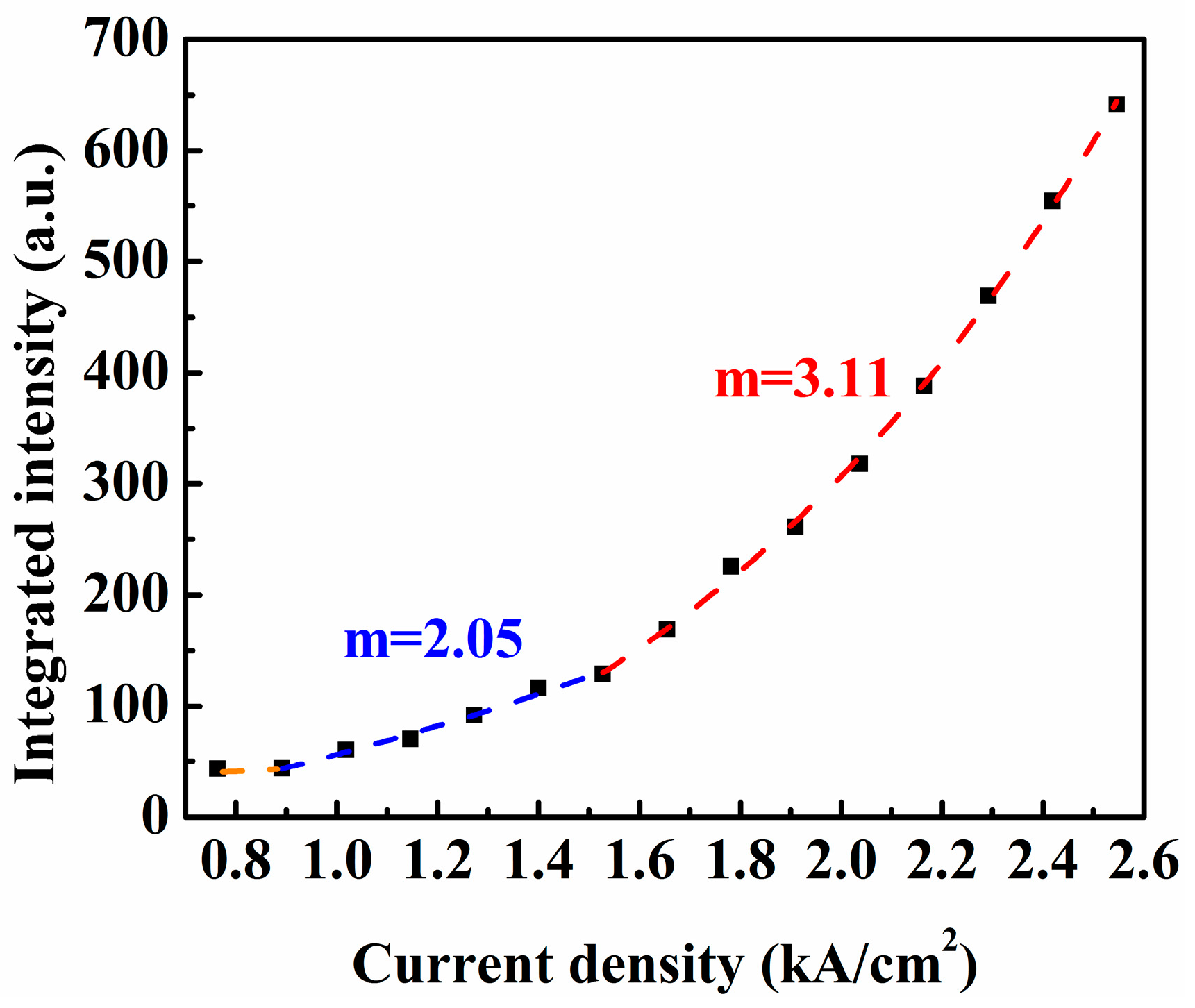
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moore, G.E. Cramming more components onto integrated circuits. Electronics 1965, 38, 114–117. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Saito, S. Ge-on-Si photonic devices for photonic-electronic integration on a Si platform. IEICE Electron. Express 2014, 11, 1–17. [Google Scholar] [CrossRef]
- Haensch, W.; Nowak, E.J.; Dennard, R.H.; Solomon, P.M.; Bryant, A.; Dokumaci, O.H.; Kumar, A.; Wang, X.; Johnson, J.B.; Fischetti, M.V. Silicon CMOS devices beyond scaling. IBM J. Res. Dev. 2006, 50, 339–361. [Google Scholar] [CrossRef]
- Kirchain, R.; Kimerling, L. A roadmap for nanophotonics. Nat. Photonics 2007, 1, 303–305. [Google Scholar] [CrossRef]
- Lipson, M. Overcoming the limitations of microelectronics using Si nanophotonics: Solving the coupling, modulation and switching challenges. Nanotechnology 2004, 15, S622–S627. [Google Scholar] [CrossRef]
- Maeda, T.; Ikeda, K.; Nakaharai, S.; Tezuka, T.; Sugiyama, N.; Moriyama, Y.; Takagi, S. High mobility Ge-on-insulator p-channel MOSFETs using Pt germanide Schottky source/drain. IEEE Electron Device Lett. 2005, 26, 102–104. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, H.-D.; Morse, M.; Paniccia, M.J.; Zadka, M.; Litski, S.; Sarid, G.; Pauchard, A.; Kuo, Y.-H.; Chen, H.-W.; et al. Monolithic germanium/silicon avalanche photodiodes with 340 GHz gain–bandwidth product. Nat. Photonics 2009, 3, 59–63. [Google Scholar] [CrossRef]
- Kuo, Y.-H.; Lee, Y.K.; Ge, Y.S.; Ren, S.; Roth, J.E.; Kamins, T.I.; Miller, D.A.B.; Harris, J.S. Quantum-confined Stark effect in Ge/SiGe quantum wells on Si for optical modulators. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1503–1513. [Google Scholar] [CrossRef]
- Sun, X.C.; Liu, J.F.; Kimerling, L.C.; Michel, J. Toward a germanium laser for integrated silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 124–131. [Google Scholar]
- Ghrib, A.; de Kersauson, M.; EI Kurdi, M.; Jakomin, R.; Beaudoin, G.; Sauvage, S.; Fishman, G.; Ndong, G.; Chaigneau, M.; Ossikovski, R.; et al. Control of tensile strain in germanium waveguides through silicon nitride layers. Appl. Phys. Lett. 2012, 100, 201104. [Google Scholar] [CrossRef]
- Cai, Y.; Han, Z.H.; Wang, X.X.; Camacho-Aguilera, R.E.; Kimerling, L.C.; Michel, J.; Liu, J.F. Analysis of threshold current behavior for bulk and quantum-well germanium laser structures. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1901009. [Google Scholar]
- Lin, G.Y.; Wang, C.; Li, C.; Chen, C.W.; Huang, Z.W.; Huang, W.; Chen, S.Y.; Lai, H.K.; Jin, C.Y.; Sun, J.M. Strong electroluminescence from direct band and defects in Ge n+/p shallow junctions at room temperature. Appl. Phys. Lett. 2016, 108, 191107. [Google Scholar] [CrossRef]
- Nam, D.; Sukhdeo, D.; Cheng, S.-L.; Roy, A.; Huang, K.C.-Y.; Brongersma, M.; Nishi, Y.; Saraswat, K. Electroluminescence from strained germanium membranes and implications for an efficient Si-compatible laser. Appl. Phys. Lett. 2012, 100, 131112. [Google Scholar] [CrossRef]
- Oehme, M.; Gollhofer, M.; Widmann, D.; Schmid, M.; Kaschel, M.; Kasper, E.; Schulze, J. Direct bandgap narrowing in Ge LED’s on Si substrates. Opt. Express 2013, 21, 2206–2211. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.C.; Liu, J.F.; Kimerling, L.C.; Michel, J. Room-temperature direct bandgap electroluminesence from Ge-on-Si light-emitting diodes. Opt. Lett. 2009, 34, 1198–1200. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.X.; Cheng, B.W.; Xue, C.L.; Xue, H.Y.; Su, S.J.; Bai, A.Q.; Luo, L.P.; Yu, Y.D.; Wang, Q.M. Electroluminescence from Ge on Si substrate at room temperature. Appl. Phys. Lett. 2009, 95, 092102. [Google Scholar] [CrossRef]
- Huang, S.H.; Lu, W.F.; Li, C.; Huang, W.; Lai, H.K.; Chen, S.Y. A CMOS-compatible approach to fabricate an ultra-thin germanium-on-insulator with large tensile strain for Si-based light emission. Opt. Express 2013, 21, 640–646. [Google Scholar] [CrossRef] [PubMed]
- Camacho-Aguilera, R.E.; Cai, Y.; Patel, N.; Bessette, J.T.; Romagnoli, M.; Kiemerling, L.C.; Michel, J. An electrically pumped germanium laser. Opt. Express 2012, 20, 11316–11320. [Google Scholar] [CrossRef] [PubMed]
- Kuo, Y.-H.; Lee, Y.K.; Ge, Y.S.; Ren, S.; Roth, J.E.; Kamins, T.; Miller, D.A.B.; Harris, J.S. Strong quantum-confined Stark effect in germanium quantum-well structures on silicon. Nature 2005, 27, 1334–1336. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.H.; Dumcenco, D.; Huang, Y.S.; Hsu, H.P.; Lai, C.H.; Lin, T.Y.; Chrastina, D.; Isella, G.; Gatti, E.; Tiong, K.K. Above-room-temperature photoluminescence from a strain-compensated Ge/Si0.15Ge0.85 multiple-quantum-well structure. Appl. Phys. Lett. 2012, 100, 141905. [Google Scholar] [CrossRef]
- Fei, E.T.; Chen, X.C.; Zang, K.; Huo, Y.J.; Shambat, G.; Miller, G.; Liu, X.; Dutt, R.; Kamins, T.I.; Vuckovic, J.; et al. Investigation of germanium quantum-well light sources. Opt. Express 2015, 23, 22424–22430. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Hu, W.X.; Li, C.; Li, Y.M.; Xue, C.L.; Li, C.B.; Zuo, Y.H.; Cheng, B.W.; Wang, Q.M. Room temperature direct-bandgap electroluminescence from n-type strain-compensated Ge/SiGe multiple quantum wells. Appl. Phys. Lett. 2012, 101, 231108. [Google Scholar] [CrossRef]
- He, C.; Liu, Z.; Zhang, X.; Huang, W.Q.; Xue, C.L.; Cheng, B.W. Direct-bandgap electroluminescence from tensile-strained Ge/SiGe multiple quantum wells at room temperature. Chin. Phys. B 2014, 23, 116103. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Li, C.; Lai, H.K.; Chen, S.Y.; Yu, J.Z. The influence of low-temperature Ge seed layer on growth of high-quality Ge epilayer on Si(100) by ultrahigh vacuum chemical vapor deposition. J. Cryst. Growth 2008, 310, 2508–2513. [Google Scholar] [CrossRef]
- Chen, Y.H.; Li, C.; Zhou, Z.W.; Lai, H.K.; Chen, S.Y.; Ding, W.C.; Cheng, B.W.; Yu, Y.D. Room temperature photoluminescence of tensile-strained Ge/Si0.13Ge0.87 quantum wells grown on silicon-based germanium virtual substrate. Appl. Phys. Lett. 2009, 94, 141902. [Google Scholar] [CrossRef]
- Sah, C.T.; Noyce, R.N.; Shockley, W. Carrier generation and recombination in pn junctions and pn junction characteristics. Proc. IRE 1957, 45, 1228–1243. [Google Scholar] [CrossRef]
- Mayes, K.; Yasan, A.; McClintock, R.; Shiell, D.; Darvish, S.R.; Kung, P.; Razeghi, M. High-power 280 nm AlGaN light-emitting diodes based on an asymmetric single-quantum well. Appl. Phys. Lett. 2004, 84, 1046–1048. [Google Scholar] [CrossRef]
- Van de Walle, C.G. Band lineups and deformation potentials in the model-solid theory. Phys. Rev. B 1989, 39, 1871–1883. [Google Scholar] [CrossRef]
- Bassani, F.; Brust, D. Effect of alloying and pressure on the band structure of germanium and silicon. Phys. Rev. 1963, 131, 1524–1529. [Google Scholar] [CrossRef]
- Weber, J.; Alonso, M.I. Near-band-gap photoluminescence of Si-Ge alloys. Phys. Rev. B 1989, 40, 5683–5693. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Wada, K.; Liu, J.F.; Cannon, D.D.; Luan, H.C.; Michel, J.; Kimerling, L.C. Strain-induced enhancement of near-infrared absorption in Ge epitaxial layers grown on Si substrate. J. Appl. Phys. 2005, 98, 013501. [Google Scholar] [CrossRef]
- Wortman, J.J.; Evans, R.A. Young’s modulus, shear modulus, and poisson’s ratio in silicon and germanium. J. Appl. Phys. 1965, 36, 153–156. [Google Scholar] [CrossRef]
- Chaisakul, P.; Marris-Morini, D.; Isella, G.; Chrastina, D.; Izard, N.; Roux, X.L.; Edmond, S.; Coudevylle, J.-R.; Vivien, L. Room temperature direct gap electroluminescence from Ge/Si0.15Ge0.85 multiple quantum well waveguide. Appl. Phys. Lett. 2011, 99, 141106. [Google Scholar] [CrossRef]
- Sun, X.C.; Liu, J.F.; Kimerling, L.C.; Michel, J. Direct gap photoluminescence of n-type tensile-strained Ge-on-Si. Appl. Phys. Lett. 2009, 95, 011911. [Google Scholar] [CrossRef]
- Varshni, Y.P. Temperature dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Lautenschlager, P.; Allen, P.B.; Cardona, M. Temperature dependence of band gaps in Si and Ge. Phy. Rev. B 1985, 31, 2163–2171. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, G.; Chen, N.; Zhang, L.; Huang, Z.; Huang, W.; Wang, J.; Xu, J.; Chen, S.; Li, C. Room Temperature Electroluminescence from Tensile-Strained Si0.13Ge0.87/Ge Multiple Quantum Wells on a Ge Virtual Substrate. Materials 2016, 9, 803. https://doi.org/10.3390/ma9100803
Lin G, Chen N, Zhang L, Huang Z, Huang W, Wang J, Xu J, Chen S, Li C. Room Temperature Electroluminescence from Tensile-Strained Si0.13Ge0.87/Ge Multiple Quantum Wells on a Ge Virtual Substrate. Materials. 2016; 9(10):803. https://doi.org/10.3390/ma9100803
Chicago/Turabian StyleLin, Guangyang, Ningli Chen, Lu Zhang, Zhiwei Huang, Wei Huang, Jianyuan Wang, Jianfang Xu, Songyan Chen, and Cheng Li. 2016. "Room Temperature Electroluminescence from Tensile-Strained Si0.13Ge0.87/Ge Multiple Quantum Wells on a Ge Virtual Substrate" Materials 9, no. 10: 803. https://doi.org/10.3390/ma9100803
APA StyleLin, G., Chen, N., Zhang, L., Huang, Z., Huang, W., Wang, J., Xu, J., Chen, S., & Li, C. (2016). Room Temperature Electroluminescence from Tensile-Strained Si0.13Ge0.87/Ge Multiple Quantum Wells on a Ge Virtual Substrate. Materials, 9(10), 803. https://doi.org/10.3390/ma9100803




