Delineation of First-Order Elastic Property Closures for Hexagonal Metals Using Fast Fourier Transforms
Abstract
:1. Introduction
2. Representation of ODF Using FFTs and Texture Hulls for HCP Metals
| Symmetries 1–4 | Symmetries 5–8 | Symmetries 9–12 |
|---|---|---|
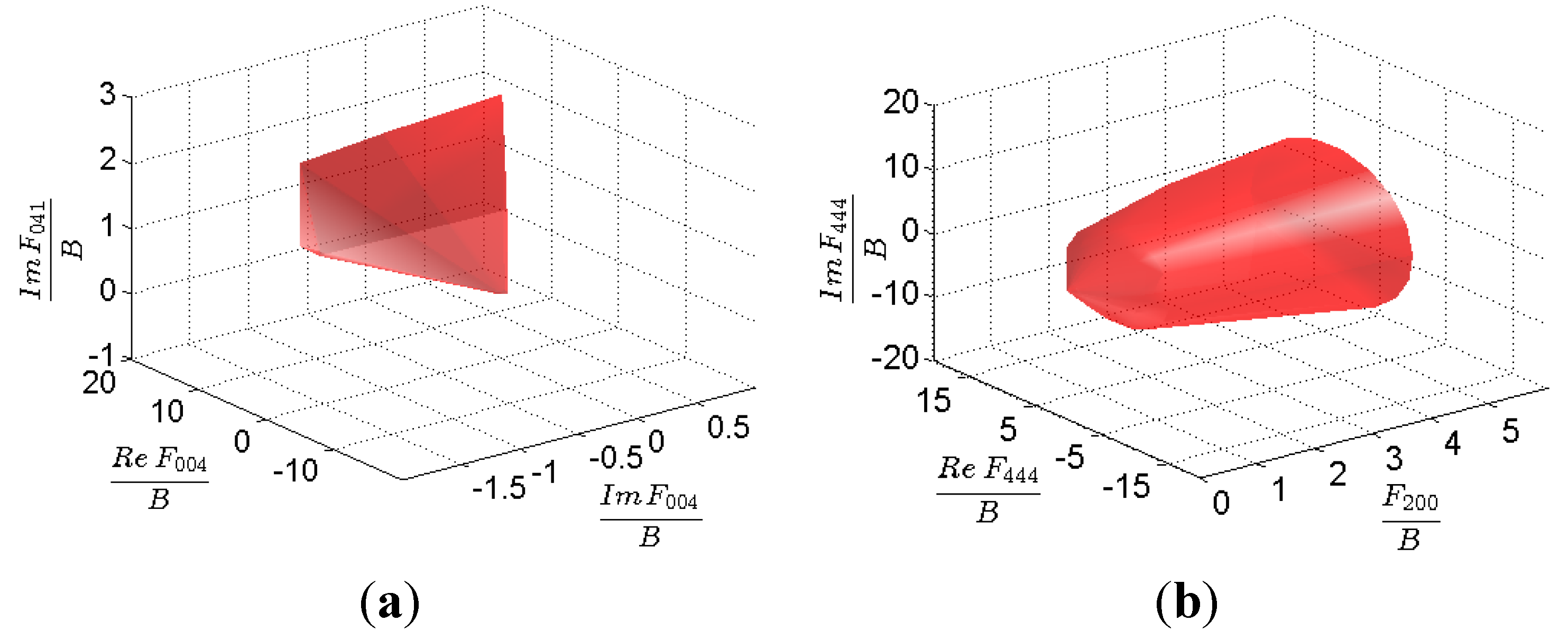
3. Property Closures
3.1. Elastic Stiffness for HCP Metals
3.2. Representation of the Elastic Stiffness for HCP Metals Using FFTs
3.3. First-Order Elastic Stiffness Bounds
3.4. Homogenization of the Elastic Properties in Fourier Space
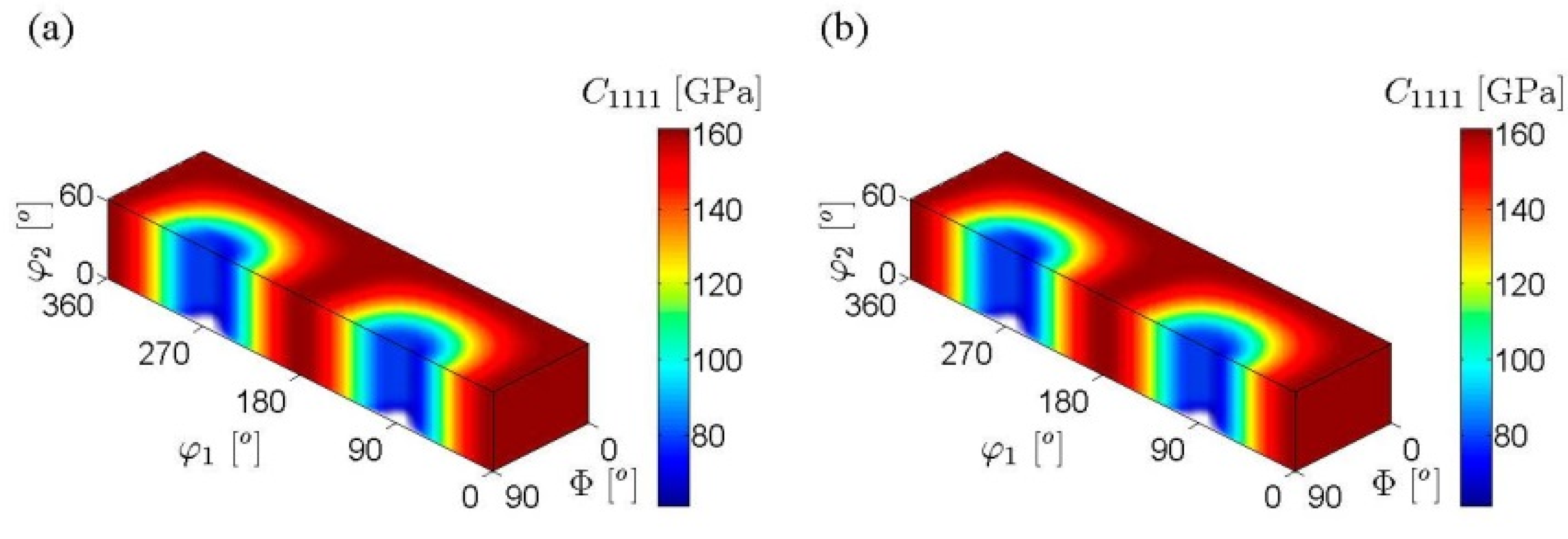
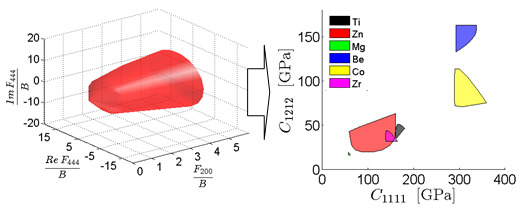
3.5. Computation of Property Closures for HCP Metals
3.6. Atlases of Property Closures for HCP Metals
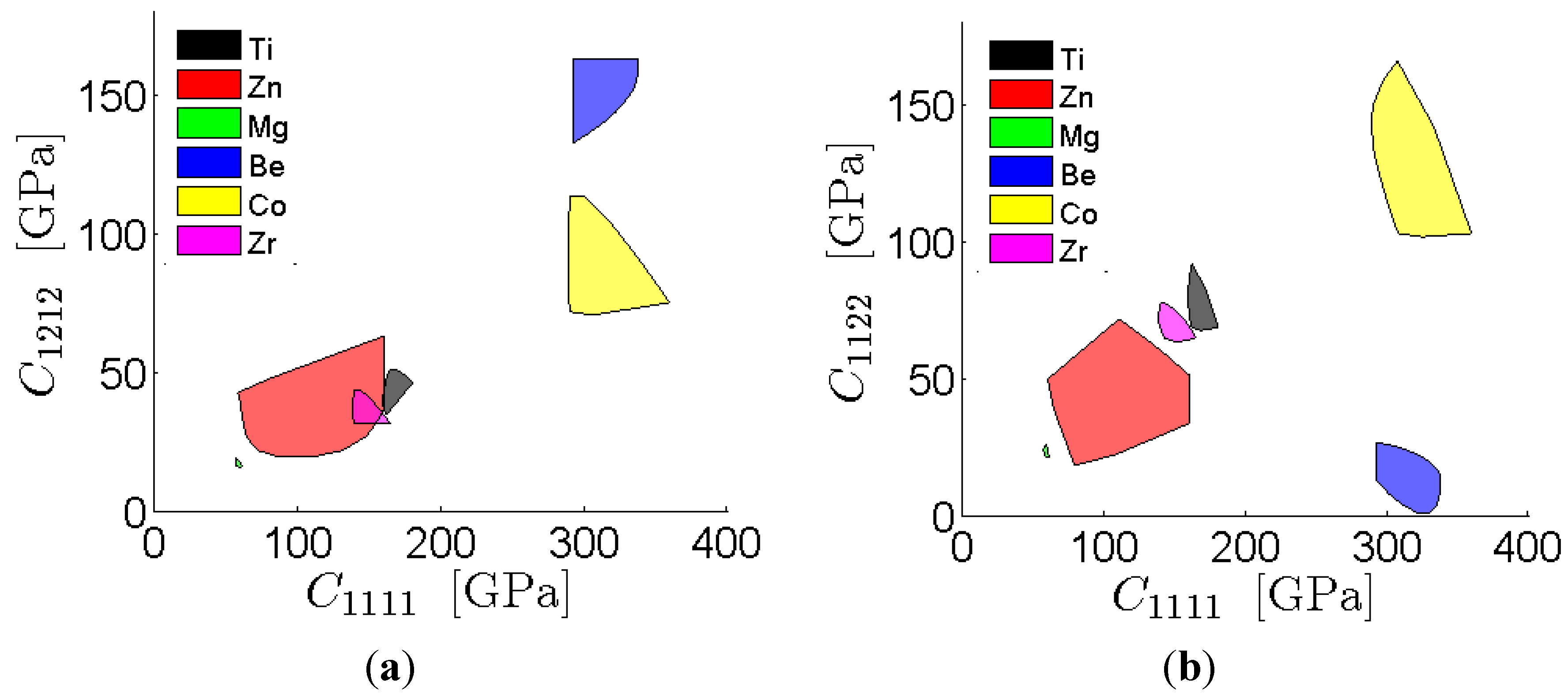
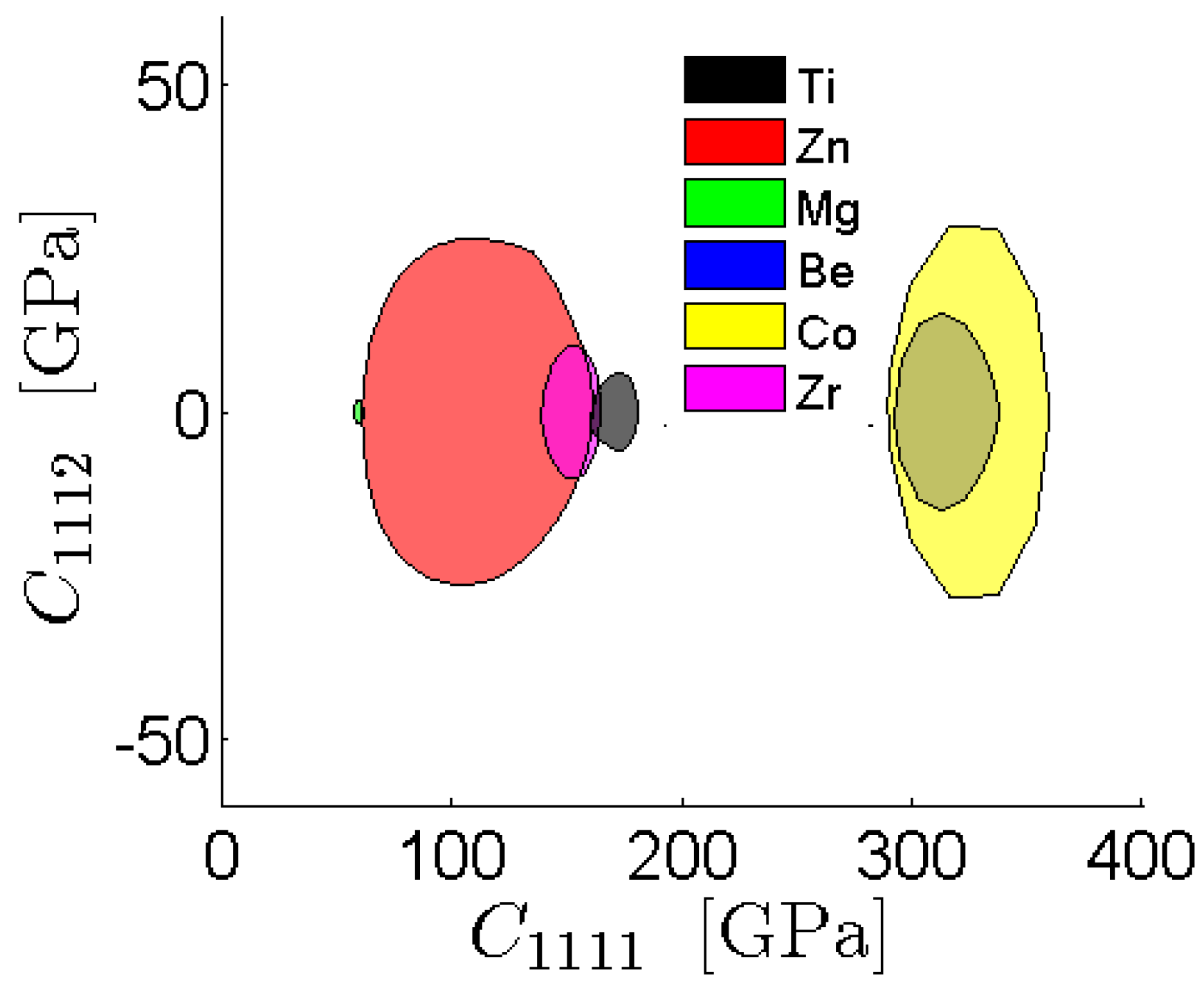
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| k1 k2 k3 | C1111 | k1 k2 k3 | C1112 | k1 k2 k3 | C1113 |
| 0 0 0 | 3.645 × 107 + 0j | 0 0 0 | 1.346 × 10−3 + 0j | 0 0 0 | 3.474 × 10−4 + 0j |
| 0 0 2 | 2.916 × 106 − 8.017 × 10−4j | 0 0 2 | −1.024 × 10−3 − 1.458 × 106j | 0 2 1 | 1.458 × 106 − 1.752 × 10−3j |
| 0 0 4 | 2.187 × 106 + 1.490 × 10−3j | 0 0 4 | −3.287 × 10−4 − 2.187 × 106j | 0 2 3 | 1.458 × 106 − 9.201 × 10−4j |
| 0 2 0 | 2.916 × 106 − 8.017 × 10−4j | 0 2 4 | 5.437 × 10−4 + 1.458 × 106j | 0 2 357 | −1.458 × 106 + 8.970 × 10−4j |
| 0 2 4 | −1.458 × 106 − 2.353 × 10−4j | 0 2 356 | 3.103 × 10−4 − 1.458 × 106j | 0 2 359 | −1.458 × 106 + 1.470 × 10−3j |
| 0 2 356 | −1.458 × 106 − 1.324 × 10−3j | 0 4 2 | 5.819 × 10−4 + 7.290 × 105j | 0 4 1 | 2.187 × 106 − 3.252 × 10−3j |
| 0 4 0 | 2.187 × 106 + 1.490 × 10−3j | 0 4 4 | −1.197 × 10−3 − 3.645 × 105j | 0 4 3 | −7.290 × 105 + 7.335 × 10−4j |
| 0 4 2 | −1.458 × 106 − 2.353 × 10−4j | 0 4 356 | −3.065 × 10−4 + 3.645 × 105j | 0 4 357 | 7.290 × 105 + 1.229 × 10−3j |
| 0 4 4 | 3.645 × 105 − 4.225 × 10−4j | 0 4 358 | −1.105 × 10−3 − 7.290 × 105j | 0 4 359 | −2.187 × 106 + 1.318 × 10−3j |
| 0 4 356 | 3.645 × 105 − 2.071 × 10−12j | – | – | – | – |
| 0 4 358 | −1.458 × 106 + 1.324 × 10−3j | – | – | – | – |
| k1 k2 k3 | C1122 | k1 k2 k3 | C1123 | k1 k2 k3 | C1133 |
| 0 0 0 | 4.374 × 106 + 0j | 0 0 0 | −8.664 × 10−4 + 0j | 0 0 0 | 5.832 × 106 + 0j |
| 0 0 4 | −2.187 × 106 + 7.111 × 10−4j | 0 2 1 | −3.505 × 10−3 + 1.458 × 106j | 0 0 2 | −2.916 × 106 + 1.366 × 10−5j |
| 0 2 0 | −2.916 × 106 + 3.868 × 10−3j | 0 2 3 | 2.036 × 10−3 − 1.458 × 106j | 0 4 0 | −2.916 × 106 + 3.465 × 10−3j |
| 0 2 4 | 1.458 × 106 − 2.976 × 10−3j | 0 2 357 | −1.196 × 10−3 − 1.458 × 106j | 0 4 2 | 1.458 × 106 − 2.873 × 10−3j |
| 0 2 356 | 1.458 × 106 − 2.763 × 10−3j | 0 2 359 | 2.458 × 10−3 + 1.458 × 106j | 0 4 358 | 1.458 × 106 − 2.842 × 10−3j |
| 0 4 0 | 7.290 × 105 − 4.308 × 10−3j | 0 4 1 | 4.336 × 10−3 − 7.290 × 105j | – | – |
| 0 4 4 | −3.645 × 105 + 2.327 × 10−3j | 0 4 3 | −3.380 × 10−3 + 7.290 × 105j | – | – |
| 0 4 356 | −3.645 × 105 + 3.997 × 10−3j | 0 4 357 | 2.269 × 10−4 + 7.290 × 105j | – | – |
| – | – | 0 4 359 | −2.354 × 10−3 − 7.290 × 105j | – | – |
| k1 k2 k3 | C1212 | k1 k2 k3 | C1312 | k1 k2 k3 | C1313 |
| 0 0 0 | 1.604 × 107 + 0j | 0 0 0 | 5.001 × 10−4 + 0j | 0 0 0 | 1.166 × 107 + 0j |
| 0 0 4 | −2.187 × 106 + 1.968 × 10−3j | 0 2 1 | −2.863 × 10−3 − 1.458 × 106j | 0 2 0 | −2.916 × 106 + 1.449 × 10−3j |
| 0 2 0 | 2.916 × 106 − 3.666 × 10−4j | 0 2 3 | 1.106 × 10−4 − 1.458 × 106j | 0 2 2 | −1.458 × 106 − 2.397 × 10−3j |
| 0 2 4 | 1.458 × 106 − 3.097 × 10−3j | 0 2 357 | −1.002 × 10−3 − 1.458 × 106j | 0 2 358 | −1.458 × 106 − 2.518 × 10−3j |
| 0 2 356 | 1.458 × 106 − 2.027 × 10−3j | 0 2 359 | −1.417 × 10−3 − 1.458 × 106j | 0 4 0 | −2.916 × 106 + 2.298 × 10−4j |
| 0 4 0 | 7.290 × 105 + 3.823 × 10−3j | 0 4 1 | −7.437 × 10−4 − 7.290 × 105j | 0 4 2 | 1.458 × 106 + 1.402 × 10−3j |
| 0 4 4 | −3.645 × 105 + 1.073 × 10−3j | 0 4 3 | −6.925 × 10−4 + 7.290 × 105j | 0 4 358 | 1.458 × 106 + 5.424 × 10−4j |
| 0 4 356 | −3.645 × 105 + 3.916 × 10−3j | 0 4 357 | −3.324 × 10−4 + 7.290 × 105j | – | – |
| – | – | 0 4 359 | −8.323 × 10−5 − 7.290 × 105j | – | – |
| k1 k2 k3 | C2212 | k1 k2 k3 | C2213 | k1 k2 k3 | C2222 |
| 0 0 0 | −2.227 × 10−3 + 0j | 0 0 0 | 1.855 × 10−3 + 0j | 0 0 0 | 3.645 × 107 + 0j |
| 0 0 2 | −8.014 × 10−4 − 1.458 × 106j | 0 2 1 | −1.458 × 106 + 2.242 × 10−3j | 0 0 2 | −2.916 × 106 + 2.652 × 10−3j |
| 0 0 4 | 1.646 × 10−3 + 2.187 × 106j | 0 2 3 | −1.458 × 106 − 9.985 × 10−4j | 0 0 4 | 2.187 × 106 − 2.554 × 10−3j |
| 0 2 4 | −1.432 × 10−3 − 1.458 × 106j | 0 2 357 | 1.458 × 106 − 9.966 × 10−4j | 0 2 0 | 2.916 × 106 + 1.752 × 10−3j |
| 0 2 356 | −1.473 × 10−3 + 1.458 × 106j | 0 2 359 | 1.458 × 106 + 2.525 × 10−3j | 0 2 4 | −1.458 × 106 − 8.290 × 10−5j |
| 0 4 2 | 1.079 × 10−4 + 7.290 × 105j | 0 4 1 | 7.290 × 105 − 9.776 × 10−4j | 0 2 356 | −1.458 × 106 − 3.054 × 10−3j |
| 0 4 4 | 1.413 × 10−3 + 3.645 × 105j | 0 4 3 | 7.290 × 105 + 4.229 × 10−3j | 0 4 0 | 2.187 × 106 − 7.525 × 10−4j |
| 0 4 356 | 2.592 × 10−4 − 3.645 × 105j | 0 4 357 | −7.290 × 105 − 1.011 × 10−4j | 0 4 2 | 1.458 × 106 − 2.064 × 10−3j |
| 0 4 358 | −4.406 × 10−4 − 7.290 × 105j | 0 4 359 | −7.290 × 105 − 3.638 × 10−3j | 0 4 4 | 3.645 × 105 − 2.895 × 10−4j |
| – | – | – | – | 0 4 356 | 3.645 × 105 + 8.692 × 10−4j |
| – | – | – | – | 0 4 358 | 1.458 × 106 + 1.344 × 10−3j |
| k1 k2 k3 | C2223 | k1 k2 k3 | C2233 | k1 k2 k3 | C2312 |
| 0 0 0 | −3.273 × 10−4 + 0j | 0 0 0 | 5.832 × 106 + 0j | 0 0 0 | −5.371 × 10−4 + 0j |
| 0 2 1 | 6.770 × 10−5 − 1.458 × 106j | 0 0 2 | 2.916 × 106 − 8.777 × 10−4j | 0 2 1 | 1.458 × 106 − 9.363 × 10−4j |
| 0 2 3 | 1.475 × 10−3 + 1.458 × 106j | 0 4 0 | −2.916 × 106 + 4.489 × 10−3j | 0 2 3 | −1.458 × 106 − 4.469 × 10−4j |
| 0 2 357 | 1.473 × 10−3 + 1.458 × 106j | 0 4 2 | −1.458 × 106 + 3.561 × 10−3j | 0 2 357 | 1.458 × 106 − 3.113 × 10−4j |
| 0 2 359 | −1.745 × 10−3 − 1.458 × 106j | 0 4 358 | −1.458 × 106 + 2.759 × 10−3j | 0 2 359 | −1.458 × 106 + 2.436 × 10−3j |
| 0 4 1 | −2.036 × 10−3 − 2.187 × 106j | – | – | 0 4 1 | 7.290 × 105 − 3.767 × 10−4j |
| 0 4 3 | 4.109 × 10−4 − 7.290 × 105j | – | – | 0 4 3 | 7.290 × 105 + 7.465 × 10−4j |
| 0 4 357 | 1.317 × 10−4 − 7.290 × 105j | – | – | 0 4 357 | −7.290 × 105 − 4.772 × 10−4j |
| 0 4 359 | −1.982 × 10−3 − 2.187 × 106j | – | – | 0 4 359 | −7.290 × 105 + 6.635 × 10−4j |
| k1 k2 k3 | C2313 | k1 k2 k3 | C2323 | k1 k2 k3 | C3312 |
| 0 0 0 | −4.698 × 10−4 + 0j | 0 0 0 | 1.166 × 107 + 0j | 0 0 0 | 5.534 × 10−4 + 0j |
| 0 2 2 | 2.663 × 10−3 + 1.458 × 106j | 0 2 0 | −2.916 × 106 + 3.338 × 10−3j | 0 0 2 | 2.781 × 10−4 + 2.916 × 106j |
| 0 2 358 | −1.665 × 10−3 − 1.458 × 106j | 0 2 2 | 1.458 × 106 + 2.699 × 10−3j | 0 4 2 | −6.452 × 10−3 − 1.458 × 106j |
| 0 4 2 | −3.239 × 10−3 − 1.458 × 106j | 0 2 358 | 1.458 × 106 + 3.103 × 10−3j | 0 4 358 | 5.710 × 10−3 + 1.458 × 106j |
| 0 4 358 | 2.674 × 10−3 + 1.458 × 106j | 0 4 0 | −2.916 × 106 + 1.859 × 10−3j | – | – |
| – | – | 0 4 2 | −1.458 × 106 + 6.743 × 10−4j | – | – |
| – | – | 0 4 358 | −1.458 × 106 − 9.184 × 10−4j | – | – |
| k1 k2 k3 | C3313 | k1 k2 k3 | C3323 | k1 k2 k3 | C3333 |
| 0 0 0 | 3.737 × 10−4 + 0j | 0 0 0 | 3.272 × 10−4 + 0j | 0 0 0 | 3.499 × 107 + 0j |
| 0 4 1 | −2.916 × 106 + 1.377 × 10−3j | 0 4 1 | 2.203 × 10−3 + 2.916 × 106j | 0 4 0 | 5.832 × 106 + 2.951 × 10−11j |
| 0 4 359 | 2.916 × 106 − 2.212 × 10−3j | 0 4 359 | 3.092 × 10−4 + 2.916 × 106j | – | – |
| k1 k2 k3 | C1111 | k1 k2 k3 | C1112 | k1 k2 k3 | C1113 |
| 0 0 0 | 1.021 × 107 + 0j | 0 0 0 | −1.346 × 10−3 + 0j | 0 0 0 | −3.474 × 10−4 + 0j |
| 0 0 2 | −2.916 × 106 + 4.497 × 10−4j | 0 0 2 | 1.024 × 10−3 + 1.458 × 106j | 0 2 1 | −1.458 × 106 + 1.752 × 10−3j |
| 0 0 4 | −2.187 × 106 − 3.121 × 10−3j | 0 0 4 | 3.287 × 10−4 + 2.187 × 106j | 0 2 3 | −1.458 × 106 + 9.201 × 10−4j |
| 0 2 0 | −2.916 × 106 + 4.497 × 10−4j | 0 2 4 | −5.437 × 10−4 − 1.458 × 106j | 0 2 357 | 1.458 × 106 − 8.970 × 10−4j |
| 0 2 4 | 1.458 × 106 + 1.246 × 10−3j | 0 2 356 | −3.103 × 10−4 + 1.458 × 106j | 0 2 359 | 1.458 × 106 − 1.470 × 10−3j |
| 0 2 356 | 1.458 × 106 + 5.795 × 10−4j | 0 4 2 | −5.819 × 10−4 − 7.290 × 105j | 0 4 1 | −2.187 × 106 + 3.252 × 10−3j |
| 0 4 0 | −2.187 × 106 − 3.121 × 10−3j | 0 4 4 | 1.197 × 10−3 + 3.645 × 105j | 0 4 3 | 7.290 × 105 − 7.335 × 10−4j |
| 0 4 2 | 1.458 × 106 + 1.246 × 10−3j | 0 4 356 | 3.065 × 10−4 − 3.645 × 105j | 0 4 357 | −7.290 × 105 − 1.229 × 10−3j |
| 0 4 4 | −3.645 × 105 − 3.397 × 10−4j | 0 4 358 | 1.105 × 10−3 + 7.290 × 105j | 0 4 359 | 2.187 × 106 − 1.318 × 10−3j |
| 0 4 356 | −3.645 × 105 + 7.221 × 10−12j | – | – | – | – |
| 0 4 358 | 1.458 × 106 − 5.795 × 10−4j | – | – | – | – |
| k1 k2 k3 | C1122 | k1 k2 k3 | C1123 | k1 k2 k3 | C1133 |
| 0 0 0 | 1.895 × 107 + 0j | 0 0 0 | −1.405 × 10−3 + 0j | 0 0 0 | 2.916 × 107 + 0j |
| 0 0 4 | 2.187 × 106 + 2.054 × 10−3j | 0 2 1 | 3.890 × 10−3 + 4.374 × 106j | 0 0 2 | −2.916 × 106 + 2.518 × 10−3j |
| 0 2 0 | −8.748 × 106 − 5.686 × 10−3j | 0 2 3 | 1.772 × 10−3 + 1.458 × 106j | 0 2 0 | 5.832 × 106 − 5.718 × 10−4j |
| 0 2 4 | −1.458 × 106 − 1.370 × 10−4j | 0 2 357 | 1.828 × 10−3 + 1.458 × 106j | 0 2 2 | 2.916 × 106 − 3.981 × 10−3j |
| 0 2 356 | −1.458 × 106 + 2.013 × 10−3j | 0 2 359 | 1.475 × 10−3 + 4.374 × 106j | 0 2 358 | 2.916 × 106 + 4.465 × 10−4j |
| 0 4 0 | −7.290 × 105 − 1.318 × 10−2j | 0 4 1 | 1.098 × 10−3 + 7.290 × 105j | 0 4 0 | 2.916 × 106 − 5.226 × 10−4j |
| 0 4 4 | 3.645 × 105 + 5.098 × 10−3j | 0 4 3 | 3.059 × 10−3 − 7.290 × 105j | 0 4 2 | −1.458 × 106 + 9.562 × 10−3j |
| 0 4 356 | 3.645 × 105 + 4.815 × 10−3j | 0 4 357 | −1.042 × 10−3 − 7.290 × 105j | 0 4 358 | −1.458 × 106 + 7.009 × 10−3j |
| – | – | 0 4 359 | −8.954 × 10−4 + 7.290 × 105j | – | – |
| k1 k2 k3 | C1212 | k1 k2 k3 | C1312 | k1 k2 k3 | C1313 |
| 0 0 0 | −4.374 × 106 + 0j | 0 0 0 | 8.664 × 10−4 + 0j | 0 0 0 | −5.832 × 106 + 0j |
| 0 0 4 | 2.187 × 106 − 7.102 × 10−4j | 0 2 1 | 3.505 × 10−3 − 1.458 × 106j | 0 0 2 | 2.916 × 106 − 1.366 × 10−5j |
| 0 2 0 | 2.916 × 106 − 3.869 × 10−3j | 0 2 3 | −2.036 × 10−3 + 1.458 × 106j | 0 4 0 | 2.916 × 106 − 3.465 × 10−3j |
| 0 2 4 | −1.458 × 106 + 2.976 × 10−3j | 0 2 357 | 1.196 × 10−3 + 1.458 × 106j | 0 4 2 | −1.458 × 106 + 2.873 × 10−3j |
| 0 2 356 | −1.458 × 106 + 2.764 × 10−3j | 0 2 359 | −2.458 × 10−3 − 1.458 × 106j | 0 4 358 | −1.458 × 106 + 2.842 × 10−3j |
| 0 4 0 | −7.290 × 105 + 4.309 × 10−3j | 0 4 1 | −4.336 × 10−3 + 7.290 × 105j | – | – |
| 0 4 4 | 3.645 × 105 − 2.328 × 10−3j | 0 4 3 | 3.380 × 10−3 − 7.290 × 105j | – | – |
| 0 4 356 | 3.645 × 105 − 3.997 × 10−3j | 0 4 357 | −2.269 × 10−4 − 7.290 × 105j | – | – |
| – | – | 0 4 359 | 2.354 × 10−3 + 7.290 × 105j | – | – |
| k1 k2 k3 | C2212 | k1 k2 k3 | C2213 | k1 k2 k3 | C2222 |
| 0 0 0 | 2.227 × 10−3 + 0j | 0 0 0 | 1.553 × 10−3 + 0j | 0 0 0 | 1.021 × 107 + 0j |
| 0 0 2 | 8.014 × 10−4 + 1.458 × 106j | 0 2 1 | −4.374 × 106 − 8.811 × 10−5j | 0 0 2 | 2.916 × 106 − 2.431 × 10−3j |
| 0 0 4 | −1.646 × 10−3 − 2.187 × 106j | 0 2 3 | 1.458 × 106 − 2.859 × 10−3j | 0 0 4 | −2.187 × 106 + 2.792 × 10−3j |
| 0 2 4 | 1.432 × 10−3 + 1.458 × 106j | 0 2 357 | −1.458 × 106 + 6.060 × 10−4j | 0 2 0 | −2.916 × 106 − 2.517 × 10−3j |
| 0 2 356 | 1.473 × 10−3 − 1.458 × 106j | 0 2 359 | 4.374 × 106 + 1.237 × 10−4j | 0 2 4 | 1.458 × 106 + 1.090 × 10−3j |
| 0 4 2 | −1.079 × 10−4 − 7.290 × 105j | 0 4 1 | −7.290 × 105 − 6.559 × 10−4j | 0 2 356 | 1.458 × 106 + 1.432 × 10−3j |
| 0 4 4 | −1.413 × 10−3 − 3.645 × 105j | 0 4 3 | −7.290 × 105 − 3.227 × 10−3j | 0 4 0 | −2.187 × 106 − 5.437 × 10−4j |
| 0 4 356 | −2.592 × 10−4 + 3.645 × 105j | 0 4 357 | 7.290 × 105 + 2.268 × 10−4j | 0 4 2 | −1.458 × 106 + 2.247 × 10−3j |
| 0 4 358 | 4.406 × 10−4 + 7.290 × 105j | 0 4 359 | 7.290 × 105 + 3.400 × 10−3j | 0 4 4 | −3.645 × 105 − 1.823 × 10−3j |
| – | – | – | – | 0 4 356 | −3.645 × 105 + 1.969 × 10−4j |
| – | – | – | – | 0 4 358 | −1.458 × 106 − 3.514 × 10−3j |
| k1 k2 k3 | C2223 | k1 k2 k3 | C2233 | k1 k2 k3 | C2312 |
| 0 0 0 | 3.273 × 10−4 + 0j | 0 0 0 | 2.916 × 107 + 0j | 0 0 0 | −1.855 × 10−3 + 0j |
| 0 2 1 | −6.770 × 10−5 + 1.458 × 106j | 0 0 2 | 2.916 × 106 + 2.189 × 10−3j | 0 2 1 | 1.458 × 106 − 2.242 × 10−3j |
| 0 2 3 | −1.475 × 10−3 − 1.458 × 106j | 0 2 0 | 5.832 × 106 + 3.827 × 10−4j | 0 2 3 | 1.458 × 106 + 9.985 × 10−4j |
| 0 2 357 | −1.473 × 10−3 − 1.458 × 106j | 0 2 2 | −2.916 × 106 − 8.557 × 10−4j | 0 2 357 | −1.458 × 106 + 9.966 × 10−4j |
| 0 2 359 | 1.745 × 10−3 + 1.458 × 106j | 0 2 358 | −2.916 × 106 + 2.756 × 10−3j | 0 2 359 | −1.458 × 106 − 2.525 × 10−3j |
| 0 4 1 | 2.036 × 10−3 + 2.187 × 106j | 0 4 0 | 2.916 × 106 − 1.242 × 10−3j | 0 4 1 | −7.290 × 105 + 9.776 × 10−4j |
| 0 4 3 | −4.109 × 10−4 + 7.290 × 105j | 0 4 2 | 1.458 × 106 − 5.018 × 10−3j | 0 4 3 | −7.290 × 105 − 4.229 × 10−3j |
| 0 4 357 | −1.317 × 10−4 + 7.290 × 105j | 0 4 358 | 1.458 × 106 − 7.378 × 10−3j | 0 4 357 | 7.290 × 105 + 1.011 × 10−4j |
| 0 4 359 | 1.982 × 10−3 + 2.187 × 106j | – | – | 0 4 359 | 7.290 × 105 + 3.638 × 10−3j |
| k1 k2 k3 | C2313 | k1 k2 k3 | C2323 | k1 k2 k3 | C3312 |
| 0 0 0 | −5.534 × 10−4 + 0j | 0 0 0 | −5.832 × 106 + 0j | 0 0 0 | −1.994 × 10−3 + 0j |
| 0 0 2 | −2.781 × 10−4 − 2.916 × 106j | 0 0 2 | −2.916 × 106 + 8.777 × 10−4j | 0 0 2 | 2.216 × 10−3 + 2.916 × 106j |
| 0 4 2 | 6.452 × 10−3 + 1.458 × 106j | 0 4 0 | 2.916 × 106 − 4.489 × 10−3j | 0 2 2 | −3.090 × 10−3 − 2.916 × 106j |
| 0 4 358 | −5.710 × 10−3 − 1.458 × 106j | 0 4 2 | 1.458 × 106 − 3.561 × 10−3j | 0 2 358 | −1.514 × 10−3 + 2.916 × 106j |
| – | – | 0 4 358 | 1.458 × 106 − 2.759 × 10−3j | 0 4 2 | 3.003 × 10−3 + 1.458 × 106j |
| – | – | – | – | 0 4 358 | −1.255 × 10−4 − 1.458 × 106j |
| k1 k2 k3 | C3313 | k1 k2 k3 | C3323 | k1 k2 k3 | C3333 |
| 0 0 0 | −3.737 × 10−4 + 0j | 0 0 0 | −3.272 × 10−4 + 0j | 0 0 0 | 1.166 × 107 + 0j |
| 0 4 1 | 2.916 × 106 − 1.377 × 10−3j | 0 4 1 | −2.203 × 10−3 − 2.916 × 106j | 0 4 0 | −5.832 × 106 − 1.367 × 10−3j |
| 0 4 359 | −2.916 × 106 + 2.212 × 10−3j | 0 4 359 | −3.092 × 10−4 − 2.916 × 106j | – | – |
| k1 k2 k3 | C1111 | k1 k2 k3 | C1112 | k1 k2 k3 | C1113 |
| 0 0 0 | 6.561 × 106 + 0j | 0 0 0 | 3.823 × 10−3 + 0j | 0 0 0 | −1.282 × 10−3 + 0j |
| 0 0 2 | −4.374 × 106 + 1.160 × 10−3j | 0 0 2 | −2.355 × 10−3 + 2.187 × 106j | 0 2 1 | −2.187 × 106 + 1.105 × 10−3j |
| 0 0 4 | 1.093 × 106 − 2.072 × 10−3j | 0 0 4 | 1.071 × 10−3 − 1.093 × 106j | 0 2 3 | 7.290 × 105 − 2.142 × 10−3j |
| 0 2 0 | −4.374 × 106 + 1.160 × 10−3j | 0 2 2 | 6.666 × 10−4 − 1.458 × 106j | 0 2 357 | −7.290 × 105 − 2.591 × 10−3j |
| 0 2 2 | 2.916 × 106 − 1.262 × 10−3j | 0 2 4 | 3.187 × 10−4 + 7.290 × 105j | 0 2 359 | 2.187 × 106 + 1.453 × 10−3j |
| 0 2 4 | −7.290 × 105 + 1.499 × 10−3j | 0 2 356 | −1.668 × 10−3 − 7.290 × 105j | 0 4 1 | 1.093 × 106 − 1.071 × 10−3j |
| 0 2 356 | −7.290 × 105 − 6.593 × 10−4j | 0 2 358 | 2.999 × 10−3 + 1.458 × 106j | 0 4 3 | −3.645 × 105 + 2.670 × 10−3j |
| 0 2 358 | 2.916 × 106 − 2.659 × 10−10j | 0 4 2 | −3.242 × 10−4 + 3.645 × 105j | 0 4 357 | 3.645 × 105 + 2.440 × 10−3j |
| 0 4 0 | 1.093 × 106 − 2.072 × 10−3j | 0 4 4 | −6.012 × 10−4 − 1.823 × 105j | 0 4 359 | −1.093 × 106 − 1.311 × 10−3j |
| 0 4 2 | −7.290 × 105 + 1.499 × 10−3j | 0 4 356 | 8.978 × 10−4 + 1.823 × 105j | – | – |
| 0 4 4 | 1.823 × 105 + 9.732 × 10−5j | 0 4 358 | −1.676 × 10−3 − 3.645 × 105j | – | – |
| 0 4 356 | 1.823 × 105 + 9.683 × 10−12j | – | – | – | – |
| 0 4 358 | −7.290 × 105 + 6.593 × 10−4j | – | – | – | – |
| k1 k2 k3 | C1122 | k1 k2 k3 | C1123 | k1 k2 k3 | C1133 |
| 0 0 0 | 2.187 × 106 + 0j | 0 0 0 | −2.897 × 10−4 + 0j | 0 0 0 | 2.916 × 106 + 0j |
| 0 0 4 | −1.094 × 106 + 8.084 × 10−4j | 0 2 1 | −4.025 × 10−4 + 7.290 × 105j | 0 0 2 | −1.458 × 106 − 1.382 × 10−4j |
| 0 2 0 | −1.458 × 106 + 1.200 × 10−3j | 0 2 3 | 2.409 × 10−4 − 7.290 × 105j | 0 4 0 | −1.458 × 106 − 6.165 × 10−6j |
| 0 2 4 | 7.290 × 105 − 1.126 × 10−3j | 0 2 357 | −4.364 × 10−4 − 7.290 × 105j | 0 4 2 | 7.290 × 105 + 4.241 × 10−4j |
| 0 2 356 | 7.290 × 105 − 1.900 × 10−4j | 0 2 359 | 1.795 × 10−4 + 7.290 × 105j | 0 4 358 | 7.290 × 105 + 1.654 × 10−4j |
| 0 4 0 | 3.645 × 105 − 8.533 × 10−4j | 0 4 1 | 8.402 × 10−4 − 3.645 × 105j | – | – |
| 0 4 4 | −1.823 × 105 + 2.970 × 10−4j | 0 4 3 | −7.023 × 10−4 + 3.645 × 105j | – | – |
| 0 4 356 | −1.823 × 105 + 5.990 × 10−4j | 0 4 357 | −1.036 × 10−3 + 3.645 × 105j | – | – |
| – | – | 0 4 359 | 4.759 × 10−4 − 3.645 × 105j | – | – |
| k1 k2 k3 | C1212 | k1 k2 k3 | C1312 | k1 k2 k3 | C1313 |
| 0 0 0 | 2.187 × 106 + 0j | 0 0 0 | −2.897 × 10−4 + 0j | 0 0 0 | 2.916 × 106 + 0j |
| 0 0 4 | −1.094 × 106 + 8.084 × 10−4j | 0 2 1 | −4.025 × 10−4 + 7.290 × 105j | 0 0 2 | −1.458 × 106 − 1.382 × 10−4j |
| 0 2 0 | −1.458 × 106 + 1.200 × 10−3j | 0 2 3 | 2.409 × 10−4 − 7.290 × 105j | 0 4 0 | −1.458 × 106 − 6.165 × 10−6j |
| 0 2 4 | 7.290 × 105 − 1.126 × 10−3j | 0 2 357 | −4.364 × 10−4 − 7.290 × 105j | 0 4 2 | 7.290 × 105 + 4.241 × 10−4j |
| 0 2 356 | 7.290 × 105 − 1.900 × 10−4j | 0 2 359 | 1.795 × 10−4 + 7.290 × 105j | 0 4 358 | 7.290 × 105 + 1.654 × 10−4j |
| 0 4 0 | 3.645 × 105 − 8.533 × 10−4j | 0 4 1 | 8.402 × 10−4 − 3.645 × 105j | – | – |
| 0 4 4 | −1.823 × 105 + 2.970 × 10−4j | 0 4 3 | −7.023 × 10−4 + 3.645 × 105j | – | – |
| 0 4 356 | −1.823 × 105 + 5.990 × 10−4j | 0 4 357 | −1.036 × 10−3 + 3.645 × 105j | – | – |
| – | – | 0 4 359 | 4.759 × 10−4 − 3.645 × 105j | – | – |
| k1 k2 k3 | C2212 | k1 k2 k3 | C2213 | k1 k2 k3 | C2222 |
| 0 0 0 | 2.792 × 10−3 + 0j | 0 0 0 | 3.074 × 10−5 + 0j | 0 0 0 | 6.561 × 106 + 0j |
| 0 0 2 | 2.951 × 10−3 + 2.187 × 106j | 0 2 1 | −7.290 × 105 + 2.330 × 10−4j | 0 0 2 | 4.374 × 106 + 7.014 × 10−4j |
| 0 0 4 | 2.232 × 10−3 + 1.093 × 106j | 0 2 3 | −7.290 × 105 + 5.117 × 10−4j | 0 0 4 | 1.093 × 106 + 1.030 × 10−3j |
| 0 2 2 | −3.103 × 10−3 − 1.458 × 106j | 0 2 357 | 7.290 × 105 + 5.010 × 10−4j | 0 2 0 | −4.374 × 106 + 9.433 × 10−4j |
| 0 2 4 | −2.957 × 10−3 − 7.290 × 105j | 0 2 359 | 7.290 × 105 + 5.058 × 10−4j | 0 2 2 | −2.916 × 106 + 1.423 × 10−4j |
| 0 2 356 | −5.481 × 10−4 + 7.290 × 105j | 0 4 1 | 3.645 × 105 − 1.666 × 10−4j | 0 2 4 | −7.290 × 105 − 1.449 × 10−4j |
| 0 2 358 | −1.477 × 10−3 + 1.458 × 106j | 0 4 3 | 3.645 × 105 + 1.777 × 10−4j | 0 2 356 | −7.290 × 105 + 8.615 × 10−4j |
| 0 4 2 | 1.298 × 10−3 + 3.645 × 105j | 0 4 357 | −3.645 × 105 − 3.247 × 10−4j | 0 2 358 | −2.916 × 106 + 1.174 × 10−3j |
| 0 4 4 | 1.733 × 10−3 + 1.823 × 105j | 0 4 359 | −3.645 × 105 − 1.046 × 10−3j | 0 4 0 | 1.093 × 106 − 2.872 × 10−3j |
| 0 4 356 | 2.726 × 10−4 − 1.823 × 105j | – | – | 0 4 2 | 7.290 × 105 − 1.485 × 10−3j |
| 0 4 358 | 9.600 × 10−4 − 3.645 × 105j | – | – | 0 4 4 | 1.823 × 105 − 3.610 × 10−4j |
| – | – | – | – | 0 4 356 | 1.823 × 105 + 5.363 × 10−4j |
| – | – | – | – | 0 4 358 | 7.290 × 105 − 2.104 × 10−3j |
| k1 k2 k3 | C2223 | k1 k2 k3 | C2233 | k1 k2 k3 | C2312 |
| 0 0 0 | 1.254 × 10−3 + 0j | 0 0 0 | 2.916 × 106 + 0j | 0 0 0 | 3.074 × 10−5 + 0j |
| 0 2 1 | −1.485 × 10−3 + 2.187 × 106j | 0 0 2 | 1.458 × 106 − 4.806 × 10−4j | 0 2 1 | −7.290 × 105 + 2.330 × 10−4j |
| 0 2 3 | −2.290 × 10−3 + 7.290 × 105j | 0 4 0 | −1.458 × 106 + 1.795 × 10−4j | 0 2 3 | −7.290 × 105 + 5.117 × 10−4j |
| 0 2 357 | 1.152 × 10−3 + 7.290 × 105j | 0 4 2 | −7.290 × 105 + 2.234 × 10−4j | 0 2 357 | 7.290 × 105 + 5.010 × 10−4j |
| 0 2 359 | 3.268 × 10−4 + 2.187 × 106j | 0 4 358 | −7.290 × 105 − 4.228 × 10−4j | 0 2 359 | 7.290 × 105 + 5.058 × 10−4j |
| 0 4 1 | 6.655 × 10−4 − 1.093 × 106j | – | – | 0 4 1 | 3.645 × 105 − 1.666 × 10−4j |
| 0 4 3 | 1.517 × 10−3 − 3.645 × 105j | – | – | 0 4 3 | 3.645 × 105 + 1.777 × 10−4j |
| 0 4 357 | −1.949 × 10−3 − 3.645 × 105j | – | – | 0 4 357 | −3.645 × 105 − 3.247 × 10−4j |
| 0 4 359 | −8.841 × 10−4 − 1.093 × 106j | – | – | 0 4 359 | −3.645 × 105 − 1.046 × 10−3j |
| k1 k2 k3 | C2313 | k1 k2 k3 | C2323 | k1 k2 k3 | C3312 |
| 0 0 0 | −1.640 × 10−3 + 0j | 0 0 0 | 2.916 × 106 + 0j | 0 0 0 | −1.640 × 10−3 + 0j |
| 0 0 2 | 1.228 × 10−3 + 1.458 × 106j | 0 0 2 | 1.458 × 106 − 4.806 × 10−4j | 0 0 2 | 1.228 × 10−3 + 1.458 × 106j |
| 0 4 2 | −1.516 × 10−3 − 7.290 × 105j | 0 4 0 | −1.458 × 106 + 1.795 × 10−4j | 0 4 2 | −1.516 × 10−3 − 7.290 × 105j |
| 0 4 358 | −4.549 × 10−5 + 7.290 × 105j | 0 4 2 | −7.290 × 105 + 2.234 × 10−4j | 0 4 358 | −4.549 × 10−5 + 7.290 × 105j |
| – | – | 0 4 358 | −7.290 × 105 − 4.228 × 10−4j | – | – |
| k1 k2 k3 | C3313 | k1 k2 k3 | C3323 | k1 k2 k3 | C3333 |
| 0 0 0 | 1.518 × 10−3 + 0j | 0 0 0 | 5.058 × 10−4 + 0j | 0 0 0 | 1.750 × 107 + 0j |
| 0 2 1 | −2.916 × 106 + 1.574 × 10−3j | 0 2 1 | 1.420 × 10−3 + 2.916 × 106j | 0 2 0 | 1.166 × 107 + 1.264 × 10−1j |
| 0 2 359 | 2.916 × 106 − 2.529 × 10−3j | 0 2 359 | 1.340 × 10−3 + 2.916 × 106j | 0 4 0 | 2.916 × 106 + 5.968 × 10−2j |
| 0 4 1 | −1.458 × 106 − 1.493 × 10−3j | 0 4 1 | −9.979 × 10−4 + 1.458 × 106j | – | – |
| 0 4 359 | 1.458 × 106 + 2.746 × 10−4j | 0 4 359 | −1.115 × 10−3 + 1.458 × 106j | – | – |
References
- Murat, F.; Tartar, L. Optimality conditions and homogenization. In Non-Linear Variational Problems; Pitman: London, UK, 1985. [Google Scholar]
- Cherkaev, A.V. Variational Methods for Structural Optimization; Springer: New York, NY, USA, 2000. [Google Scholar]
- Cherkaev, A.V.; Gibiansky, L.V. Extremal structures of multiphase heat conducting composites. Int. J. Solids Struct. 1996, 33, 2609–2623. [Google Scholar] [CrossRef]
- Lurie, K.A. A stable spatio-temporal G-closure and Gm-closure of a set of isotropic dielectrics with respect to one-dimensional wave propagation. Wave Motion 2004, 40, 95–110. [Google Scholar] [CrossRef]
- Adams, B.L.; Henrie, A.; Henrie, B.; Lyon, M.; Kalidindi, S.R.; Garmestani, H. Microstructure-sensitive design of a compliant beam. J. Mech. Phys. Solids 2001, 49, 1639–1663. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Houskamp, J.R.; Lyons, M.; Adams, B.L. Microstructure sensitive design of an orthotropic plate subjected to tensile load. Int. J. Plast. 2004, 20, 1561–1575. [Google Scholar] [CrossRef]
- Wu, X.; Proust, G.; Knezevic, M.; Kalidindi, S.R. Elastic-plastic property closures for hexagonal close-packed polycrystalline metals using first-order bounding theories. Acta Mater. 2007, 55, 2729–2737. [Google Scholar] [CrossRef]
- Knezevic, M.; Landry, N.W. Procedures for reducing large datasets of crystal orientations using generalized spherical harmonics. Mech. Mater. 2015, 88, 73–86. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Houskamp, J.R. Application of the spectral methods of microstructure design to continuous fiber reinforced composites. J. Compos. Mater. 2007, 41, 909–930. [Google Scholar] [CrossRef]
- Bunge, H.-J. Texture Analysis in Materials Science. Mathematical Methods; Cuvillier Verlag: Göttingen, Germany, 1993. [Google Scholar]
- Zuo, L.; Humbert, M.; Esling, C. Elastic properties of polycrystals in the voigt-reuss-hill approximation. J. Appl. Crystallogr. 1992, 25, 751–755. [Google Scholar] [CrossRef]
- Proust, G.; Kalidindi, S.R. Procedures for construction of anisotropic elastic-plastic property closures for face-centered cubic polycrystals using first-order bounding relations. J. Mech. Phys. Solids 2006, 54, 1744–1762. [Google Scholar] [CrossRef]
- Knezevic, M.; Kalidindi, S.R. Fast computation of first-order elastic-plastic closures for polycrystalline cubic-orthorhombic microstructures. Comput. Mater. Sci. 2007, 39, 643–648. [Google Scholar] [CrossRef]
- Duvvuru, H.K.; Knezevic, M.; Mishra, R.K.; Kalidindi, S.R. Application of microstructure sensitive design to fcc polycrystals. Mater. Sci. Forum 2007, 546, 675–680. [Google Scholar] [CrossRef]
- Knezevic, M.; Kalidindi, S.R.; Mishra, R.K. Delineation of first-order closures for plastic properties requiring explicit consideration of strain hardening and crystallographic texture evolution. Int. J. Plast. 2008, 24, 327–342. [Google Scholar] [CrossRef]
- Knezevic, M.; Kalidindi, S.R.; Fullwood, D. Computationally efficient database and spectral interpolation for fully plastic taylor-type crystal plasticity calculations of face-centered cubic polycrystals. Int. J. Plast. 2008, 24, 1264–1276. [Google Scholar] [CrossRef]
- Fuentes-Cobas, L.E.; Muñoz-Romero, A.; Montero-Cabrera, M.E.; Fuentes-Montero, L.; Fuentes-Montero, M.E. Predicting the coupling properties of axially-textured materials. Materials 2013, 6, 4967–4984. [Google Scholar] [CrossRef]
- Paul, B. Prediction of elastic constants of multiphase materials. Trans. Metall. Soc. AIME 1960, 218, 36–41. [Google Scholar]
- Hill, R. The elastic behavior of a crystalline aggregate. Proc. R. Soc. Lond. Sect. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Lyon, M.; Adams, B.L. Gradient-based non-linear microstructure design. J. Mech. Phys. Solids 2004, 52, 2569–2586. [Google Scholar] [CrossRef]
- Kim, I.Y.; de Weck, O.L. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation. Struct. Multidiscip. Optim. 2005, 29, 149–158. [Google Scholar] [CrossRef]
- Fast, T.; Knezevic, M.; Kalidindi, S.R. Application of microstructure sensitive design to structural components produced from hexagonal polycrystalline metals. Comput. Mater. Sci. 2008, 43, 374–383. [Google Scholar] [CrossRef]
- Sintay, D.S.; Adams, B.L. Microstructure design for a rotating disk: With application to turbine engines. In Proceedings of the IDETC/CIE, 31st Design Automation Conference, Long Beach, CA, USA, 24–28 September 2005.
- Houskamp, J.R.; Proust, G.; Kalidindi, S.R. Integration of microstructure-sensitive design with finite element methods: Elastic-plastic case studies in fcc polycrystals. Int. J. Multiscale Comput. Eng. 2007, 5, 261–272. [Google Scholar]
- Saheli, G.; Garmestani, H.; Adams, B.L. Microstructure design of a two phase composite using two-point correlation functions. J. Comput. Aided Mater. Des. 2004, 11, 103–115. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Binci, M.; Fullwood, D.; Adams, B.L. Elastic properties closures using second-order homogenization theories: Case studies in composites of two isotropic constituents. Acta Mater. 2006, 54, 3117–3126. [Google Scholar] [CrossRef]
- Sigmund, O.; Torquato, S. Design of materials with extreme thermal expansion using a three-phase topology optimization method. J. Mech. Phys. Solids 1997, 45, 1037–1067. [Google Scholar] [CrossRef]
- Sigmund, O.; Torquato, S. Composites with extremal thermal expansion coefficients. Appl. Phys. Lett. 1996, 69, 3203–3205. [Google Scholar] [CrossRef]
- Torquato, S. Modeling of physical properties of composite materials. Int. J. Solids Struct. 2000, 37, 411–422. [Google Scholar] [CrossRef]
- Xu, B.; Arias, F.; Brittain, S.T.; Zhao, X.-M.; Grzybowski, B.; Torquato, S.; Whitesides, G.M. Making negative poisson’s ratio microstructures by soft lithography. Adv. Mater. 1999, 11, 1186–1189. [Google Scholar] [CrossRef]
- Mayeur, J.; Beyerlein, I.; Bronkhorst, C.; Mourad, H. The influence of grain interactions on the plastic stability of heterophase interfaces. Materials 2014, 7, 302–322. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic strain in metals. J. Inst. Metals 1938, 62, 307–324. [Google Scholar]
- Knezevic, M.; Drach, B.; Ardeljan, M.; Beyerlein, I.J. Three dimensional predictions of grain scale plasticity and grain boundaries using crystal plasticity finite element models. Comput. Methods Appl. Mech. Eng. 2014, 277, 239–259. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M. A dislocation density based elasto-plastic self-consistent model for the prediction of cyclic deformation: Application to al6022-t4. Int. J. Plast. 2015, 72, 200–217. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M.; Beyerlein, I.J.; Tomé, C.N. An elasto-plastic self-consistent model with hardening based on dislocation density, twinning and de-twinning: Application to strain path changes in hcp metals. Mater. Sci. Eng. A 2015, 638, 262–274. [Google Scholar] [CrossRef]
- Jahedi, M.; Ardeljan, M.; Beyerlein, I.J.; Paydar, M.H.; Knezevic, M. Enhancement of orientation gradients during simple shear deformation by application of simple compression. J. Appl. Phys. 2015, 117. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J.; Brown, D.W.; Sisneros, T.A.; Tomé, C.N. A polycrystal plasticity model for predicting mechanical response and texture evolution during strain-path changes: Application to beryllium. Int. J. Plast. 2013, 49, 185–198. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J.; Lovato, M.L.; Tomé, C.N.; Richards, A.W.; McCabe, R.J. A strain-rate and temperature dependent constitutive model for bcc metals incorporating non-schmid effects: Application to tantalum-tungsten alloys. Int. J. Plast. 2014, 62, 93–104. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J.; Nizolek, T.; Mara, N.A.; Pollock, T.M. Anomalous basal slip activity in zirconium under high-strain deformation. Mater. Res. Lett. 2013, 1, 133–140. [Google Scholar] [CrossRef]
- Knezevic, M.; Capolungo, L.; Tomé, C.N.; Lebensohn, R.A.; Alexander, D.J.; Mihaila, B.; McCabe, R.J. Anisotropic stress-strain response and microstructure evolution of textured a-uranium. Acta Mater. 2012, 60, 702–715. [Google Scholar] [CrossRef]
- Knezevic, M.; Carpenter, J.S.; Lovato, M.L.; McCabe, R.J. Deformation behavior of the cobalt-based superalloy haynes 25: Experimental characterization and crystal plasticity modeling. Acta Mater. 2014, 63, 162–168. [Google Scholar] [CrossRef]
- Knezevic, M.; McCabe, R.J.; Tomé, C.N.; Lebensohn, R.A.; Chen, S.R.; Cady, C.M.; Gray Iii, G.T.; Mihaila, B. Modeling mechanical response and texture evolution of α-uranium as a function of strain rate and temperature using polycrystal plasticity. Int. J. Plast. 2013, 43, 70–84. [Google Scholar] [CrossRef]
- Knezevic, M.; Zecevic, M.; Beyerlein, I.J.; Bingert, J.F.; McCabe, R.J. Strain rate and temperature effects on the selection of primary and secondary slip and twinning systems in hcp Zr. Acta Mater. 2015, 88, 55–73. [Google Scholar] [CrossRef]
- Lentz, M.; Klaus, M.; Beyerlein, I.J.; Zecevic, M.; Reimers, W.; Knezevic, M. In situ X-ray diffraction and crystal plasticity modeling of the deformation behavior of extruded Mg-Li-(Al) alloys: An uncommon tension-compression asymmetry. Acta Mater. 2015, 86, 254–268. [Google Scholar] [CrossRef]
- Lentz, M.; Klaus, M.; Wagner, M.; Fahrenson, C.; Beyerlein, I.J.; Zecevic, M.; Reimers, W.; Knezevic, M. Effect of age hardening on the deformation behavior of an Mg-Y-Nd alloy: In-situ X-ray diffraction and crystal plasticity modeling. Mater. Sci. Eng. A 2015, 628, 396–409. [Google Scholar] [CrossRef]
- Fromm, B.S.; Adams, B.L.; Ahmadi, S.; Knezevic, M. Grain size and orientation distributions: Application to yielding of a-titanium. Acta Mater. 2009, 57, 2339–2348. [Google Scholar] [CrossRef]
- Carpenter, J.S.; Nizolek, T.; McCabe, R.J.; Knezevic, M.; Zheng, S.J.; Eftink, B.P.; Scott, J.E.; Vogel, S.C.; Pollock, T.M.; Mara, N.A.; et al. Bulk texture evolution of nanolamellar Zr-Nb composites processed via accumulative roll bonding. Acta Mater. 2015, 92, 97–108. [Google Scholar] [CrossRef]
- Van Houtte, P. Fast calculation of average taylor factors and mandel spins for all possible strain modes. Int. J. Plast. 2001, 17, 807–818. [Google Scholar] [CrossRef]
- Shaffer, J.B.; Knezevic, M.; Kalidindi, S.R. Building texture evolution networks for deformation processing of polycrystalline fcc metals using spectral approaches: Applications to process design for targeted performance. Int. J. Plast. 2010, 26, 1183–1194. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Duvvuru, H.K.; Knezevic, M. Spectral calibration of crystal plasticity models. Acta Mater. 2006, 54, 1795–1804. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Knezevic, M.; Niezgoda, S.; Shaffer, J. Representation of the orientation distribution function and computation of first-order elastic properties closures using discrete fourier transforms. Acta Mater. 2009, 57, 3916–3923. [Google Scholar] [CrossRef]
- Knezevic, M.; Al-Harbi, H.F.; Kalidindi, S.R. Crystal plasticity simulations using discrete fourier transforms. Acta Mater. 2009, 57, 1777–1784. [Google Scholar] [CrossRef]
- Al-Harbi, H.F.; Knezevic, M.; Kalidindi, S.R. Spectral approaches for the fast computation of yield surfaces and first-order plastic property closures for polycrystalline materials with cubic-triclinic textures. CMC Comput. Mater. Contin. 2010, 15, 153–172. [Google Scholar] [CrossRef]
- Zecevic, M.; McCabe, R.J.; Knezevic, M. A new implementation of the spectral crystal plasticity framework in implicit finite elements. Mech. Mater. 2015, 84, 114–126. [Google Scholar] [CrossRef]
- Mihaila, B.; Knezevic, M.; Cardenas, A. Three orders of magnitude improved efficiency with high-performance spectral crystal plasticity on GPU platforms. Int. J. Numer. Methods Eng. 2014, 97, 785–798. [Google Scholar] [CrossRef]
- Knezevic, M.; Savage, D.J. A high-performance computational framework for fast crystal plasticity simulations. Comput. Mater. Sci. 2014, 83, 101–106. [Google Scholar] [CrossRef]
- Savage, D.J.; Knezevic, M. Computer implementations of iterative and non-iterative crystal plasticity solvers on high performance graphics hardware. Comput. Mech. 2015, in press. [Google Scholar] [CrossRef]
- Bunge, H. Texture analysis in Materials Science; Butterworths: London, UK, 1982. [Google Scholar]
- Carslaw, H.S. Introduction to the Theory of Fourier’s Series and Integrals, 2nd ed.; MacMillan and Co. Limited: London, UK, 1921. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: Oxford, UK, 1992. [Google Scholar]
- Briggs, W.L.; Henson, V.E. The DFT: An Owner’s Manual for the Discrete Fourier Transform; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995. [Google Scholar]
- Brigham, E.O. The Fast Fourier Transform and Its Applications; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Cooley, J.W.; Tukey, J.W. Algorithm for the machine computation of complex fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Duhamel, P.; Vetterli, M. Fast fourier transforms: A tutorial review and a state of the art. Signal Process. 1990, 19, 259–299. [Google Scholar]
- Adams, B.L.; Gao, X.; Kalidindi, S.R. Finite approximations to the second-order properties closure in single phase polycrystals. Acta Mater. 2005, 53, 3563–3577. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chawla, K.K. Mechanical Behavior of Materials; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Zecevic, M.; McCabe, R.J.; Knezevic, M. Spectral database solutions to elasto-viscoplasticity within finite elements: Application to a cobalt-based fcc superalloy. Int. J. Plast. 2015, 70, 151–165. [Google Scholar] [CrossRef]
- Knezevic, M.; McCabe, R.J.; Lebensohn, R.A.; Tomé, C.N.; Liu, C.; Lovato, M.L.; Mihaila, B. Integration of self-consistent polycrystal plasticity with dislocation density based hardening laws within an implicit finite element framework: Application to low-symmetry metals. J. Mech. Phys. Solids 2013, 61, 2034–2046. [Google Scholar] [CrossRef]
- Knezevic, M.; Lebensohn, R.A.; Cazacu, O.; Revil-Baudard, B.; Proust, G.; Vogel, S.C.; Nixon, M.E. Modeling bending of α-titanium with embedded polycrystal plasticity in implicit finite elements. Mater. Sci. Eng. A 2013, 564, 116–126. [Google Scholar] [CrossRef]
- Knezevic, M.; Jahedi, M.; Korkolis, Y.P.; Beyerlein, I.J. Material-based design of the extrusion of bimetallic tubes. Comput. Mater. Sci. 2014, 95, 63–73. [Google Scholar] [CrossRef]
- Knezevic, M.; McCabe, R.J.; Lebensohn, R.A.; Tomé, C.N.; Mihaila, B. Finite Element Implementation of a Self-Consistent Polycrystal Plasticity Model: Application to α-Uranium, Proceedings; Materials Science and Technology Division, Los Alamos National Laboratory: Los Alamos, NM, USA, 2012; Volume 2, pp. 789–796. [Google Scholar]
- Jahedi, M.; Paydar, M.H.; Knezevic, M. Enhanced microstructural homogeneity in metal-matrix composites developed under high-pressure-double-torsion. Mater. Charact. 2015, 104, 92–100. [Google Scholar] [CrossRef]
- Jahedi, M.; Paydar, M.H.; Zheng, S.; Beyerlein, I.J.; Knezevic, M. Texture evolution and enhanced grain refinement under high-pressure-double-torsion. Mater. Sci. Eng. A 2014, 611, 29–36. [Google Scholar] [CrossRef]
- Jahedi, M.; Knezevic, M.; Paydar, M. High-pressure double torsion as a severe plastic deformation process: Experimental procedure and finite element modeling. J. Mater. Eng. Perform. 2015, 24, 1471–1482. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landry, N.W.; Knezevic, M. Delineation of First-Order Elastic Property Closures for Hexagonal Metals Using Fast Fourier Transforms. Materials 2015, 8, 6326-6345. https://doi.org/10.3390/ma8095303
Landry NW, Knezevic M. Delineation of First-Order Elastic Property Closures for Hexagonal Metals Using Fast Fourier Transforms. Materials. 2015; 8(9):6326-6345. https://doi.org/10.3390/ma8095303
Chicago/Turabian StyleLandry, Nicholas W., and Marko Knezevic. 2015. "Delineation of First-Order Elastic Property Closures for Hexagonal Metals Using Fast Fourier Transforms" Materials 8, no. 9: 6326-6345. https://doi.org/10.3390/ma8095303
APA StyleLandry, N. W., & Knezevic, M. (2015). Delineation of First-Order Elastic Property Closures for Hexagonal Metals Using Fast Fourier Transforms. Materials, 8(9), 6326-6345. https://doi.org/10.3390/ma8095303