The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams
Abstract
:1. Introduction
2. Segmental Moment-Rotation Approach
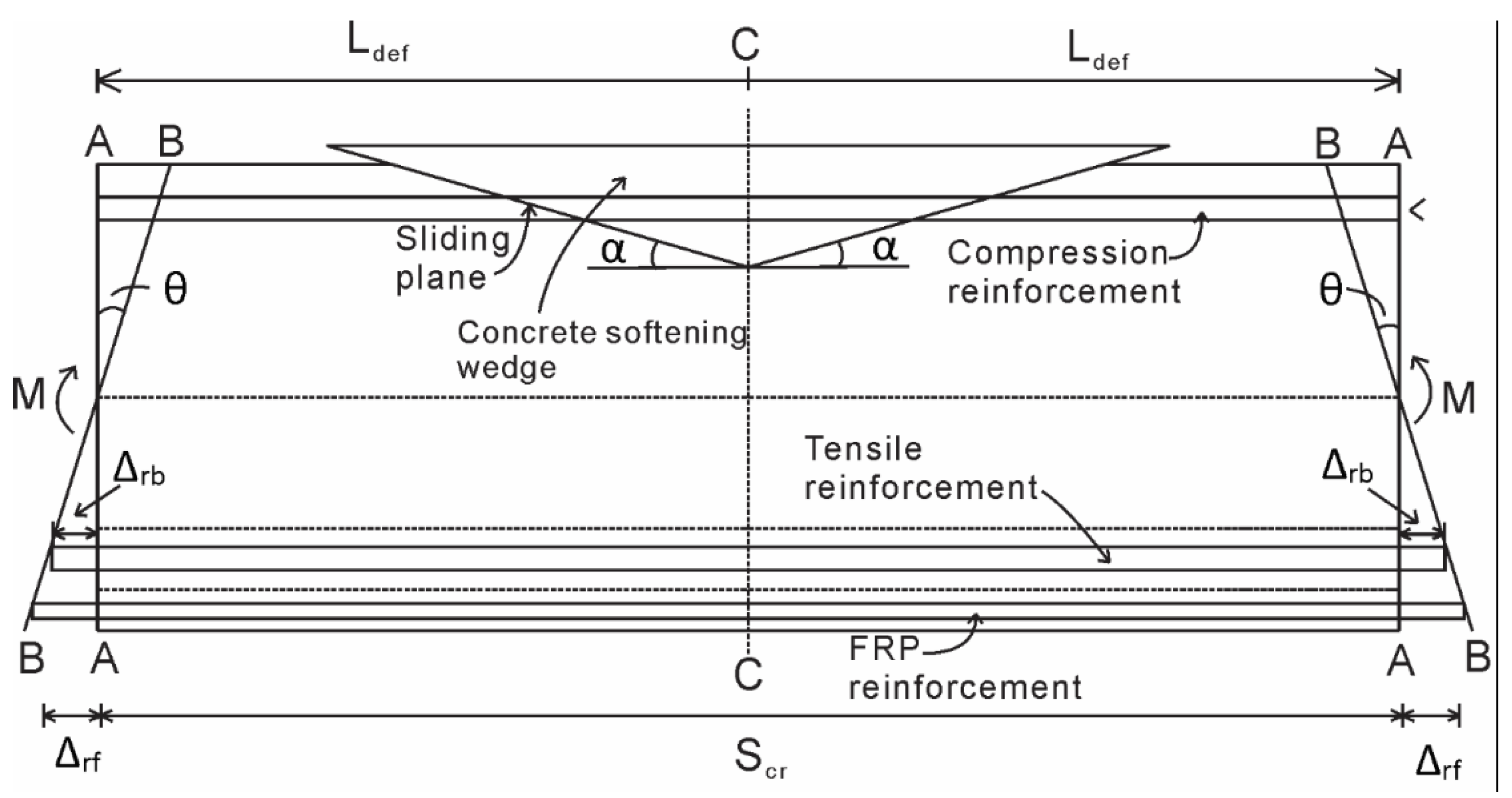
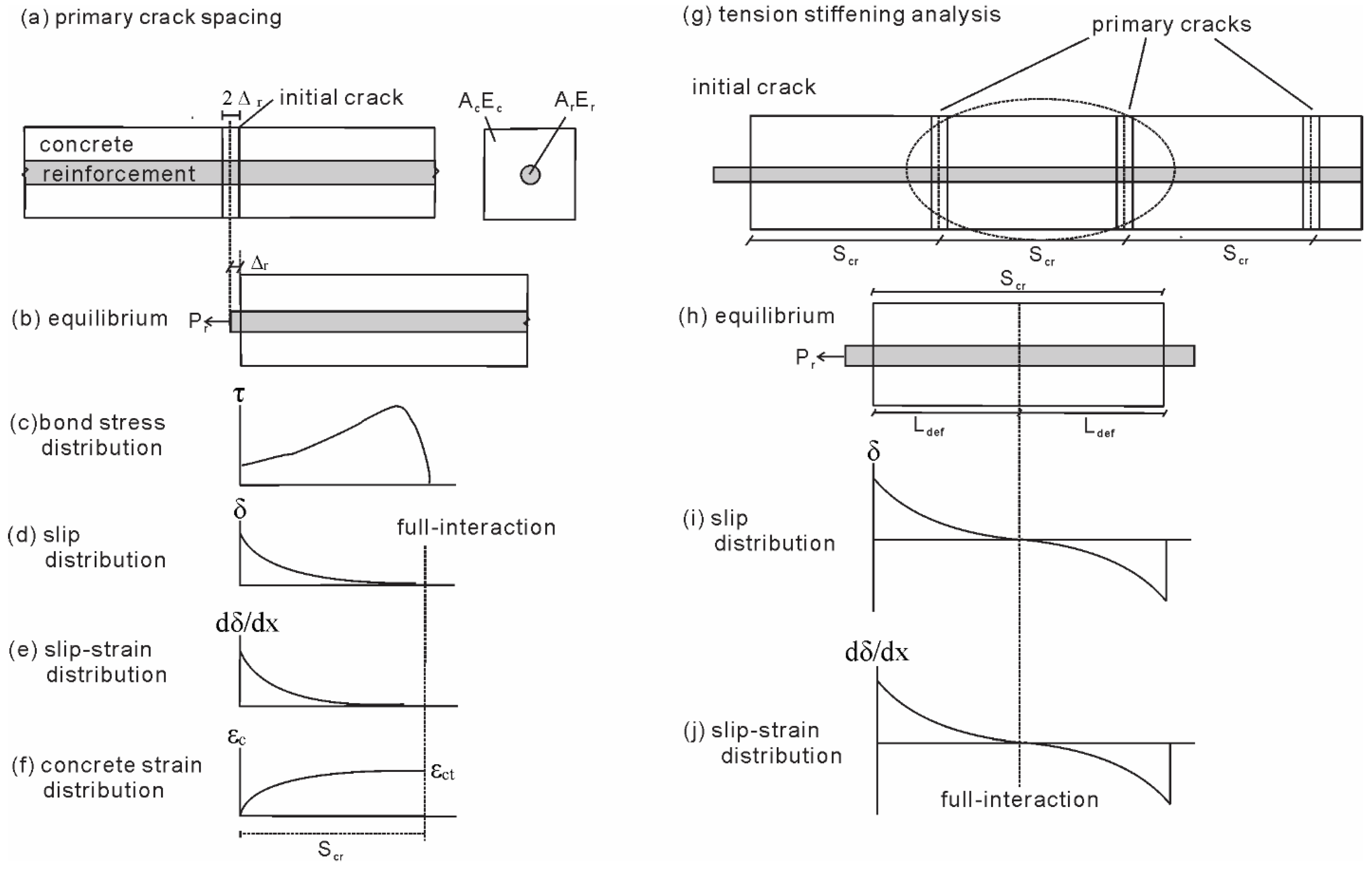
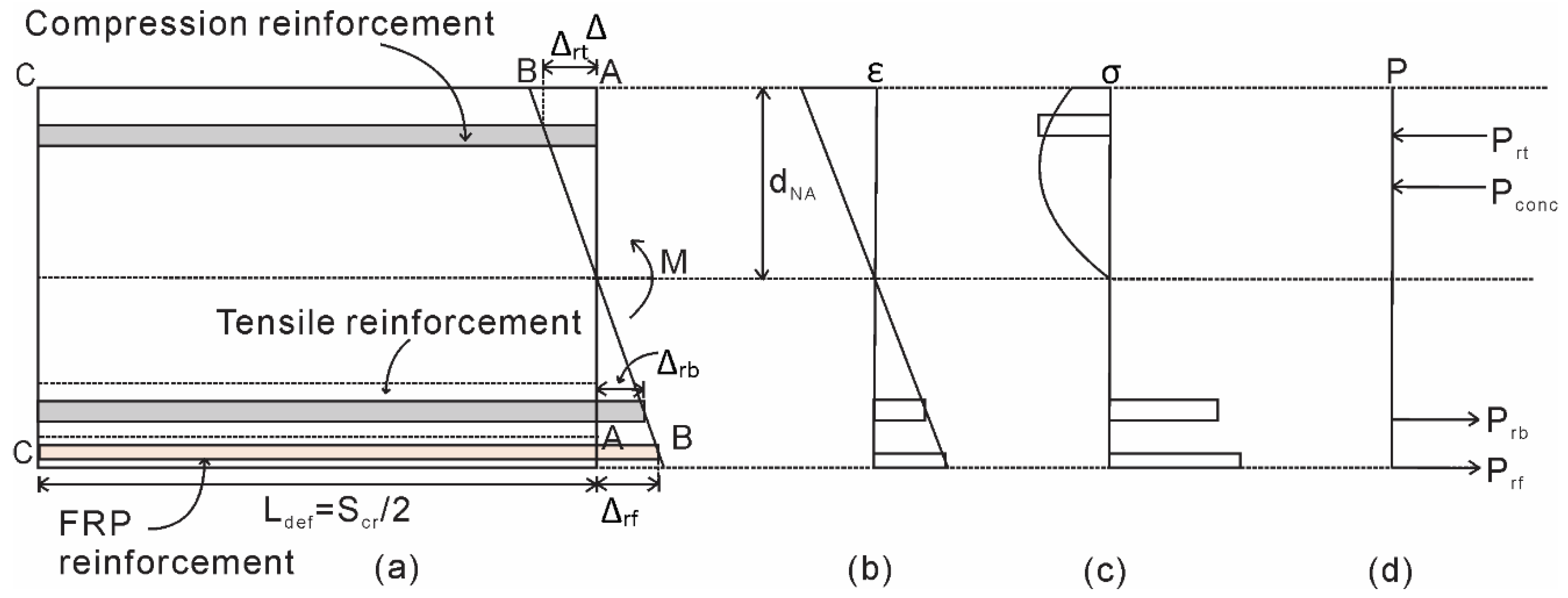
2.1. Partial-Interaction Tension Stiffening Analysis
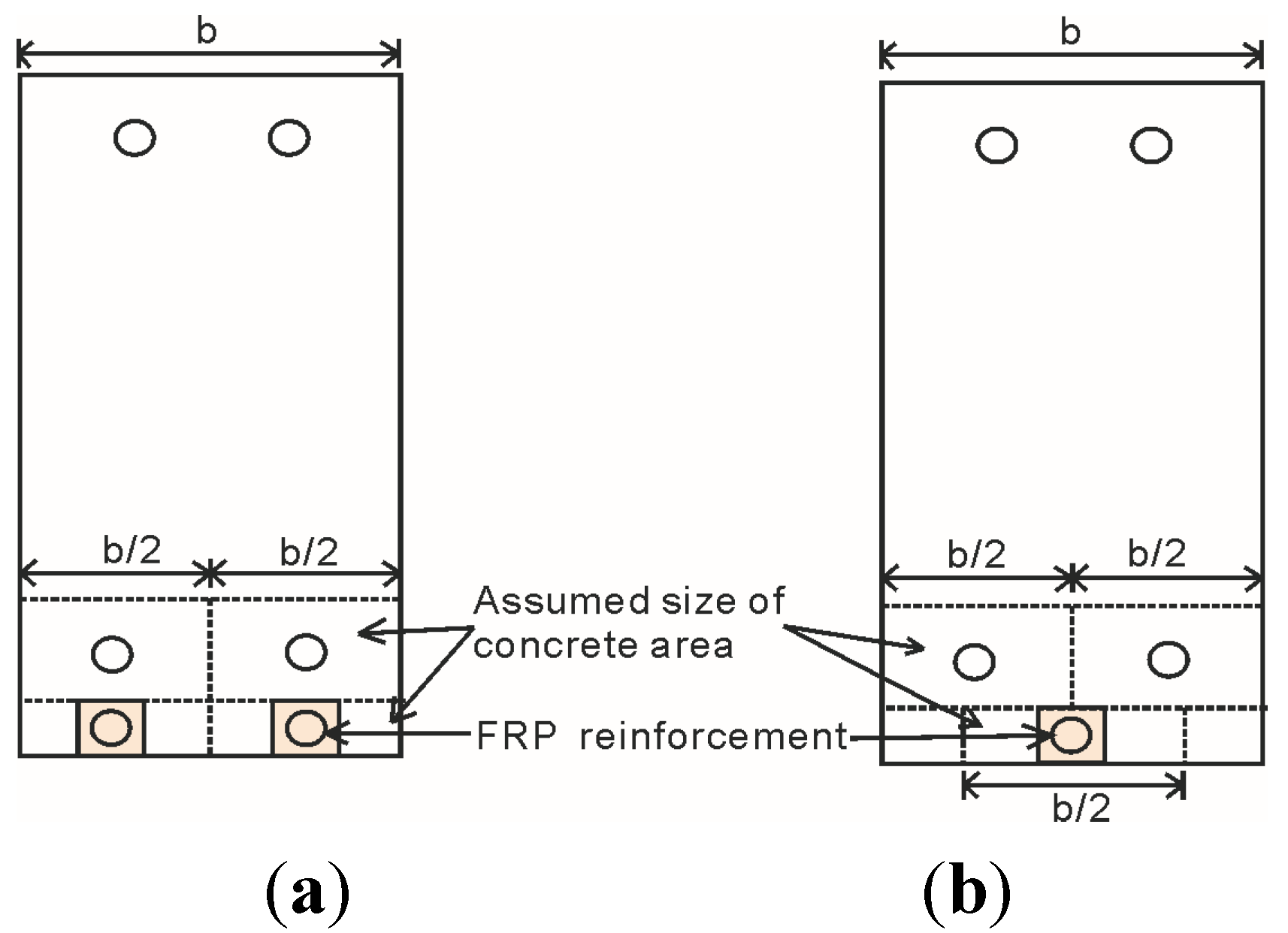
2.2. Size-Dependent Stress-Strain of Concrete
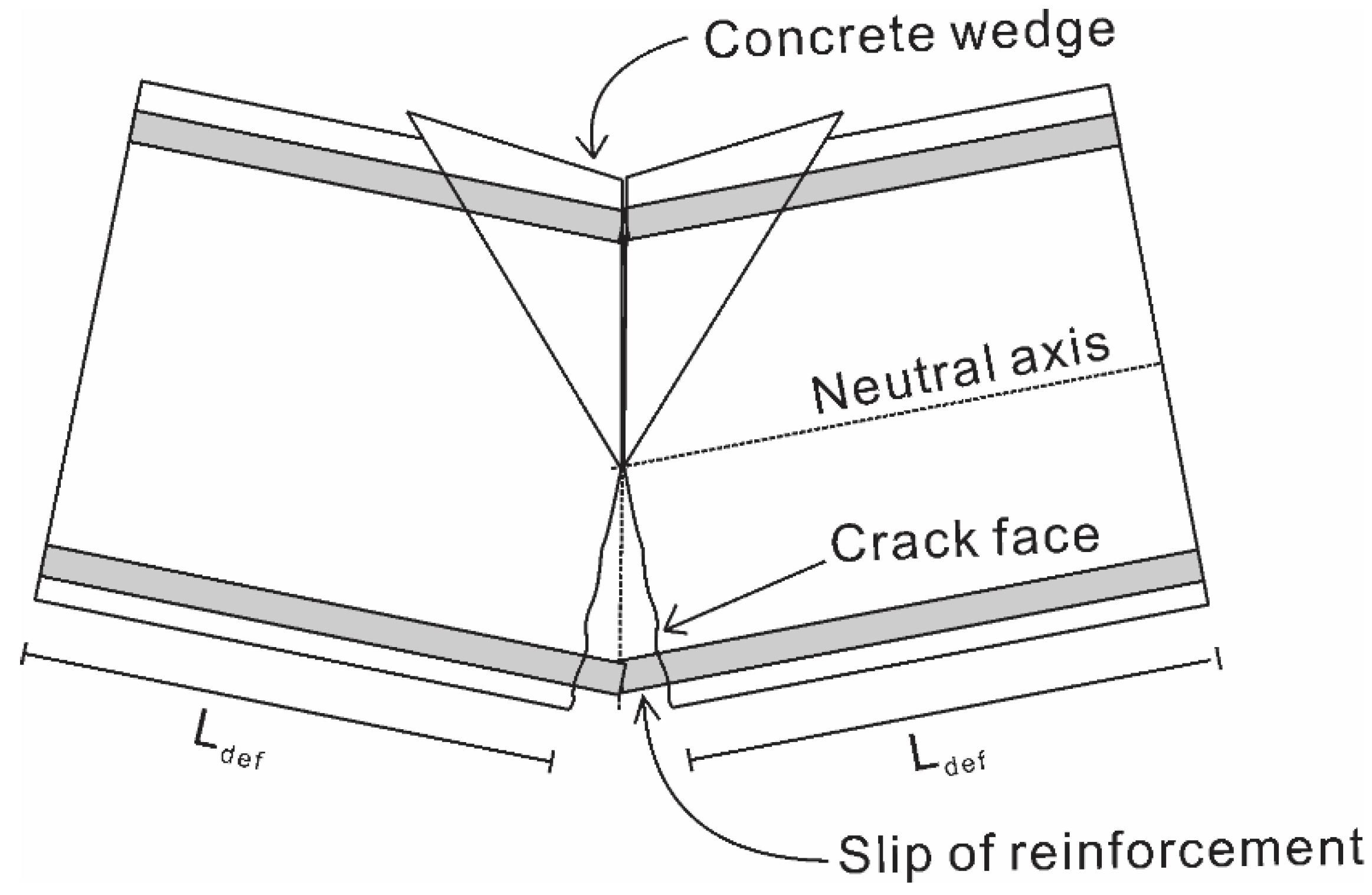
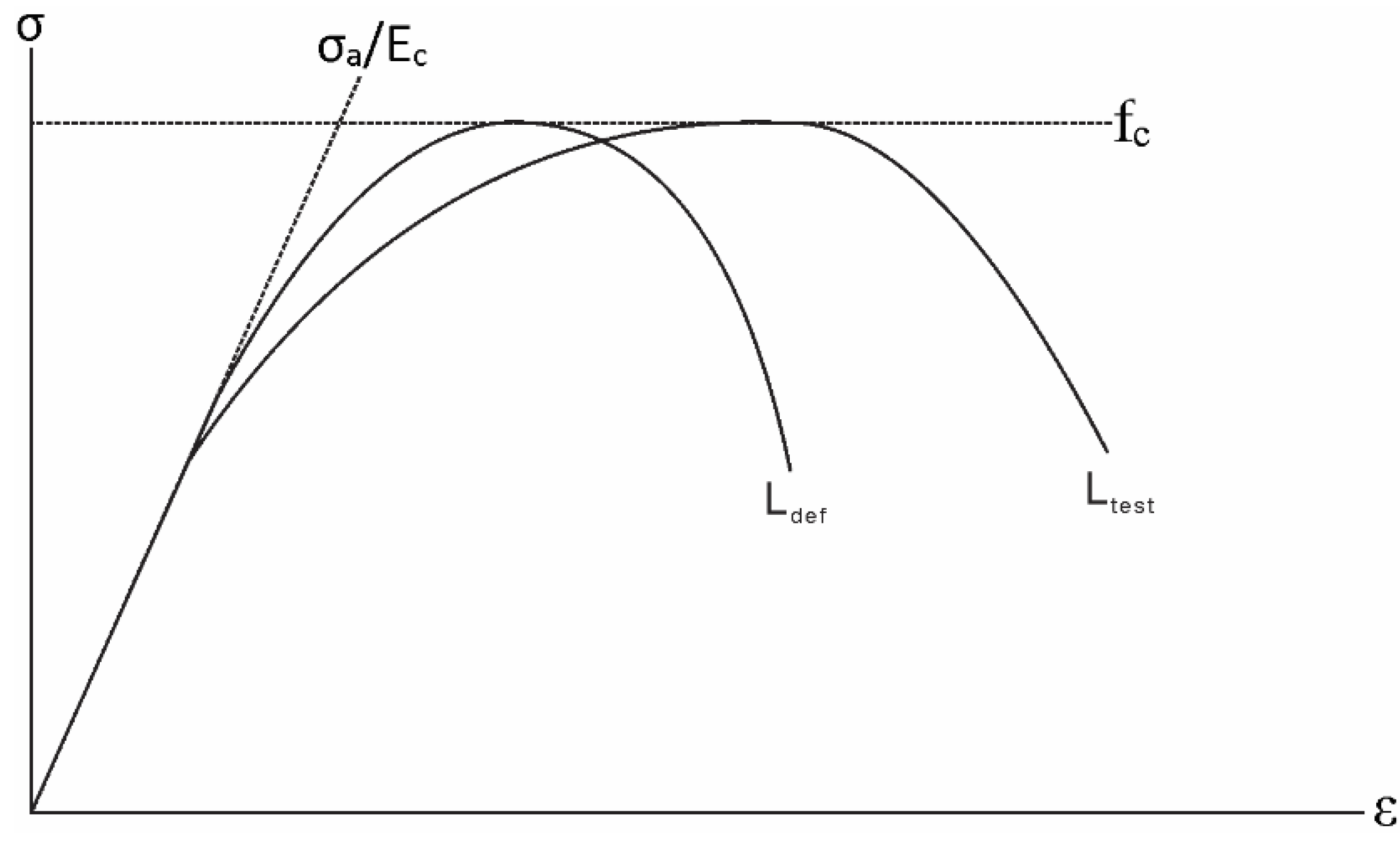
2.3. Hinge Analysis
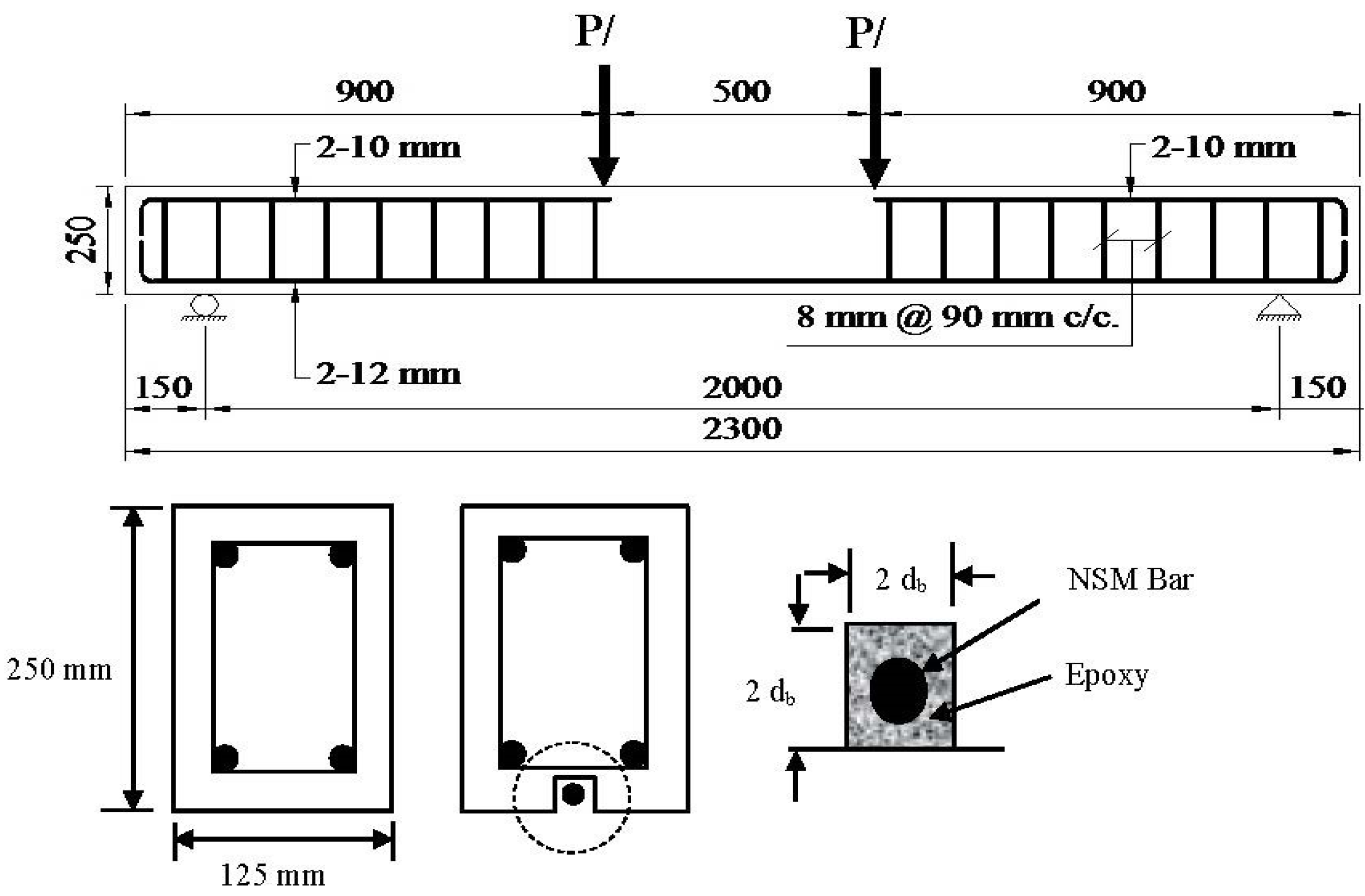
3. Experimental Program
| Specimen name & details | Bonded length (mm) | Beam length (mm) | Shape of NSM CFRP reinforcement | Number of NSM FRP reinforcements |
|---|---|---|---|---|
| CB (Control beam) | - | 2000 | - | - |
| A1 (Strengthened beam) | 1800 | 2000 | bar | 1 |
| A2 (Strengthened beam) | 1900 | 2000 | bar | 1 |
| Jung-1 [22] | 2700 | 3000 | bar | 1 |
| Capozucca-1 [23] | 1300 | 1500 | bar | 2 |
| Teng-1 [24] | 1800 | 3000 | strip | 1 |
| Teng-2 [24] | 2900 | 3000 | strip | 1 |
Materials and Samples
| Material | Compressive strength (MPa) | Flexure strength (MPa) | Yield stress (MPa) | Ultimate strength (MPa) | Elastic modulus (GPa) | Strain at failure (%) |
|---|---|---|---|---|---|---|
| Concrete | 43.24 (cube) 35.63 (Cylinder) | 5.01 | - | - | 30.1 | - |
| Steel- Φ 12 mm | - | - | 520 | 587 | 200 | 20 |
| Steel- Φ 10 mm | - | - | 529 | 578 | 200 | 21 |
| Steel- Φ 8 mm | - | - | 380 | 450 | 200 | 29 |
| CFRP- Φ 12 mm | - | - | - | 2400 | 165 | - |
| Temperature | 15 °C | 35 °C |
|---|---|---|
| Compressive strength | 70–80 MPa | 85–95 MPa |
| Tensile strength | 14–17 MPa | 16–19 MPa |
| Shear strength | 24–27 MPa | 26–31 MPa |

4. Results and discussion
4.1. Experimental Results
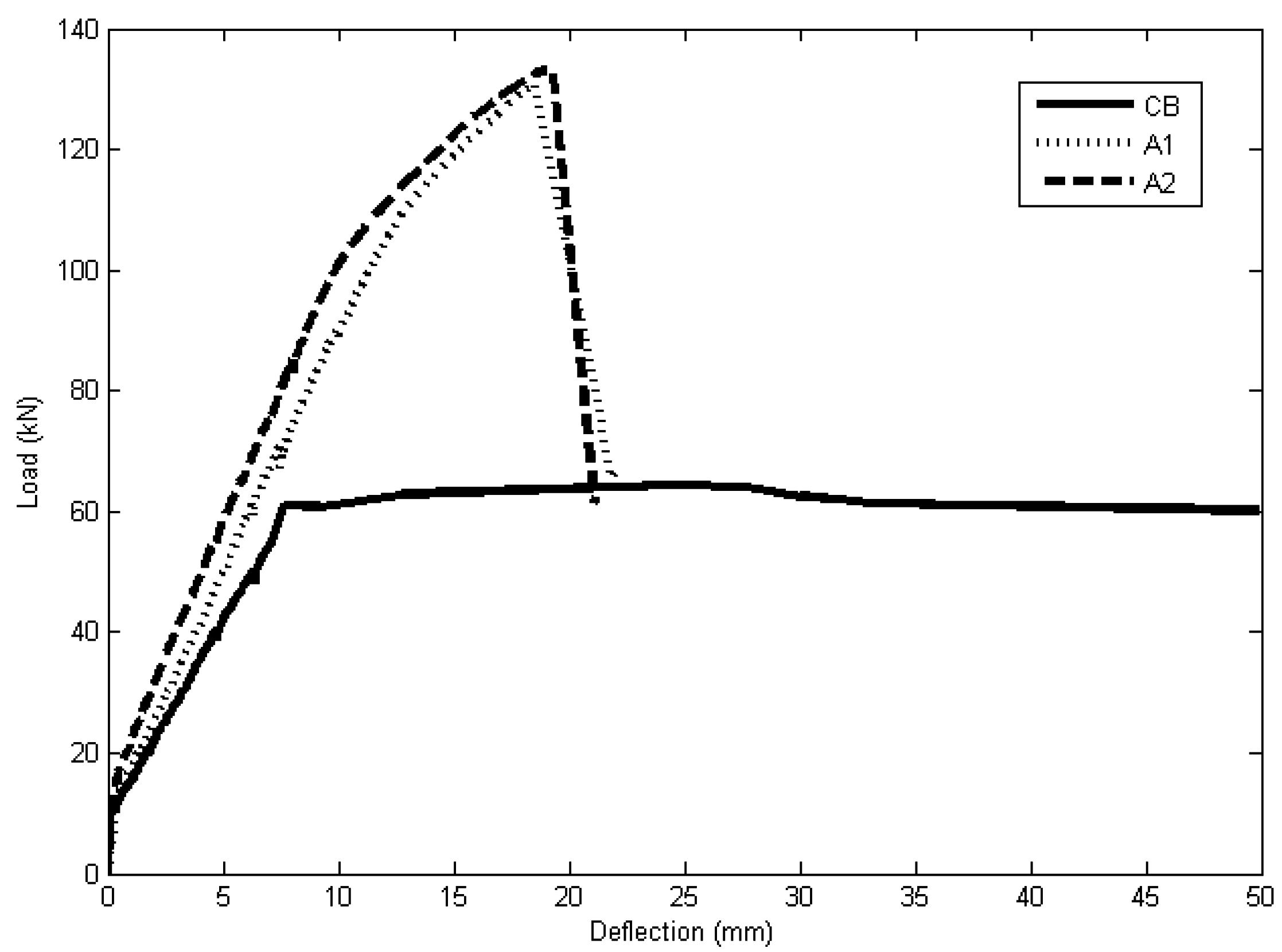
| Specimen name | Pcr (kN) | Py (kN) | Δy (mm) | Pu (kN) | Δu (mm) | Failure mode |
|---|---|---|---|---|---|---|
| CB | 10.6 | 61.0 | 7.7 | 64.4 | 24.7 | Flexure failure (Concrete crushing after steel yielding) |
| A1 | 14.0 | 110.6 | 13.0 | 130.8 | 18.6 | Debonding (Concrete cover separation) |
| A2 | 15.0 | 104.5 | 10.7 | 133.2 | 19.2 | Debonding (Concrete cover separation) |

4.2. Validation of Segmental Moment-Rotation Approach
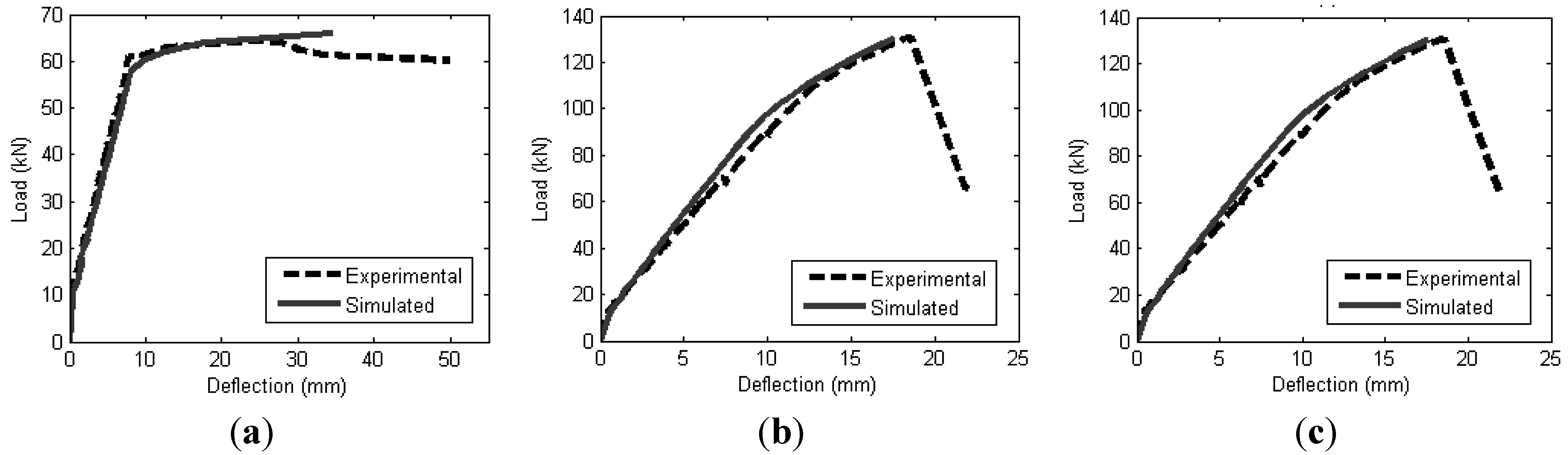
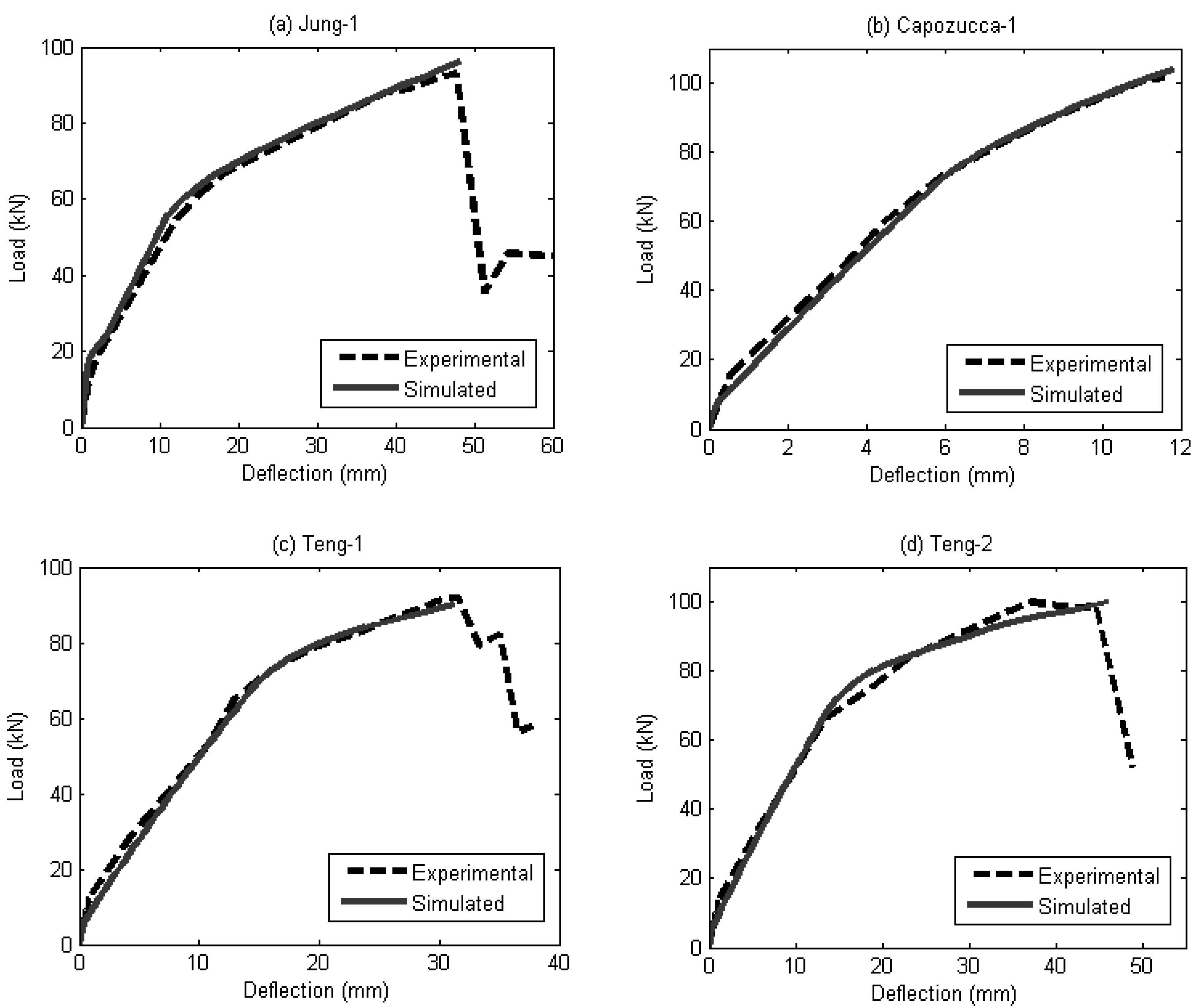
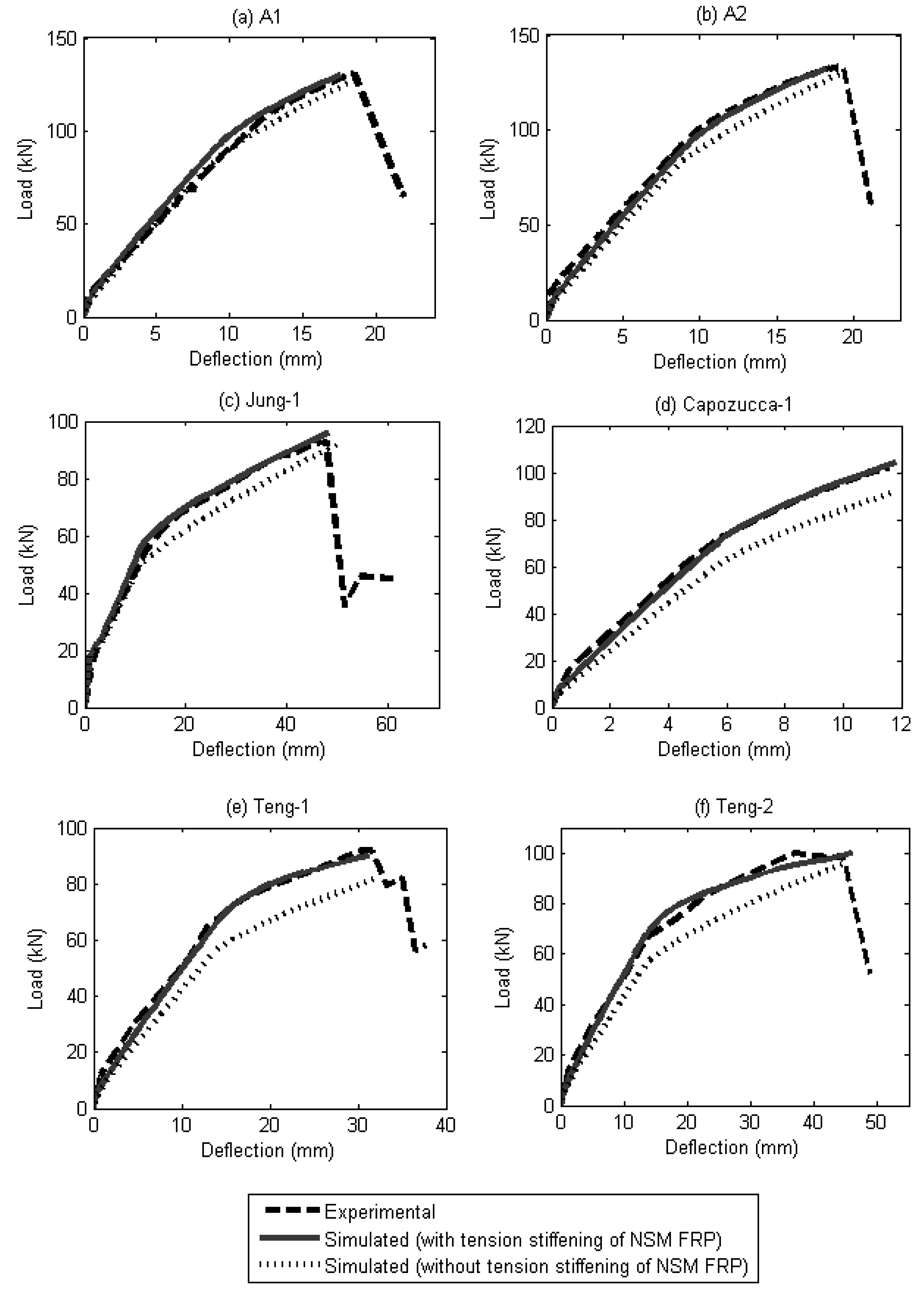
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, J.; Samali, B.; Ye, L.; Bakoss, S. Behaviour of concrete beam-column connections reinforced with hybrid FRP sheet. Compos. Struct. 2002, 57, 357–365. [Google Scholar] [CrossRef]
- Mancusi, G.; Feo, L.; Berardi, V.P. Concrete open-wall systems wrapped with FRP under torsional loads. Materials 2012, 5, 2055–2068. [Google Scholar] [CrossRef]
- Ekenel, M.; Rizzo, A.; Myers, J.J.; Nanni, A. Flexural fatigue behavior of reinforced concrete beams strengthened with FRP fabric and precured laminate systems. J. Compos. Constr. 2006, 10, 433–442. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Oudah, F.; El-Hacha, R. Fatigue behavior of RC beams strengthened with prestressed NSM CFRP rods. Compos. Struct. 2012, 94, 1333–1342. [Google Scholar] [CrossRef]
- Sharaky, I.A.; Torres, L.; Sallam, H.E.M. Experimental and analytical investigation into the flexural performance of RC beams with partially and fully bonded NSM FRP bars/strips. Compos. Struct. 2015, 122, 113–126. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Nanni, A. Bond between near-surface mounted fiber-reinforced polymer rods and concrete in structural strengthening. Am. Concr. Inst. Struct. J. 2002, 99, 123–132. [Google Scholar]
- De Lorenzis, L.; Rizzo, A.; La Tegola, A. A modified pull-out test for bond of near-surface mounted FRP rods in concrete. Compos. Part B Eng. 2002, 33, 589–603. [Google Scholar] [CrossRef]
- Al-Mahmoud, F.; Castel, A.; François, R.; Tourneur, C. Anchorage and tension-stiffening effect between near-surface-mounted CFRP rods and concrete. Cem. Concr. Compos. 2011, 33, 346–352. [Google Scholar] [CrossRef]
- Bischoff, P.H. Reevaluation of deflection prediction for concrete beams reinforced with steel and fiber reinforced polymer bars. J. Struct. Eng. 2005, 131, 752–767. [Google Scholar] [CrossRef]
- Coleman, J.; Spacone, E. Localization issues in force-based frame elements. J. Struct. Eng. 2001, 127, 1257–1265. [Google Scholar] [CrossRef]
- Panagiotakos, T.B.; Fardis, M.N. Deformations of reinforced concrete members at yielding and ultimate. Am. Concr. Inst. Struct. J. 2001, 98, 135–148. [Google Scholar]
- Haskett, M.; Oehlers, D.J.; Mohamed Ali, M.S.; Wu, C. Yield penetration hinge rotation in reinforced concrete beams. J. Struct. Eng. 2009, 135, 130–138. [Google Scholar] [CrossRef]
- Haskett, M.; Oehlers, D.J.; Ali, M.S.M.; Sharma, S.K. Evaluating the shear-friction resistance across sliding planes in concrete. Eng. Struct. 2011, 33, 1357–1364. [Google Scholar] [CrossRef]
- Chen, Y.; Visintin, P.; Oehlers, D.J.; Alengaram, U.J. Size dependent stress-strain model for unconfined concrete. J. Struct. Eng. 2013, 140, 04013088. [Google Scholar] [CrossRef]
- Muhamad, R.; Ali, M.S.M.; Oehlers, D.; Sheikh, A.H. Load-slip relationship of tension reinforcement in reinforced concrete members. Eng. Struct. 2011, 33, 1098–1106. [Google Scholar] [CrossRef]
- Visintin, P.; Oehlers, D.J.; Wu, C.; Haskett, M. A mechanics solution for hinges in RC beams with multiple cracks. Eng. Struct. 2012, 36, 61–69. [Google Scholar] [CrossRef]
- Knight, D.; Visintin, P.; Oehlers, D.J.; Ali, M.S.M. Simulating RC beams with unbonded FRP and steel prestressing tendons. Compos. Part B Eng. 2014, 60, 392–399. [Google Scholar] [CrossRef]
- Oehlers, D.J.; Visintin, P.; Haskett, M.; Sebastian, W.M. Flexural ductility fundamental mechanisms governing all RC members in particular FRP RC. Constr. Build. Mater. 2013, 49, 985–997. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Walraven, J.; Frenay, J.; Pruijssers, A. Influence of concrete strength and load history on the shear friction capacity of concrete members. J. Prestress. Concr. Inst. 1987, 32, 66–84. [Google Scholar]
- Jung, W.T.; Park, Y.H.; Park, J.S.; Kang, J.Y.; You, Y.J. Experimental investigation on flexural behavior of RC beams strengthened by NSM CFRP reinforcements. Am. Concr. Inst. Spec. Publ. 2005, 795–806. [Google Scholar]
- Capozucca, R. Analysis of bond-slip effects in RC beams strengthened with NSM CFRP rods. Compos. Struct. 2013, 102, 110–123. [Google Scholar] [CrossRef]
- Teng, J.; De Lorenzis, L.; Wang, B.; Li, R.; Wong, T.N.; Lam, L. Debonding failures of RC beams strengthened with near surface mounted CFRP strips. J. Compos. Constr. 2006, 10, 92–105. [Google Scholar] [CrossRef]
- BSI Standards Publication. Testing Hardened Concrete. Compressive Strength of Test Specimens; BS EN 12390-2:2009; British Standards Institute: London, UK, 2009. [Google Scholar]
- ASTM International. Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM C39/C39M-14a; American Society for Testing and Materials International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- BSI Standards Publication. Testing Hardened Concrete. Flexural Strength of Test Specimens; BS EN 12390-2:2009; British Standards Institute: London, UK, 2009. [Google Scholar]
- ASTM International. Standard Specification for Deformed and Plain Carbon-Steel Bars for Concrete Reinforcement; ASTM A615/A615M-14; American Society for Testing and Materials International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Sikadur®-30. Product Data Sheet-Adhesive for bonding reinforcement. Available online: http://mys.sika.com/en/solutions_products/02/02a013/02a013sa06/02a013sa06100/02a013sa06105.html (accessed on 2 June 2014).
- Hassan, T.K.; Rizkalla, S.H. Bond mechanism of near-surface-mounted fiber-reinforced polymer bars for flexural strengthening of concrete structures. Am. Concr. Inst. Struct. J. 2004, 101, 830–839. [Google Scholar]
- Zhang, S.S.; Teng, J.G.; Yu, T. Bond–slip model for CFRP strips near-surface mounted to concrete. Eng. Struct. 2013, 56, 945–953. [Google Scholar] [CrossRef]
- De Lorenzis, L. Anchorage length of near-surface mounted fiber-reinforced polymer rods for concrete strengthening? Analytical modeling. Am. Concr. Inst. Struct. J. 2004, 101, 375–386. [Google Scholar]
- El-Hacha, R.; Rizkalla, S.H. Near-surface-mounted fiber-reinforced polymer reinforcements for flexural strengthening of concrete structures. Am. Concr. Inst. Struct. J. 2004, 101, 717–726. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shukri, A.A.; Darain, K.M.u.; Jumaat, M.Z. The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams. Materials 2015, 8, 4131-4146. https://doi.org/10.3390/ma8074131
Shukri AA, Darain KMu, Jumaat MZ. The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams. Materials. 2015; 8(7):4131-4146. https://doi.org/10.3390/ma8074131
Chicago/Turabian StyleShukri, Ahmad Azim, Kh Mahfuz ud Darain, and Mohd Zamin Jumaat. 2015. "The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams" Materials 8, no. 7: 4131-4146. https://doi.org/10.3390/ma8074131
APA StyleShukri, A. A., Darain, K. M. u., & Jumaat, M. Z. (2015). The Tension-Stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams. Materials, 8(7), 4131-4146. https://doi.org/10.3390/ma8074131






