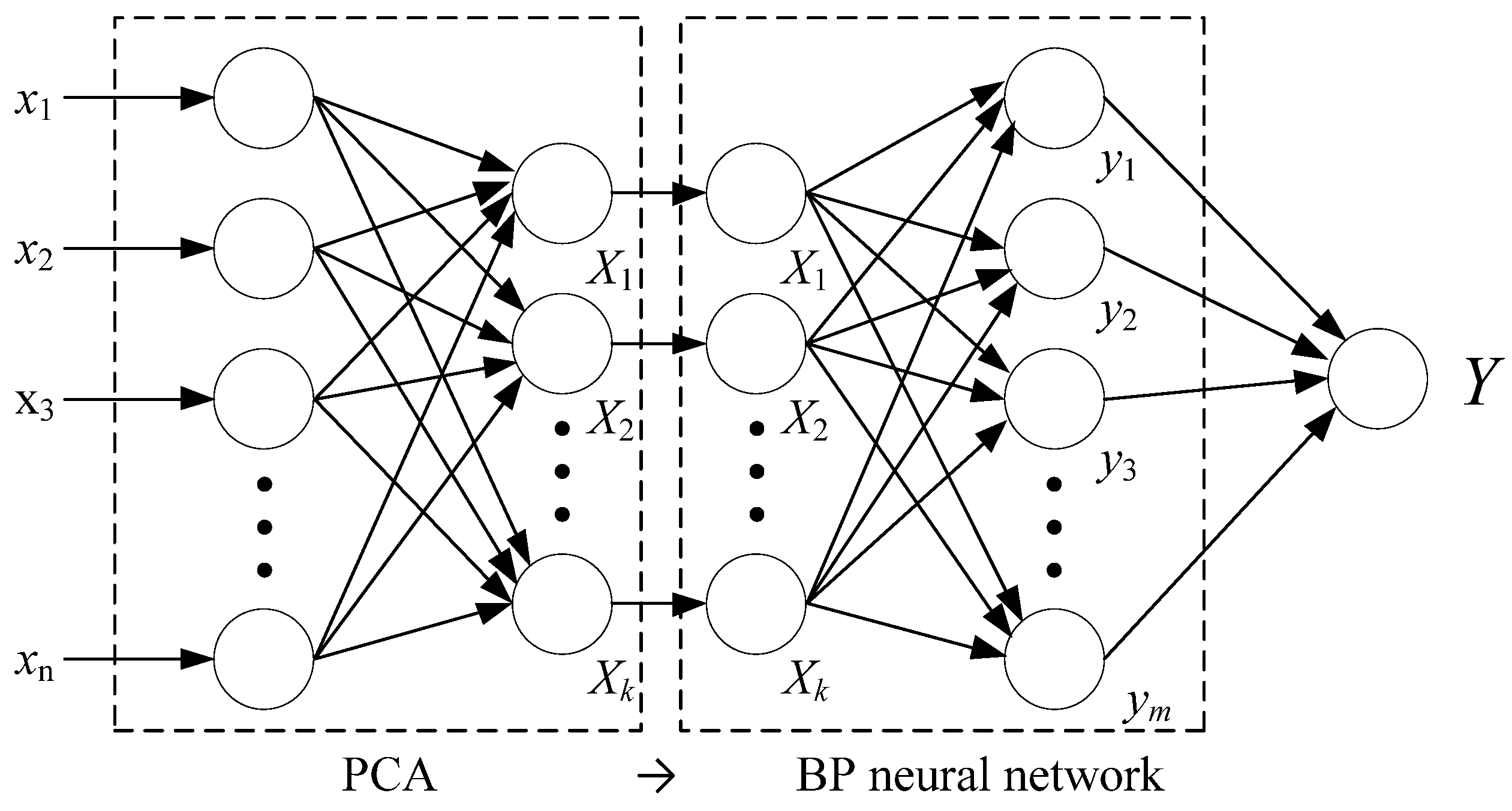
3.1. The Background of the PCA Method
In complex problems, the PCA method is an effective technique for reducing data dimensions to prevent information repetitions and redundancies to address principal contradictions [
34,
35,
36,
37]. The PCA method is a statistical procedure by which an information matrix of possibly correlated original sample data is converted into a set of values for linearly uncorrelated variables known as principal components by using an orthogonal transformation. Without loss of original sample information, the PCA method focuses on the crux of problems not only to reduce information dimensions but also to eliminate any information redundancy and nonlinearity. In this study, a prediction index system for rheological parameters of cemented tailing backfill was developed, and then a data matrix of samples was obtained according to experimental results. Rheological parameters of cemented tailing backfill can be considered a question involving
n sets of experimental samples and
p numbers of influencing factors (
p <
n) based on the following data matrix:
where
X is an
n ×
p matrix representing
n sets of data in which each data set consists of
p variables and
xij represents parameters to be tested.
Given dimensional inconsistencies in factors influencing rheological parameters of cemented tailing backfill, and it is necessary to standardize sample data as follows:
where
denotes the mean of the
j-th variable;
denotes the standard deviation of the
j-th variable;
i = 1, 2, …,
n; and
j = 1, 2, …,
p.
Standardized data were rearranged such that
p numbers of combined variables were obtained by a linear combination of original variables (
x1,
x2,…,
xp):
where
is the loading of the principle component representing the weight of the
j-th variable projected onto the
i-th principle component.
In addition, the coefficients
had to meet the requirement
, k = 1,2, …, p, which were determined by the following principles:
(i) yi should be linearly uncorrelated with yj (i ≠ j; i, j = 1,2, …, p).
(ii) y1 is the first principal component and has the largest variance in a linear combination of x1, x2, …, xp. That is, it accounts for as much variability in data as possible. y2 is the second principal component and has the largest variance in a linear combination of x1, x2, …, xp, which are linearly uncorrelated with y1. Similarly, yp is the p-th principal component and has the largest variance in a linear combination of x1, x2, …, xp, which are linearly uncorrelated with y1, y2, …, yp−1.
As stated earlier, rearranged integrated variables were defined as the first, second … and p-th principal components of original variables such that y1 had the highest ratio of the total variance and other integrated variables y2, y3, …, yp had gradually decreasing variances. The number of principle components was chosen based on the accumulated contribution ratio of variances such that the larger the accumulated contribution, the less the information loss. However, more calculations were required in both cases. Accordingly, the suitable accumulated contribution ratio was set to approximately 80%, and only several largest principle components were picked for constructing the next model to simplify the structure of the system and grasp the essence of the question.
3.2. The Application of the PCA Method for Reducing Rheological Property Data
Although prediction models for rheological properties based on artificial intelligence methods have been introduced [
17,
18], correlations and overlaps between input data have been ignored, which can have unfavorable effects on the accuracy of prediction models. To overcome this limitation, the PCA method was adopted before constructing prediction models with the BP neural network. New input factors (principal components) were obtained by the orthogonal transformation of original input factors. The number of input factors was reduced effectively almost without any change in original information, and correlations between input factors were eliminated, improving the precision and efficiency of calculations.
Standardized preprocessing [
34,
35,
36,
37] was employed using the experimental results for rheological properties of cemented tailing backfill tabulated in
Table 6. Then a Pearson correlation analysis was conducted to investigate the interrelationships between four input factors tabulated in
Table 7. There were distinct correlations between the specific weight and solid concentration of cemented tailing backfill, as well as between the slump and the solid concentration, indicating the existence of some information overlap between input factors, and therefore the use of principle components was required.
Table 6.
The standardized processing of index data.
Table 6.
The standardized processing of index data.
| Item | PC-1 | PC-2 | PC-3 | PC-4 |
|---|
| 1 | −1.43303 | −1.31339 | −1.24818 | 1.01734 |
| 2 | −1.43303 | −0.43780 | −1.35077 | 1.11851 |
| 3 | −1.43303 | 0.43780 | −1.35077 | 1.18596 |
| 4 | −1.43303 | 1.31339 | −1.35077 | 1.28713 |
| 5 | −0.85982 | −1.31339 | −0.83782 | 1.01734 |
| 6 | −0.85982 | −0.43780 | −0.83782 | 1.01734 |
| 7 | −0.85982 | 0.43780 | −0.83782 | 1.05106 |
| 8 | -0.85982 | 1.31339 | −0.83782 | 1.08478 |
| 9 | −0.28661 | −1.31339 | −0.32487 | 0.34286 |
| 10 | −0.28661 | −0.43780 | −0.32487 | 0.51148 |
| 11 | −0.28661 | 0.43780 | −0.32487 | 0.68010 |
| 12 | −0.28661 | 1.31339 | −0.42746 | 0.78127 |
| 13 | 0.28661 | −1.31339 | 0.18808 | −0.43279 |
| 14 | 0.28661 | −0.43780 | 0.18808 | −0.36534 |
| 15 | 0.28661 | 0.43780 | 0.18808 | −0.33162 |
| 16 | 0.28661 | 1.31339 | 0.18808 | −0.56769 |
| 17 | 0.85982 | −1.31339 | 0.70103 | −1.10727 |
| 18 | 0.85982 | −0.43780 | 0.70103 | −1.03982 |
| 19 | 0.85982 | 0.43780 | 0.70103 | −1.14099 |
| 20 | 0.85982 | 1.31339 | 0.70103 | −1.10727 |
| 21 | 1.43303 | −1.31339 | 1.62434 | −1.27589 |
| 22 | 1.43303 | −0.43780 | 1.62434 | −1.24216 |
| 23 | 1.43303 | 0.43780 | 1.62434 | −1.20844 |
| 24 | 1.43303 | 1.31339 | 1.62434 | −1.27589 |
Table 7.
A Pearson correlation analysis of factors influencing rheological properties.
Table 7.
A Pearson correlation analysis of factors influencing rheological properties.
| Pearson Correlation Analysis |
|---|
| Rheological properties | Solid Concentration (%) | Tailing/Cement ratio | Specific Weight (kg/m3) | Slump (m) |
|---|
| Solid concentration (%) | Pearson correlation coefficient | 1 | 0.000 | 0.992 ** | −0.969 ** |
| Significance (two-sided) | 0.000 | 1.000 | 0.000 | 0.000 |
| N | 24 | 24 | 24 | 24 |
| Tailing/cement ratio | Pearson correlation coefficient | 0.000 | 1 | −0.012 | 0.041 |
| Significance (two-sided) | 1.000 | 0.000 | 0.957 | 0.849 |
| N | 24 | 24 | 24 | 24 |
| Specific weight (kg/m3) | Pearson correlation coefficient | 0.992 ** | -0.012 | 1 | -0.955 ** |
| Significance (two-sided) | 0.000 | 0.957 | 0.000 | 0.000 |
| N | 24 | 24 | 24 | 24 |
| Slump (m) | Pearson correlation coefficient | −0.969 ** | 0.041 | −0.955 ** | 1 |
| Significance (two-sided) | 0.000 | 0.849 | 0.000 | 0.000 |
| N | 24 | 24 | 24 | 24 |
Analyses were conducted using data in
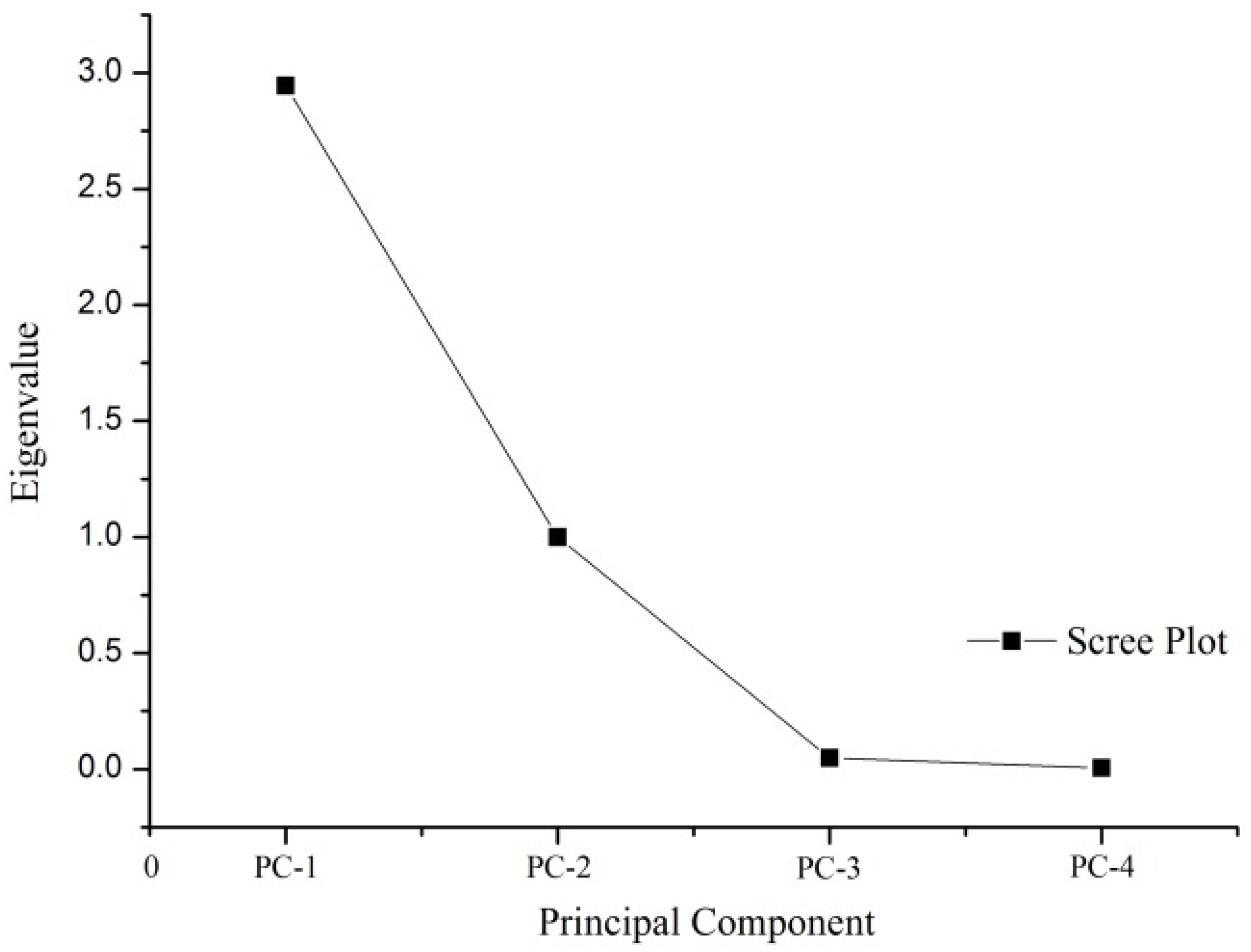
Table 6 based on SPSS (Statistical Package for the Social Sciences) and its PCA function, and principle components and scree plots were obtained. As shown in
Figure 3, the X-axis shows principal components sorted by the decreasing fraction of the total variance explained, and the Y-axis shows corresponding eigenvalues. Based on the scree plots, there large differences in eigenvalues between PC-1 and PC-2 and between PC-3 and PC-4, indicating that the first two components of the rearranged information matrix included original information. Therefore, PC-1 and PC-2 were considered the most important indices, and PC-3 and PC-4 were considered non-significant indices. The scree plot was consistent with the cumulative contribution of the first two sets of data in
Table 8. Despite some errors in the substitution of two sets of data in the rearranged information matrix for the original four sets of data, test data accounted for 98.634% of information in the original sample, produced reliable calculations, and enhanced computing efficiency because of a reduced number of factors. In addition, the results satisfy the requirement that the ratio of required information accounts for more than 75%–85% of original information in the PCA. Further, the results in
Table 8 are consistent with
Figure 3.
Figure 3.
A PCA scree plot.
Figure 3.
A PCA scree plot.
Table 8.
Variance and cumulative contributions of PC-1, PC-2, PC-3, and PC-4.
Table 8.
Variance and cumulative contributions of PC-1, PC-2, PC-3, and PC-4.
| Components | Initial Eigenvalue | Accumulated Contributions |
|---|
| Total | Variance (%) | Accumulation (%) | Total | Variance (%) | Accumulation (%) |
|---|
| PC-1 | 2.945 | 73.622 | 73.622 | 2.965 | 73.622 | 73.622 |
| PC-2 | 1.000 | 25.012 | 98.634 | 1.000 | 25.012 | 98.634 |
| PC-3 | 0.048 | 1.210 | 99.844 | | | |
| PC-4 | 0.006 | 0.156 | 100.000 | | | |
A coefficient matrix of principle components was calculated and tabulated based on SPSS in
Table 9 for relationships between two principle components and original data:
Principal components (PCs) were determined using the standardized data in
Table 6 according to the aforementioned formula. The prediction model was constructed using the results tabulated in
Table 10.
Table 9.
The weight factor matrix of principle components.
Table 9.
The weight factor matrix of principle components.
| Coefficient | Principle Component |
|---|
| Z1 | Z2 |
|---|
| PC1 | 0.338 | 0.027 |
| PC2 | 0.009 | 0.999 |
| PC3 | 0.337 | 0.015 |
| PC4 | 0.334 | 0.016 |
Table 10.
Experimental data with the PCA method.
Table 10.
Experimental data with the PCA method.
| No. | Z1 | Z2 | Yield Stress (Pa) | Viscosity (Pa·s) |
|---|
| 1 | −1.23297 | 1.27439 | 43.85 | 1.35 |
| 2 | −1.30922 | 0.399356 | 48.74 | 1.51 |
| 3 | −1.33962 | −0.47488 | 50.92 | 1.57 |
| 4 | −1.3813 | −1.34893 | 35.62 | 1.09 |
| 5 | −0.90094 | 1.290709 | 73.51 | 2.27 |
| 6 | −0.90882 | 0.416121 | 67.44 | 2.08 |
| 7 | −0.92796 | −0.4583 | 65.50 | 2.03 |
| 8 | −0.9471 | −1.33271 | 66.48 | 2.05 |
| 9 | −0.30905 | 1.30441 | 142.15 | 4.41 |
| 10 | −0.37325 | 0.430723 | 111.05 | 3.43 |
| 11 | −0.43745 | −0.44297 | 80.47 | 2.48 |
| 12 | −0.51369 | −1.31801 | 94.42 | 2.91 |
| 13 | 0.31663 | 1.31757 | 175.96 | 5.44 |
| 14 | 0.286221 | 0.443342 | 177.56 | 5.46 |
| 15 | 0.267078 | −0.43108 | 154.19 | 4.79 |
| 16 | 0.338045 | −1.30693 | 124.95 | 3.86 |
| 17 | 0.908515 | 1.331271 | 300.05 | 9.38 |
| 18 | 0.878106 | 0.457043 | 341.78 | 10.82 |
| 19 | 0.904017 | −0.4181 | 338.25 | 7.56 |
| 20 | 0.884874 | −1.2925 | 322.47 | 9.24 |
| 21 | 1.469734 | 1.351618 | 533.92 | 12.11 |
| 22 | 1.450588 | 0.47721 | 542.38 | 13.06 |
| 23 | 1.431445 | −0.39721 | 521.31 | 10.97 |
| 24 | 1.446093 | −1.27216 | 532.10 | 12.53 |