A Six-Fold Symmetric Metamaterial Absorber
Abstract
:1. Introduction
2. Results and Discussion
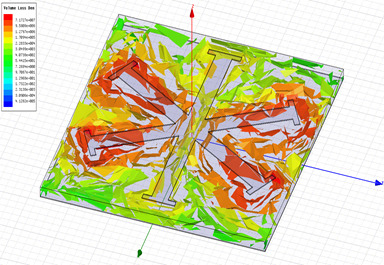
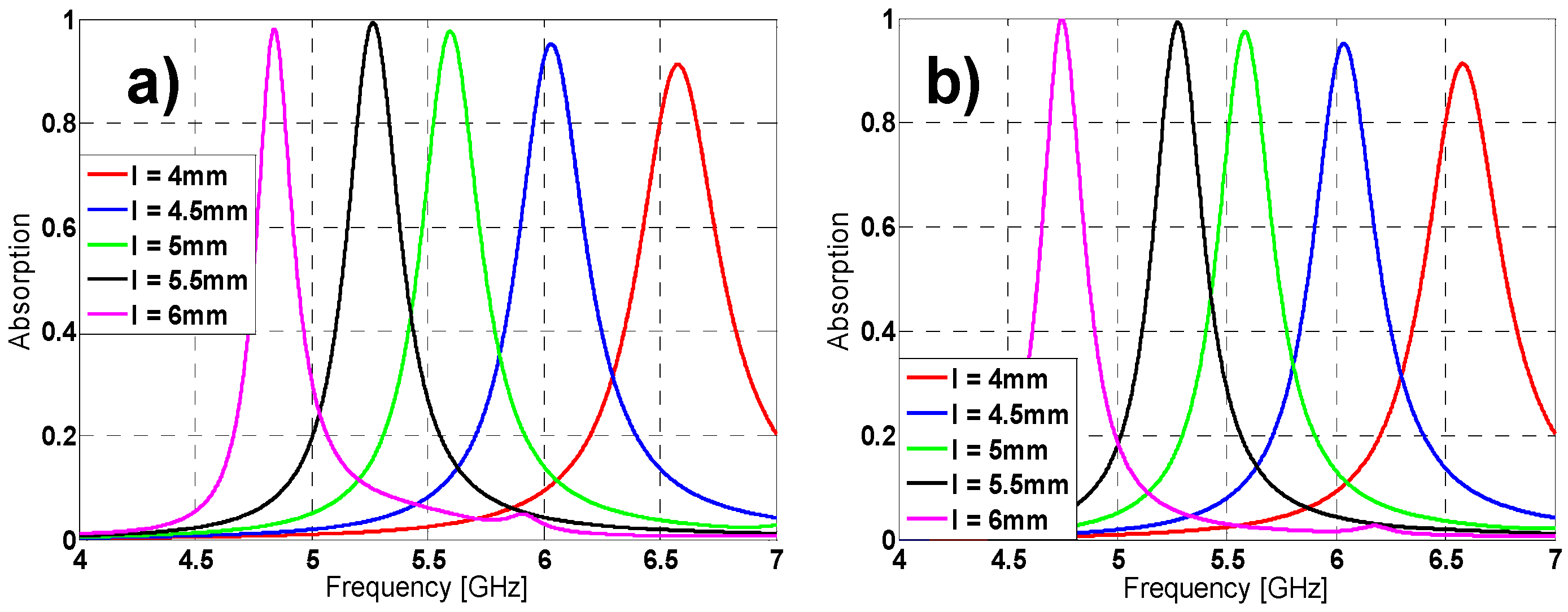
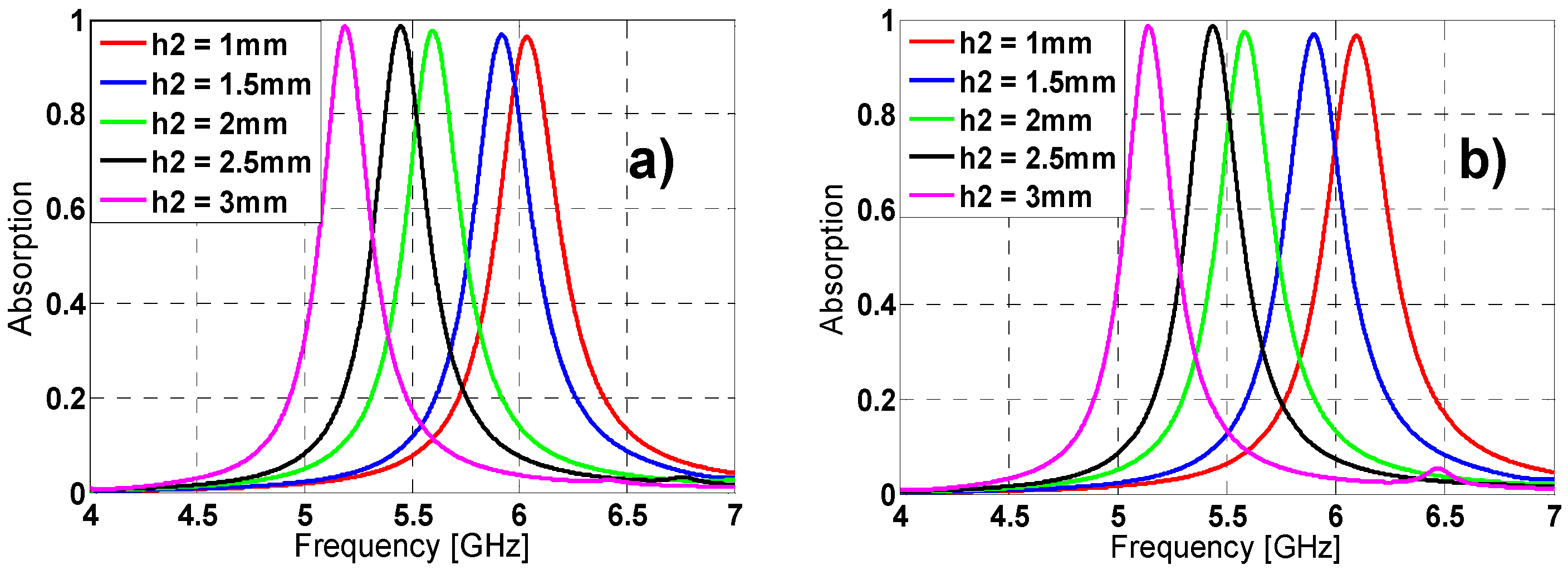
2.1. Metamaterial Absorber Design and Characterization
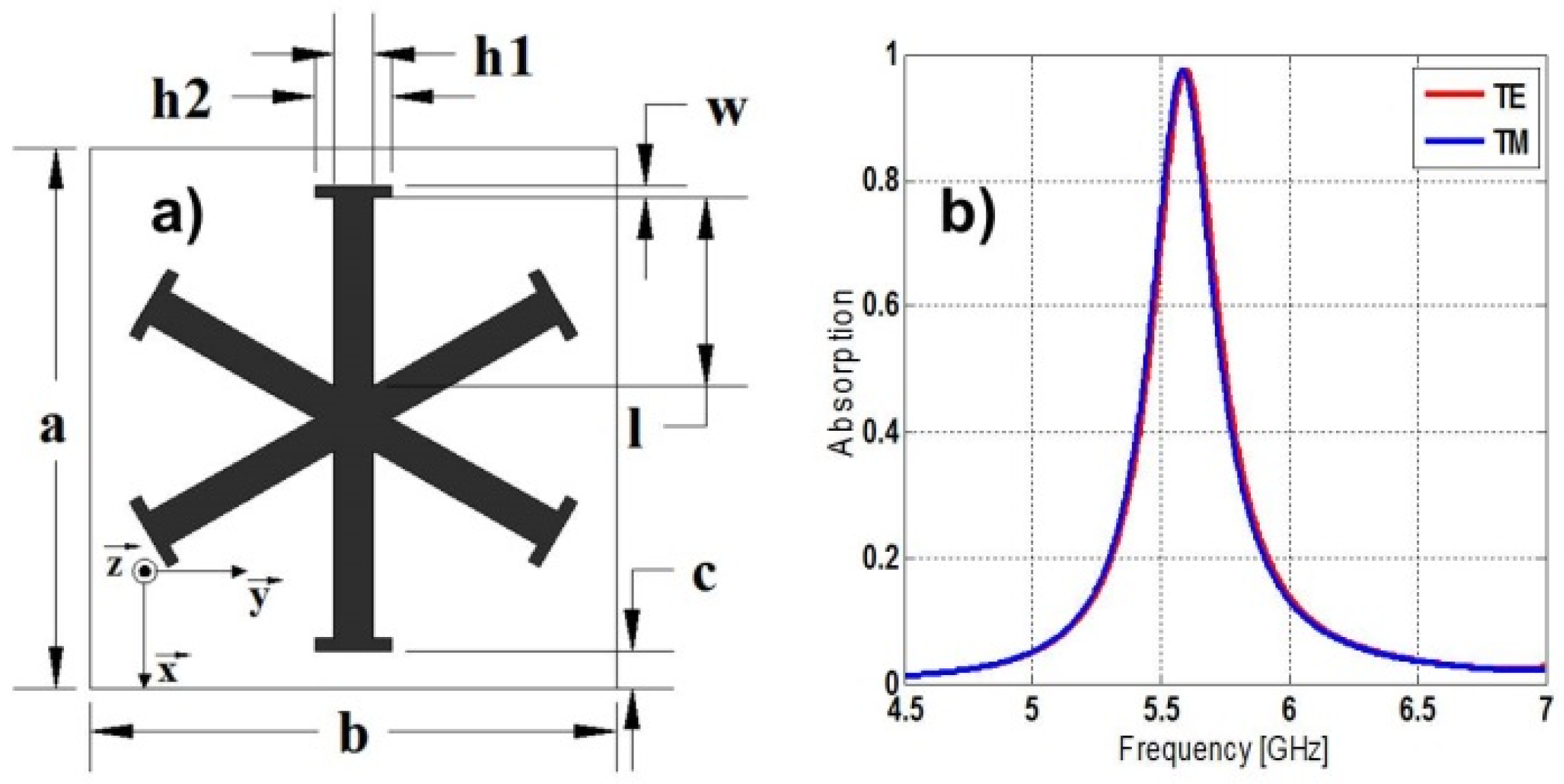
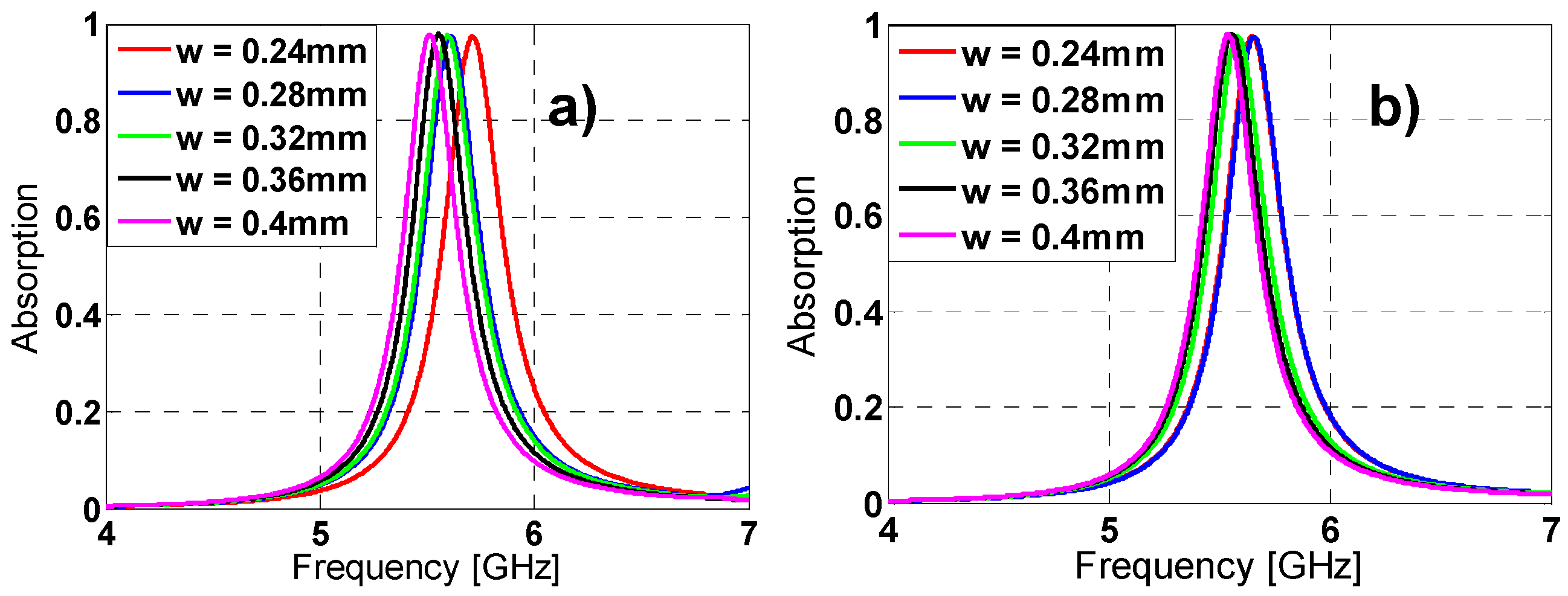
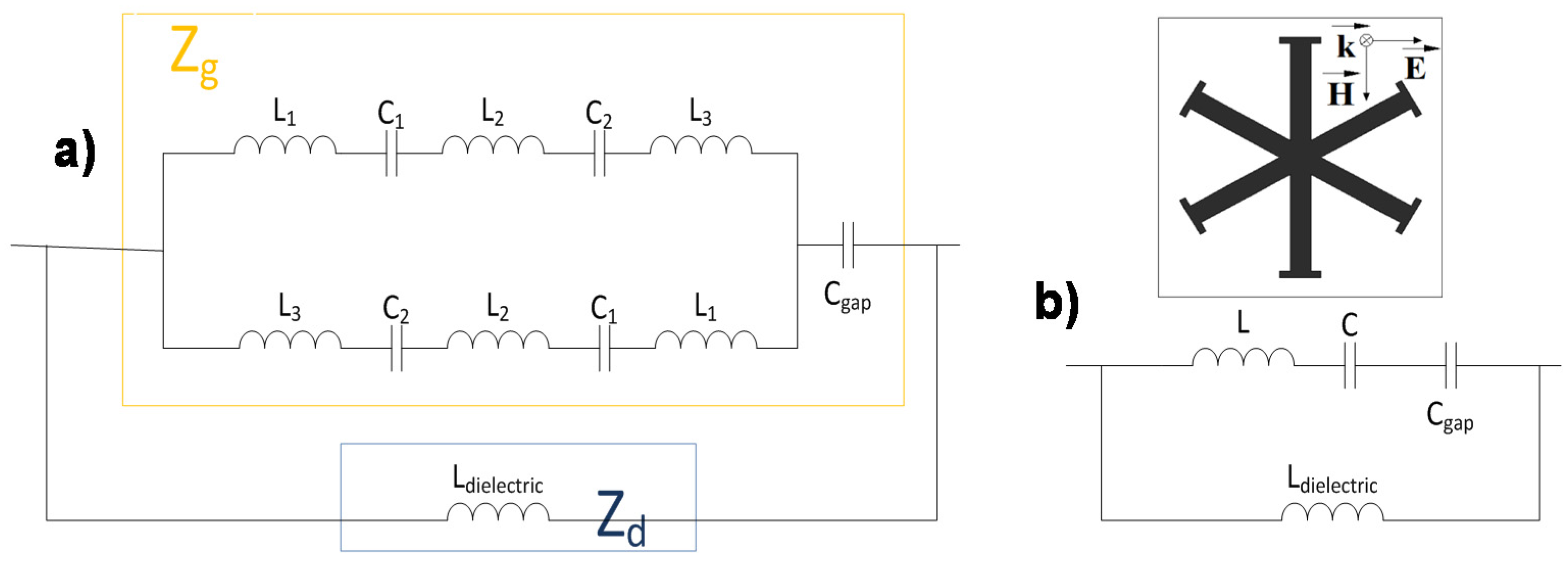
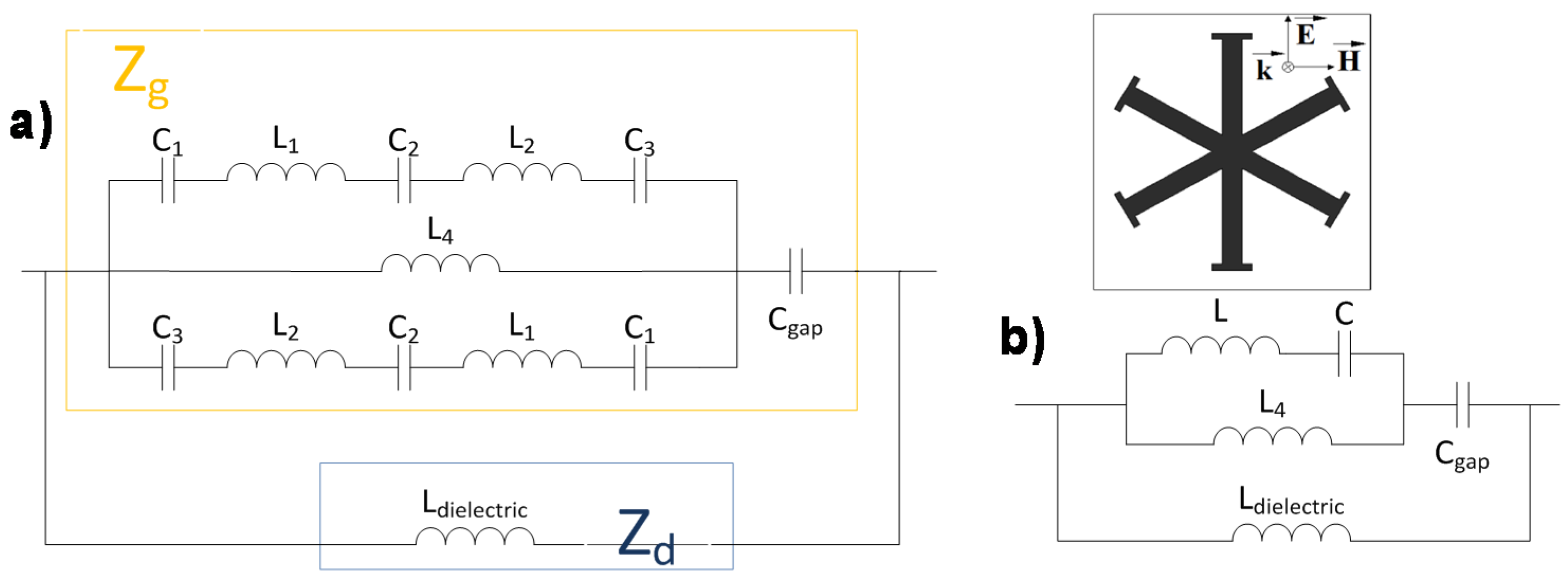
2.2. Equivalent Circuit Model
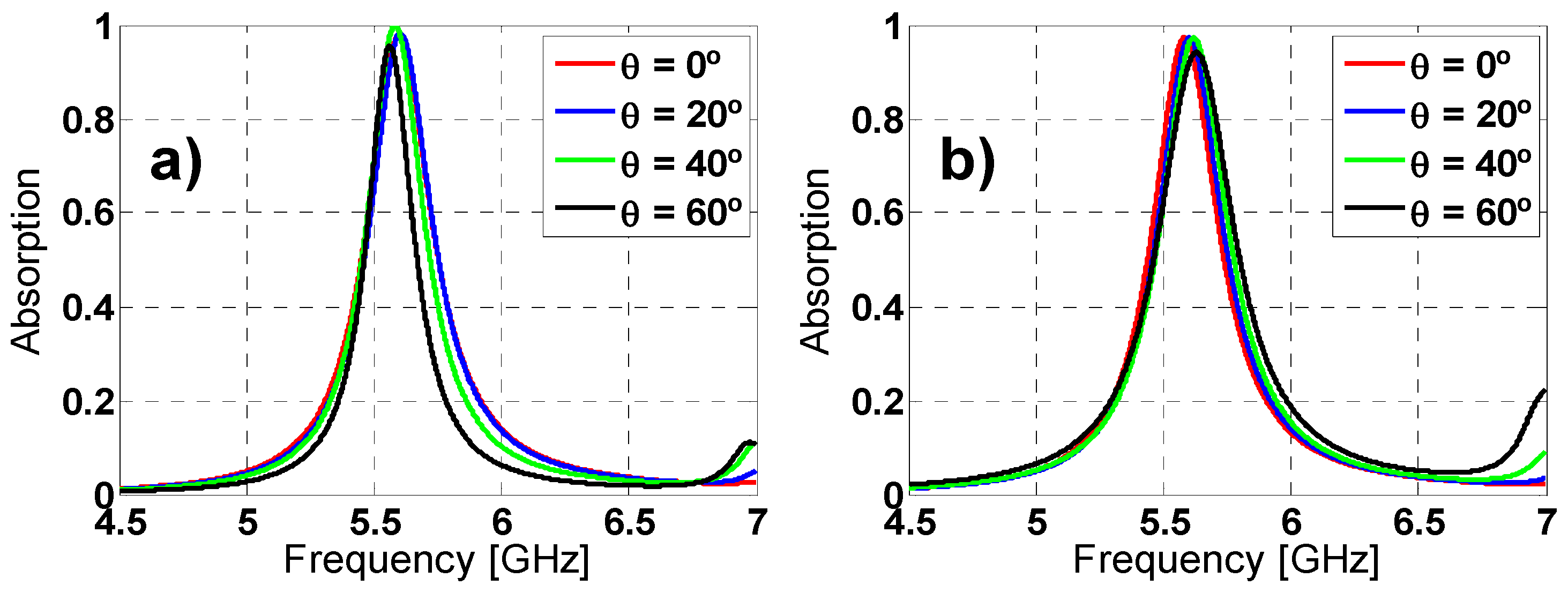
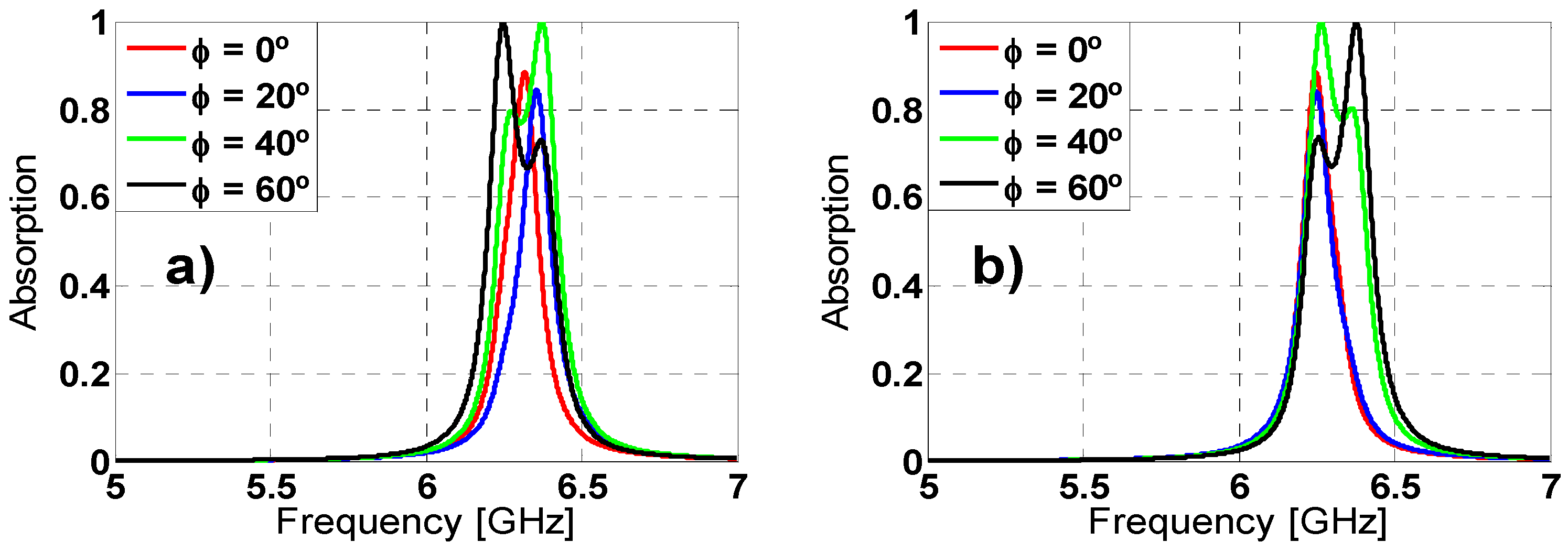
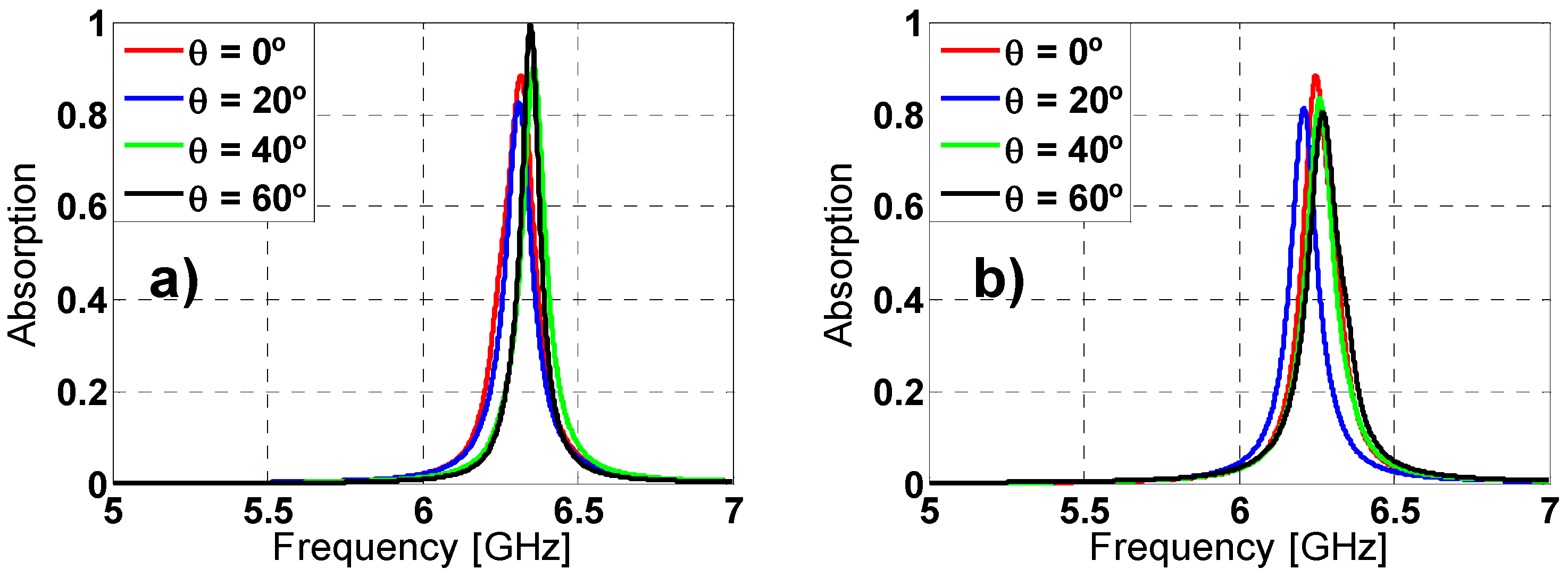
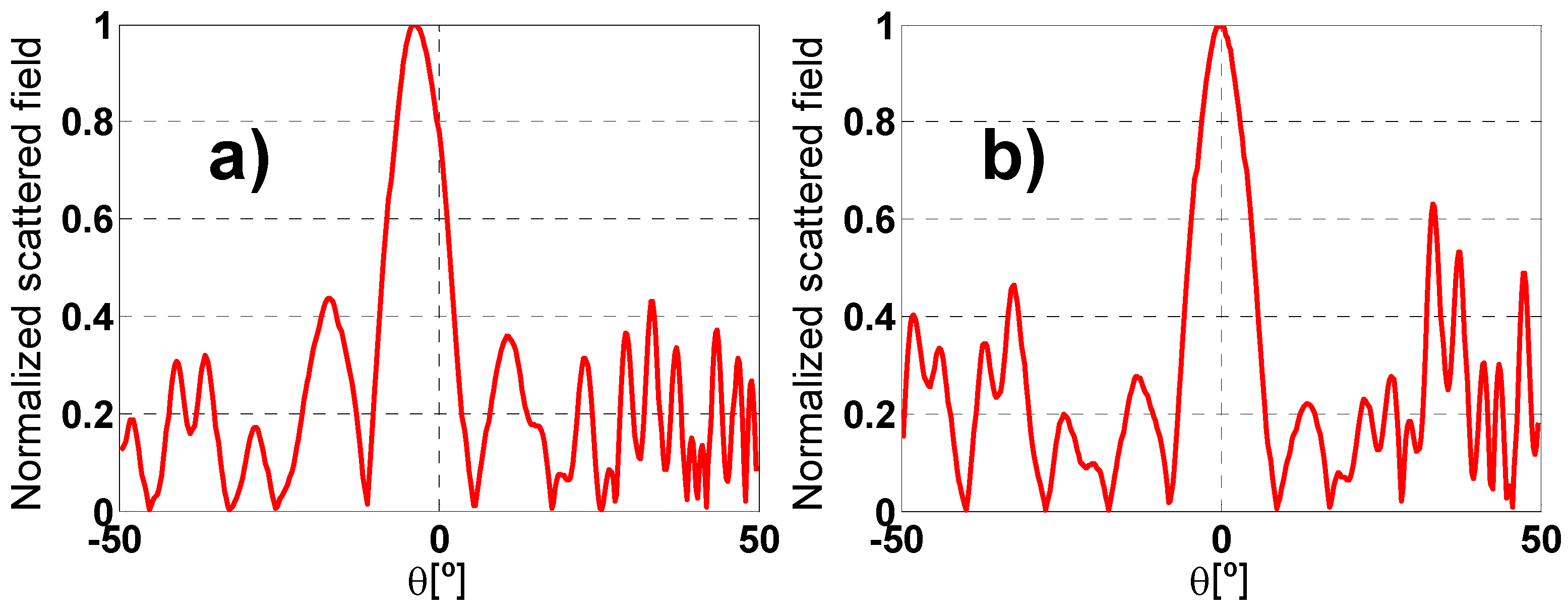
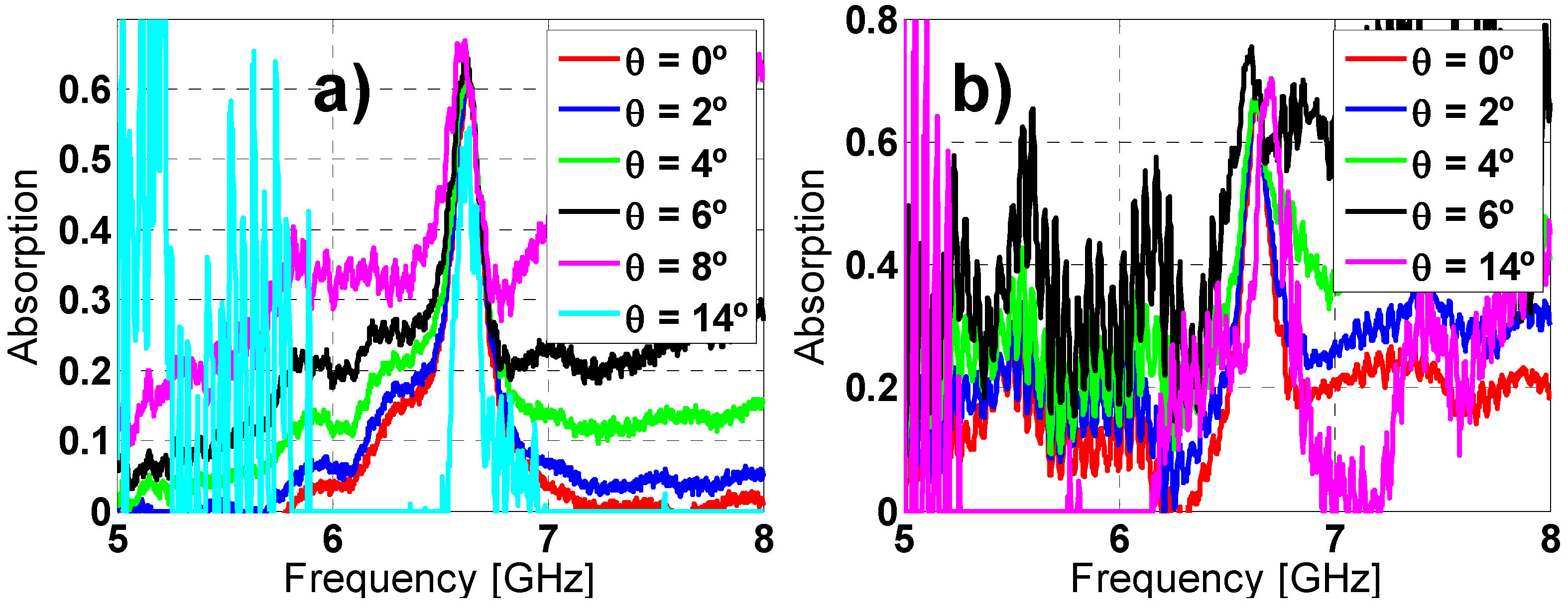
2.3. Angular Stability

2.4. Comparison with the State of the Art
| Prototype | Resonant Frequency [GHz] | Thickness * [mm] | Electrical Thickness | FWHM (simulation) [%] | Polarization Insensitive | Angle of incidence insensitive |
|---|---|---|---|---|---|---|
| Paper | 5.599 | 1.07 | λfr/50 | 5.55 | Yes | Yes |
| [3] | 11.65 | 0.737 | λfr/34.94 | 4 | No | Till 16° |
| [13] | 5.57 | 0.57 | λfr/94.49 | 3.9 | Yes | Yes but worse than in this paper |
| [30] | 9.5 | 1.034 | λfr/30.54 | 3.79 | Yes | Yes but worse than in this paper |
| [31] | 10.05 | 0.76 | λfr/39 | 4.8 | Yes | Yes but worse than in this paper |
| [32] | 10.14 | 1 | λfr/29.586 | 4.7 | Yes | Yes |
| [33] | 11.3 | 0.418 | λfr/63 | 4.2 | Yes | Till 25° |
| [34] | 8.10 | 1.07 | λfr/34.61 | 4.68 | No | No |
| [35] | 10 | 0.87 | λfr/34.48 | 4.9 | Yes | Yes |
2.5. Flexible Metamaterial
| Dielectric | εr | tanδ | Thickness (mm) |
|---|---|---|---|
| Arlon 25n | 3.28 | 0.0025 | 0.457 |
| RO3003 | 3 | 0.0013 | 0.800 |
| RO4003C | 3.38 | 0.0027 | 0.203 |
| RO4003C | 3.38 | 0.0027 | 0.406 |
| Dielectric | Polarization (fr [GHz]) | Thickness (mm) | Electric thickness |
|---|---|---|---|
| FR4 | TE (5.599) | 1.07 | ~λr/50 |
| FR4 | TM (5.583) | 1.07 | ~λr/50 |
| Arlon 25n | TE(6.319) | 0.493 | ~λr/96.26 |
| Arlon 25n | TM(6.249) | 0.493 | ~λr/97.33 |
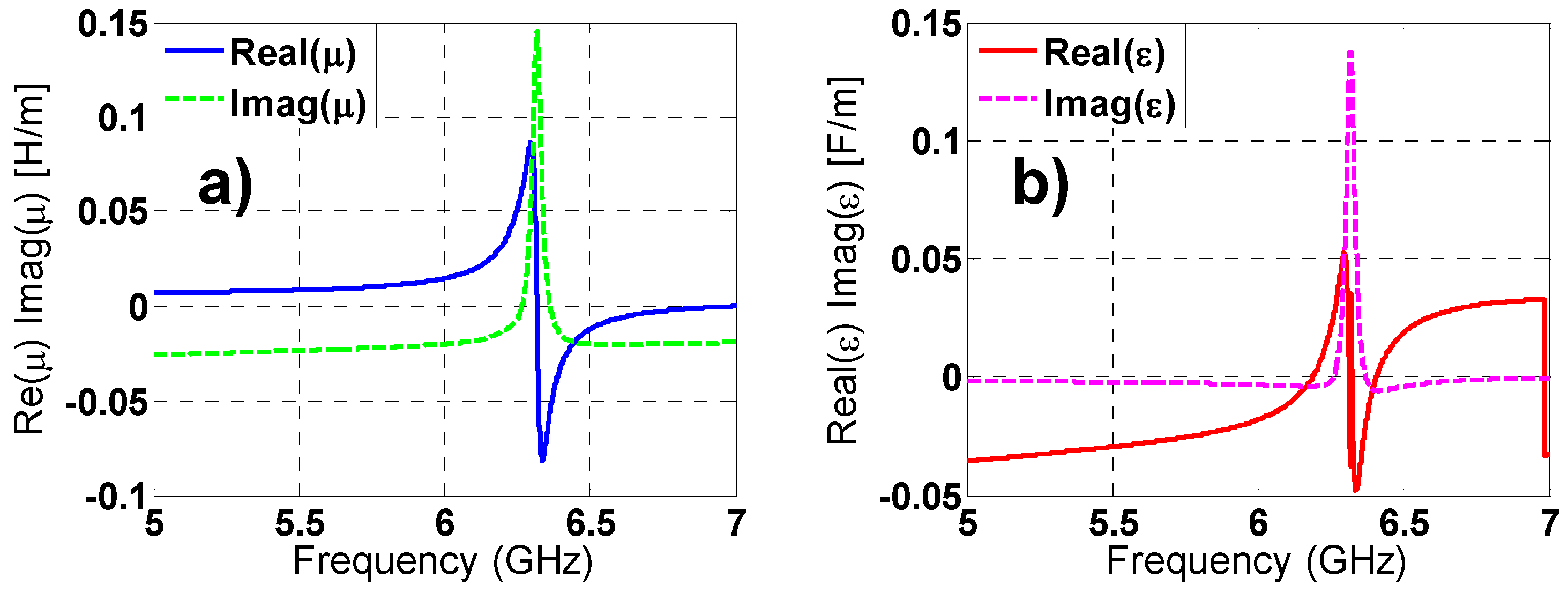
2.6. Constitutive Parameters of Metamaterial Absorber
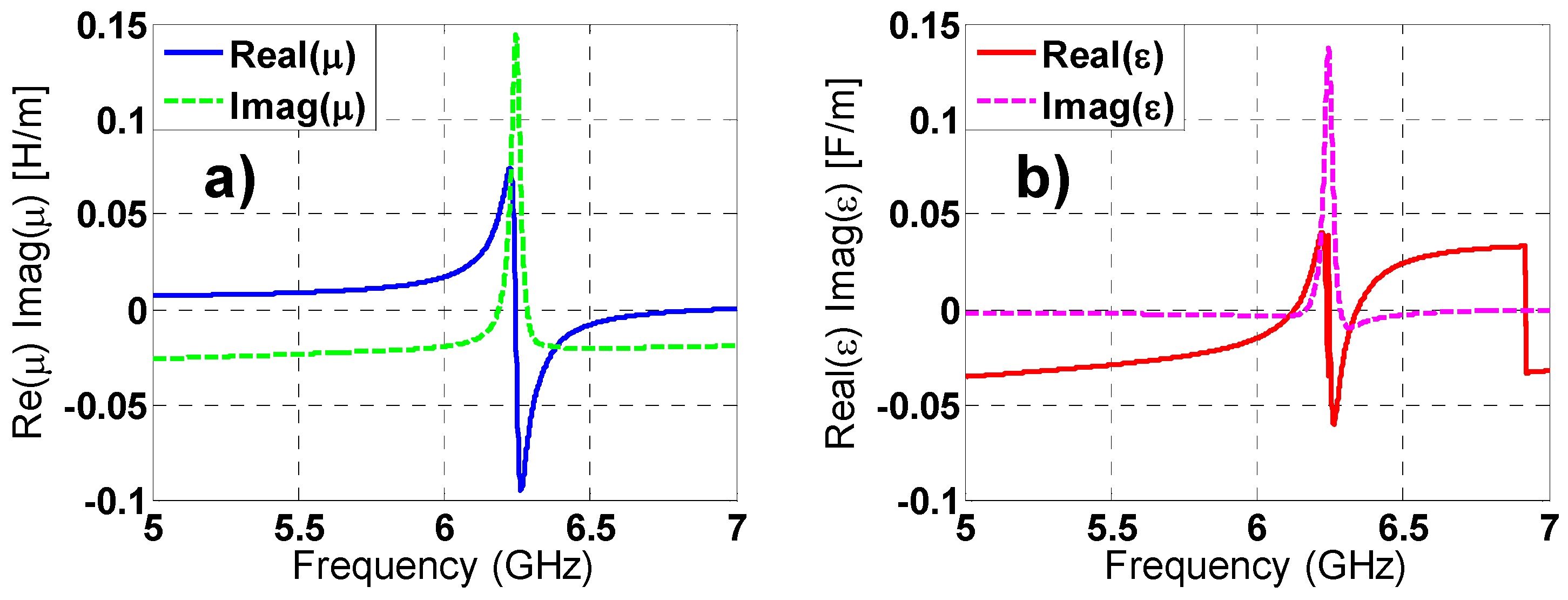
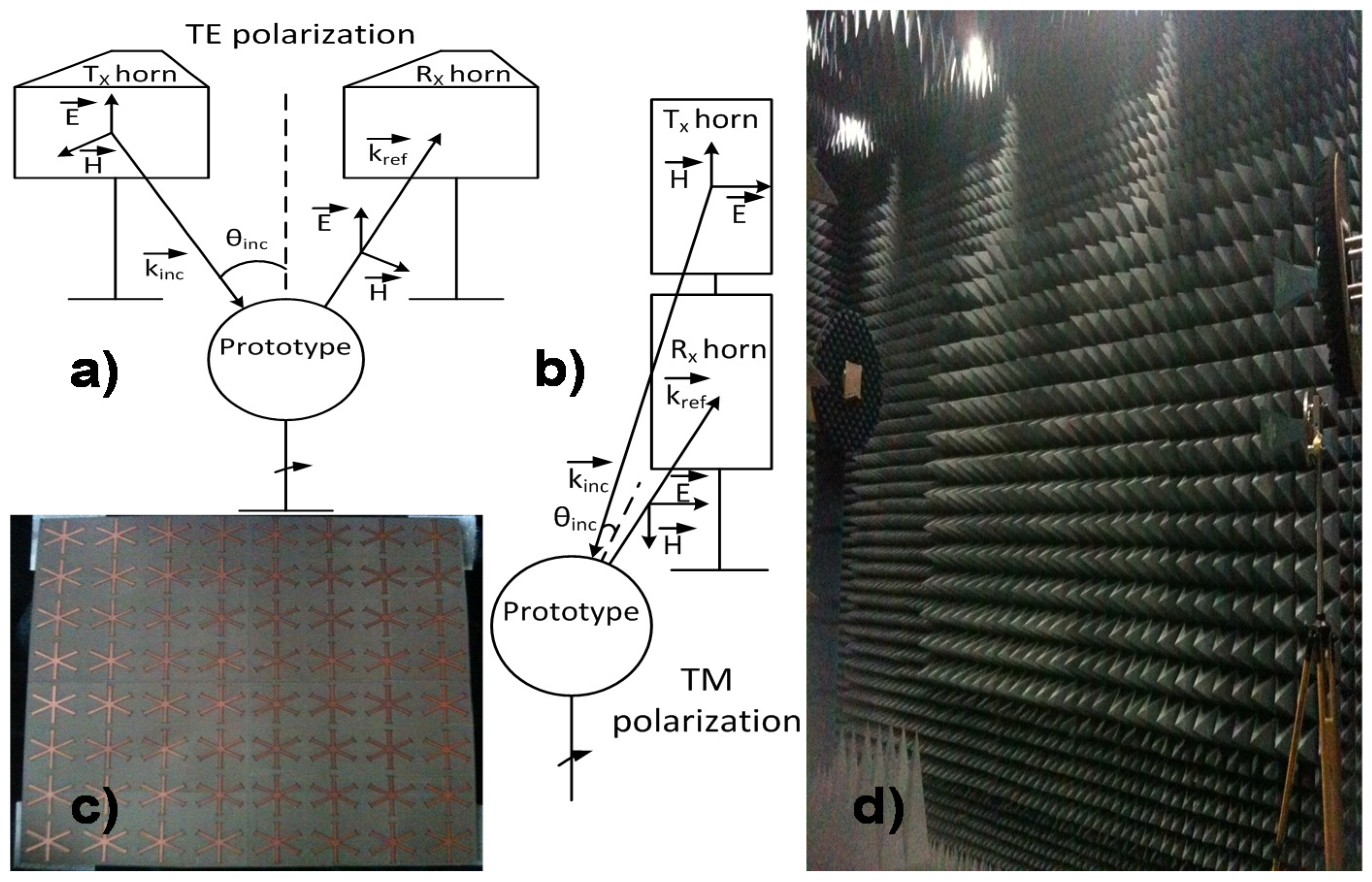
3. Experimental Section
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075. [Google Scholar] [CrossRef]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Che, S.F.; Cahill, R.; Fusco, V.F.; Goussetis, G. Design of a salisbury screen absorber using frequency selective surfaces to improve bandwidth and angular stability performance. IET Microw. Antennas Propag. 2011, 5, 149–156. [Google Scholar] [CrossRef]
- Kafesaki, M.; Tsiapa, I.; Katsarakis, N.; Koschny, Th.; Soukoulis, C.M.; Economou, E.N. Left-handed metamaterials: The fishnet structure and its variations. Phys. Rev. B 2007, 75, 235114–235123. [Google Scholar] [CrossRef]
- Pham, V.T.; Park, J.W.; Lam, V.D.; Jang, W.H.; Choi, E.H.; Nikitov, S.A; Young, P.L. Negative refractive index at the third-order resonance of flower-shaped metamaterial. Lightwave Technol. 2012, 30, 3451–3455. [Google Scholar]
- Bingnan, W.; Thomas, K.; Costas, M.S. Wide-angle and polarization-independent chiral metamaterial absorber. Phys. Rev. B 2009, 80, 033108. [Google Scholar] [CrossRef]
- Yang, H.; Cao, X.-Y.; Gao, J.; Yuan, W.; Li, Z.; Shang, K. Low RCS metamaterial absorber and extending bandwidth based on electromagnetic resonances. Prog. Electromagn. Res. M 2013, 33, 31–44. [Google Scholar] [CrossRef]
- Luo, H.; Wang, T.; Gong, R.-Z.; Nie, Y.; Wang, X. Extending the bandwidth of electric ring resonator metamaterial absorber. Chin. Phys. Lett. 2011, 28, 034204. [Google Scholar] [CrossRef]
- Zhong, S.M.; He, S.L. Ultrathin and lightweight microwave absorbers made of Mu-near-zero metamaterials. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- He, X.-J.; Wang, Y.; Wang, J.; Gui, T.; Wu, Q. Dual-band terahertz metamaterial absorber with polarization insensitivity and wide incident angle. Prog. Electromagn. Res. 2011, 115, 381–397. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Zillohu, A.U.; Strunskus, T.; Faupel, F.; Elbahri, M. Plasmonic tunable metamaterial absorber as ultraviolet protection film. Appl. Phys. Lett. 2014, 104, 041103. [Google Scholar] [CrossRef]
- Liu, T.; Cao, X.; Gao, J.; Zheng, Q.; Li, W.; Yang, H. RCS Reduction of waveguide slot antenna with metamaterial absorber. IEEE Trans. Antennas Propag. 2013, 61, 1479–1484. [Google Scholar] [CrossRef]
- Nicholas, F.; Hyesog, L.; Cheng, S.; Xiang, Z. Sub-diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Wu, B.-I.; Zhang, B.; Au Kong, J. Electromagnetic wave interactions with a metamaterial cloak. Phys. Rev. Lett. 2007, 99, 063903. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Li, S.; Sun, H. Metamaterials application in sensing. Sensors 2012, 12, 2742–2765. [Google Scholar] [CrossRef] [PubMed]
- Cong, L.; Tan, S.; Yahiaoui, R.; Yan, F.; Zhang, W.; Singh, R. Experimental demonstration of ultrasensitive sensing with terahertz metamaterial absorbers: A comparison with the metasurfaces. Appl. Phys. Lett. 2015, 106, 031107. [Google Scholar] [CrossRef]
- Cao, W.; Singh, R.; Zhang, C.; Han, J.; Tonouchi, M.; Zhang, W. Plasmon-induced transparency in metamaterials: Active near field coupling between bright superconducting and dark metallic mode resonators. Appl. Phys. Lett. 2013, 103, 101106. [Google Scholar] [CrossRef]
- Chowdhury, D.R.; Singh, R.; Taylor, A.J.; Chen, H.T.; Azad, A.K. Ultrafast manipulation of near field coupling between bright and dark modes in terahertz metamaterial. Appl. Phys. Lett. 2013, 102, 011122. [Google Scholar] [CrossRef]
- Singh, R.; Xiong, J.; Azad, A.K.; Yang, H.; Trugman, S.A.; Jia, Q.X.; Taylor, A.J.; Chen, H.-T. Optical tuning and ultrafast dynamics of high-temperature superconducting terahertz metamaterials. Nanophotonics 2012, 1, 117–123. [Google Scholar] [CrossRef]
- Gu, J.; Singh, R.; Azad, A.K.; Han, J.; Taylor, A.J.; O’Hara, J.F.; Zhang, W. An active hybrid plasmonic metamaterial. Opt. Mater. Express 2012, 2, 31–37. [Google Scholar] [CrossRef]
- Chowdhury, D.R.; Singh, R.; Reiten, M.; Zhou, J.; Taylor, A.J.; O’Hara, J.F. Tailored resonator coupling for modifying the terahertz metamaterial response. Opt. Express 2011, 19, 10679–10685. [Google Scholar]
- Tao, H.; Bingham, C.M.; Strikwerda, A.C.; Pilon, D.; Shrekenhamer, D.; Landy, N.I.; Fan, K.; Zhang, X.; Padilla, W.J.; Averitt, R.D. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication and characterization. Phys. Rev. B 2008, 78, 241103. [Google Scholar] [CrossRef]
- Avitzour, Y.; Urzhumov, Y.A.; Shvets, G. Wide-angle infrared absorber based on a negative-index plasmonic metamaterial. Phys. Rev. B 2009, 79, 045131. [Google Scholar] [CrossRef]
- Diem, M.; Koschny, T.; Soukoulis, C.M. Wide-angle perfect absorber/thermal emitter in the terahertz regime. Phys. Rev. B 2009, 79, 033101. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [PubMed]
- Luukkonen, O.; Simovski, C.; Granet, G.; Goussetis, G.; Lioubtchenko, D.; Raisanen, A.V.; Tretyakov, S.A. Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Trans. Antenna Propag. 2008, 56, 1624–1632. [Google Scholar] [CrossRef]
- Ziolkowski, R.W. Design, fabrication, and testing of double negative metamaterials. IEEE Trans. Antennas Propag. 2003, 51, 1516–1529. [Google Scholar] [CrossRef]
- De Cos, M.E.; Alvarez, Y.; Las-Heras, F. Novel broadband artificial magnetic conductor with hexagonal unit cell. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 615–618. [Google Scholar]
- Zhu, B.; Wang, Z.-B.; Yu, Z.-Z.; Zhang, Q.; Zhao, J.-M.; Feng, Y.-J.; Tian, J. Planar metamaterial microwave absorber for all wave polarizations. Chin. Phys. Lett. 2008, 26, 114102. [Google Scholar]
- Fallahzadeh, S.; Forooraghi, K.; Atlasbaf, Z. Design, simulation and measurement of a dual linear polarization insensitive planar resonant metamaterial absorber. Prog. Electromagn. Res. Lett. 2012, 35, 135–144. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, Z.; Huang, C.; Feng, Y.; Zhao, J.; Jiang, T. Polarization insensitive metamaterial absorber with wide incident angle. Prog. Electromagn. Res. 2010, 101, 231–239. [Google Scholar] [CrossRef]
- Lee, J.; Yoon, Y.J.; Lim, S. Ultra-thin polarization independent absorber using hexagonal interdigital metamaterial. ETRI J. 2012, 34, 126–129. [Google Scholar] [CrossRef]
- Ghosh, S.; Sarkar, D.; Bhattacharyya, S.; Sriavstava, K.V. Design of an ultra-thin dual band microwave metamaterial absorber. In Proceedings of the 6th Antenna Test & Measurement Society (ATMS) Conference, Kolkata, India, 18–20 December 2013; pp. 38–41.
- Ayop, O.; Rahim, M.K.A.; Murad, N.A.; Samsuri, N.A. Polarization insensitive and wide operating angle metamaterial absorber at X-band. In Proceedings of the IEEE Asia-Pacific Conference on Applied Electromagnetics (APACE), Johor Bahru, Malaysia, 8–10 December 2014; pp. 245–249.
- Costa, F.; Genovesi, S.; Monorchio, A.; Manara, G. A circuit-based model for the interpretation of perfect metamaterial absorbers. IEEE Trans. Antennas Propag. 2013, 61, 1201–1209. [Google Scholar] [CrossRef]
- De Cos, M.E.; Las-Heras, F. On the advantages of loop-based unit-cell’s metallization regarding the angular stability of artificial magnetic conductors. Appl. Phys. A 2015, 118, 699–708. [Google Scholar]
- Lee, J.; Lim, S. Bandwidth-enhanced and polarisation-insensitive metamaterial absorber using double resonance. Electron. Lett. 2011, 47, 8–9. [Google Scholar] [CrossRef]
- De Cos, M.E.; Alvarez, Y.; Hadarig, R.C.; Las-Heras, F. Novel SHF-band uniplanar artificial magnetic conductor. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 44–47. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández Álvarez, H.; De Cos Gómez, M.E.; Las-Heras, F. A Six-Fold Symmetric Metamaterial Absorber. Materials 2015, 8, 1590-1603. https://doi.org/10.3390/ma8041590
Fernández Álvarez H, De Cos Gómez ME, Las-Heras F. A Six-Fold Symmetric Metamaterial Absorber. Materials. 2015; 8(4):1590-1603. https://doi.org/10.3390/ma8041590
Chicago/Turabian StyleFernández Álvarez, Humberto, María Elena De Cos Gómez, and Fernando Las-Heras. 2015. "A Six-Fold Symmetric Metamaterial Absorber" Materials 8, no. 4: 1590-1603. https://doi.org/10.3390/ma8041590
APA StyleFernández Álvarez, H., De Cos Gómez, M. E., & Las-Heras, F. (2015). A Six-Fold Symmetric Metamaterial Absorber. Materials, 8(4), 1590-1603. https://doi.org/10.3390/ma8041590