Process Design of Aluminum Tailor Heat Treated Blanks
Abstract
:1. Introduction
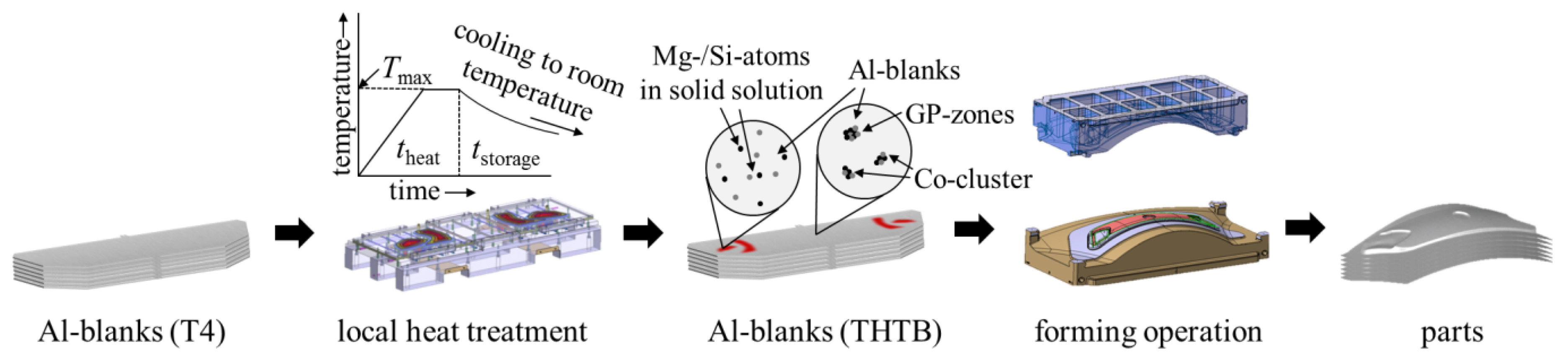
2. A Material Model for Tailor Heat Treated Blanks
2.1. General Approach to Describe the Plastic Behavior of Tailor Heat Treated Blanks (THTB)
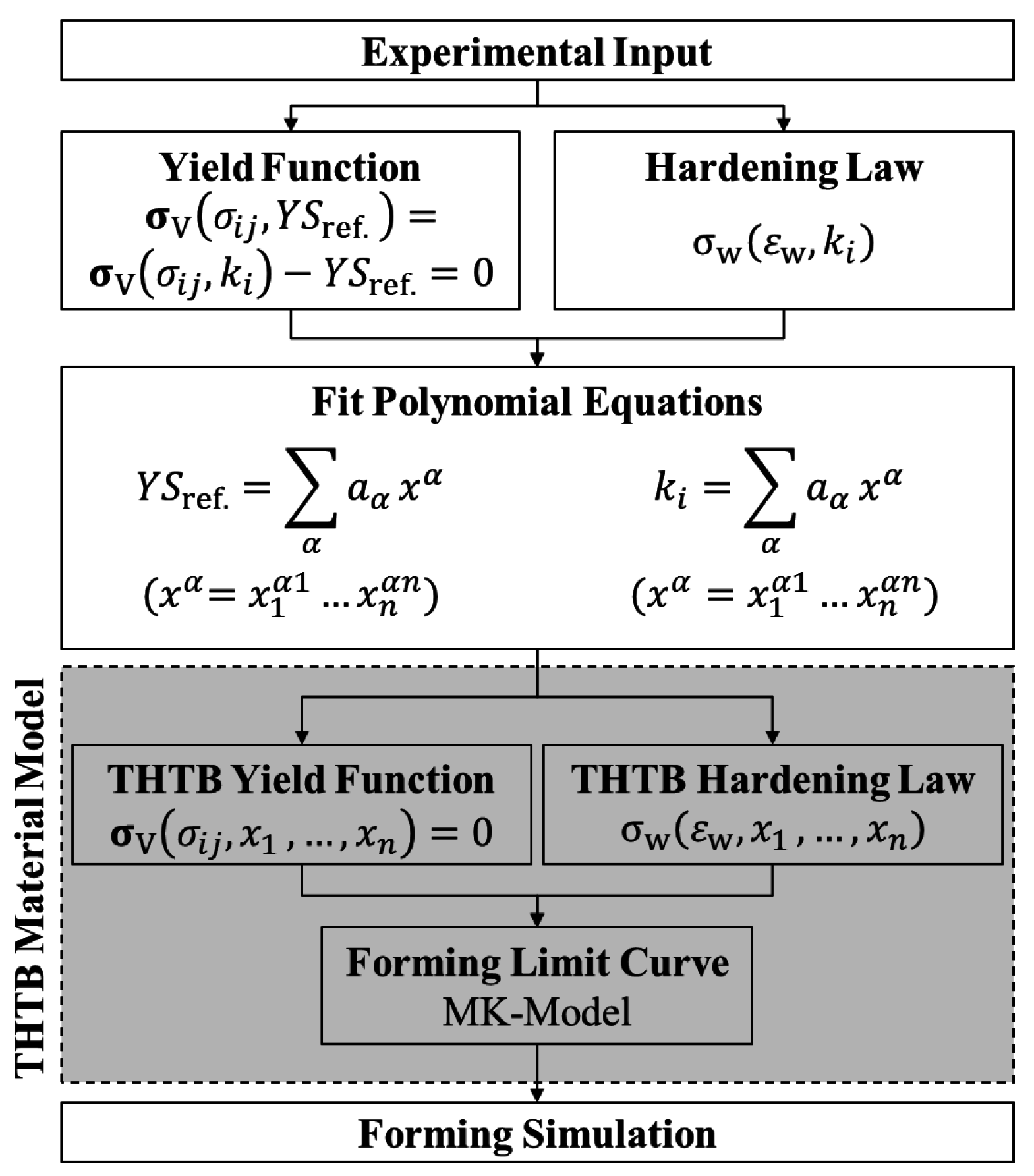
2.2. Application of the THTB Material Model to AA6014PX
2.2.1. Analysis of the Yield Surface and Flow Curve of the State T4
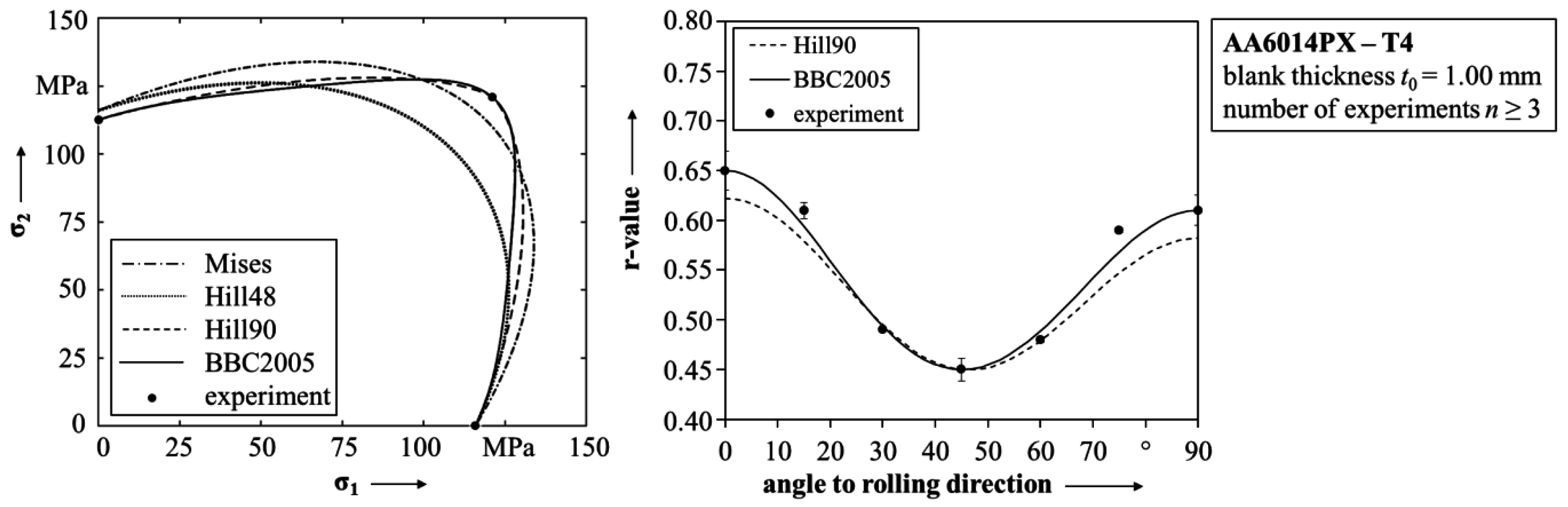
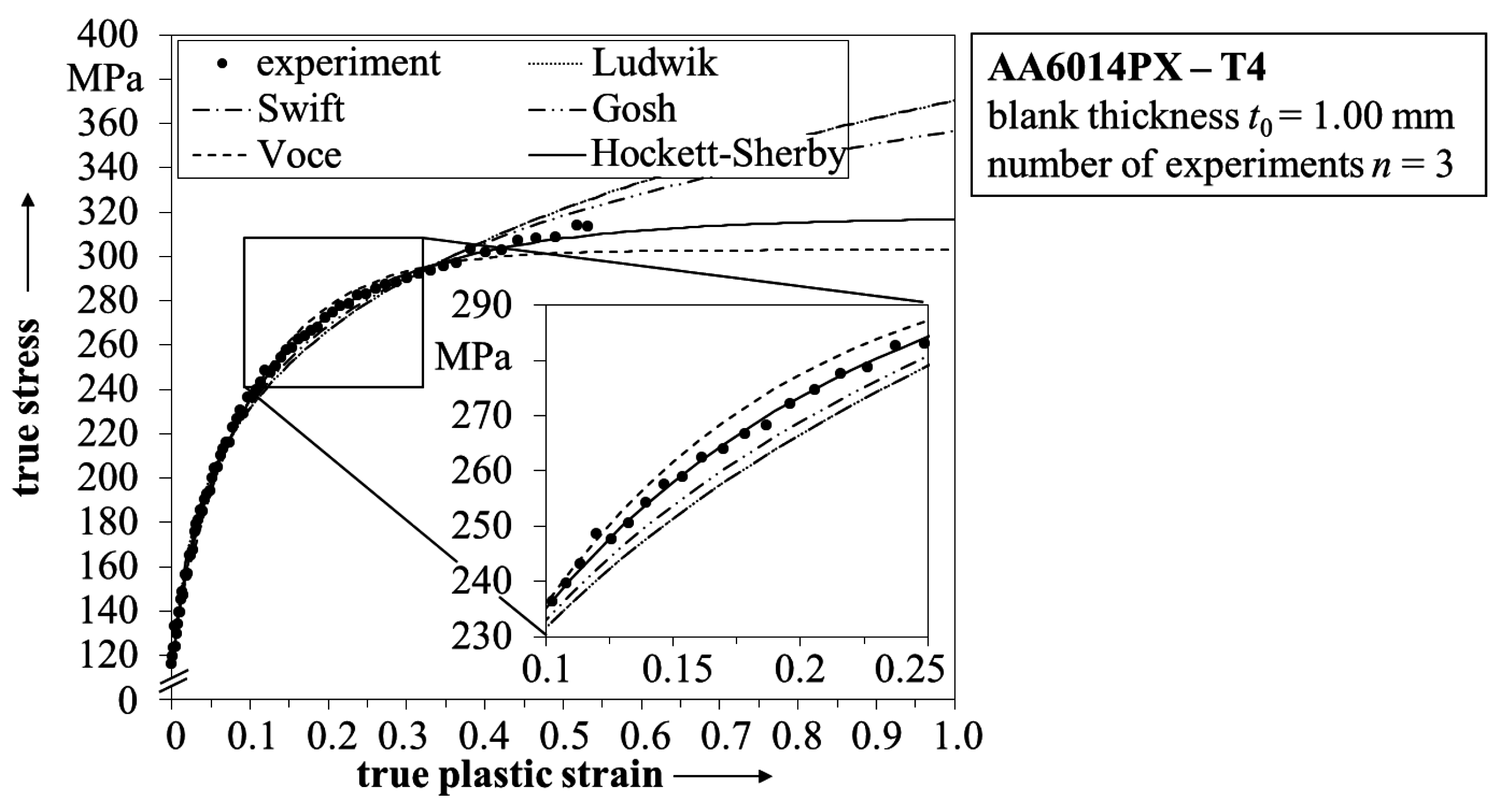
2.2.2. Determination of the THTB Material Model
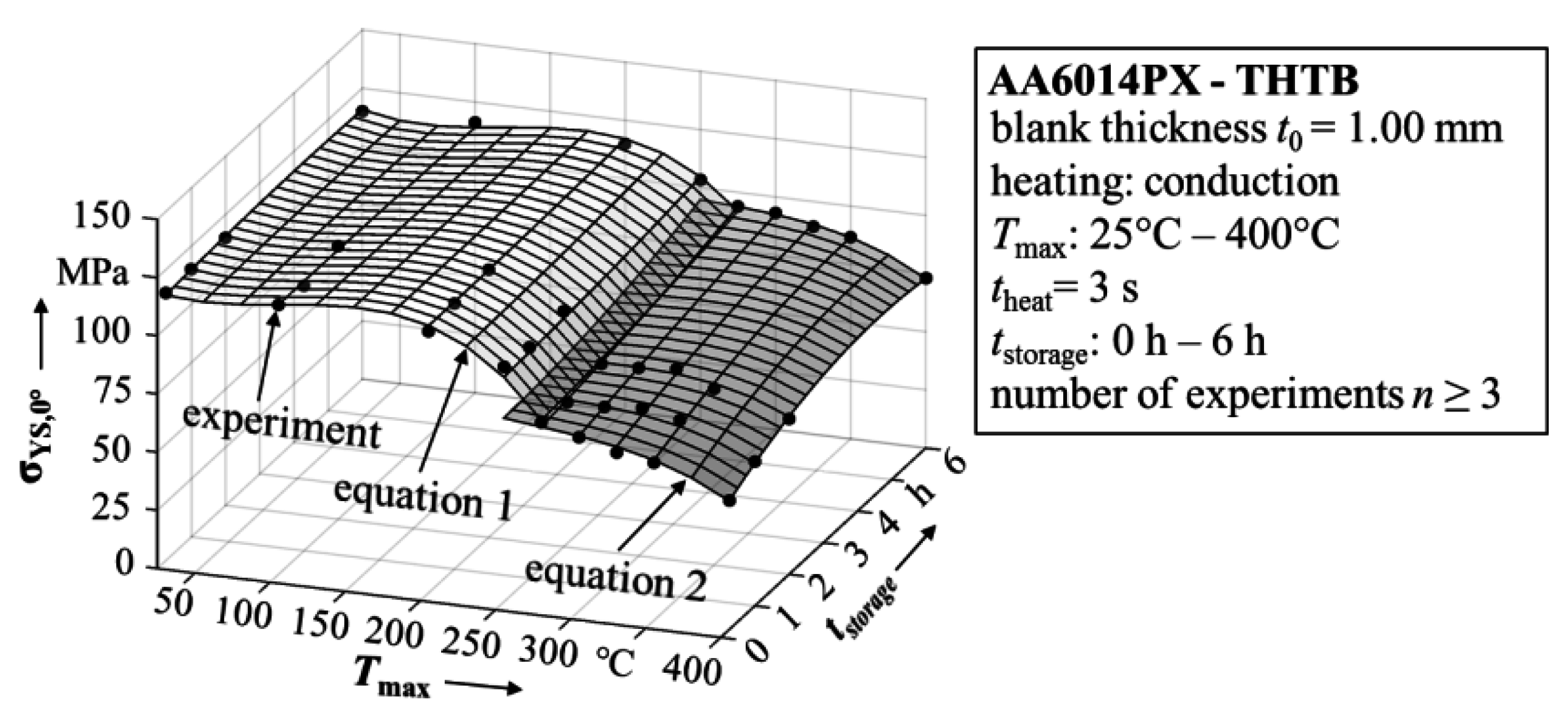
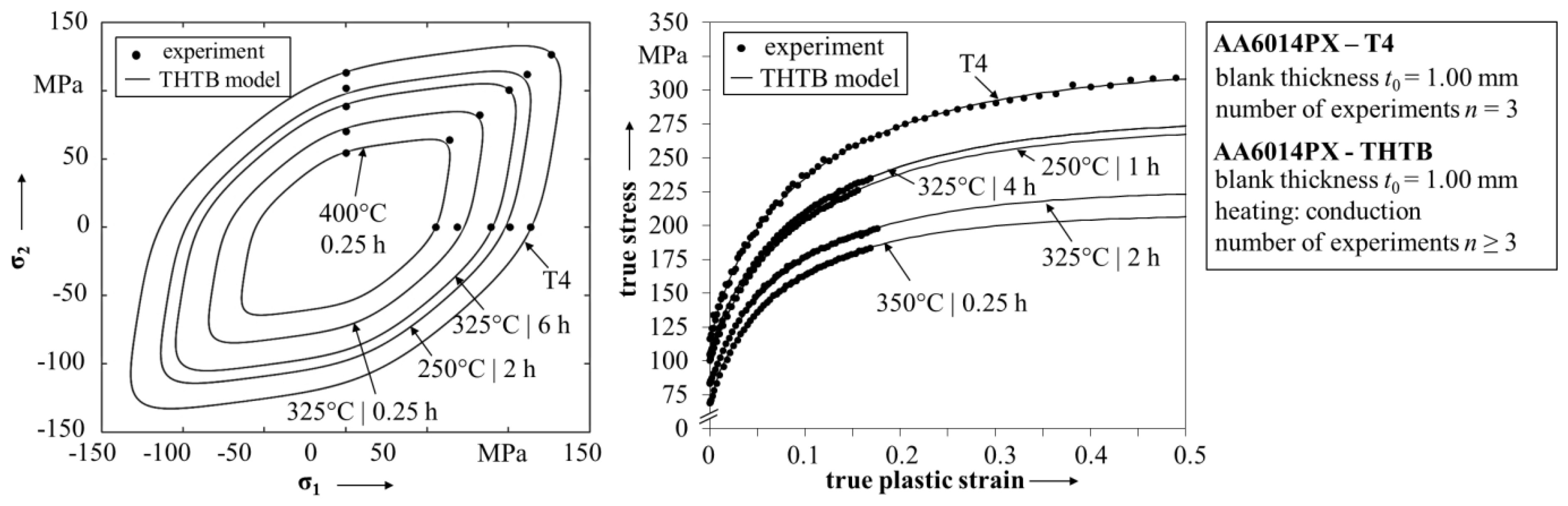
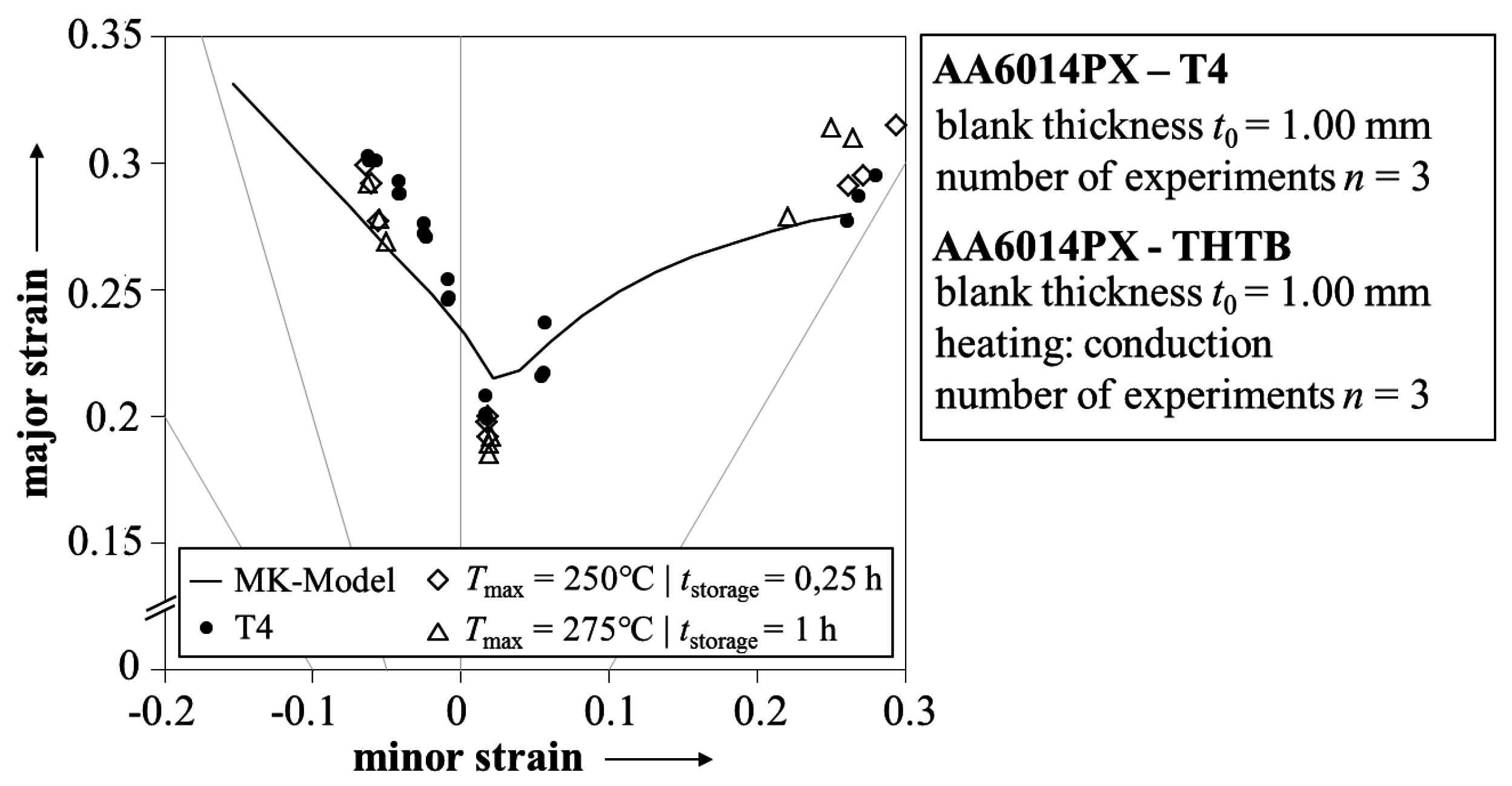
3. Process Design of Aluminum Tailor Heat Treated Blanks

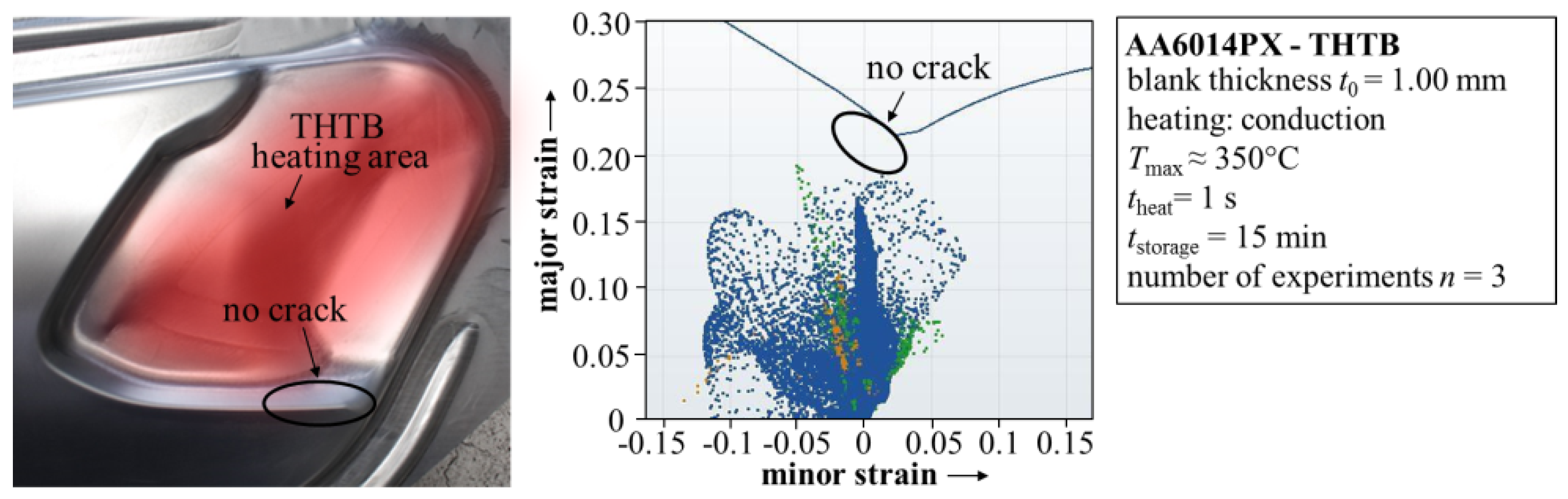



4. Summary and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A: Yield Functions
| Variable | T4 value | Description | Method |
|---|---|---|---|
| σYS,0° | 115 ± 1 MPa | yield strength under uniaxial loading for 0°/45°/90° to the rolling direction | uniaxial tensile test [18] |
| σYS,45° | 116 ± 1 MPa | ||
| σYS,90° | 112 ± 2 MPa | ||
| σYS,b | 121 ± 3 MPa | yield strength under biaxial loading (σ1 = σ2, σ3 = 0) | biaxial tensile test [19] |
| r0° | 0.65 ± 0.019 | anisotropy value under uniaxial loading for 0°/45°/90° to the rolling direction | uniaxial tensile test [18] |
| r45° | 0.45 ± 0.015 | ||
| r90° | 0.61 ± 0.015 | ||
| rb | 0.92 ± 0.025 | anisotropy value under biaxial loading (σ1 = σ2, σ3 = 0) | layer compression test [38] |
Appendix B: Flow Curves
Appendix C
| Variable | a | M | N | P | Q | R | S | T |
|---|---|---|---|---|---|---|---|---|
| T4-solution | 1.3758 | 0.2351 | 0.3990 | 0.4449 | 0.5115 | 0.5018 | 0.5395 | 0.5591 |
| Parameter | σYS,0° | σsat. | C | |||
|---|---|---|---|---|---|---|
| Fit 1 | Fit 2 | Fit 1 | Fit 2 | Fit 1 | Fit 2 | |
| p00 | 117.3 | 215.2 | 314.7 | 335.0 | 6.067 | −27.36 |
| p10 | −0.2086 | −1.365 | −0.2422 | 0.1494 | −0.01509 | 0.2996 |
| p01 | 1.949 | −17.73 | 3.783 | −136.8 | 0.1234 | 1.666 |
| p20 | 0002894 | 0.00475 | 0.005042 | −0.003417 | 3.536 × 10−9 | −8.428 × 10−4 |
| p11 | −0.02748 | 0.07863 | −0.02099 | 0.7111 | −8.024 × 10−4 | −0.01783 |
| p02 | −0.1993 | 2.775 | –0.4793 | 6.53 | −0.018 | 0.4022 |
| p30 | −9.567 × 10−6 | −5.877 × 10−6 | −1.906 × 10−5 | 5.53 × 10−6 | 2.386 × 10−7 | 7.725 × 10−7 |
| p21 | 8.671 × 10−5 | −2.659 × 10−5 | 5.829 × 10−5 | 8.257 × 10−4 | −2.521 × 10−6 | 3.06 × 10−5 |
| p12 | 0.001369 | −0.009505 | 0.001415 | −0.0202 | 1.891 × 10−4 | −3.901 × 10−4 |
| p03 | - | - | - | - | - | −0.02772 |
References
- Goede, M.; Stehlin, M.; Rafflenbeul, L.; Kopp, G.; Beeh, E. Super light car—Lightweight construction thanks to a multi-material design and function integration. Eur. Transp. Res. Rev. 2009, 1, 5–10. [Google Scholar] [CrossRef]
- Miller, W.; Zhuang, L.; Bottema, J.; Wittebrood, A.; De Smet, P.; Haszler, A.; Vieregge, A. Recent development in aluminium alloys for the automotive industry. Mater. Sci. Eng. 2000, A280, 37–49. [Google Scholar] [CrossRef]
- Kleiner, M.; Geiger, M.; Klaus, A. Manufacturing of lightweight components by metal forming. CIRP Ann. Manuf. Technol. 2003, 52, 521–542. [Google Scholar] [CrossRef]
- Geiger, M.; Merklein, M.; Vogt, U. Aluminum tailored heat treated blanks. Prod. Eng. Res. Dev. 2009, 3, 401–410. [Google Scholar] [CrossRef]
- Merklein, M.; Johannes, M.; Lechner, M.; Kuppert, A. A review on tailored blanks—Production, applications and evaluation. J. Mater. Process. Technol. 2014, 214, 151–164. [Google Scholar] [CrossRef]
- Merklein, M.; Vogt, U. Application of tailored heat treated blanks under quasi series conditions. Key Eng. Mater. 2007, 344, 383–390. [Google Scholar] [CrossRef]
- Edwards, G.A.; Stiller, K.; Dunlop, G.; Couper, M.J. The precipitation sequence in Al-Mg-Si alloys. Acta Mater. 1998, 46, 3893–3904. [Google Scholar] [CrossRef]
- Lechner, M.; Kuppert, A.; Hagenah, H.; Merklein, M. Optimization of the heat treatment layout and blank outline of THTB. Key Eng. Mater. 2013, 554–557, 2465–2471. [Google Scholar] [CrossRef]
- Geiger, M.; Merklein, M.; Staud, D.; Kaupper, M. An inverse approach to the numerical design of the process sequence of tailored heat treated blanks. Prod. Eng. Res. Dev. 2008, 2, 15–20. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609–620. [Google Scholar] [CrossRef]
- Banabic, D.; Bunge, H.-J.; Pöhlandt, K.; Tekkaya, A.E. Formability of Metallic Materials—Plastic Anisotropy, Formability Testing, Forming Limits; Springer: Berlin, Germany, 2000. [Google Scholar]
- Hill, R. A Theory of the yielding and plastic flow of anisotropic metals. Proc. Soc. Math. Phys. Eng. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]
- Banabic, D.; Aretz, H.; Comsa, D.S.; Paraianu, L. An improved analytical description of orthotropy in metallic sheets. Int. J. Plast. 2005, 21, 493–512. [Google Scholar] [CrossRef]
- Banabic, D.; Barlat, F.; Cazacu, O.; Kuwabara, T. Advances in anisotropy and formability. Int. J. Mater. Form. 2010, 3, 165–189. [Google Scholar] [CrossRef]
- Hockett, J.E.; Sherby, O.D. Large strain deformation of polycrystalline metals at low homologous temperatures. J. Mech. Phys. Solids 1975, 23, 87–98. [Google Scholar] [CrossRef]
- Vogt, U. Seriennahe Auslegung von Aluminium Tailored Heat Treated Blanks. In Fertigungstechnik—Erlangen 208; Merklein, M., Franke, J., Geiger, M., Schmidt, M., Eds.; Meisenbach: Bamberg, Germany, 2009. [Google Scholar]
- Peters, P.; Manopulo, N.; Lange, C.; Hora, P. A strain rate dependent anisotropic hardening model and its validation through deep drawing experiments. Int. J. Mater. Form. 2014, 7, 447–457. [Google Scholar] [CrossRef]
- EN 10002-1, Metallic Materials—Tensile Testing—Part 1: Method of Testing at Ambient Temperature. Beuth: Berlin, Germany, 2001. Available online: http://www.beuth.de/en/standard/din-en-10002-1/40710666 (accessed on 2 December 2015).
- EN ISO 16808, Metallic Materials—Sheet and Strip—Determination of Biaxial Stress-Strain Curve by Means of Bulge Test with Optical Measuring Systems. Beuth: Berlin, Germany, 2014. Available online: http://www.iso.org/iso/iso_catalogue/catalogue_tc/catalogue_detail.htm?csnumber=57777 (accessed on 2 December 2015).
- Merklein, M.; Biasutti, M. Development of a biaxial tensile machine for characterization of sheet metals. J. Mater. Process. Technol. 2013, 213, 939–946. [Google Scholar] [CrossRef]
- EN ISO 12004-2, Metallic Materials—Sheet and Strip—Determination of Forming-Limit Curves—Part 2: Determination of Forming-Limit Curves in the Laboratory. Beuth: Berlin, Germany, 2008. Available online: http://www.iso.org/iso/iso_catalogue/catalogue_tc/catalogue_detail.htm?csnumber=43621 (accessed on 2 December 2015).
- Mises, R.V. Mechanik der plastischen Formänderung von Kristallen. Z. Für Angew. Math. Mech. 1928, 8, 161–185. [Google Scholar] [CrossRef]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente der Technologischen Mechanik; Springer: Berlin, Germany, 1909. [Google Scholar]
- Hollomon, J.H. Tensile deformation. Trans. Metall. Soc. AIME 1945, 162, 268–290. [Google Scholar]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Banabic, D.; Sester, M. Influence of material models on the accuracy of the sheet forming simulation. Mater. Manuf. Proc. 2012, 27, 304–308. [Google Scholar] [CrossRef]
- Kim, J.-H.; Serpantié, A.; Barlat, F.; Pierron, F.; Lee, M.-G. Characterization of the post-necking strain hardening behavior using the virtual fields method. Int. J. Solids Struct. 2013, 50, 3829–3842. [Google Scholar] [CrossRef]
- Coppieters, S.; Kuwabara, T. Identification of post-necking hardening phenomena in ductile sheet metal. Exp. Mech. 2014, 54, 1355–1371. [Google Scholar] [CrossRef]
- Lechner, M.; Johannes, M.; Kuppert, A.; Merklein, M. Influence of pre-straining and heat treatment on the yield surface of precipitation hardenable aluminum alloys. Phys. Procedia 2014, 56, 1400–1409. [Google Scholar] [CrossRef]
- Merklein, M. Charakterisierung von Blechwerkstoffen für den Leichtbau; Meisenbach: Bamberg, Germany, 2006. [Google Scholar]
- Bichiş, I.; Banabic, D.; Comsa, D.S. Research on the shock heat treatment method used for modifying the formability of aluminium alloys. In Proceedings of the 10th International Conference on Modern Technologies in Manufacturing, Cluj-Napoca, Romania, 6–8 October 2011.
- Kleiner, M.; Chatti, S.; Klaus, A. Metal forming techniques for lightweight construction. J. Mater. Process. Technol. 2006, 177, 2–7. [Google Scholar] [CrossRef]
- Kerausch, M. Simulationsgestützte Prozessauslegung für das Umformen lokal wärmebehandelter Aluminiumplatinen. In Fertigungstechnik—Erlangen 187; Geiger, M., Feldmann, K., Eds.; Meisenbach: Bamberg, Germany, 2006. [Google Scholar]
- Geiger, M.; Merklein, M.; Kerausch, M. Finite element simulation of deep drawing of tailored heat treated blanks. CIRP Ann. Manuf. Technol. 2004, 53, 223–226. [Google Scholar] [CrossRef]
- Hogg, M. Herstellung und Umformung lokal wärmebehandelter Platinen. In Beiträge zur Umformtechnik 53; Siegert, K., Liewald, M., Eds.; DGM Informationsgesellschaft: Frankfurt, Germany, 2006. [Google Scholar]
- Merklein, M.; Kuppert, A. A method for the layer compression test considering the anisotropic material behavior. Int. J. Mater. Form. 2009, 2, 483–486. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kahrimanidis, A.; Lechner, M.; Degner, J.; Wortberg, D.; Merklein, M. Process Design of Aluminum Tailor Heat Treated Blanks. Materials 2015, 8, 8524-8538. https://doi.org/10.3390/ma8125476
Kahrimanidis A, Lechner M, Degner J, Wortberg D, Merklein M. Process Design of Aluminum Tailor Heat Treated Blanks. Materials. 2015; 8(12):8524-8538. https://doi.org/10.3390/ma8125476
Chicago/Turabian StyleKahrimanidis, Alexander, Michael Lechner, Julia Degner, Daniel Wortberg, and Marion Merklein. 2015. "Process Design of Aluminum Tailor Heat Treated Blanks" Materials 8, no. 12: 8524-8538. https://doi.org/10.3390/ma8125476
APA StyleKahrimanidis, A., Lechner, M., Degner, J., Wortberg, D., & Merklein, M. (2015). Process Design of Aluminum Tailor Heat Treated Blanks. Materials, 8(12), 8524-8538. https://doi.org/10.3390/ma8125476






