Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics
Abstract
:1. Introduction
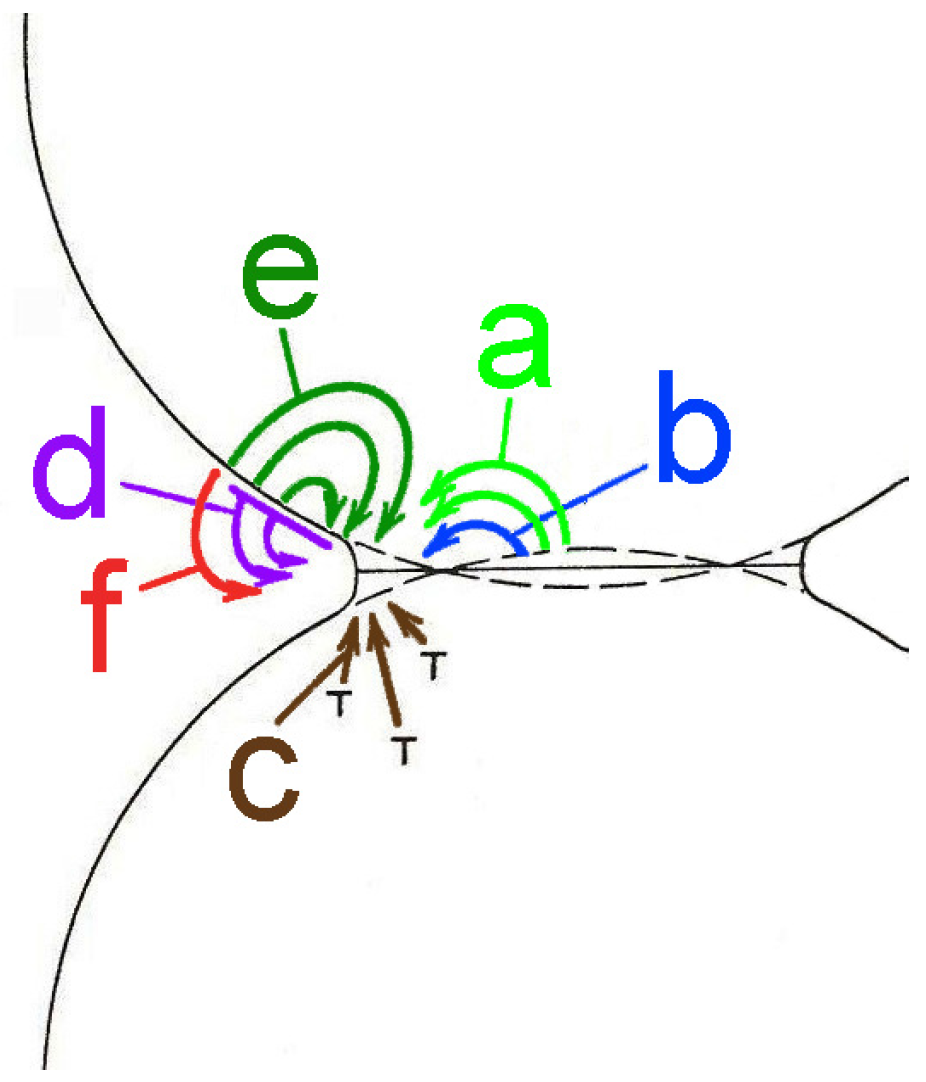
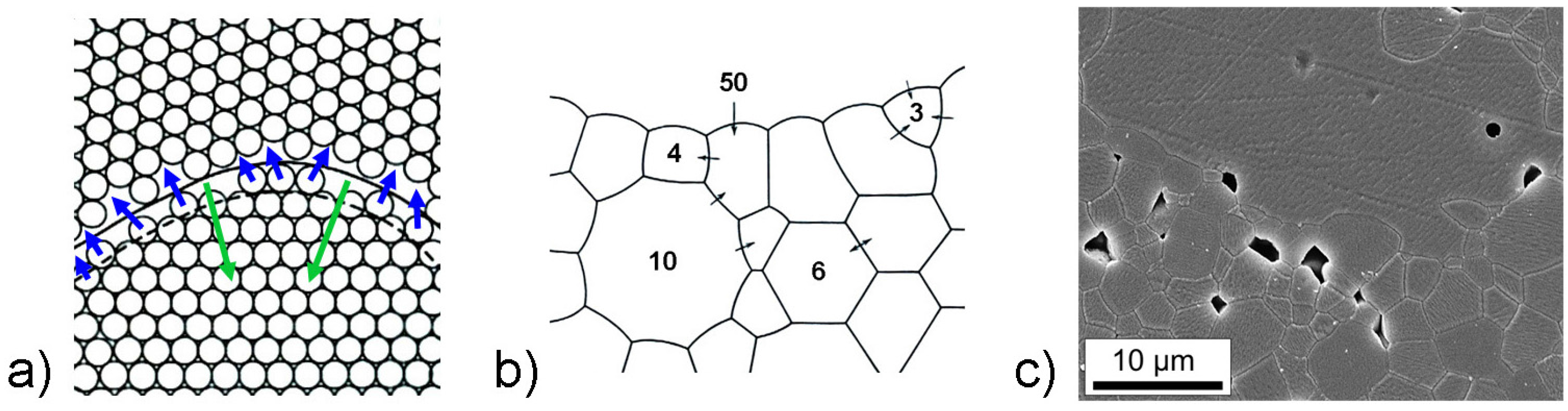
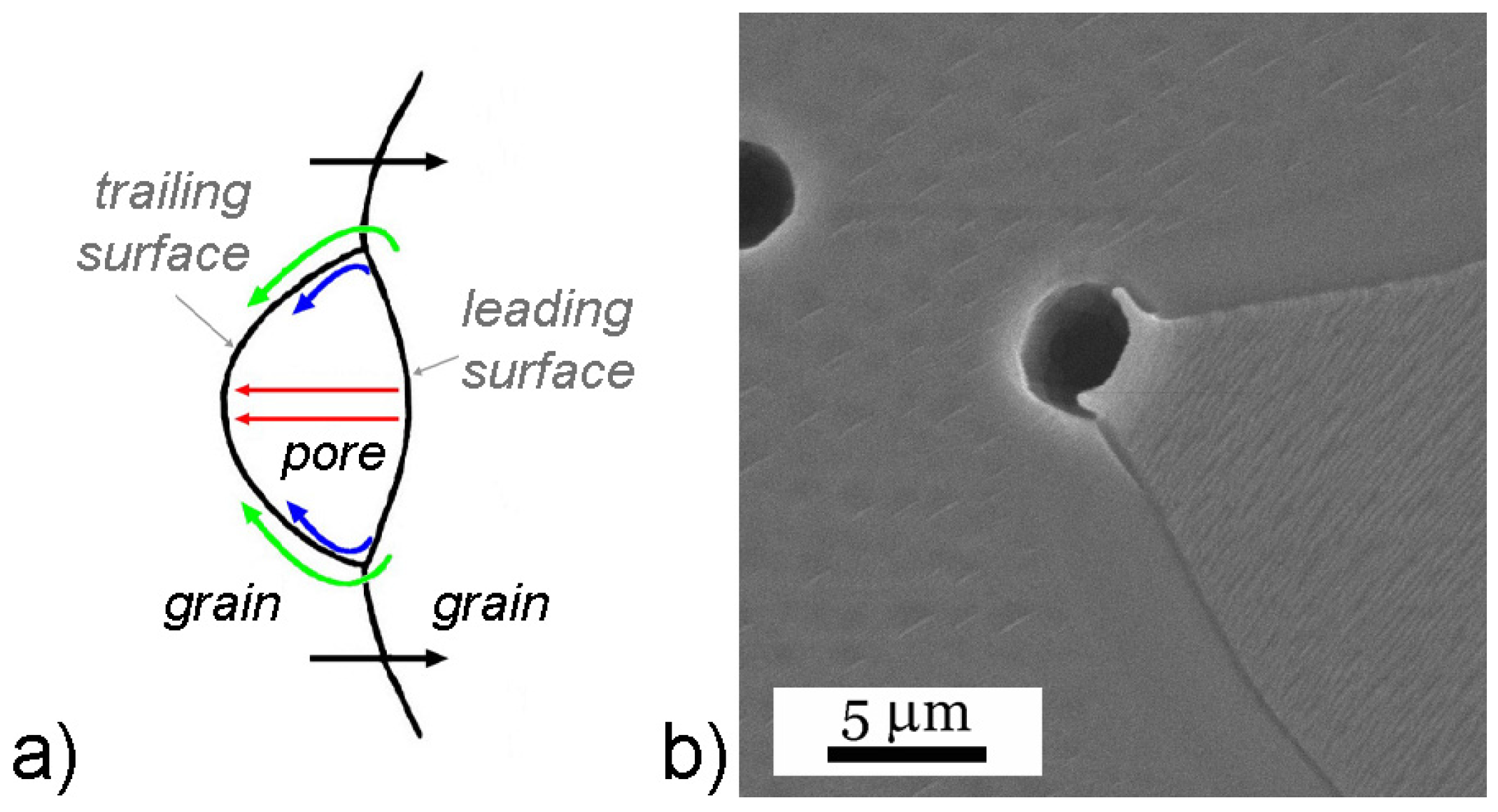
2. Sintering of Ceramic Materials—Fundamentals
3. Sodium Potassium Niobate System
3.1. Phase Relations
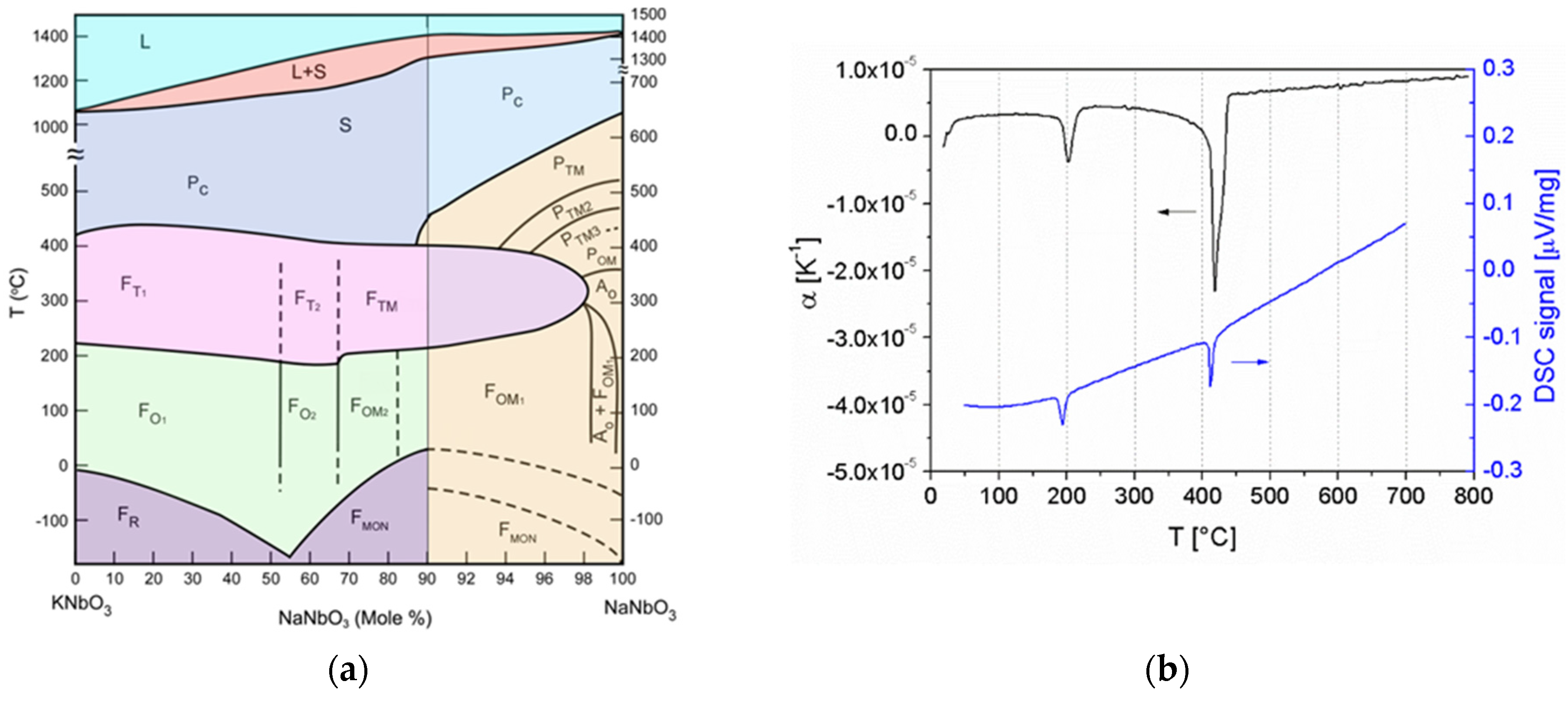
3.2. Solid-State Synthesis of Powders
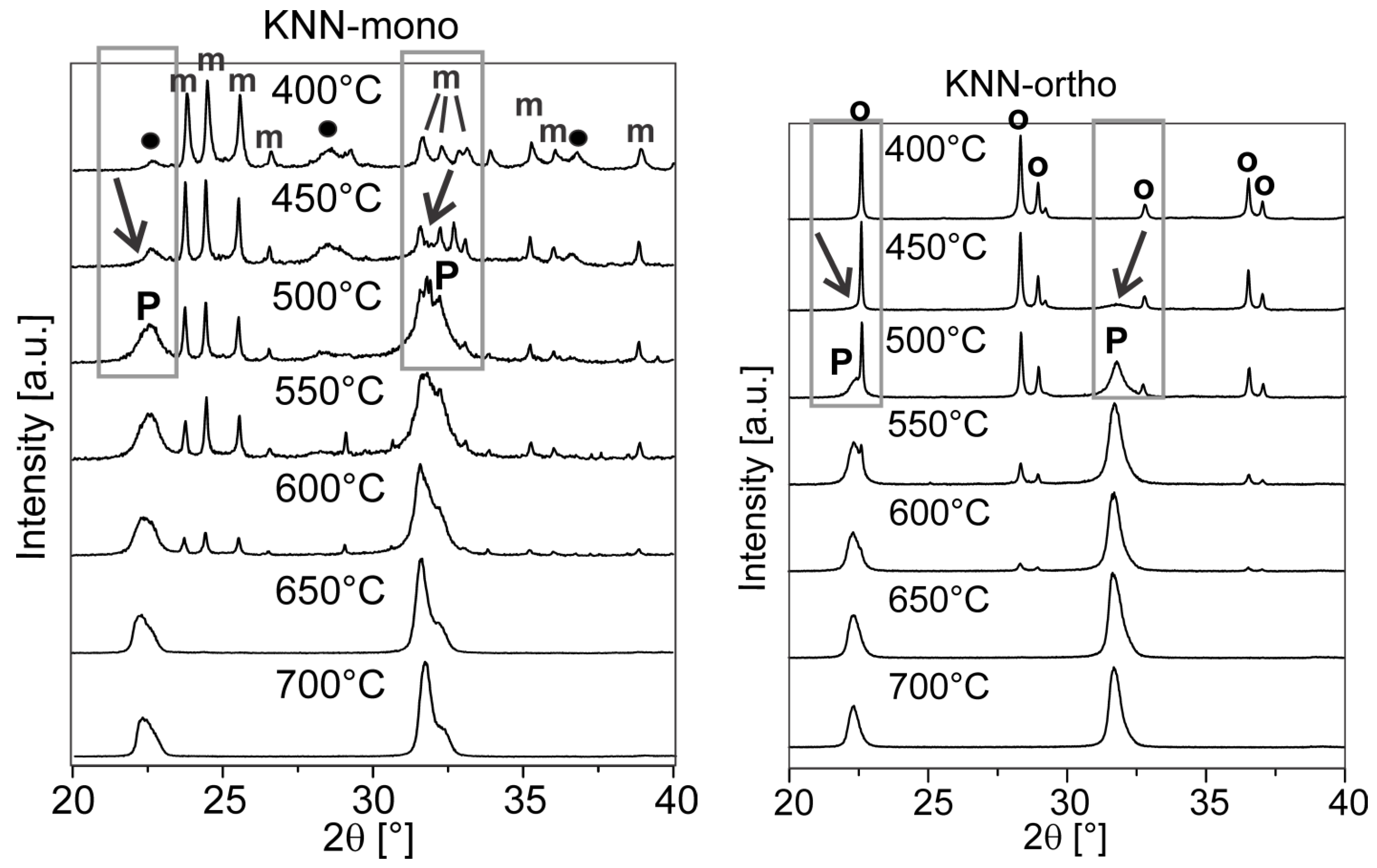
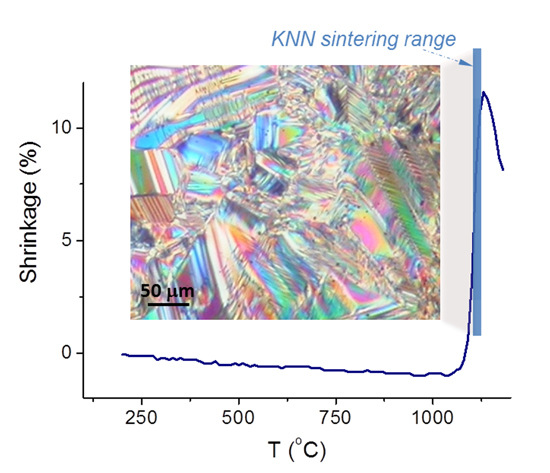
3.3. Solid-State Sintering of KNN
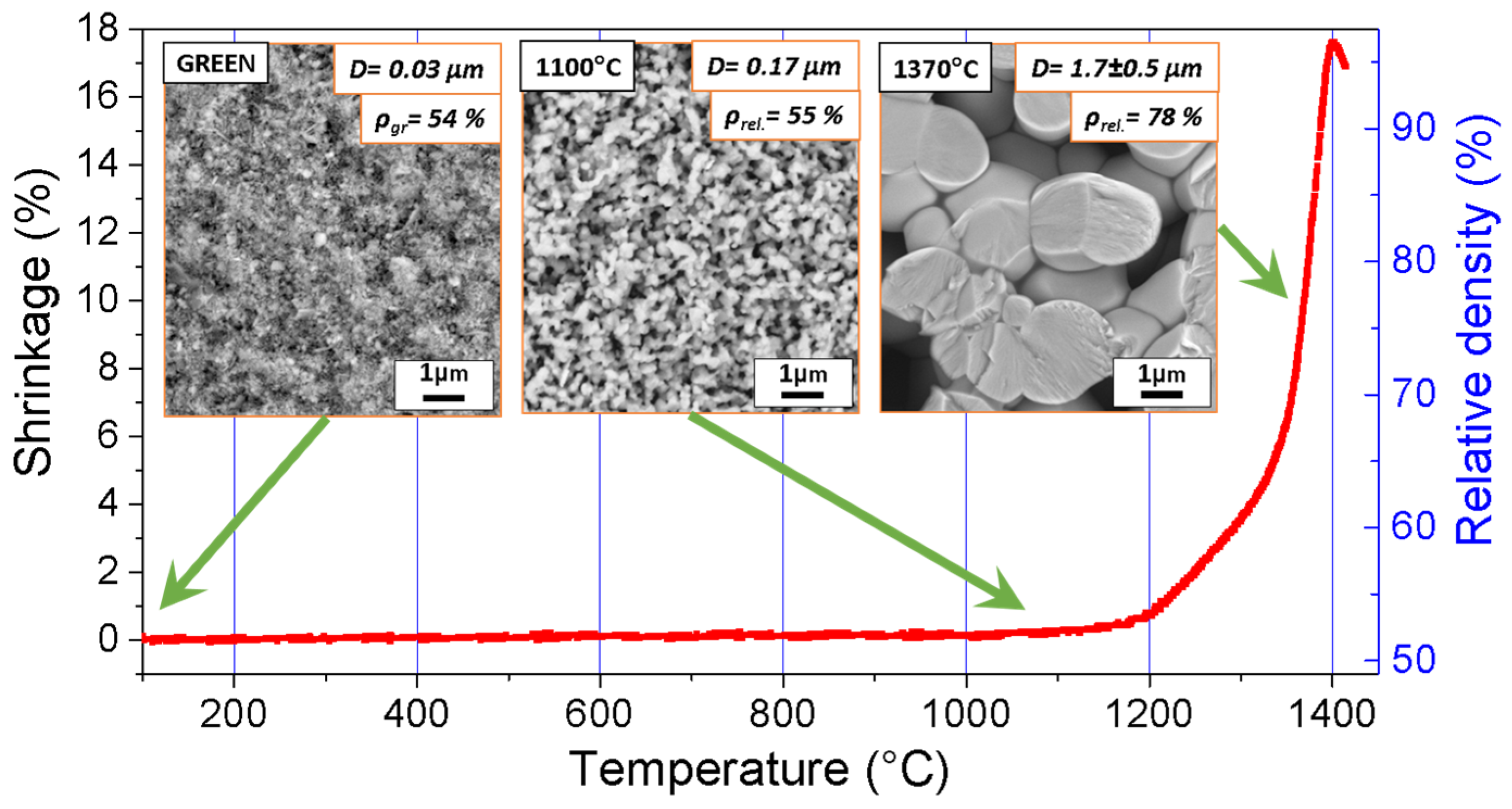
3.3.1. Sintering Mechanisms in NaNbO3
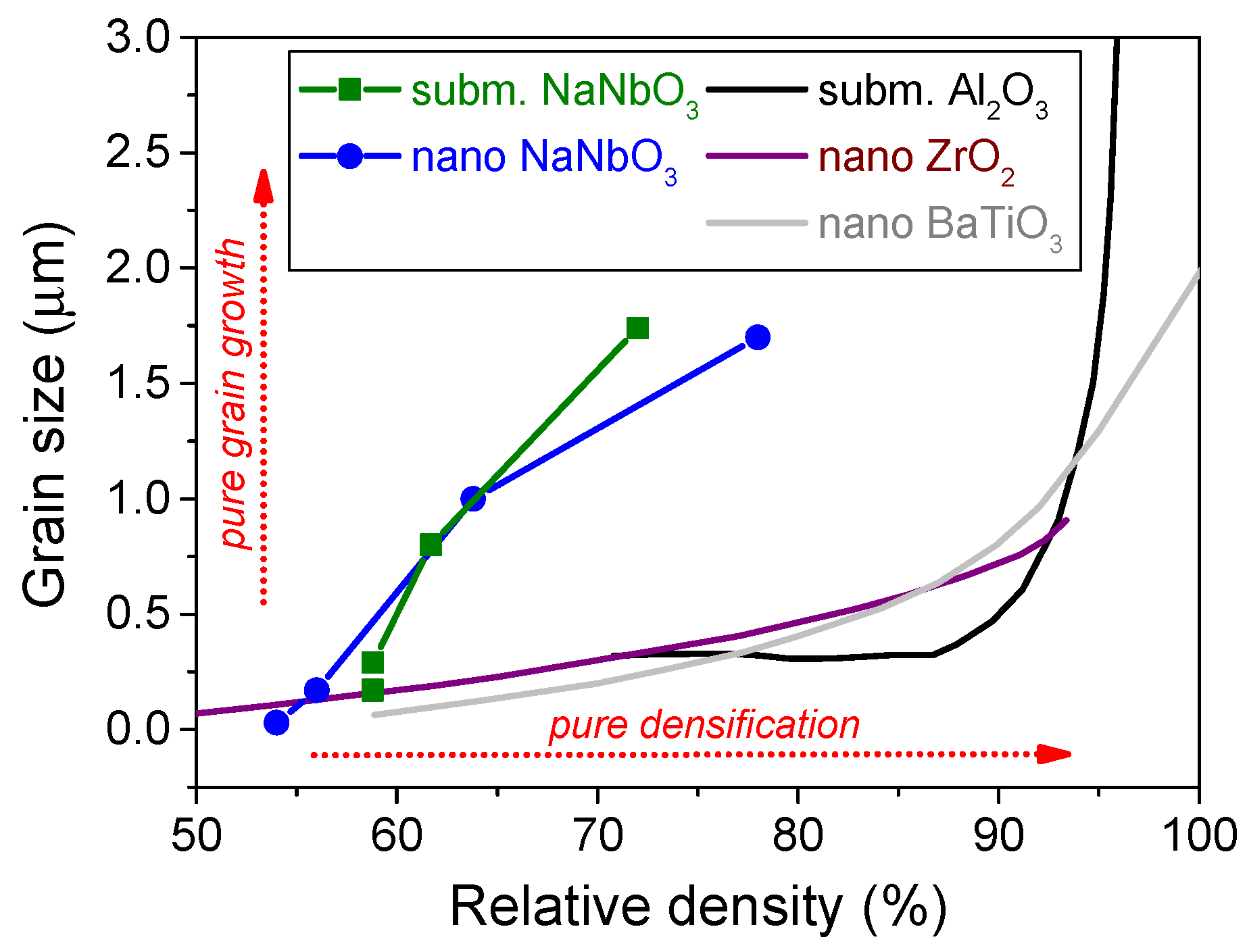
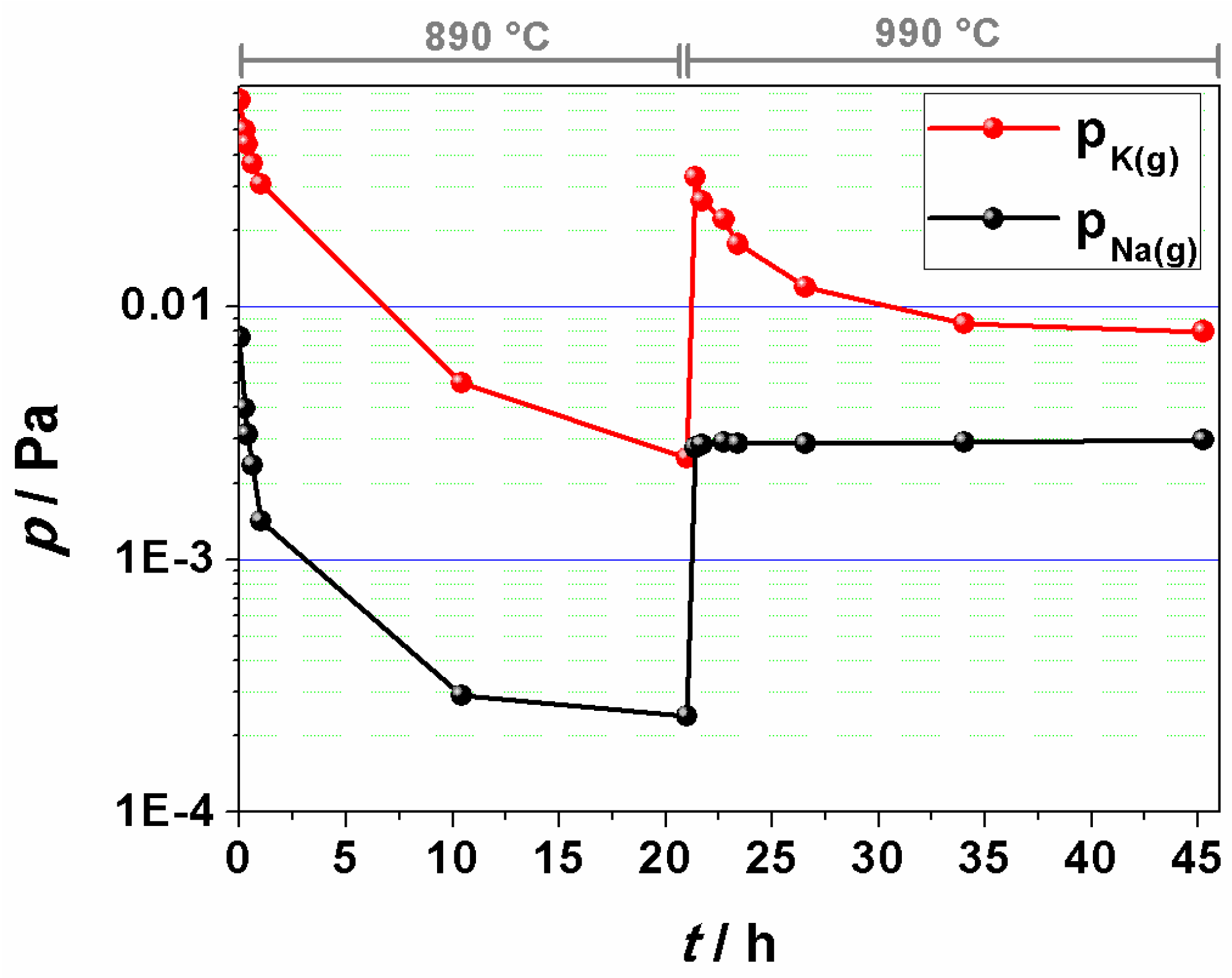
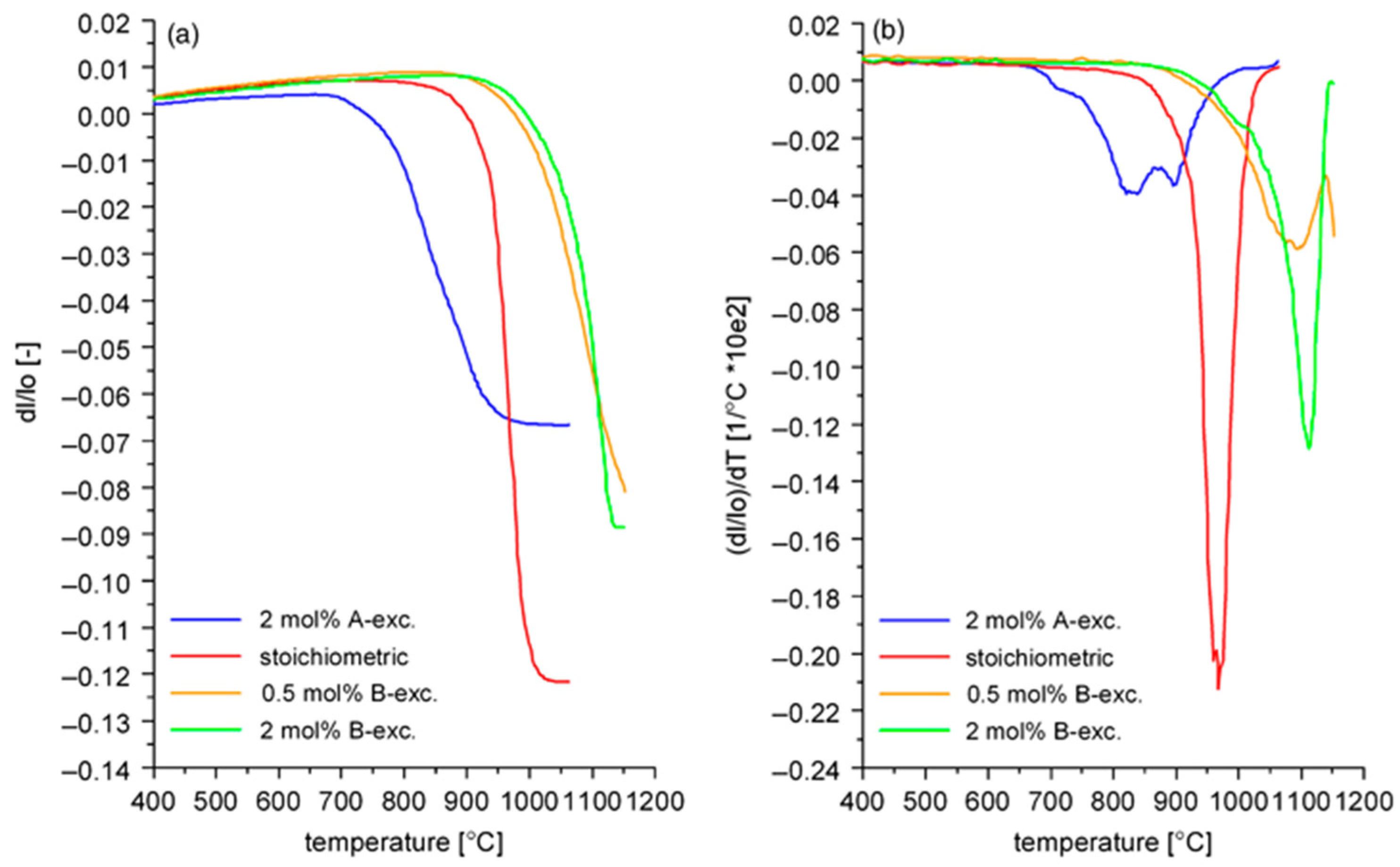
3.3.2. Solid-State Sintering of KNN: Stoichiometry and Microstructure


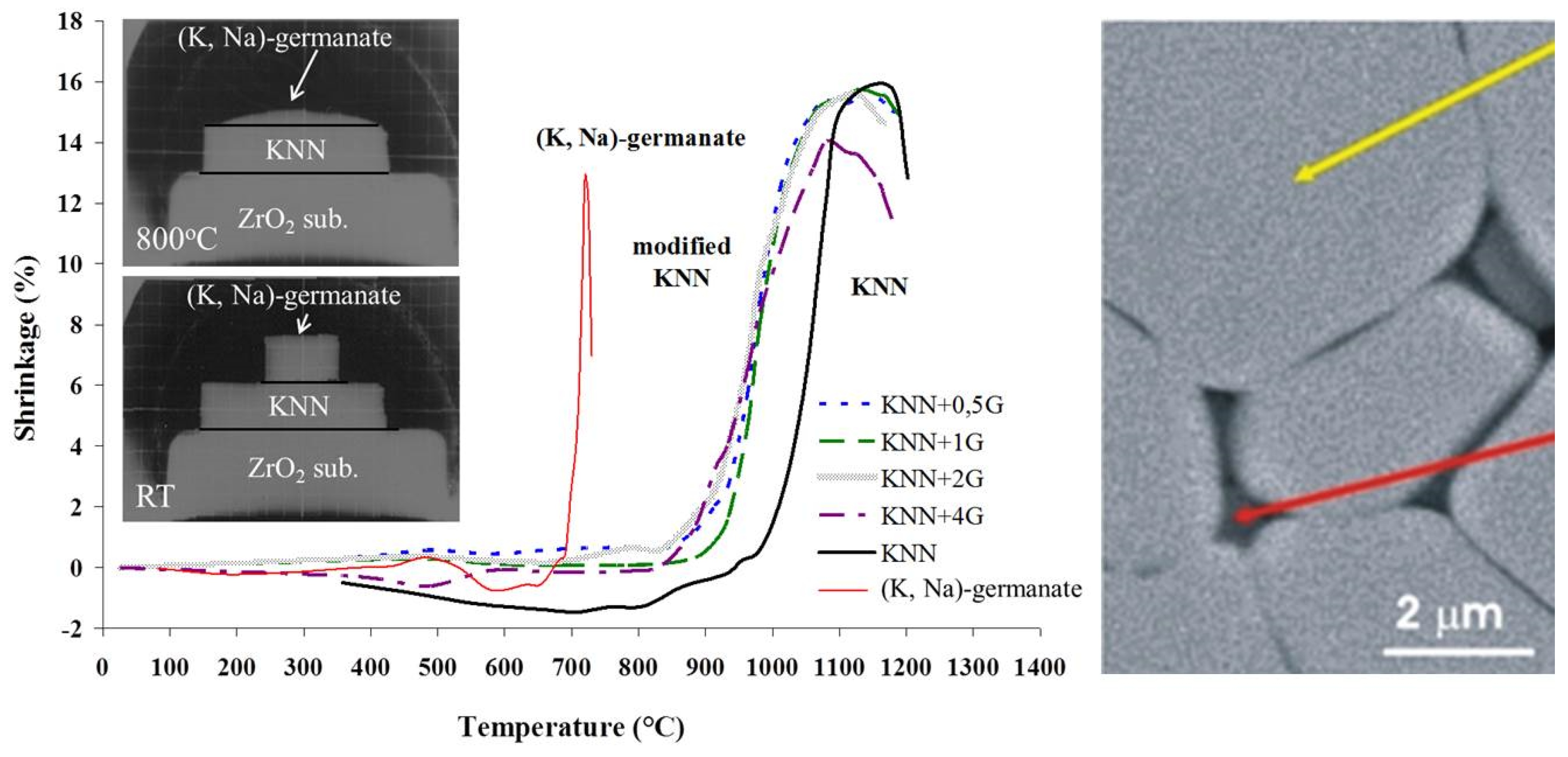
3.4. Liquid-Phase Sintering
| Properties | KNN + 0.5 mol % K4CuNb8O23 | KNN + 0.38 mol % K5.4Cu1.3Ta10O29 | KNN + 0.5 mol % K1.94Zn1.06Ta5.19O15 | KNN + 1.0 mol % ZnO | KNN + 1 wt % (K,Na)-Germanate | KNN + 0.45 wt % Na2B4O7∙10H2O |
|---|---|---|---|---|---|---|
| Sintering Temperature (°C) | 1095 | 1125 | 1070 | 1050 | 1000 | 1020 |
| Density (g/cm3, %) | 4.40 (97.6) | 4.60 * | ≈4.35 (96.3) | 4.25 * | 4.31 (95.6) | ≈95.5 * |
| Curie Temperature (°C) | 410 | ≈390 | 390 | ≈400 | ≈400 | - |
| d33 | 180 pm/V | 190 pm/V | 126 pC/N | 123 pC/N | 120 pC/N | 132 pC/N |
| kp (/) | 0.39 | 0.41 | 0.42 | 0.4 | 0.40 | 0.35 |
| Qm (/) | 1210 | 1300 | ≈60 | ≈140 | 77 | 109 |
| Reference | [71] | [111] | [113] | [112] | [115] | [114] |
3.5. Controlled-Atmosphere Sintering of K0.5Na0.5NbO3-Based Ceramics

3.6. Chemical Modifications
3.6.1. Doping
3.6.2. Solid Solutions KNN + ABO3
3.7. Alternatives to Conventional Sintering Methods
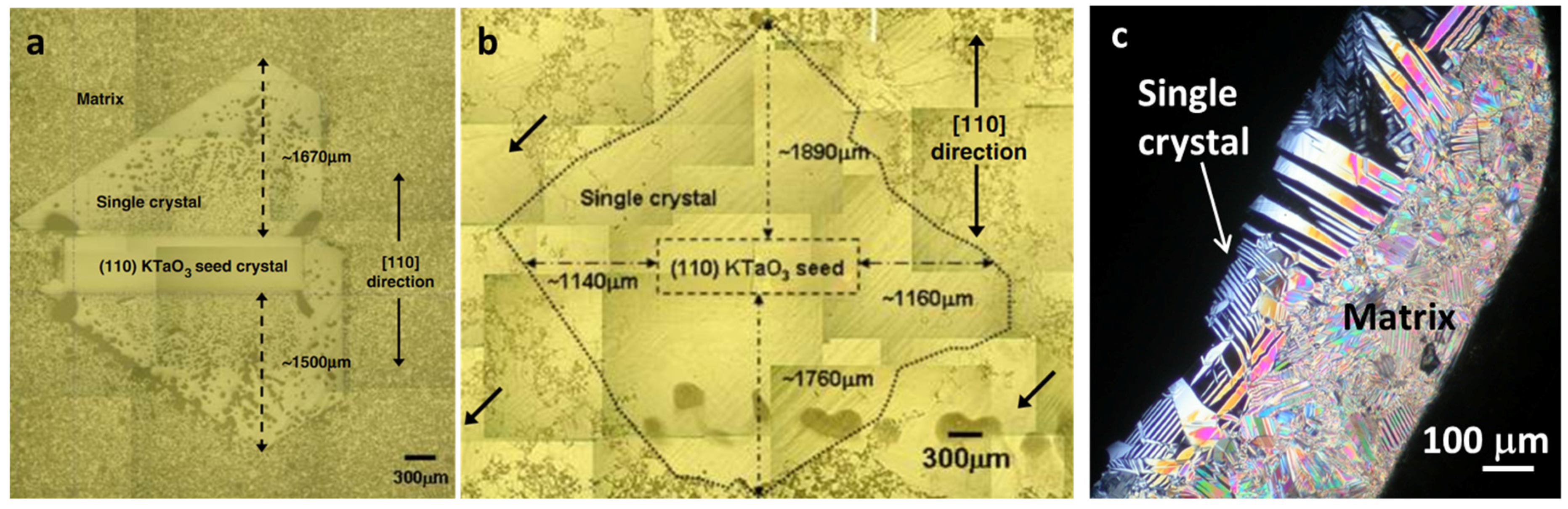
3.8. Solid-State Crystal Growth
3.9. KNN Versus PZT: Sintering and Vapour Pressure
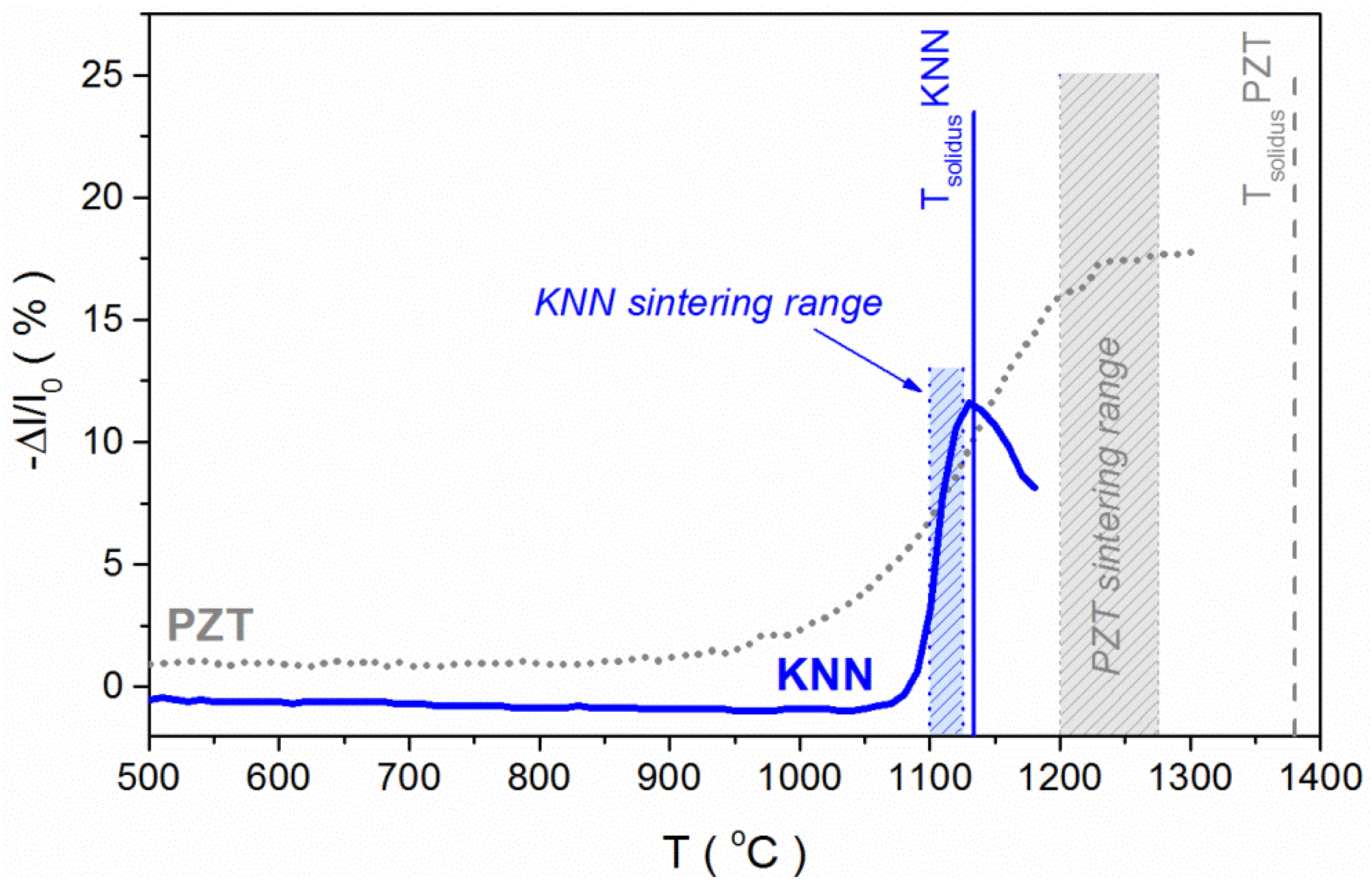
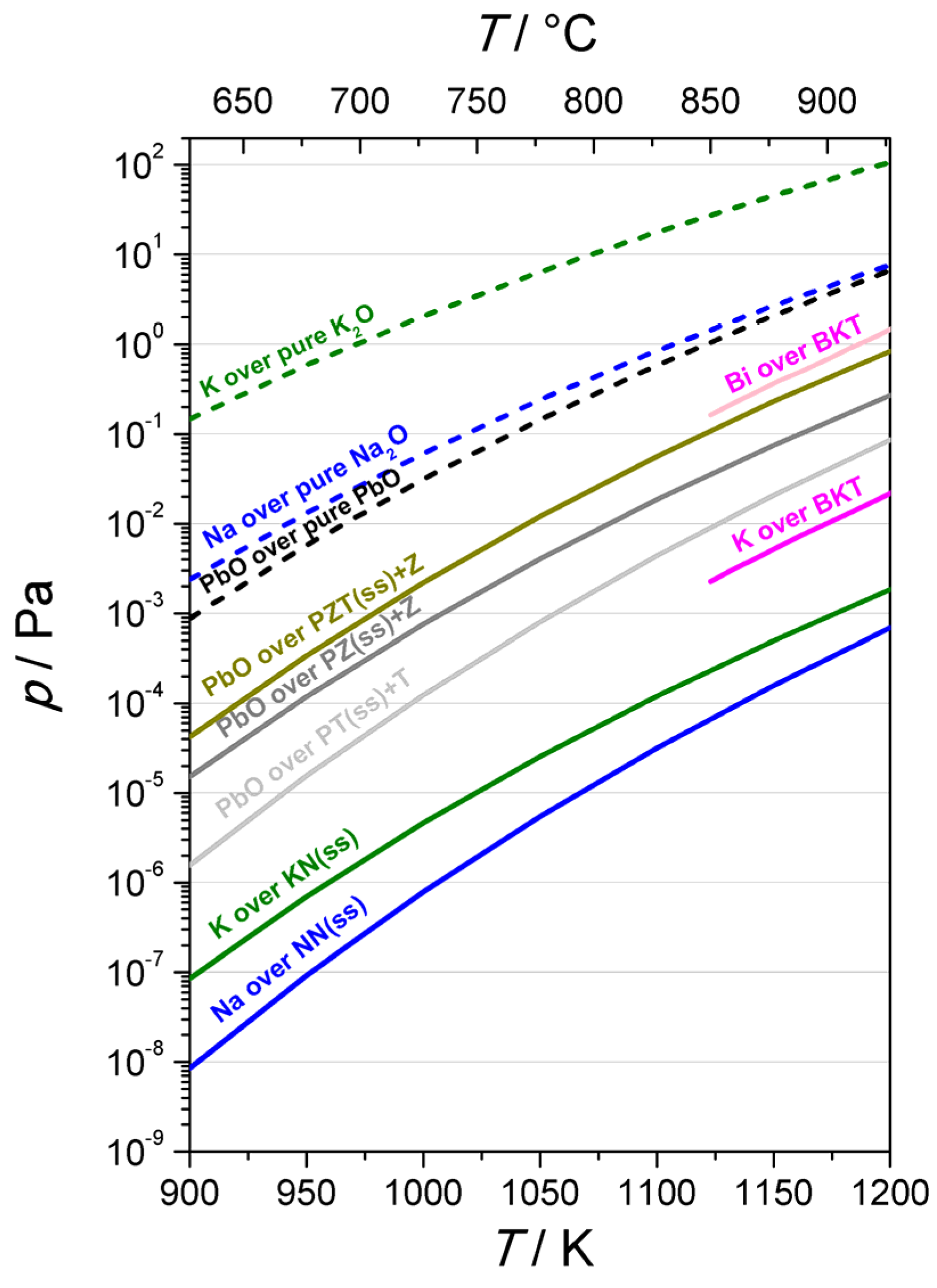
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Setter, N. Piezoelectric Materials in Devices; EPFL Swiss Federal Institute of Technology: Lausanne, Switzerland, 2002. [Google Scholar]
- Haertling, G.H. Ferroelectric ceramics: History and technology. J. Am. Ceram. Soc. 1999, 82, 797–818. [Google Scholar] [CrossRef]
- European Standards, Directive 2011/65/EU on the Restriction of the Use of Certain Hazardous Substances in Electrical and Electronic Equipment; European Standardisation Organisation: Brussels, Belgium, 2011.
- Japan Electronics and Information Technology Industries Association. JIS C 0950: The Marking for Presence of the Specific Chemical Substances for Electrical and Electronic Equipment; Japanese Standards Association: Tokyo, Japan, 2005; p. 26. [Google Scholar]
- U.S. California Senate. Bill No. 50: Solid Waste: Hazardous Electronic Waste, 2004. Available online: ftp://www.leginfo.ca.gov/pub/03-04/bill/sen/sb_0001-0050/sb_50_bill_20040929_chaptered.html (accessed on 27 November 2015).
- Shrout, T.R.; Zhang, S.J. Lead-free piezoelectric ceramics: Alternatives for PZT? J. Electr. 2007, 19, 113–126. [Google Scholar] [CrossRef]
- Panda, P.K. Review: Environmental friendly lead-free piezoelectric materials. J. Mater. Sci. 2009, 44, 5049–5062. [Google Scholar] [CrossRef]
- Rödel, J.; Jo, W.; Seifert, K.T.P.; Anton, E.M.; Granzow, T.; Damjanovic, D. Perspective on the development of lead-free piezoceramics. J. Am. Ceram. Soc. 2009, 92, 1153–1177. [Google Scholar] [CrossRef]
- Rödel, J.; Webber, K.G.; Dittmer, R.; Jo, W.; Kimura, M.; Damjanovic, D. Transferring lead-free piezoelectric ceramics into application. J. Eur. Ceram. Soc. 2015, 35, 1659–1681. [Google Scholar] [CrossRef]
- Wu, J.G.; Xiao, D.Q.; Zhu, J.G. Potassium-sodium niobate lead-free piezoelectric materials: Past, present, and future of phase boundaries. Chem. Rev. 2015, 115, 2559–2595. [Google Scholar] [CrossRef] [PubMed]
- Matthias, B.T.; Remeika, J.P. Dielectric properties of sodium and potassium niobates. Phys. Rev. 1951, 82, 727–729. [Google Scholar] [CrossRef]
- Shirane, G.; Newnham, R.; Pepinsky, R. Dielectric properties and phase transitions of NaNbO3 and (Na,K)NbO3. Phys. Rev. 1954, 96, 581–588. [Google Scholar] [CrossRef]
- Egerton, L.; Dillon, D.M. Piezoelectric and dielectric properties of ceramics in the system potassium-sodium niobate. J. Am. Ceram. Soc. 1959, 42, 438–442. [Google Scholar] [CrossRef]
- Saito, Y.; Takao, H.; Tani, T.; Nonoyama, T.; Takatori, K.; Homma, T.; Nagaya, T.; Nakamura, M. Lead-free piezoceramics. Nature 2004, 432, 84–87. [Google Scholar] [CrossRef] [PubMed]
- Malic, B.; Bencan, A.; Rojac, T.; Kosec, M. Lead-free piezoelectrics based on alkaline niobates: Synthesis, sintering and microstructure. Acta Chim. Slov. 2008, 55, 719–726. [Google Scholar]
- Kosec, M.; Malič, B.; Benčan, A.; Rojac, T. KNN-Based Piezoelectric Ceramics. In Piezoelectric and Acoustic Materials for Transducer Applications; Safari, A., Akdoğan, E.K., Eds.; Springer: New York, NY, USA, 2010; pp. 81–102. [Google Scholar]
- Priya, S.; Nahm, S. Lead-Free Piezoelectrics; Springer: New York, NY, USA, 2012. [Google Scholar]
- Li, J.-F.; Wang, K.; Zhu, F.-Y.; Cheng, L.-Q.; Yao, F.-Z. (K,Na)NbO3-based lead-free piezoceramics: Fundamental aspects, processing technologies, and remaining challenges. J. Am. Ceram. Soc. 2013, 96, 3677–3696. [Google Scholar] [CrossRef]
- Wang, K.; Yao, F.-Z.; Jo, W.; Gobeljic, D.; Shvartsman, V.V.; Lupascu, D.C.; Li, J.-F.; Rödel, J. Temperature-insensitive (K,Na)NbO3-based lead-free piezoactuator ceramics. Adv. Funct. Mater. 2013, 23, 4079–4086. [Google Scholar] [CrossRef]
- Wang, R.; Wang, K.; Yao, F.-Z.; Li, J.-F.; Schader, F.H.; Webber, K.G.; Jo, W.; Rödel, J. Temperature stability of lead-free niobate piezoceramics with engineered morphotropic phase boundary. J. Am. Ceram. Soc. 2015, 98, 2177–2182. [Google Scholar] [CrossRef]
- Park, B.C.; Hong, I.K.; Jang, H.D.; Tran, V.D.N.; Tai, W.P.; Lee, J.S. Highly enhanced mechanical quality factor in lead-free (K0.5Na0.5)NbO3 piezoelectric ceramics by co-doping with K5.4Cu1.3Ta10O29 and CuO. Mater. Lett. 2010, 64, 1577–1579. [Google Scholar] [CrossRef]
- Gurdal, E.A.; Ural, S.O.; Park, H.Y.; Nahm, S.; Uchino, K. High power (Na0.5K0.5)NbO3-based lead-free piezoelectric transformer. Jpn. J. Appl. Phys. 2011, 50. [Google Scholar] [CrossRef]
- Yao, F.Z.; Patterson, E.A.; Wang, K.; Jo, W.; Rodel, J.; Li, J.F. Enhanced bipolar fatigue resistance in CaZrO3-modified (K,Na) NbO3 lead-free piezoceramics. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Yao, F.-Z.; Wang, K.; Shen, Y.; Li, J.-F. Robust CaZrO3-modified (K,Na)NbO3-based lead-free piezoceramics: High fatigue resistance insensitive to temperature and electric field. J. Appl. Phys. 2015, 118. [Google Scholar] [CrossRef]
- Jaffe, B.; Cook, W.R.; Jaffe, H. Piezoelectric Ceramics; Academic Press: London, UK, 1971. [Google Scholar]
- Nilsson, K.; Lidman, J.; Ljungstrom, K.; Kjellman, C. Biocompatible Material for Implants. U.S. Patent US6526984 B1, 4 March 2003. [Google Scholar]
- Kawada, S.; Kimura, M.; Higuchi, Y.; Takagi, H. (K,Na)NbO3-based multilayer piezoelectric ceramics with nickel inner electrodes. Appl. Phys. Express 2009, 2. [Google Scholar] [CrossRef]
- Bantignies, C.; Filoux, C.; Mauchamp, P.; Dufait, R.; Pham Thi, M.; Rouffaud, R.; Gregoire, J.M.; Levassort, F. Lead-free high-frequency linear-array transducer (30 MHz) for in vivo skin imaging. In Proceedings of IEEE International Ultrasonics Symposium, Prague, Czech Republic, 21–25 July 2013; pp. 785–788.
- Hong, C.-H.; Han, H.-S.; Lee, J.-S.; Wang, K.; Yao, F.-Z.; Li, J.-F.; Gwon, J.-H.; Quyet, N.V.; Jung, J.-K.; Jo, W. Ring-type rotary ultrasonic motor using lead-free ceramics. J. Sens. Sci. Technol. 2015, 24, 228–231. [Google Scholar] [CrossRef]
- Kobayashi, K.; Doshida, Y.; Mizuno, Y.; Randall, C.A. Possibility of cofiring a nickel inner electrode in a (Na0.5K0.5)NbO3–LiF piezoelectric actuator. Jpn. J. Appl. Phys. 2013, 52. [Google Scholar] [CrossRef]
- ERAS®KN (Non-resonant Type Knock Sensor). Available online: www.ngkntk.co.jp/english/product/sensors/knock/eras-kn.html (accessed on 10 January 2015).
- Guo, M.; Lam, K.H.; Lin, D.M.; Wang, S.; Kwok, K.W.; Chan, H.L.W.; Zhao, X.Z. A Rosen-type piezoelectric transformer employing lead-free K0.5Na0.5NbO3 ceramics. J. Mater. Sci. 2008, 43, 709–714. [Google Scholar] [CrossRef]
- Acker, J.; Kungl, H.; Hoffmann, M.J. Influence of alkaline and niobium excess on sintering and microstructure of sodium-potassium Niobate (K0.5Na0.5)NbO3. J. Am. Ceram. Soc. 2010, 93, 1270–1281. [Google Scholar] [CrossRef]
- Wang, Y.; Damjanovic, D.; Klein, N.; Hollenstein, E.; Setter, N. Compositional inhomogeneity in Li- and Ta-modified (K,Na)NbO3 ceramics. J. Am. Ceram. Soc. 2007, 90, 3485–3489. [Google Scholar] [CrossRef]
- Rojac, T.; Benčan, A.; Uršič, H.; Malič, B.; Kosec, M. Synthesis of a Li- and Ta-modified (K,Na)NbO3 solid solution by mechanochemical activation. J. Am. Ceram. Soc. 2008, 91, 3789–3791. [Google Scholar] [CrossRef]
- Härdtl, K.H.; Rau, H. PbO vapour pressure in Pb(Ti1-xZrx)O3 system. Solid State Commun. 1969, 7, 41–45. [Google Scholar] [CrossRef]
- Holman, R.L.; Fulrath, R.M. Intrinsic nonstoichiometry in lead zirconate lead Titanate system determined by Knudsen effusion. J. Appl. Phys. 1973, 44, 5227–5236. [Google Scholar] [CrossRef]
- Kingon, A.I.; Clark, J.B. Sintering of PZT ceramics. 1. Atmosphere control. J. Am. Ceram. Soc. 1983, 66, 253–256. [Google Scholar] [CrossRef]
- Kingon, A.I.; Clark, J.B. Sintering of PZT ceramics. 2. Effect of PbO content on densification kinetics. J. Am. Ceram. Soc. 1983, 66, 256–260. [Google Scholar] [CrossRef]
- Rahaman, M.N. Ceramic Processing and Sintering, 2nd ed.; Marcel Dekker: New York, NY, USA, 2003. [Google Scholar]
- German, R.M. Sintering Theory and Practice; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Kingery, W.D.; Bowen, H.K.; Uhlmann, D.R. Introduction to Ceramics; John Wiley & Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
- Kang, S.-J.L. Sintering: Densification, Grain Growth, and Microstructure; Elsevier Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Burke, J.E. The Development of Pore-Free Ceramics. In Sintering Key Papers; Somiya, S., Moriyoshi, Y., Eds.; Elsevier Science Publishing: London, UK; New York, NY, USA, 1989; pp. 3–17. [Google Scholar]
- Koruza, J.; Malic, B.; Kosec, M. Microstructure evolution during sintering of sodium niobate. J. Am. Ceram. Soc. 2011, 94, 4174–4178. [Google Scholar] [CrossRef]
- Rollett, A.D.; Srolovitz, D.J.; Anderson, M.P. Simulation and theory of abnormal grain growth—Anisotropic grain boundary energies and mobilities. Acta Metall. 1989, 37, 1227–1240. [Google Scholar] [CrossRef]
- Lee, B.K.; Chung, S.Y.; Kang, S.J.L. Grain boundary faceting and abnormal grain growth in BaTiO3. Acta Mater. 2000, 48, 1575–1580. [Google Scholar] [CrossRef]
- Horn, D.S.; Messing, G.L. Anisotropic grain growth in TiO2-doped alumina. Mater. Sci. Eng. A 1995, 195, 169–178. [Google Scholar] [CrossRef]
- Bateman, C.A.; Bennison, S.J.; Harmer, M.P. Mechanism for the role of magnesia in the sintering of alumina containing small amounts of a liquid phase. J. Am. Ceram. Soc. 1989, 72, 1241–1244. [Google Scholar] [CrossRef]
- Hsueh, C.H.; Evans, A.G.; Coble, R.L. Microstructure development during final intermediate stage sintering—I. Pore grain-boundary separation. Acta Metall. 1982, 30, 1269–1279. [Google Scholar] [CrossRef]
- Nichols, F.A. Further comments on the theory of grain growth in porous compacts. J. Am. Ceram. Soc. 1968, 51, 468. [Google Scholar] [CrossRef]
- Brook, R.J. Pore-grain boundary interactions and grain growth. J. Am. Ceram. Soc. 1969, 52, 56–57. [Google Scholar] [CrossRef]
- Tennery, V.J. High-temperature phase transitions in NaNbO3. J. Am. Ceram. Soc. 1965, 48, 537–539. [Google Scholar] [CrossRef]
- Megaw, H.D. 7 Phases of sodium niobate. Ferroelectrics 1974, 7, 87–89. [Google Scholar] [CrossRef]
- Koruza, J.; Tellier, J.; Malič, B.; Bobnar, V.; Kosec, M. Phase transitions of sodium niobate powder and ceramics, prepared by solid state synthesis. J. Appl. Phys. 2010, 108, 113509. [Google Scholar] [CrossRef]
- Tellier, J.; Malic, B.; Dkhil, B.; Jenko, D.; Cilensek, J.; Kosec, M. Crystal structure and phase transitions of sodium potassium niobate perovskites. Solid State Sci. 2009, 11, 320–324. [Google Scholar] [CrossRef]
- Malic, B.; Razpotnik, H.; Koruza, J.; Kokalj, S.; Cilensek, J.; Kosec, M. Linear thermal expansion of lead-free piezoelectric K0.5Na0.5NbO3 ceramics in a wide temperature range. J. Am. Ceram. Soc. 2011, 94, 2273–2275. [Google Scholar] [CrossRef]
- Tennery, V.J.; Hang, K.W. Thermal and X-Ray diffraction studies of NaNbO3-KNbO3 system. J. Appl. Phys. 1968, 39, 4749–4753. [Google Scholar] [CrossRef]
- Li, J.-F.; Wang, K.; Zhang, B.-P.; Zhang, L.-M. Ferroelectric and piezoelectric properties of fine-grained Na0.5K0.5NbO3 lead-free piezoelectric ceramics prepared by spark plasma sintering. J. Am. Ceram. Soc. 2006, 89, 706–709. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.-F. Analysis of crystallographic evolution in (Na,K)NbO3-based lead-free piezoceramics by X-ray diffraction. Appl. Phys. Lett. 2007, 91. [Google Scholar] [CrossRef]
- Guo, Y.P.; Kakimoto, K.; Ohsato, H. (Na0.5K0.5)NbO3-LiTaO3 lead-free piezoelectric ceramics. Mater. Lett. 2005, 59, 241–244. [Google Scholar] [CrossRef]
- Hollenstein, E.; Davis, M.; Damjanovic, D.; Setter, N. Piezoelectric properties of Li- and Ta-modified (K0.5Na0.5)NbO3 ceramics. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.-F. Domain engineering of lead-free Li-modified (K,Na)NbO3 polycrystals with highly enhanced piezoelectricity. Adv. Funct. Mater. 2010, 20, 1924–1929. [Google Scholar] [CrossRef]
- Park, H.Y.; Ahn, C.W.; Song, H.C.; Lee, J.H.; Nahm, S.; Uchino, K.; Lee, H.G.; Lee, H.J. Microstructure and piezoelectric properties of 0.95(Na0.5K0.5)NbO3-0.05BaTiO3 ceramics. Appl. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Park, H.Y.; Cho, K.H.; Paik, D.S.; Nahm, S.; Lee, H.G.; Kim, D.H. Microstructure and piezoelectric properties of lead-free (1-x)(Na0.5K0.5)NbO3-xCaTiO3 ceramics. J. Appl. Phys. 2007, 102. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Wang, K.; Li, F.; Li, J.-F.; Zhang, X.-W.; Wang, Q.-M. High and frequency-insensitive converse piezoelectric coefficient obtained in AgSbO3-modified (Li,K,Na)(Nb,Ta)O3 lead-free piezoceramics. J. Am. Ceram. Soc. 2013, 96, 519–523. [Google Scholar]
- Dai, Y.J.; Zhang, X.W.; Chen, K.P. Morphotropic phase boundary and electrical properties of K1-xNaxNbO3 lead-free ceramics. Appl. Phys. Lett. 2009, 94. [Google Scholar] [CrossRef]
- Tomoaki, K.; Tsunehiro, K.; Kazuhiro, Y.; Subaru, M.; Masatoshi, A. Morphotropic phase boundary slope of (K,Na,Li)NbO3–BaZrO3 binary system adjusted using third component (Bi,Na)TiO3 additive. Jpn. J. Appl. Phys. 2013, 52. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.; Xiao, D.; Zhu, J.; Cheng, X.; Zheng, T.; Zhang, B.; Lou, X. Giant piezoelectricity in potassium-sodium niobate lead-free ceramics. J. Am. Ceram. Soc. 2014, 136, 2905–2910. [Google Scholar] [CrossRef] [PubMed]
- Powell, B.R.J. Processing of Sodium Potassium Niobate Ceramics. Master’s Thesis, University of California, Berkeley, CA, USA, 1971. [Google Scholar]
- Matsubara, M.; Yamaguchi, T.; Kikuta, K.; Hirano, S. Sinterability and piezoelectric properties of (K,Na)NbO3 ceramics with novel sintering aid. Jpn. J. Appl. Phys. 2004, 43, 7159–7163. [Google Scholar] [CrossRef]
- Malic, B.; Bernard, J.; Holc, J.; Jenko, D.; Kosec, M. Alkaline-earth doping in (K,Na)NbO3 based piezoceramics. J. Eur. Ceram. Soc. 2005, 25, 2707–2711. [Google Scholar] [CrossRef]
- Hagh, N.M.; Jadidian, B.; Safari, A. Property-processing relationship in lead-free (K,Na,Li) NbO3-solid solution system. J. Electr. 2007, 18, 339–346. [Google Scholar] [CrossRef]
- Malic, B.; Bernard, J.; Bencan, A.; Kosec, M. Influence of zirconia addition on the microstructure of K0.5Na0.5NbO3 ceramics. J. Eur. Ceram. Soc. 2008, 28, 1191–1196. [Google Scholar] [CrossRef]
- Malic, B.; Jenko, D.; Bernard, J.; Cilensek, J.; Kosec, M. Synthesis and sintering of (K,Na)NbO3 based ceramics. In Proceedings of the 2002 Materials Research Society (MRS) Fall Meeting & Exhibit, Boston, MA, USA, 2–5 December 2002.
- Shafer, M.W.; Roy, R. Phase equilibria in the system Na2O-Nb2O5. J. Am. Ceram. Soc. 1959, 42, 482–486. [Google Scholar] [CrossRef]
- Appendino, P. Contributo allo studio del sistema Na2O-Nb2O5. Ann. di Chim. 1973, 63, 547–556. [Google Scholar]
- Irle, E.; Blachnik, R.; Gather, B. The phase diagrams of Na2O and K2O with Nb2O5 and the ternary system Nb2O5-Na2O-Yb2O3. Thermochim. Acta 1991, 179, 157–169. [Google Scholar] [CrossRef]
- Reisman, A.; Holtzberg, F. Phase equilibria in the system K2CO3-Nb2O5 by the method of differential thermal analysis. J. Am. Chem. Soc. 1955, 77, 2115–2119. [Google Scholar] [CrossRef]
- Montorsi, M.; Appendino, P.; Vallino, M. Solid-state equilibria in system niobium pentoxide and lithium and strontium metaniobates. Ann. Chim. 1976, 66, 233–240. [Google Scholar]
- Malic, B.; Jenko, D.; Holc, J.; Hrovat, M.; Kosec, M. Synthesis of sodium potassium niobate: A diffusion couples study. J. Am. Ceram. Soc. 2008, 91, 1916–1922. [Google Scholar] [CrossRef]
- Hreščak, J.; Bencan, A.; Rojac, T.; Malič, B. The influence of different niobium pentoxide precursors on the solid-state synthesis of potassium sodium niobate. J. Eur. Ceram. Soc. 2013, 33, 3065–3075. [Google Scholar] [CrossRef]
- Bizeto, M.A.; Constantino, V.R.L. Structural aspects and thermal behavior of the proton-exchanged layered niobate K4Nb6O17. Mater. Res. Bull. 2004, 39, 1729–1736. [Google Scholar] [CrossRef]
- Bomlai, P.; Songsurin, C.; Muensit, N.; Milne, S.J. Structural and electrical properties of (1–x)Na0.465K0.465Li0.07Nb0.93Ta0.07O3-xMnO lead-free piezoelectric ceramics synthesized at low sintering temperatures. ScienceAsia 2010, 36, 231–236. [Google Scholar] [CrossRef]
- Haugen, A.B.; Madaro, F.; Bjorkeng, L.P.; Grande, T.; Einarsrud, M.A. Sintering of sub-micron K0.5Na0.5NbO3 powders fabricated by spray pyrolysis. J. Eur. Ceram. Soc. 2015, 35, 1449–1457. [Google Scholar] [CrossRef]
- Popovič, A.; Bencze, L.; Koruza, J.; Malič, B. Vapour pressure and mixing thermodynamic properties of the KNbO3-NaNbO3 system. RSC Adv. 2015, 5, 76249–76256. [Google Scholar] [CrossRef]
- Cho, C.R.; Grishin, A. Background oxygen effects on pulsed laser deposited Na0.5K0.5NbO3 films: From superparaelectric state to ferroelectricity. J. Appl. Phys. 2000, 87, 4439–4448. [Google Scholar] [CrossRef]
- Kupec, A.; Malic, B.; Tellier, J.; Tchernychova, E.; Glinsek, S.; Kosec, M. Lead-free ferroelectric potassium sodium niobate thin films from solution: Composition and structure. J. Am. Ceram. Soc. 2012, 95, 515–523. [Google Scholar] [CrossRef]
- Koruza, J.; Malic, B.; Noshchenko, O.; Kosec, M. Top-down processing of NaNbO3 nanopowder. J. Nanomater. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
- Koruza, J.; Malic, B. Initial stage sintering mechanism of NaNbO3 and implications regarding the densification of alkaline niobates. J. Eur. Ceram. Soc. 2014, 34, 1971–1979. [Google Scholar] [CrossRef]
- Kosec, M.; Kolar, D. Activated sintering and electrical properties of NaKNbO3. Mater. Res. Bull. 1975, 10, 335–339. [Google Scholar] [CrossRef]
- Nobre, M.A.L.; Longo, E.; Leite, E.R.; Varela, J.A. Synthesis and sintering of ultra fine NaNbO3 powder by use of polymeric precursors. Mater. Lett. 1996, 28, 215–220. [Google Scholar]
- Shiratori, Y.; Magrez, A.; Dornseiffer, J.; Haegel, F.H.; Pithan, C.; Waser, R. Polymorphism in micro-, submicro-, and nanocrystalline NaNbO3. J. Phys. Chem. B 2005, 109, 20122–20130. [Google Scholar] [PubMed]
- Wang, J.D.; Raj, R. Estimate of the Activation-energies for boundary diffusion from rate-controlled sintering of pure alumina, and alumina doped with zirconia or titania. J. Am. Ceram. Soc. 1990, 73, 1172–1175. [Google Scholar]
- Srdić, V.V.; Winterer, M.; Hahn, H. Sintering behavior of nanocrystalline zirconia prepared by chemical vapor synthesis. J. Am. Ceram. Soc. 2000, 83, 729–736. [Google Scholar]
- Polotai, A.; Breece, K.; Dickey, E.; Randall, C.; Ragulya, A. A novel approach to sintering nanocrystalline barium titanate ceramics. J. Am. Ceram. Soc. 2005, 88, 3008–3012. [Google Scholar] [CrossRef]
- German, R.M.; Munir, Z.A. Surface-area reduction during isothermal sintering. J. Am. Ceram. Soc. 1976, 59, 379–383. [Google Scholar] [CrossRef]
- Lehl, H. Niob. Teil B 4, Alkalioxoniobate, Niobverbindungen mit weiteren Kationen, Kohlenstoffverbindungen des Niob. In Gmelins Handbuch der Anorganischen Chemie; Chemie: Weinheim, Germany, 1973; pp. 1–473. [Google Scholar]
- Bron, V.A. Some crystal-chemical relationships in the activated sintering of highly refractory oxides in the solid phase. Powder Metall. Metal Ceram. 1964, 1, 339–344. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Defect studies of doped and undoped barium titanate using computer simulation techniques. J. Phys. Chem. Solids 1986, 47, 89–97. [Google Scholar] [CrossRef]
- Jenko, D.; Bencan, A.; Malic, B.; Holc, J.; Kosec, M. Electron microscopy studies of potassium sodium niobate ceramics. Microsc. Microanal. 2005, 11, 572–580. [Google Scholar] [CrossRef] [PubMed]
- Jenko, D. Sinteza keramike na osnovi (K,Na)NbO3 [Synthesis of (K,Na)NbO3 based Ceramics]. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2006. [Google Scholar]
- Madaro, F.; Saeterli, R.; Tolchard, J.R.; Einarsrud, M.A.; Holmestad, R.; Grande, T. Molten salt synthesis of K4Nb6O17, K2Nb4O11 and KNb3O8 crystals with needle- or plate-like morphology. Cryst. Eng. Comm. 2011, 13, 1304–1313. [Google Scholar] [CrossRef]
- Hoffmann, M.J.; Kungl, H.; Acker, J.; Elsässer, C.; Körbel, S.; Marton, P.; Eichel, R.-A.; Erünal, E.; Jakes, P. Influence of the A/B stoichiometry on defect structure, sintering, and microstructure in undoped and Cu-doped KNN. In Lead-Free Piezoelectrics; Priya, S., Nahm, S., Eds.; Springer: New York, NY, USA, 2012; pp. 209–251. [Google Scholar]
- Zhen, Y.H.; Li, J.F. Normal sintering of (K,Na)NbO3-based ceramics: Influence of sintering temperature on densification, microstructure, and electrical properties. J. Am. Ceram. Soc. 2006, 89, 3669–3675. [Google Scholar] [CrossRef]
- Pavlic, J.; Malic, B.; Rojac, T. Microstructural, structural, dielectric and piezoelectric properties of potassium sodium niobate thick films. J. Eur. Ceram. Soc. 2014, 34, 285–295. [Google Scholar] [CrossRef]
- Acker, J.; Kungl, H.; Schierholz, R.; Wagner, S.; Eichel, R.A.; Hoffmann, M.J. Microstructure of sodium-potassium niobate ceramics sintered under high alkaline vapor pressure atmosphere. J. Eur. Ceram. Soc. 2014, 34, 4213–4221. [Google Scholar] [CrossRef]
- German, R.; Suri, P.; Park, S. Review: Liquid phase sintering. J. Mater. Sci. 2009, 44, 1–39. [Google Scholar] [CrossRef]
- Matsubara, M.; Yamaguchi, T.; Sakamoto, W.; Kikuta, K.; Yogo, T.; Hirano, S. Processing and piezoelectric properties of lead-free (K,Na)(Nb,Ta)O3 ceramics. J. Am. Ceram. Soc. 2005, 88, 1190–1196. [Google Scholar] [CrossRef]
- Matsubara, M.; Yamaguchi, T.; Kikuta, K.; Hirano, S. Synthesis and characterization of (K0.5Na0.5)(Nb0.7Ta0.3)O3 piezoelectric ceramics sintered with sintering aid K5.4Cu1.3Ta10O29. Jpn. J. Appl. Phys. 2005, 44, 6618–6623. [Google Scholar] [CrossRef]
- Matsubara, M.; Yamaguchi, T.; Kikuta, K.; Hirano, S. Sintering and piezoelectric properties of potassium sodium niobate ceramics with newly developed sintering aid. Jpn. J. Appl. Phys. 2005, 44, 258–263. [Google Scholar] [CrossRef]
- Park, S.H.; Ahn, C.W.; Nahm, S.; Song, J.S. Microstructure and piezoelectric properties of ZnO-added (Na0.5K0.5)NbO3 ceramics. Jpn. J. Appl. Phys. 2004, 43, L1072–L1074. [Google Scholar] [CrossRef]
- Ryu, J.; Choi, J.J.; Hahn, B.D.; Park, D.S.; Yoon, W.H.; Kim, K.Y. Sintering and piezoelectric properties of KNN ceramics doped with KZT. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 2510–2515. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.P.; Zhang, F.L.; Zhou, J.Q.; Zhang, X.W.; Li, C.W.; An, L.N. Effect of borax addition on sintering and electrical properties of (K0.5Na0.5)NbO3 lead-free piezoceramics. Ceram. Int. 2015, 41, 10232–10236. [Google Scholar] [CrossRef]
- Bernard, J.; Bencan, A.; Rojac, T.; Holc, J.; Malic, B.; Kosec, M. Low-temperature sintering of K0.5Na0.5NbO3 ceramics. J. Am. Ceram. Soc. 2008, 91, 2409–2411. [Google Scholar] [CrossRef]
- Bernard, J. Low-Temperature Sintering of Piezoelectric Ceramics KNN. Ph.D. Thesis, Jozef Stefan International Postgraduate School, Ljubljana, Slovenia, 2012. [Google Scholar]
- Kim, M.-S.; Jeon, S.; Lee, D.-S.; Jeong, S.-J.; Song, J.-S. Lead-free NKN-5LT piezoelectric materials for multilayer ceramic actuator. J. Electr. 2009, 23, 372–375. [Google Scholar] [CrossRef]
- Liu, C.; Liu, P.; Kobayashi, K.; Randall, C.A. Base metal Co-fired (Na,K)NbO3 structures with enhanced piezoelectric performance. J. Electr. 2014, 32, 301–306. [Google Scholar] [CrossRef]
- Fisher, J.G.; Kang, S.-J.L. Microstructural changes in (Na0.5K0.5)NbO3 ceramics sintered in various atmospheres. J. Eur. Ceram. Soc. 2009, 29, 2581–2588. [Google Scholar] [CrossRef]
- Fisher, J.G.; Rout, D.; Moon, K.-S.; Kang, S.-J.L. Structural changes in potassium sodium niobate ceramics sintered in different atmospheres. J. Alloys Compd. 2009, 479, 467–472. [Google Scholar] [CrossRef]
- Fisher, J.G.; Rout, D.; Moon, K.-S.; Kang, S.-J.L. High-temperature X-ray diffraction and Raman spectroscopy study of (K0.5Na0.5)NbO3 ceramics sintered in oxidizing and reducing atmospheres. Mater. Chem. Phys. 2010, 120, 263–271. [Google Scholar] [CrossRef]
- Choi, S.-Y.; Kang, S.-J.L. Sintering kinetics by structural transition at grain boundaries in barium titanate. Acta Mater. 2004, 52, 2937–2943. [Google Scholar] [CrossRef]
- Kobayashi, K.; Doshida, Y.; Mizuno, Y.; Randall, C.A. A route forwards to narrow the performance gap between PZT and lead-free piezoelectric ceramic with low oxygen partial pressure processed (Na0.5K0.5)NbO3. J. Am. Ceram. Soc. 2012, 95, 2928–2933. [Google Scholar] [CrossRef]
- Shimizu, H.; Kobayashi, K.; Mizuno, Y.; Randall, C.A. Advantages of low partial pressure of oxygen processing of alkali niobate: NaNbO3. J. Am. Ceram. Soc. 2014, 97, 1791–1796. [Google Scholar] [CrossRef]
- Kang, S.-J.L.; Jung, Y.-I.; Jung, S.-H.; Fisher, J.G. Interface structure-dependent grain growth behavior in polycrystals. In Microstructural Design of Advanced Engineering Materials; Molodov, D.A., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA.: Weinheim, Germany, 2013; pp. 299–322. [Google Scholar]
- Jung, S.H.; Kang, S.-J.L. An explanation for the formation of polyhedral abnormal grains in single-phase systems. Scr. Mater. 2014, 82, 49–52. [Google Scholar] [CrossRef]
- Kang, S.-J.L.; Lee, M.G.; An, S.M. Microstructural evolution during sintering with control of the interface structure. J. Am. Ceram. Soc. 2009, 92, 1464–1471. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. Lond. 1951, 243A, 299–358. [Google Scholar] [CrossRef]
- Williams, E.D.; Bartelt, N.C. Thermodynamics of surface morphology. Science 1991, 251, 393–400. [Google Scholar] [CrossRef] [PubMed]
- Chiang, Y.M.; Birnie, D.; Kingery, W.D. Physical Ceramics: Principles for Ceramic Science and Engineering; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Wang, H.-Q.; Dai, Y.-J.; Zhang, X.-W. Microstructure and hardening mechanism of K0.5Na0.5NbO3 lead-free ceramics with CuO doping sintered in different atmospheres. J. Am. Ceram. Soc. 2012, 95, 1182–1184. [Google Scholar] [CrossRef]
- Kobayashi, K.; Doshida, Y.; Mizuno, Y.; Randall, C.A. Piezoelectric and dielectric properties of Sn-doped (Na0.5K0.5)NbO3 ceramics processed under low oxygen partial pressure atmosphere. Jpn. J. Appl. Phys. 2014, 53. [Google Scholar] [CrossRef]
- Taub, J.; Ramajo, L.; Castro, M.S. Phase structure and piezoelectric properties of Ca- and Ba-doped K1/2Na1/2NbO3 lead-free ceramics. Ceram. Int. 2013, 39, 3555–3561. [Google Scholar] [CrossRef]
- Vendrell, X.; García, J.E.; Bril, X.; Ochoa, D.A.; Mestres, L.; Dezanneau, G. Improving the functional properties of (K0.5Na0.5)NbO3 piezoceramics by acceptor doping. J. Eur. Ceram. Soc. 2015, 35, 125–130. [Google Scholar] [CrossRef]
- Zuo, R.; Rödel, J.; Chen, R.; Li, L. Sintering and electrical properties of lead-free Na0.5K0.5NbO3 piezoelectric ceramics. J. Am. Ceram. Soc. 2006, 89, 2010–2015. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.-F.; Liu, N. Piezoelectric properties of low-temperature sintered Li-modified (Na,K)NbO3 lead-free ceramics. Appl. Phys. Lett. 2008, 93. [Google Scholar] [CrossRef]
- Wang, K.; Li, J.-F. Low-temperature sintering of Li-modified (K,Na)NbO3 lead-free ceramics: Sintering behavior, microstructure, and electrical properties. J. Am. Ceram. Soc. 2010, 93, 1101–1107. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Li, J.-F.; Wang, K.; Zhang, X.-W. Phase structure and electrical properties of (Li,Ta)-doped (K,Na)NbO3 lead-free piezoceramics in the vicinity of Na/K = 50/50. J. Mater. Sci. 2011, 46, 5111–5116. [Google Scholar] [CrossRef]
- Zang, G.Z.; Wang, J.F.; Chen, H.C.; Su, W.B.; Wang, C.M.; Qi, P.; Ming, B.Q.; Du, J.; Zheng, L.M.; Zhang, S.J.; et al. Perovskite (Na0.5K0.5)1–x(LiSb)xNb1-xO3 lead-free piezoceramics. Appl. Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
- Wu, J.G.; Xiao, D.Q.; Wang, Y.Y.; Wu, W.J.; Zhang, B.; Zhu, J.G. Improved temperature stability of CaTiO3-modified [(K0.5Na0.5)0.96)Li0.04](Nb0.91Sb0.05Ta0.04)O3 lead-free piezoelectric ceramics. J. Appl. Phys. 2008, 104. [Google Scholar] [CrossRef]
- Jaeger, R.E.; Egerton, L. Hot pressing of potassium-sodium niobates. J. Am. Ceram. Soc. 1962, 45, 209–213. [Google Scholar] [CrossRef]
- Haertling, G.H. Properties of hot-pressed ferroelectric alkali niobate ceramics. J. Am. Ceram. Soc. 1967, 50, 329–330. [Google Scholar] [CrossRef]
- Egerton, L.; Bieling, C.A. Isostatically hot-pressed sodium-potassium niobate transducer material for ultrasonic devices. Am. Ceram. Soc. Bull. 1968, 47, 1151–1156. [Google Scholar]
- Nazeri-Eshghi, A.; Kuang, A.X.; Mackenzie, J.D. Preparation and properties of KNbO3 via the Sol-Gel method. J. Mater. Sci. 1990, 25, 3333–3337. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.-P.; Li, J.-F.; Zhang, L.-M. Lead-free Na0.5K0.5NbO3 piezoelectric ceramics fabricated by spark plasma sintering: Annealing effect on electrical properties. J. Electr. 2007, 21, 251–254. [Google Scholar] [CrossRef]
- Hungría, T.; Galy, J.; Castro, A. Spark plasma sintering as a useful technique to the nanostructuration of piezo-ferroelectric materials. Adv. Eng. Mater. 2009, 11, 615–631. [Google Scholar] [CrossRef]
- Shen, Z.-Y.; Li, J.-F.; Wang, K.; Xu, S.; Jiang, W.; Deng, Q. Electrical and mechanical properties of fine-grained Li/Ta-modified (Na,K)NbO3-based piezoceramics prepared by spark plasma sintering. J. Am. Ceram. Soc. 2010, 93, 1378–1383. [Google Scholar] [CrossRef]
- Fang, C.Y.; Randall, C.A.; Lanagan, M.T.; Agrawal, D.K. Microwave processing of electroceramic materials and devices. J. Electr. 2009, 22, 125–130. [Google Scholar] [CrossRef]
- Oghbaei, M.; Mirzaee, O. Microwave versus conventional sintering: A review of fundamentals, advantages and applications. J. Alloys Compd. 2010, 494, 175–189. [Google Scholar] [CrossRef]
- Feizpour, M.; Bafrooei, H.B.; Hayati, R.; Ebadzadeh, T. Microwave-assisted synthesis and sintering of potassium sodium niobate lead-free piezoelectric ceramics. Ceram. Int. 2014, 40, 871–877. [Google Scholar] [CrossRef]
- Bafandeh, M.R.; Gharahkhani, R.; Abbasi, M.H.; Saidi, A.; Lee, J.S.; Han, H.S. Improvement of piezoelectric and ferroelectric properties in (K,Na)NbO3- based ceramics via microwave sintering. J. Electr. 2014, 33, 128–133. [Google Scholar] [CrossRef]
- Harmer, M.P.; Brook, R.J. Fast firing—Microstructural benefits. Trans. J. Br. Ceram. Soc. 1981, 80, 147–148. [Google Scholar]
- Huckabee, M.L.; Palmour, H. Rate Controlled sintering of fine-grained Al2O3. Am. Ceram. Soc. Bull. 1972, 51, 574–576. [Google Scholar]
- Chen, I.W.; Wang, X.H. Sintering dense nanocrystalline ceramics without final-stage grain growth. Nature 2000, 404, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.G.; Bai, W.F.; Shen, B.; Zhai, J.W. Improved piezoelectric properties of (KxNa1–x)0.94Li0.06NbO3 lead-free ceramics fabricated by combining two-step sintering. J. Alloys Compd. 2012, 534, 13–19. [Google Scholar] [CrossRef]
- Kang, S.-J.L.; Park, J.H.; Ko, S.Y.; Lee, H.Y. Solid-state conversion of single crystals: The principle and the state-of-the-art. J. Am. Ceram. Soc. 2015, 98, 347–360. [Google Scholar] [CrossRef]
- Benčan, A.; Tchernychova, E.; Uršič, H.; Kosec, M.; Fisher, J. Growth and Characterization of Single Crystals of Potassium Sodium Niobate by Solid State Crystal Growth. In Ferroelectrics-Material Aspects; Lallart, M., Ed.; InTech: Rijeka, Croatia, 2011; pp. 87–108. [Google Scholar]
- Kizaki, Y.; Noguchi, Y.; Miyayama, M. Defect control for low leakage current in K0.5Na0.5NbO3 single crystals. Appl. Phys. Lett. 2006, 89. [Google Scholar] [CrossRef]
- Davis, M.; Klein, N.; Damjanovic, D.; Setter, N.; Gross, A.; Wesemann, V.; Vernay, S.; Rytz, D. Large and stable thickness coupling coefficients of [001]C-oriented KNbO3 and Li-modified (K,Na)NbO3 single crystals. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
- Gupta, S.; Priya, S. Ferroelectric properties and dynamic scaling of <100> oriented (K0.5Na0.5)NbO3 single crystals. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Zhou, Z.X.; Guo, R.Y.; Bhalla, A.S. Piezoelectric and ferroelectric properties of lead-free niobium-rich potassium lithium tantalate niobate single crystals. Mater. Res. Bull. 2014, 49, 206–209. [Google Scholar] [CrossRef]
- Fisher, J.G.; Benčan, A.; Holc, J.; Kosec, M.; Vernay, S.; Rytz, D. Growth of potassium sodium niobate single crystals by solid state crystal growth. J. Cryst. Growth 2007, 303, 487–492. [Google Scholar] [CrossRef]
- Fisher, J.G.; Benčan, A.; Bernard, J.; Holc, J.; Kosec, M.; Vernay, S.; Rytz, D. Growth of (Na,K,Li)(Nb,Ta)O3 single crystals by solid state crystal growth. J. Eur. Ceram. Soc. 2007, 27, 4103–4106. [Google Scholar] [CrossRef]
- Farooq, M.U.; Fisher, J.G. Growth of (Na0.5K0.5)NbO3–SrTiO3 lead-free piezoelectric single crystals by the solid state crystal growth method and their characterization. Ceram. Int. 2014, 40, 3199–3207. [Google Scholar] [CrossRef]
- Fisher, J.G.; Bencan, A.; Kosec, M.; Vernay, S.; Rytz, D. Growth of dense single crystals of potassium sodium niobate by a combination of solid-state crystal growth and hot pressing. J. Am. Ceram. Soc. 2008, 91, 1503–1507. [Google Scholar] [CrossRef]
- Bencan, A.; Tchernychova, E.; Godec, M.; Fisher, J.; Kosec, M. Compositional and structural study of a (K0.5Na0.5)NbO3 single crystal prepared by solid state crystal growth. Microsc. Microanal. 2009, 15, 435–440. [Google Scholar] [CrossRef] [PubMed]
- Ursic, H.; Bencan, A.; Skarabot, M.; Godec, M.; Kosec, M. Dielectric, ferroelectric, piezoelectric, and electrostrictive properties of K0.5Na0.5NbO3 single crystals. J. Appl. Phys. 2010, 107. [Google Scholar] [CrossRef]
- Dvoršek, M. Piezokeramika na osnovi PbO-ZrO2-TiO2-Sb2O5-Nb2O5 sistemov [Piezoceramics based on PbO-ZrO2-TiO2-Sb2O5-Nb2O5 Systems]. Master’s Thesis, University of Ljubljana, Ljubljana, Slovenia, 1989. [Google Scholar]
- Northrop, D.A. Vaporization of lead zirconate-lead titanate materials. J. Am. Ceram. Soc. 1967, 50, 441–445. [Google Scholar] [CrossRef]
- Fushimi, S.; Ikeda, T. Phase equilibrium in system PbO-TiO2-ZrO2. J. Am. Ceram. Soc. 1967, 50, 129–132. [Google Scholar] [CrossRef]
- König, J.; Spreitzer, M.; Jancar, B.; Suvorov, D.; Samardzija, Z.; Popovic, A. The thermal decomposition of K0.5Bi0.5TiO3 ceramics. J. Eur. Ceram. Soc. 2009, 29, 1695–1701. [Google Scholar] [CrossRef]
- Popovič, A.; Bencze, L.; Koruza, J.; Malič, B.; Kosec, M. Knudsen effusion mass spectrometric approach to the thermodynamics of Na2O-Nb2O5 system. Int. J. Mass Spectrom. 2012, 309, 70–78. [Google Scholar] [CrossRef]
- Popovic, A.; Malic, B.; Bencze, L. Knudsen cell mass spectrometric investigation of the PbO-ZrO2-TiO2 system. Rapid Commun. Mass Spectrom. 1999, 13, 1129–1137. [Google Scholar] [CrossRef]
- Drowart, J.; Colin, R.; Exsteen, G. Mass-spectrometric study of vaporization of lead monoxide—Dissociation energy of PbO. Trans. Faraday Soc. 1965, 61, 1376–1383. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malič, B.; Koruza, J.; Hreščak, J.; Bernard, J.; Wang, K.; Fisher, J.G.; Benčan, A. Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics. Materials 2015, 8, 8117-8146. https://doi.org/10.3390/ma8125449
Malič B, Koruza J, Hreščak J, Bernard J, Wang K, Fisher JG, Benčan A. Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics. Materials. 2015; 8(12):8117-8146. https://doi.org/10.3390/ma8125449
Chicago/Turabian StyleMalič, Barbara, Jurij Koruza, Jitka Hreščak, Janez Bernard, Ke Wang, John G. Fisher, and Andreja Benčan. 2015. "Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics" Materials 8, no. 12: 8117-8146. https://doi.org/10.3390/ma8125449
APA StyleMalič, B., Koruza, J., Hreščak, J., Bernard, J., Wang, K., Fisher, J. G., & Benčan, A. (2015). Sintering of Lead-Free Piezoelectric Sodium Potassium Niobate Ceramics. Materials, 8(12), 8117-8146. https://doi.org/10.3390/ma8125449