Light Steel-Timber Frame with Composite and Plaster Bracing Panels
Abstract
:1. Introduction
2. Description of the System
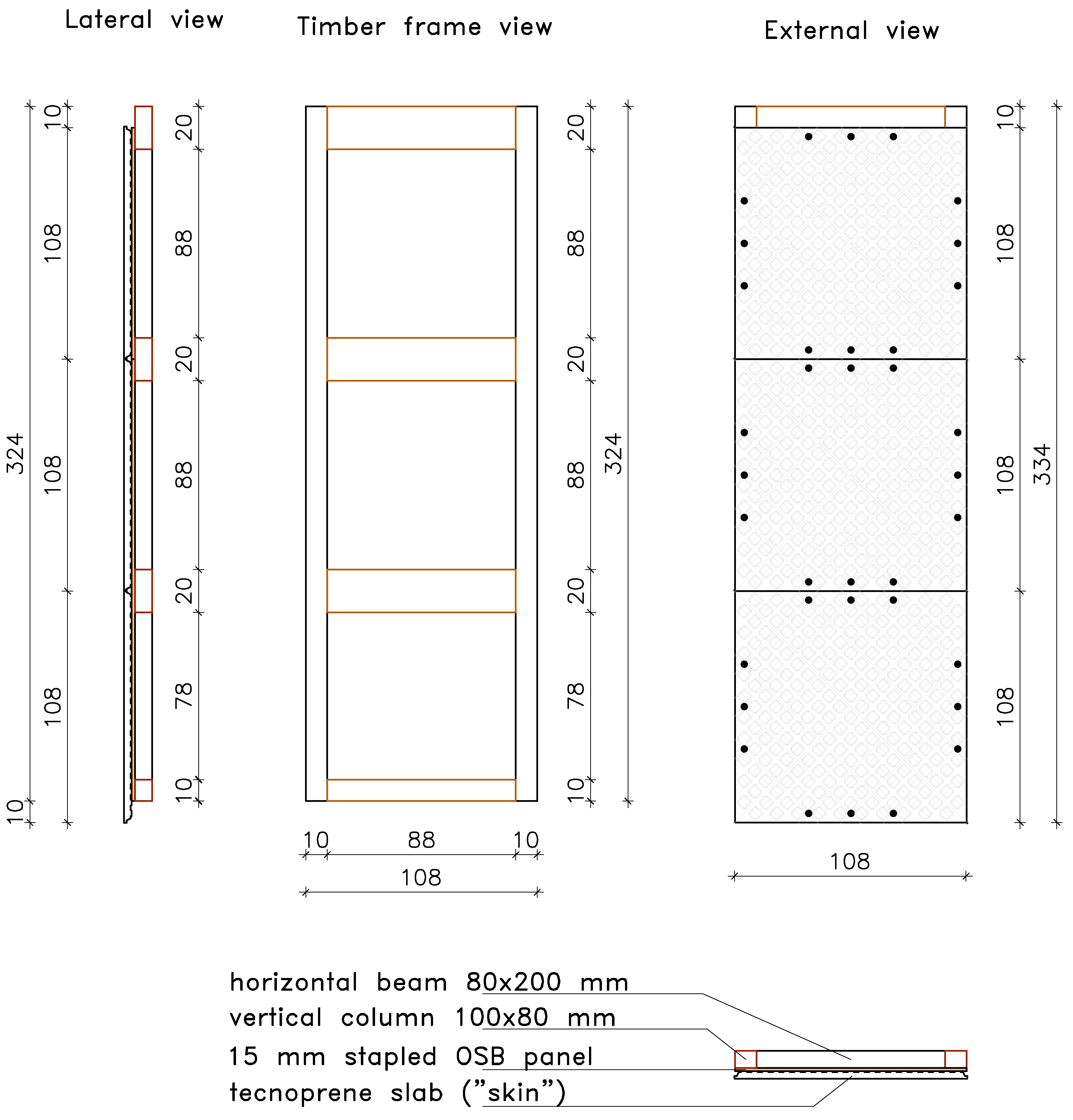

- The lightweight panel facilitates the realization of the buildings.
- The special 3D shape improves the adherence with the plaster and allows the creation of a ventilation chamber between the OSB and the external layer (i.e., a continuous natural airflow from the ground level to the roof), improving the durability of the wooden parts and providing good insulation properties to the building.



3. Experimental Test
3.1. Test Setup and Procedure
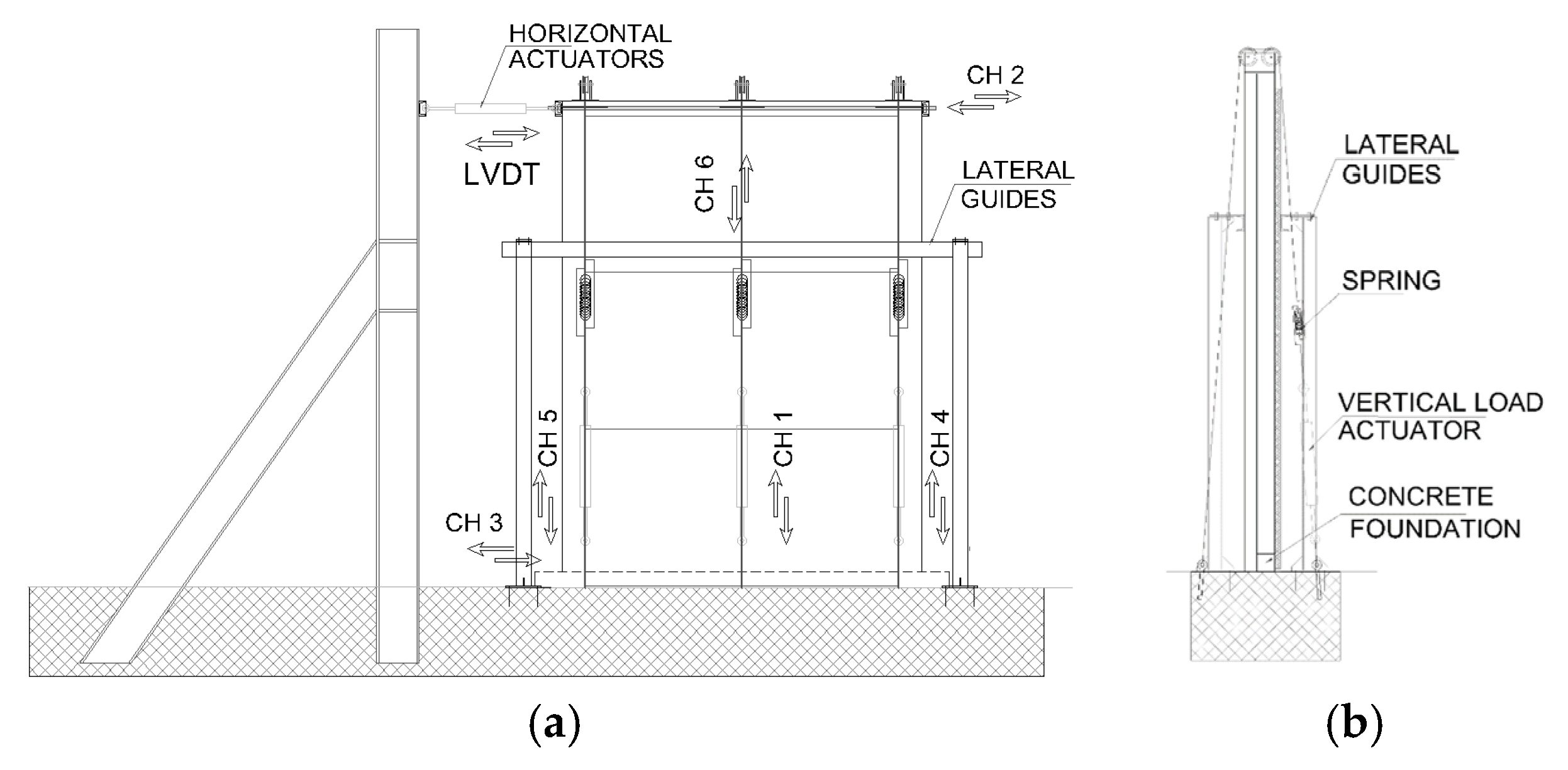

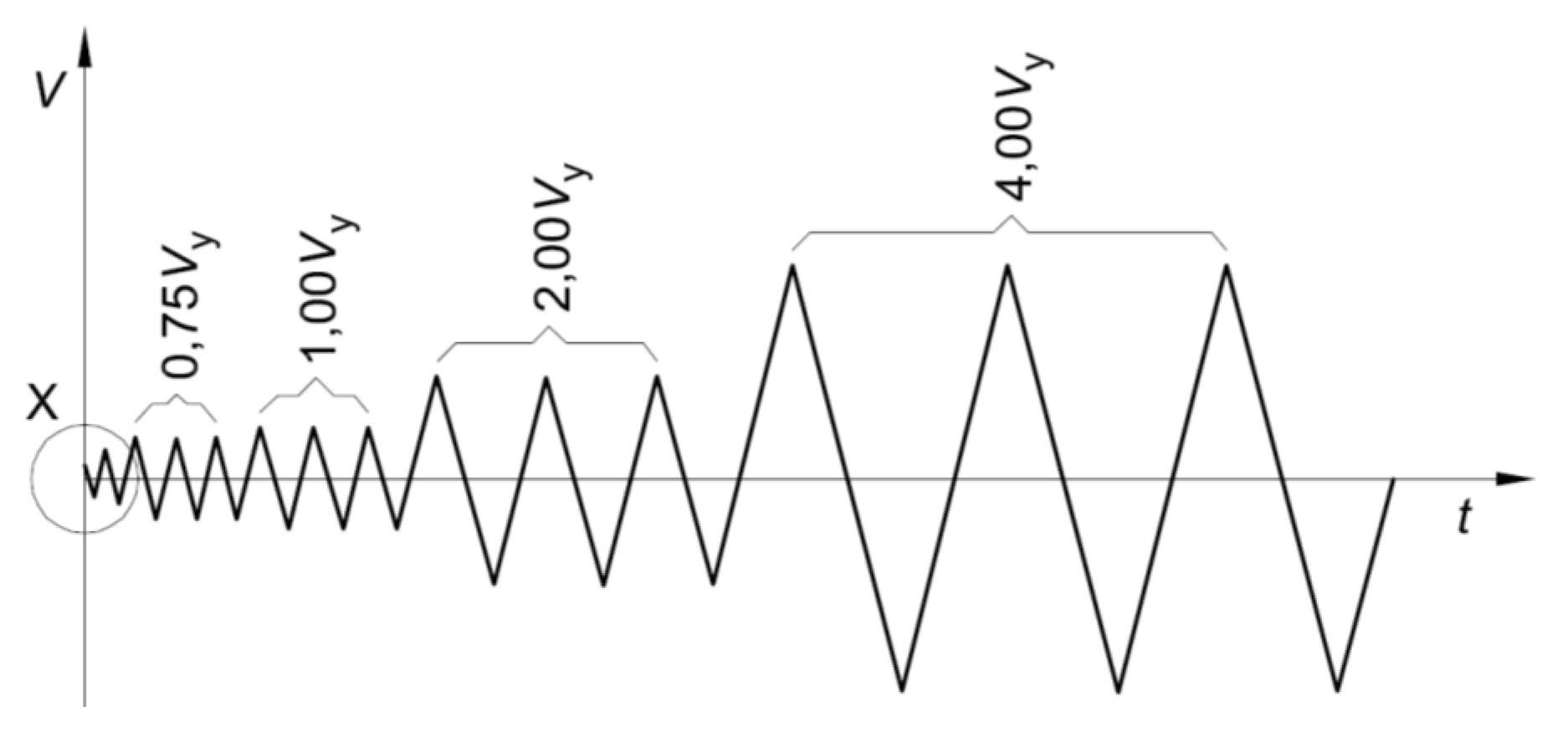
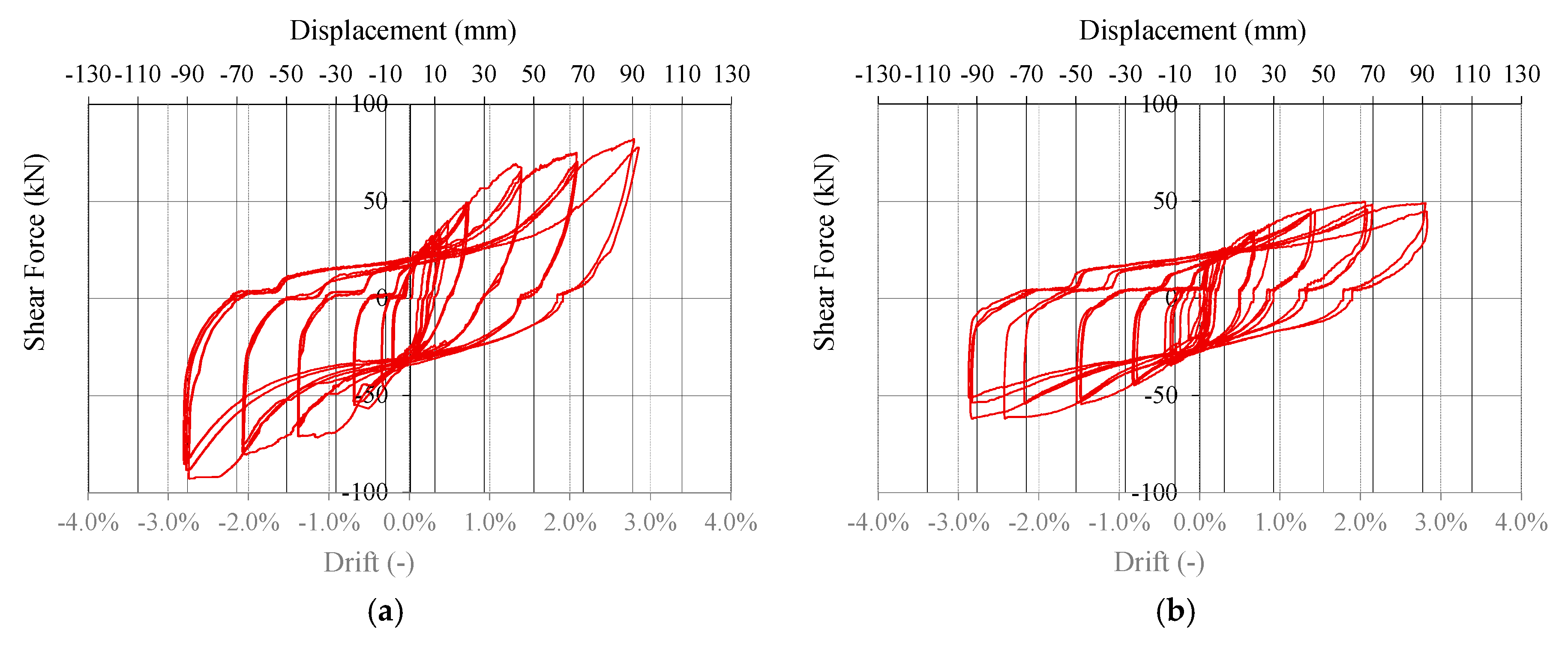
3.2. Test Results

- The in-plane shear resistance of skin and OSB panel and the shear resistance of the relative connectors.
- The axial and shear resistance of the connections at foundation.
- The shear resistance of frame-to-column joints.

3.3. Analysis of Experimental Results
3.3.1. Ductility Estimation
| Parameters | Notations (units) | ENa | EEEP | EEEH |
|---|---|---|---|---|
| Ultimate displacement | Vmax (mm) | 92.0 | 92.0 | 92.0 |
| Ultimate force | Fmax (kN) | 86.0 | 65.9 | 86.0 |
| Elastic stiffness | ke (kN/mm) | 7.5 | 4.5 | 5.0 |
| Hardening stiffness | kp (kN/mm) | 0.5 | 0.0 | 0.5 |
| Yielding displacement | Vy (mm) | 5.6 | 14.7 | 8.6 |
| Yielding force | Fy (kN) | 41.7 | 65.9 | 43.2 |
| Ductility ratio | μ = Vu/Vy (-) | 16.5 | 6.2 | 10.7 |
| Parameters | Notations (units) | EEEP |
|---|---|---|
| Ultimate displacement | Vmax (mm) | 90.0 |
| Ultimate force | Fmax (kN) | 47.4 |
| Elastic stiffness | ke (kN/mm) | 4.1 |
| Hardening stiffness | kp (kN/mm) | 0.0 |
| Yielding displacement | Vy (mm) | 11.6 |
| Yielding force | Fy (kN) | 47.4 |
| Ductility ratio | μ = Vu/Vy (-) | 7.7 |
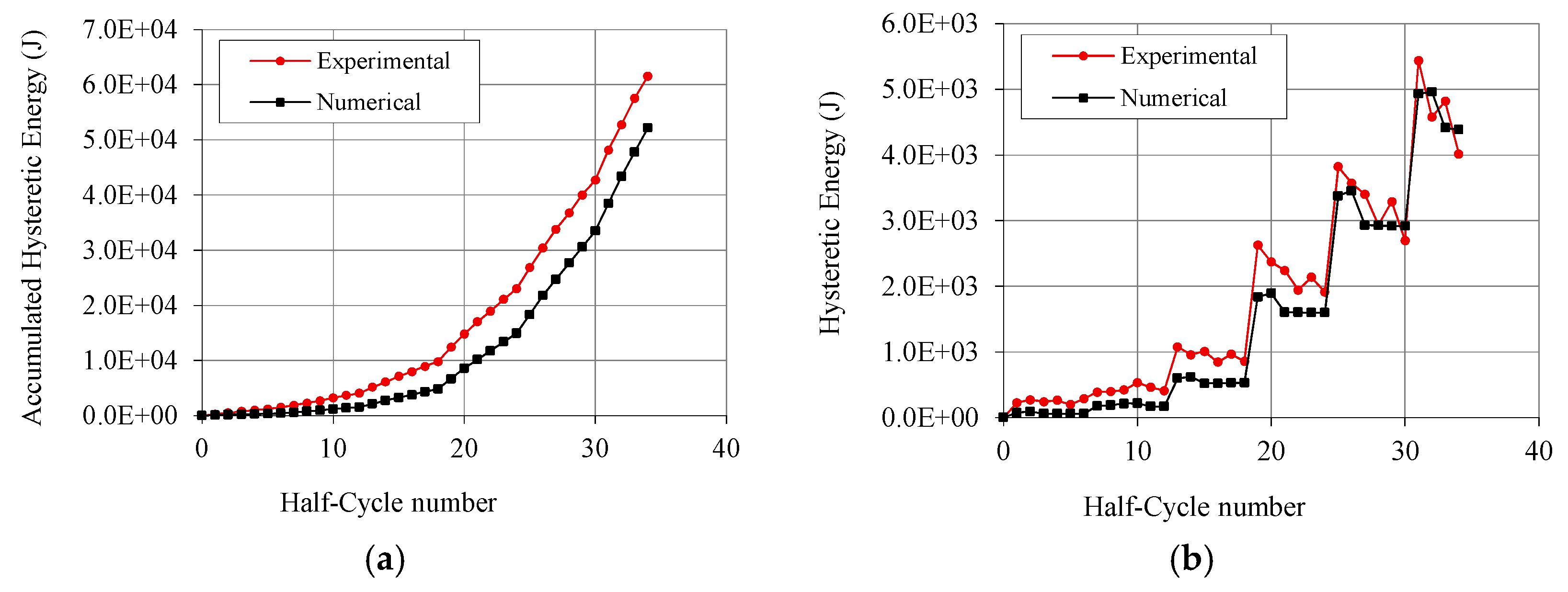
3.3.2. Strength Degradation and Viscous Damping Ratio
| Cycle Amplitude (mm) | Strength Reduction (%) | νeq (%) |
|---|---|---|
| Wall A | ||
| 20 | 5.9 | 23.8 |
| 40 | 5.9 | 20.9 |
| 60 | 7.6 | 19.6 |
| 80 | 11.4 | 18.6 |
| Wall B | ||
| 20 | 3.4 | 31.2 |
| 40 | 4.9 | 24.3 |
| 60 | 8.9 | 24.9 |
| 80 | 16.2 | 25.8 |
4. Numerical Simulations
4.1. Nonlinear Model
- Execution of quasi-static cyclic loading tests, according to EN12512 [24], of an entire wall specimen representative of the studied system and recording of applied lateral force vs. displacement of wall and connections, as shown above.
- Calibration based on test results of each nonlinear hysteretic spring representing connection elements and bracing system, in terms of equivalence of hysteresis cycles and dissipated energy for each element.
- Assembling of linear and nonlinear elements to reproduce the tested wall specimen and to simulate the cyclic-loading test.
- Comparison of numerical and experimental curves of the wall in terms of hysteresis cycles and energy dissipation, in order to validate the model.
- Modeling of the case-study building and execution of NLDA.
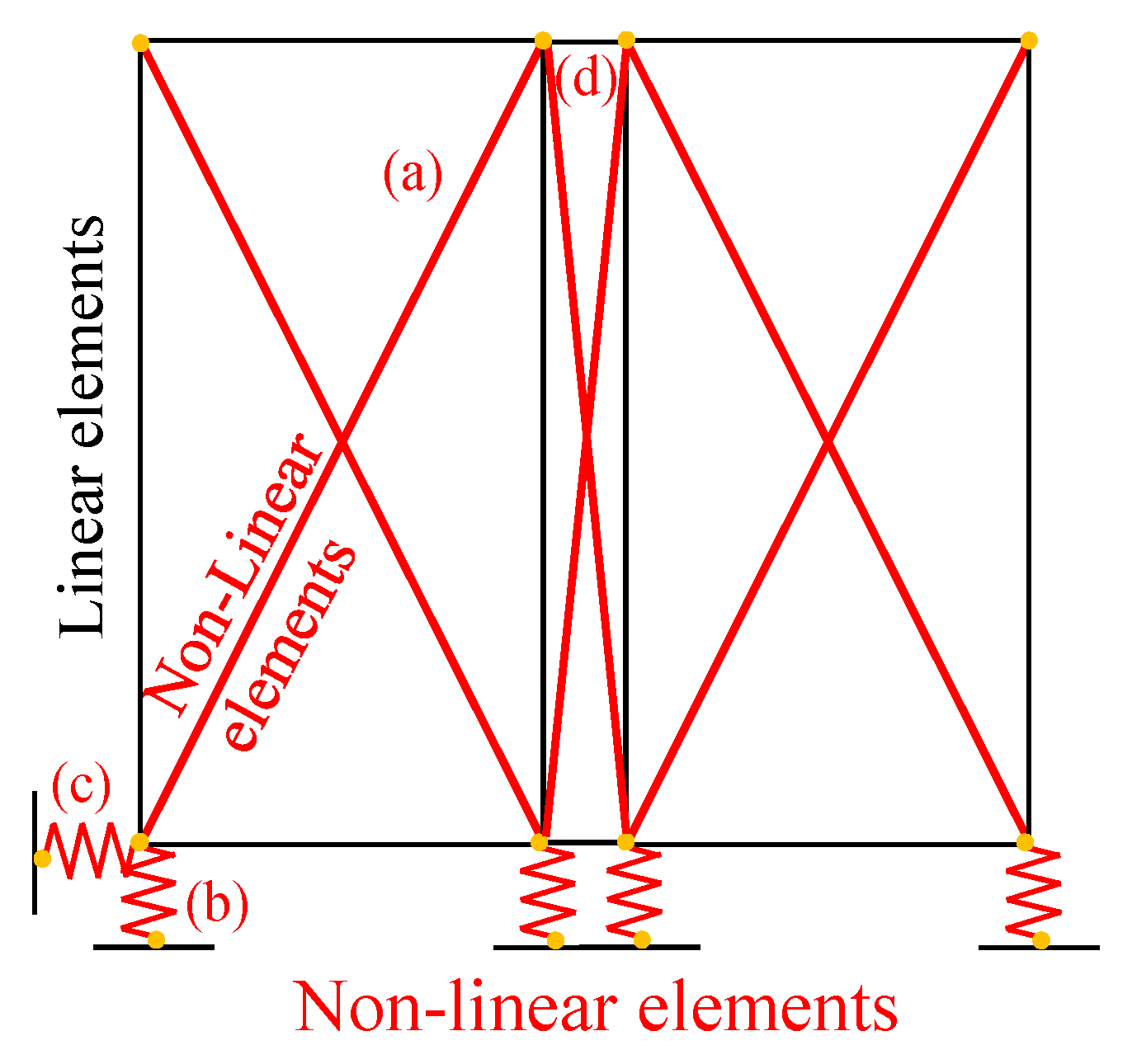
| Main Parameters | Units | Bracing Panel (a) | Hold-Downs (b) | Base Shear Screws (c) | Vertical Joints (d) |
|---|---|---|---|---|---|
| Elastic stiffness | kN/mm | 7.00 | 64.04 | 617.50 | 33.25 |
| First yielding force | kN | 14.00 | 38.42 | 24.70 | 26.60 |
| Post-elastic stiffness | kN/mm | 1.22 | 11.70 | 105.55 | 6.48 |
4.2. Simulation of Tests
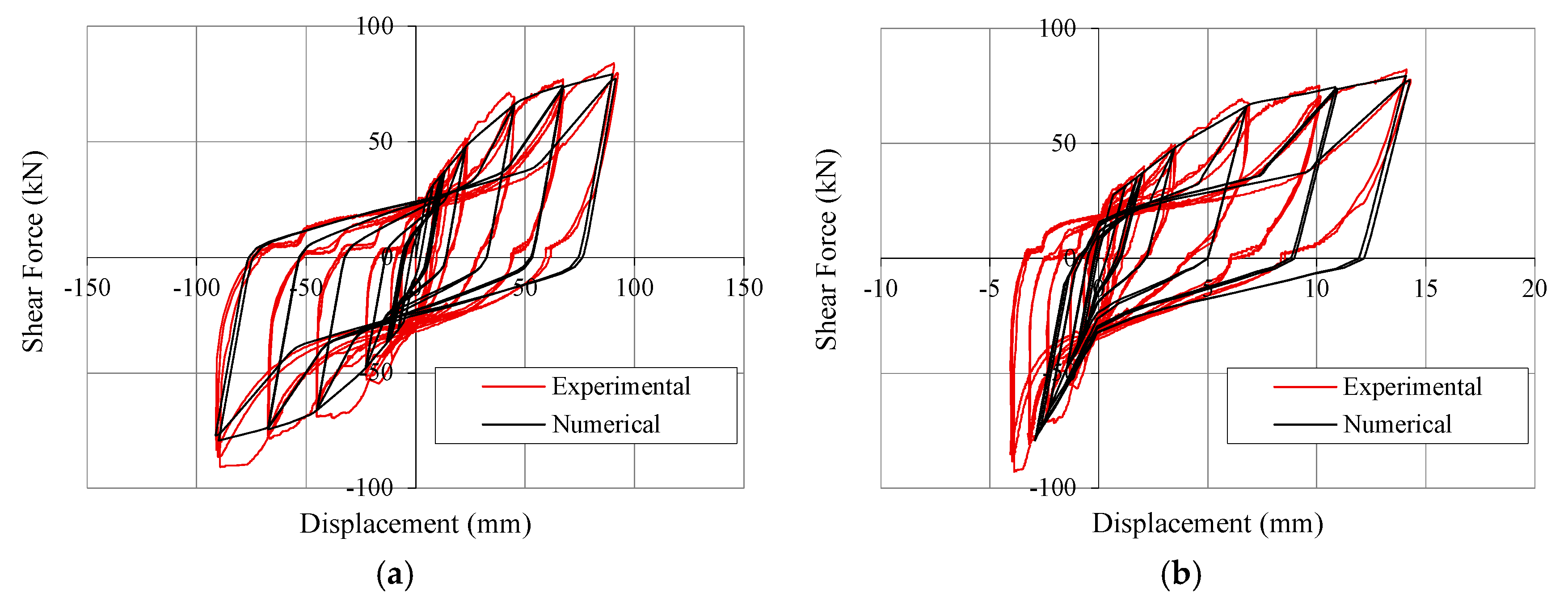
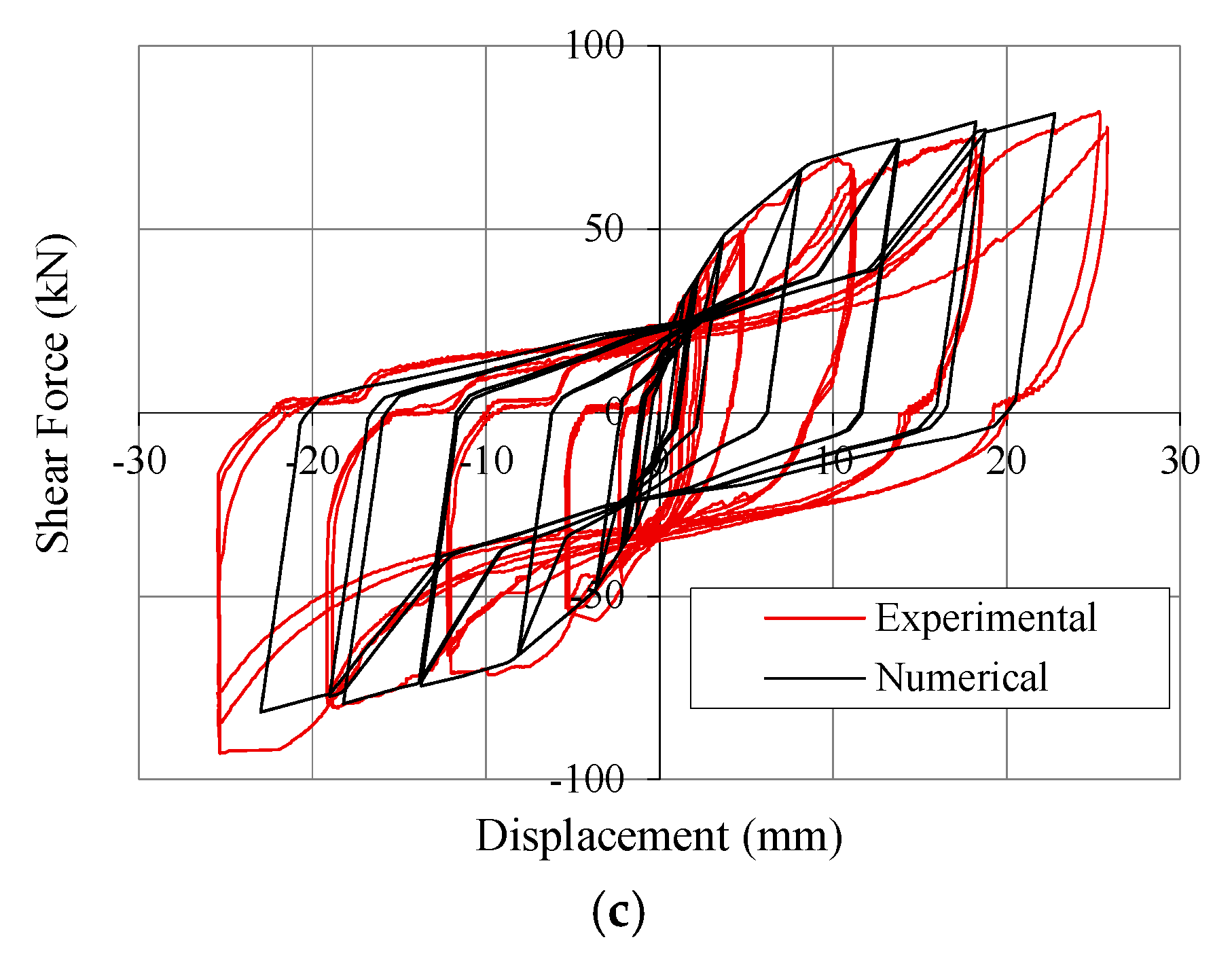
4.3. Case-Study Building and Design Criteria
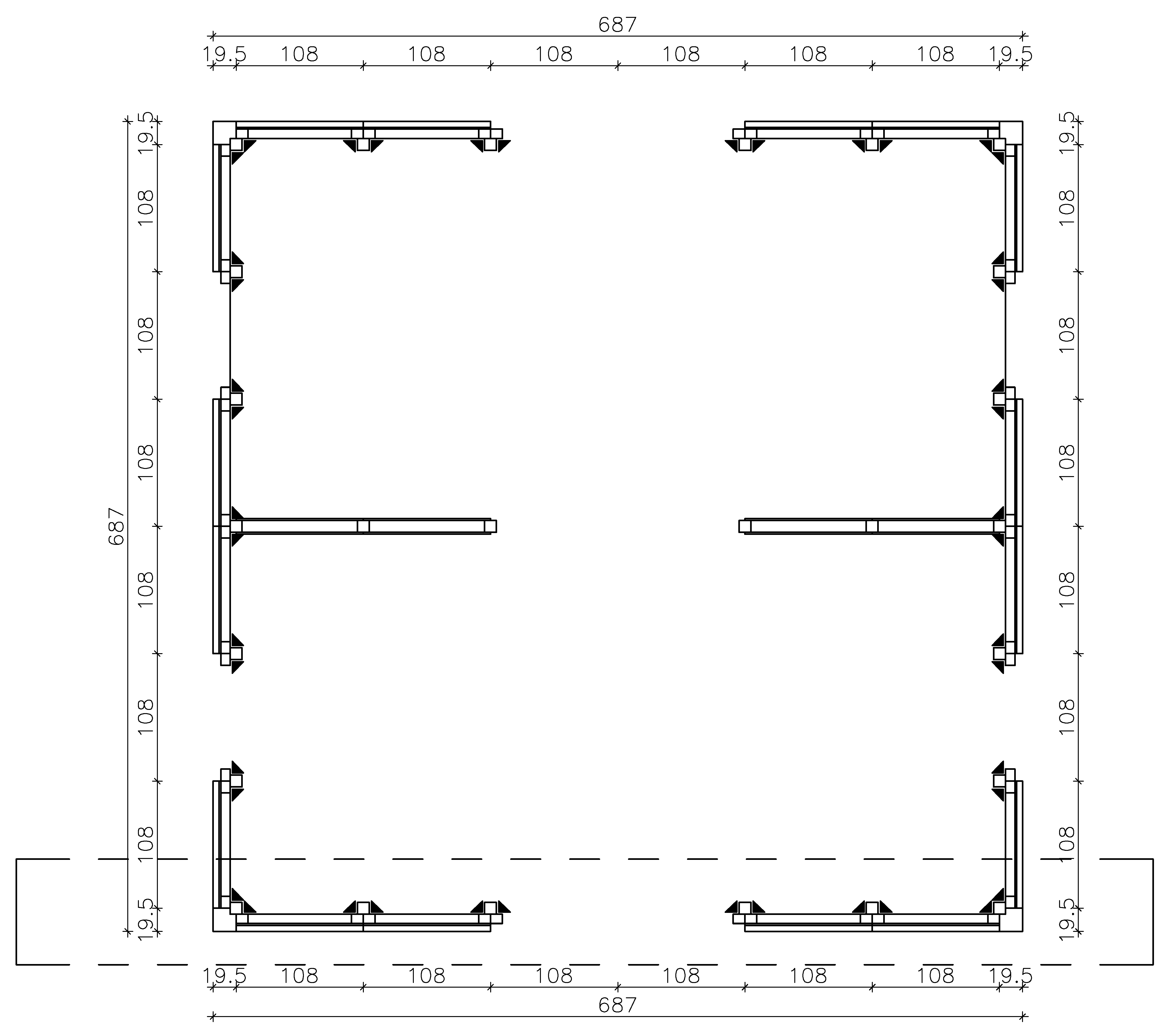
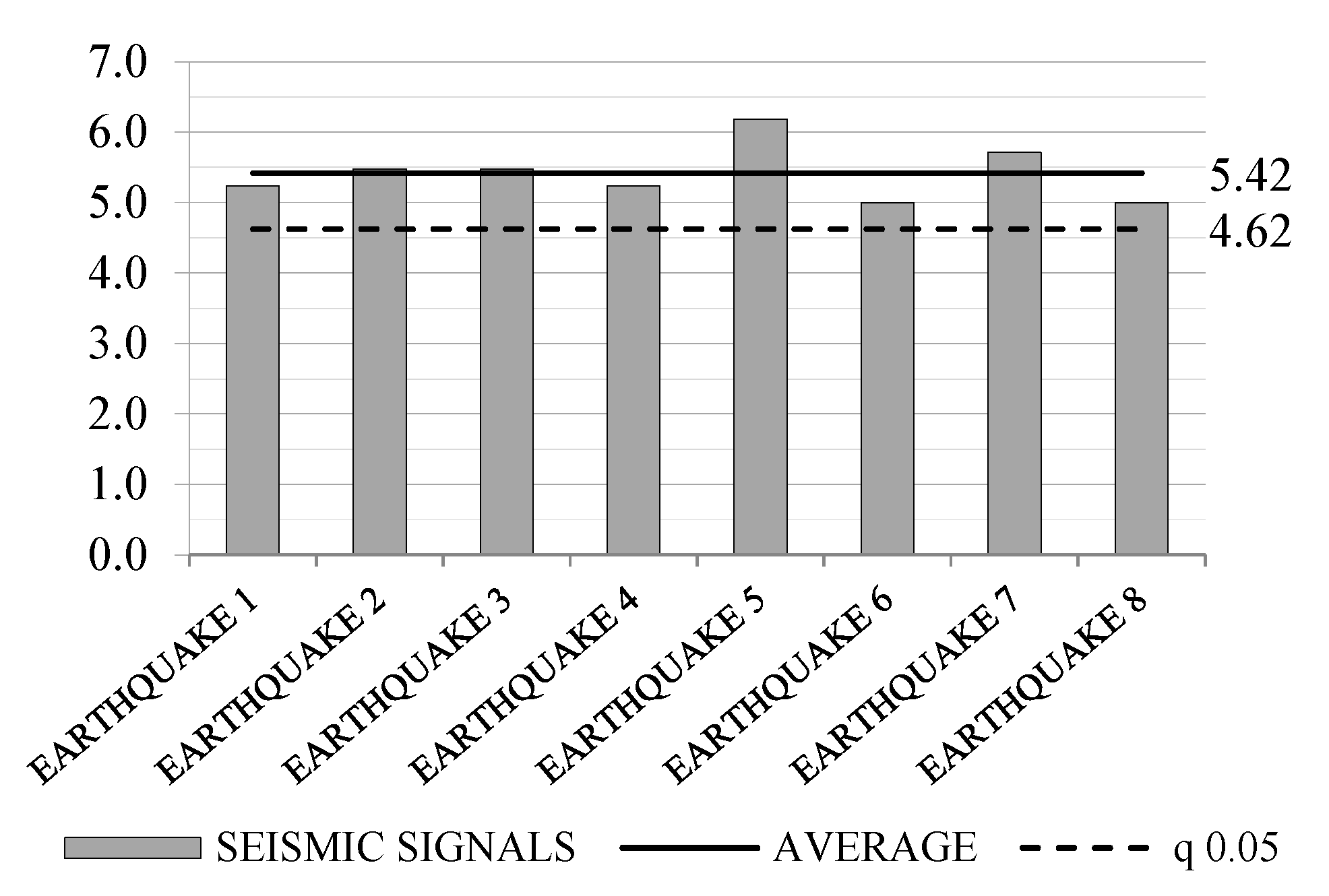
4.4. Evaluation of q-Factor
| Seismic Signals | |||||||
|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
| 5.2 | 5.5 | 5.5 | 5.2 | 6.2 | 5.0 | 5.7 | 5.0 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Karacabeyli, E.; Ceccotti, A. Seismic force modification factor for design of multi-storey wood-frame platform construction. In Proceedings of the 30th Meeting of Working Commission W18-Timber Structures, Vancouver, BC, Canada; 25–28 August 1997. [Google Scholar]
- Källsner, B.; Girhammar, U.A. Analysis of fully anchored light-frame timber shear walls—Elastic model. Mater. Struct. 2009, 42, 301–320. [Google Scholar] [CrossRef]
- Casagrande, D.; Rossi, S.; Sartori, T.; Tomasi, R. Proposal of an analytical procedure and a simplified numerical model for elastic response of single-storey timber shear-walls. Constr. Build. Mater. 2015. [Google Scholar] [CrossRef]
- Casagrande, D.; Rossi, S.; Tomasi, R; Mischi, G. A predictive analytical model for the elasto-plastic behavior of a light timber-frame shear-wall. Constr. Build. Mater. 2015. [Google Scholar] [CrossRef]
- Germano, F.; Metelli, G.; Giuriani, E. Experimental results on the role of sheathing-to-frame and base connections of a European timber framed shear wall. Constr. Build. Mater. 2015, 80, 315–328. [Google Scholar] [CrossRef]
- Van De Lindt, J.W.; Pei, S.; Pryor, S.E.; Shimizu, H.; Isoda, H. Experimental seismic response of a full-scale six-story light-frame wood building. J. Struct. Eng. 2010, 136, 1262–1272. [Google Scholar] [CrossRef]
- Gattesco, N.; Boem, I. Seismic performances and behavior factor of post-and-beam timber buildings braced with nailed shear walls. Eng. Struct. 2015, 100, 674–685. [Google Scholar] [CrossRef]
- De la Roche, I.; Dangerfield, J.A.; Karacabeyli, E. Wood products and sustainable construction. N. Z. Timber Des. J. 2003, 12, 9–13. [Google Scholar]
- Khorasani, Y. Feasibility study of hybrid wood steel structures. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, April 2011. [Google Scholar]
- Stiemer, S.; Tesfamariam, S.; Karacabeyli, E.; Propovski, M. Development of steel-wood hybrid systems for buildings under dynamic loads. In Proceedings of the 7th International Specialty Conference on Behavior of Steel Structures in Seismic Areas (STESSA), Santiago, Chile, 9–11 January 2012.
- Dickof, C.; Stiemer, S.F.; Bezabeh, M.A.; Tesfamariam, S. CLT—Steel hybrid system: Ductility and overstrength values based on static pushover analysis. J. Perform. Constr. Facil. 2014, 28. [Google Scholar] [CrossRef]
- Zhang, X.; Fairhurst, M.; Tannert, T. Ductility estimation for a novel timber–steel hybrid system. J. Struct. Eng. 2015. [Google Scholar] [CrossRef]
- Li, Z.; He, M.; Lam, F.; Li, M.; Ma, R.; Ma, Z. Finite element modeling and parametric analysis of timber–steel hybrid structures. Struct. Design Tall Spec. Build. 2014, 23, 1045–1063. [Google Scholar] [CrossRef]
- He, M.; Li, Z.; Lam, F.; Ma, R.; Ma, Z. Experimental investigation on lateral performance of timber-steel hybrid shear wall systems. J. Struct. Eng. 2013. [Google Scholar] [CrossRef]
- Uang, C.; Gatto, K. Effects of finish materials and dynamic loading on the cyclic response of woodframe shearwalls. J. Struct. Eng. 2003, 129, 1394–1402. [Google Scholar] [CrossRef]
- Tomazevic, M. Earthquake-Resistant Design of Masonry Buildings, 1st ed.; Imperial College Press: London, UK, 1999; pp. 221–222. [Google Scholar]
- Zisi, N. The Influence of Brick Veneer on Racking Behavior of Light Frame Wood Shear Walls. Ph.D. Thesis, University of Tennessee, Knoxville, Tennessee, August 2009. [Google Scholar]
- Zisi, N.V.; Bennett, R.M. Shear behavior of corrugated tie connections in anchored brick veneer–wood frame wall systems. J. Mater. Civil Eng. 2010, 23, 120–130. [Google Scholar] [CrossRef]
- Filiatrault, A.; Christovasilis, I.P.; Wanitkorkul, A.; van de Lindt, J.W. Experimental seismic response of a full-scale light-frame wood building. J. Struct. Eng. 2010, 136, 246–254. [Google Scholar] [CrossRef]
- Pozza, L.; Scotta, R.; Trutalli, D.; Polastri, A. Behavior factor for innovative massive timber shear walls. Bull. Earthq. Eng. 2015. [Google Scholar] [CrossRef]
- Van De Lindt, J. Evolution of wood shear wall testing, modeling, and reliability analysis: Bibliography. Pract. Period. Struct. Design Constr. 2004, 9, 44–53. [Google Scholar] [CrossRef]
- Ellingwood, B.R.; Rosowsky, D.V.; Pang, W. Performance of light-frame wood residential construction subjected to earthquakes in regions of moderate seismicity. J. Struct. Eng. 2008, 134, 1353–1363. [Google Scholar] [CrossRef]
- Kirkham, W.J.; Gupta, R.; Miller, T.H. State of the art: Seismic behavior of wood-frame residential structures. J. Struct. Eng. 2013. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). Timber Structures. Test Methods. Cyclic Testing of Joints Made with Mechanical Fasteners; EN 12512; CEN: Brussels, Belgium, 2001. [Google Scholar]
- Pozza, L.; Scotta, R.; Trutalli, D.; Polastri, A.; Ceccotti, A. Concrete-plated wooden shear walls: structural details, testing and seismic characterization. J. Struct. Eng. 2015. [Google Scholar] [CrossRef]
- European Committee for Standardization (CEN). Oriented Strand Boards (OSB)—Definitions, Classifications and Specifications; EN 300:2006; CEN: Brussels, Belgium, 2006. [Google Scholar]
- European Committee for Standardization (CEN). Structural Timber—Strength Classes; EN 338; CEN: Brussels, Belgium, 2009. [Google Scholar]
- European Committee for Standardization (CEN). Mechanical Properties of Fasteners Made of Carbon Steel and Alloy Steel—Part 1: Bolts, Screws and Studs with Specified Property Classes—Coarse Thread and Fine Pitch Thread; ISO 898-1:2013; CEN: Brussels, Belgium, 2013. [Google Scholar]
- European Committee for Standardization (CEN). Hexagon Washer Head Drilling Screws with Tapping Screw Thread; EN 15480; CEN: Brussels, Belgium, 1999. [Google Scholar]
- German Institute for Standardization. DIN 571: Hexagon Head Wood Screws; German Institute for Standardization: Berlin, Germany, 2010. [Google Scholar]
- European Committee for Standardization (CEN). Eurocode 8—Design of Structures for Earthquake Resistance, Part 1: General Rules, Seismic Actions and Rules for Buildings; EN 1998-1; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Muñoz, W.; Mohammad, M.; Salenikovich, A.; Quenneville, P. Need for a harmonized approach for calculations of ductility of timber assemblies. In Proceedings of the 41st Meeting of the Working Commission W18-Timber Structures, St. Andrews, NB, Canada; 23–29 August 2008. [Google Scholar]
- Foliente, G.C. Issues in seismic performance testing and evaluation of timber structural systems. In Proceedings of the International Wood Engineering Conference, New Orleans, LA, USA; 1996; pp. 29–36. [Google Scholar]
- Foschi, R.O.; Bonac, T. Load slip characteristic for connections with common nails. Wood Sci. Technol. 1977, 9, 118–123. [Google Scholar]
- Gavric, I.; Fragiacomo, M.; Ceccotti, A. Cyclic behavior of CLT wall systems: Experimental tests and analytical prediction models. J. Struct. Eng. 2015. [Google Scholar] [CrossRef]
- Pozza, L.; Scotta, R.; Trutalli, D.; Pinna, M.; Polastri, A.; Bertoni, P. Experimental and numerical analyses of new massive wooden shear-wall systems. Buildings 2014, 4, 355–374. [Google Scholar] [CrossRef]
- Ceccotti, A. New technologies for construction of medium-rise buildings in seismic regions: The XLAM case. Struct. Eng. Int. 2008, 18, 156–165. [Google Scholar] [CrossRef]
- Fajfar, P. A nonlinear analysis method for performance based seismic design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Ceccotti, A.; Sandhaas, C. A proposal for a standard procedure to establish the seismic behavior factor q of timber buildings. In Proceedings of the 11th World Conference on Timber Engineering, Riva del Garda, Italy, 20–24 June 2010.
- Open System for Earthquake Engineering Simulation. Available online: http://opensees.berkeley.edu (accessed on 23 October 2015).
- Lowes, L.N.; Altoontash, A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading. J. Struct. Eng. 2003, 129, 1686–1697. [Google Scholar] [CrossRef]
- Ceccotti, A.; Sandhaas, C.; Okabe, M.; Yasumura, M.; Minowa, C.; Kawai, N. SOFIE project—3D shaking table test on a seven-storey full-scale cross-laminated timber building. Earthq. Eng. Struct. Dyn. 2013, 42, 2003–2021. [Google Scholar] [CrossRef]
- Gelfi, P. SIMQKE_GR, Version 2.7. University of Brescia: Italy, 2012. Available online: http://dicata.ing.unibs.it/gelfi (accessed on 23 October 2015).
- European Committee for Standardization (CEN). Eurocode—Basis of Structural Design; EN 1990; CEN: Brussels, Belgium, 2001. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scotta, R.; Trutalli, D.; Fiorin, L.; Pozza, L.; Marchi, L.; De Stefani, L. Light Steel-Timber Frame with Composite and Plaster Bracing Panels. Materials 2015, 8, 7354-7370. https://doi.org/10.3390/ma8115386
Scotta R, Trutalli D, Fiorin L, Pozza L, Marchi L, De Stefani L. Light Steel-Timber Frame with Composite and Plaster Bracing Panels. Materials. 2015; 8(11):7354-7370. https://doi.org/10.3390/ma8115386
Chicago/Turabian StyleScotta, Roberto, Davide Trutalli, Laura Fiorin, Luca Pozza, Luca Marchi, and Lorenzo De Stefani. 2015. "Light Steel-Timber Frame with Composite and Plaster Bracing Panels" Materials 8, no. 11: 7354-7370. https://doi.org/10.3390/ma8115386
APA StyleScotta, R., Trutalli, D., Fiorin, L., Pozza, L., Marchi, L., & De Stefani, L. (2015). Light Steel-Timber Frame with Composite and Plaster Bracing Panels. Materials, 8(11), 7354-7370. https://doi.org/10.3390/ma8115386






