Fabrication of Microdots Using Piezoelectric Dispensing Technique for Viscous Fluids
Abstract
:1. Introduction
| Technique | E-Jet Printer | Aerosol Jet Printing | High-Viscosity Jetting System | Piezoelectric Inkjet Printing |
|---|---|---|---|---|
| Dispensing components | Printhead with conducting nozzle and DC power | Ultrasonic atomizer and deposition head | Micro-valve printhead | Piezoelectric printhead |
| Nozzle size | 0.3–200 μm | 100–200 μm | 50–400 μm | 10–100 μm |
| Fluid characterization | Electrically charged fluid | Major solvent with high boiling point/low vapor pressure (compared to those of ethylene glycol) | No limitation | No limitation |
| Mechanism | Electrohydrodynamic | Atomization | Mechanical and pneumatic forces | Mechanical force |
| Recommended rheology | <18 cP 30–48 mN·m−1 | 0.7–5 cP | 20–100,000 cP | < 40 cP 20–70 mN·m−1 |
| Printing feature size | 240 nm–210 μm | 5–150 μm | 10–150 μm, typically 50 μm | 30–300 μm |
2. Experimental Setup
2.1. Experimental Apparatus
2.2. Preparation of Fluid
2.3. Experimental Conditions

3. Mathematical Method
4. Results and Discussion
4.1. Liquid Column Formation
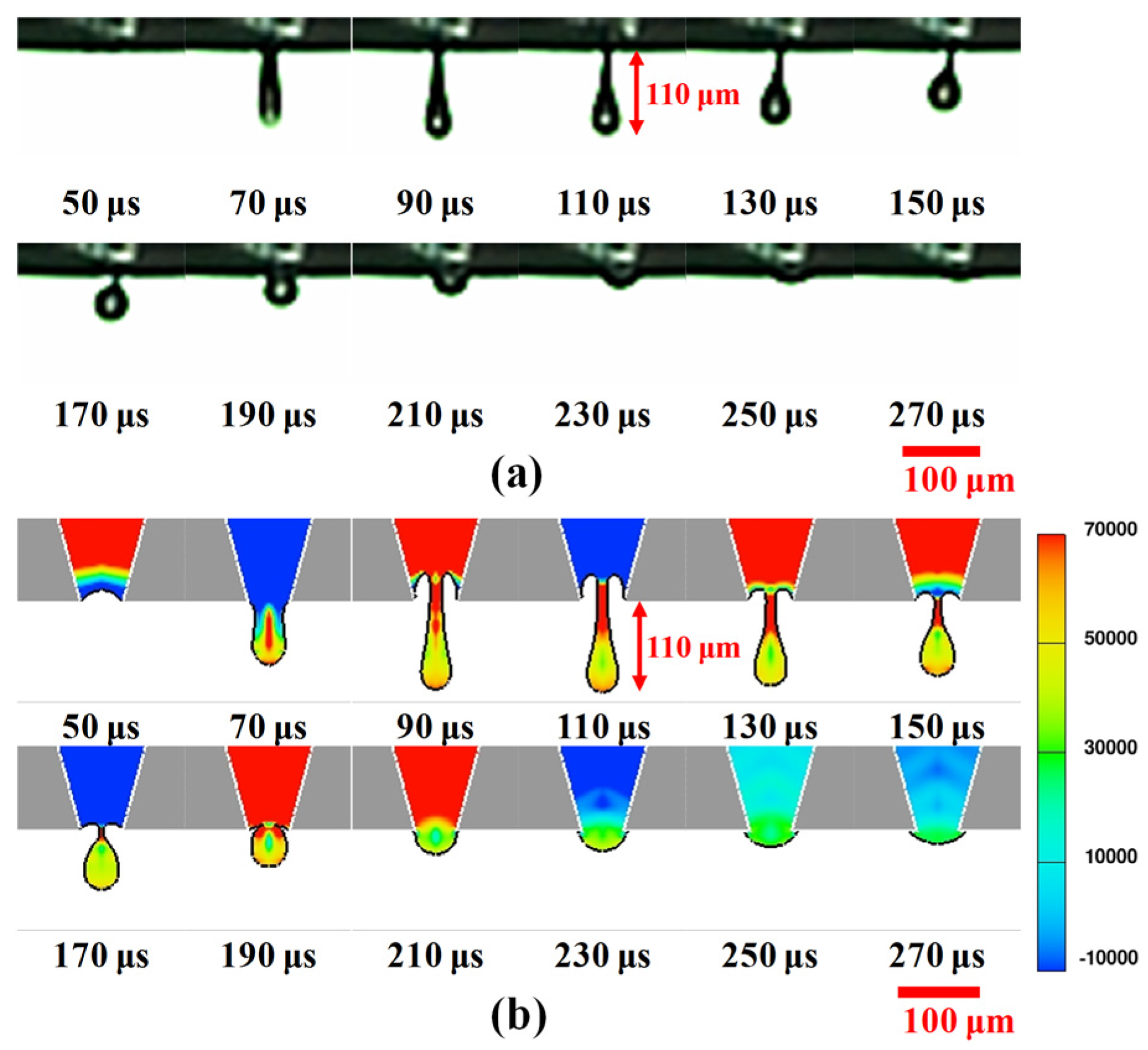
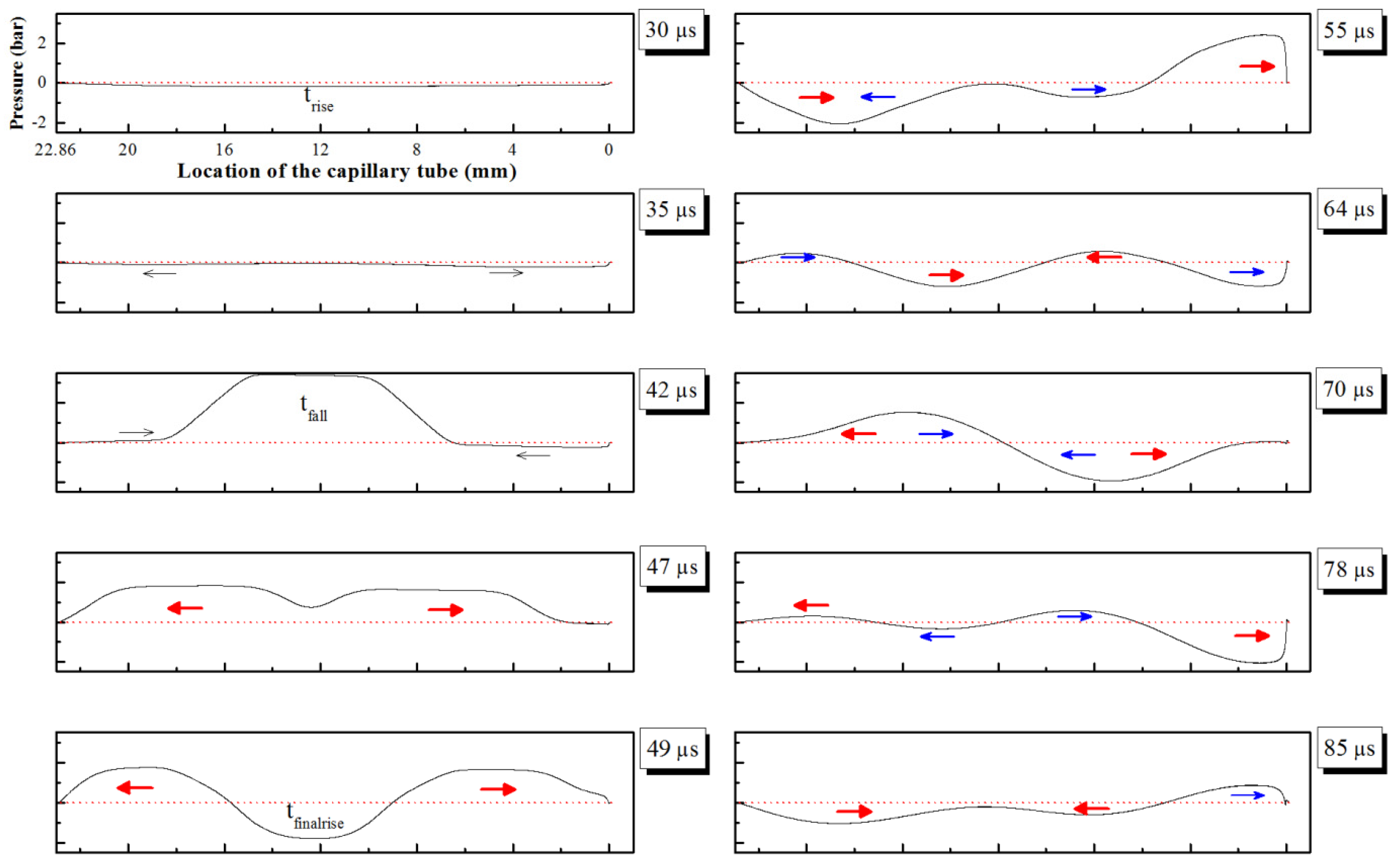
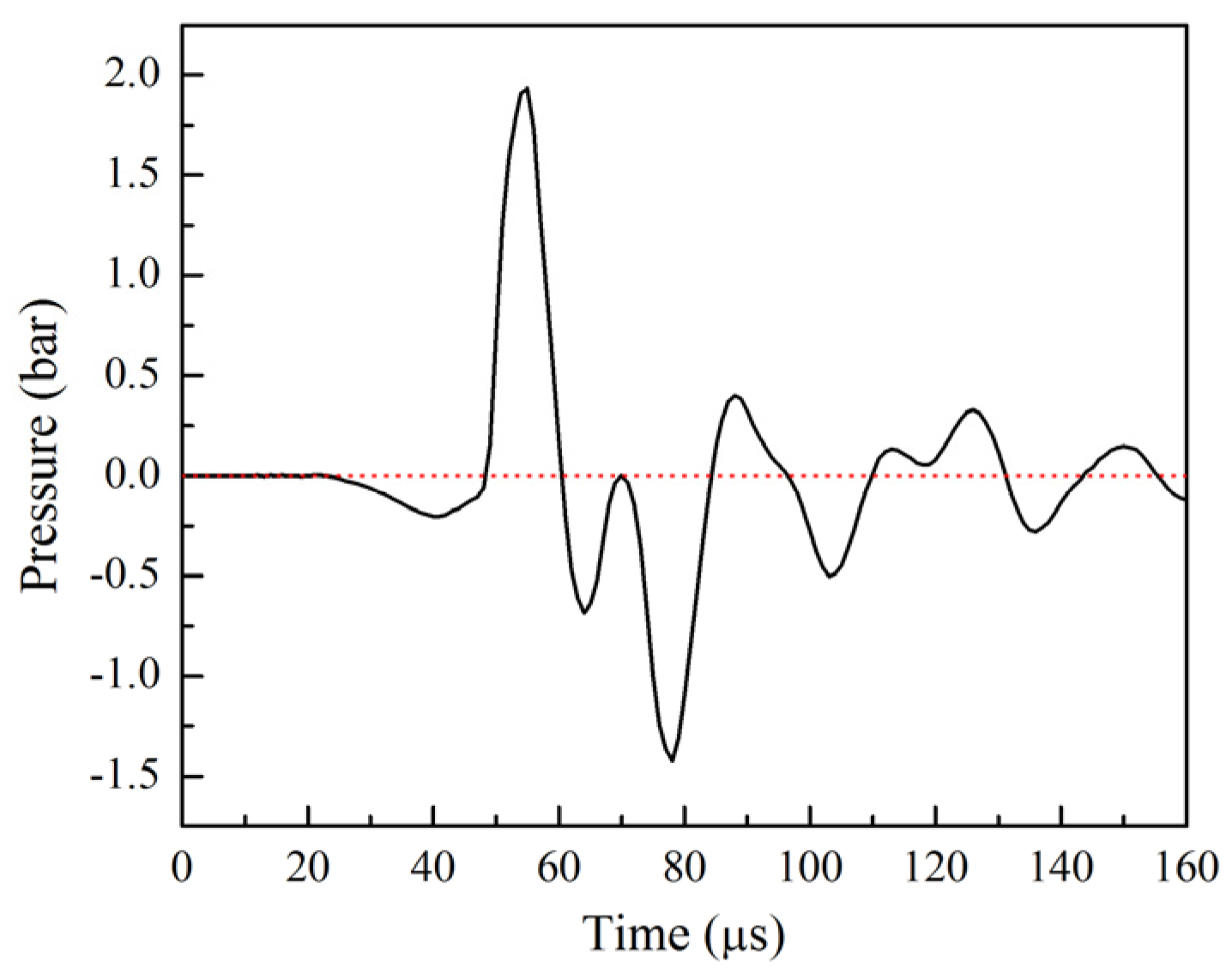
4.2. Analysis of Pressure Distribution Along Capillary Tube
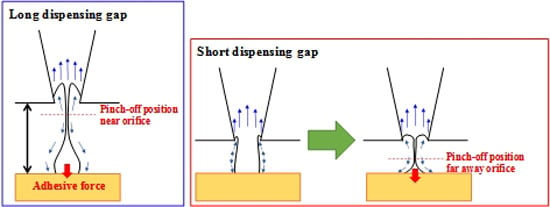
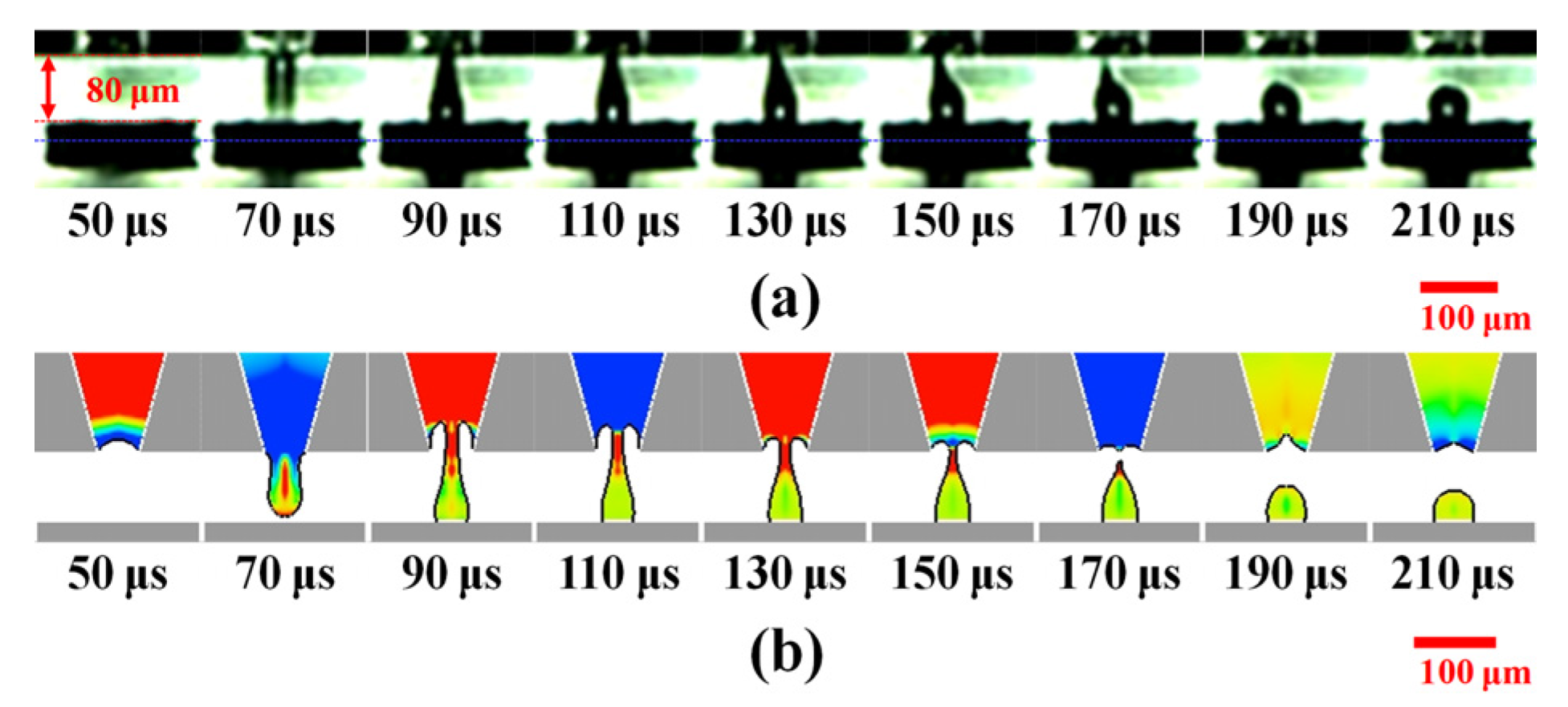
4.3. Fabrication of Micro Dots
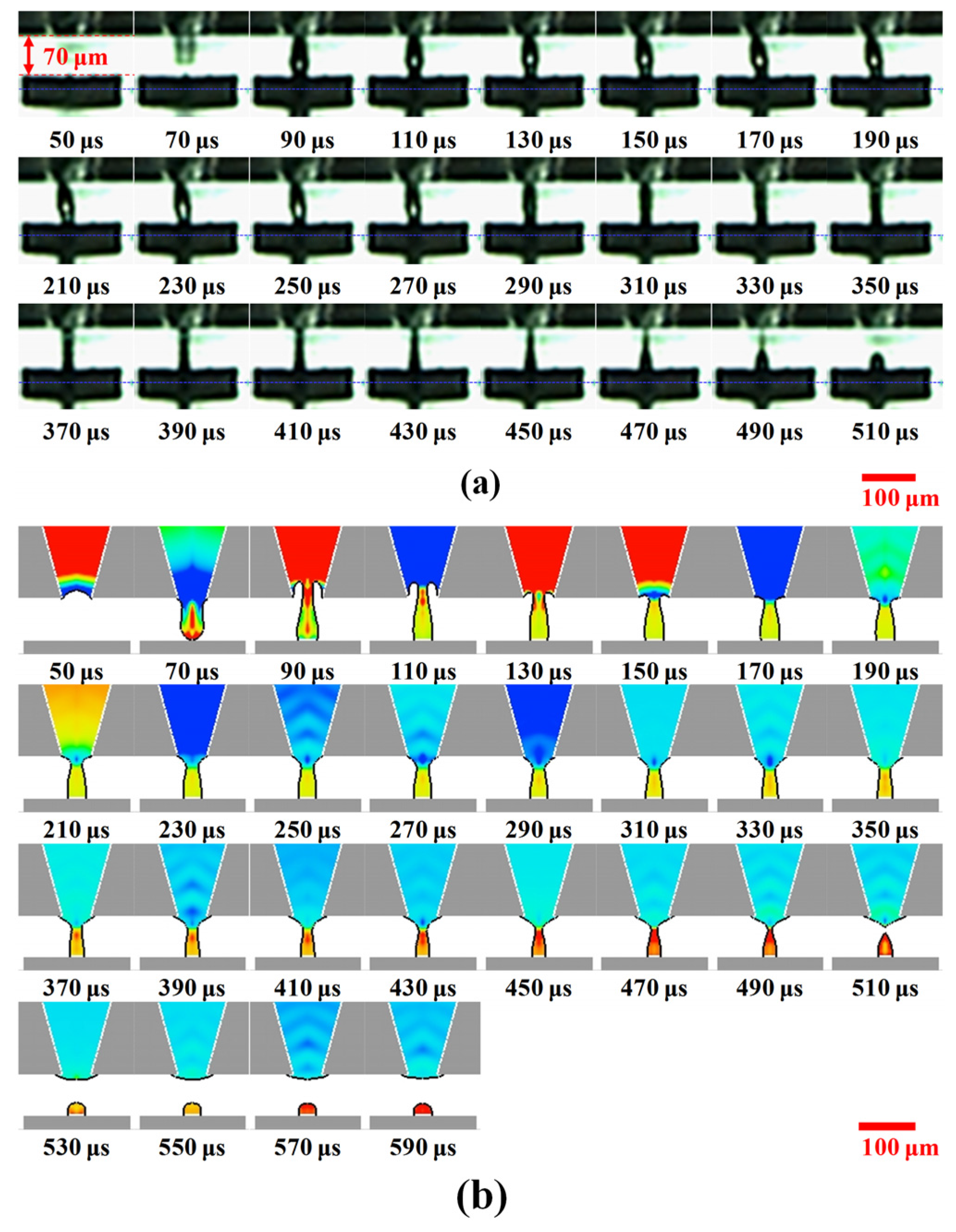
4.4. Fluid Dispensing Mechanism
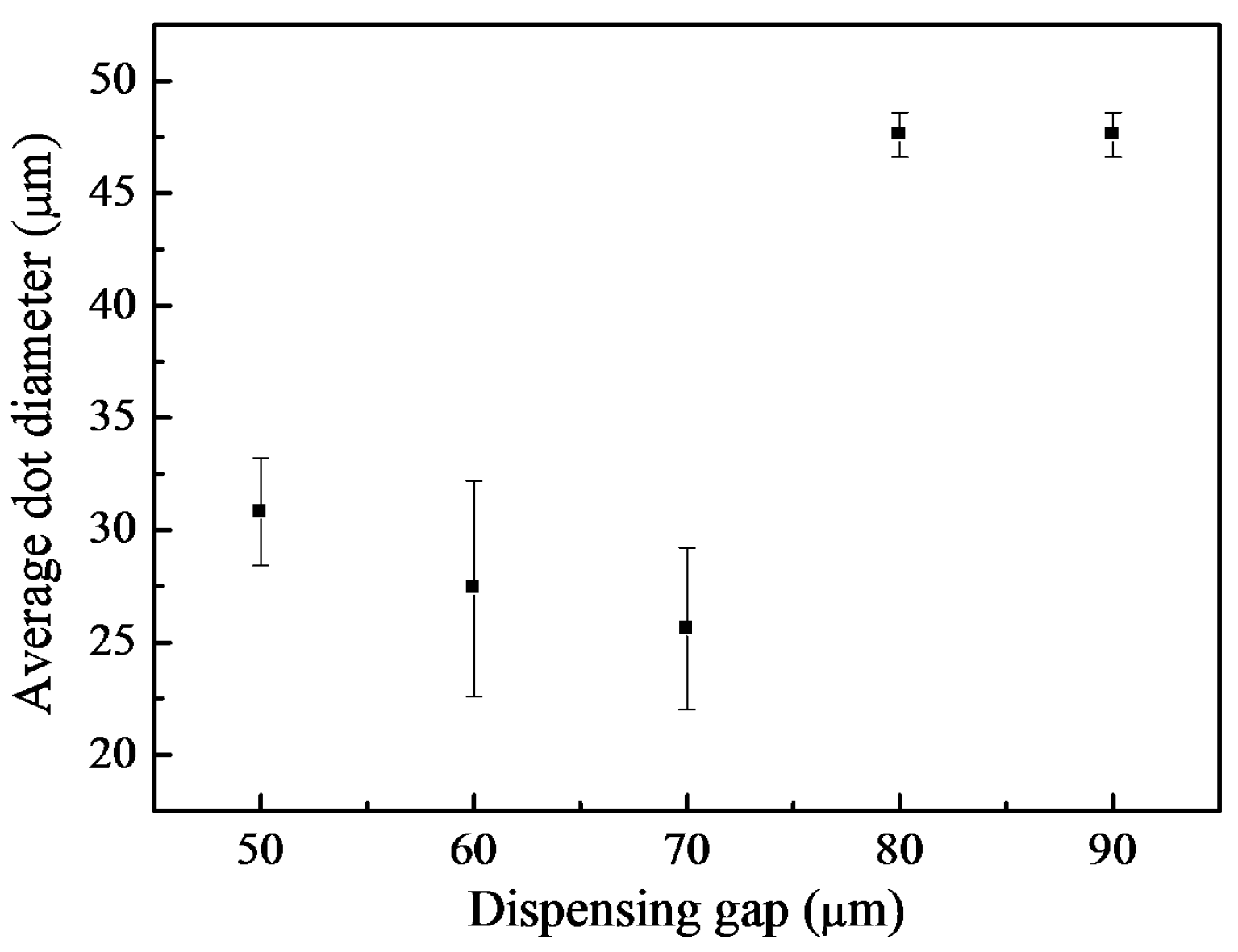
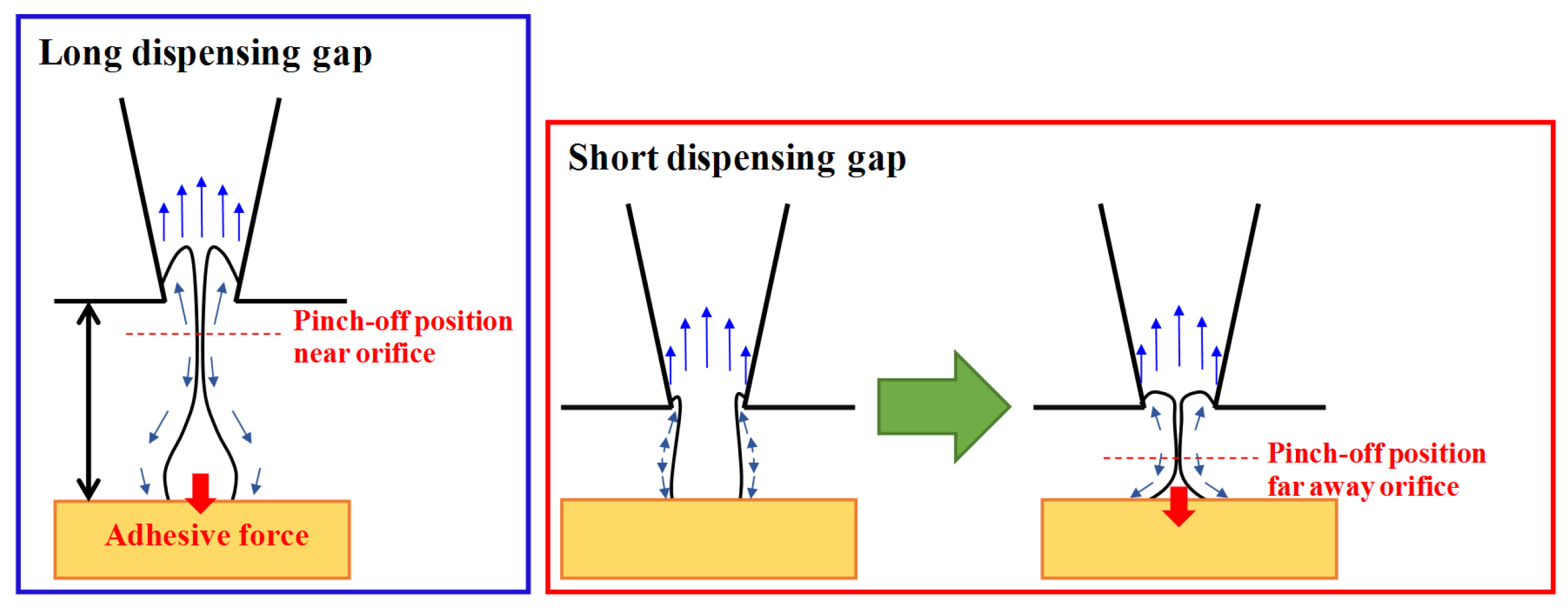
5. Conclusions
- The liquid column of the aqueous glycerol solution was extruded by the lower actuation pulse obtained with a bipolar waveform.
- The liquid column was directly detached near the orifice for the dispensing gaps of 80 and 90 μm. However, the liquid junction was formed for the dispensing gaps of 50 and 70 μm which were closed to the natural length of 65 μm.
- Dots with a diameter of 48 μm were obtained for dispensing gaps of 80 and 90 μm.
- Microdots with diameters half that of the orifice were fabricated with dispensing gaps of below 70 μm.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tu, K.N. Reliability challenges in 3D IC packaging technology. Microelectron. Reliab. 2011, 51, 517–523. [Google Scholar] [CrossRef]
- Park, J.U.; Hardy, M.; Kang, S.J.; Barton, K.; Adair, K.; Mukhopadhyay, D.K.; Lee, C.Y.; Strano, M.S.; Alleyne, A.G.; Georgiadis, J.G.; et al. High-resolution lectrohydrodynamic jet printing. Nat. Mater. 2007, 6, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Barton, K.; Mishra, S.; Shorter, K.A.; Alleyne, A.; Ferreira, P.; Rogers, J. A desktop electrohydrodynamic jet printing system. Mechatronics 2010, 20, 611–616. [Google Scholar]
- Sutanto, E.; Shigeta, K.; Kim, Y.K.; Graf, P.G.; Hoelzle, D.J.; Barton, K.L.; Alleyne, A.G.; Ferreira, P.M.; Rogers, J.A. A multimaterial electrohydrodynamic jet (E-jet) printing system. J. Micromech. Microeng. 2012, 22. [Google Scholar] [CrossRef]
- Mahajan, A.; Frisbie, C.D.; Francis, L.F. Optimization of aerosol jet printing for high-resolution, high-aspect ratio silver lines. ACS Appl. Mater. Interfaces 2013, 5, 4856–4864. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ng, J.H.; Fuh, Y.H.; Wong, Y.S.; Loh, H.; Xu, Q. Comparison of micro-dispensing performance between micro-valve and piezoelectric printhead. Microsyst. Technol. 2009, 15, 1437–1448. [Google Scholar]
- Yang, H.; He, Y.; Tuck, C.; Wildman, R.; Ashcroft, I.; Dickens, P.; Hague, R. High Viscosity Jetting System for 3D Reactive Inkjet Printing. In Proceeding of 24th Annual International Solid Freeform Fabrication Symposium: An Additive Manufacturing Conference, Austin, TX, USA, 12–14 August 2013; pp. 505–513.
- Mitzi, D.B. Solution Processing of Inorganic Materials; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 384–386. [Google Scholar]
- Hon, K.K.B.; Li, L.; Hutchings, I.M. Direct writing technology-advances and developments. CIRP Ann Manuf. Technol. 2008, 57, 601–620. [Google Scholar] [CrossRef]
- Lee, E.R. Microdrop Generation; CRC Press: New York, NY, USA, 2003; pp. 59–67. [Google Scholar]
- Tekin, E.; Smith, P.J.; Schubert, U.S. Inkjet printing as a deposition and patterning tool for polymers and inorganic particles. Soft Matter. 2008, 4, 703–713. [Google Scholar] [CrossRef]
- Tsai, M.H.; Hwang, W.S. Effects of pulse voltage on the droplet formation of alcohol and ethylene glycol in a piezoelectric inkjet printing process with bipolar pulse. Mater. Trans. 2008, 49, 331–338. [Google Scholar] [CrossRef]
- Gan, H.Y.; Shan, X.; Eriksson, T.; Lok, B.K.; Lam, Y.C. Reduction of droplet volume by controlling actuating waveforms in inkjet printing for micro-pattern formation. J. Micromech. Microeng. 2009, 19. [Google Scholar] [CrossRef]
- Van Dam, D.B.; Clerc, C.L. Experimental study of the impact of an ink-jet printed droplet on a solid substrate. Phys. Fluids 2004, 16, 3403–3414. [Google Scholar] [CrossRef]
- An, S.M.; Lee, S.Y. Observation of the spreading and receding behavior of a shear-thinning liquid drop impacting on dry solid surfaces. Exp. Therm. Fluid Sci. 2012, 37, 37–45. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar]
- Brown, P.S.; Berson, A.; Talbot, E.L.; Wood, T.J.; Schofield, W.C.E.; Bain, C.D.; Badyal, J.P.S. Impact of picoliter droplets on superhydrophobic surfaces with ultralow spreading ratios. Langmuir 2011, 27, 13897–13903. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.U.; Basaran, O.A. A new method for significantly reducing drop radius without reducing nozzle radius in drop-on-demand drop production. Phys. Fluids 2002, 14, L1–L4. [Google Scholar] [CrossRef]
- Tsai, M.H.; Hwang, W.S.; Chou, H.H.; Hsieh, P.H. Effects of pulse voltage on inkjet printing of a silver nanopowder suspension. Nanotechnology 2008, 19. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.J.; Tsai, M.H.; Hwang, W.S.; Wu, J.T.; Hsu, S.L.C.; Chou, H.H. Application of silver nitrate solution and inkjet printing in the fabrication of microstructural patterns on glass substrates. J. Phys. Chem. C 2012, 116, 4612–4620. [Google Scholar] [CrossRef]
- Cheng, N.S. Formula for the viscosity of a glycerol-water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Khossravi, D.; Connors, K. Solvent effects on chemical processes. 3. Surface tension of binary aqueous organic solvents. J. Solution Chem. 1993, 22, 321–330. [Google Scholar] [CrossRef]
- Wijshoff, H. The dynamics of the piezo inkjet printhead operation. Phys. Rep. 2010, 491, 77–177. [Google Scholar]
- Shin, D.Y.; Grassia, P.; Derby, B. Oscillatory incompressible fluid flow in a tapered tube with a free surface in an inkjet print head. J. Fluids Eng. 2005, 127, 98–109. [Google Scholar] [CrossRef]
- Liu, Y.F.; Pai, Y.F.; Tsai, M.H.; Hwang, W.S. Investigation of driving waveform and resonance pressure in piezoelectric inkjet printing. Appl. Phys. A Mater. Sci. Process. 2012, 109, 323–329. [Google Scholar] [CrossRef]
- Dong, H.; Carr, W.W.; Morris, J.F. An experimental study of drop-on-demand drop formation. Phys. Fluids 2006, 18. [Google Scholar] [CrossRef]
- Dong, H.; Carr, W.W.; Morris, J.F. Visualization of drop-on-demand inkjet: Drop formation and deposition. Rev. Sci. Instrum. 2006, 77. [Google Scholar] [CrossRef]
- Fromm, J.E. Numerical calculation of the fluid dynamics of drop-on-demand jets. IBM J. Res. Dev. 1984, 28, 322–333. [Google Scholar] [CrossRef]
- Liu, Y.F.; Tsai, M.H.; Pai, Y.F.; Hwang, W.S. Control of droplet formation by operating waveform for inks with various viscosities in piezoelectric inkjet printing. Appl. Phys. A Mater. Sci. Process. 2013, 111, 509–516. [Google Scholar] [CrossRef]
- Bogy, D.B.; Talke, F. Experimental and theoretical study of wave propagation phenomena in drop-on-demand ink jet devices. IBM J. Res. Dev. 1984, 28, 314–321. [Google Scholar] [CrossRef]
- Chen, L.; Bonaccurso, E. Effects of surface wettability and liquid viscosity on the dynamic wetting of individual drops. Phys. Rev. E 2014, 90. [Google Scholar] [CrossRef]
- Eggers, J. Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 1993, 71, 3458–3460. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Ashgriz, N.; Chandra, S. Droplet generation from pulsed micro-jets. Exp. Therm. Fluid Sci. 2008, 32, 1679–1686. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, H.-L.; Hwang, W.-S.; Wang, J.-K.; Peng, W.-C.; Chen , S.-H. Fabrication of Microdots Using Piezoelectric Dispensing Technique for Viscous Fluids. Materials 2015, 8, 7006-7016. https://doi.org/10.3390/ma8105355
Tsai H-L, Hwang W-S, Wang J-K, Peng W-C, Chen S-H. Fabrication of Microdots Using Piezoelectric Dispensing Technique for Viscous Fluids. Materials. 2015; 8(10):7006-7016. https://doi.org/10.3390/ma8105355
Chicago/Turabian StyleTsai, Ho-Lin, Weng-Sing Hwang, Jhih-Kai Wang, Wen-Chih Peng, and Shin-Hau Chen . 2015. "Fabrication of Microdots Using Piezoelectric Dispensing Technique for Viscous Fluids" Materials 8, no. 10: 7006-7016. https://doi.org/10.3390/ma8105355
APA StyleTsai, H.-L., Hwang, W.-S., Wang, J.-K., Peng, W.-C., & Chen , S.-H. (2015). Fabrication of Microdots Using Piezoelectric Dispensing Technique for Viscous Fluids. Materials, 8(10), 7006-7016. https://doi.org/10.3390/ma8105355