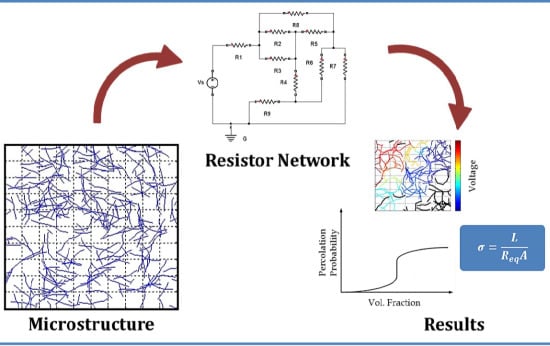
Modeling Percolation in Polymer Nanocomposites by Stochastic Microstructuring
Abstract
:1. Introduction
1.1. Percolation Behavior
1.2. Electrical Conductivity
2. Procedure
2.1. Generating and Analyzing the Microstructure
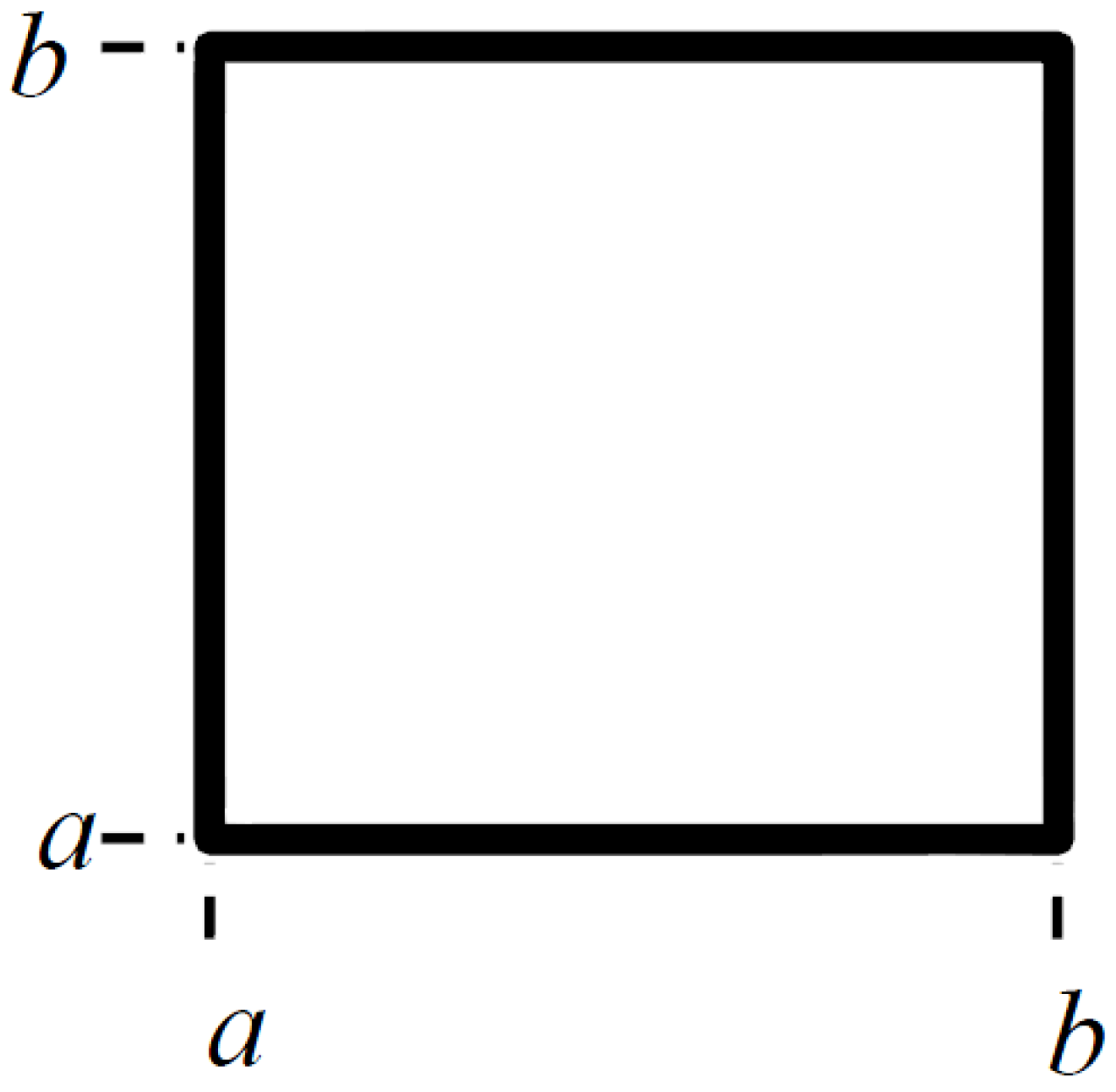
2.1.1. Generating the Geometry
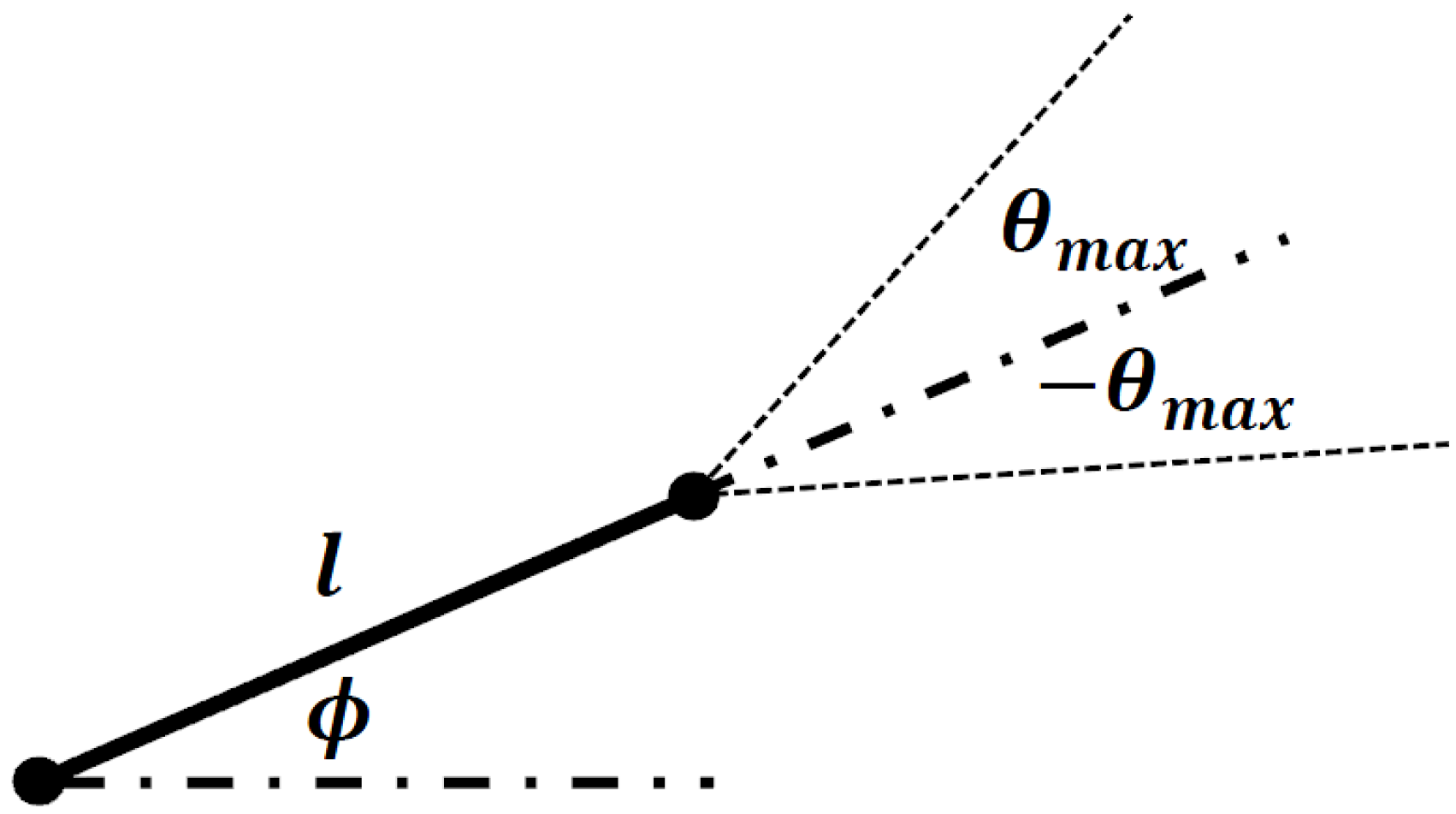
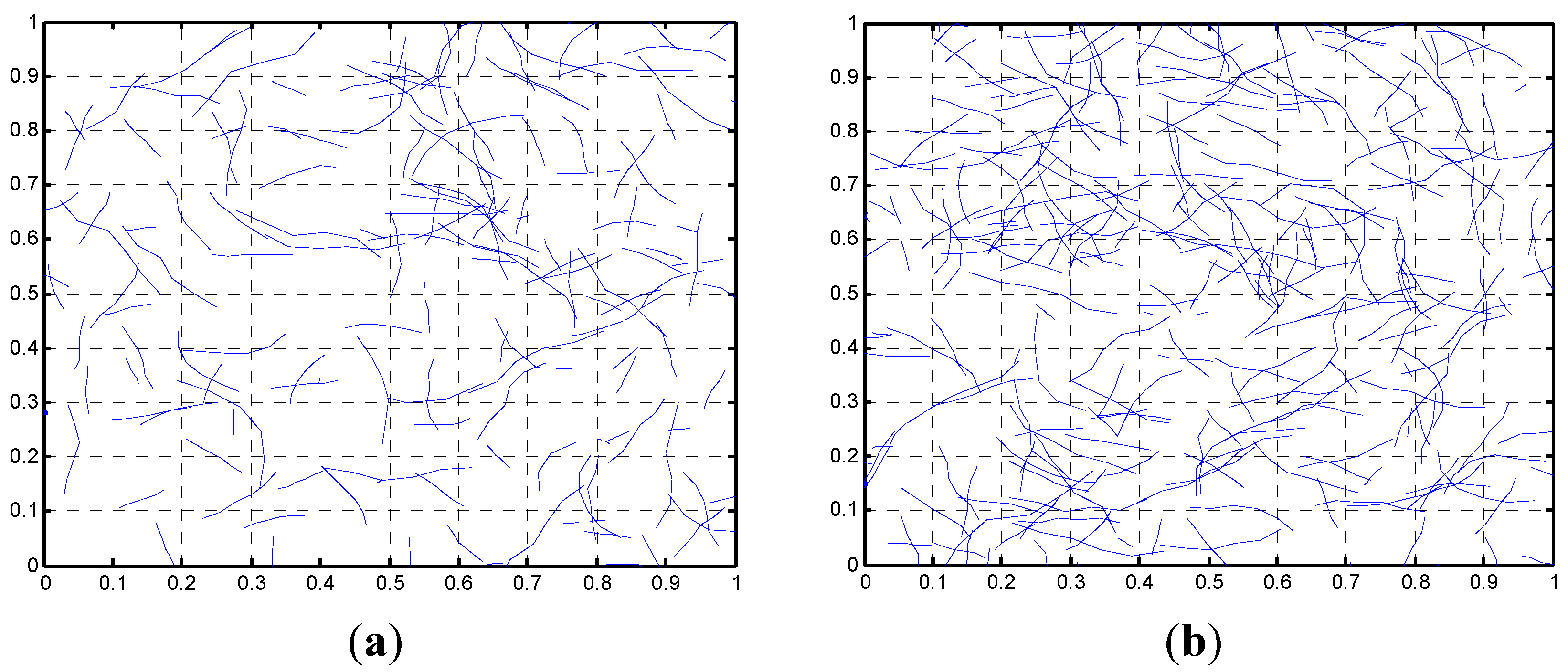
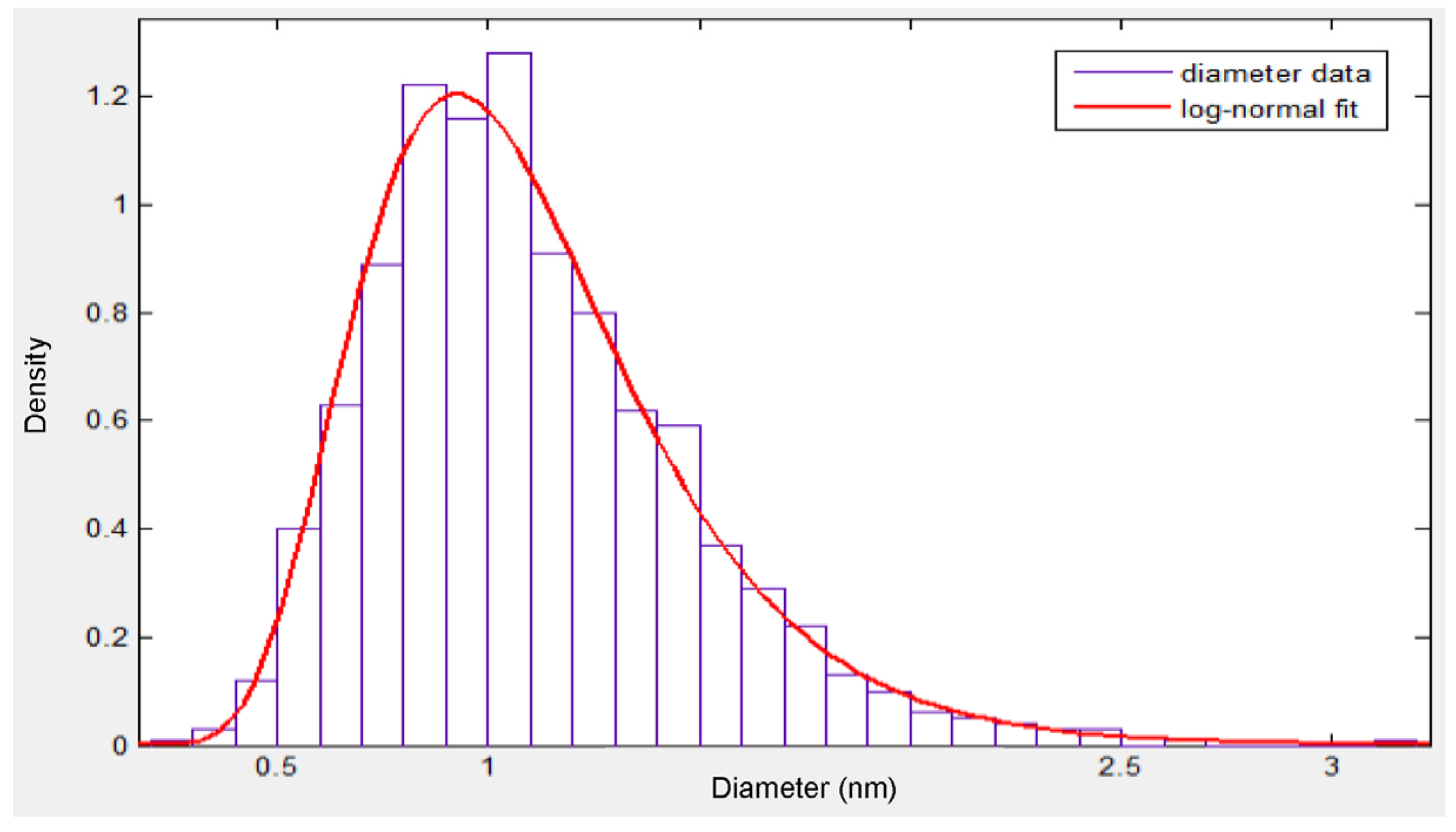
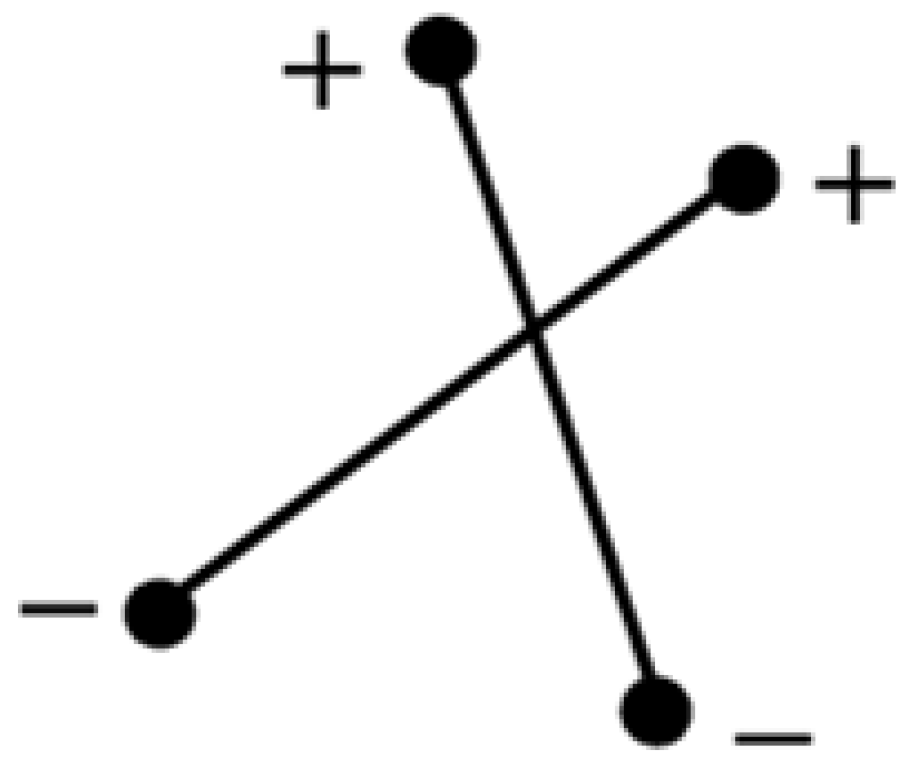
2.1.2. Network Interactions
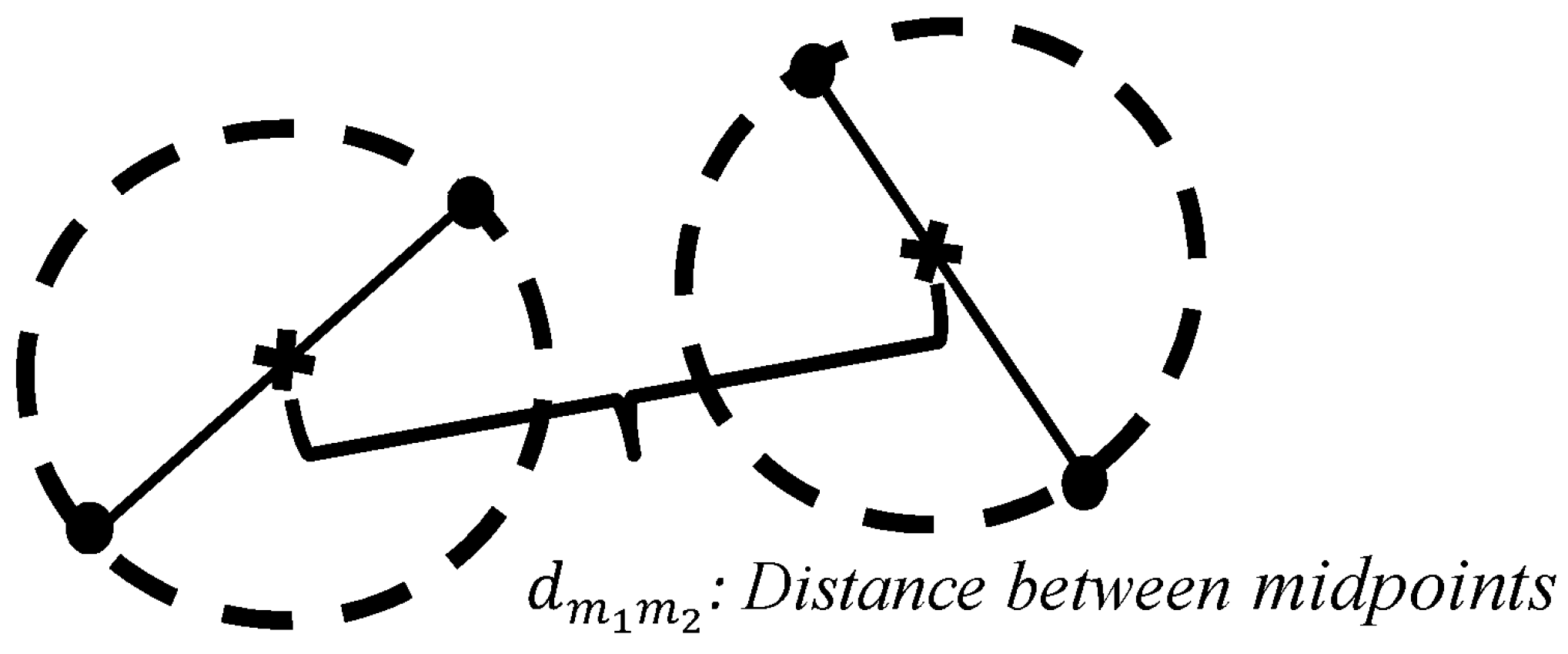
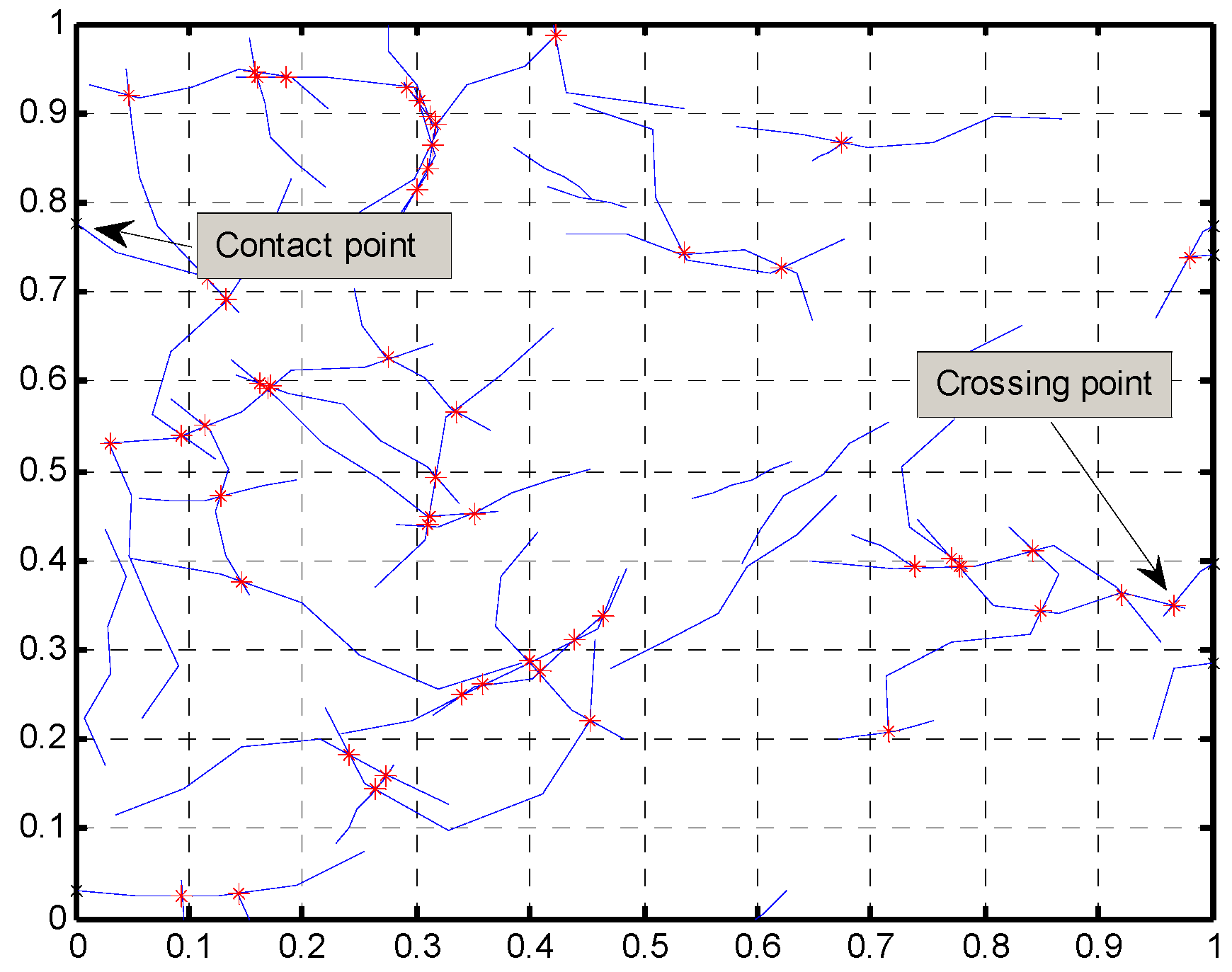
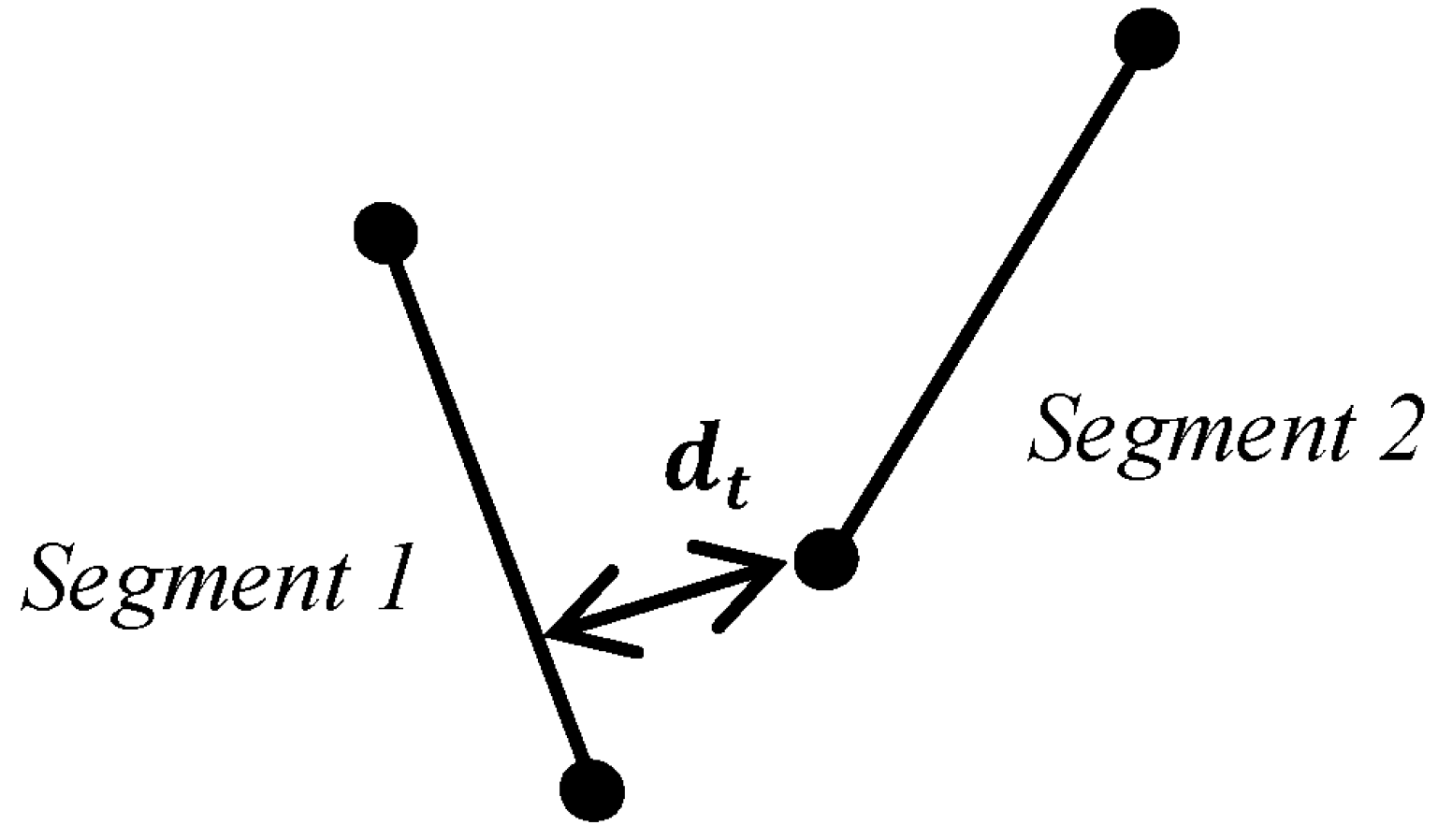
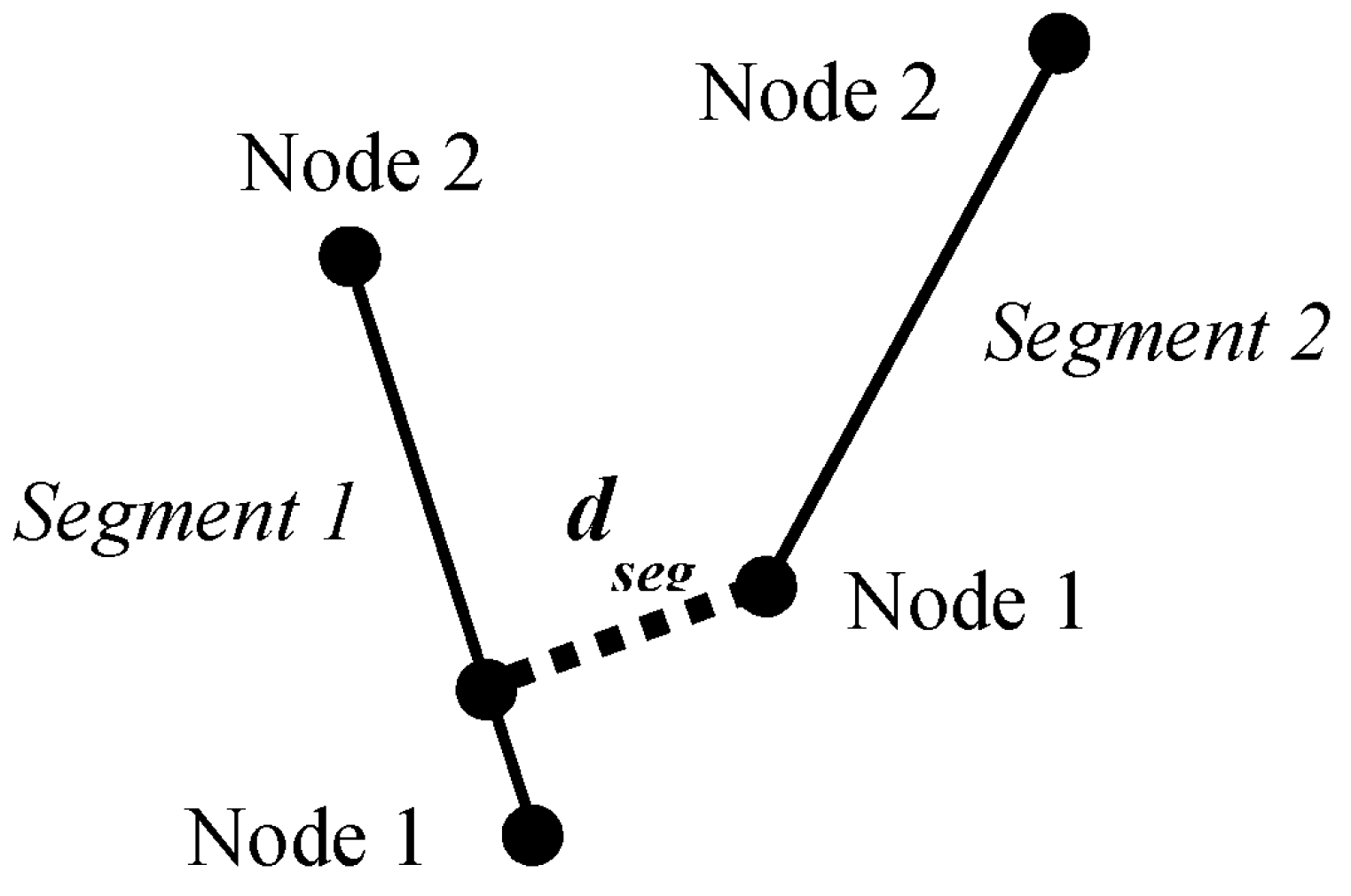
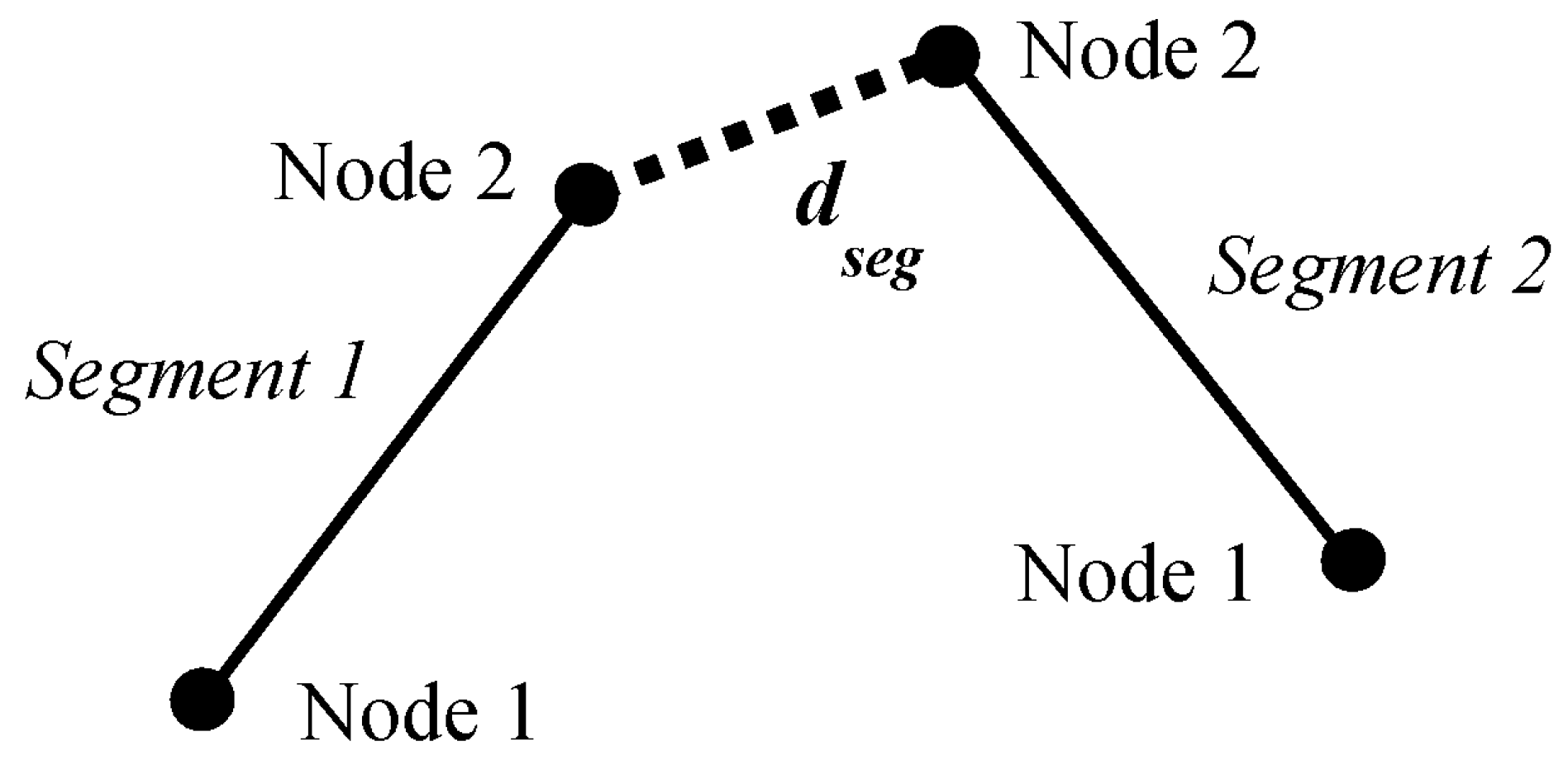
| Matrix Material | Distance (nm) |
|---|---|
| Polyethylene (PE) | 2.00 |
| Polyimide (PI) | 2.50 |
| Polyvinyl Alcohol (PVA) | 2.27 |
2.2. Solution via Node-Voltage Analysis
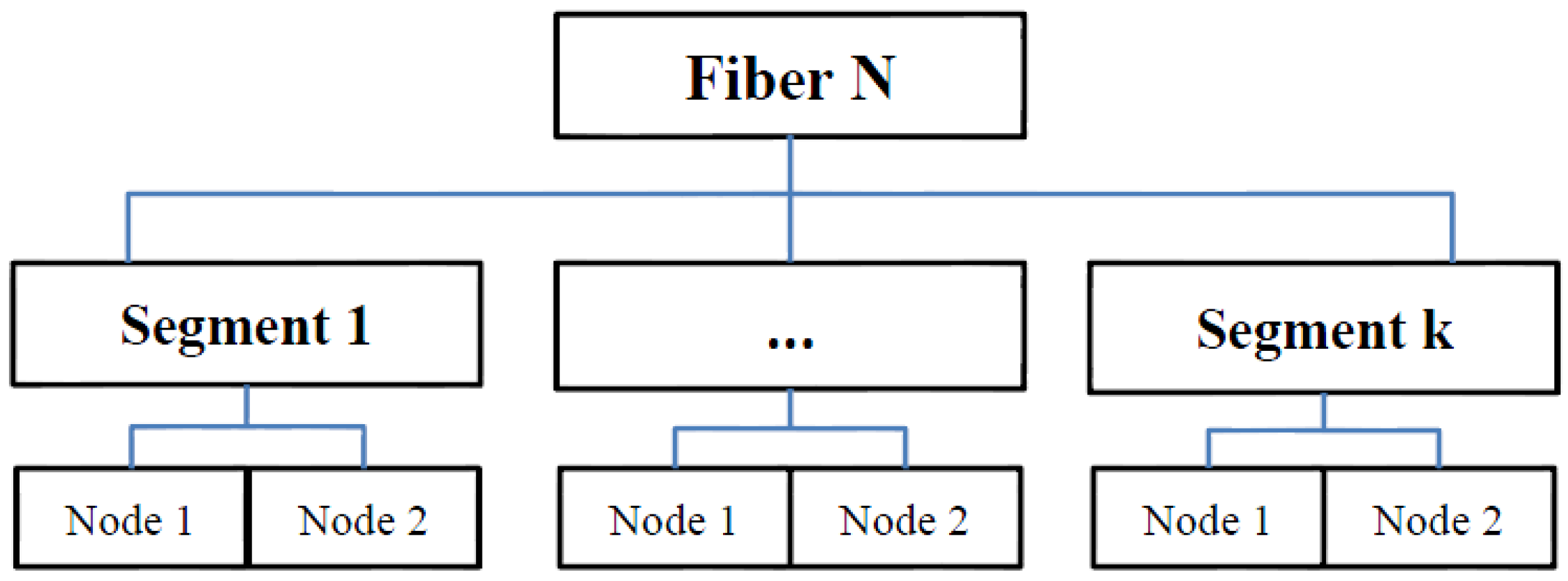
2.2.1. Converting Fiber Network into Set of Equations
| Matrix Material | Barrier Height (eV) |
|---|---|
| Polyethylene (PE) | 4.43 [16] |
| Polyimide (PI) | 4.56 [16] |
| Polyvinyl Alcohol (PVA) | 2.58 [16] |
| Epoxy | 0.5–2.5 [18] |
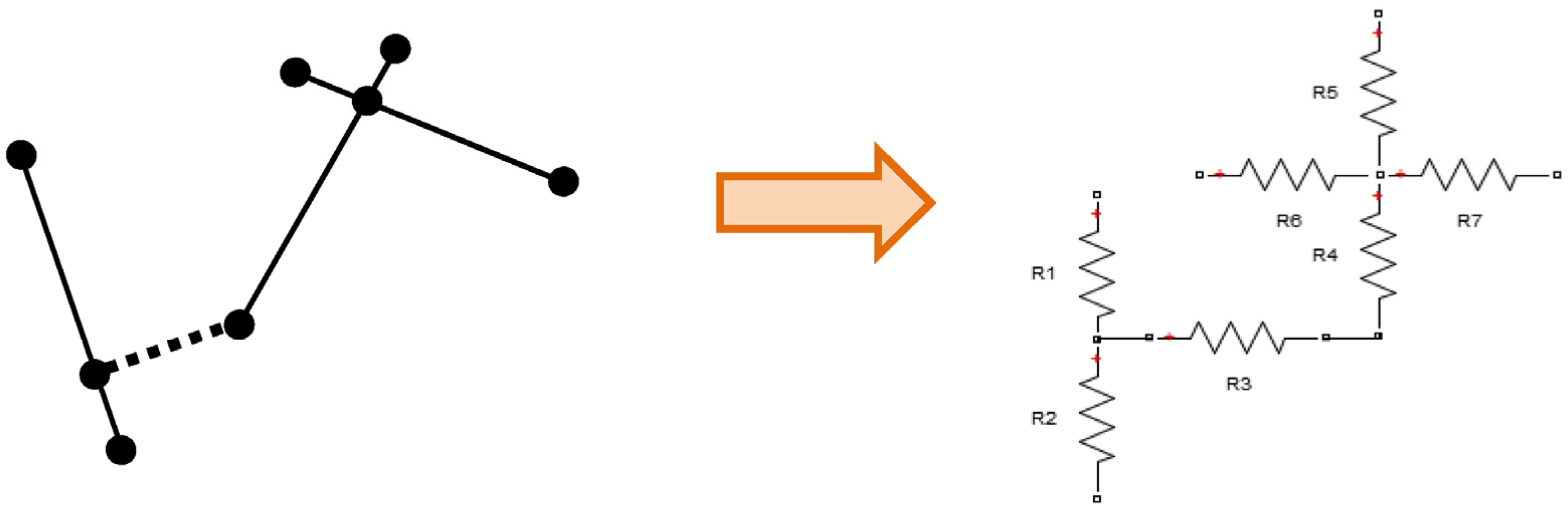
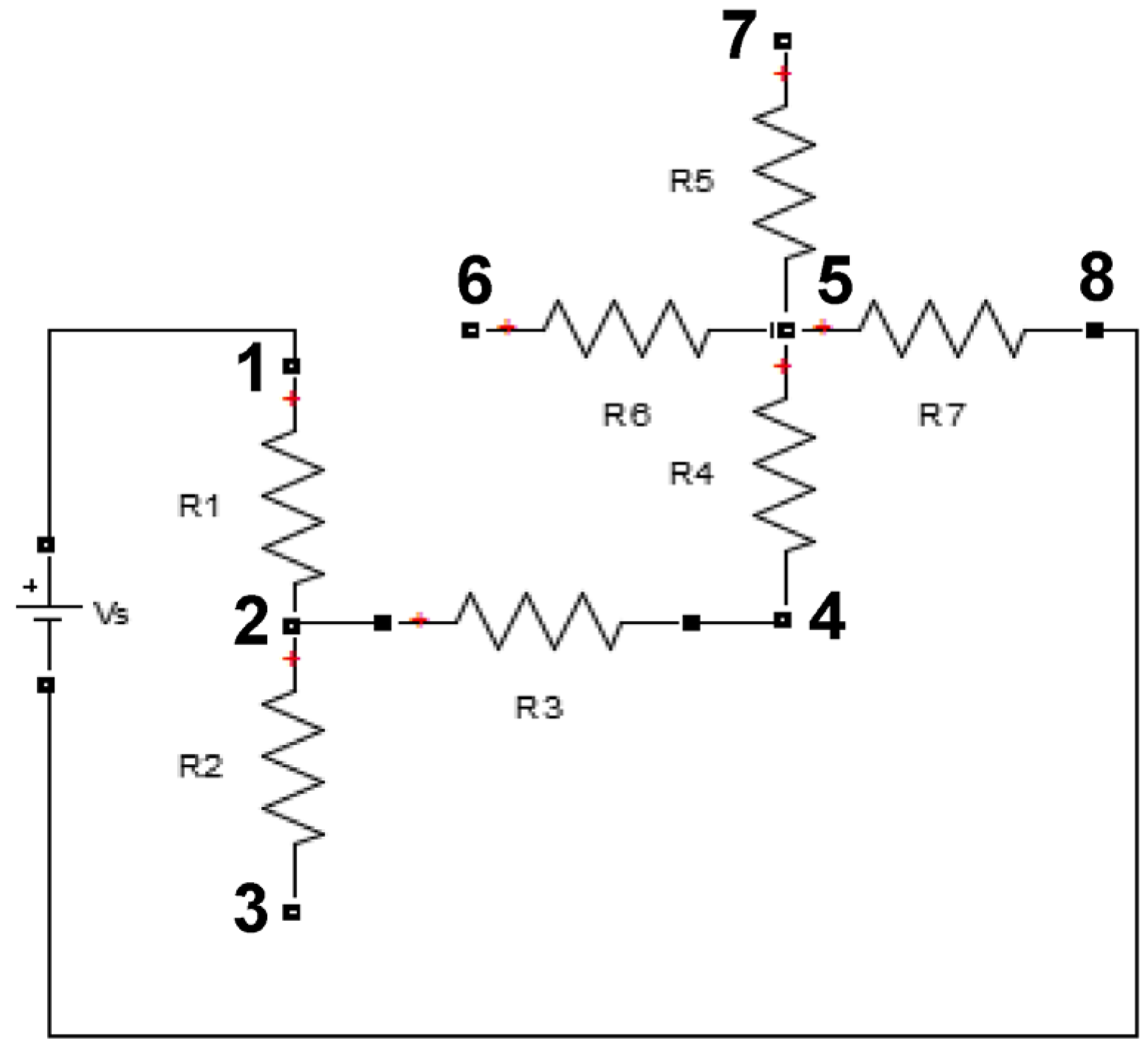
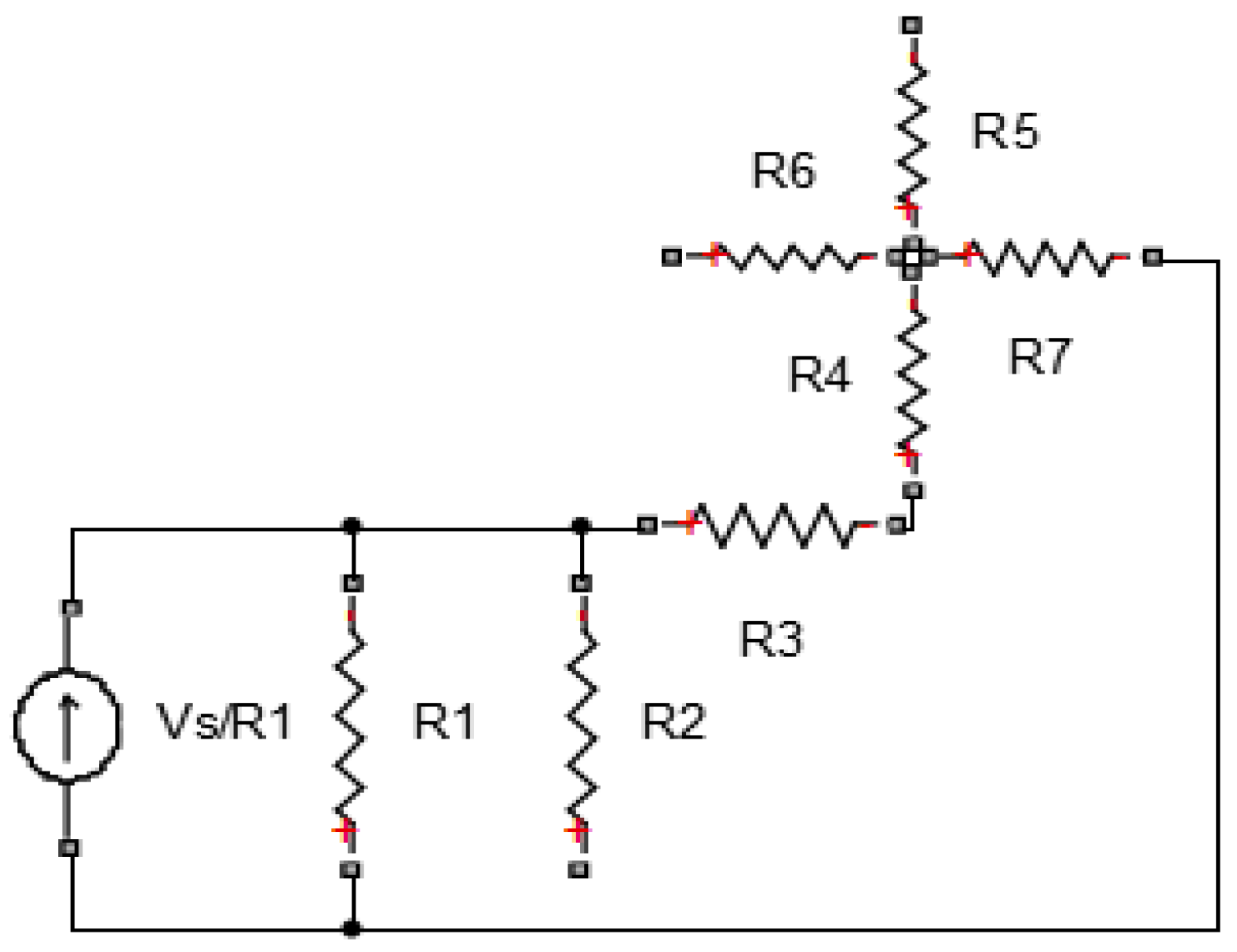
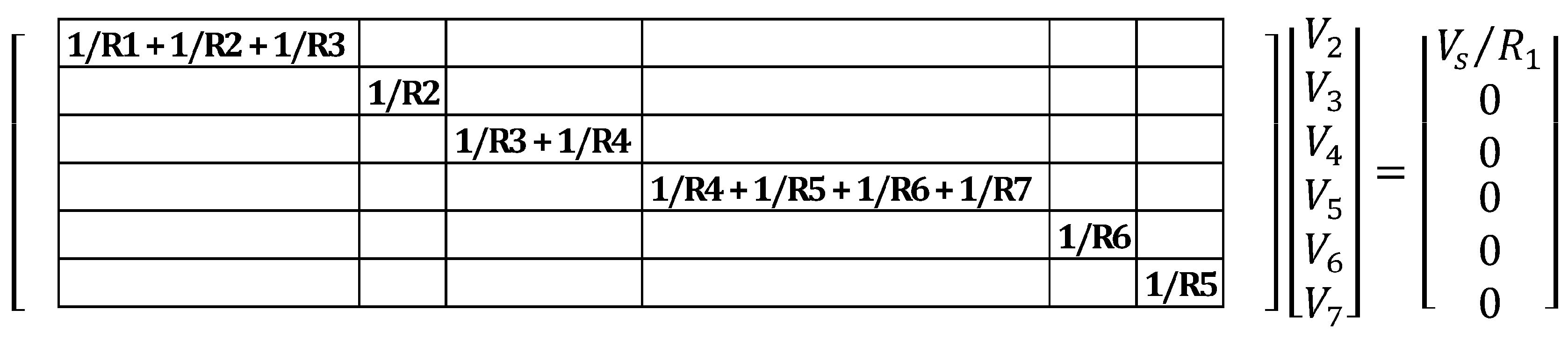
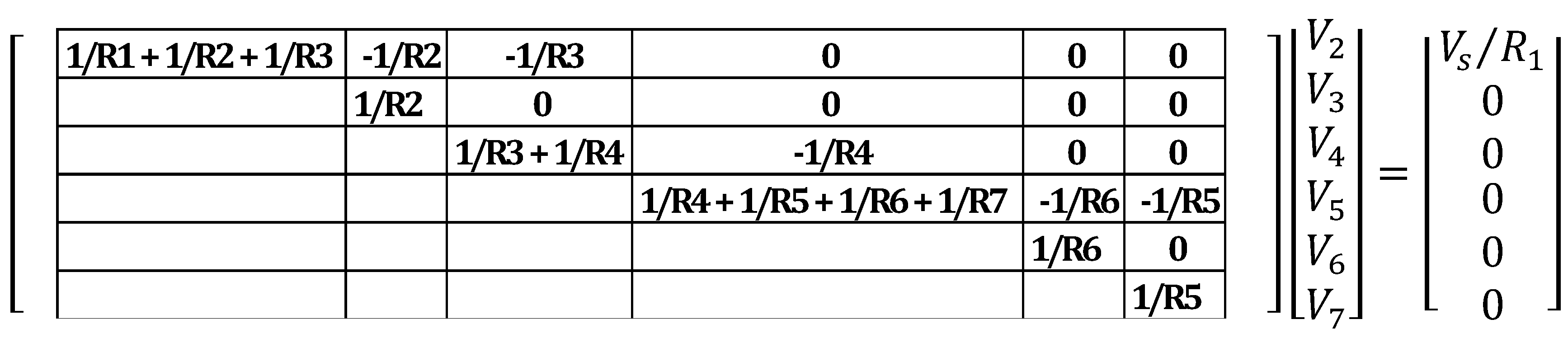

2.2.2. Boundary Conditions
2.2.3. Solving System of Equations
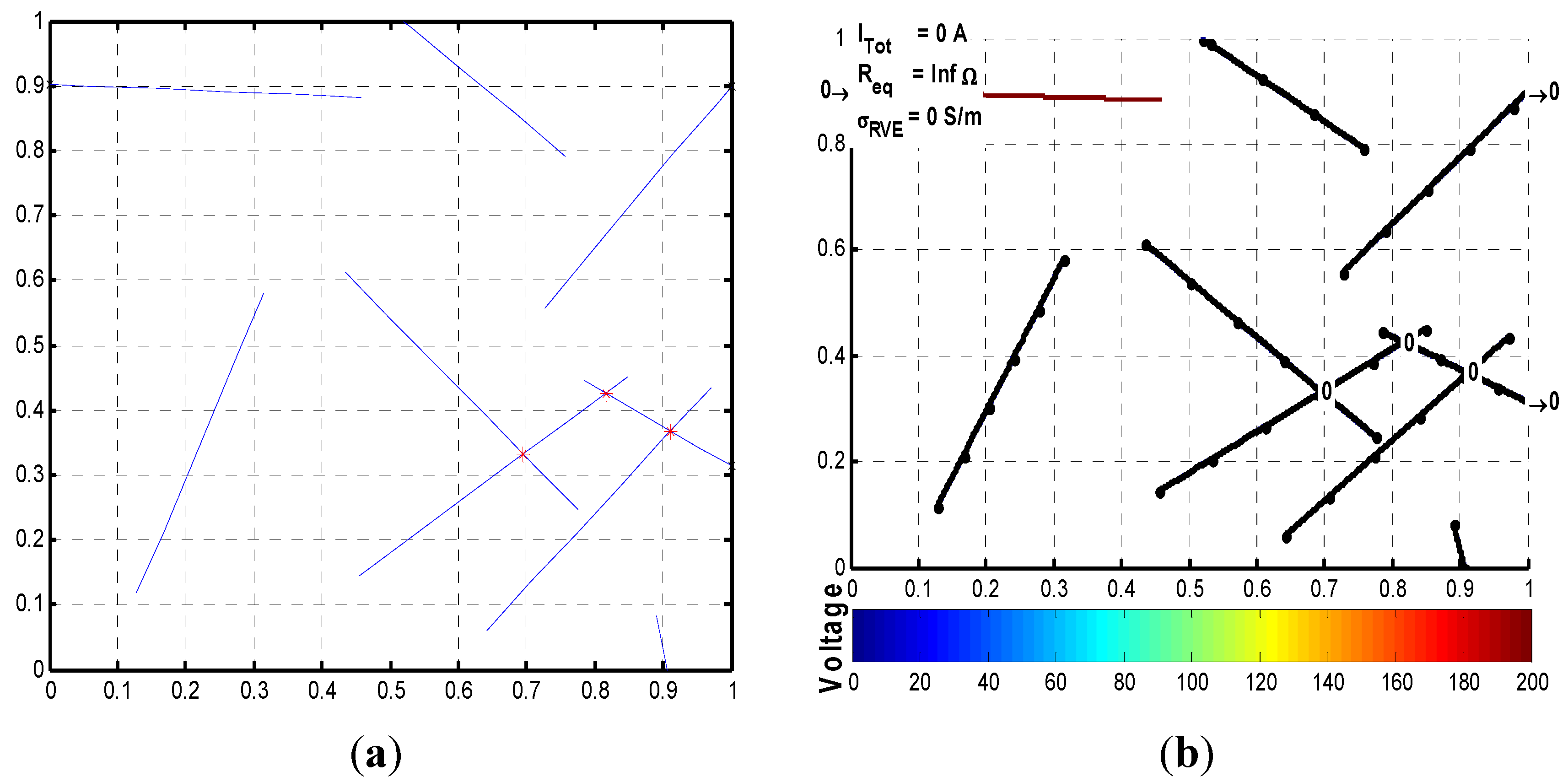
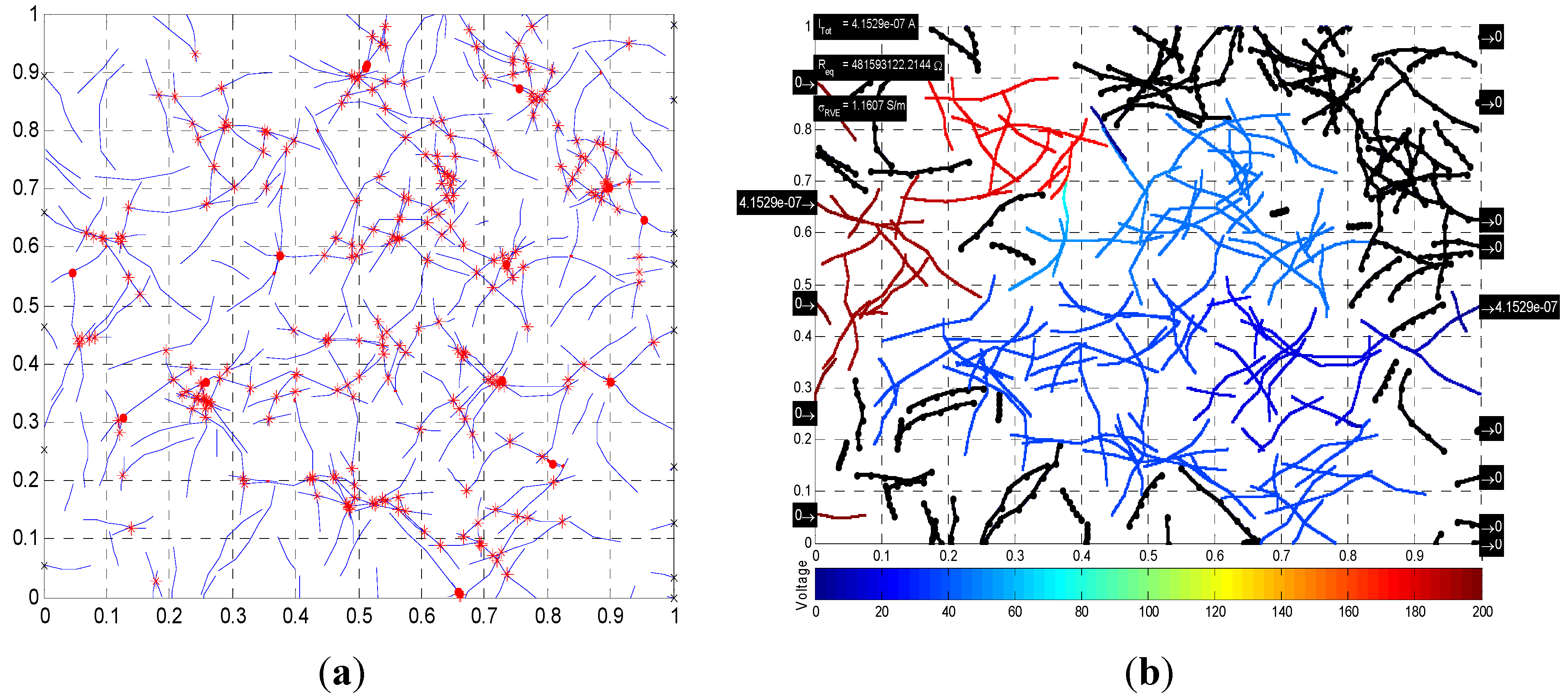
3. Results and Discussion
3.1. Percolation Behavior
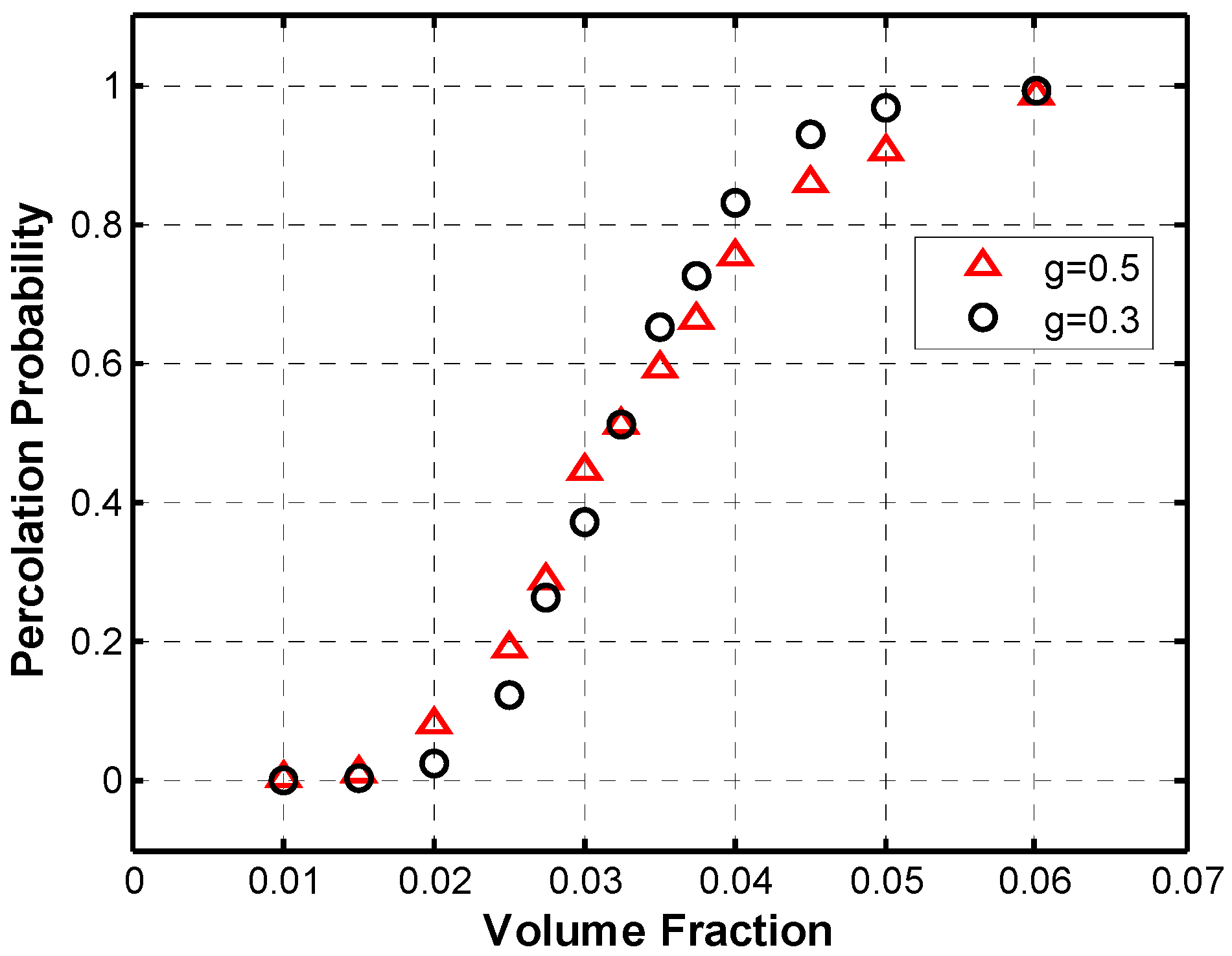
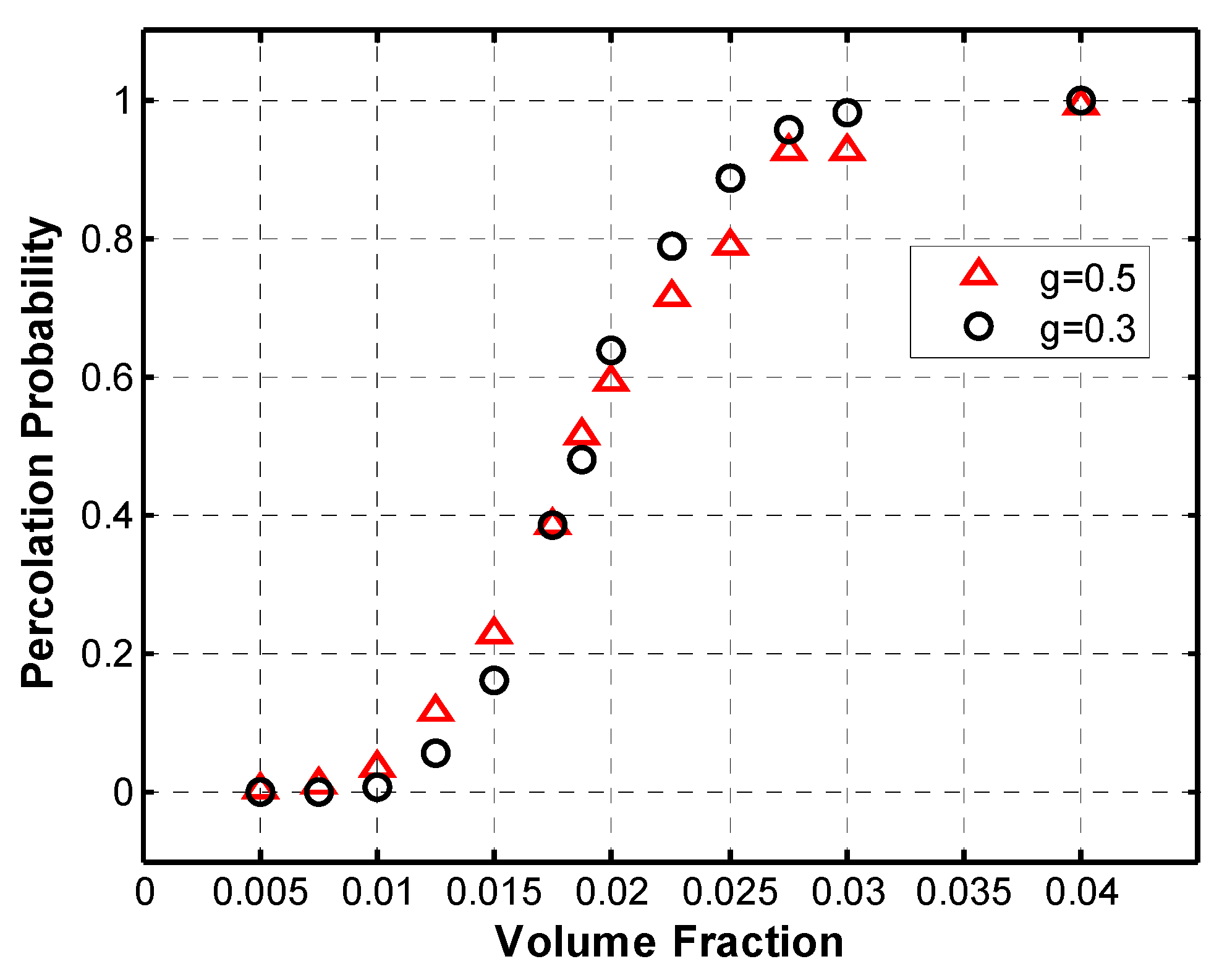
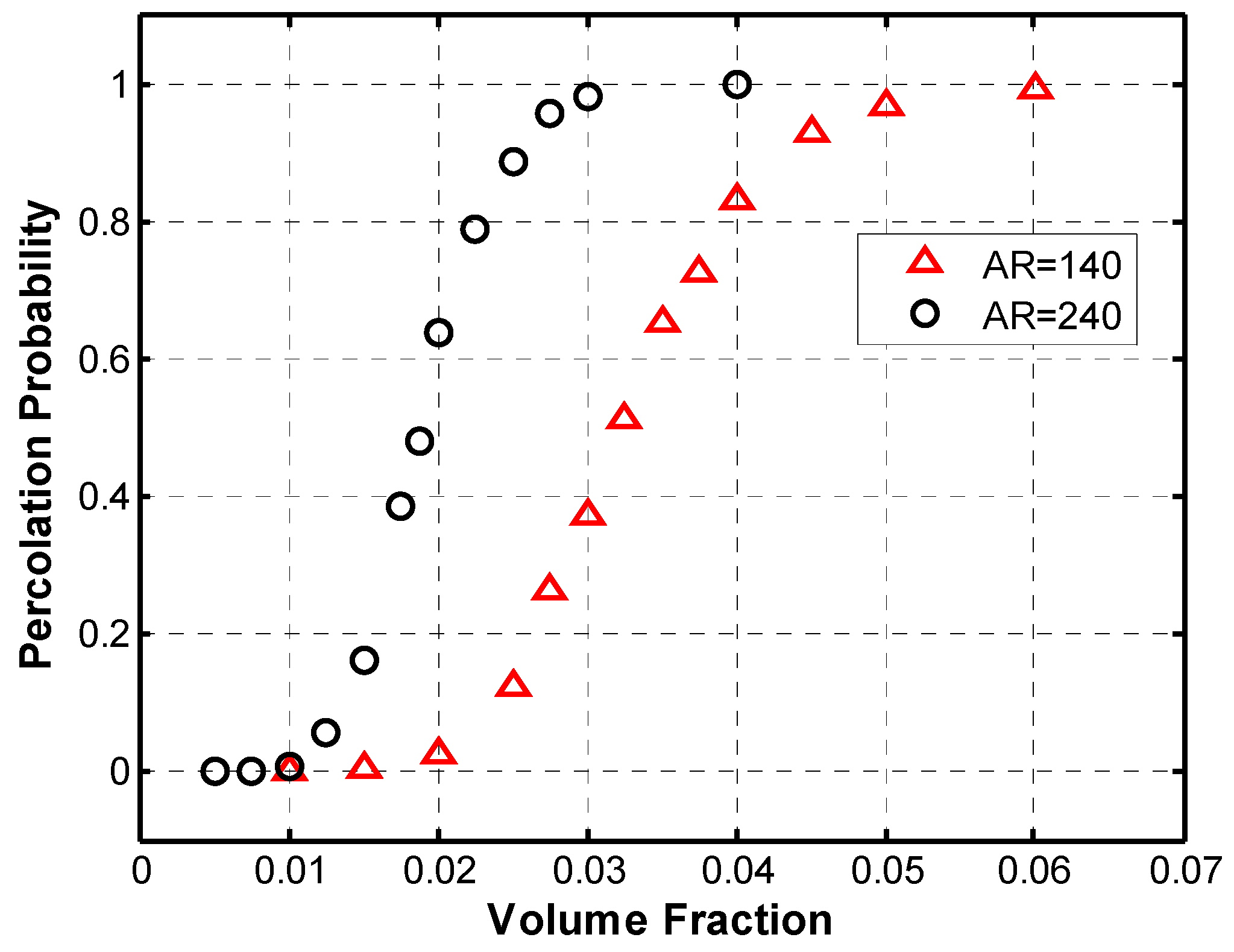
| Author | Aspect Ratio | CNT Type | Matrix Type | Percolation Threshold |
|---|---|---|---|---|
| This work | 140–240 | SWCNTs | PE (thermoplastic) | 1.75–3.25 vol. % |
| Potschke et al. [30] | 100–667 | MWCNTs | PC (thermoplastic) | 1.47–2.94 vol. % |
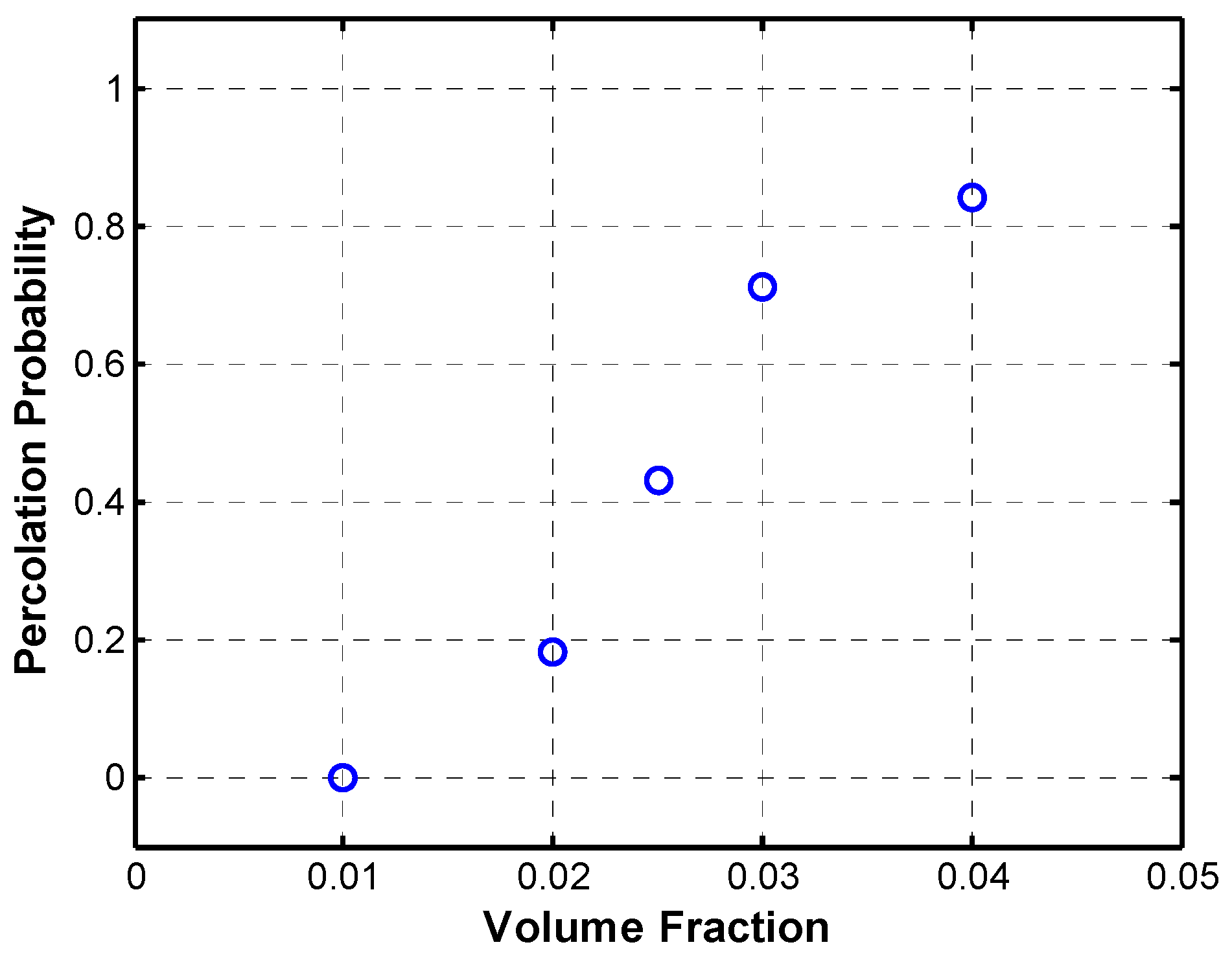
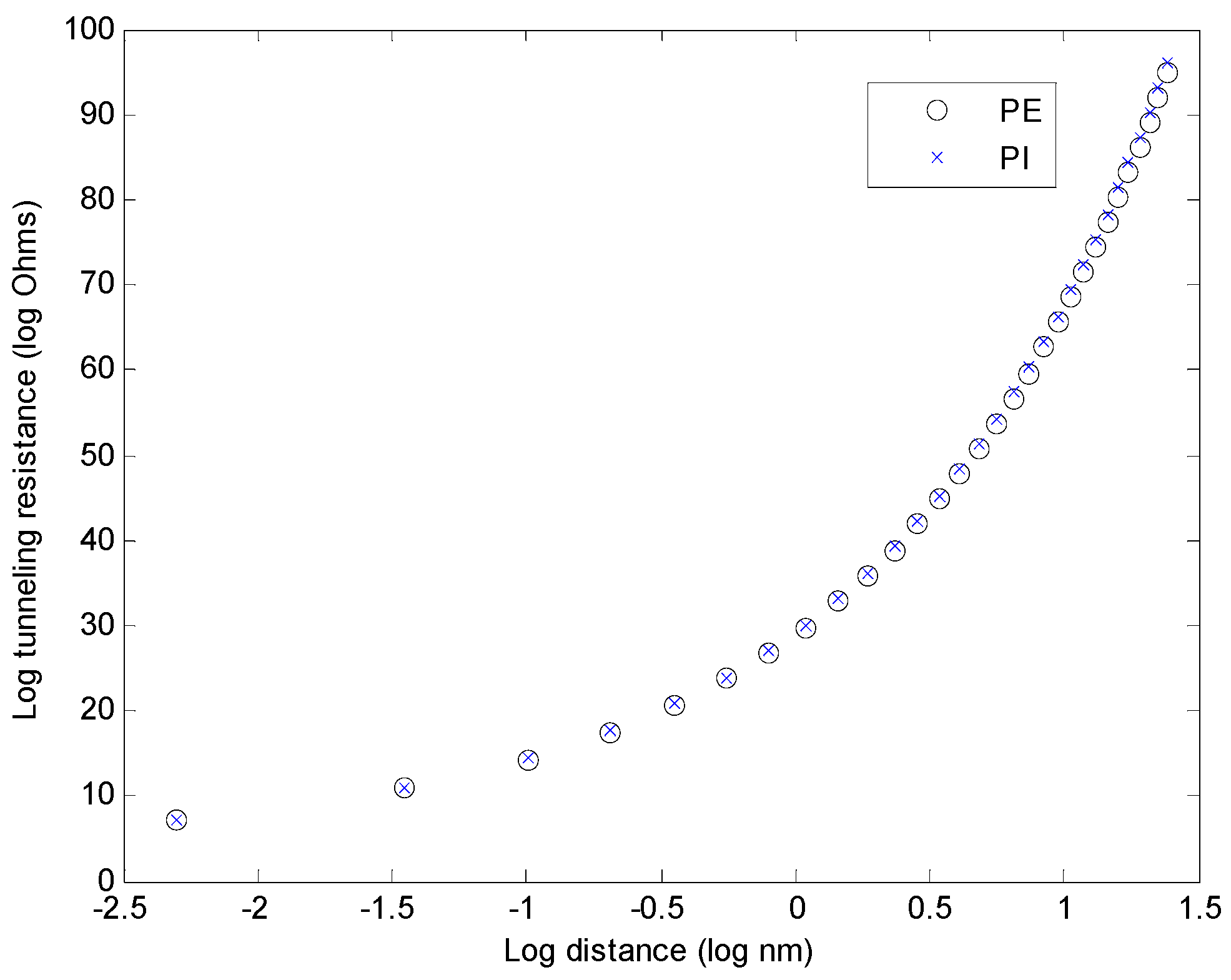
3.2. Tunneling Behavior
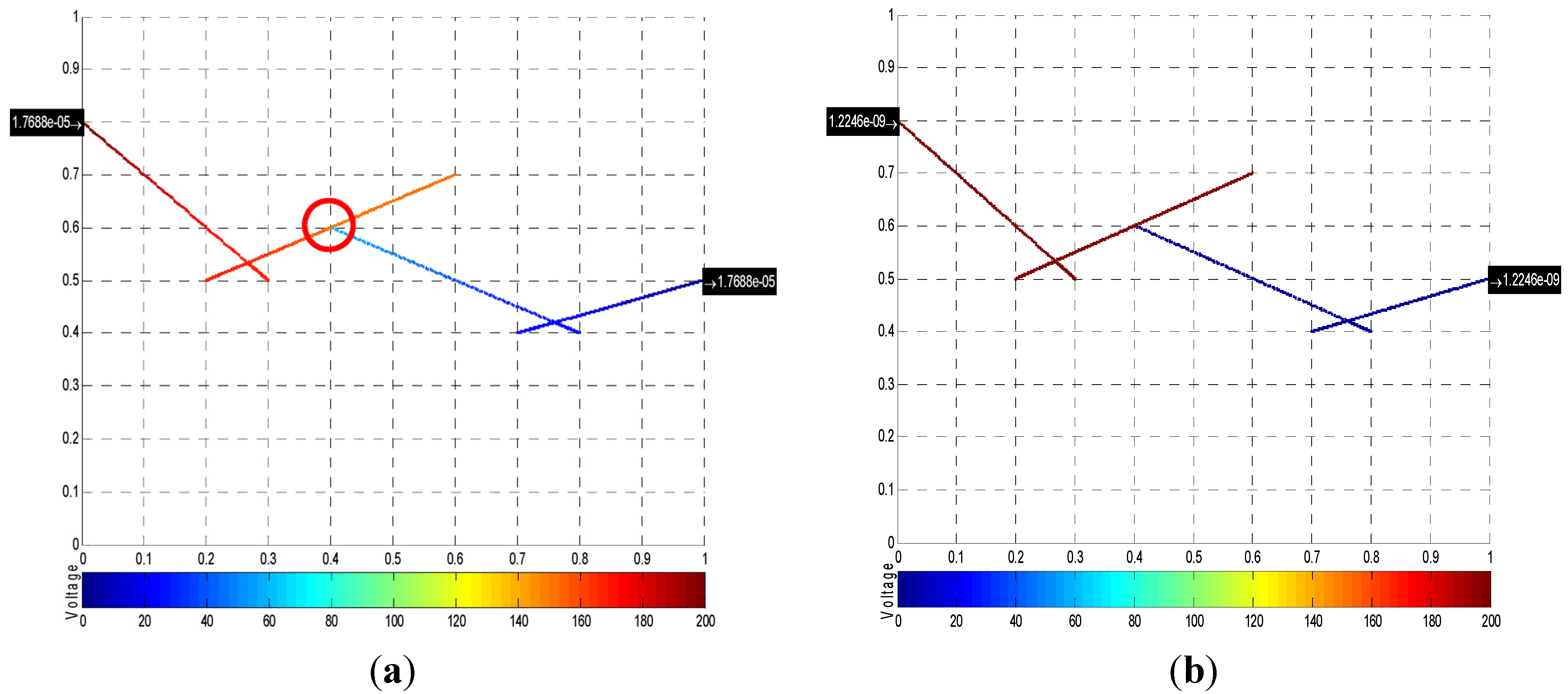
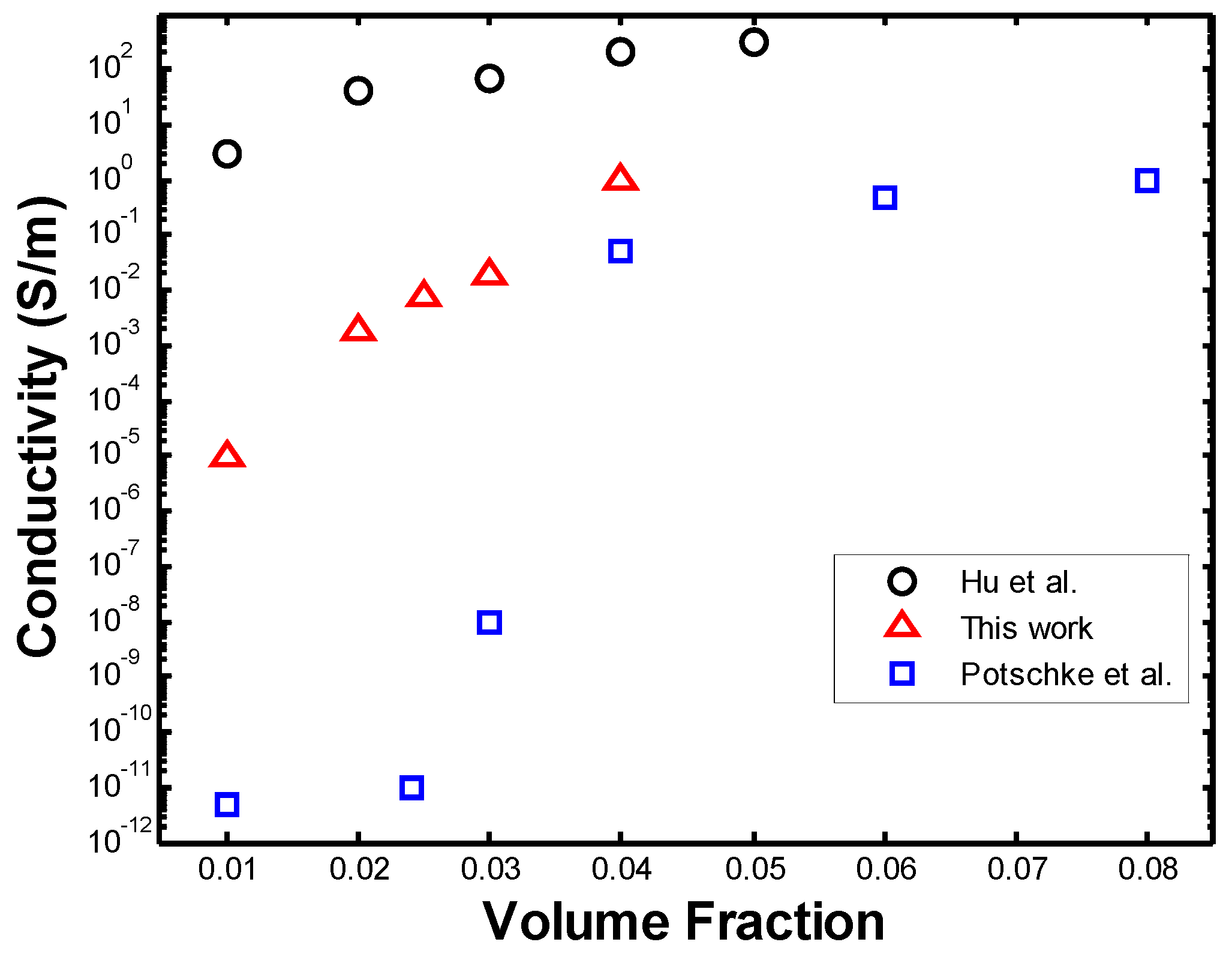
3.3. Electrical Conductivity
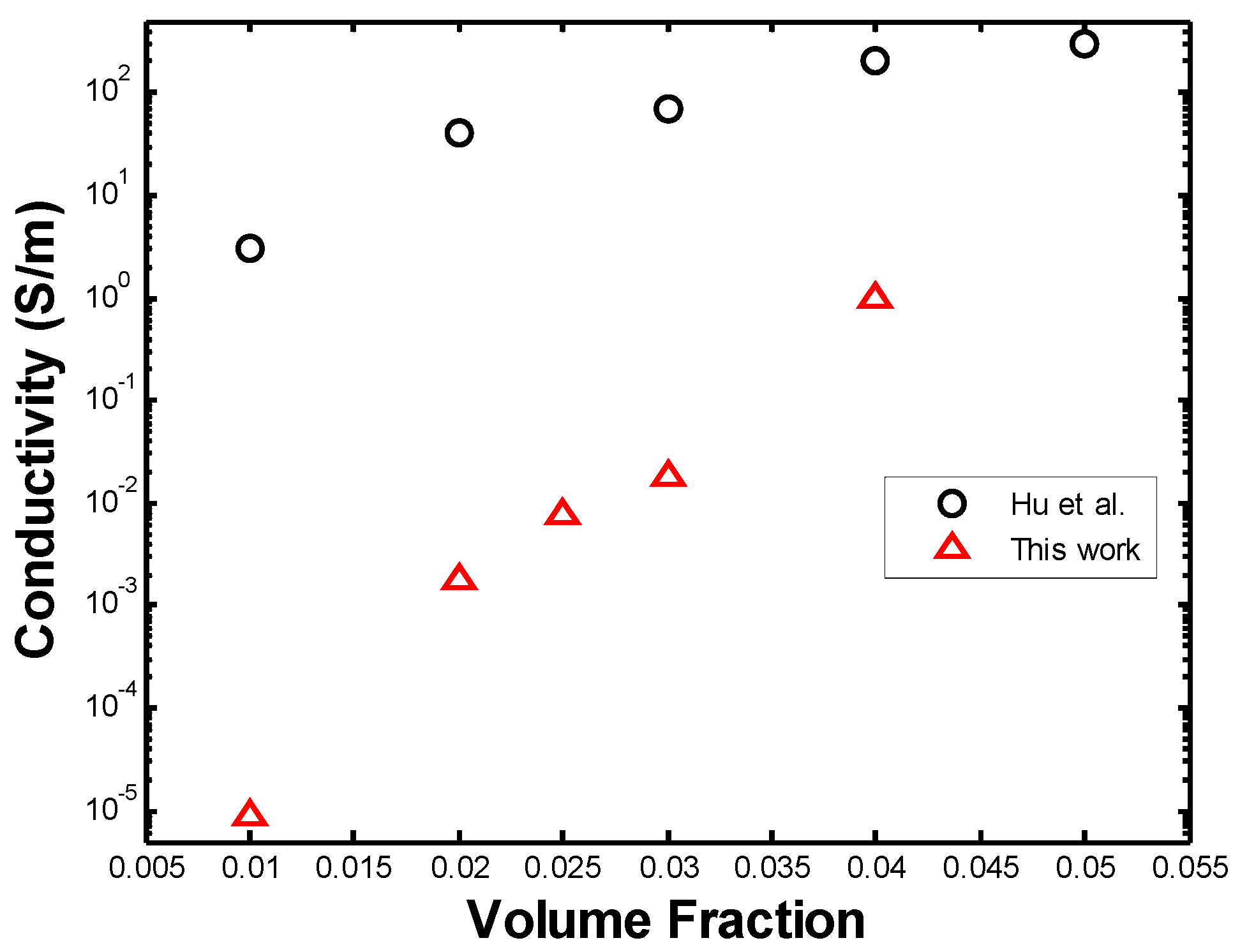
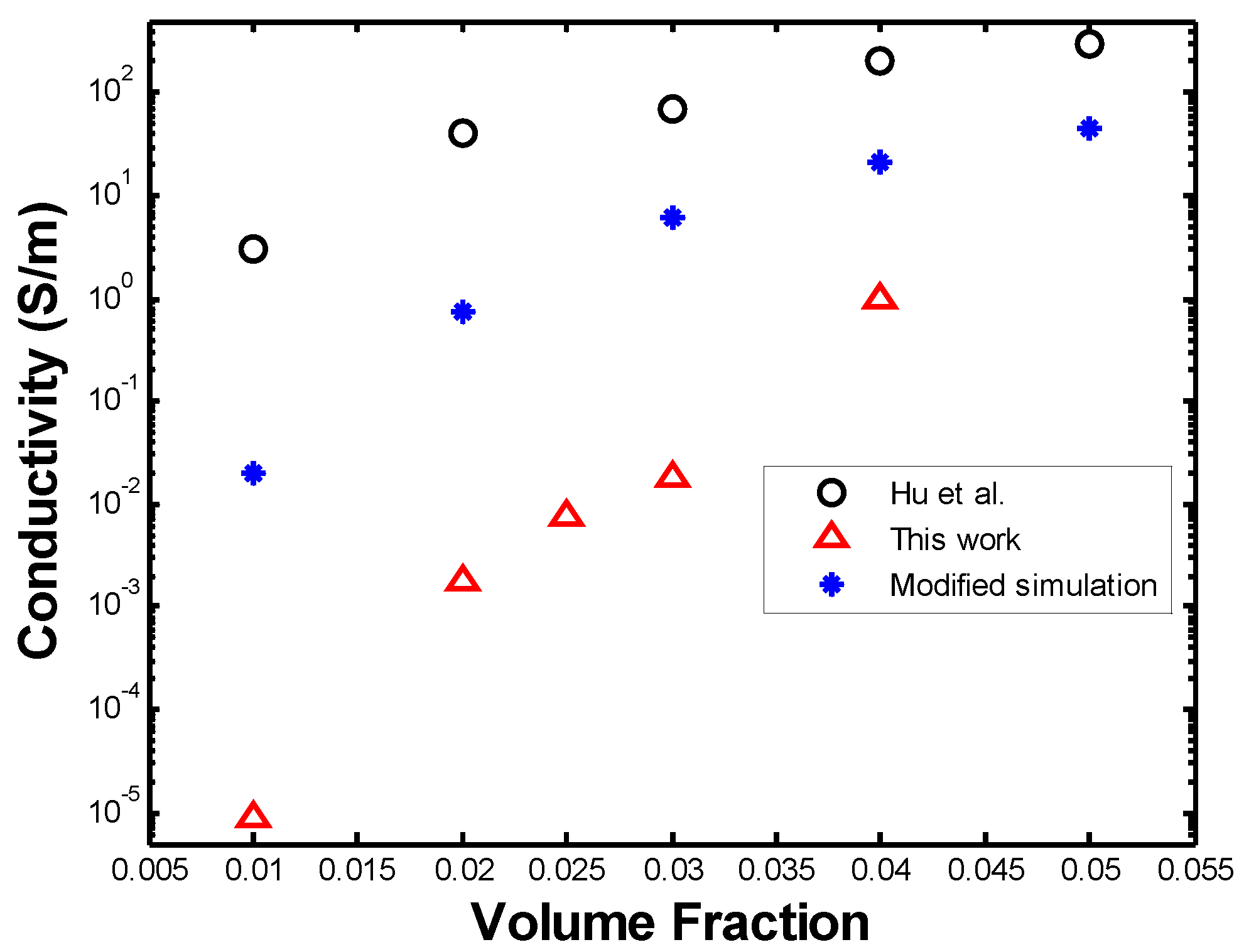
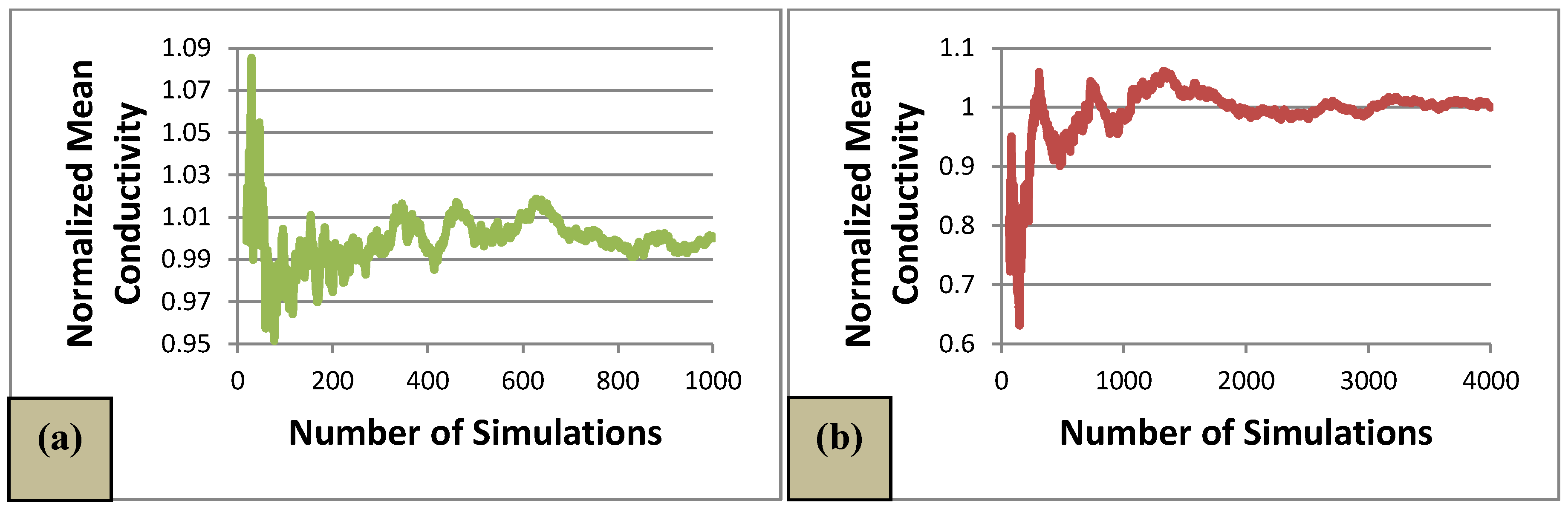

4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dovaston, N.G.; Male, S.E. Conductors and Superconductors. In Electrical Engineer’s Reference Book; Reed Educational and Professional Publishing Ltd.: Boston, MA, USA, 1993; pp. 11/1–11/12. [Google Scholar]
- Spanos, P.D.; Esteva, M. Effect of stochastic nanotube waviness on the elastic and thermal properties of nanocomposites by fiber embedment in finite elements. J. Comput. Theor. Nanosci. 2009, 6, 2317–2333. [Google Scholar] [CrossRef]
- Wernik, J.M.; Meguid, S.A. Recent developments in multifunctional nanocomposites using carbon nanotubes. Appl. Mech. Rev. 2010, 63. [Google Scholar] [CrossRef]
- Mintmire, J.W.; White, C.T. Electronic and structural properties of carbon nanotubes. Carbon 1995, 33, 893–902. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Saito, R. Physics of carbon nanotubes. Carbon 1995, 33, 883–891. [Google Scholar] [CrossRef]
- Ebbesen, T.W.; Lezec, H.J.; Hiura, H.; Bennett, J.W.; Ghaemi, H.F.; Thio, T. Electrical conductivity of individual carbon nanotubes. Nature 1996, 382, 54–56. [Google Scholar] [CrossRef]
- Tans, S.J.; Devoret, M.H.; Dai, H.; Thess, A.; Smalley, R.E.; Geerligs, L.J.; Dekker, C. Individual single-wall carbon nanotubes as quantum wires. Nature 1997, 386, 474–477. [Google Scholar] [CrossRef]
- Gojny, F.H.; Wichmann, M.H.; Fiedler, B.; Kinloch, I.A.; Bauhofer, W.; Windle, A.H.; Schulte, K. Evaluation and identification of electrical and thermal conduction mechanisms in carbon nantoube/epoxy composites. Polymer 2006, 47, 2036–2045. [Google Scholar] [CrossRef]
- Bauhofer, W.; Kovacs, J.Z. A review and analysis of electrical percolation in carbon nanotube polymer composites. Compos. Sci. Technol. 2009, 69, 1486–1498. [Google Scholar] [CrossRef]
- Seidel, G.D.; Lagoudas, D.C. A micromechanics model for the electrical conductivity of nanotube-polymer nanocomposites. J. Compos. Mater. 2009, 43, 917–941. [Google Scholar] [CrossRef]
- Dalmas, F.; Dendievel, R.; Chazeau, L.; Cavaille, J.-Y.; Gauthier, C. Carbon nanotube-filled polymer composites. Numerical simulation of electrical conductivity in three-dimensional entangled fibrous networks. Acta Mater. 2006, 54, 2923–2931. [Google Scholar] [CrossRef]
- Hu, N.; Masuda, Z.; Yan, C.; Fukunaga, H.; Hashida, T. Electrical properties of polymer nanocomposites with carbon nanotube fillers. Nanotechnology 2008, 19. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chou, T.-W. Continuum percolation of nanocomposites with fillers of arbitrary shapes. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
- Li, J.; Ma, C.; Chow, W.S.; To, C.K.; Tang, B.Z.; Kim, J.-K. Correlations between percolation threshold, dispersion state, and aspect ratio of carbon nanotubes. Adv. Funct. Mater. 2007, 17, 3207–3215. [Google Scholar] [CrossRef]
- Lu, C.; Mai, Y.-W. Anomalous electrical conductivity and percolation in carbon nanotube composites. J. Mater. Sci. 2008, 43, 6012–6015. [Google Scholar] [CrossRef]
- Sun, X.; Song, M. Highly conductive carbon nanotube/polymer nanocomposites achievable? Macromol. Theory Simul. 2009, 18, 155–161. [Google Scholar] [CrossRef]
- White, S.I.; DiDonna, B.; Mu, M.; Lubensky, T.; Winey, K. Simulations and electrical conductivity of percolated networks of finite rods with various degrees of axial alignment. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Xu, S.; Rezvanian, O.; Peters, K.; Zikry, M.A. Tunneling effects and electrical conductivity of cnt polymer composites. In MRS Proceeding; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Zeng, X.; Xu, X.; Shenai, P.M.; Kovalev, E.; Baudot, C.; Mathews, N.; Zhao, Y. Characteristics of the electrial percolation in carbon nanotubes/polymer nanocomposites. J. Phys. Chem. 2011, 115, 21685–21690. [Google Scholar]
- Flandin, L.; Verdier, M.; Boutherin, B.; Brechet, Y.; Cavaillé, J.-Y. A 3-d numerical simulation of AC electrical properties of short fiber composites. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 805–814. [Google Scholar] [CrossRef]
- Merabia, S.; Sotta, P.; Long, D.R. A microscopic model for the reinforcement and the nonlinear behavior of filled elastomers and thermoplastic elastomers (Payne and Mullins effects). Macromolecules 2008, 41, 8252–8266. [Google Scholar] [CrossRef]
- Merabia, S.; Sotta, P.; Long, D.R. Unique plastic and recovery behavior of nanofilled elastomers and thermoplastic elastomers (Payne and Mullins effects). J. Polym. Sci. Part B Polym. Phys. 2010, 48, 1495–1508. [Google Scholar] [CrossRef]
- Yacobi, B.G. Semiconductor Materials: An Introduction to Basic Principles; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2003. [Google Scholar]
- Sheng, P. Fluctuation-induced tunneling conduction in disordered materials. Phys. Rev. B 1980, 21, 2180–2195. [Google Scholar]
- Wang, S.; Liang, Z.; Wang, B.; Zhang, C. Statistical characterization of single-wall carbon nanotube length distribution. Nanotechnology 2006, 17, 634–639. [Google Scholar]
- Bao, H.-D.; Sun, Y.; Xiong, Z.-Y.; Guo, Z.-X.; Yu, J. Effects of the dispersion state and aspect ratio of carbon nanotubes on their electrical percolation threshold in a polymer. J. Appl. Polym. Sci. 2012, 128. [Google Scholar] [CrossRef]
- Taya, M. Electronic Composites; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Buldum, A.; Lu, J.P. Contact Resistance between Carbon Nanotubes; Department of Physics and Astronomy, The University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 2000. [Google Scholar]
- Gómez, A.; Martínez, J.L.; Rosendo, J.A.; Romero, E.; Riquelme, J.M. Fundamentos de Teoría de Circuitos; Internation Thomson Editores Spain: Madrid, Spain, 2007. [Google Scholar]
- Potschke, P.; Fornes, T.; Paul, D. Rheological behavior of multiwalled carbon nanotube/polycarbonate composites. Polymer 2002, 43, 3247–3255. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, M.; Esteva, M.; Martínez-Romero, O.; Baez, J.; Elías-Zúñiga, A. Modeling Percolation in Polymer Nanocomposites by Stochastic Microstructuring. Materials 2015, 8, 6697-6718. https://doi.org/10.3390/ma8105334
Soto M, Esteva M, Martínez-Romero O, Baez J, Elías-Zúñiga A. Modeling Percolation in Polymer Nanocomposites by Stochastic Microstructuring. Materials. 2015; 8(10):6697-6718. https://doi.org/10.3390/ma8105334
Chicago/Turabian StyleSoto, Matias, Milton Esteva, Oscar Martínez-Romero, Jesús Baez, and Alex Elías-Zúñiga. 2015. "Modeling Percolation in Polymer Nanocomposites by Stochastic Microstructuring" Materials 8, no. 10: 6697-6718. https://doi.org/10.3390/ma8105334
APA StyleSoto, M., Esteva, M., Martínez-Romero, O., Baez, J., & Elías-Zúñiga, A. (2015). Modeling Percolation in Polymer Nanocomposites by Stochastic Microstructuring. Materials, 8(10), 6697-6718. https://doi.org/10.3390/ma8105334