Application of Hydrophilic Silanol-Based Chemical Grout for Strengthening Damaged Reinforced Concrete Flexural Members
Abstract
:1. Introduction
2. Development and Properties of HCGS
2.1. Development of HCGS
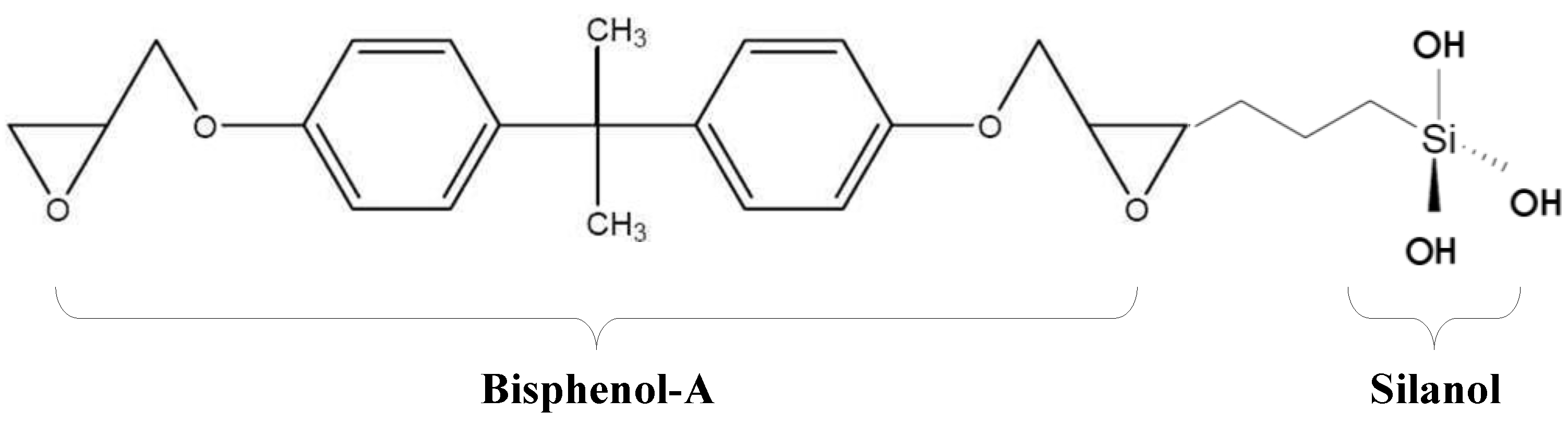
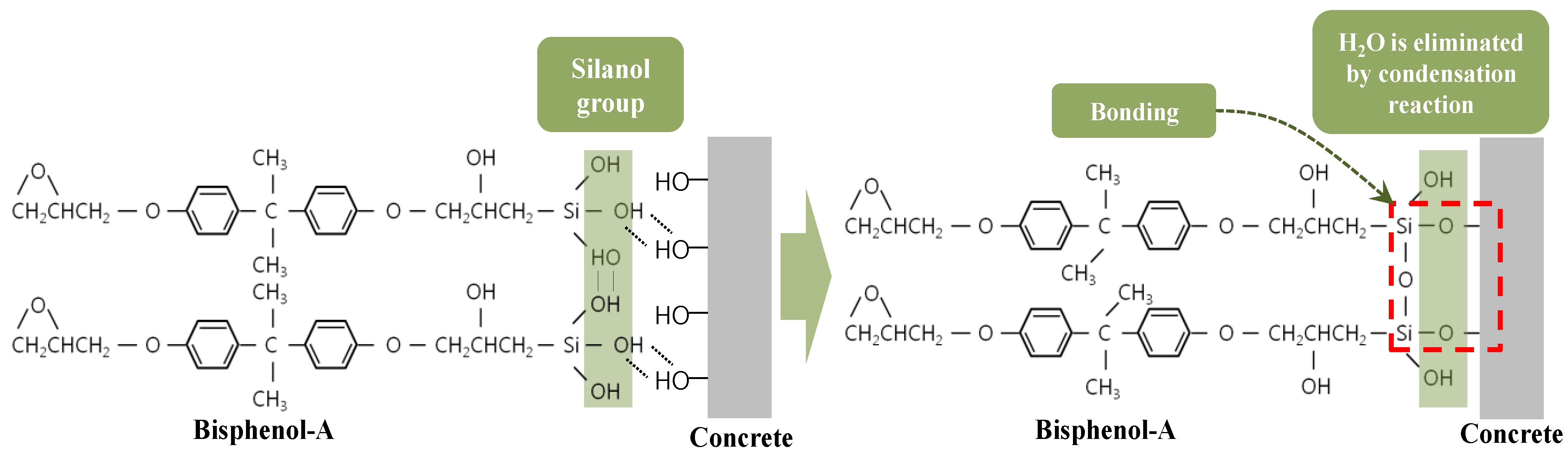
2.2. Material Characteristics of HCGS
| Tests | HCGS | Epoxy | Ref. Standards | |
|---|---|---|---|---|
| Compressive strength (MPa) | 59.1 | 51.3 | ASTM C109 [24] | |
| Modulus of rupture (MPa) | 20.1 | 8.2 | ASTM C293 [25] | |
| Bond strength | Standard (MPa) | 3.6 | 1.9 | ASTM C1583 [26] |
| Cyclic heat temperature (MPa) | 2.1 | 1.5 | ||
| Alkali resistance (Compressive Strength) (MPa) | 57.4 | 50.4 | ASTM C227 [27] | |
| Water permeability (g) | 1 | 2 | ISO.12572 [28] | |
| Water absorption coefficient (kg/m2∙h0.5) | 0.06 | 0.11 | ISO.15148 [29] | |
| Water vapor transmission, Sd (m) | 1.2 | 1.7 | ASTM E 96 [30] | |
| Chloride ion permeation resistance (Coulombs) | 427 | 3926 | ASTM C1202 [31] | |
| Changing rate of length (%) | −0.06 | −0.10 | ASTM C157 [32] | |
| Carbonation depth (mm) | 1.9 | 3.2 | ISO DIS 1920-12.2 [33] | |

3. Experimental Program
3.1. Specimens and Material Characteristics
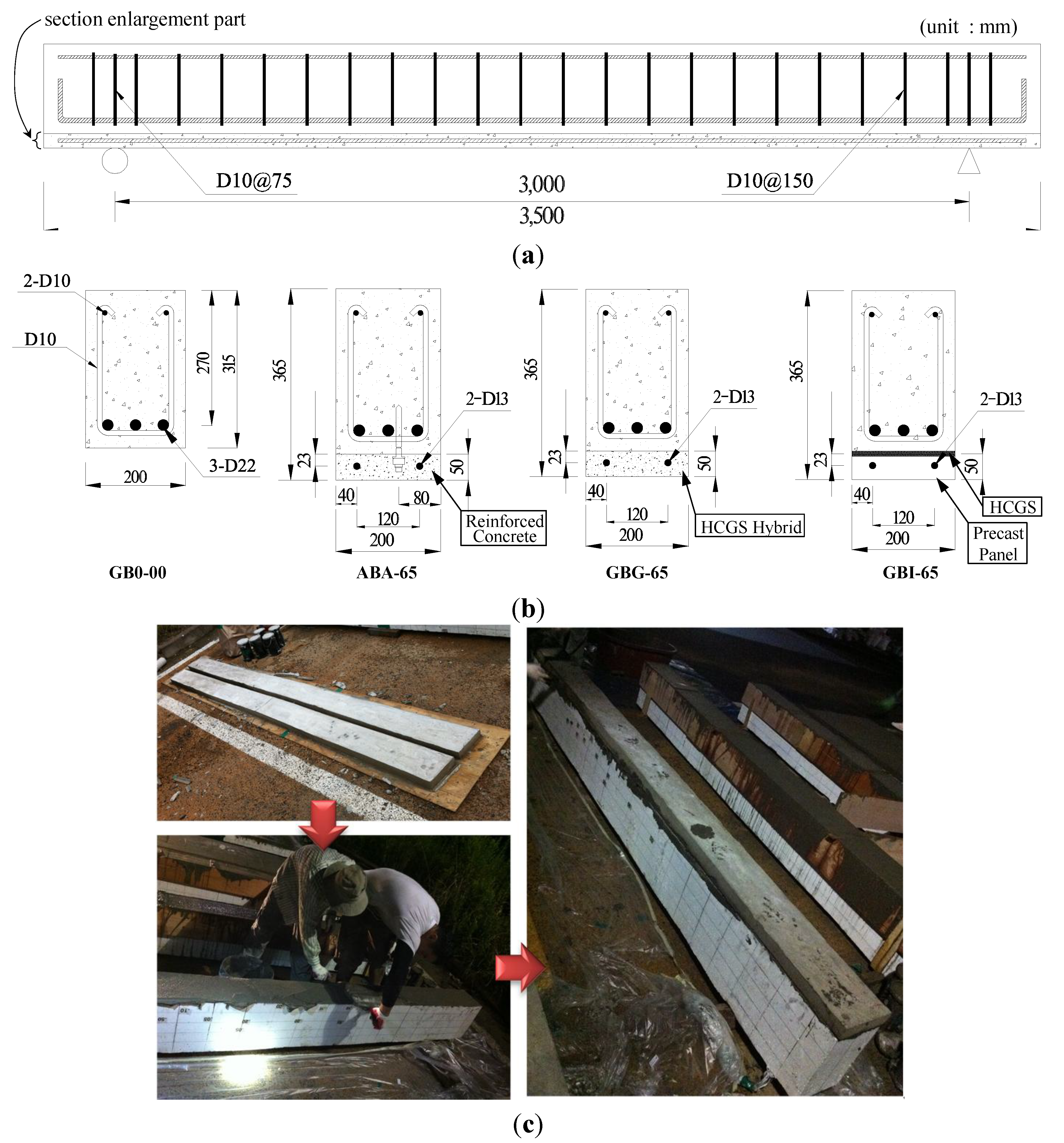
| Specimen | fck (MPa) | fsp (MPa) | Material | Longitudinal reinforcement | Transverse reinforcement | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Steel bars | fyl (MPa) | Steel bars | fyl (MPa) | Steel bars | fyl (MPa) | Steel bars | fyt (MPa) | ||||
| GB0-00 | 34.39 | 2.86 | – | 3-D22 | 421 | – | – | 2-D10 | 486 | D10 | 486 |
| ABA-65 | 33.89 | 3.07 | In-place concrete with Anchors | 3-D22 | 505 | 2-D13 | 503 | 2-D10 | 486 | D10 | 486 |
| GBG-65 | 33.18 | 3.60 | HCGS hybrid | 3-D22 | 505 | 2-D13 | 503 | 2-D10 | 486 | D10 | 486 |
| GBI-65 | 30.75 | 3.04 | HCGS | 3-D22 | 505 | 2-D13 | 503 | 2-D10 | 486 | D10 | 486 |
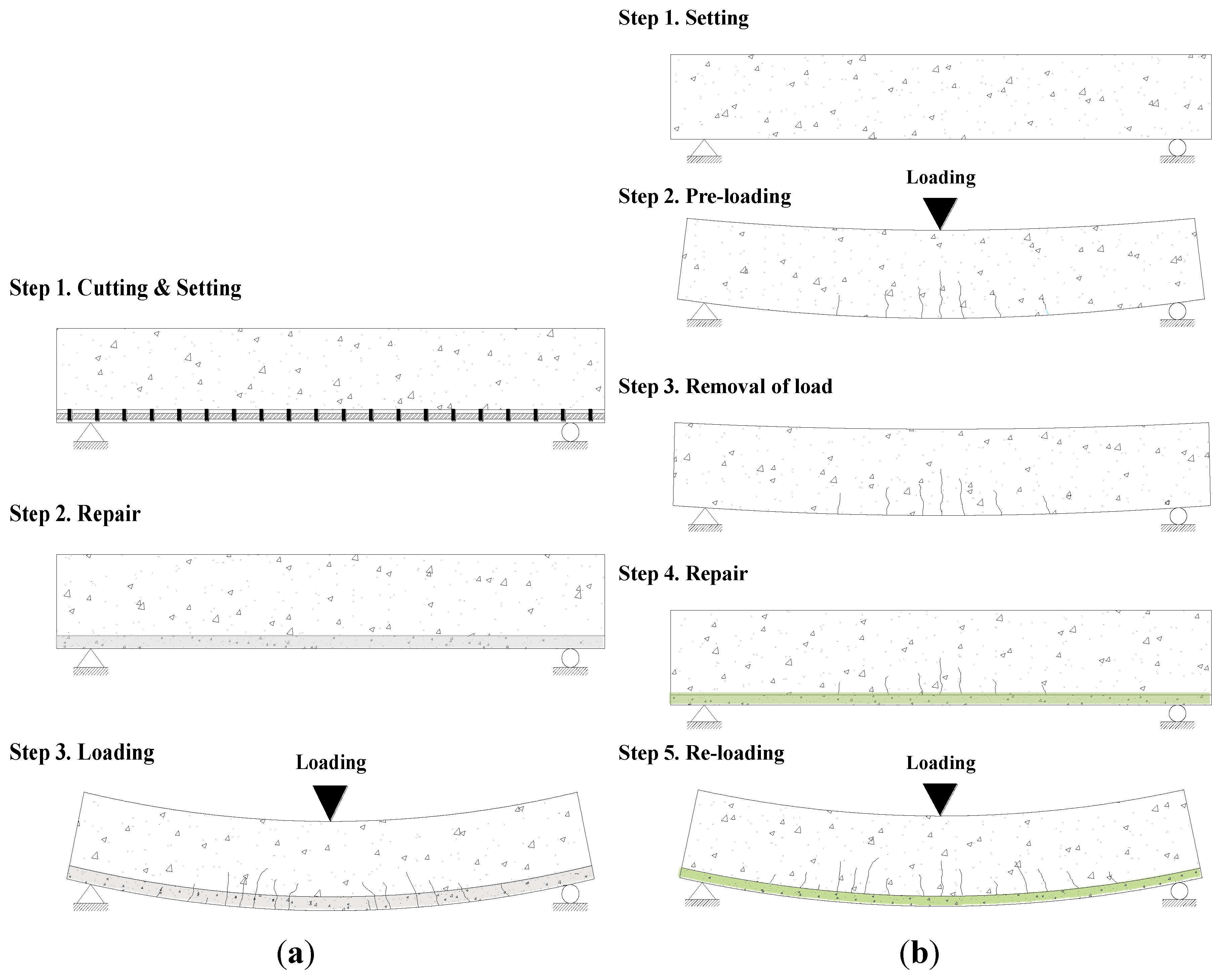
3.2. Loading and Measurements
| Type | Mechanical/Physical Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Anchor | Ɩp | dp | Ɩ | As | fuk | fyk | W | MRd,s | Sw | dw |
| 110 | 13.1 | 160 | 76.2 | 500 | 400 | 93.9 | 45.1 | 19 | 24 | |
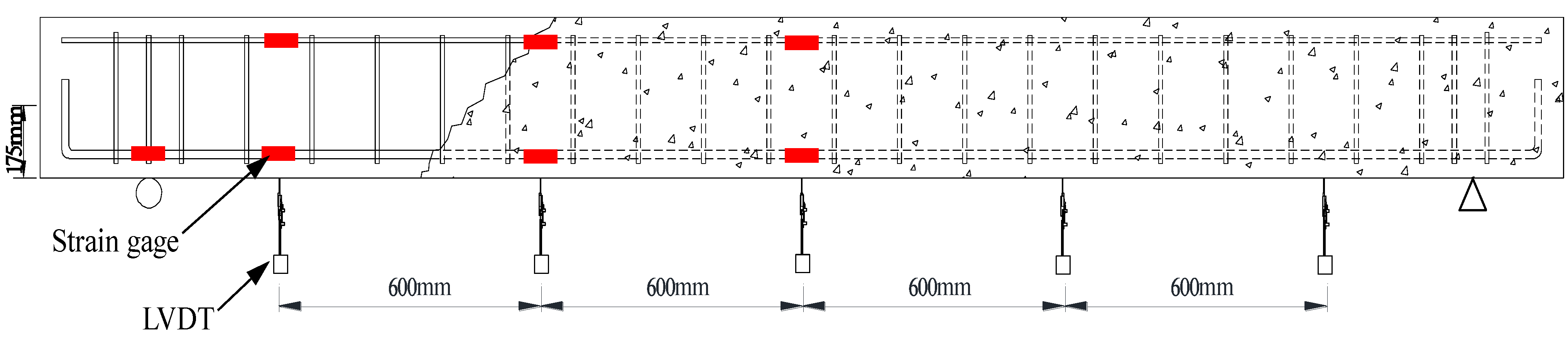
3.3. Load-Deflection Behavior of the Test Specimens
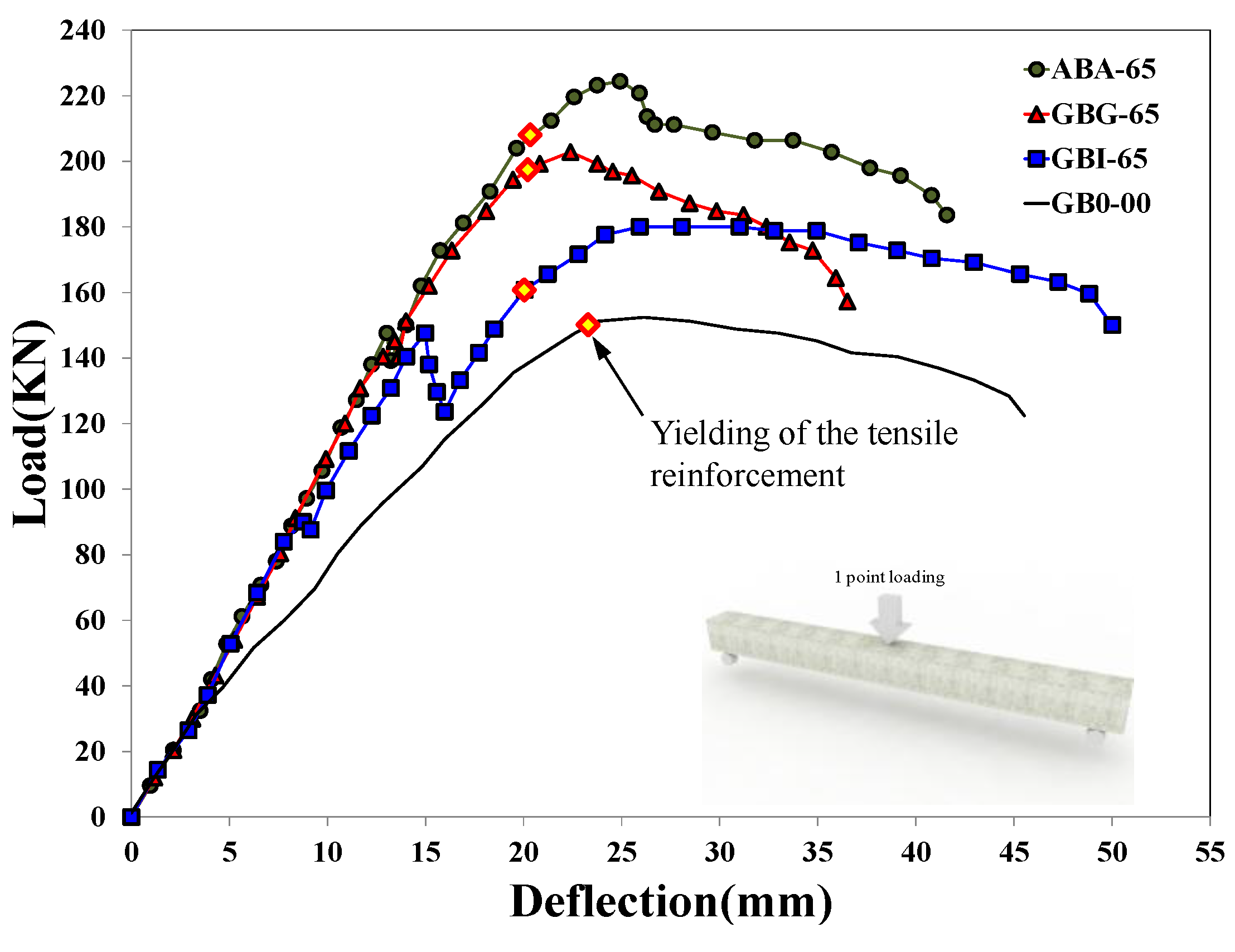
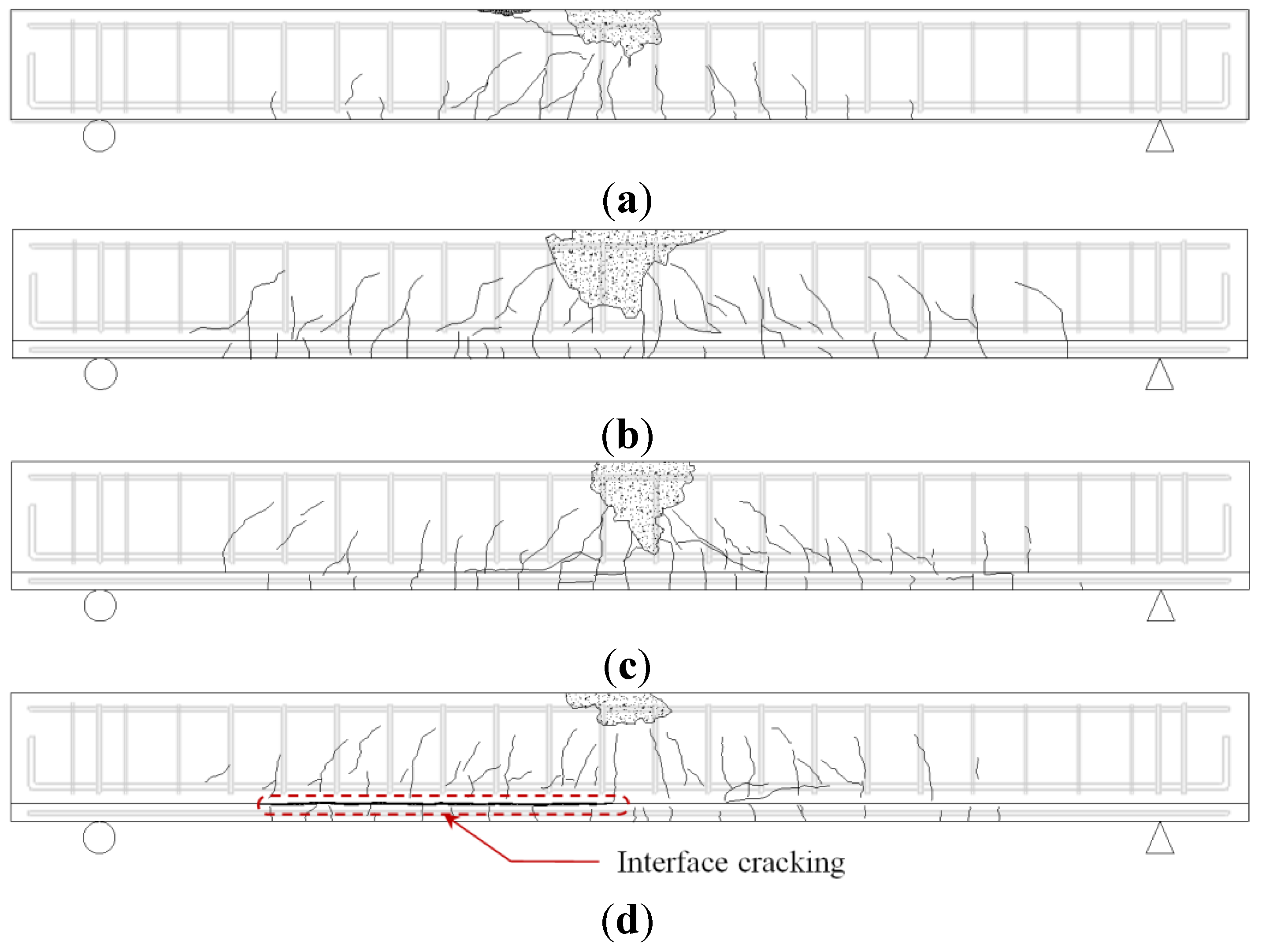
4. Evaluation of the Test Results
4.1. Partial Interaction Theory (PIT)
- (1)
- Concrete is a homogeneous and isotropic material;
- (2)
- The shear connection at the interface (bonding at interface) between composite components is continuous and constant along the longitudinal direction of the member;
- (3)
- The base and the expanded sections remain in plane even after flexural deformation, and their curvatures are the same;
- (4)
- Separation in a vertical direction does not occur, and thus only shear stress is taken into account for the analysis.
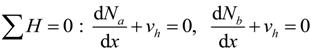
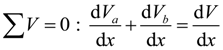
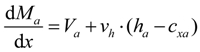
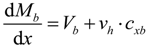
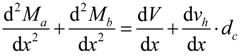
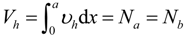
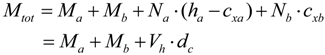
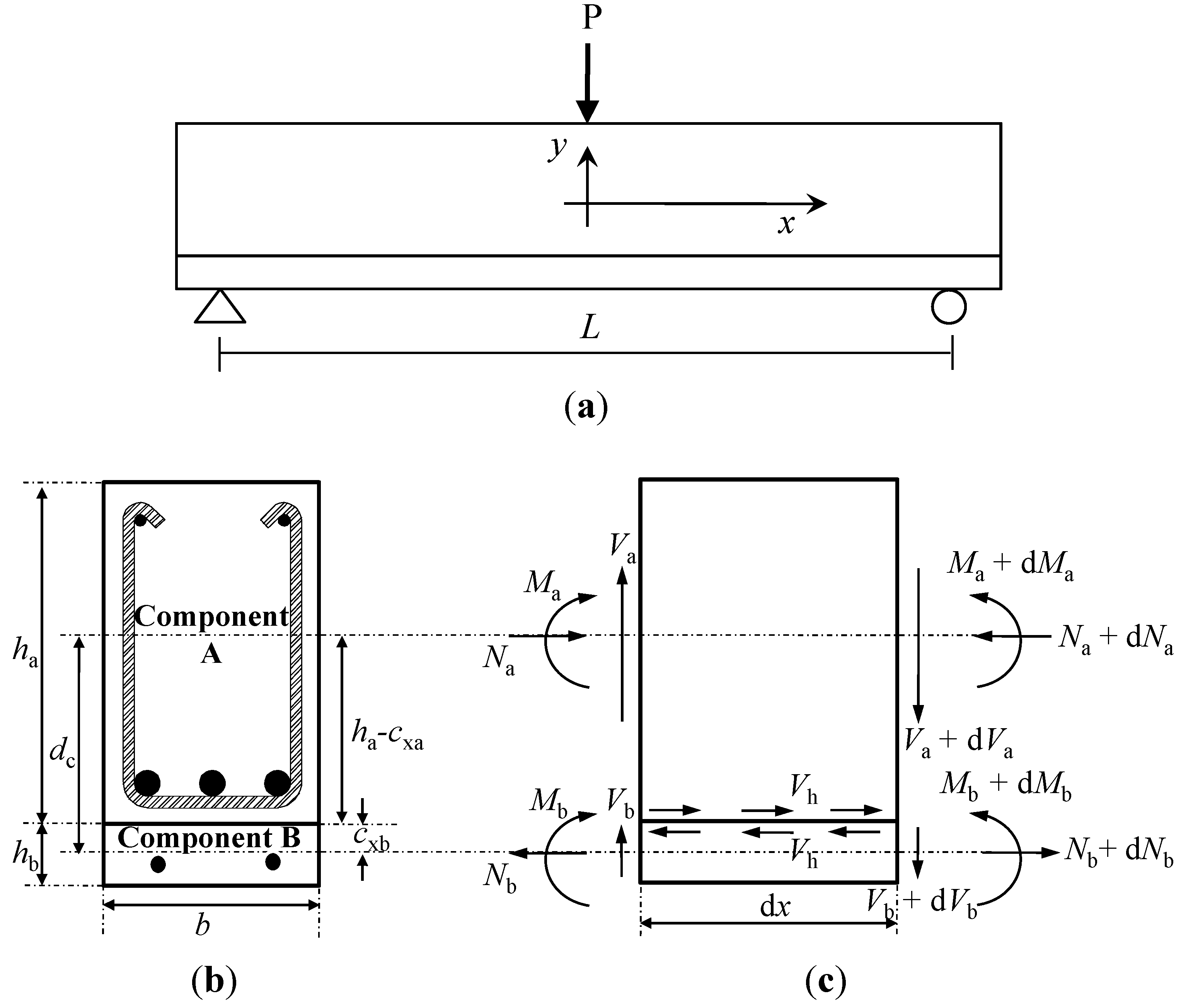
4.2. Analysis Methodology
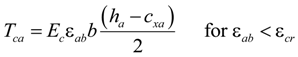
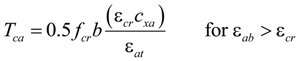
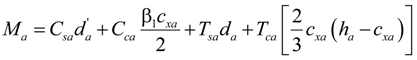
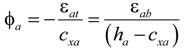
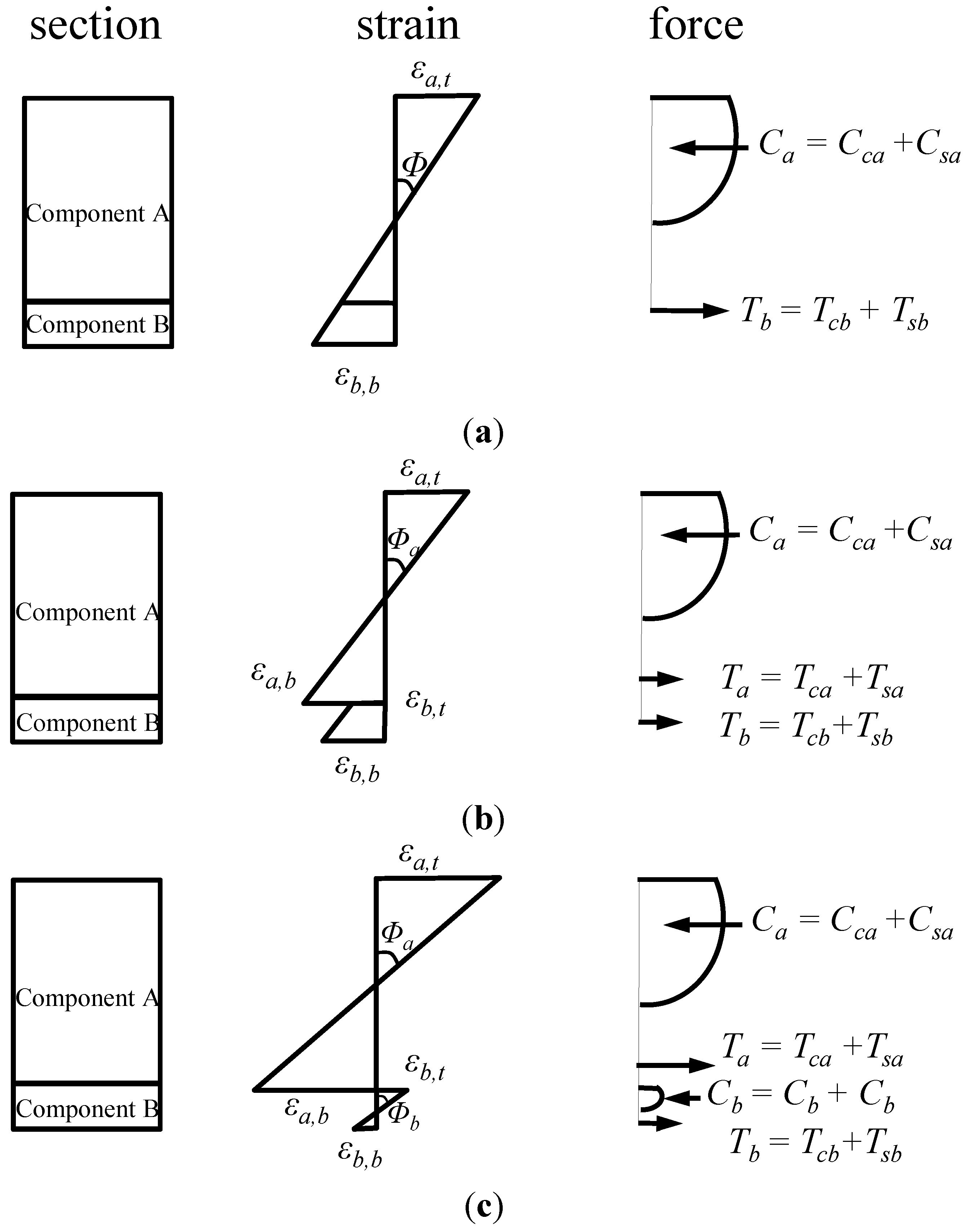
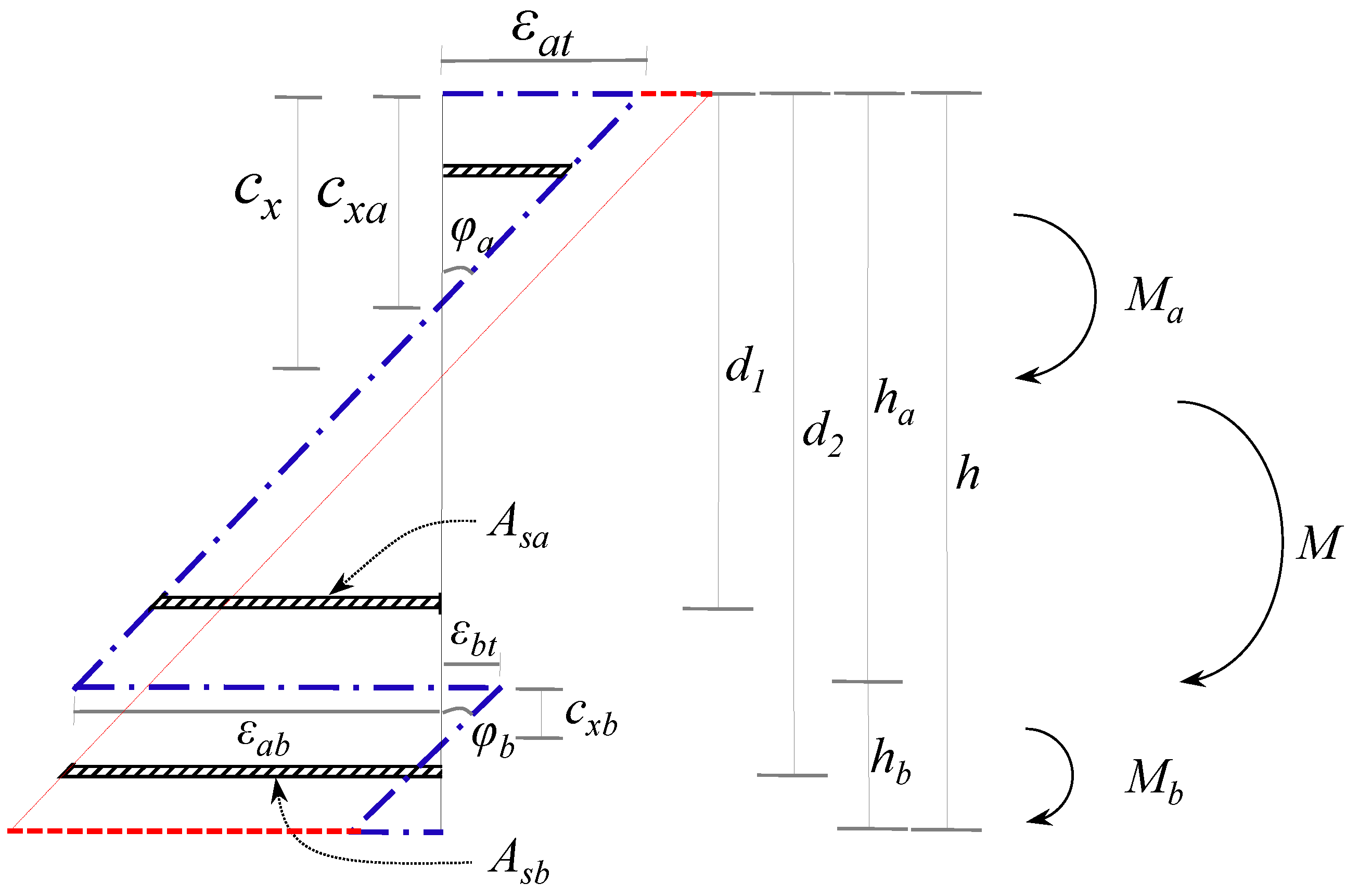
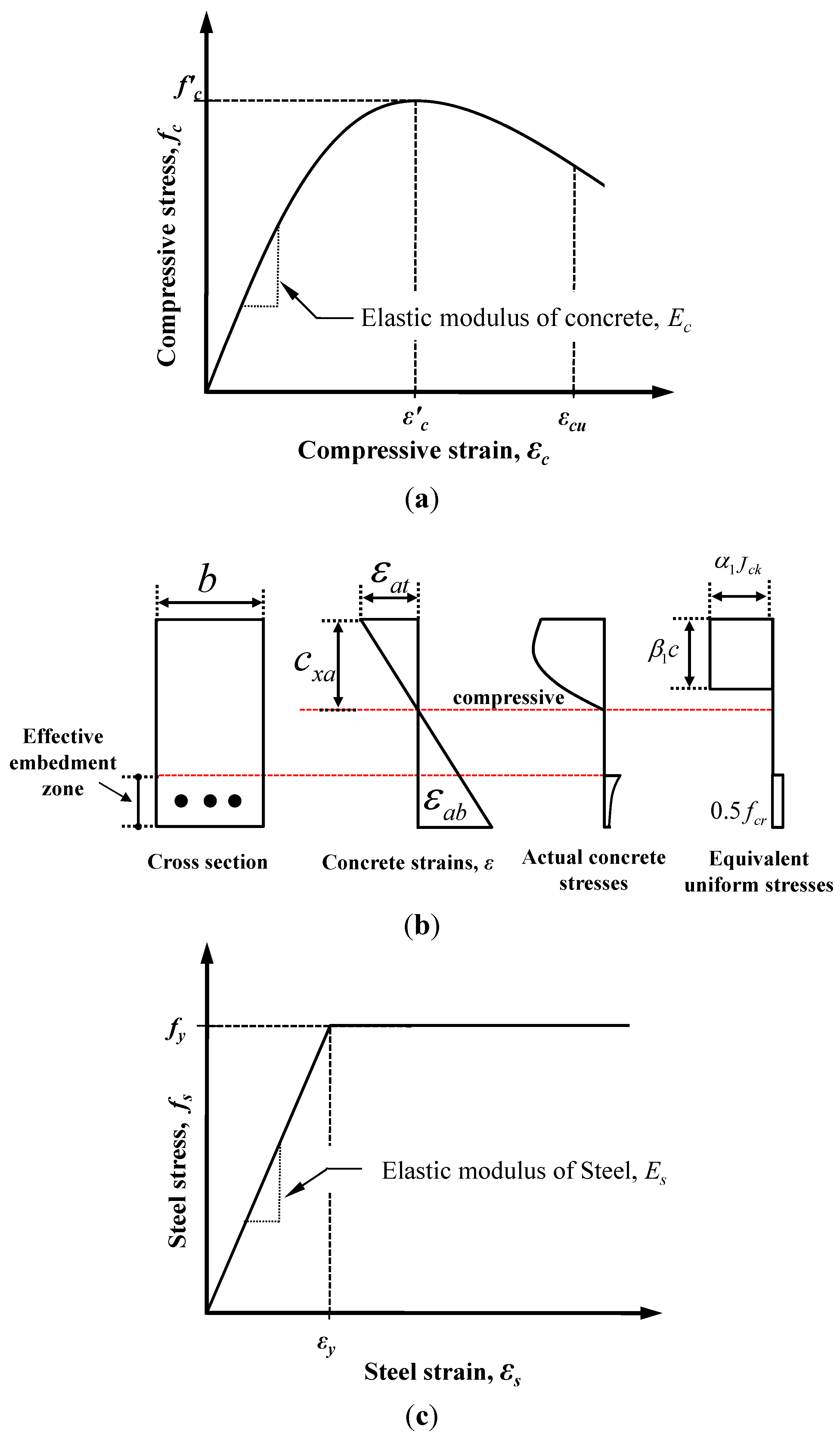
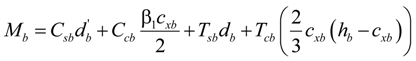
4.3. Comparison of the Analysis and Experimental Results
 ) can be estimated, as follows:
) can be estimated, as follows:
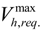 = Asbfsb,y
= Asbfsb,y
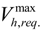 ) can be entirely transmitted at the interface was almost consistent with that obtained by assuming full composite behavior. In addition, the analysis result obtained by assuming non-composite behavior (i.e.,
) can be entirely transmitted at the interface was almost consistent with that obtained by assuming full composite behavior. In addition, the analysis result obtained by assuming non-composite behavior (i.e., 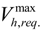 = 0) showed approximately 20% higher strength and similar initial flexural stiffness compared to the non-strengthened specimen GB0-00. It should be noted that specimen GB0-00 had steel bars with a lower yield strength as indicated in Table 2, and, if their yield strength had been the same as the steel bars used in other specimens, the moment capacity would have been even closer to that of the non-composite section.
= 0) showed approximately 20% higher strength and similar initial flexural stiffness compared to the non-strengthened specimen GB0-00. It should be noted that specimen GB0-00 had steel bars with a lower yield strength as indicated in Table 2, and, if their yield strength had been the same as the steel bars used in other specimens, the moment capacity would have been even closer to that of the non-composite section.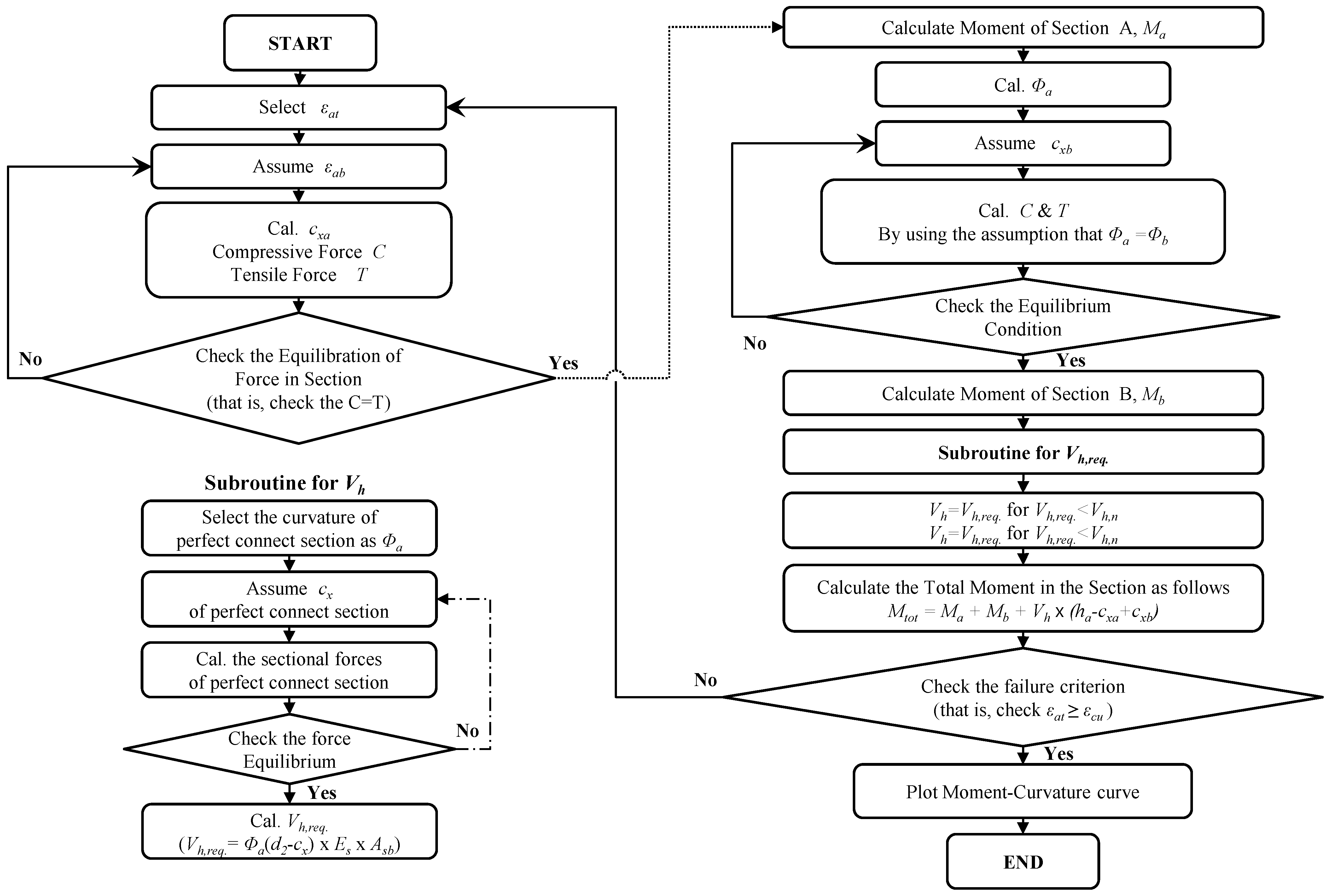

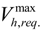 . In addition, the flexural moment of specimen GBI-65 strengthened by the panel strengthening method decreased temporarily due to severe interfacial cracking occurring at 112.5 kN·m, and then it showed similar behavior to the analysis results estimated by the analysis assuming 25% shear capacity of
. In addition, the flexural moment of specimen GBI-65 strengthened by the panel strengthening method decreased temporarily due to severe interfacial cracking occurring at 112.5 kN·m, and then it showed similar behavior to the analysis results estimated by the analysis assuming 25% shear capacity of 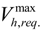 . Afterward, its behavior became similar to the analysis result with non-composite action at the interface (i.e.,
. Afterward, its behavior became similar to the analysis result with non-composite action at the interface (i.e., 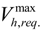 = 0). In this case, i.e., the non-composite behavior, about 15.0% of the flexural capacity was enhanced by structural strengthening compared to the control specimen.
= 0). In this case, i.e., the non-composite behavior, about 15.0% of the flexural capacity was enhanced by structural strengthening compared to the control specimen.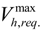 ) required at the interface. This result indicates that the amount of shear connectors (or anchors) can be significantly reduced for structural strengthening using the HCGS hybrid (specimen GBG-65), and it is expected that the constructability of strengthening work can be greatly improved. Specimen GBI-65 strengthened by the panel strengthening method showed improved initial stiffness compared to the non-strengthened specimen GB0-00, but poorer flexural behavior at the ultimate state, similar to the non-composite member analysis result, in which the complete separation behavior was assumed, i.e.,
) required at the interface. This result indicates that the amount of shear connectors (or anchors) can be significantly reduced for structural strengthening using the HCGS hybrid (specimen GBG-65), and it is expected that the constructability of strengthening work can be greatly improved. Specimen GBI-65 strengthened by the panel strengthening method showed improved initial stiffness compared to the non-strengthened specimen GB0-00, but poorer flexural behavior at the ultimate state, similar to the non-composite member analysis result, in which the complete separation behavior was assumed, i.e., 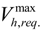 = 0. Accordingly, in order to use the panel strengthening method in practice, additional considerations would yet be necessary for the proper application of the HCGS to the interface of the damaged member depending on the flatness condition of the bottom surface. Although there were some differences between the observed values of the ultimate curvatures and the analysis results, it is to be noted that the PIT-based analysis is meaningful because it gives an indication of the levels of compositeness of the strengthened members.
= 0. Accordingly, in order to use the panel strengthening method in practice, additional considerations would yet be necessary for the proper application of the HCGS to the interface of the damaged member depending on the flatness condition of the bottom surface. Although there were some differences between the observed values of the ultimate curvatures and the analysis results, it is to be noted that the PIT-based analysis is meaningful because it gives an indication of the levels of compositeness of the strengthened members.5. Conclusions
- (1)
- The HCGS introduced in this study showed superior basic material characteristics compared to existing epoxy binding materials. In particular, a more powerful binding structure was established by forming a Si-O ionic bond between the cement hydration products within the concrete, leading to excellent bond performance and durability.
- (2)
- Specimen ABA-65, strengthened by the section enlargement method using shear connectors showed the most enhanced flexural capacity, and specimen GBG-65 strengthened by the section enlargement method utilizing the HCGS hybrid showed somewhat lower maximum load but similar flexural behavior with specimen ABA-65 due to the superior bond performance of the HCGS even though no shear connector was provided at the interface.
- (3)
- In specimen GBI-65, strengthened by the panel strengthening method, interfacial separation (i.e., horizontal shear failure) was observed, and only minor strengthening effect was obtained, compared to the other strengthened specimens. It is expected, however, that constructability can be enhanced by proper surface treatment or placing a small amount of shear connectors.
- (4)
- Flexural behavior analyses on the test specimens were performed using PIT-based flexural behavior analysis. This analysis method reasonably reflected the effect of horizontal shear developed at the interface. On this basis, the degrees of connections of the composite members were able to be estimated quantitatively.
- (5)
- In the analysis of the specimens, it was found that specimen ABA-65 showed behavior close to full interaction, and specimen GBG-65 showed about 70% of the horizontal shear capacity of the fully composite member.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Newman, A. Structural Renovation of Buildings: Methods, Details, and Design Examples; McGraw-Hill: New York, NY, USA, 2001; p. 867. [Google Scholar]
- American Concrete Institute. Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix (FRCM) Systems for Repair and Strengthening Concrete and Masonry Structures; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- D’Ambrisi, A.; Focacci, F. Flexural strengthening of RC Beams with cement based composites. J. Compos. Constr. 2011, 15, 707–720. [Google Scholar] [CrossRef]
- Pellegrino, C.; D’Antino, T. Experimental behavior of existing precast prestressed reinforced concrete elements strengthened with cementitious composites. Compos. Part B Eng. 2013, 55, 31–40. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Focacci, F.; Caporale, A. Strengthening of masonry-unreinforced concrete railway bridges with PBO-FRCM materials. Compos. Struct. 2013, 102, 193–204. [Google Scholar] [CrossRef]
- Ombres, L. Debonding Analysis of reinforced concrete beams strengthened with fibre reinforced cementitious mortar. Eng. Fract. Mech. 2012, 81, 94–109. [Google Scholar] [CrossRef]
- Täljsten, B.; Blanksvärd, T. Mineral-based bonding of carbon FRP to strengthen concrete structures. J. Compos. Constr. 2007, 11, 120–128. [Google Scholar]
- Lee, J.Y.; Hwang, H.B.; Doh, J.H. Effective strain of RC Beams strengthened in shear with FRP. Compos. Part B Eng. 2012, 42, 754–765. [Google Scholar]
- El-Mihilmy, M.T.; Tedesco, J.W. Prediction of anchorage failure for reinforced concrete beams strengthened with fiber-reinforced polymer plates. ACI Struct. J. 2001, 98, 301–314. [Google Scholar]
- Smith, S.T.; Teng, J.G. Interfacial stresses in plated beams. Eng. Struct. 2001, 23, 857–871. [Google Scholar] [CrossRef]
- Cai, C.S.; Nie, J.; Shi, X.M. Interface slip effect on bonded plate repairs of concrete beams. Eng. Struct. 2007, 29, 1084–1095. [Google Scholar] [CrossRef]
- Täljsten, B. Strengthening of beams by plate bonding. J. Mater. Civ. Eng. ASCE 1997, 9, 215–231. [Google Scholar] [CrossRef]
- Malec, A.M.; Saadatmanesh, H.; Ehsani, M.R. Prediction of failure load of R/C Beams strengthened with FRP plate due to stress concentration at the plate end. ACI Struct. J. 1998, 95, 142–152. [Google Scholar]
- Alam, M.S.; Kanakubo, T.; Yasojima, A. Shear-peeling bond strength between continuous fiber sheet and concrete. ACI Struct. J. 2012, 109, 75–82. [Google Scholar]
- Pešić, N.; Pilakoutas, K. Concrete beans with externally bonded flexural FRP-reinforcement: Analytical investigation of debonding failure. Compos. Part B Eng. 2003, 34, 327–338. [Google Scholar]
- Silfwerbrand, J. Shear bond strength in repaired concrete structures. Mater. Struct. 2003, 36, 419–424. [Google Scholar] [CrossRef]
- Tsioulou, O.T.; Dritsos, S.E. A theoretical model to predict interface slip due to bending. Mater. Struct. 2011, 44, 825–843. [Google Scholar] [CrossRef]
- Ju, H.; Lee, D.H.; Kim, K.S.; Kim, D.H.; Kwak, J.Y. Properties and applications of non-shrinkage chemical grout for repairing and strengthening of concrete structures. World J. Eng. 2012, 9, 423–428. [Google Scholar] [CrossRef]
- Kim, K.S.; Ju, H.; Kim, D.H.; Hwang, J.H.; Oh, J.Y.; Kang, H. Flexural behavior of reinforced concrete beams strengthened by hydrophilic chemical grout using silanol. Adv. Sci. Lett. (in press).
- Callister, W.D. Materials Science and Engineering: An Introduction, 7th ed.; John Wiley & Sons: New York, NY, USA, 2007; p. 832. [Google Scholar]
- Mehta, P.K.; Monteiro, P.J.M. Concrete: Microstucture, Properties and Materials, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006; p. 659. [Google Scholar]
- Neville, A.M. Properties of Concrete, 4th ed.; John Wiley & Sons: New York, NY, USA, 1996; p. 844. [Google Scholar]
- Korean Standards Information Center. Polymer Modified Cement Mortar for Maintenance in Concrete Structure: Agency for Technology and Standards; Korean Standards Information Center: Seoul, Korea, 2007; p. 19. [Google Scholar]
- ASTM international. Standard Test Method for Compressive Strength of Hydraulic Cement Mortars; ASTM: West Conshohocken, PA, 2013; p. 10. [Google Scholar]
- ASTM international. Standard Test Method for Flexural Strength of Concrete; ASTM: West Conshohocken, PA, 2010; p. 3. [Google Scholar]
- ASTM international. Standard Test Method for Tensile Strength of Concrete Surfaces and the Bond Strength or Tensile Strength of Concrete Repair and Overlay Materials by Direct Tension; ASTM: West Conshohocken, PA, 2013; p. 5. [Google Scholar]
- ASTM international. Standard Test Method for Tensile Strength of Concrete Surfaces and the Bond Strength or Tensile Strength of Concrete Repair and Overlay Materials by Direct Tension; ASTM: West Conshohocken, PA, 2010; p. 6. [Google Scholar]
- ASTM international. Standard Test Method for Potential Alkali Reactivity of Cement-Aggregate Combinations; ASTM: West Conshohocken, PA, 2013; p. 5. [Google Scholar]
- International Organization for Standardization. Hygrothermal Performance of Building Materials and Products—Determination of Water Vapour Transmission Properties; International Organization for Standardization: Geneva, Switzerland, 2001; p. 34. [Google Scholar]
- ASTM international. Standard Test Methods for Water Vapor Transmission of Materials. ASTM: West Conshohocken, PA, 2013; p. 13. [Google Scholar]
- ASTM international. Standard Test Method for Electrical Indication of Concrete’s Ability to Resist Chloride Ion Penetration; ASTM: West Conshohocken, PA, 2012; p. 8. [Google Scholar]
- ASTM international. Standard Test Method for Length Change of Hardened Hydraulic-Cement Mortar and Concrete; ASTM: West Conshohocken, PA, 2008; p. 7. [Google Scholar]
- International Organization for Standardization. Testing of concrete—Part 12: Determination of the carbonation resistance of concrete—Accelerated carbonation method; International Organization for Standardization: Geneva, Switzerland, 2014; p. 18. [Google Scholar]
- HILTI Korea. Fastening Technology Manual; HILTI Korea Co.: Seoul, Korea, 2003. [Google Scholar]
- Plum, D.R.; Horne, M.R. The analysis of continuous composite beams with partial interaction. Proc. Inst. Civ. Eng. 1975, 59, 625–643. [Google Scholar]
- Fabbrocino, G.; Manfredi, G.; Cosenza, E. Non-linear analysis of composite beams under positive bending. Comput. Struct. 1999, 70, 77–89. [Google Scholar] [CrossRef]
- Fabbrocino, G.; Manfredi, G.; Cosenza, E. Analysis of continuous composite beams including partial interaction and bond. J. Struct. Eng. ASCE 2000, 126, 1288–1294. [Google Scholar] [CrossRef]
- Newmark, N.M.; Siess, C.P.; Viest, I.M. Tests and analysis of composite beams with incomplete interaction. Proc. Soc. Exp. Stress Anal. 1951, 9, 75–92. [Google Scholar]
- Nie, J.; Cai, C.S. Steel-concrete composite beams considering shear slip effects. J. Struct. Eng. ASCE 2003, 129, 495–506. [Google Scholar] [CrossRef]
- Arizumi, Y.; Hamada, S.; Kajita, T. Elastic-plastic analysis of composite beams with incomplete interaction by finite element method. Comput. Struct. 1981, 14, 453–462. [Google Scholar] [CrossRef]
- Saiidi, M.; Vrontinos, S.; Douglas, B. Model for the response of reinforced concrete beams strengthened by concrete overlays. ACI Struct. J. 1990, 87, 687–695. [Google Scholar]
- Collins, M.P.; Mitchell, D. Prestressed Concrete Structures; Prentice-Hall: Bergen County, NJ, USA, 1991; p. 766. [Google Scholar]
- Kim, K.S.; Lee, D.H. Nonlinear analysis method for continuous post-tensioned concrete members with unbonded tendons. Eng. Struct. 2012, 40, 487–500. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, D.H. Flexural behavior model for post-tensioned concrete members with unbonded tendons. Comput. Concr. 2012, 10, 241–258. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, D.H.; Choi, S.M.; Choi, Y.H.; Jung, S.H. flexural behavior of prestressed composite beams with corrugated web: Part I. Development and analysis. Compos. Part B Eng. 2011, 42, 1603–1616. [Google Scholar]
- Wight, J.K.; MacGregor, J.G. Reinforced Concrete: Mechanics and Design, 6th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2011; p. 1176. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ju, H.; Lee, D.H.; Cho, H.-C.; Kim, K.S.; Yoon, S.; Seo, S.-Y. Application of Hydrophilic Silanol-Based Chemical Grout for Strengthening Damaged Reinforced Concrete Flexural Members. Materials 2014, 7, 4823-4844. https://doi.org/10.3390/ma7064823
Ju H, Lee DH, Cho H-C, Kim KS, Yoon S, Seo S-Y. Application of Hydrophilic Silanol-Based Chemical Grout for Strengthening Damaged Reinforced Concrete Flexural Members. Materials. 2014; 7(6):4823-4844. https://doi.org/10.3390/ma7064823
Chicago/Turabian StyleJu, Hyunjin, Deuck Hang Lee, Hae-Chang Cho, Kang Su Kim, Seyoon Yoon, and Soo-Yeon Seo. 2014. "Application of Hydrophilic Silanol-Based Chemical Grout for Strengthening Damaged Reinforced Concrete Flexural Members" Materials 7, no. 6: 4823-4844. https://doi.org/10.3390/ma7064823
APA StyleJu, H., Lee, D. H., Cho, H.-C., Kim, K. S., Yoon, S., & Seo, S.-Y. (2014). Application of Hydrophilic Silanol-Based Chemical Grout for Strengthening Damaged Reinforced Concrete Flexural Members. Materials, 7(6), 4823-4844. https://doi.org/10.3390/ma7064823







