Unified Formulation for a Triaxial Elastoplastic Constitutive Law for Concrete
Abstract
:1. Introduction
2. Triaxial Constitutive Formulation
2.1. Yield Surface Criterion
- is the mean normal stress or hydrostatic pressure expressed by:
- ρ is the deviatoric stress defined by:is the second invariant of the deviatoric stress tensor s:
- θ is the polar angle that determines the direction of the octahedral shear stress and locates the stress state relative to the meridians of tension and compression around the hydrostatic axis. The angle θ is defined as follows:is the third invariant of the deviatoric stress tensor s defined by:
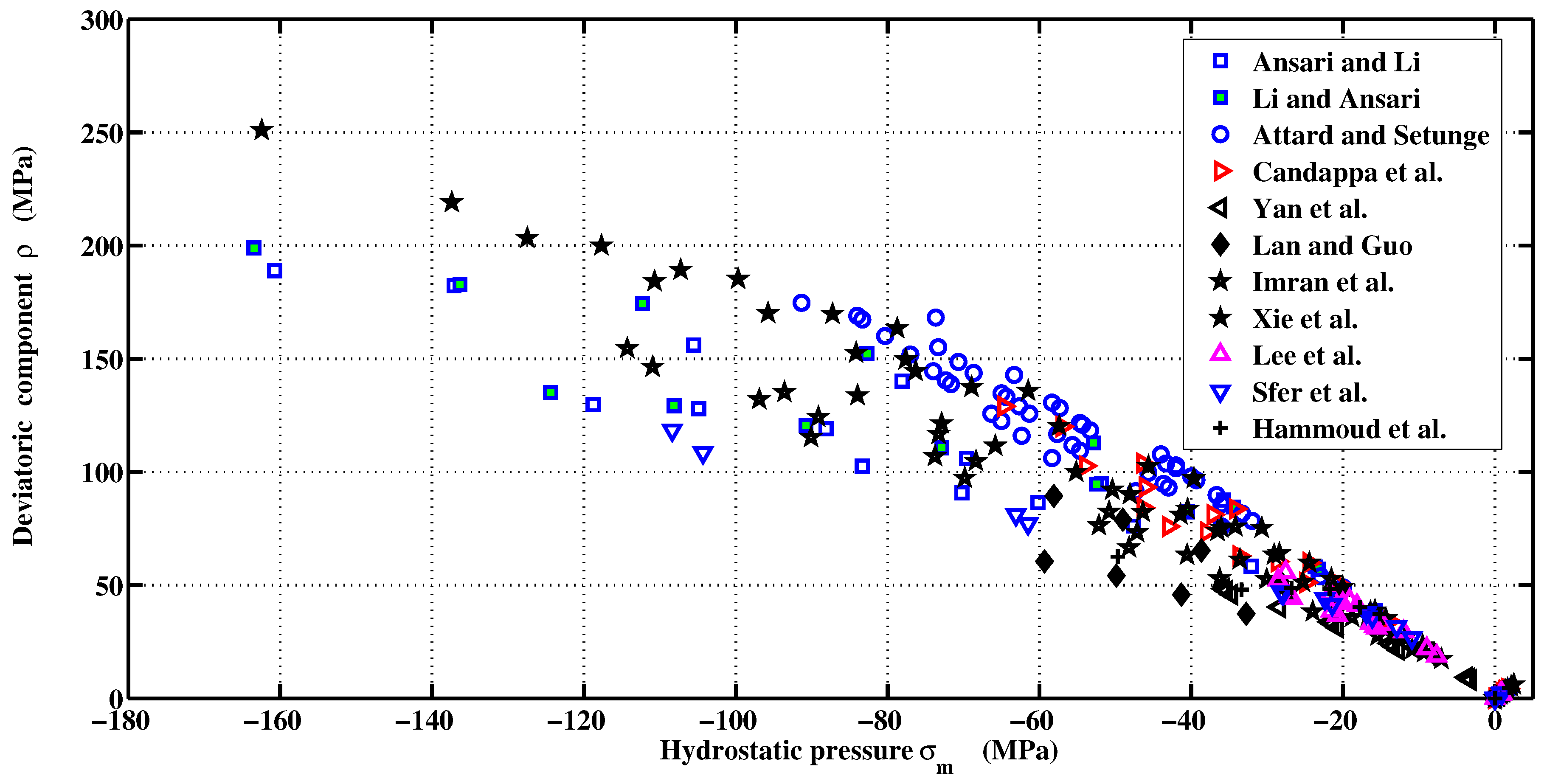
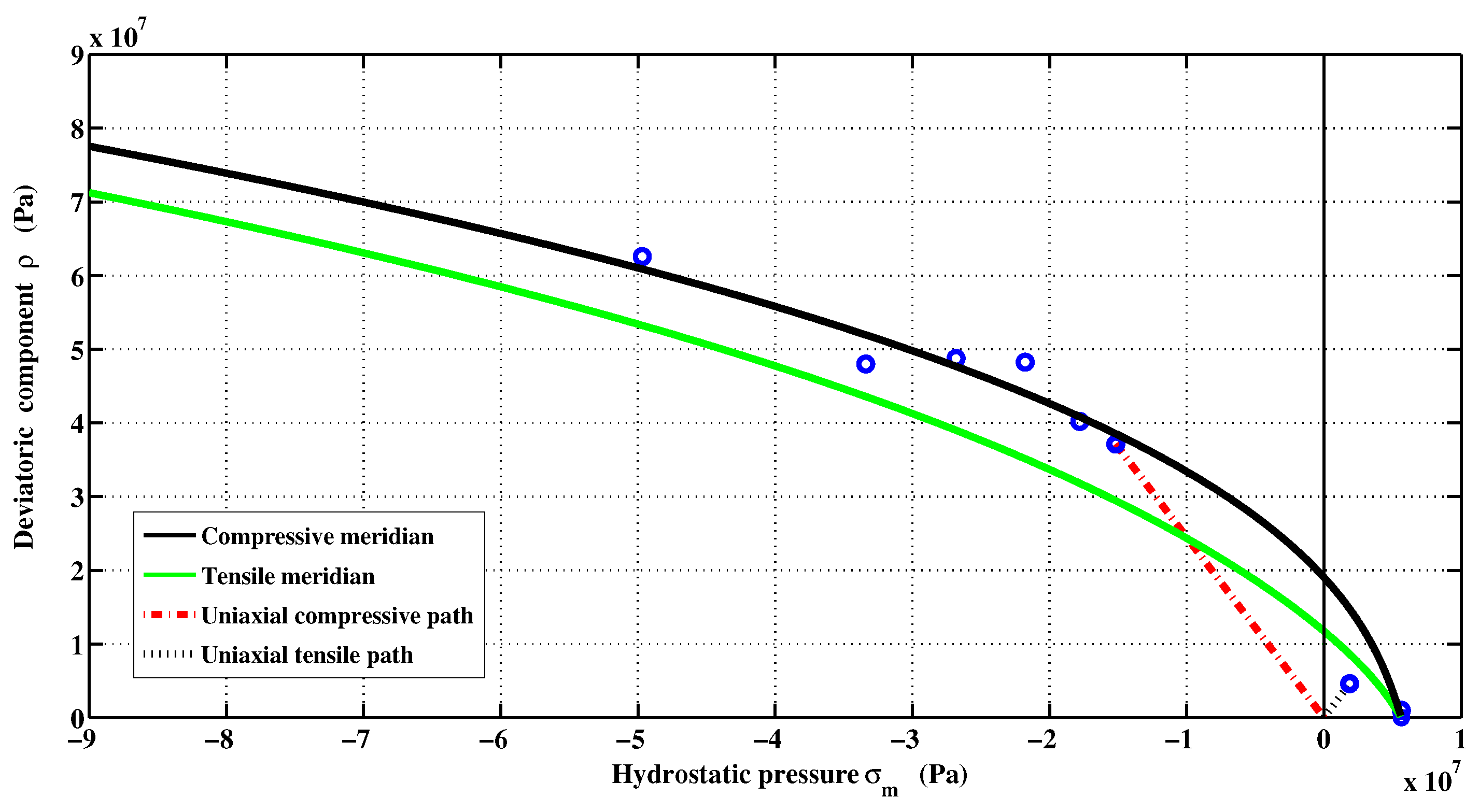
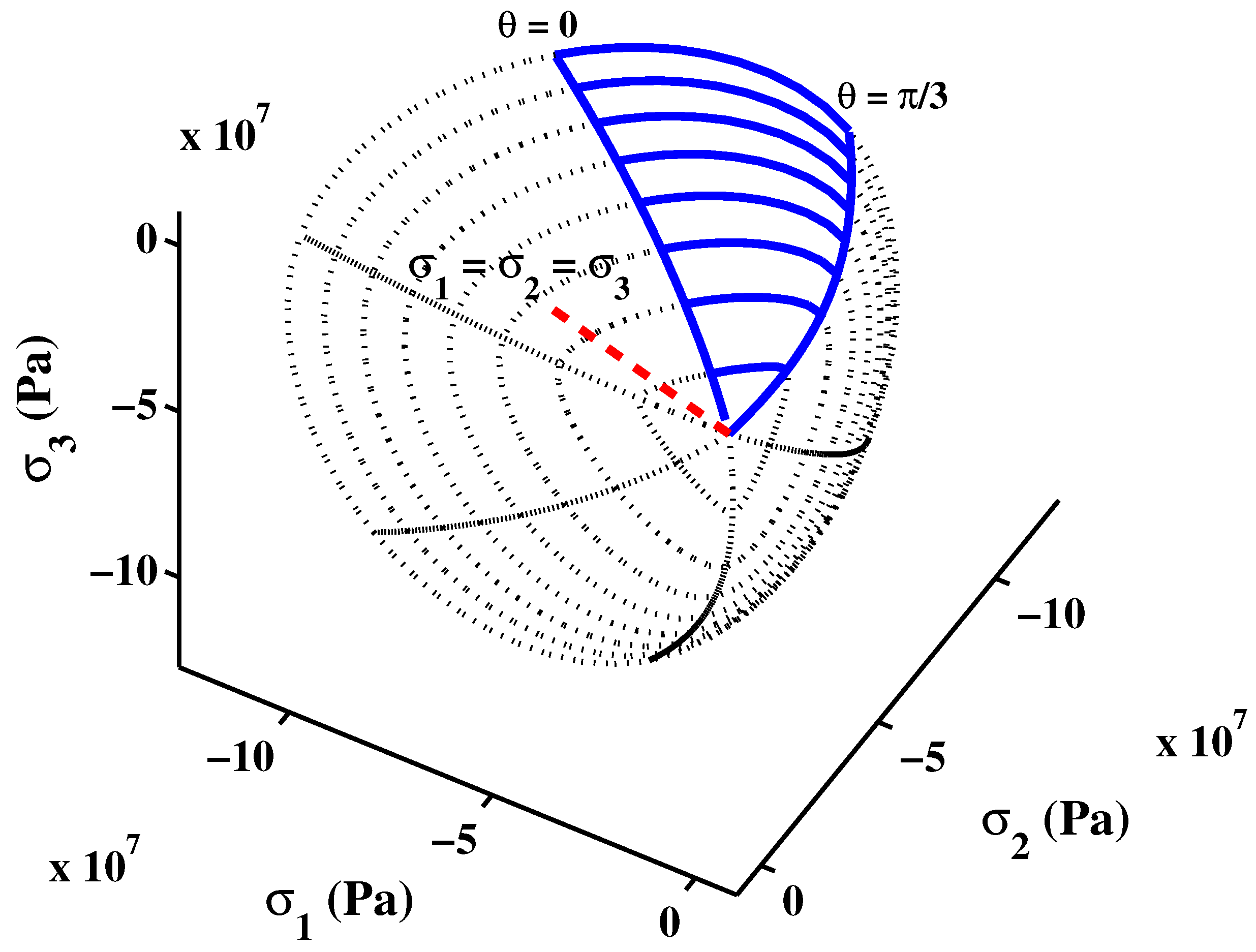
2.2. Isotropic Loading Surfaces in Pre- and Post-Peak
2.2.1. Isotropic Hardening
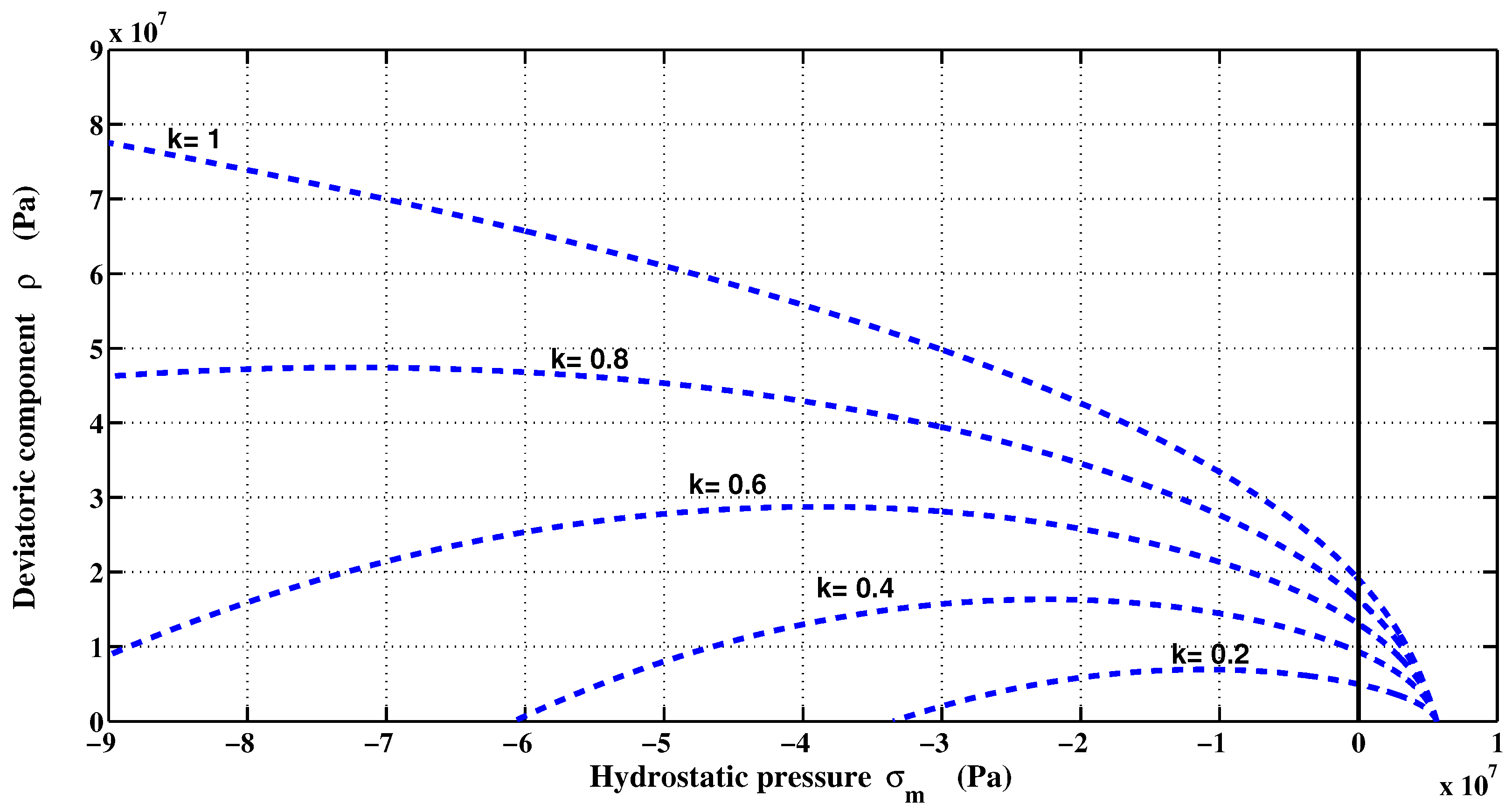
2.2.2. Isotropic Softening
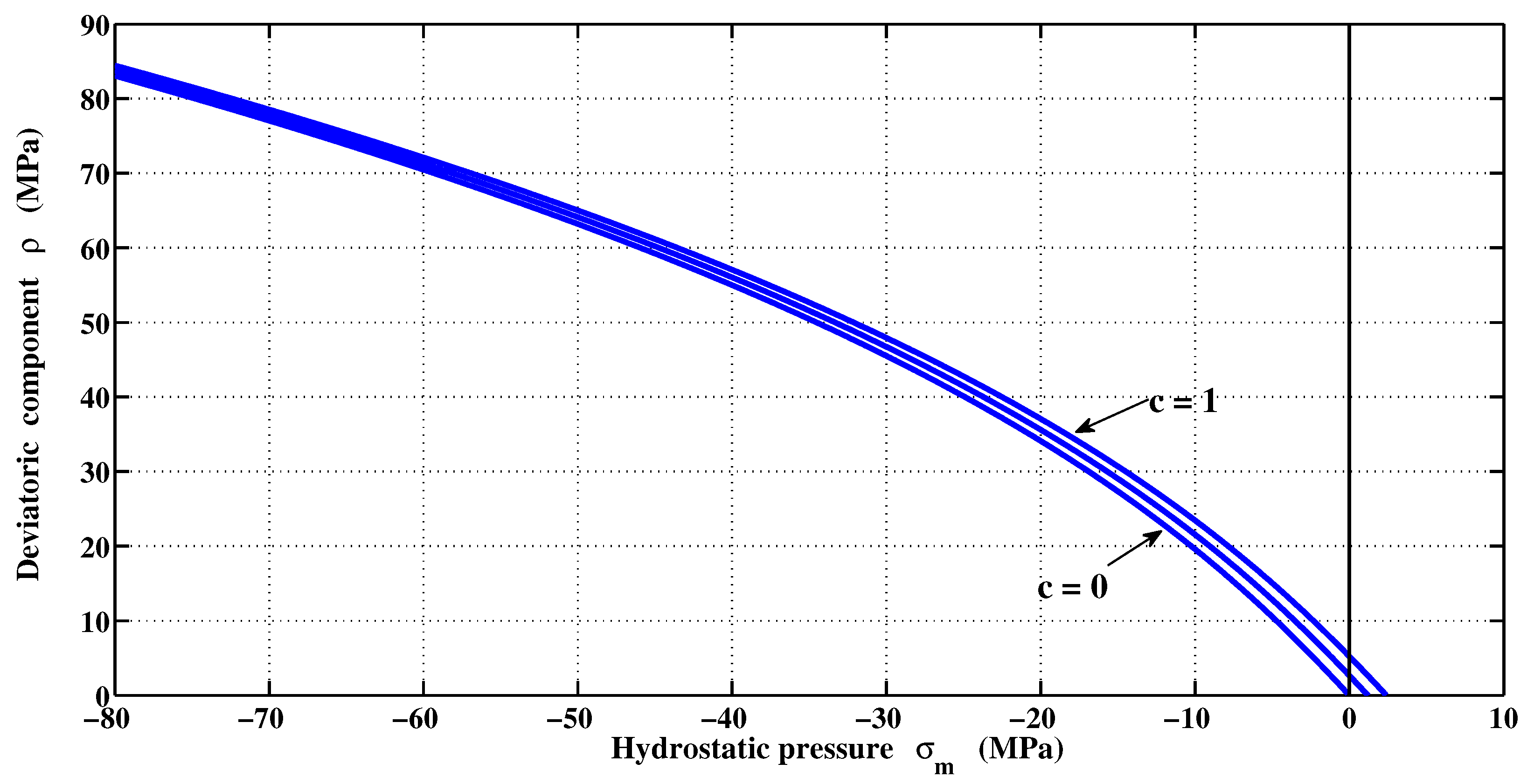
3. Plastic Potential Function
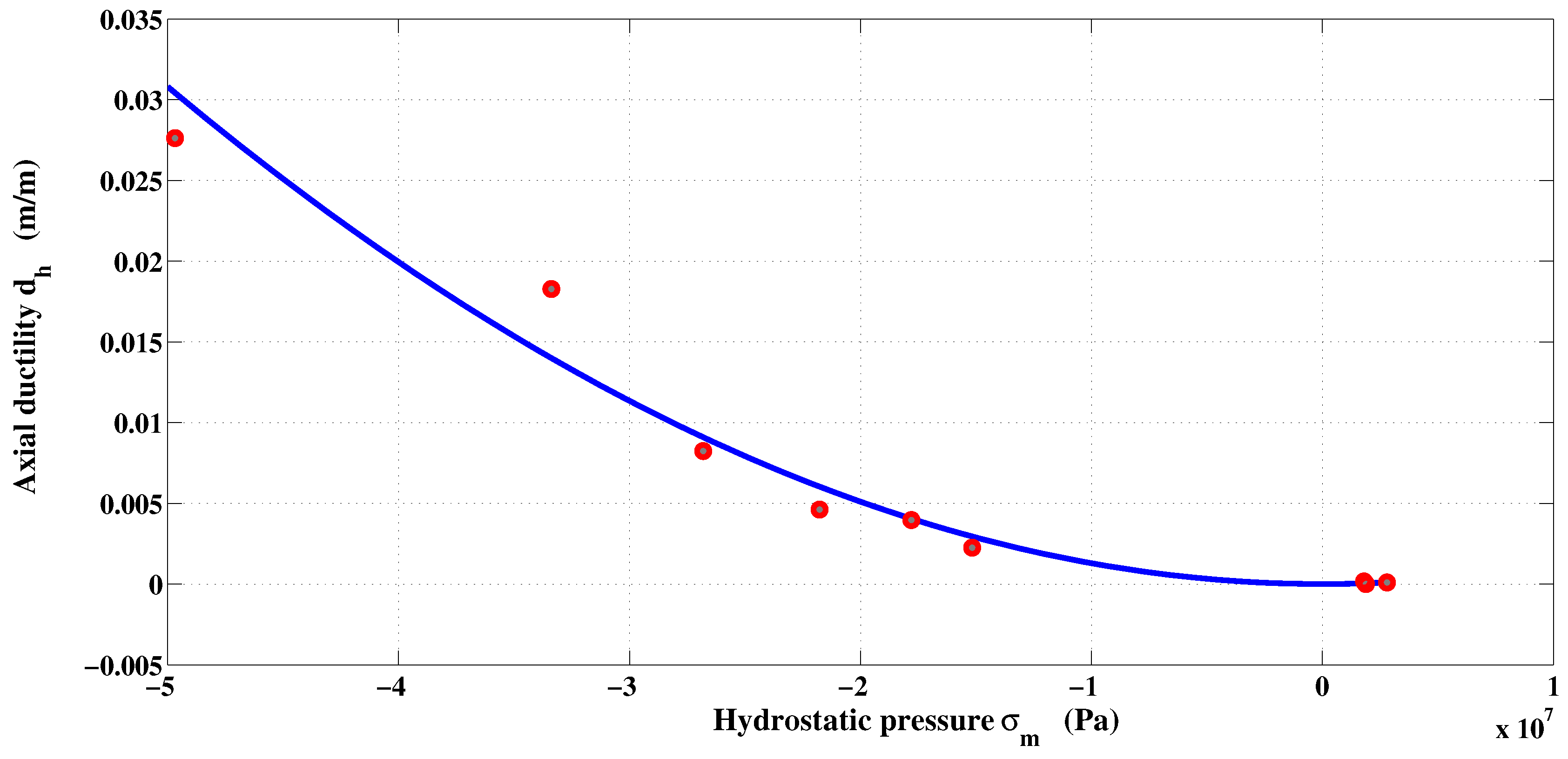
4. Hardening and Softening Parameter Functions
5. Algorithmic Formulation
5.1. Evaluation of Convenient Stress for Plastic Potential
5.2. Resolution Scheme
- Calculating the first elastic prediction:
- In the presence of non-associated flow, identify a particular value of ρ for and calculate the gradient .
- Compute and the stresses at point C: , where is the elastic test point; is elasticity tensor; and is effective plastic modulus (g is generic variable, for hardening and for softening).
- Update the equivalent plastic strain in hardening (softening) and the strength parameter during the hardening(softening).
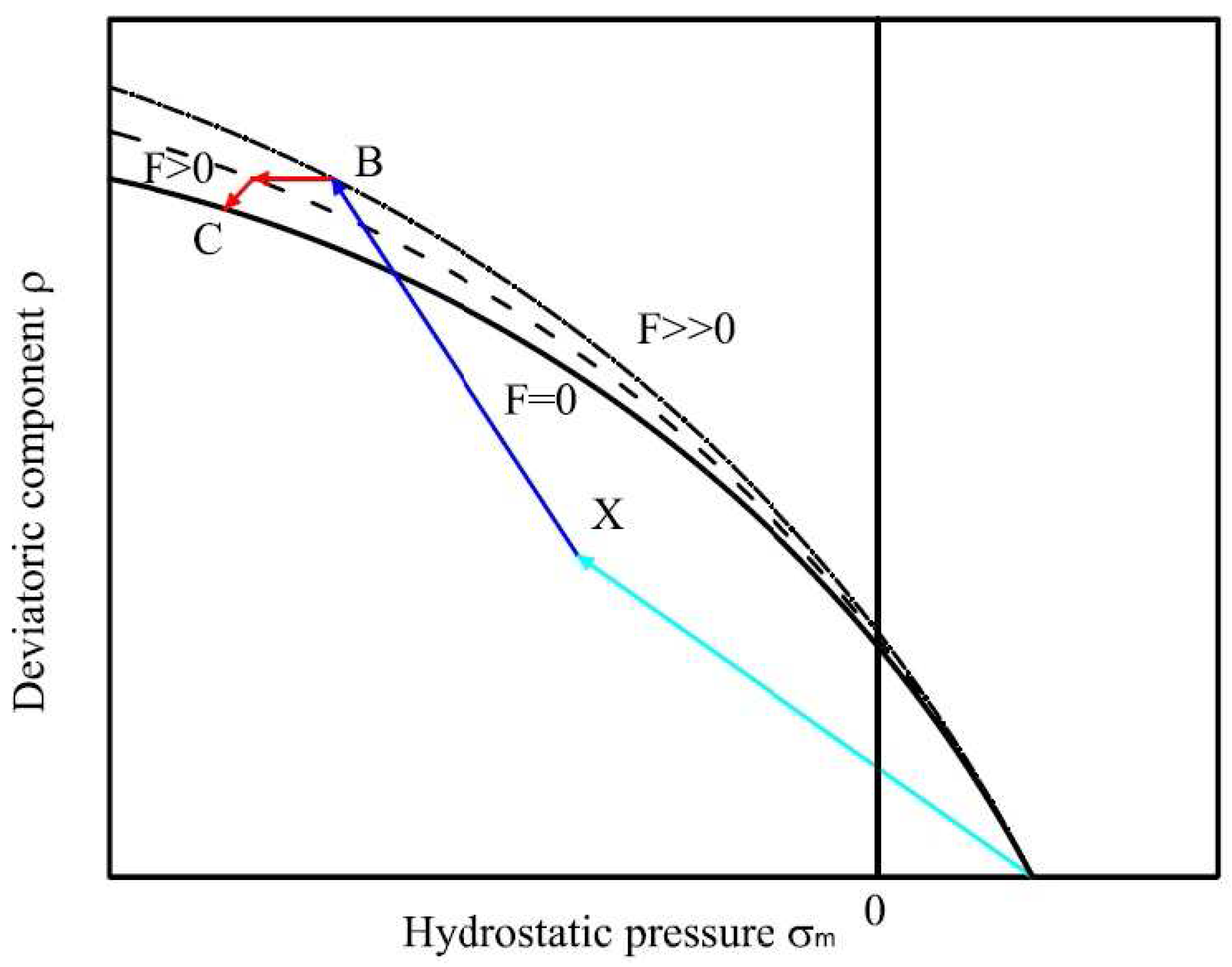
- Beginning the implicit backward-Euler method:
- 5.
- Calculate F and at the current point C.
- 6.
- Minimize the potential for and calculate the gradient .
- 7.
- Calculate the residual .
- 8.
- Compute the change of the plastic multiplier:and then change the stresses
- 9.
- Update the stresses at the point C: , then calculate the changes in plastic multiplier at point B (Figure 7):
- 10.
- Update the equivalent plastic strain and the strength parameter during the hardening(softening).
- 11.
- Repeat the procedure from step 5 until and F are below a certain tolerance.
6. Calibration
- It should promote a positive change in volumetric plastic in the region of positive pressure related to the mode of crack opening.
- It should promote a change in plastic form in the region of negative pressure related to the mode of cracking or splitting in shear compression.
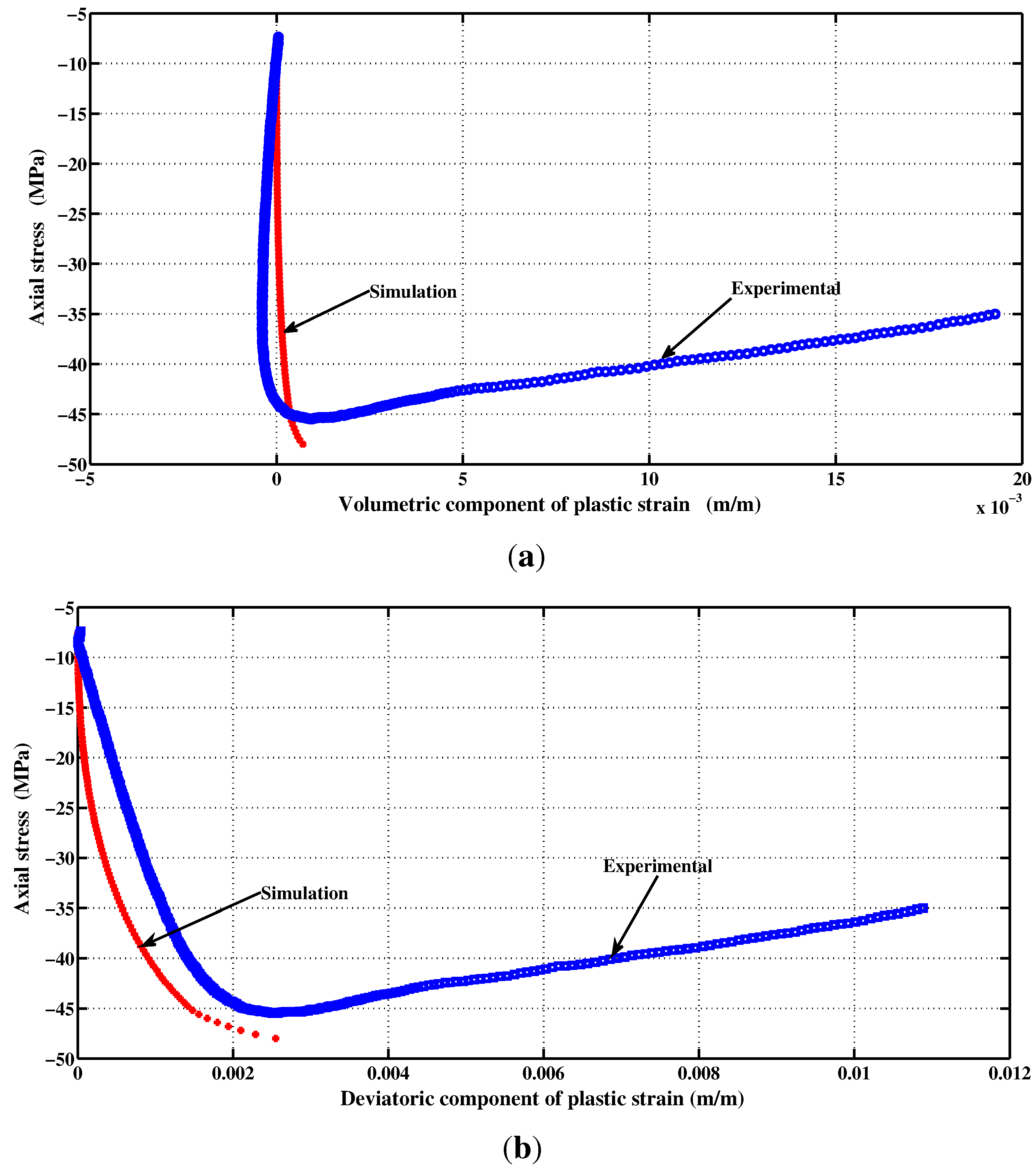
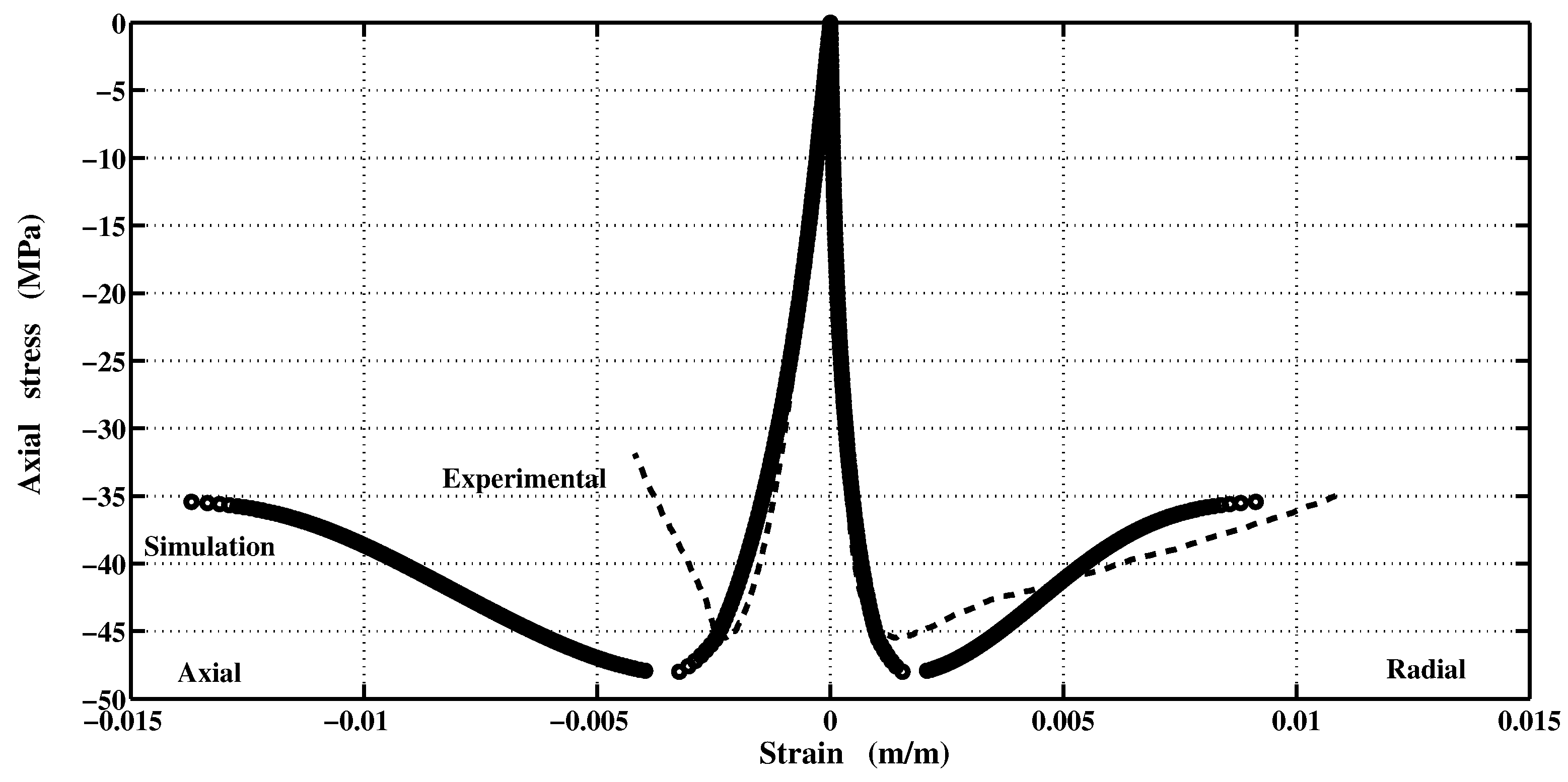
7. Numerical Experiments for Various Loading Scenarios
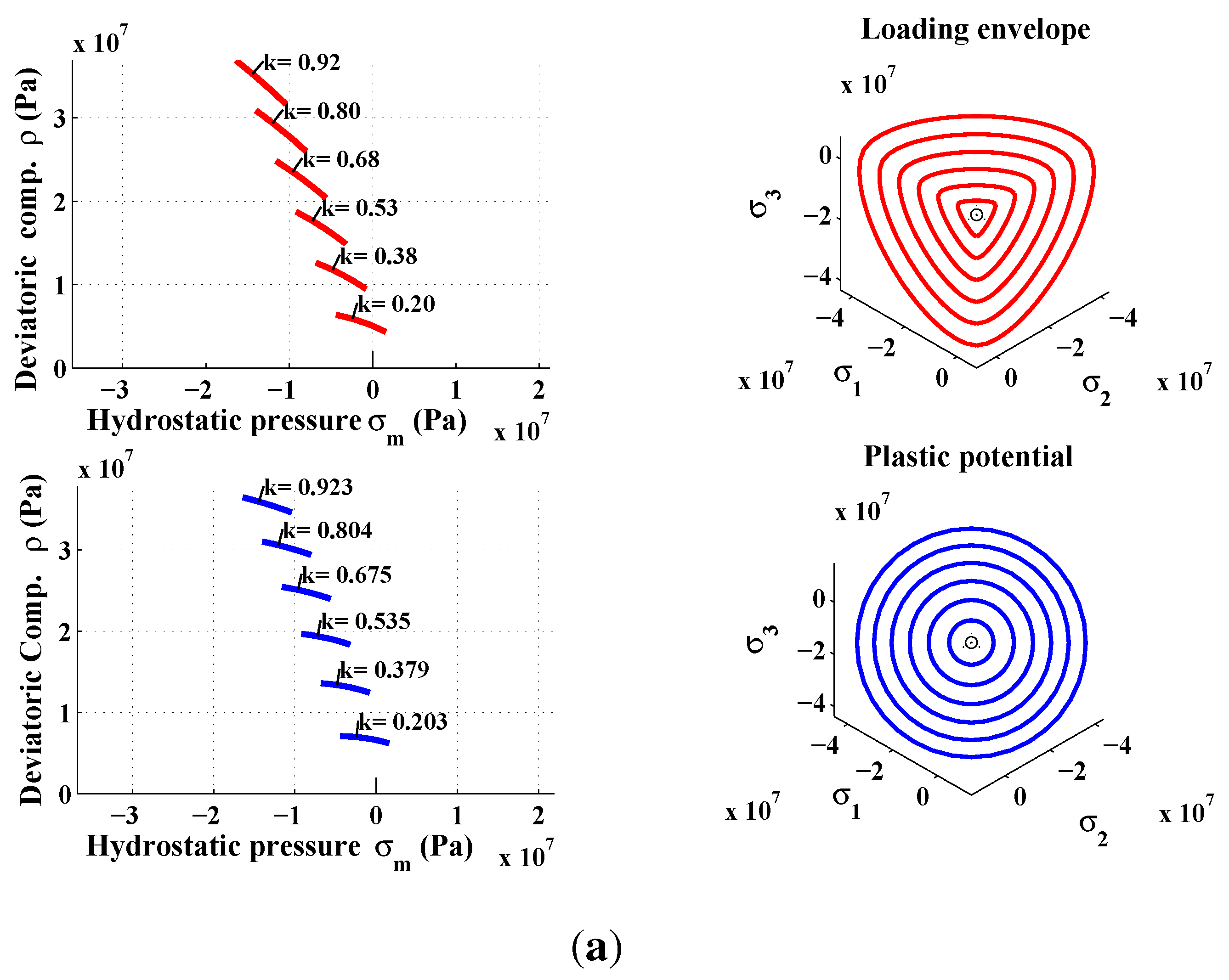
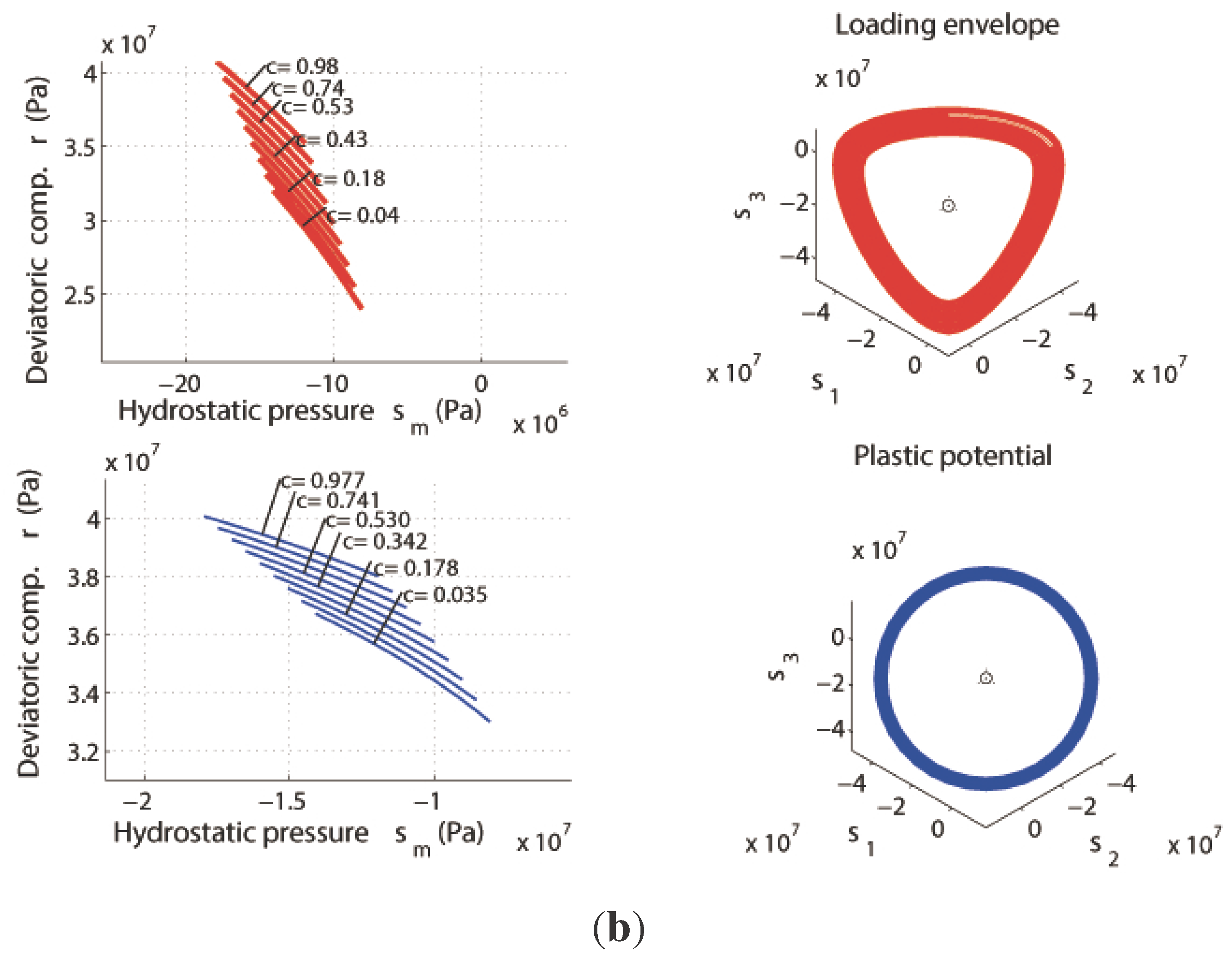
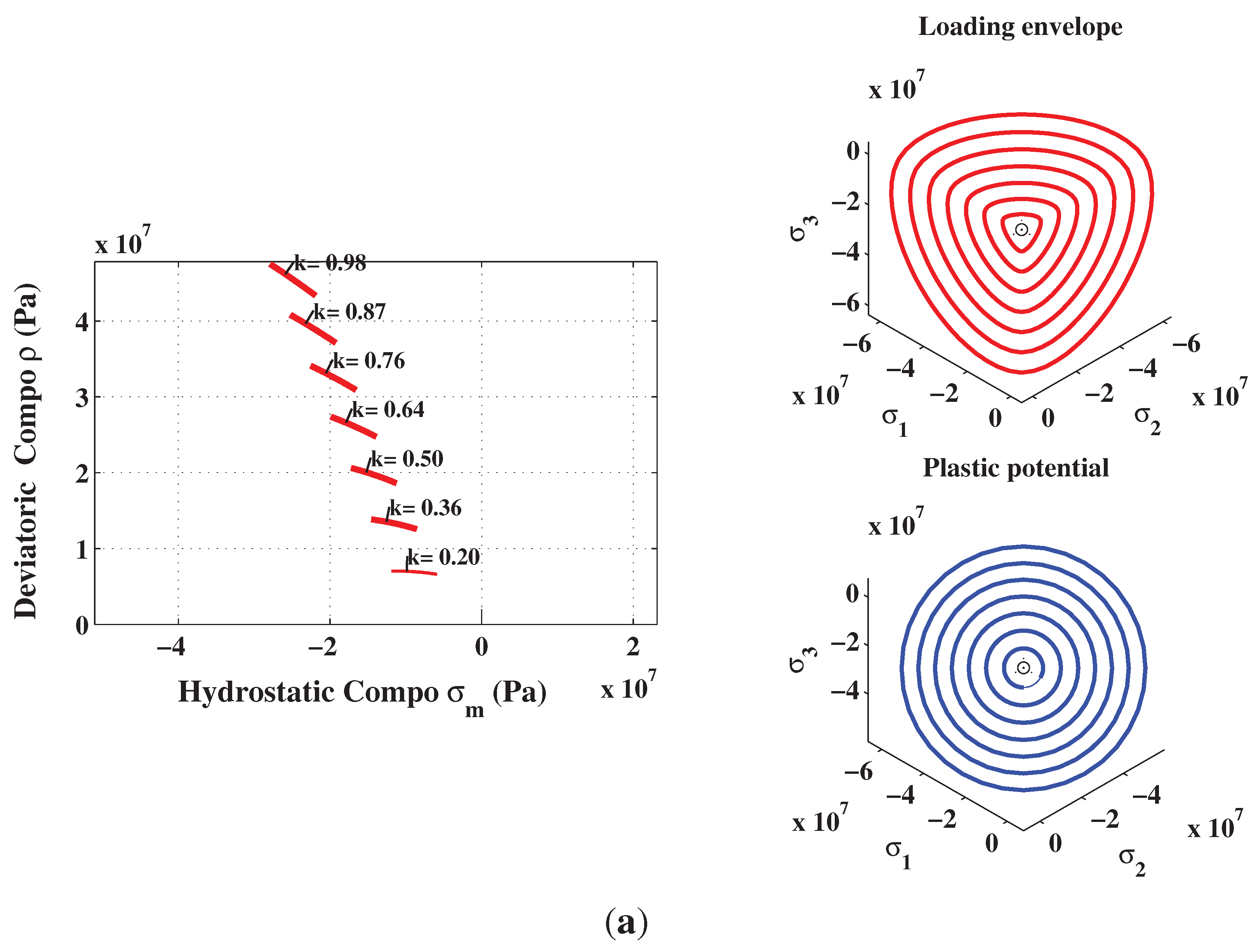
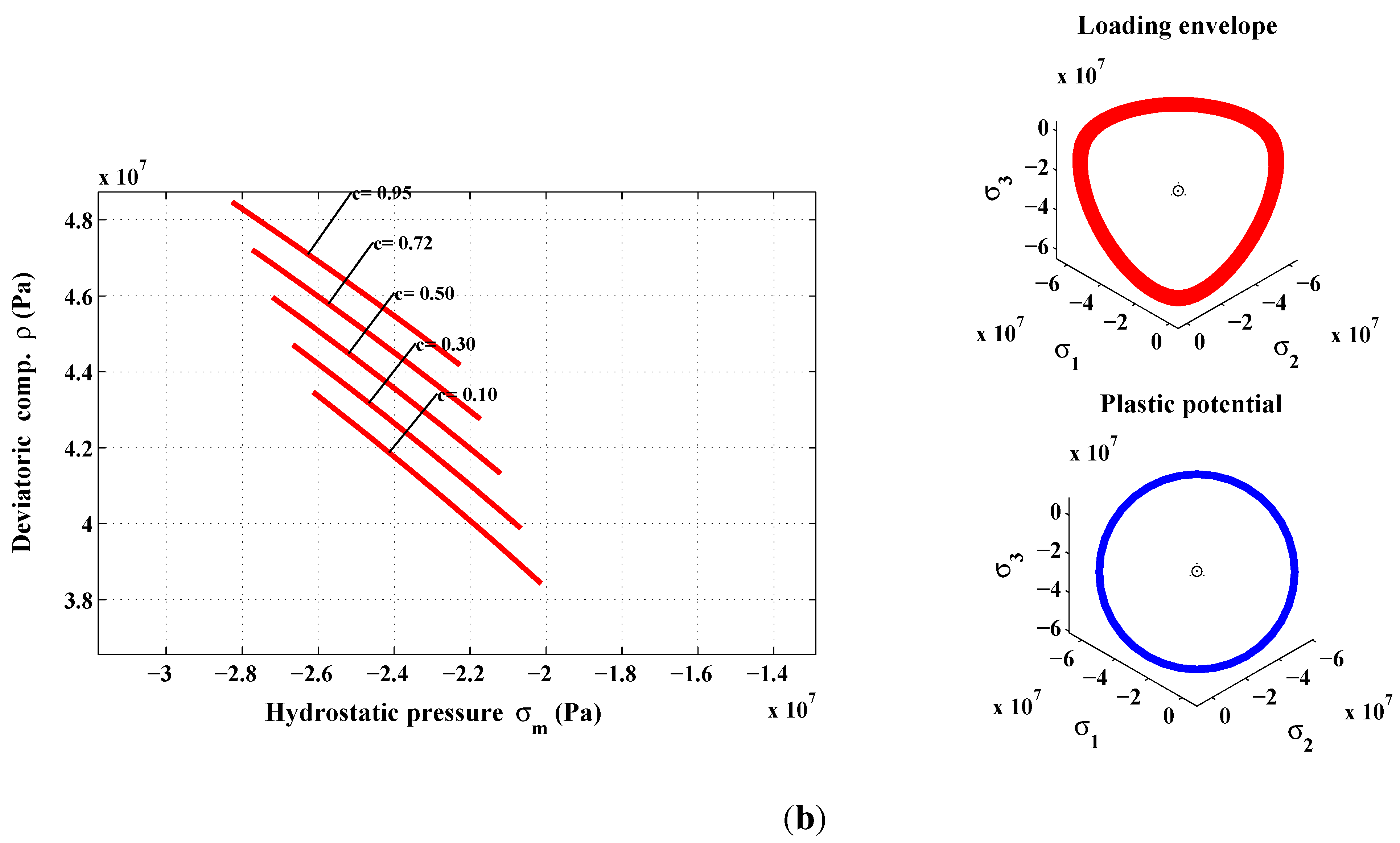
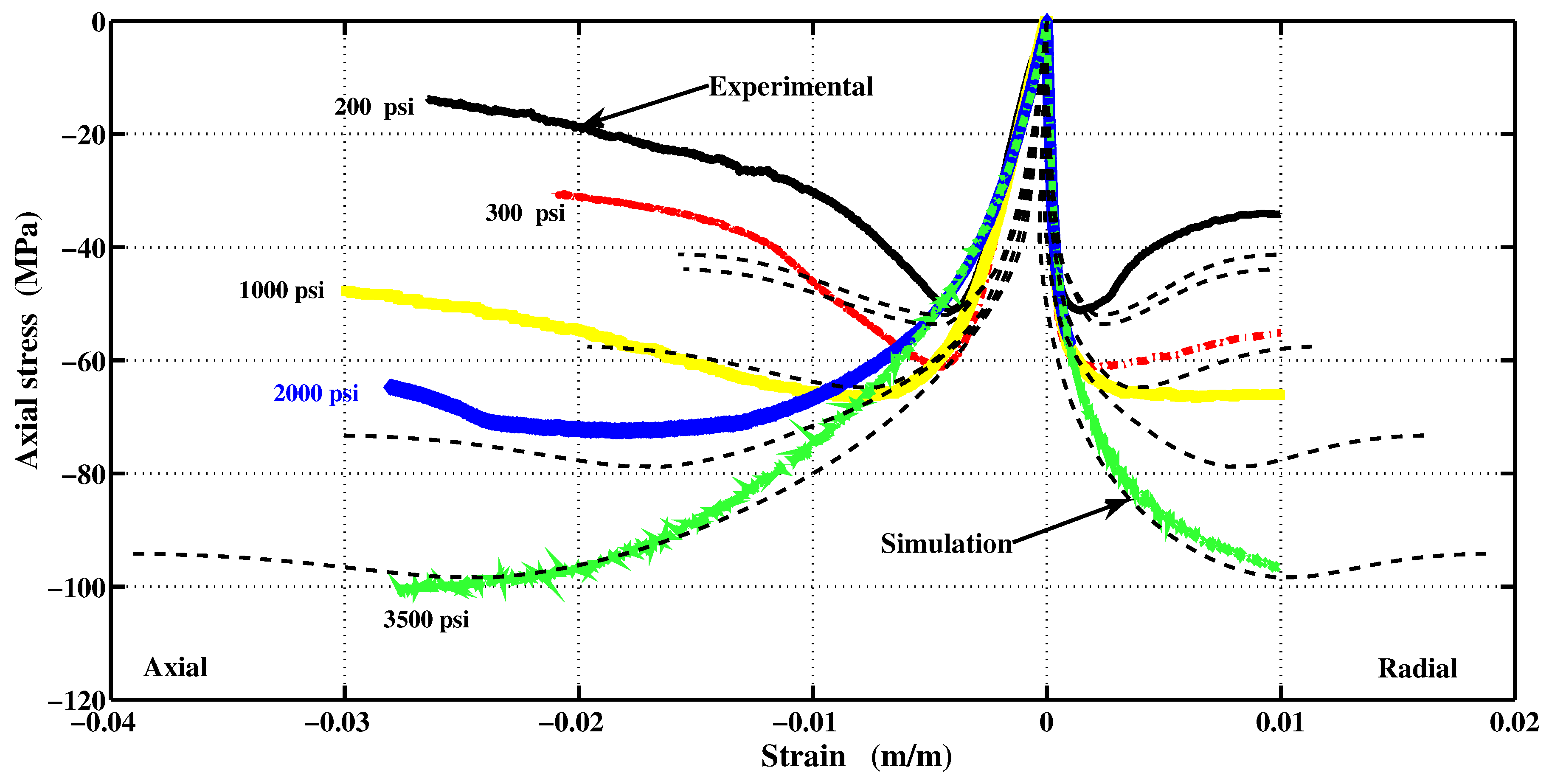
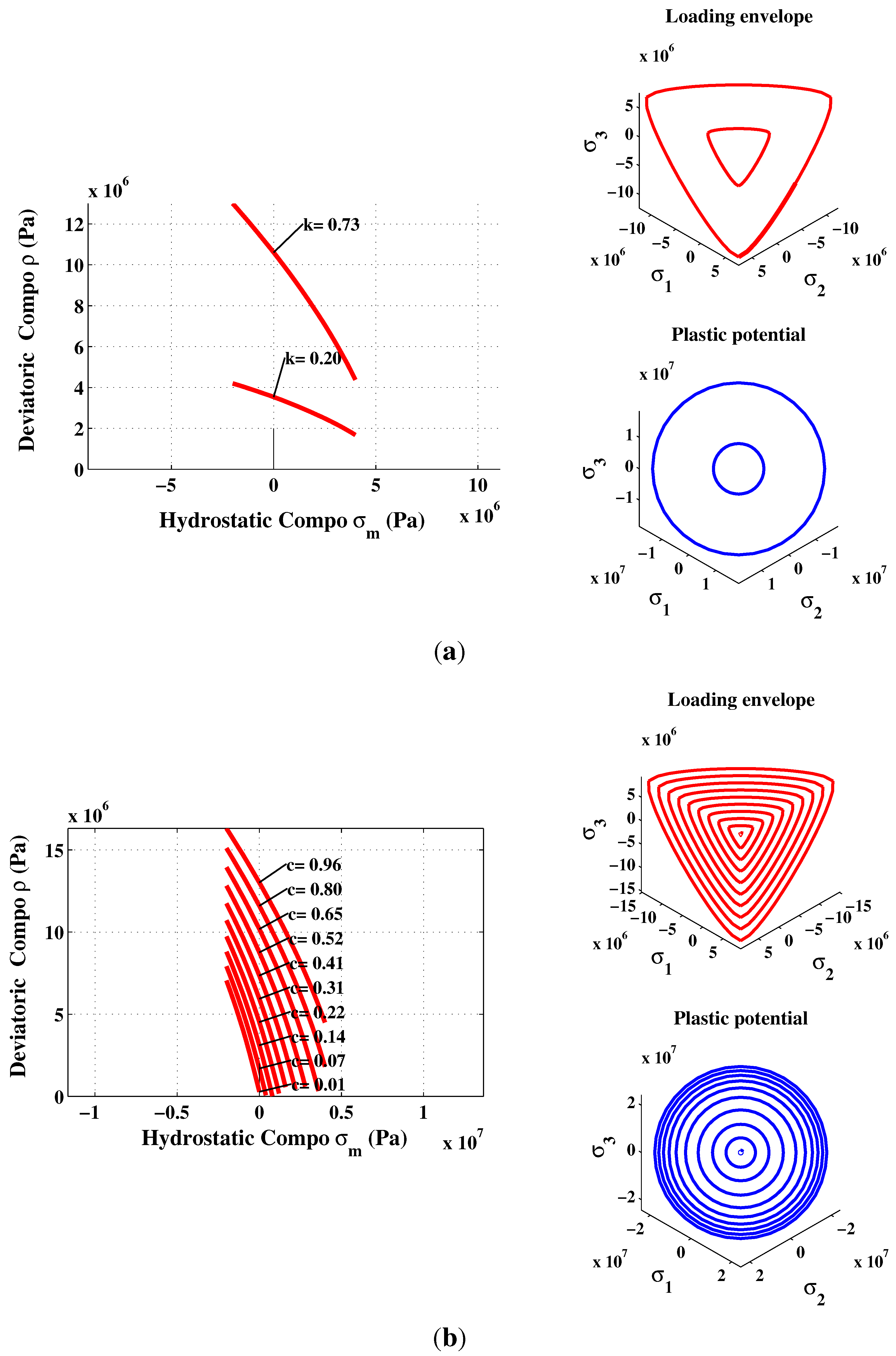
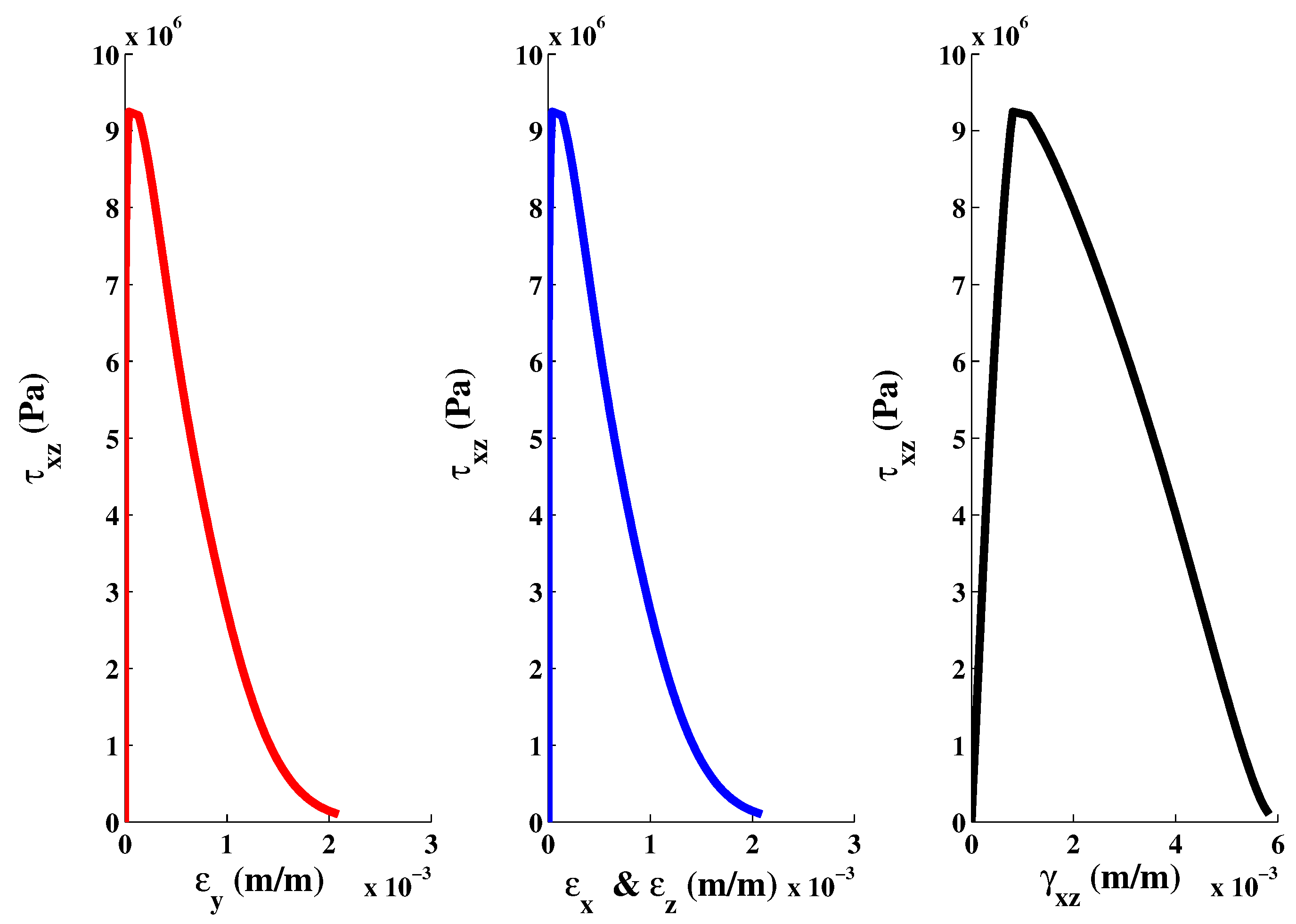
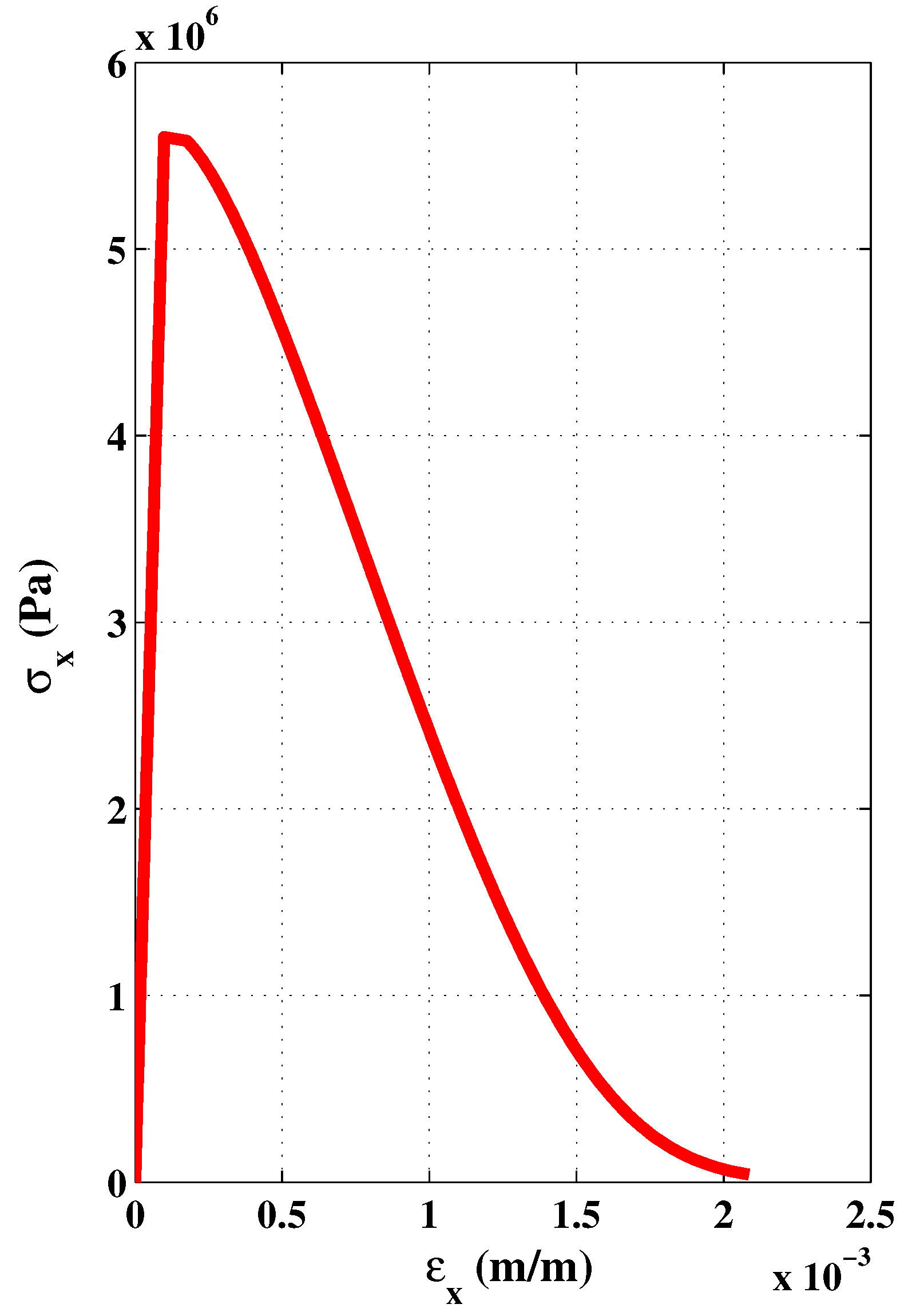
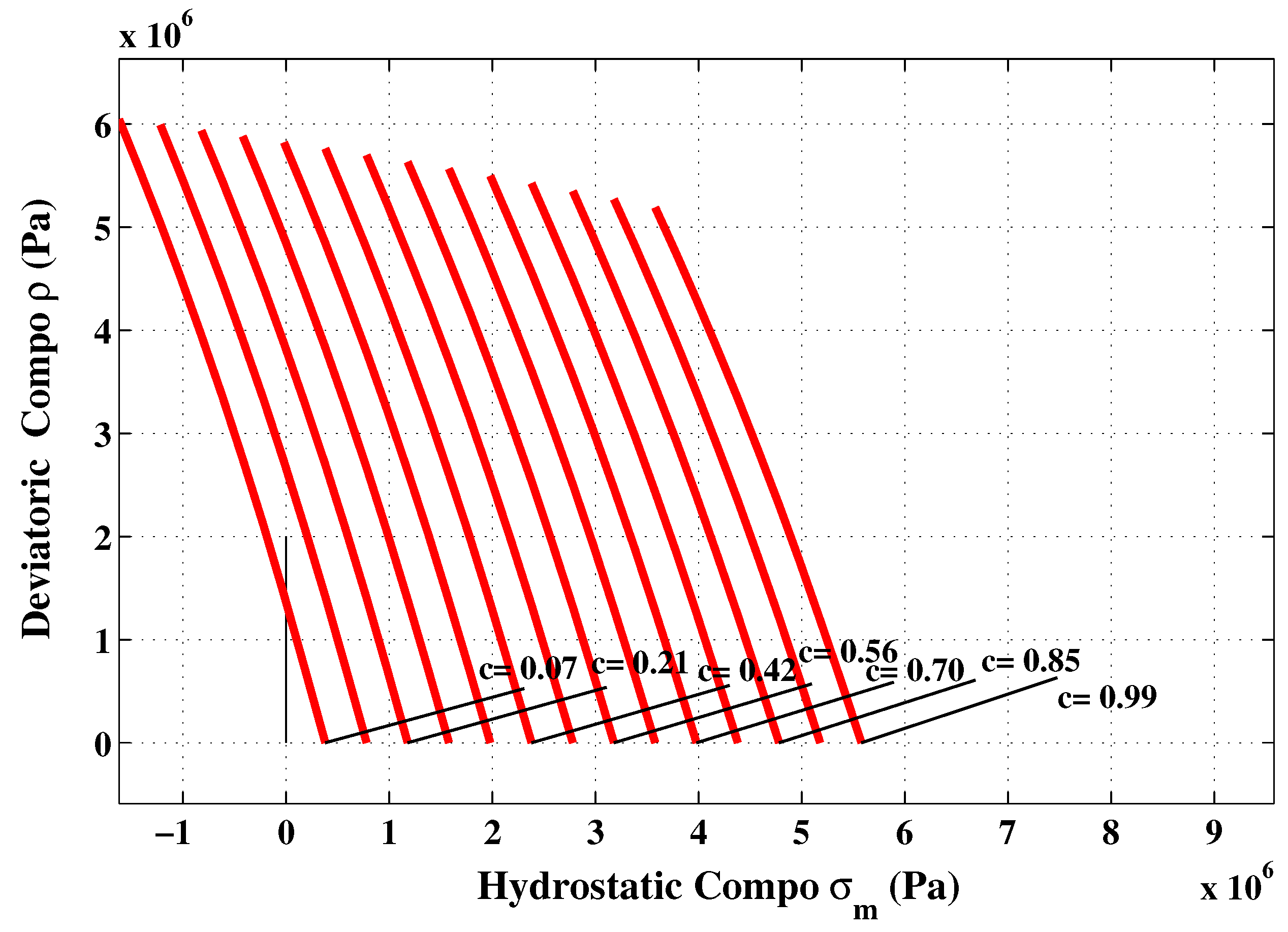
8. Conclusions
- A five parameters loading surface, which was adapted and calibrated by a simple procedure.
- Uncoupled hardening and softening functions following the accumulation of plastic strain and ductility evolution.
- A new ductility function was proposed and fitted experimentally.
- A new nonlinear plastic potential function was developed and calibrated using database of test results (uniaxial compression).
- As the failure criterion and plastic potential do not undergo the same stress states, a projection procedure has been adopted and applied to the concrete case. The calculation of normal is accurate and verified through numerical simulations.
Acknowledgements
Conflicts of Interest
References
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: New York, NY, USA, 1950. [Google Scholar]
- Babu, R.; Benipal, G.; Singh, A. Constitutive modelling of concrete: An overview. Asian J. Civil Eng. Build. Hous. 2005, 6, 211–246. [Google Scholar]
- Chen, A.; Chen, W. Constitutive relations for concrete. J. Eng. Mech. Div. 1975, 101, 465–481. [Google Scholar]
- Lin, F.B.; Bazant, Z.; Chern, J.C.; Marchertas, A. Concrete model with normality and sequential identification. Comput. Struct. 1987, 26, 1011–1025. [Google Scholar] [CrossRef]
- Pekau, O.; Zhang, Z. Strain-space cracking model for concrete and its application. Comput. Struct. 1994, 51, 151–162. [Google Scholar] [CrossRef]
- Menetrey, P.; Willam, K. A triaxial failure criterion for concrete and its generalization. ACI Struct. J. 1995, 92, 311–318. [Google Scholar]
- Kang, H. Triaxial Constitutive Model for Plain and Reinforced Concrete Behavior. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1997. [Google Scholar]
- Kang, H.; Willam, K. Localisation characteristics of triaxial concrete model. J. Eng. Mech. 1999, 125, 941–950. [Google Scholar] [CrossRef]
- Grassl, P.; Lundgren, K.; Gylltoft, K. Concrete in compression: A plasticity theory with a novel hardening law. Int. J. Solids Struct. 2002, 39, 5205–5223. [Google Scholar] [CrossRef]
- Papanikolaou, V.; Kappos, A. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef]
- Imran, I.; Pantazopoulou, S. Plasticity model for concrete under triaxial compression. J. Eng. Mech. 2001, 127, 281–290. [Google Scholar] [CrossRef]
- Aubertin, M.; Li, L.; Simon, R.; Bussiere, B. A General Plasticity and Failure Criterion for Materials of Variable Porosity; Technical Report EPM-RT-2003-11; École Polytechnique de Montréal: Montréal, QC, Canada, 2003. [Google Scholar]
- Drucker, D.; Prager, W. Soil mechanics and plastic analysis for limit design. Q. Appl. Math. 1952, 10, 157–165. [Google Scholar]
- Chen, W.F. Plasticity in Reinforced Concrete; J. Ross Publishing: Plantation, FL, USA, 2007. [Google Scholar]
- Lade, P.; Duncan, J. Cubical triaxial tests on cohesionless soil. J. Soils Mech. Found. Div. 1973, 99, 793–812. [Google Scholar] [CrossRef]
- Lade, P.; Duncan, J. Elastoplastic stress-strain theory for cohesionless soil. J. Geotech. Eng. 1975, 101, 1035–1052. [Google Scholar]
- Lade, P. Elastoplastic stress-strain theory cohesionless soil with curved yield surfaces. Int. J. Solids Struct. 1977, 13, 1019–1035. [Google Scholar] [CrossRef]
- Schreyer, H. Smooth limit surfaces for metals, concrete and geotechnical materials. J. Eng. Mech. 1989, 115, 1960–1975. [Google Scholar] [CrossRef]
- Hane, D.; Chen, W. Constitutive modeling in analysis of concrete structures. J. Eng. Mech. 1987, 113, 577–593. [Google Scholar] [CrossRef]
- Ohtani, Y.; Chen, W. A plastic softening model for concrete materials. Comput. Struct. 1989, 33, 1047–1055. [Google Scholar] [CrossRef]
- Pramono, E.; Willam, K. Fracture energy based plasticity formulation of plain concrete. J. Eng. Mech. 1989, 115, 1183–1204. [Google Scholar] [CrossRef]
- Etse, G.; Willam, K. Fracture energy formulation for inelastic behavior of plain concrete. J. Eng. Mech. 1994, 120, 1983–2011. [Google Scholar] [CrossRef]
- Crouch, R.S.; Tahar, B. Application of a Stress Return Algorithm for Elasto-Plastic Hardening-Softening Models with High Yield Surface Curvature. In Proceedings of the European Congress on Computational Methods Sciences and Engineering (CD-ROM), Barcelona, Spain, 11–14 September 2000; Onate, E., et al., Eds.; ECCOMAS: Barcelona, Espana, 2000. [Google Scholar]
- Meyer, R.; Ahrens, H.; Duddeck, H. Material model for concrete in cracked and uncracked states. J. Eng. Mech. 1989, 120, 1877–1895. [Google Scholar] [CrossRef]
- Willam, K.; Warnke, E. Constitutive Model for the Triaxial Behavior of Concrete. In Proceedings of the Concrete Structure Subjected to Triaxial Stresses, International Association for Bridge and Structural Engineering, Bergamo, Italy, 17–19 May 1974; IABSE Proceedings: Zurich, Switzerland, 1975; Volume 19, pp. 1–30. [Google Scholar]
- Li, Q.; Ansari, F. High-strength concrete in triaxial compression by different sizes of specimens. ACI Mater. J. 2000, 97, 684–689. [Google Scholar]
- Ansari, F.; Li, Q. High-strength concrete subjected to triaxial compression. ACI Mater. J. 1998, 95, 747–755. [Google Scholar]
- Candappa, D.; Sanjayan, J.; Setunge, S. Complete triaxial stress strain curves of high-strength concrete. J. Mater. Civil Eng. 2001, 13, 209–215. [Google Scholar] [CrossRef]
- Imran, I.; Pantazopoulou, S. Experimental study of plain concrete under triaxial stresses. ACI Mater. J. 1996, 93, 589–601. [Google Scholar]
- Sfer, D.; Carol, I.; Gettu, R.; Etse, G. Study of the behavior of concrete under triaxial compression. J. Eng. Mech. 2002, 128, 156–163. [Google Scholar] [CrossRef]
- Xie, J.; Elwi, A.; MacGregor, J. Mechanical properties of three high-strength concretes containing silica fuma. ACI Mater. J. 1995, 92, 1–11. [Google Scholar]
- Yan, D.; Lin, G.; Chen, G. Dynamic properties of plain concrete in triaxial stress state. ACI Mater. J. 2009, 106, 89–94. [Google Scholar]
- Attard, M.; Setunge, S. Stress-strain relationship of confined and unconfined concrete. ACI Mater. J. 1996, 93, 432–442. [Google Scholar]
- Lan, S.; Guo, Z. Experimental investigation of multiaxial compressive strength of concrete under different stress paths. ACI Mater. J. 1997, 94, 427–434. [Google Scholar]
- Lee, S.; Song, Y.; Han, S. Biaxial behavior of plain concrete of nuclear containment building. Nuclear Eng. Des. 2004, 227, 143–153. [Google Scholar] [CrossRef]
- Hammoud, R.; Yahia, A.; Boukhili, R. Triaxial compressive strength of concrete subjected to high temperatures. ASCE J. Mater. Civil Eng. 2013. [Google Scholar] [CrossRef]
- D’amours, G. Développement de lois Constitutives Thermomécaniques Pour les Matériaux à base de Carbone lors du préchauffage d’une cuve d’électrolyse (in French). Ph.D. Thesis, Université Laval, Québec, Canada, 2004. [Google Scholar]
- De Borst, R. Non-linear Analysis of Frictional Materials. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1986. [Google Scholar]
- Crisfield, M. Non-linear Finite Element Analysis of Solids and Structures; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Hammoud, R.; Boukhili, R.; Yahia, A. Unified Formulation for a Triaxial Elastoplastic Constitutive Law for Concrete. Materials 2013, 6, 4226-4248. https://doi.org/10.3390/ma6094226
Hammoud R, Boukhili R, Yahia A. Unified Formulation for a Triaxial Elastoplastic Constitutive Law for Concrete. Materials. 2013; 6(9):4226-4248. https://doi.org/10.3390/ma6094226
Chicago/Turabian StyleHammoud, Rabah, Rachid Boukhili, and Ammar Yahia. 2013. "Unified Formulation for a Triaxial Elastoplastic Constitutive Law for Concrete" Materials 6, no. 9: 4226-4248. https://doi.org/10.3390/ma6094226
APA StyleHammoud, R., Boukhili, R., & Yahia, A. (2013). Unified Formulation for a Triaxial Elastoplastic Constitutive Law for Concrete. Materials, 6(9), 4226-4248. https://doi.org/10.3390/ma6094226




