Terahertz Wave Propagation in a Nanotube Conveying Fluid Taking into Account Surface Effect
Abstract
:1. Introduction
2. Timoshenko Model for Nanotube Conveying Fluid
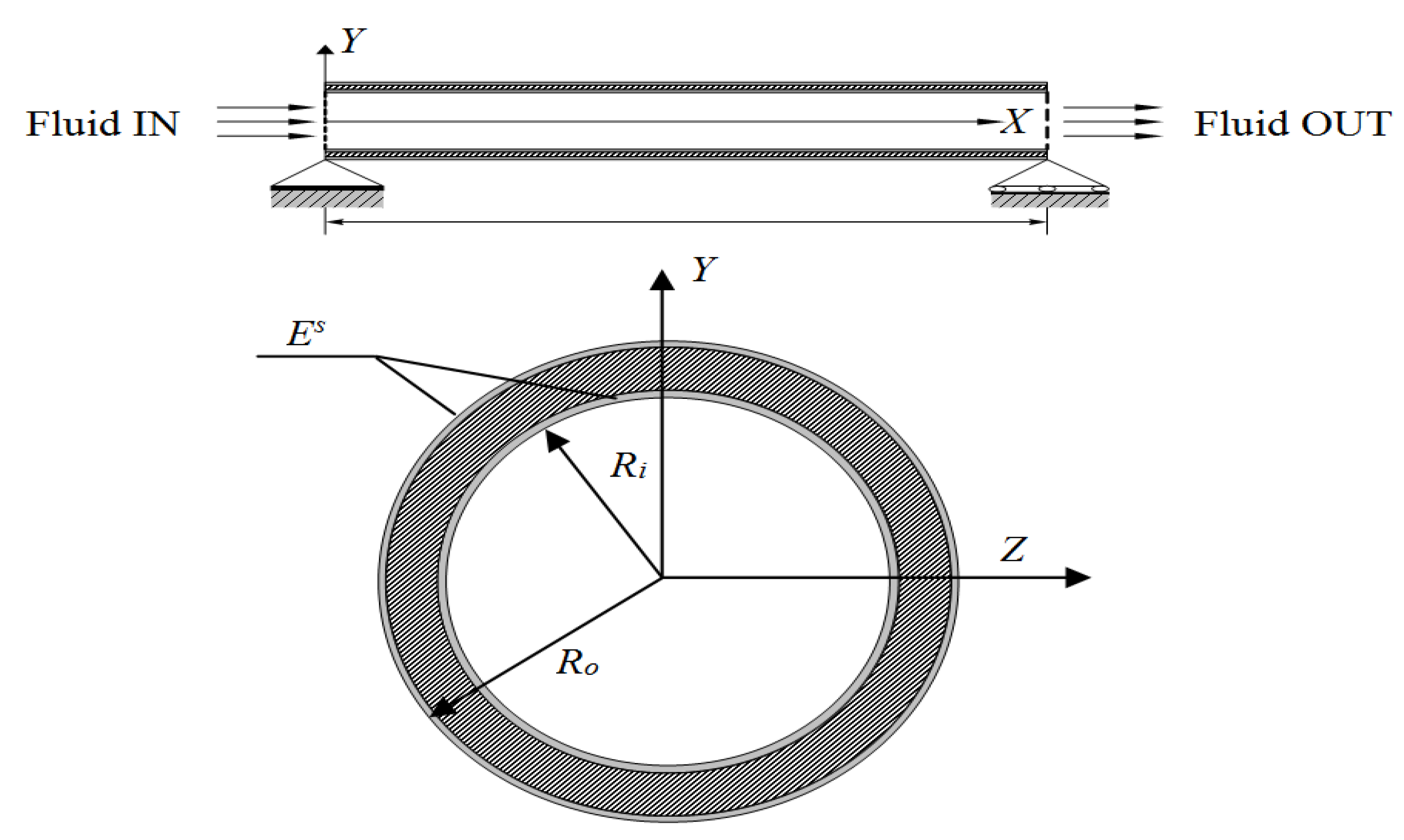
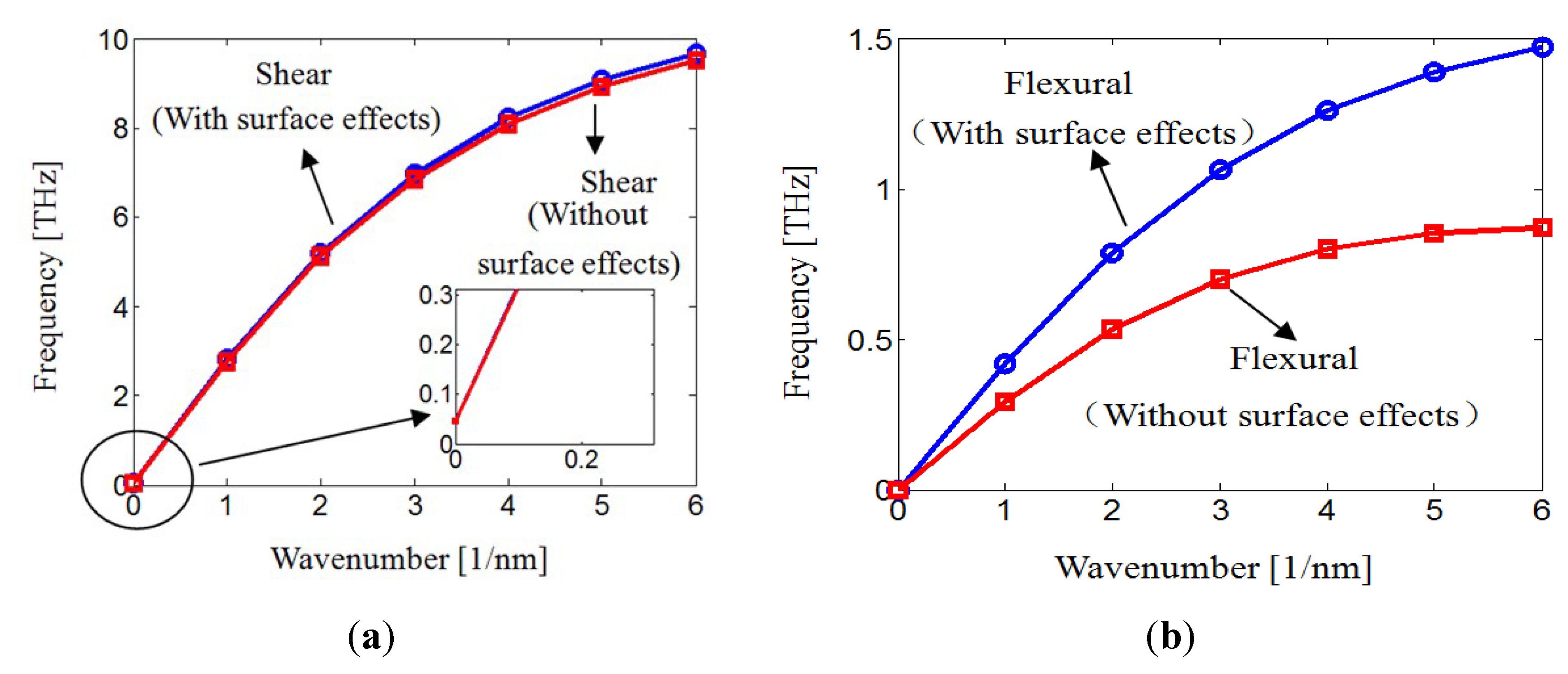
3. Numerical Results and Discussion
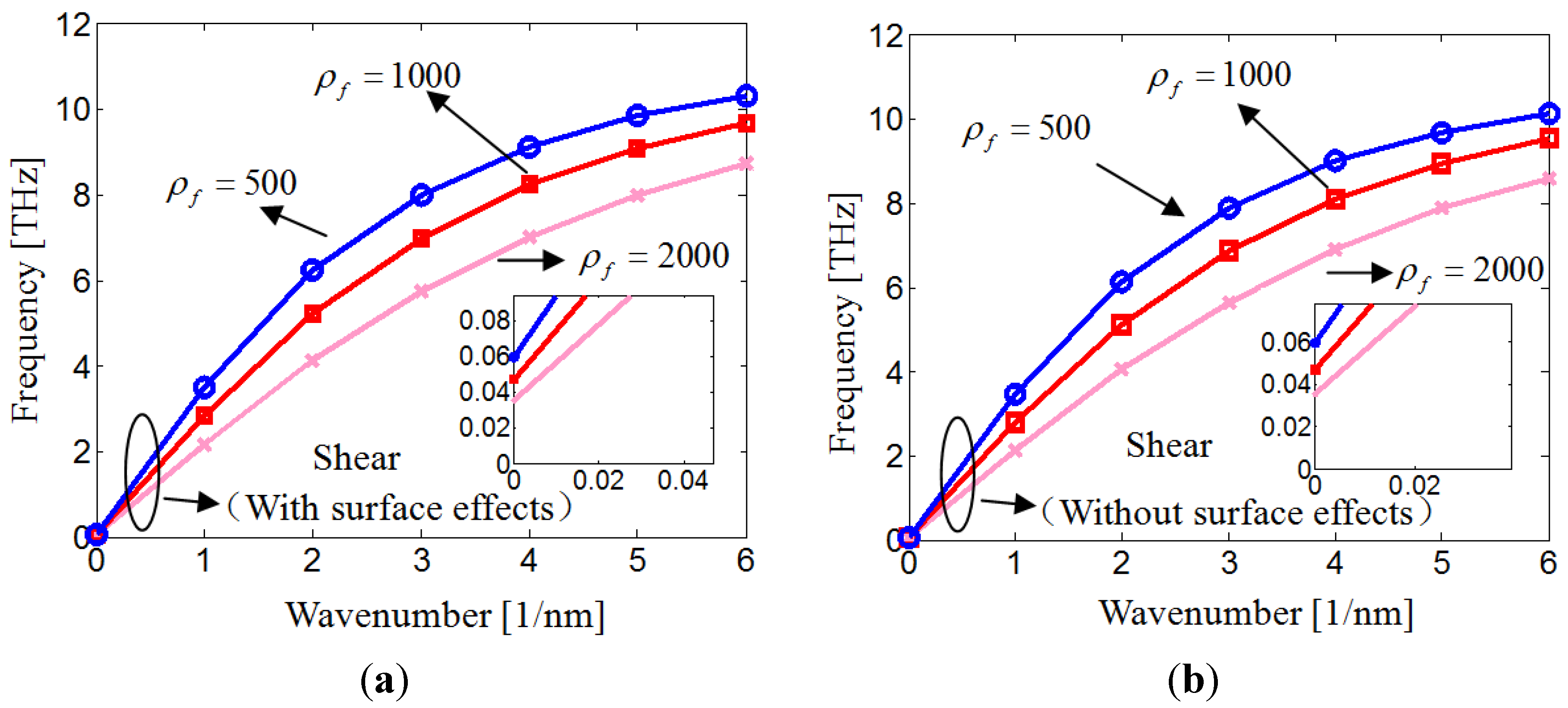
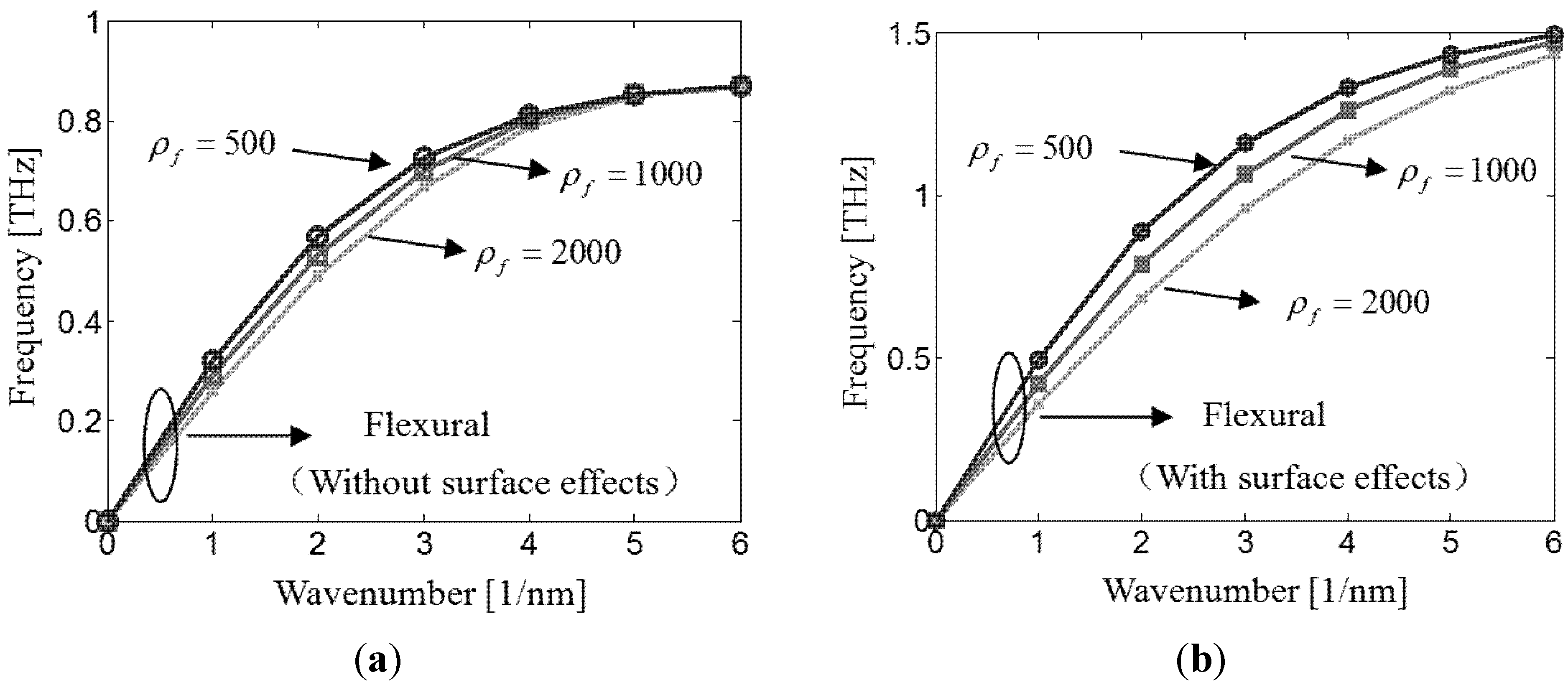
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Whitby, M.; Quirke, N. Fluid flow in carbon nanotubes and nanopipes. Nat. Nanotechnol. 2007, 2, 87–94. [Google Scholar]
- Kiani, K. Application of nonlocal beam models to double-walled carbon nanotubes under a moving nanoparticle. Part I: Theoretical formulations. Acta Mech. 2011, 216, 165–195. [Google Scholar]
- Wang, L.; Ni, Q.; Li, M.; Qian, Q. The thermal effect on vibration and instability of carbon nanotubes conveying fluid. Phys. E 2008, 40, 3179–3182. [Google Scholar]
- Yoon, J.; Ru, C.Q.; Mioduchowski, A. Vibration and instability of carbon nanotubes conveying fluid. Compos. Sci. Technol 2005, 65, 1326–1336. [Google Scholar]
- Joseph, S.; Aluru, N.R. Why are carbon nanotubes fast transporters of water. Nano Lett. 2008, 8, 452–458. [Google Scholar]
- Wang, L. A modified nonlocal beam model for vibration and stability of nanotubes conveying fluid. Phys. E 2011, 44, 25–28. [Google Scholar]
- Yan, Y.; Wang, W.Q.; Zhang, L.X. Noncoaxial vibration of fluid-filled multi-walled carbon nanotubes. Appl. Math. Model. 2010, 34, 122–128. [Google Scholar]
- Reddy, C.D.; Lu, C.; Rajendran, S.; Liew, K.M. Free vibration analysis of fluid-conveying single-walled carbon nanotubes. Appl. Phys. Lett. 2007, 90, 133122:1–133122:3. [Google Scholar]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K. Wave propagation characteristics in fluid-conveying double-walled nanotubes with scale effects. Comput. Mater. Sci. 2010, 48, 413–418. [Google Scholar]
- Ke, L.-L.; Wang, Y.-S. Flow-induced vibration and instability of embedded double-walled carbon nanotubes based on a modified couple stress theory. Phys. E 2011, 43, 1031–1039. [Google Scholar]
- Lee, H.L.; Chang, W.J. Surface effects on frequency analysis of nanotubes using nonlocal Timoshenko beam theory. J. Appl. Phys. 2010, 108, 093503:1–093503:3. [Google Scholar]
- Wang, L. Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Phys. E 2010, 43, 437–439. [Google Scholar]
- Narendar, S.; Ravinder, S.; Gopalakrishnan, S. Study of non-local wave properties of nanotubes with surface effects. Comput. Mater. Sci. 2012, 56, 179–184. [Google Scholar]
- Narendar, S.; Gopalakrishnan, S. Study of terahertz wave propagation properties in nanoplates with surface and small scale effects. Int. J. Mech. Sci. 2012, 64, 221–231. [Google Scholar]
- Wang, Y.-Z.; Cui, H.-T.; Li, F.-M.; Kishimoto, K. Effects of viscous fluid on wave propagation in carbon nanotubes. Phys. Lett. A 2011, 375, 2448–2451. [Google Scholar]
- Khosravian, N.; Rafii-Tabar, H. Computational modelling of a non-viscous fluid flow in a multi-walled carbon nanotube modelled as a Timoshenko beam. Nanotechnology 2008, 19. [Google Scholar] [CrossRef]
- Khosravian, N.; Rafii-Tabar, H. Computational modelling of the flow of viscous fluids in carbon nanotubes. J. Phys. D Appl. Phys. 2007, 40, 7046–7052. [Google Scholar]
- Ghavanloo, E.; Daneshmand, F.; Rafiei, M. Vibration and instability analysis of carbon nanotubes conveying fluid and resting on a linear viscoelastic Winkler foundation. Phys. E 2010, 42, 2218–2224. [Google Scholar]
- Narendar, S.; Gopalakrishnan, S. Terahertz wave characteristics of a single-walled carbon nanotube containing a fluid flow using the nonlocal Timoshenko beam model. Phys. E 2010, 42, 1706–1712. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, Y.-W.; Yang, T.-Z.; Zang, J.; Fang, B. Terahertz Wave Propagation in a Nanotube Conveying Fluid Taking into Account Surface Effect. Materials 2013, 6, 2393-2399. https://doi.org/10.3390/ma6062393
Zhang Y-W, Yang T-Z, Zang J, Fang B. Terahertz Wave Propagation in a Nanotube Conveying Fluid Taking into Account Surface Effect. Materials. 2013; 6(6):2393-2399. https://doi.org/10.3390/ma6062393
Chicago/Turabian StyleZhang, Ye-Wei, Tian-Zhi Yang, Jian Zang, and Bo Fang. 2013. "Terahertz Wave Propagation in a Nanotube Conveying Fluid Taking into Account Surface Effect" Materials 6, no. 6: 2393-2399. https://doi.org/10.3390/ma6062393
APA StyleZhang, Y.-W., Yang, T.-Z., Zang, J., & Fang, B. (2013). Terahertz Wave Propagation in a Nanotube Conveying Fluid Taking into Account Surface Effect. Materials, 6(6), 2393-2399. https://doi.org/10.3390/ma6062393



