3.2. Microstructure
In the SEM images of
Figure 1, the polished sections of the samples A-F are displayed. In these pictures, just the ZrB
2 matrix is shown. All the materials were nearly fully dense. Dark features correspond to secondary phases formed during sintering,
i.e., amorphous Si-O-N, ZrN and BN. The values of mean grain size and relative dispersion are reported in
Table 2. As for the mean grain size of ZrB
2 matrix, it can be noticed that samples A-F had a similar value. There is a slight tendency of the mean grain size to increase with the spread of the fiber length distribution. It was also observed that samples milled with ZrO
2, A-E, generally have a more faceted shape than those milled with the SiC media, F, suggesting a possible rounding off of the ZrB
2 powder due to the higher hardness of silicon carbide.
Figure 1.
SEM-images of the polished sections of samples: ZrB2 matrix. The dark features correspond to secondary phases (amorphous Si-O-N, ZrN and BN).
Figure 1.
SEM-images of the polished sections of samples: ZrB2 matrix. The dark features correspond to secondary phases (amorphous Si-O-N, ZrN and BN).
Fiber dispersion into the matrix is shown in
Figure 2,
Figure 3 and
Figure 4 for samples A-F. Generally speaking, no agglomeration was observed with an orientation distribution of the fibers almost isotropic in the section plane oriented perpendicularly to the hot pressing direction. This can be compared with the anisotropic distribution of fibers shown in the inset of
Figure 2a when the section was cut parallel to the hot pressing direction. As expected, the fibers showed the tendency to align their long axis perpendicular to the direction of applied pressure. In
Figure 2,
Figure 3 and
Figure 4, the effects of milling time, milling speed and milling media type on the fiber length can be directly evaluated. At a first glance, it is apparent that a gradual decrease of the fiber length with the increase of milling time occurred (compare sample A, B and C in
Figure 2). As for the milling time, the increase of milling speed up to 200 rpm effectively reduced the fiber size, but a further increase to 300 rpm did not lead to any additional improvement (compare sample B, D and E in
Figure 3). Also for the milling media, the difference among sample B and F are not so evident only observing the SEM-images (compare sample B and F in
Figure 4).
Figure 2.
(a)–(c) SEM-images of samples milled for different times showing the section perpendicular to the hot pressing direction, see labels. The inset in (a) shows the fiber distribution in a section parallel to the hot pressing direction.
Figure 2.
(a)–(c) SEM-images of samples milled for different times showing the section perpendicular to the hot pressing direction, see labels. The inset in (a) shows the fiber distribution in a section parallel to the hot pressing direction.
Figure 3.
(a)–(c) SEM-images of samples milled at different speeds, see labels. The polished sections were cut perpendicularly to the hot pressing direction.
Figure 3.
(a)–(c) SEM-images of samples milled at different speeds, see labels. The polished sections were cut perpendicularly to the hot pressing direction.
Figure 4.
(a), (b) SEM-images of samples milled with different milling media, see labels. The polished sections were cut perpendicularly to the hot pressing direction.
Figure 4.
(a), (b) SEM-images of samples milled with different milling media, see labels. The polished sections were cut perpendicularly to the hot pressing direction.
The calculated parameters of the fitted CDF curves are listed in
Table 2. Besides the mean grain size, the maximum length, the form factor m the scale factor s
0, also the main quantiles are reported. The parameters m and s
0 are indicative of the data dispersion (the higher is m the lower is the data dispersion) and the data median. The fitted CDF curves are shown in
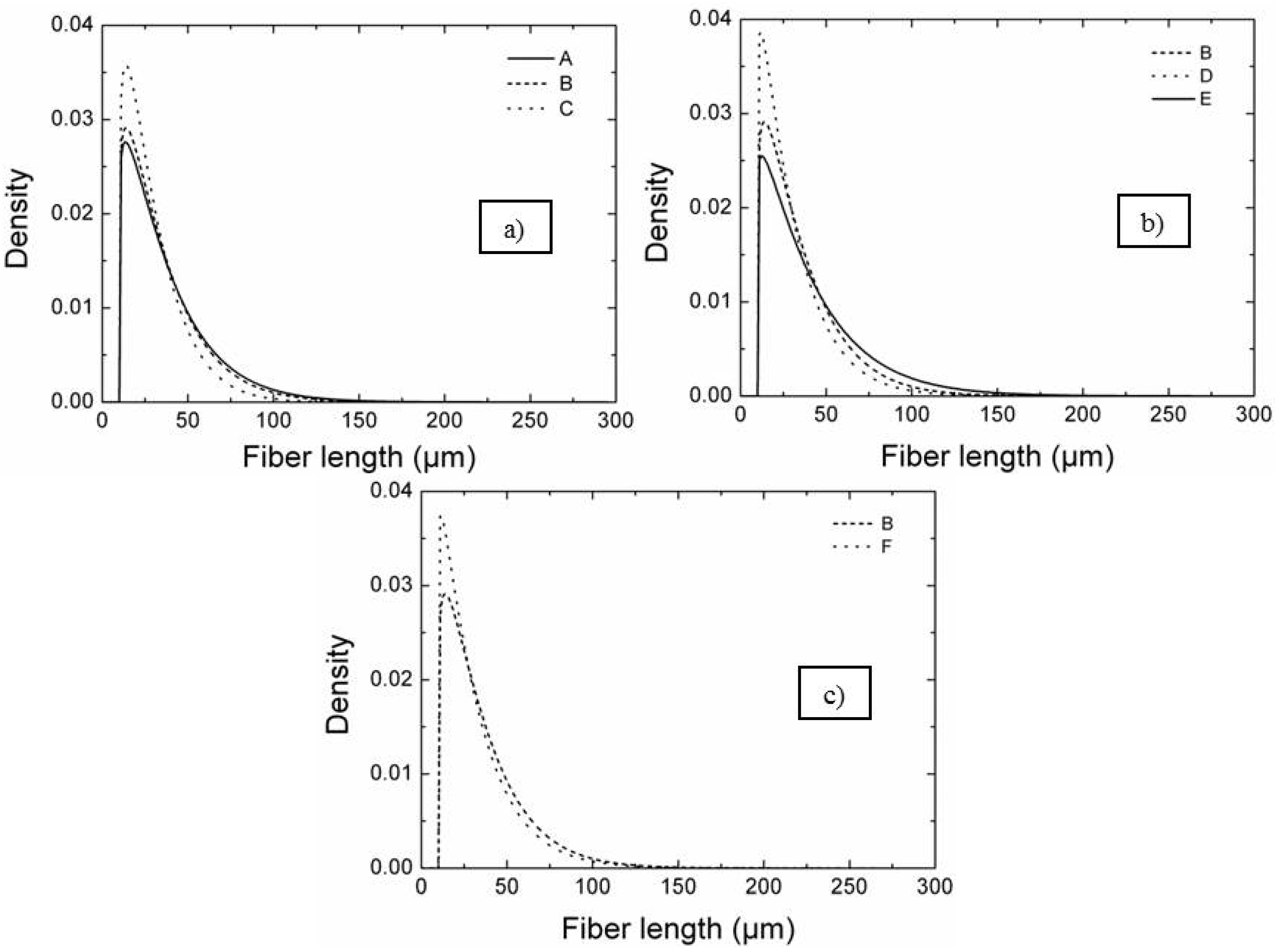
Figure 5 as PDF curves grouped according to the different milling parameters. In
Figure 5a, the effect of milling time on the length distribution can be evaluated for samples A, B and C. As can be seen, the length distribution became narrower increasing the milling time, as indicated by the increasing of the form factor m from A, milled for the shortest time, to C, milled for the longest time (
Table 2). At the same time, the median values of fiber length decreased with increasing milling time passing from 29 µm of sample A to 21 µm of sample C, as indicated by the scale factor s
0. As a consequence, the density of long fibers decreased with the increase of the milling time, as concluded from the SEM images (sample A, B and C in
Figure 2).
Table 2.
Sample label, mean grain size (m.g.s.), maximum fiber length (lmax), form factor (m), scale factor (s0) and quantiles.
Table 2.
Sample label, mean grain size (m.g.s.), maximum fiber length (lmax), form factor (m), scale factor (s0) and quantiles.
| Label | m.g.s. 1 (µm) | lmax (µm) | Form factor 2 m | Scale factor 2 s0 (µm) | Quantiles (µm) |
|---|
| ¼ | ½ | ¾ |
|---|
| ZB [9] | - | - | - | - | - | - | - |
| A | 2.9 ± 1.4 | 296 | 1.106 ± 0.004 | 29.07 ± 0.07 | 19.42 | 30.87 | 49.01 |
| B | 2.6 ± 2.0 | 248 | 1.126 ± 0.004 | 27.03 ± 0.05 | 18.93 | 29.51 | 46.12 |
| C | 2.3 ± 1.5 | 239 | 1.157 ± 0.004 | 21.50 ± 0.04 | 17.33 | 25.67 | 38.51 |
| D | 2.3 ± 1.4 | 233 | 1.068 ± 0.003 | 21.72 ± 0.04 | 16.76 | 25.41 | 39.49 |
| E | 2.3 ± 1.1 | 256 | 1.065 ± 0.002 | 33.13 ± 0.04 | 20.28 | 33.48 | 55.03 |
| F | 2.2 ± 1.9 | 274 | 1.054 ± 0.003 | 22.93 ± 0.05 | 17.03 | 26.19 | 41.26 |
Figure 5.
Probability density function curves: (a) effect of milling time on the length distribution (sample A, B and C); (b) effect of milling velocity (sample B, D and E); (c) effect of milling media hardness (sample B and F).
Figure 5.
Probability density function curves: (a) effect of milling time on the length distribution (sample A, B and C); (b) effect of milling velocity (sample B, D and E); (c) effect of milling media hardness (sample B and F).
In
Figure 5b, the fiber length PDF curves of samples B, D and E were compared to study the effect of milling speed. Initially, the distribution width decreased passing from sample B, milled at 130 rpm, to sample D, milled at 200 rpm. Further increasing the milling speed had an opposite effect. The median value of fiber length of sample E milled at 300 rpm increased and the long fiber density increased. Very likely, increasing too much the rotation speed decreased the frictional interaction between the bottle wall and milling media, thus reducing the milling effect as the milling media dropped from a lower height.
The milling media hardness effect can be evaluated by comparing the PDF curves of samples B and F (
Figure 5c), in which the powders mixtures were milled with ZrO
2 milling media (B) and with SiC milling media (F). As can be seen, increasing the milling media hardness decreased the median fiber length, which passed from 27 µm to 22 µm for sample B and F, respectively, and also the fiber length dispersion.
Besides the main parameters of the distributions, the maximum fiber length was measured for all the composites (
Table 2) and it can be observed that the values were related to the severity of milling procedure. For instance the specimen milled in the mildest conditions, 12 h at 130 rpm (A), resulted in the longest fiber length, about 300 μm. This value showed the tendency to decrease for increasing milling time, from 300 to 240 μm (samples A, B, C). As for the other conditions, the maximum length decreased when increasing the speed from 130 to 200 rpm, but then increased for further increase of the milling velocity. The use of ZrO
2 instead of SiC milling media resulted in maximum fiber length of 250 and 275, respectively, which is quite surprisingly owing to the different hardness, but could be explained with a highest range of dimensions down to smaller size of ZrO
2 media, 15, 10, 5 mm
vs. 14, 7 mm for SiC. No significant correlation was observed between l
max and any of the parameter distributions (m, s
0, and quantiles).
Another microstructural feature analyzed was the interface between matrix and fiber. During densification, a strong interface form between the matrix and SiC fibers due to ZrB
2/SiC fiber interaction [
9]. In the sintered materials, the fibers show multilayered core-shell morphology (
Figure 6):
the inner part was constituted of β-SiC crystallites, amorphous Si-C, and turbostratic carbon;
the surrounding shell was coarsened β-SiC crystallites with embedded ZrO2, ZrC, ZrSi2, Zr-C-O phases;
the outermost jagged layer was made of SiC platelets.
Figure 6.
Multilayered core-shell morphology of a SiC fiber in a ZrB2 matrix.
Figure 6.
Multilayered core-shell morphology of a SiC fiber in a ZrB2 matrix.
This arrangement is due to complex chemical reactions occurring during sintering related to the fiber chemical instability at temperatures higher than 1500 °C. Fiber evolution during sintering is presently under analysis as the extent of modification may be affected by several factors, including sintering temperature/holding time/type of sintering aid.
The chemical composition and extension of the core/rim structure was analyzed and no variation of the transformed area was found for the different milling conditions. In all cases, the area ratio between the unreacted SiC core and the transformed rim was approximately 70:30.
3.3. Mechanical Properties
The mechanical properties of the ZrB
2-based composites are shown in
Table 3, together with the unreinforced baseline material [
9].
Table 3.
Mechanical properties: fracture toughness (KIc), flexural strength (σRT), Vickers microhardness (HV1.0). Mean ± 1 standard deviation.
Table 3.
Mechanical properties: fracture toughness (KIc), flexural strength (σRT), Vickers microhardness (HV1.0). Mean ± 1 standard deviation.
| Label | KIc (MPa·m1/2) | σRT (MPa) | HV1.0 (GPa) |
|---|
| ZB [9] | 3.8 ± 0.1 | 600 ± 90 | 13.4 ± 0.6 |
| A | 5.5 ± 0.4 | 355 ± 12 | 11.8 ± 1.3 |
| B | 5.4 ± 0.4 | 389 ± 18 | 13.0 ± 0.8 |
| C | 5.2 ± 0.1 | 389 ± 24 | 13.0 ± 0.8 |
| D | 5.1 ± 0.2 | 415 ± 12 | 12.1 ± 0.9 |
| E | 5.6 ± 0.4 | 369 ± 13 | 13.9 ± 0.8 |
| F | 5.11 ± 0.02 | 368 ± 27 | 13.5 ± 1.0 |
The Vickers hardness of these composites ranges between 11.8 and 13.9 GPa. It should be however considered that the indentation marks at 9.81 N were not large enough to test both matrix and fibers so that the measured values mainly represent the hardness of the matrix. No clear relationships between hardness and milling conditions were identified. More than the milling conditions, matrix density and matrix grain size can have influenced the hardness results.
The fracture toughness of ZrB
2-based composites (5.1–5.6 MPa·m
1/2) did not significantly change for the samples milled in different milling conditions, but increased of about 45% in comparison with the unreinforced materials (3.8 MPa·m
1/2 [
9]). The Analysis of Variance (ANOVA) performed on the toughness data confirmed that there was no significant difference among samples A–F.
Figure 7 shows an example of crack path generated by a 98.1 N indentation. The crack crossed the fibers without any significant deflection, as a consequence of the strong matrix/fiber interface, which did not allow fiber debonding. Crack pinning and residual stresses were thus considered the dominant toughening mechanisms for this type of composites. However, due to the unfavorable mismatch between the thermal expansion coefficients of the matrix and the fibers [
20,
21], the residual stresses give in this case a negative contribution according to the model of Taya
et al. [
21]. Therefore, crack pinning must be considered the major toughening mechanism in these composites. From our experimental results, there was no influence of the length distribution of the SiC fiber on the fracture toughness.
Figure 7.
Crack path generated by a 98.1 N indentation.
Figure 7.
Crack path generated by a 98.1 N indentation.
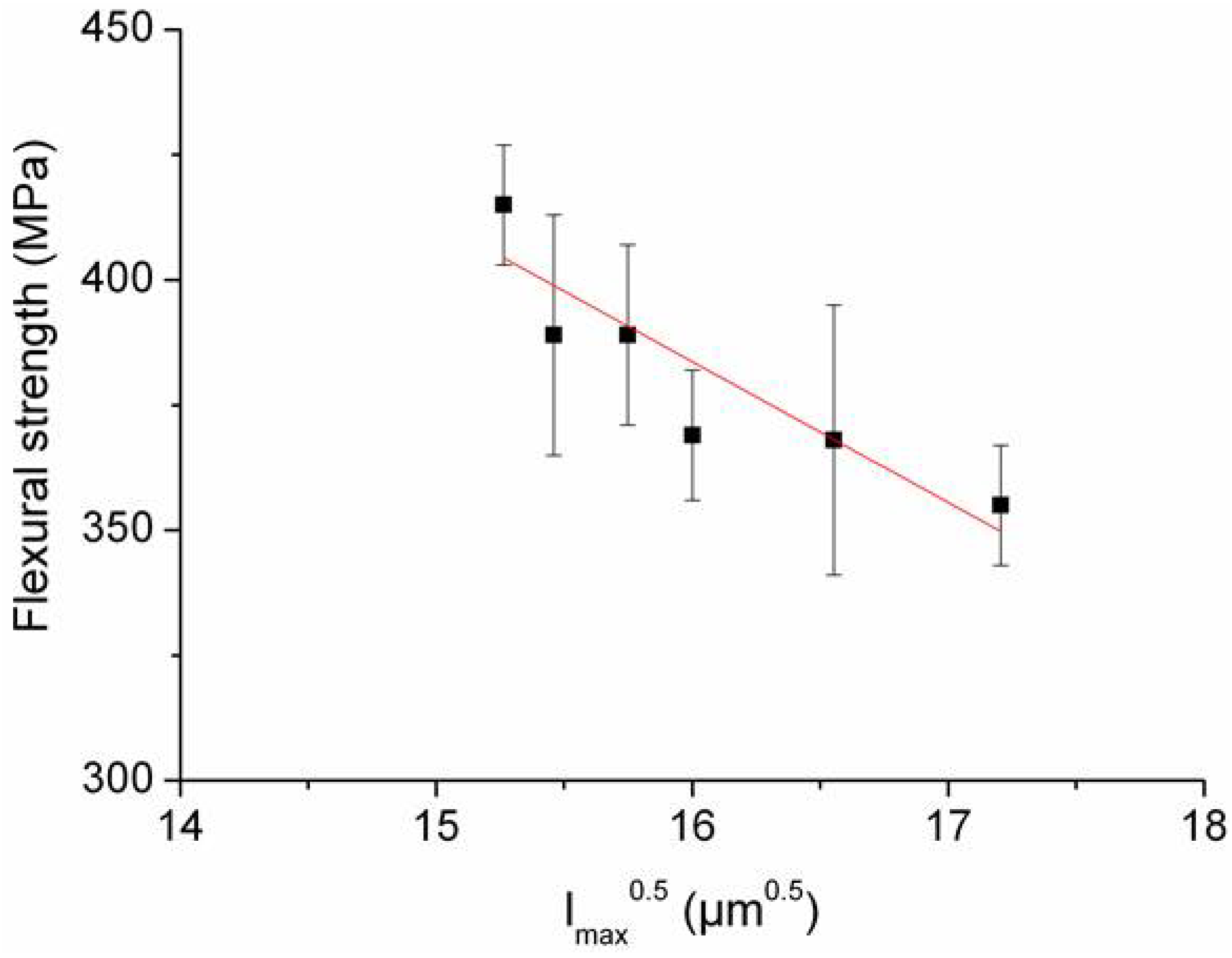
On the contrary, the ANOVA performed on the strength data (ranging from 355 to 415 MPa) indicated a significant difference among samples A–F. However, very loose correlations were found between strength and the fitted parameters of the length distributions. The best correlation was observed when the strength was evaluated against the square root of maximum fiber length (see
Figure 8), considering the longest fiber as a critical flaw.
Figure 8.
Strength vs. square root of maximum fiber length, considering the longest fiber as a critical flaw.
Figure 8.
Strength vs. square root of maximum fiber length, considering the longest fiber as a critical flaw.
However, when observing the fracture surfaces of the samples, we did not find any fiber, which was at the origin of the sample failure. Moreover, as can be seen on the fracture surfaces, an example of which are shown in
Figure 9, the short fibers are aligned perpendicular to the tensile surface. According to the Newman and Raju [
22], this is an unfavorable orientation for the fiber to act as critical flaw. With the simplifying hypothesis that the fracture origins were located on the tensile surface of the specimens with a half-penny shape of radius
c, the size
c of the critical flaws can be estimated according to Equation (1) [
23]:
where
σ is the fracture strength and
KIc the fracture toughness. Considering the values of
Table 3, the calculated size
c of the critical flaw for samples A–F were 153, 123, 114, 96, 147 and 122 µm, respectively (for comparison, the starting matrix has a critical flaw size
c of 26 µm). No feature with dimensions matching these values was observed on the fracture surfaces of the composites. It is therefore apparent that the fracture in this type of composites is somehow related to the introduction of the fibers, as the composite strength dropped in spite of the toughness increase with respect to the starting matrix, and that the critical flaws are not the fibers
per se but must be the result of the fiber/matrix and fiber/fiber interaction. An example of this could be regions where fibers tend to aggregate. In
Figure 8, such regions are outlined and it is possible to see that the distance between neighbor fibers in these regions is much shorter than the average. Since the fracture toughness is the same, the strength of the composites seems to be therefore determined by the size of these fiber aggregates, which form during processing. However, as the residual stress in the fibers is compressive, very likely it is the matrix residual stress, which can explain the strength variation in our composites. According to a micromechanical model [
24], the residual stress in the matrix just outside a short fiber is a function of three factors: (1) elastic and thermal expansion mismatch between fiber and matrix, (2) fiber volume and (3) L/d, where L and d are the long and transverse dimension of the fiber, respectively. In composites with elastic and thermal properties of the fibers and matrix as those we are considering, the radial component of the residual stress in the matrix just outside the fiber is compressive while the tangential component is tensile. The maximum value of the latter is attained just at the ends of the fiber. Of particular relevance for our composites is factor (3) since factor (1) and (2) do not vary among the composites. As shown in Reference [
24], the higher is the aspect ratio (L/d) of the fiber, the higher is the value of the matrix tangential tensile stress at the fiber ends. This can explain the apparent relationship that was observed between the flexural strength and the fiber maximum length,
Figure 8. Moreover, the possible superposition of the residual thermal stress field around neighbor fibers can also explain why fractography indicates fibers aggregates as fracture origins: high values of residual tensile stress in the matrix can be locally generated by the superposition of the tangential tensile stress around agglomerated fibers. The flexural strength is therefore determined by the combined effect of the external applied tensile stress and this local residual tensile stress.
Figure 9.
Fracture surface of sample D where the short fibers are aligned perpendicular to the tensile surface.
Figure 9.
Fracture surface of sample D where the short fibers are aligned perpendicular to the tensile surface.