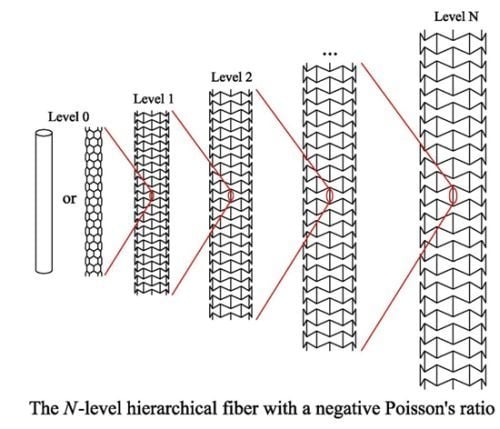
Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites
Abstract
:1. Introduction
2. Hierarchical Structures with Negative Poisson’s Ratio
2.1. Design of Hierarchical NPR Tubes
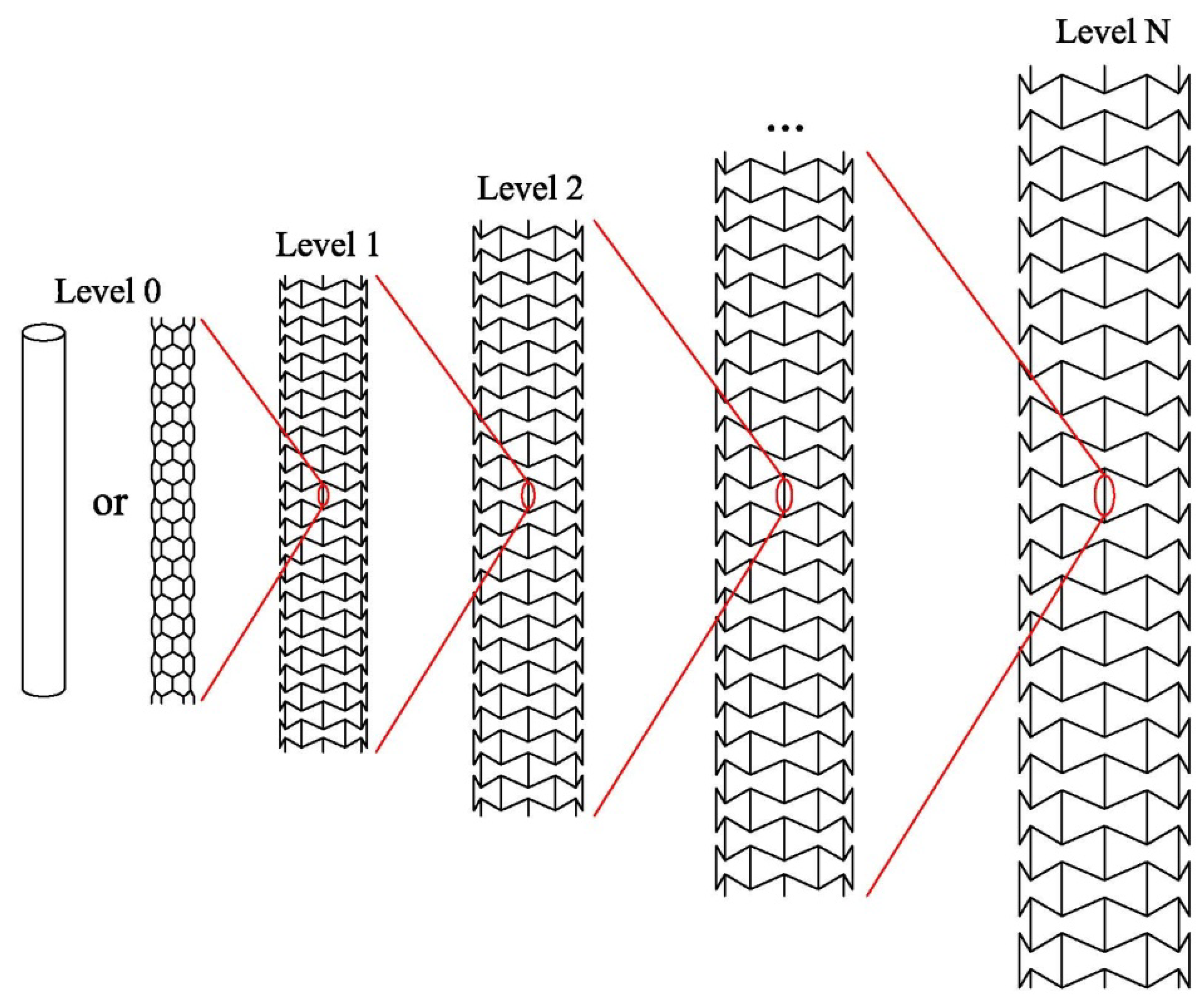
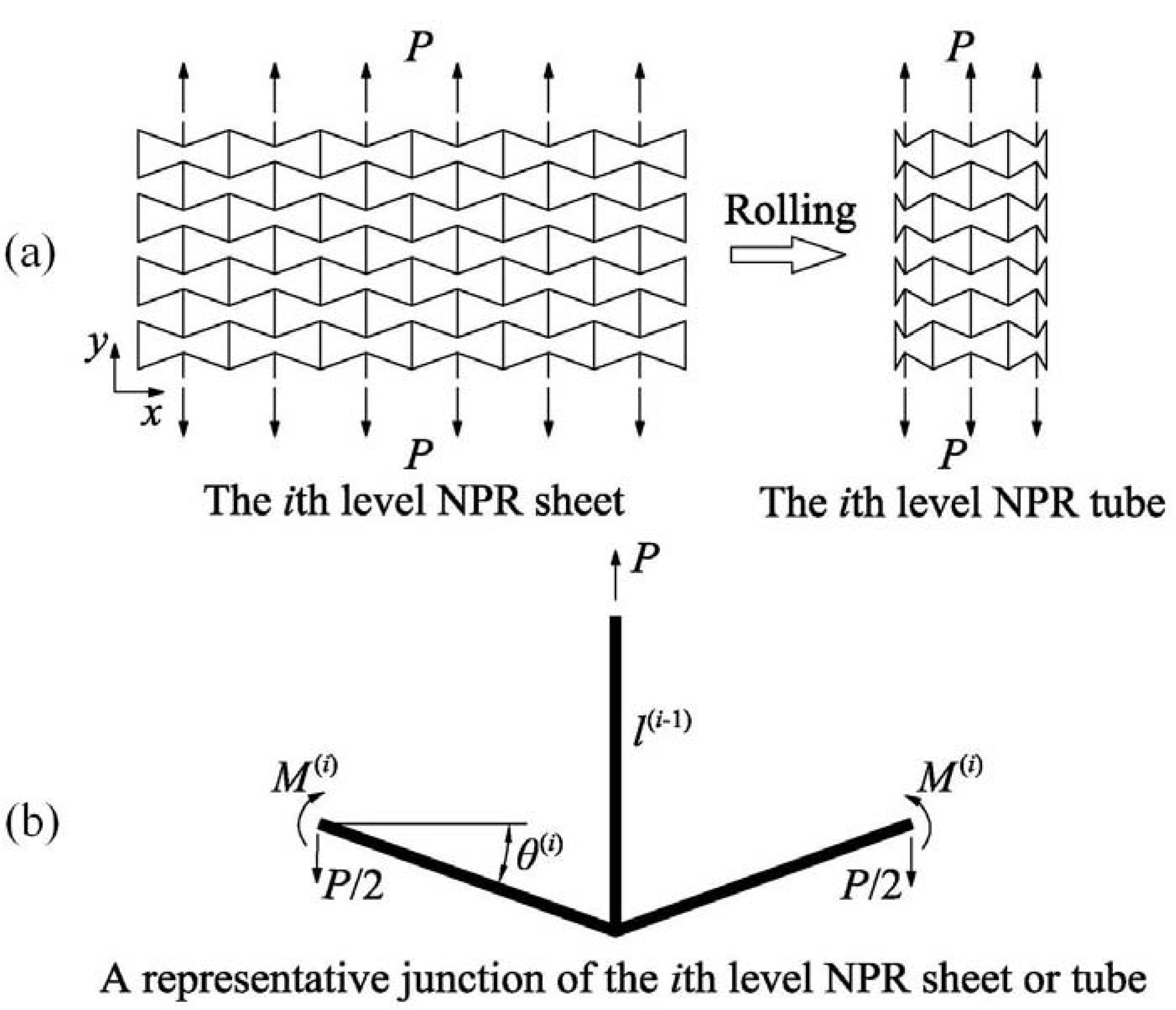
2.2. Elasticity of the Hierarchical NPR Tubes
2.2.1. The Level 1 NPR Tube
2.2.2. The Level N NPR Tube
2.2.3. Effects of the Parameters , and N
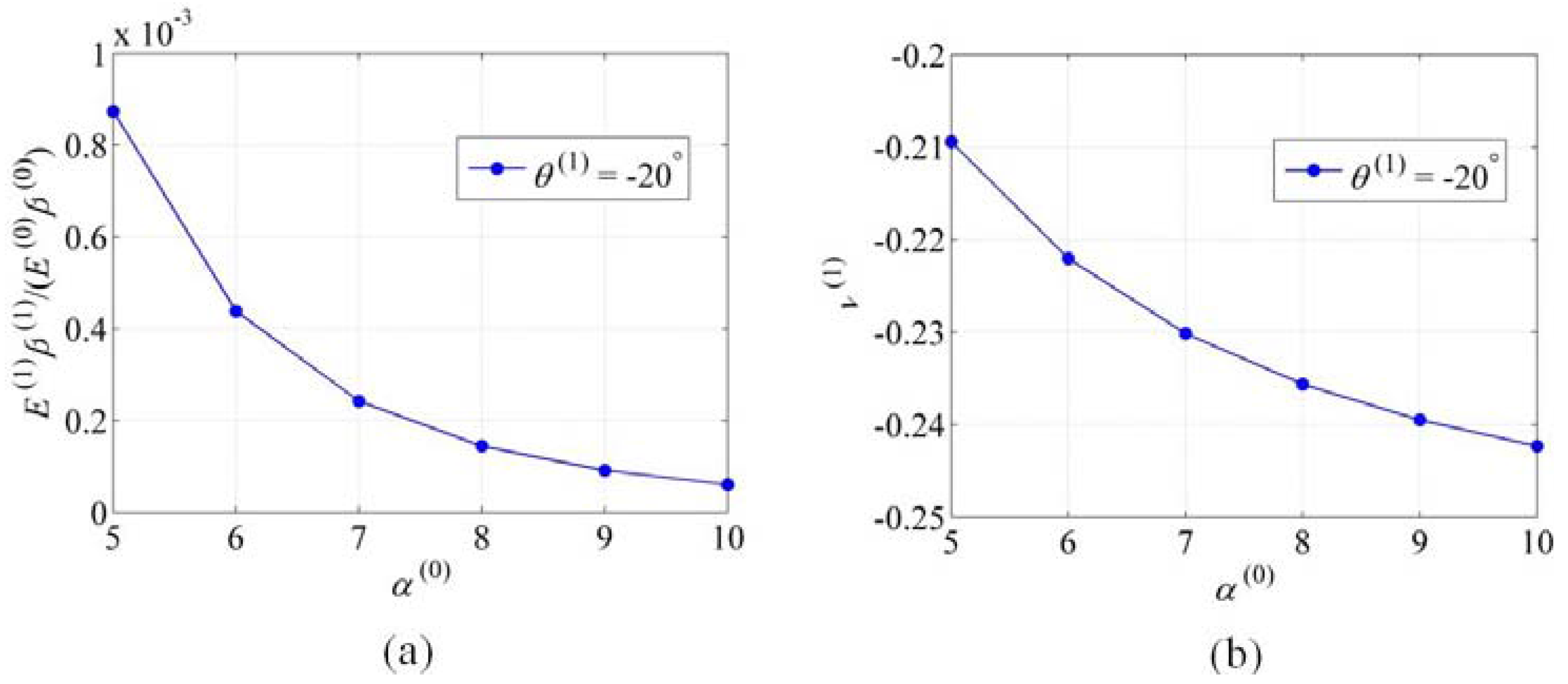
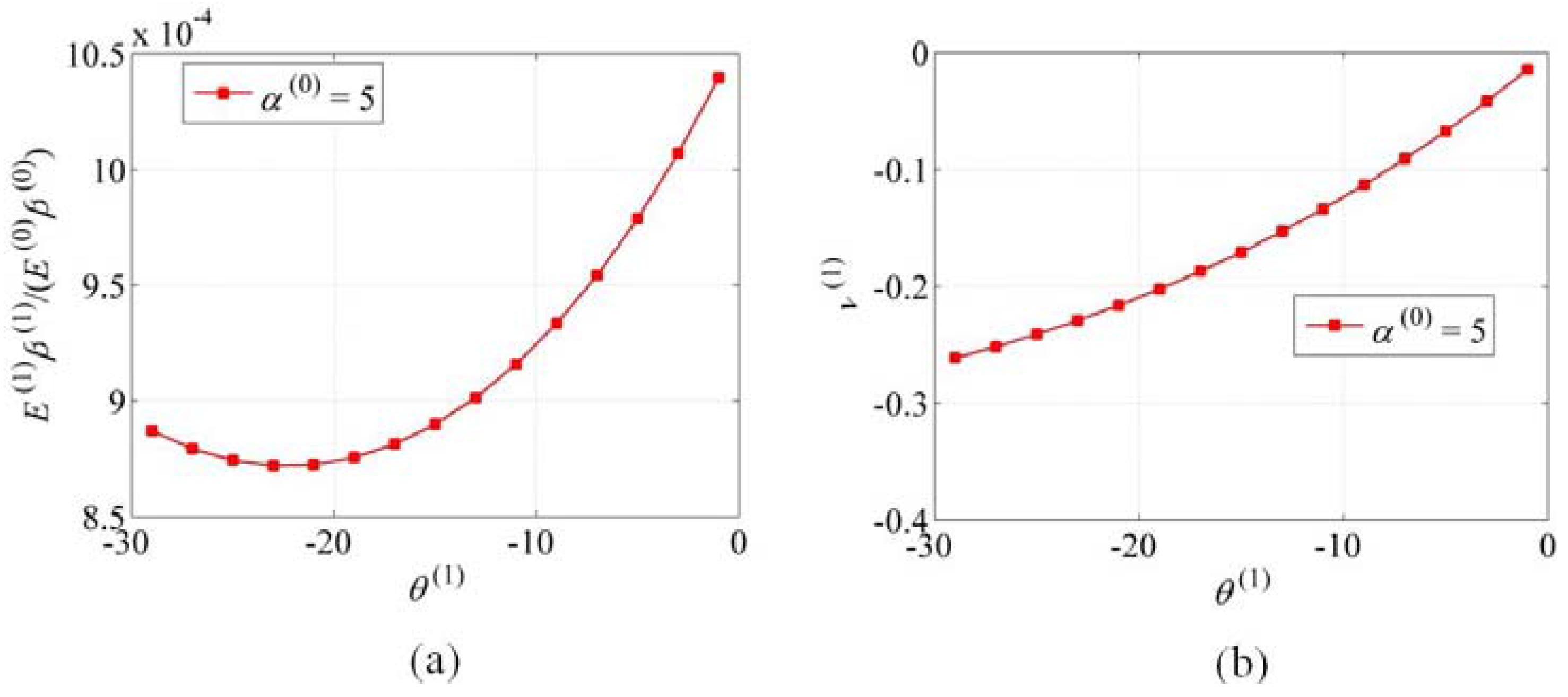
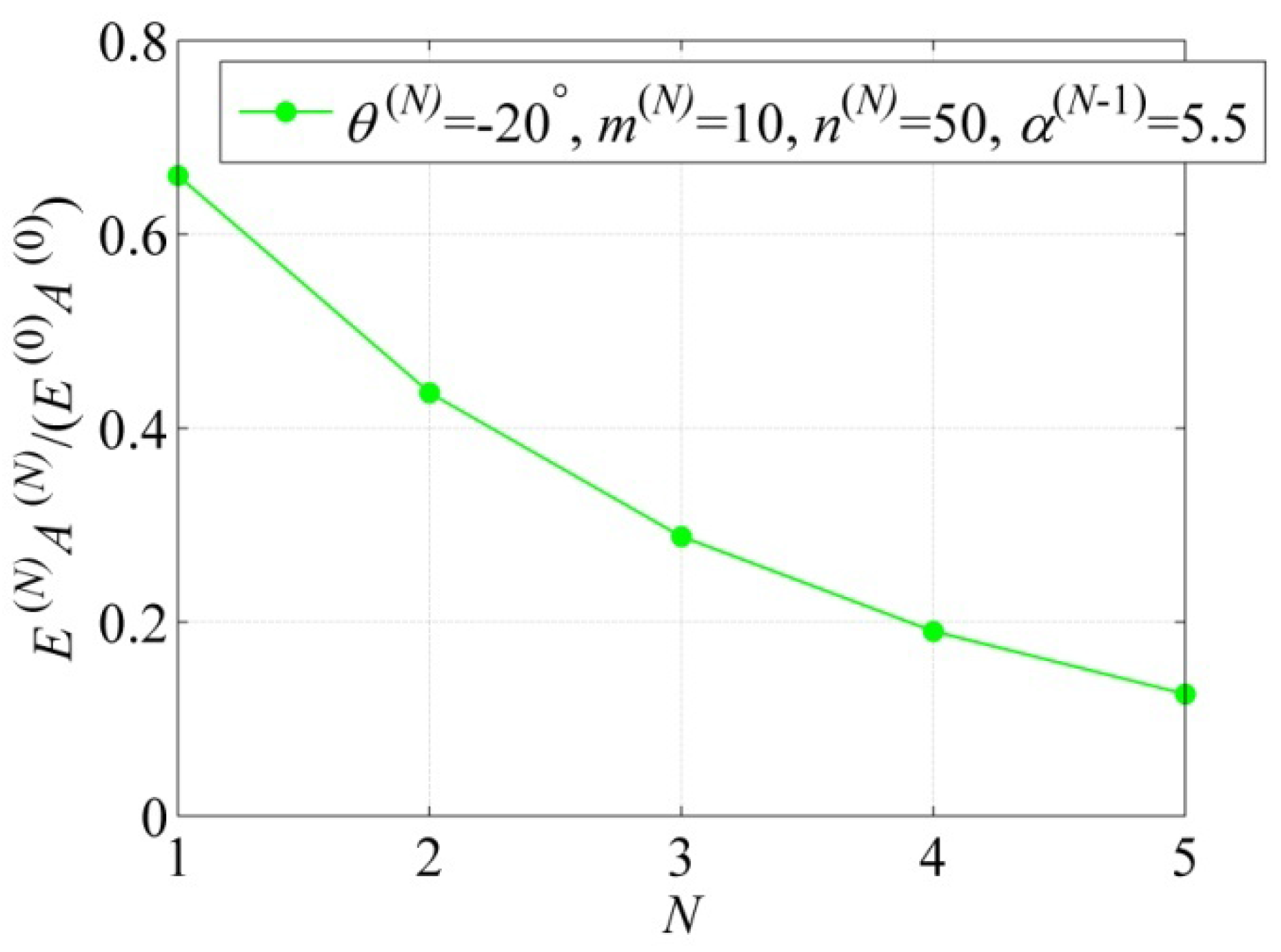
3. Conclusions
Acknowledgements
References
- Terrones, M.; Banhart, F.; Grobert, N.; Charlier, J.C.; Terrones, H.; Ajayan, P.M. Molecular junctions by joining single-walled carbon nanotubes. Phys. Rev. Lett. 2002, 89, 075505:1–075505:4. [Google Scholar] [CrossRef]
- Romo-Herrera, J.M.; Terrones, M.; Terrones, H.; Dag, S.; Meunier, V. Covalent 2D and 3D networks from 1D nanostructures: Designing new materials. Nano Lett. 2007, 7, 570–576. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared Graphene: A new 3-D network nanostructure for enhanced hydrogen storage. Nano Lett. 2008, 8, 3166–3170. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qiu, X.; Yang, F.; Yin, Y.; Fan, Q. Stretching-dominated deformation mechanism in a super square carbon nanotube network. Carbon 2009, 47, 812–819. [Google Scholar] [CrossRef]
- Li, Y.; Qiu, X.; Yang, F.; Yin, Y.; Fan, Q. The specific heat of carbon nanotube networks and their potential applications. J. Phys. D 2009, 42. [Google Scholar] [CrossRef]
- Zsoldos, I. Planar trivalent polygonal networks constructed from carbon nanotube Y-junctions. J. Geom. Phys. 2011, 61, 37–45. [Google Scholar] [CrossRef]
- Pugno, N.; Chen, Q. In plane elastic properties of hierarchical cellular solids. Eng. Proc. Phys. Eng. 2011, 10, 3026–3031. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N. Modeling the elastic anisotropy of woven hierarchical tissues. Compos. Part B Eng. 2011, 42, 2030–2037. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N. Mechanics of hierarchical 3-D nanofoams. Europhys. Lett. 2012, 97. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N. In-plane elastic buckling of hierarchical honeycomb materials. Eur. J. Mech. A 2012, 34, 120–129. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N. Competition between in-plane buckling and bending collapses in nano-honeycombs. Europhys. Lett. 2012, 98, 16005:1–16005:5. [Google Scholar]
- Coluci, V.R.; Galvao, D.S.; Jorio, A. Geometric and electronic structure of carbon nanotube networks: “Super”-carbon nanotubes. Nanotechnology 2006, 17, 617–621. [Google Scholar] [CrossRef]
- Pugno, N.M. Mimicking nacre with super-nanotubes for producing optimized super-composites. Nanotechnology 2006, 17, 5480–5484. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Gao, H. On optimal hierarchy of load-bearing biological materials. Proc. Biol. Sci. 2011, 278, 519–525. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Boyce, M.C. Bioinspired structural material exhibiting post-yield lateral expansion and volumetric energy dissipation during tension. Adv. Funct. Mater. 2010, 20, 3025–3030. [Google Scholar] [CrossRef]
- Wang, M.; Qiu, X.M.; Zhang, X. Mechanical properties of super honeycomb structures based on carbon nanotubes. Nanotechnology 2007, 18, 075711:1–075711:6. [Google Scholar]
- Wang, M.; Qiu, X.M.; Zhang, X.; Yin, Y.J. Equivalent parameter study of the mechanical properties of super carbon nanotubes. Nanotechnology 2007, 18, 295708:1–295708:6. [Google Scholar]
- Coluci, V.R.; Pugno, N.; Dantas, S.O.; Galvao, D.S.; Jorio, A. Atomistic simulations of the mechanical properties of “super” carbon nanotubes. Nanotechnology 2007, 18, 335702:1–335702:7. [Google Scholar] [CrossRef]
- Qin, Z.; Feng, X.Q.; Zou, J.; Yin, Y.J.; Yu, S.W. Molecular dynamics simulations of deformation and rupture of super carbon nanotubes under tension. J. Nanosci. Nanotechnol. 2008, 8, 6274–6282. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qiu, X.M.; Yang, F.; Wang, X.S.; Yin, Y.J. Ultra-high sensitivity of super carbon-nanotube-based mass and strain sensors. Nanotechnology 2008, 19, 165502:1–165502:6. [Google Scholar]
- Li, Y.; Qiu, X.M.; Yang, F.; Wang, X.S.; Yin, Y.J. The effective modulus of super carbon nanotubes predicted by molecular structure mechanics. Nanotechnology 2008, 19, 225701:1–225701:7. [Google Scholar]
- Li, Y.; Qiu, X.M.; Yang, F.; Wang, X.S.; Yin, Y.J.; Fan, Q.S. A comprehensive study on the mechanical properties of super carbon nanotubes. J. Phys. D 2008, 41, 155423:1–155423:6. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking. Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R.S. Properties of a chiral honeycomb with a Poisson’s ratio-1. Int. J. Mech. Sci. 1996, 39, 305–314. [Google Scholar] [CrossRef]
- Lorato, A.; Innocenti, P.; Scarpa, F.; Alderson, A.; Alderson, K.L.; Zied, K.M.; Ravirala, N.; Miller, W.; Smith, C.W.; Evans, K.E. The transverse elastic properties of chiral honeycombs. Compos. Sci. Technol. 2010, 70, 1057–1063. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Shufrin, I.; Pasternak, E.; Dyskin, A.V. Planar isotropic structures with negative Poisson’s ratio. Int. J. Solids Struct. 2012, 49, 2239–2253. [Google Scholar] [CrossRef]
- Pasternak, E.; Dyskin, A.V. Multiscale hybrid materials with negative Poisson’s ratio. In IUTAM Symposium on Scaling in Solid Mechanics; Borodich, F., Ed.; Springer: Heidelberg, Germany, 2008; pp. 49–58. [Google Scholar]
- Pasternak, E.; Dyskin, A.V. Materials with Poisson’s ratio near-1: Properties and possible realizations. In Proceeding of XXII International Congress of Theoretical and Applied Mechanics, Adelaide, Australia, 24–29 August 2008.
- Pasternak, E.; Dyskin, A.V. Materials and structures with macroscopic negative Poisson’s ratio. Int. J. Eng. Sci. 2012, 52, 103–114. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Rotation and dilation deformation mechanism for auxetic behavior in thea-cristolobite tetrahedral framework structure. Phys. Chem. Miner. 2001, 28, 711–718. [Google Scholar] [CrossRef]
- Attard, D.; Manicaro, E.; Grima, J.N. On rotating rigid parallelograms and their potential for exhibiting auxetic behavior. Phys. Status Solidi B 2009, 246, 2033–2044. [Google Scholar] [CrossRef]
- Attard, D.; Manicaro, E.; Gatt, R.; Grima, J.N. On the properties of auxetic rotating stretching squares. Phys. Status Solidi B 2009, 246, 2045–2054. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behavior from rotating rigid units. Phys. Status Solidi B 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Grima, J.N.; Cassar, R.N.; Gatt, R. On the effect of hydrostatic pressure on the auxetic character of NAT-type silicates. J. Non-Cryst. Solids 2009, 355, 1307–1312. [Google Scholar] [CrossRef]
- Grima, J.N.; Manicaro, E.; Attard, D. Auxetic behavior from connected different-sized squares and rectangles. Proc. R. Soc. A 2010, 467, 439–458. [Google Scholar] [CrossRef]
- Williams, J.J.; Smith, C.W.; Evans, K.E.; Lethbridge, Z.A.D.; Walton, R.I. An analytical model for producing negative Poisson’s ratios and its application in explaining off-axis elastic properties of the NAT-type zeolites. Acta Mater. 2007, 55, 5697–5707. [Google Scholar] [CrossRef]
- Bathurst, R.J.; Rothenburg, L. Note on a random isotropic granular material with negative Poisson’s ratio. Int. J. Eng. Sci. 1988, 26, 373–383. [Google Scholar] [CrossRef]
- Ravirala, N.; Alderson, A.; Alderson, K.L. Interlocking hexagons model for auxetic behavior. J. Mater. Sci. 2007, 42, 7433–7445. [Google Scholar]
- Lakes, R. Advances in negative Poisson’s ratio materials. Adv. Mater. 1993, 5, 293–296. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.M.; Shi, W.; Xie, B.H.; Yang, M.B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Stavroulakis, G.E. Auxetic behavior: Appearance and engineering applications. Phys. Status Solidi B 2005, 242, 710–720. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic materials. J. Aerosp. Eng. 2007, 221, 565–575. [Google Scholar]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Signal Proc. Mag. 2008, 25, 126–128. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Song, F.; Zhou, J.; Xu, X.; Xu, Y.; Bai, Y. Effect of a negative poisson ratio in the tension of ceramics. Phys. Rev. Lett. 2008, 100, 245502:1–245502:4. [Google Scholar]
- Xu, B.; Arias, F.; Brittain, S.T.; Zhao, X.M.; Grzybowski, B.; Torquato, S.; Whitesides, G.M. Making negative Poisson’s ratio microstructures by soft lithography. Adv. Mater. 1999, 11, 1186–1189. [Google Scholar] [CrossRef]
- Meng, G.; Jung, Y.J.; Cao, A.; Vajtai, R.; Ajayan, P.M. Controlled fabrication of hierarchically branched nanopores, nanotubes, and nanowires. Proc. Natl. Acad. Soc. USA 2005, 102, 7074–7078. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sun, Y.; Pugno, N. Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites. Materials 2013, 6, 699-712. https://doi.org/10.3390/ma6020699
Sun Y, Pugno N. Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites. Materials. 2013; 6(2):699-712. https://doi.org/10.3390/ma6020699
Chicago/Turabian StyleSun, Yongtao, and Nicola Pugno. 2013. "Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites" Materials 6, no. 2: 699-712. https://doi.org/10.3390/ma6020699
APA StyleSun, Y., & Pugno, N. (2013). Hierarchical Fibers with a Negative Poisson’s Ratio for Tougher Composites. Materials, 6(2), 699-712. https://doi.org/10.3390/ma6020699