Multiscale Microstructures and Microstructural Effects on the Reliability of Microbumps in Three-Dimensional Integration
Abstract
:1. Introduction
2. Modeling Methodology
2.1. Phase Field Model of Solidification
2.2. Phase Field Crystal Model of Solidification
2.3. Coupling Microstructural Evolution with Elastic Mechanics
2.4. Microstructure-Based Electromigration Modeling
| Alloy | Phase | Ef (eV) | ρ (µΩ cm) | C11 (GPa) | C12 (GPa) | C44 (GPa) | Diffusion element | D (×10−13 m2/s) | Z |
| SnPb | Sn-rich | 0.54 [27] | 14.8 [28] | 75.29 [23] | 61.56 [23] | 21.93 [23] | Sn | 6.41 [29] | −17 [30] |
| Pb | 6.41 [29] | −47 [30] | |||||||
| Pb-rich | 0.50 [27] | 30.3 [28] | 49.66 [23] | 42.31 [23] | 14.98 [23] | Sn | 2.15 [29] | −17 [30] | |
| Pb | 5.33 [29] | −47 [30] | |||||||
| SnCu | Sn-rich | 0.54 [27] | 14.8 [28] | 75.29 [23] | 61.56 [23] | 21.93 [23] | Sn | 6.41 [29] | −17 [30] |
| Cu | 201 [31] | −2 [32] | |||||||
| Cu6Sn5 | 1.28 [27] | 17.5 [33] | 164.95 [31] | 74.11 [31] | 45.42 [31] | Sn | 6.49 × 10−3 [32] | −36 [32] | |
| Cu | 7.04 × 10−3 [32] | −26 [32] |
3. Results and Discussion
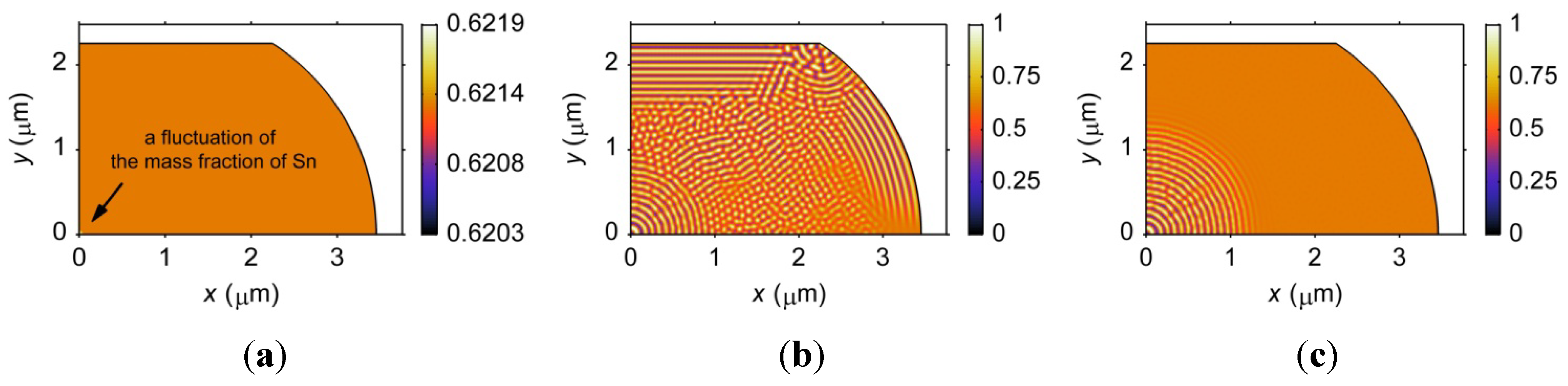
3.1. Mesoscale Microstructural Formation during Solidification
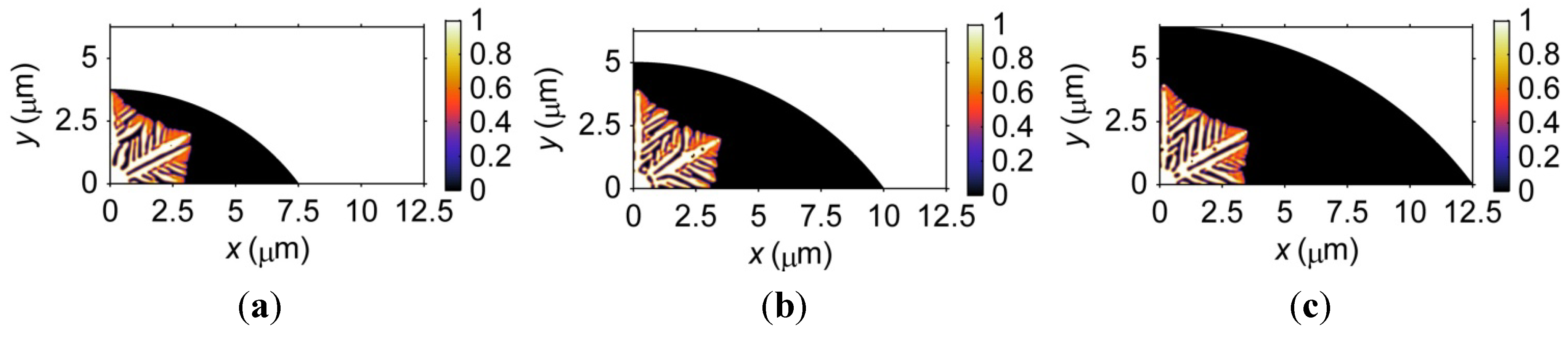
3.1.1. Size Effects on Microstructural Formation
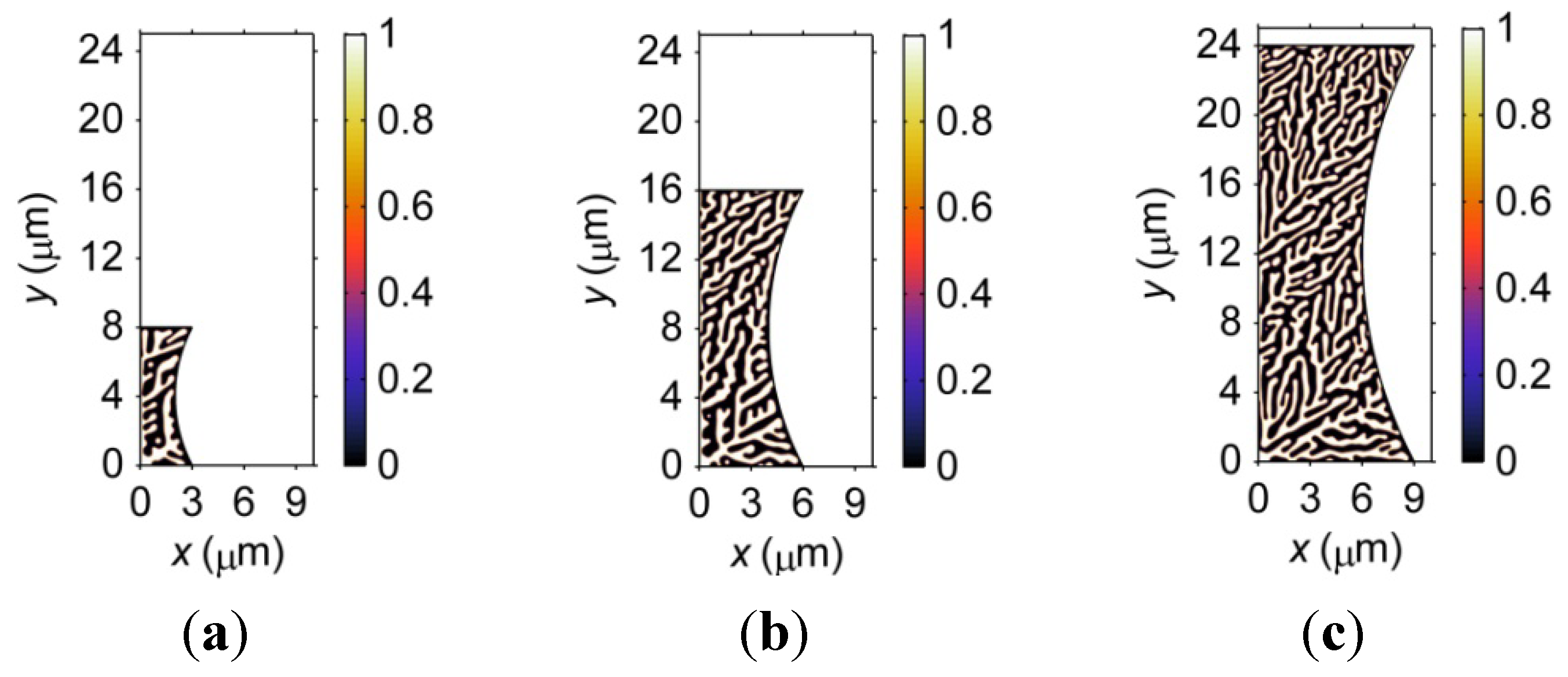
3.1.2. Geometry Effects on Microstructural Formation
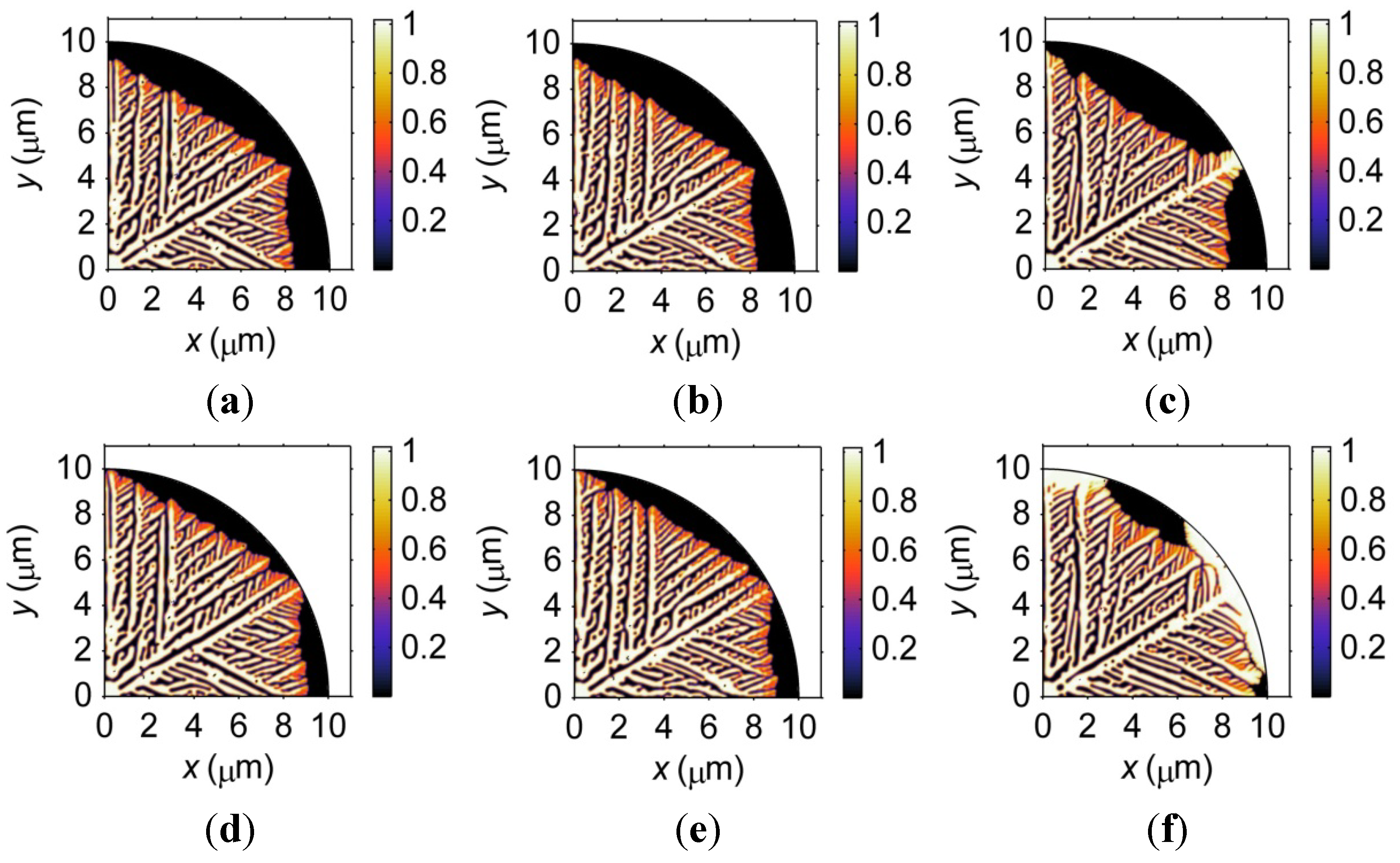
3.2. Atomic-Scale Microstructural Formation during Solidification
3.2.1. Solidification Rate
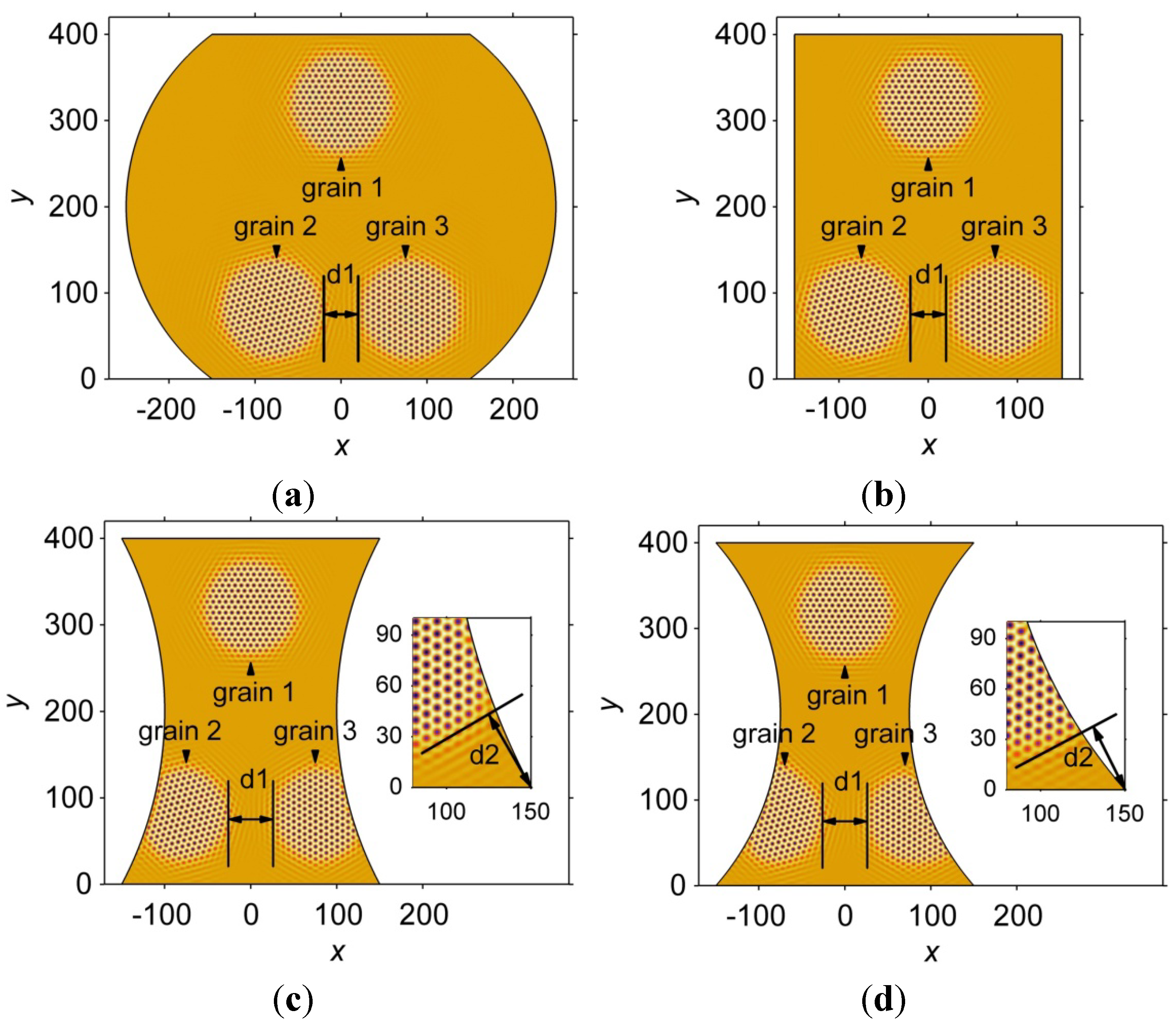
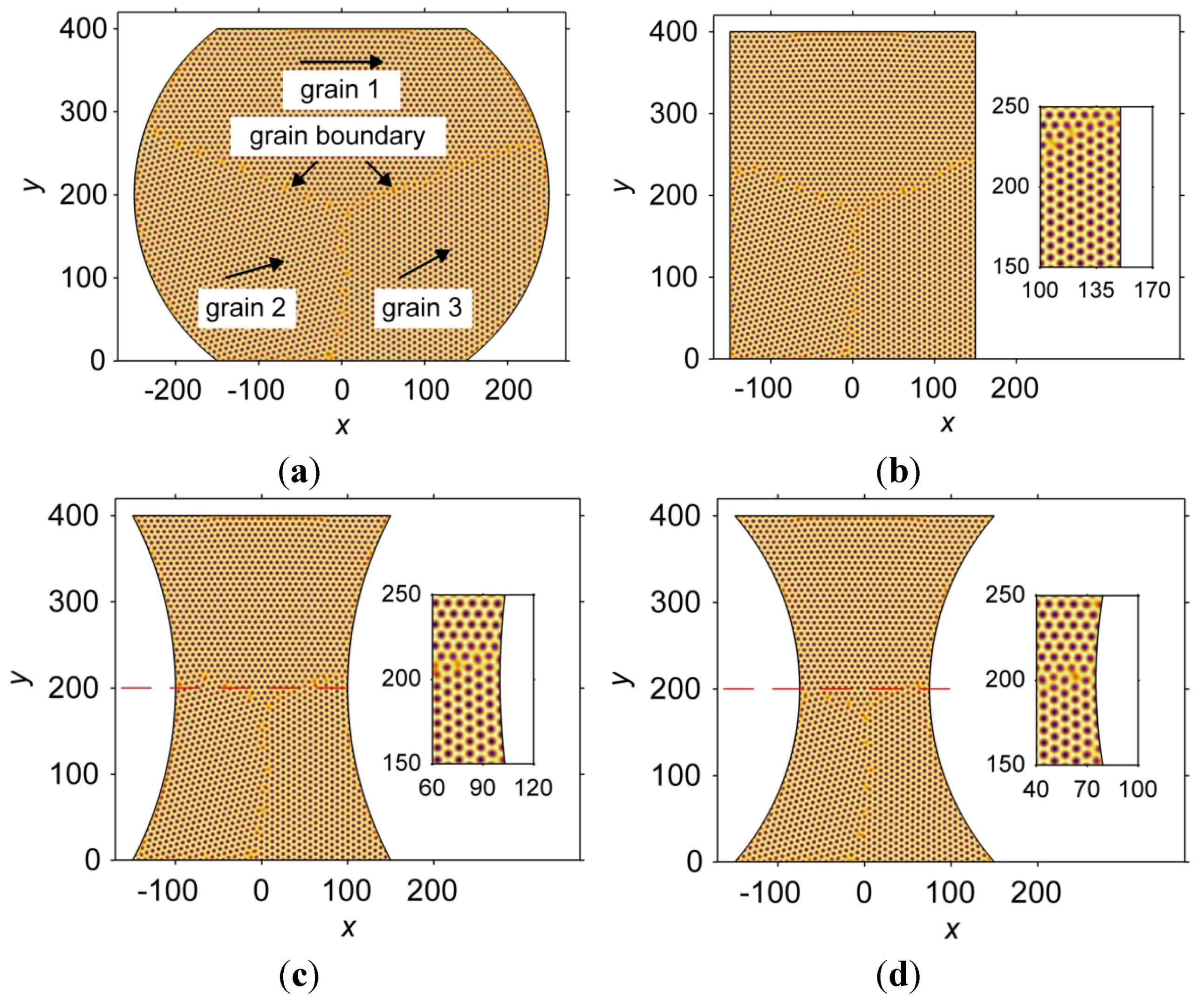
3.2.2. Grain Boundary Formation
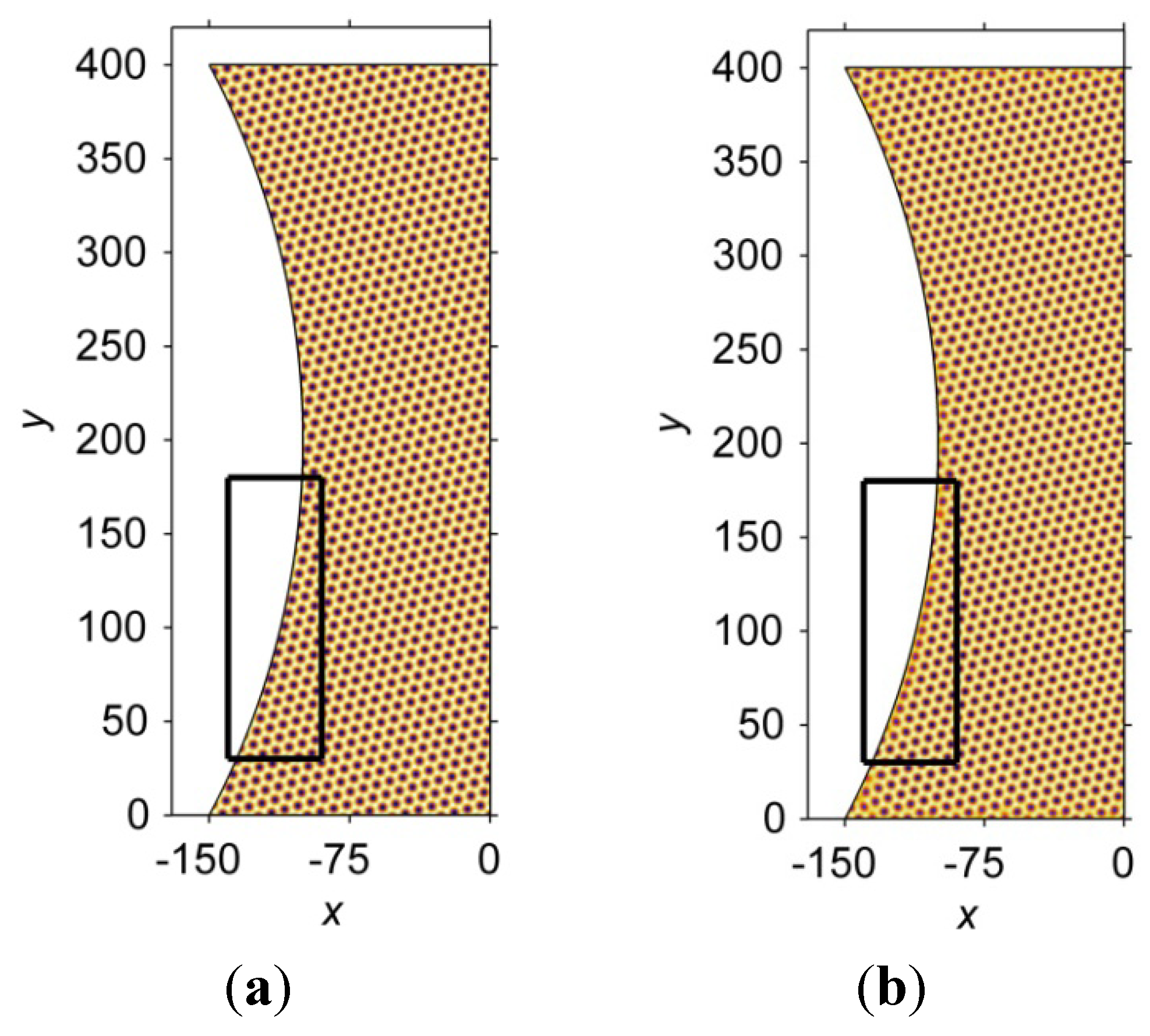
3.2.3. Atomic Arrangement
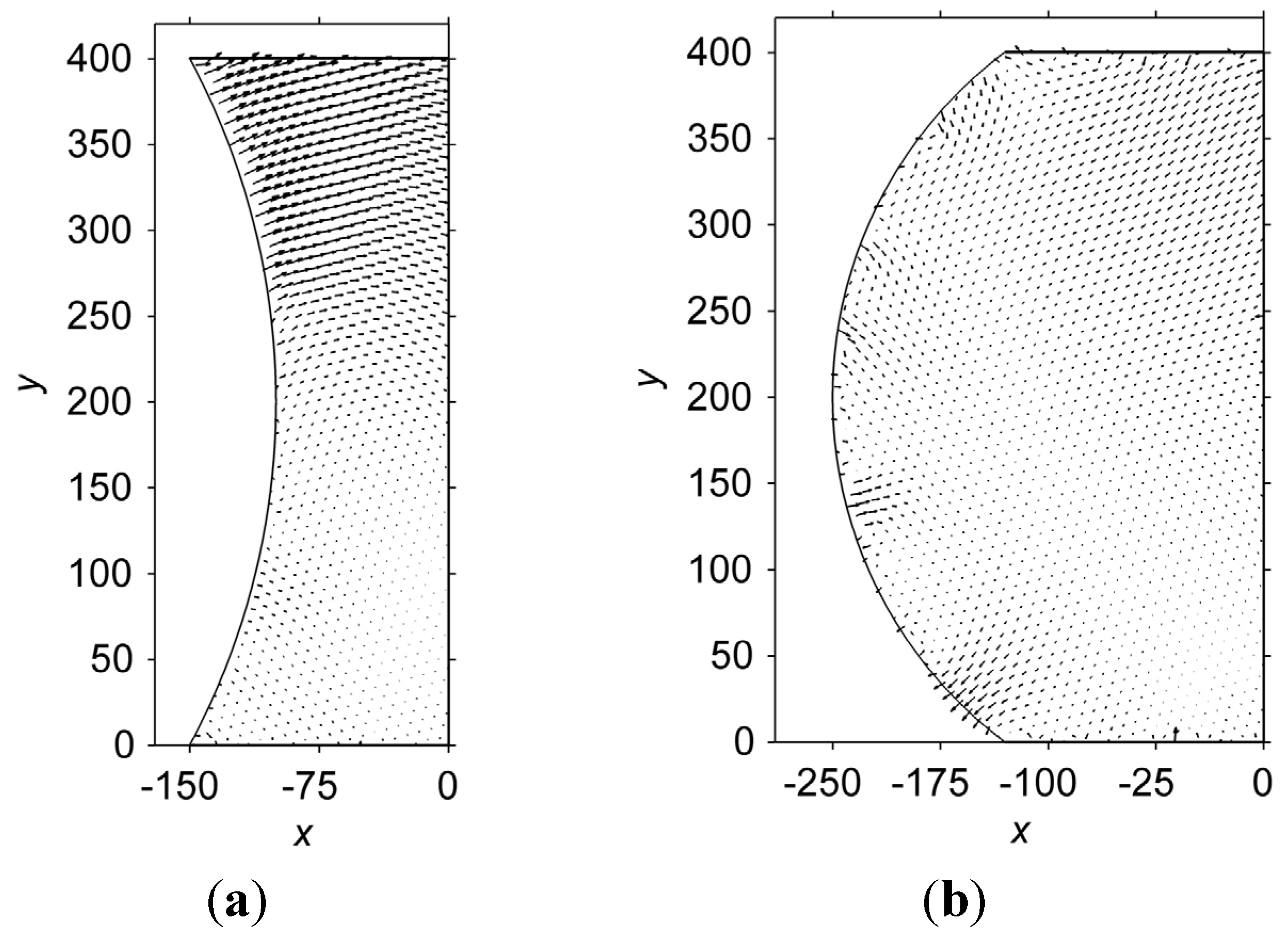
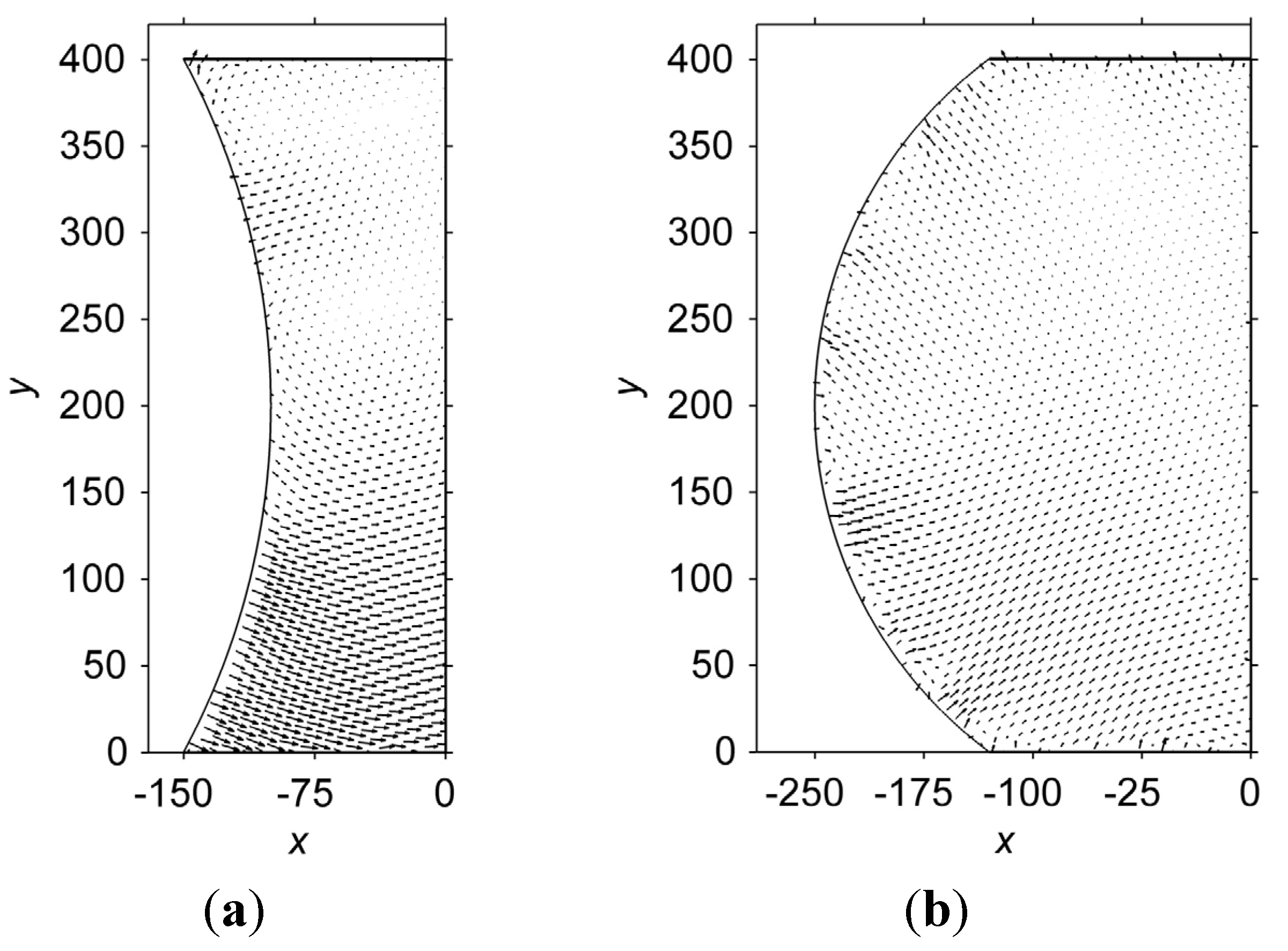
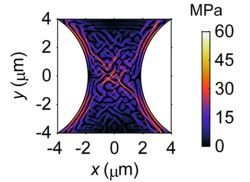
3.3. Effects of Stress on Solid State Microstructural Evolution
3.3.1. Effects of Stress on Phase Separation
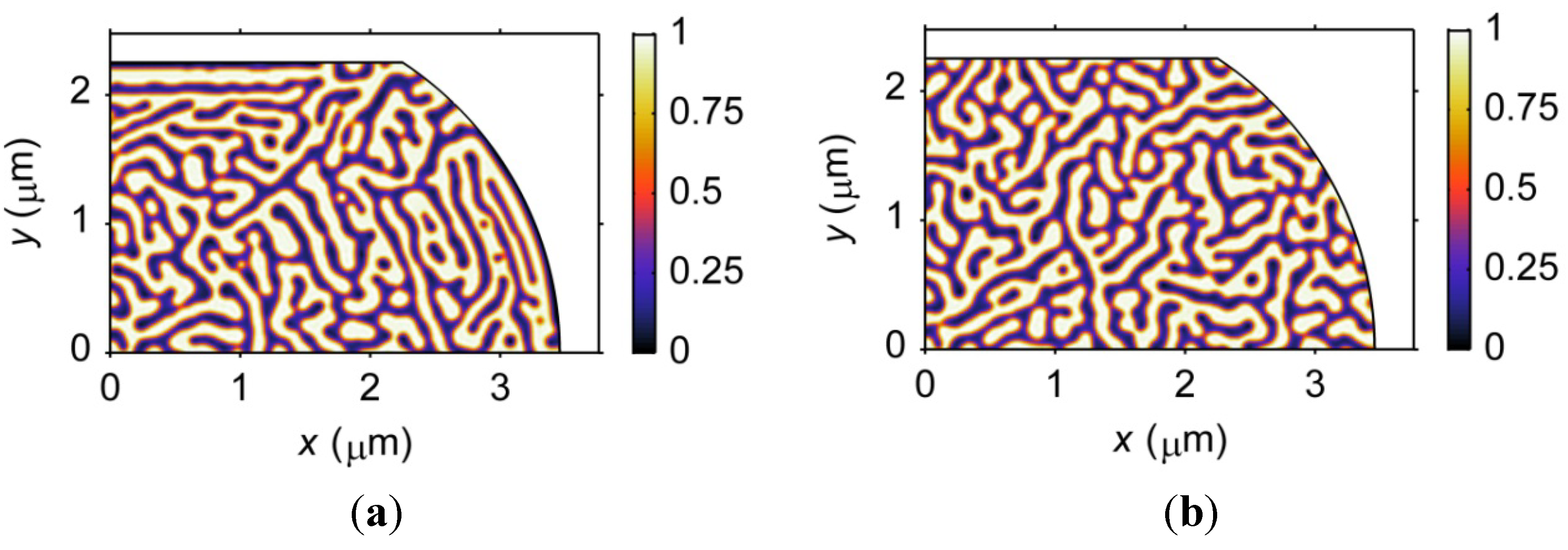
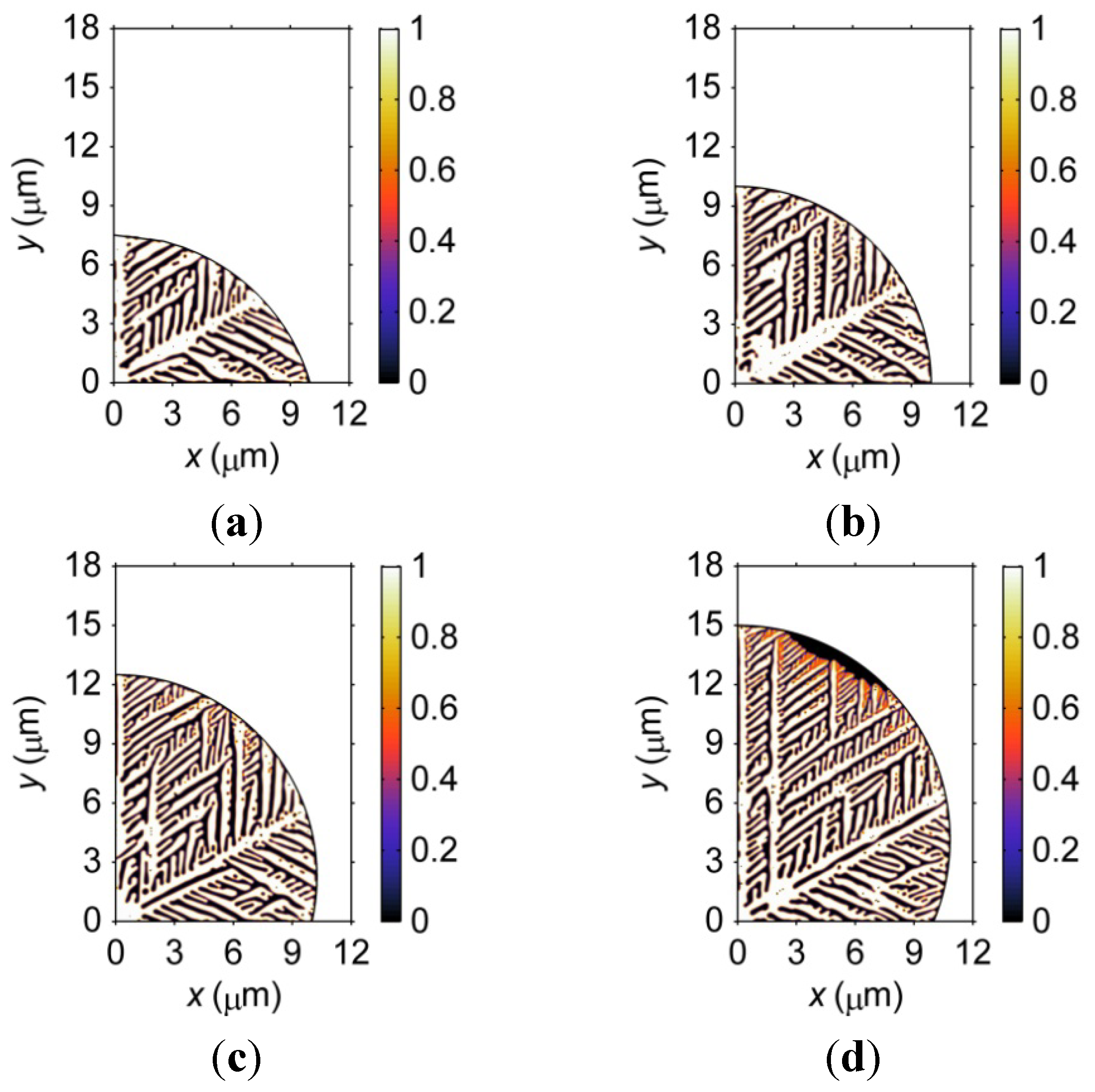
3.3.2. Size Effects on Microstructure

3.3.3. Geometry Effects on Microstructure

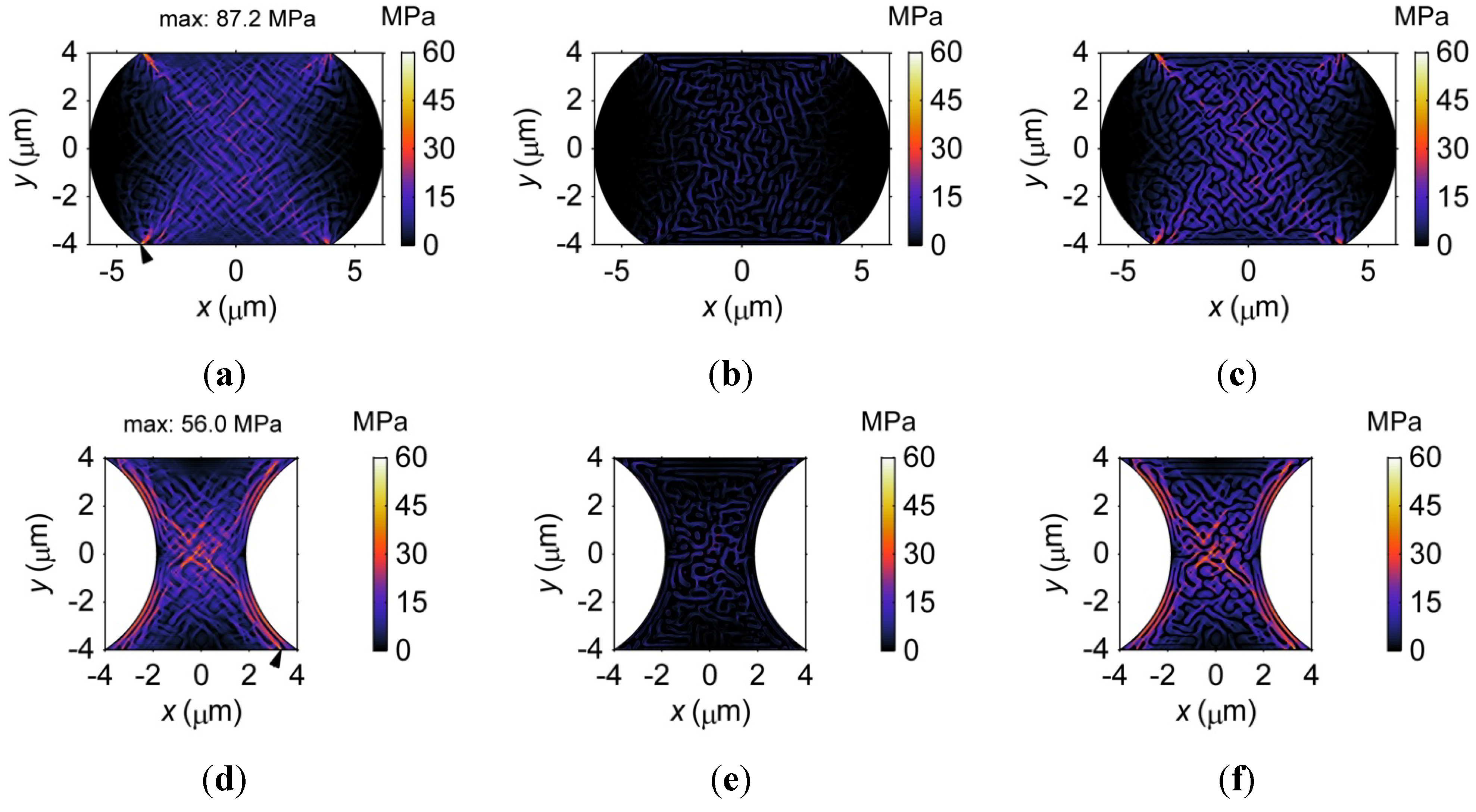
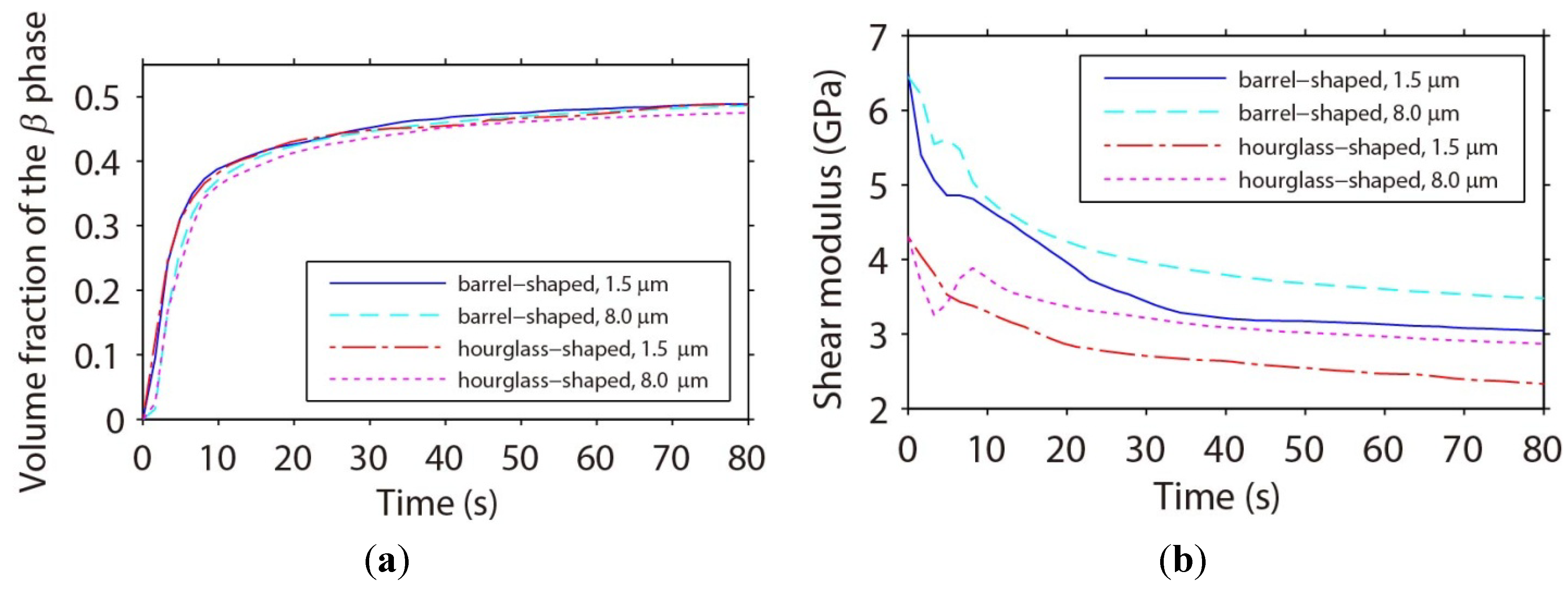
3.3.4. Shear Moduli of Microbumps
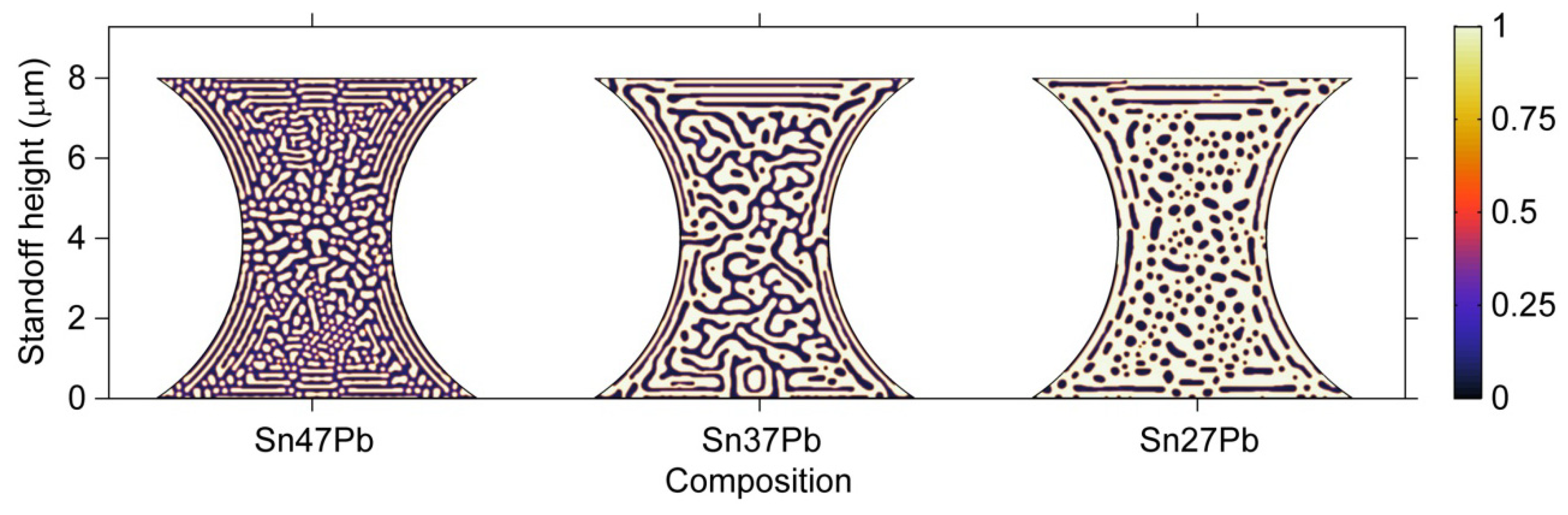
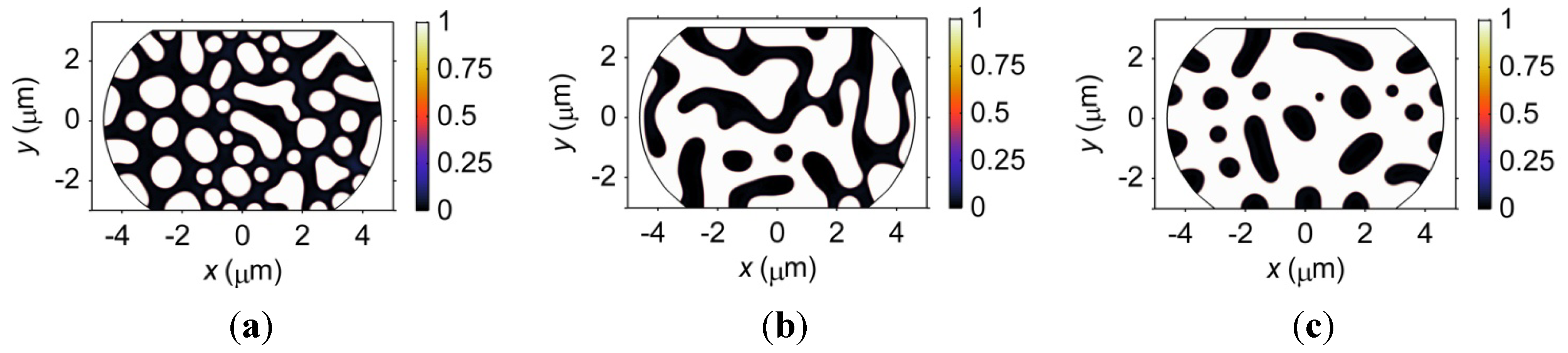
3.3.5. Composition Effects on Microstructure
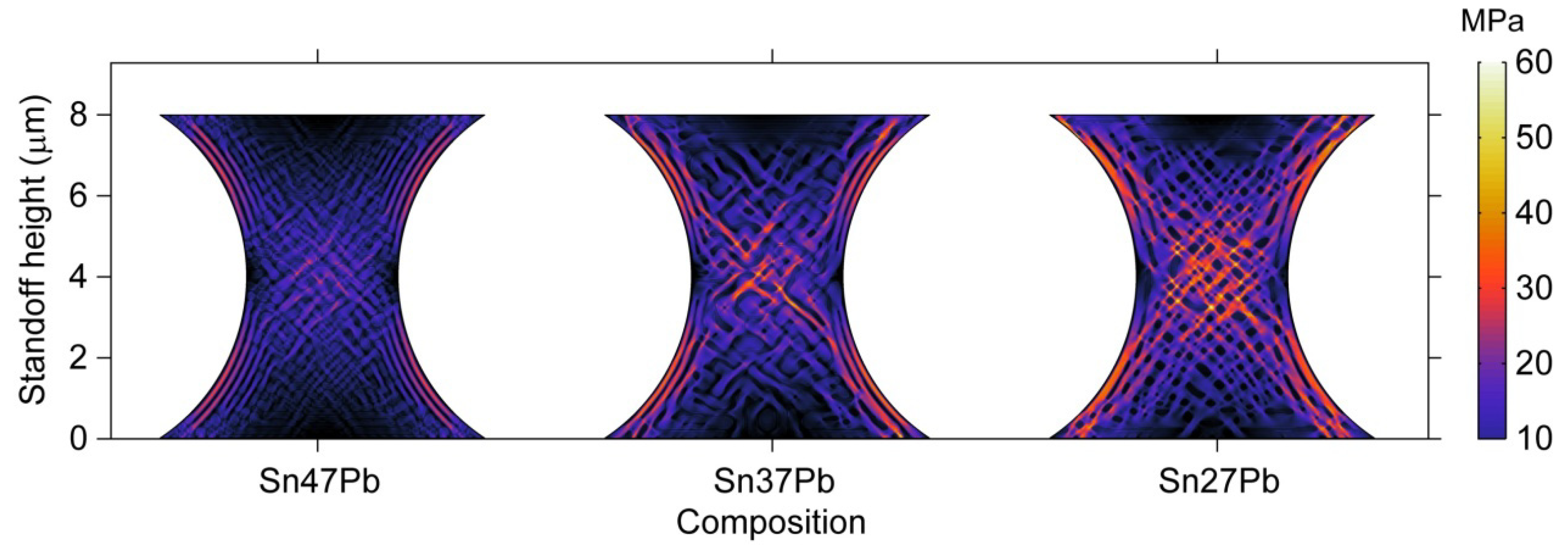
3.4. Effects of Microstructure on Electromigration
3.4.1. Electromigration in Sn27Pb and Sn15Cu Microbumps
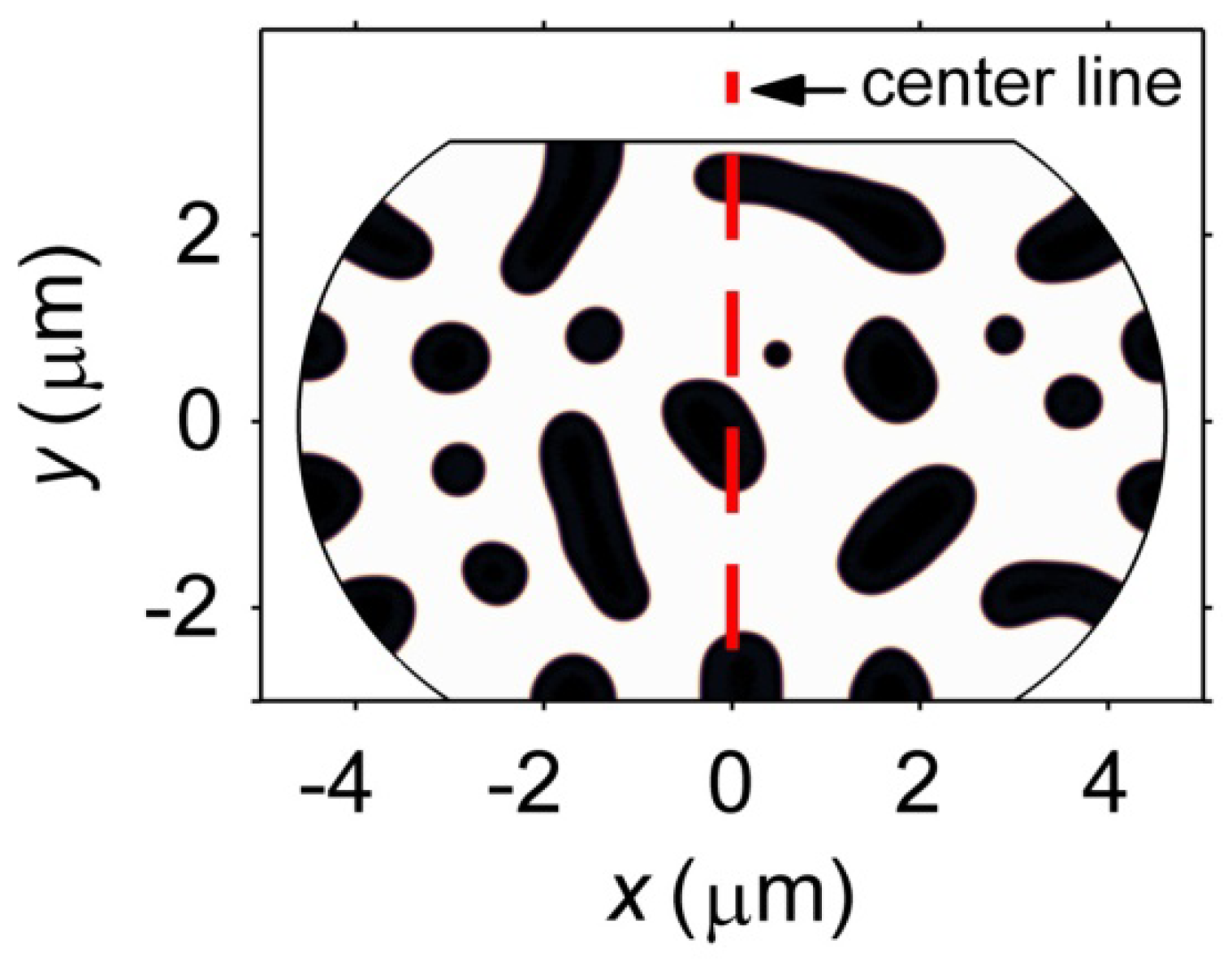
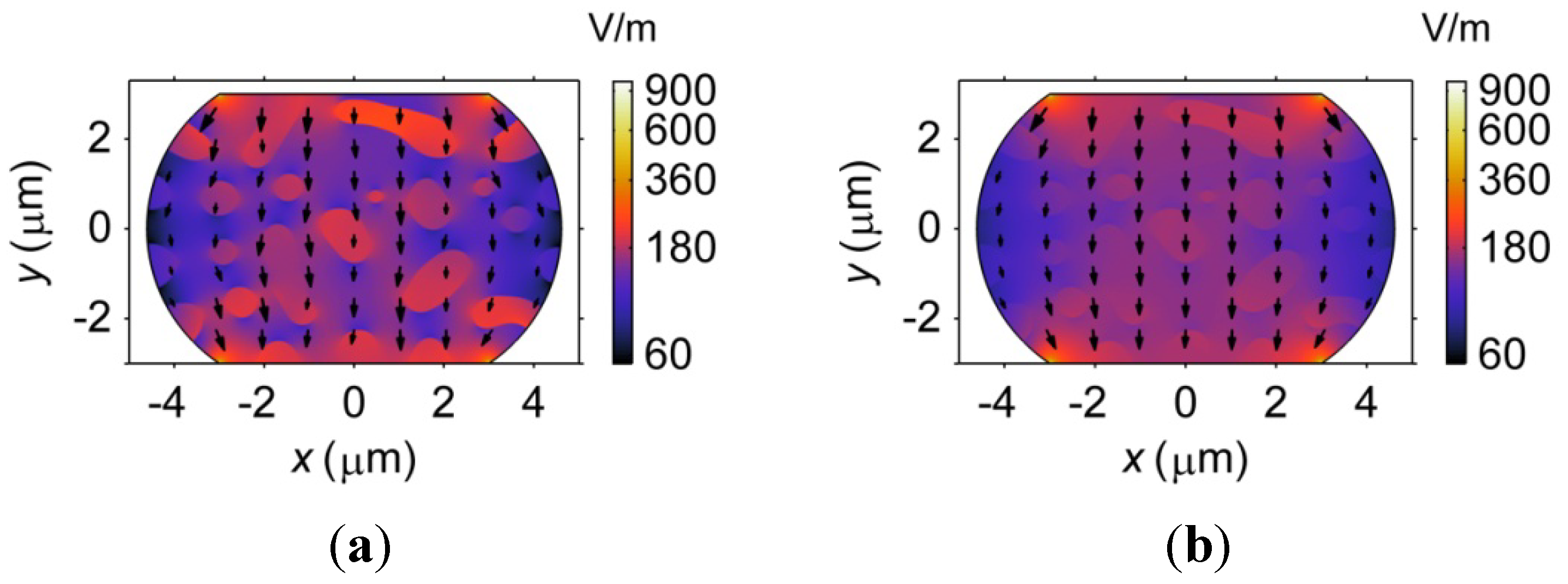
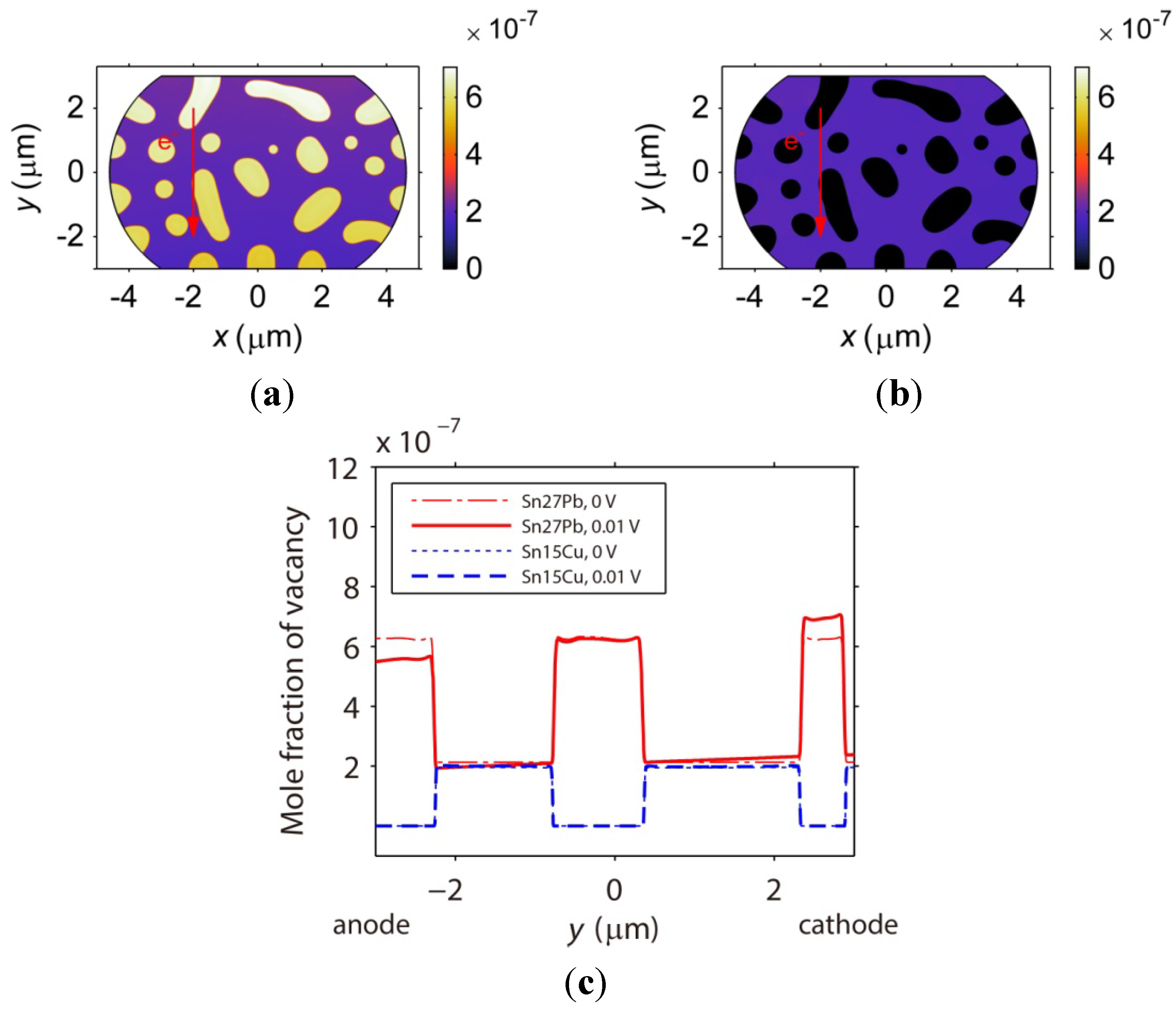
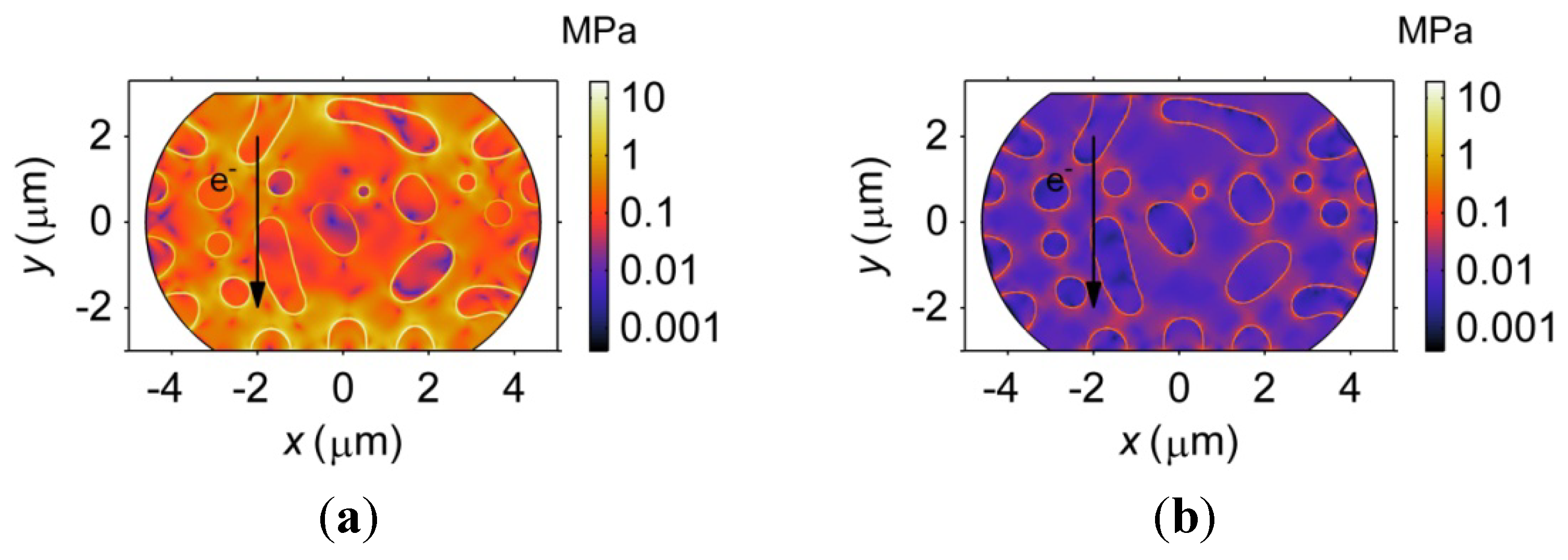
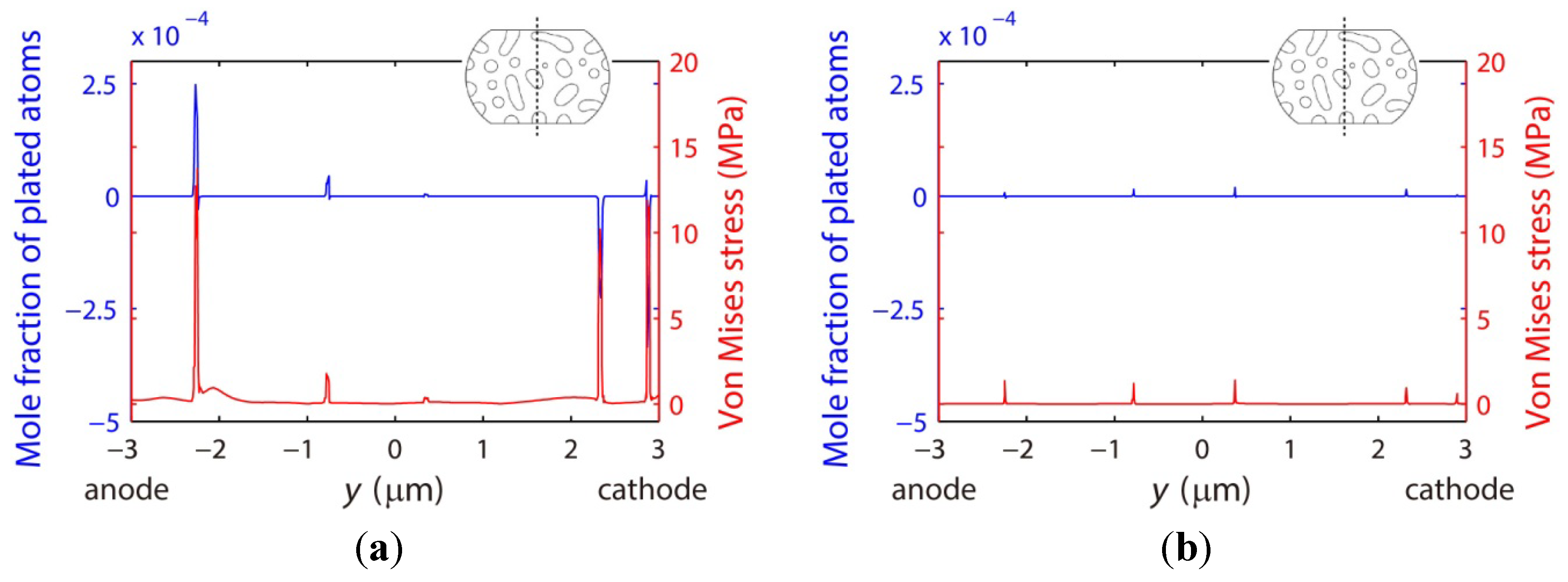
3.4.2. Effects of Phase Coarsening on Electromigration
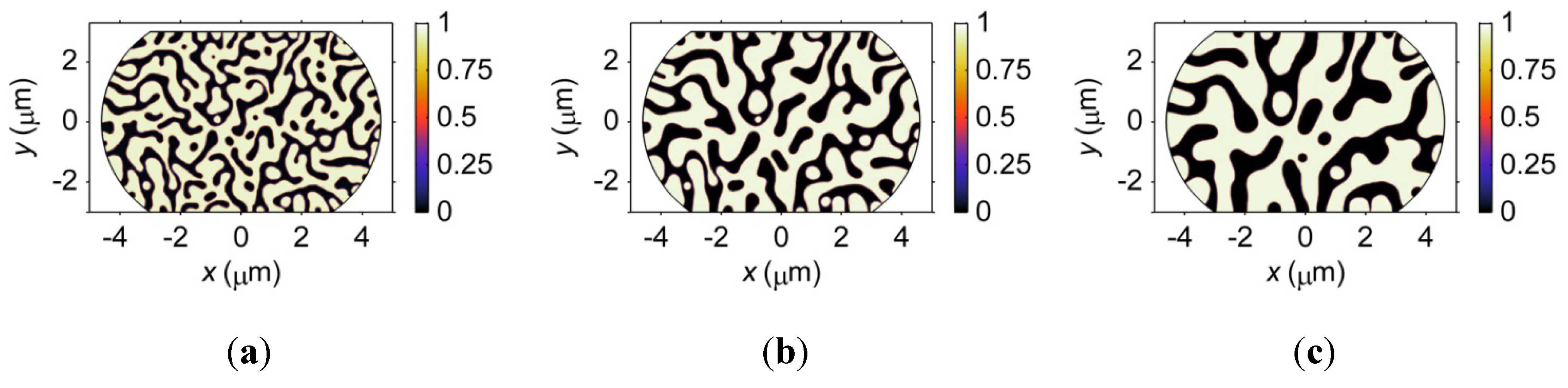
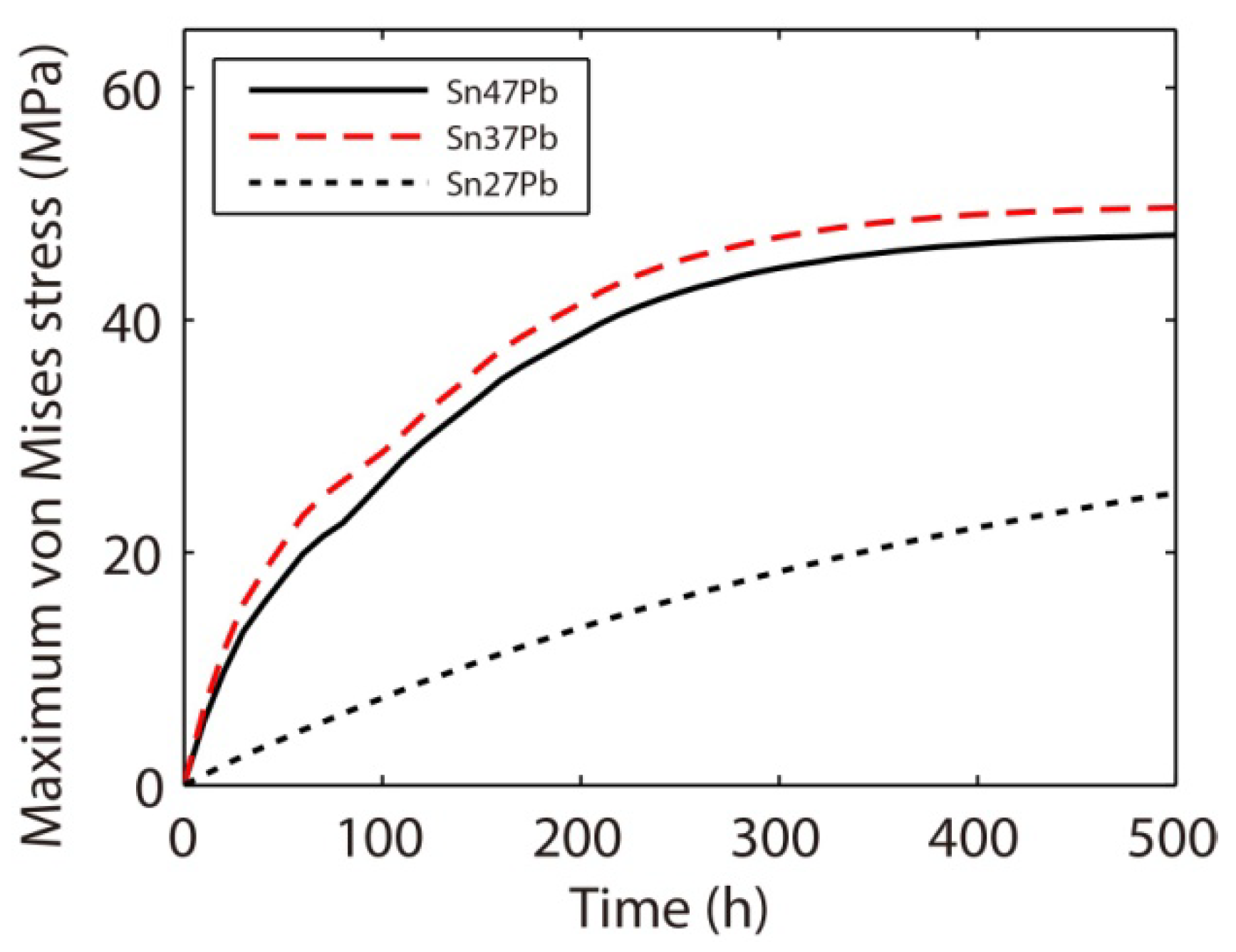
3.4.3. Effects of Composition on Electromigration
4. Conclusions
- The size and geometry of the microbumps can influence the mesoscale microstructural formation during solidification; a smaller microbump solidifies more quickly than a larger counterpart. The length of the dendritic arms increases with the size of the microbump, and a larger microbump contains finer dendrites and a relatively more homogeneous microstructure.
- The simulated atomic arrangements obtained during solidification using the phase crystal method exhibit a displacement when compared to the ideal crystal lattice due to the combined effects of the location of the nucleus and the geometry of the microbump. The magnitude of the displacement depends on the geometry of the microbump, while the distribution of the displacement is controlled by the location of the nucleus.
- Ordered phase growth along the boundaries of the microbump can be observed due to influences from the imposed external shear stress and the geometrical constraints on diffusion. The formation of the ordered phase structures reduces the shear moduli of the microbumps to minimize the strain energy. The shear moduli of the hourglass-shaped microbumps are smaller than the barrel-shaped ones and decrease faster in the smaller microbumps as the microstructures evolve with time.
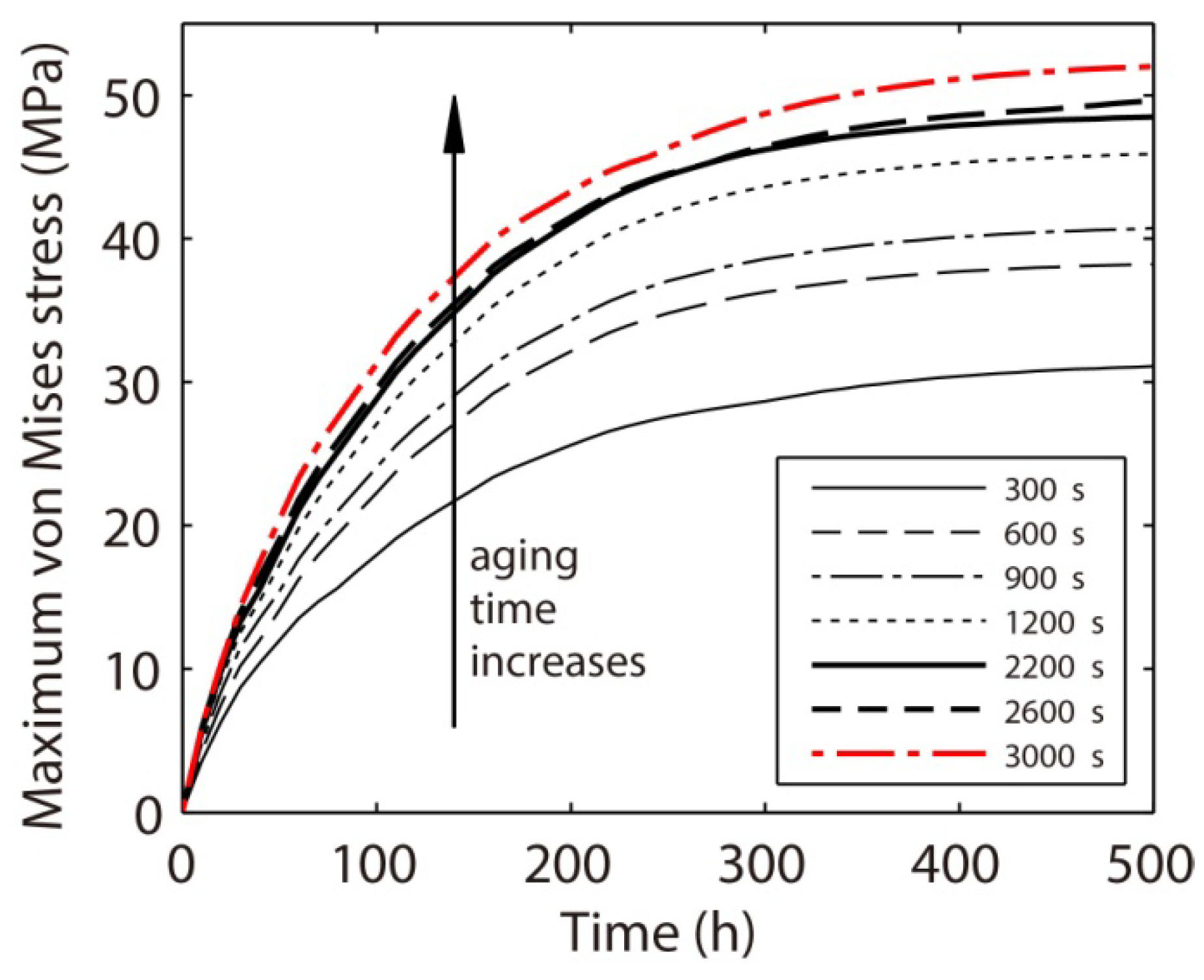
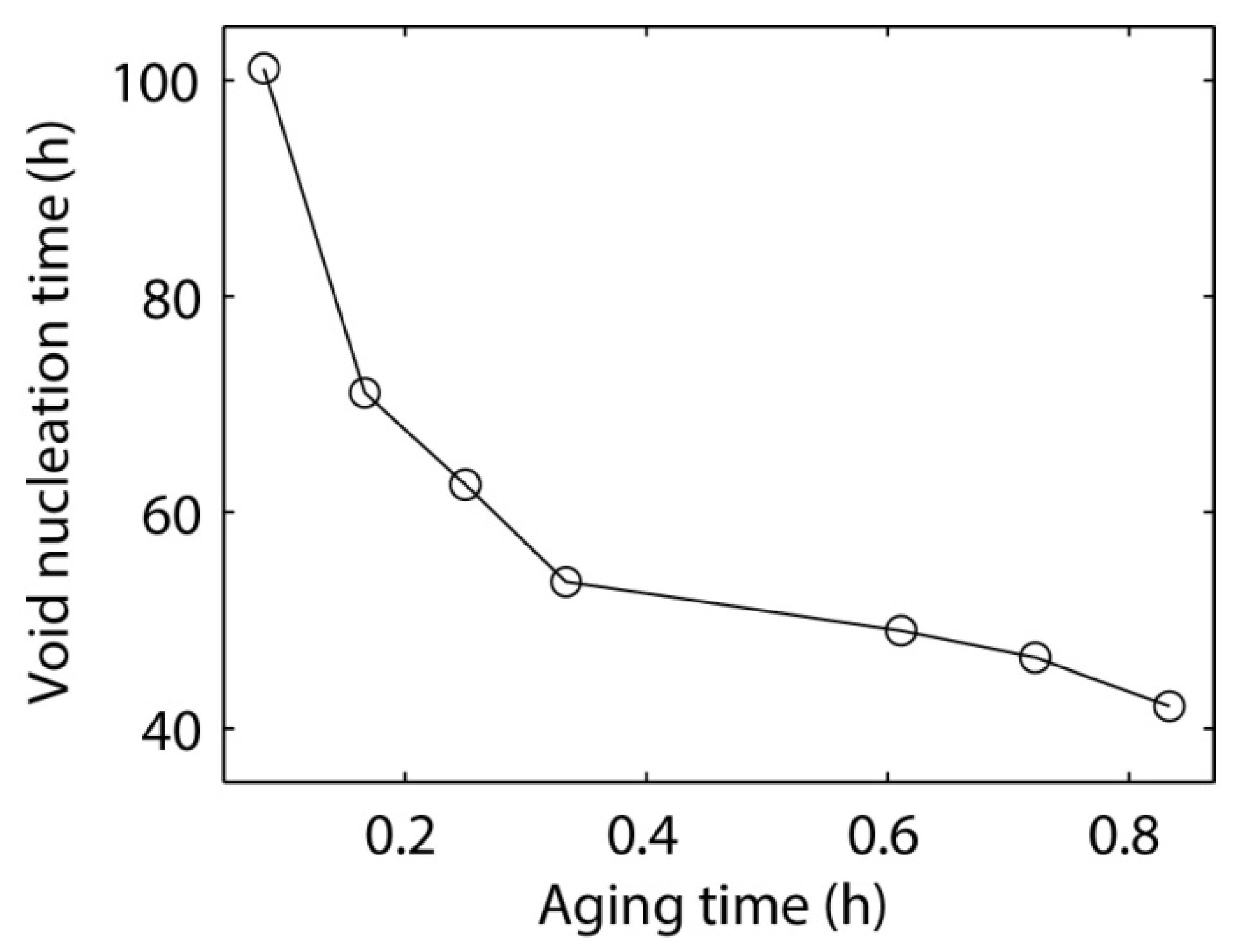
- More vacancy accumulation and stress concentration occur in the Sn27Pb microbump compared to the Sn15Cu microbump during electromigration. Hence, a lower electromigration reliability of the Sn27Pb microbump can be expected. It is also found that phase coarsening in the Sn37Pb microbump reduces the amount of interface and accelerates vacancy accumulation at the cathode and depletion at the anode. Therefore, stress can quickly increase during electromigration in Sn37Pb microbumps aged for longer times, thus increasing the risk of voiding.
- A combined effect caused by the connectivity of the Pb-rich phase and the amount of interface should be considered when comparing the electromigration behaviors of the Sn47Pb, Sn37Pb, and Sn27Pb microbumps. The maximum von Mises stress present in the Sn37Pb microbump increases with the electromigration time and depends on the composition of the microbump, which could result in nonuniformity in bump heights if the process variables are not tightly controlled.
Acknowledgments
Conflicts of Interest
References
- Lu, J.-Q. 3-D hyperintegration and packaging technologies for micro-nano systems. Proc. IEEE 2009, 97, 18–30. [Google Scholar] [CrossRef]
- IMEC Scientific Report 2012. Available online: http://www.imec.be/ScientificReport/SR2012/1115980.html (accessed on 16 August 2013).
- International Technology Roadmap for Semiconductors. Available online: http://www.itrs.net/Links/2012ITRS/Home2012.htm (accessed on 16 August 2013).
- Tummala, R.R. The future of packaging. Chip Scale Rev. 2012, 16, 9–11. [Google Scholar]
- Lau, J.H. Evolution, Challenge, and Outlook of TSV, 3D IC Integration and 3D Silicon Integration. In Proceedings of the International Symposium on Advanced Packaging Materials (APM), Xiamen, China, 25–28 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 462–488. [Google Scholar]
- Papanikolaou, A.; Soudris, D.; Radojcic, R. Three Dimensional System Integration: IC Stacking Process and Design; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bakir, M.S.; Meindl, J.D. Integrated Interconnect Technologies for 3D Nanoelectronic Systems; Artech House: Norwood, OH, USA, 2009. [Google Scholar]
- Tummala, R.R.; Swaminathan, M. Introduction to System-on-Package (SOP): Miniaturization of the Entire System; McGraw-Hill Companies: New York, NY, USA, 2008. [Google Scholar]
- Chen, C.F. Homogenization of TSV Interposer and Quick Assessment of Its Thermomechanical Influence on 3D Packages. In Proceedings of the 63rd Electronic Components and Technology Conference (ECTC), Las Vegas, NV, USA, 28–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 2249–2254. [Google Scholar]
- Hwang, S.-H.; Kim, B.-J.; Lee, H.-Y. Electrical and mechanical properties of through-silicon vias and bonding layers in stacked wafers for 3D integrated circuits. J. Electron. Mater. 2012, 41, 232–240. [Google Scholar] [CrossRef]
- Beyne, E. Electrical, Thermal and Mechanical Impact of 3D TSV and 3D Stacking Technology on Advanced CMOS Devices–Technology Directions. In Proceedings 2011 IEEE International 3D Systems Integration Conference (3DIC), Osaka, Japan, 31 January–2 February 2012; IEEE: Piscataway, NJ, USA, 2012; p. 6. [Google Scholar]
- Yu, H.; Ho, J.; He, L. Allocating power ground vias in 3D ICs for simultaneous power and thermal integrity. ACM Trans. Des. Autom. Electron. Syst. 2009, 14. [Google Scholar] [CrossRef]
- Manoj, S.; Yu, H.; Shang, Y.; Tan, C.S.; Lim, S.K. Reliable 3-D clock-tree synthesis considering nonlinear capacitive TSV model with electrical-thermal-mechanical coupling. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2013, 32, 1734–1747. [Google Scholar] [CrossRef]
- Bernstein, L. Semiconductor joining by the solid-liquid-interdiffusion (SLID) process: I. The systems Ag-In, Au-In, and Cu-In. J. Elecrochem. Soc. 1966, 113, 1282–1288. [Google Scholar] [CrossRef]
- Chang, J.-Y.; Cheng, R.-S.; Kao, K.-S. Reliable microjoints formed by solid-liquid interdiffusion (SLID) bonding within a chip-stacking architecture. IEEE Trans. Compon. Pack. Manuf. Technol. 2012, 2, 979–984. [Google Scholar] [CrossRef]
- Yang, Y.; Balaraju, J.N.; Chong, S.C. Significantly retarded interfacial reaction between an electroless Ni-W-P metallization and lead-free Sn-3.5Ag solder. J. Alloy. Compd. 2013, 565, 11–16. [Google Scholar] [CrossRef]
- Dimcic, B.; Labie, R.; de Messemaeker, J. Diffusion growth of Cu3Sn phase in the bump and thin film Cu/Sn structures. Microelectron. Reliab. 2012, 52, 1971–1974. [Google Scholar] [CrossRef]
- Rajoo, R.; Lim, S.S.; Wong, E.H. Development of stretch solder interconnections for wafer level packaging. IEEE Trans. Adv. Pack. 2008, 31, 377–385. [Google Scholar] [CrossRef]
- Liu, X.; Lu, G.-Q. Effects of solder joint shape and height on thermal fatigue lifetime. IEEE Trans. Compon. Pack. Technol. 2003, 26, 455–465. [Google Scholar] [CrossRef]
- Kim, S.G.; Kim, W.T.; Lee, J.S. Large scale simulation of dendritic growth in pure undercooled melt by phase-field model. ISIJ Int. 1999, 4, 335–340. [Google Scholar] [CrossRef]
- Elder, K.R.; Katakowski, M.; Haataja, M. Modeling elasticity in crystal growth. Phys. Rev. Lett. 2002, 88, 245701:1–245701:4. [Google Scholar] [CrossRef]
- Elder, K.R.; Grant, M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals. Phys. Rev. E 2004, 70, 051605:1–051605:20. [Google Scholar] [CrossRef]
- Dreyer, W.; Müller, W.H. Modeling diffusional coarsening in eutectic tin/lead solders: A quantitative approach. Int. J. Solids Struct. 2001, 38, 1433–1458. [Google Scholar] [CrossRef]
- Liu, X.; Xu, S.; Lu, G.-Q. Stacked solder bumping technology for improved solder joint reliability. Microelectron. Reliab. 2001, 41, 1979–1992. [Google Scholar] [CrossRef]
- Sukharev, V.; Zschech, E.; Nix, W.D. A model for electromigration-induced degradation mechanisms in dual-inlaid copper interconnects: Effect of microstructure. J. Appl. Phys. 2007, 102, 053505:1–053505:14. [Google Scholar] [CrossRef]
- Darken, L.S. Diffusion, mobility and their interrelation through free energy in binary metallic systems. Trans. AIME 1948, 175, 184–201. [Google Scholar]
- Schaefer, H.-E. Investigation of thermal equilibrium vacancies in metals by positron annihilation. Phys. Status Solidi 1987, 102, 47–65. [Google Scholar] [CrossRef]
- Li, X.-F.; Zu, F.-Q.; Ding, H.-F. Anomalous change of electrical resistivity with temperature in liquid Pb-Sn alloys. Phys. B 2005, 358, 126–131. [Google Scholar] [CrossRef]
- Gupta, D.; Vieregge, K.; Gust, W. Interface diffusion in eutectic Pb-Sn solder. Acta Mater. 1998, 47, 5–12. [Google Scholar] [CrossRef]
- Lee, T.Y.; Tu, K.N.; Kuo, S.M. Electromigration of eutectic SnPb solder interconnects for flip chip technology. J. Appl. Phys. 2001, 89, 3189–3194. [Google Scholar] [CrossRef]
- Chae, S.-H.; Chao, B.; Zhang, X.F. Invetigation of Intermetallic Compound Growth Enhanced by Electromigration in Pb-Free Solder Joints. In Proceedings of the 57th Electronic Components and Technology Conference (ECTC), Reno, NV, USA, 29 May–1 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1442–1449. [Google Scholar]
- Chao, B.; Chae, S.-H.; Zhang, X.F. Investigation of diffusion and electromigration parameters for Cu-Sn intermetallic compounds in Pb-free solders using simulated annealing. Acta Mater. 2007, 55, 2805–2814. [Google Scholar] [CrossRef]
- Peng, J.; Wu, F.S.; Liu, H. Effects of Thermal Aging on the Electrical Resistance of Sn-3.5Ag Micro SOH Solder Joints. In Proceedings of the International Conference on Electronic Packaging Technology & High Density Packaging (ICEPT-HDP), Beijing, China, 10–13 August 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1023–1026. [Google Scholar]
- Murrary, B.T.; Wheeler, A.A.; Glicksman, M.E. Simulations of experimentally observed dendritic growth behavior using a phase-field model. J. Cryst. Growth 1995, 154, 386–400. [Google Scholar] [CrossRef]
- Liu, C.Y.; Chen, C.; Tu, K.N. Electromigration in Sn-Pb solder strips as a function of alloy composition. J. Appl. Phys. 2000, 88, 5703–5709. [Google Scholar] [CrossRef]
- Sukharev, V.; Kteyan, A.; Zschech, E. Physics-based models for EM and SM simulations in three-dimensional IC structures. IEEE Trans. Device Mater. Reliab. 2012, 12, 272–284. [Google Scholar] [CrossRef]
- Kanchanomai, C.; Miyashita, Y.; Mutoh, Y. Strain-rate effects on low cycle fatigue mechanism of eutectic Sn-Pb solder. Int. J. Fatigue 2002, 24, 987–993. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huang, Z.; Xiong, H.; Wu, Z.; Conway, P.; Altmann, F. Multiscale Microstructures and Microstructural Effects on the Reliability of Microbumps in Three-Dimensional Integration. Materials 2013, 6, 4707-4736. https://doi.org/10.3390/ma6104707
Huang Z, Xiong H, Wu Z, Conway P, Altmann F. Multiscale Microstructures and Microstructural Effects on the Reliability of Microbumps in Three-Dimensional Integration. Materials. 2013; 6(10):4707-4736. https://doi.org/10.3390/ma6104707
Chicago/Turabian StyleHuang, Zhiheng, Hua Xiong, Zhiyong Wu, Paul Conway, and Frank Altmann. 2013. "Multiscale Microstructures and Microstructural Effects on the Reliability of Microbumps in Three-Dimensional Integration" Materials 6, no. 10: 4707-4736. https://doi.org/10.3390/ma6104707
APA StyleHuang, Z., Xiong, H., Wu, Z., Conway, P., & Altmann, F. (2013). Multiscale Microstructures and Microstructural Effects on the Reliability of Microbumps in Three-Dimensional Integration. Materials, 6(10), 4707-4736. https://doi.org/10.3390/ma6104707