Review of Random Phase Encoding in Volume Holographic Storage
Abstract
:1. Introduction
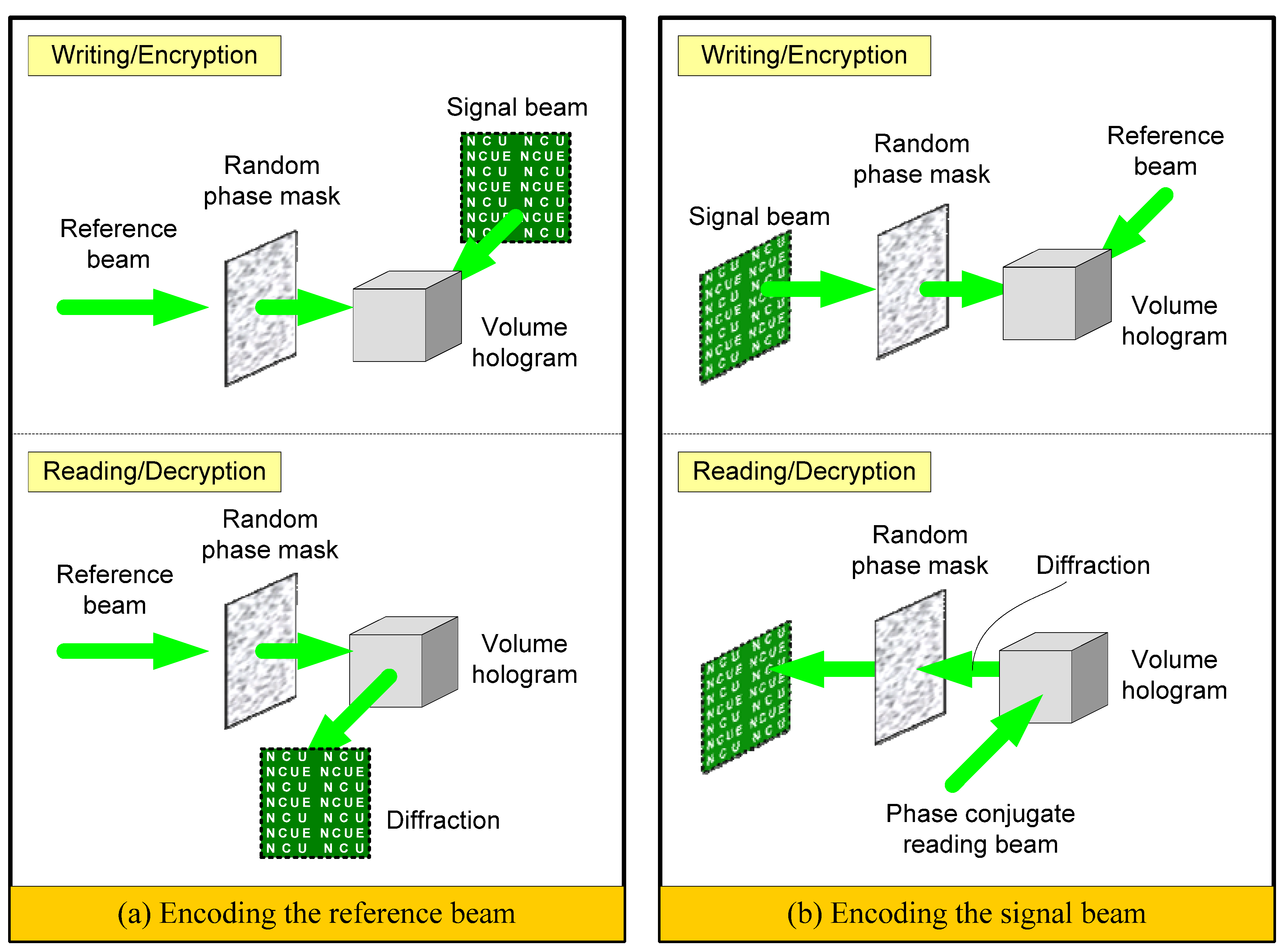
2. Random Phase Multiplexing
2.1. Shifting Selectivity
2.1.1. Lateral Shifting Selectivity
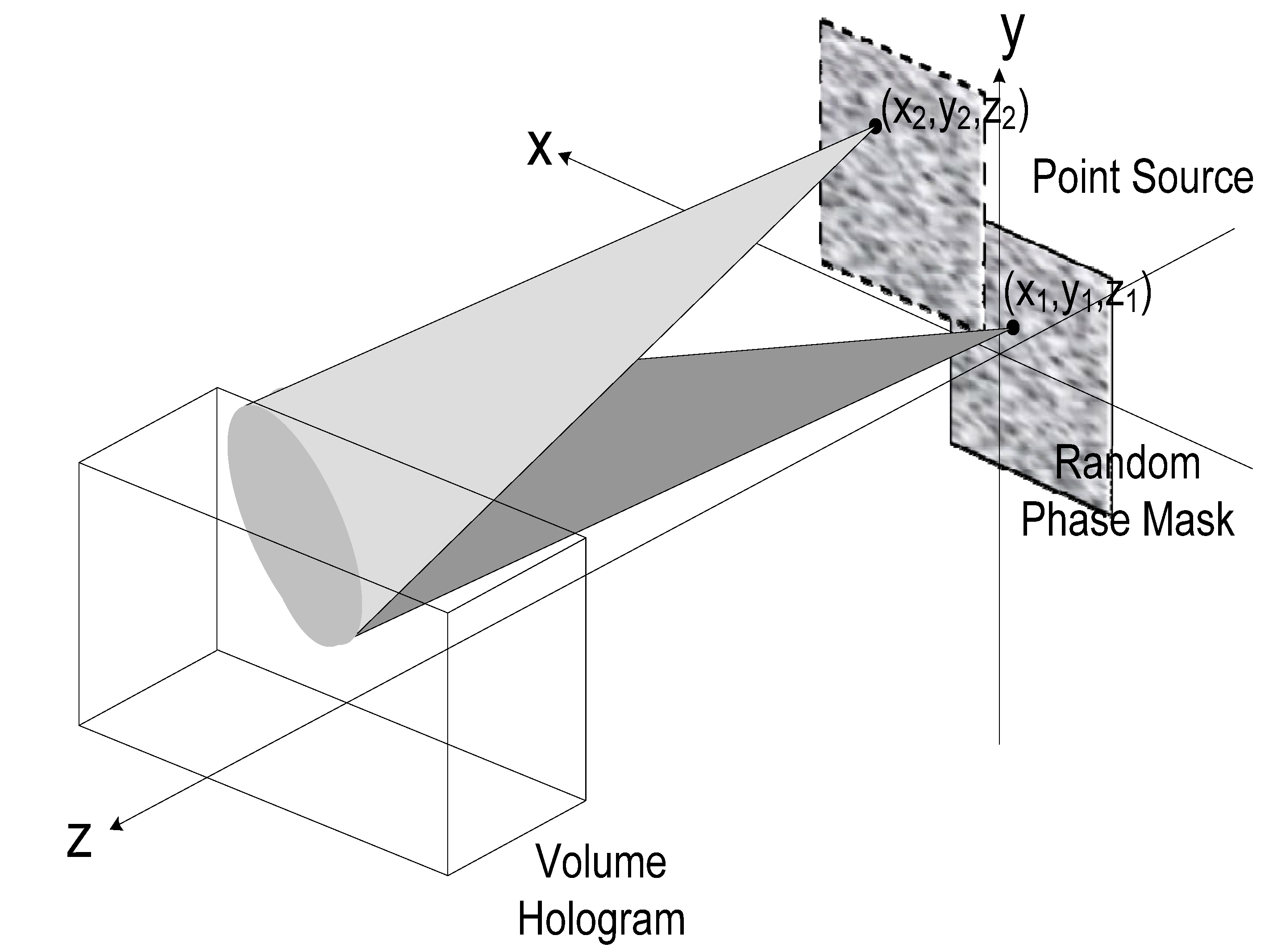
2.1.2. Longitudinal Shifting Selectivity
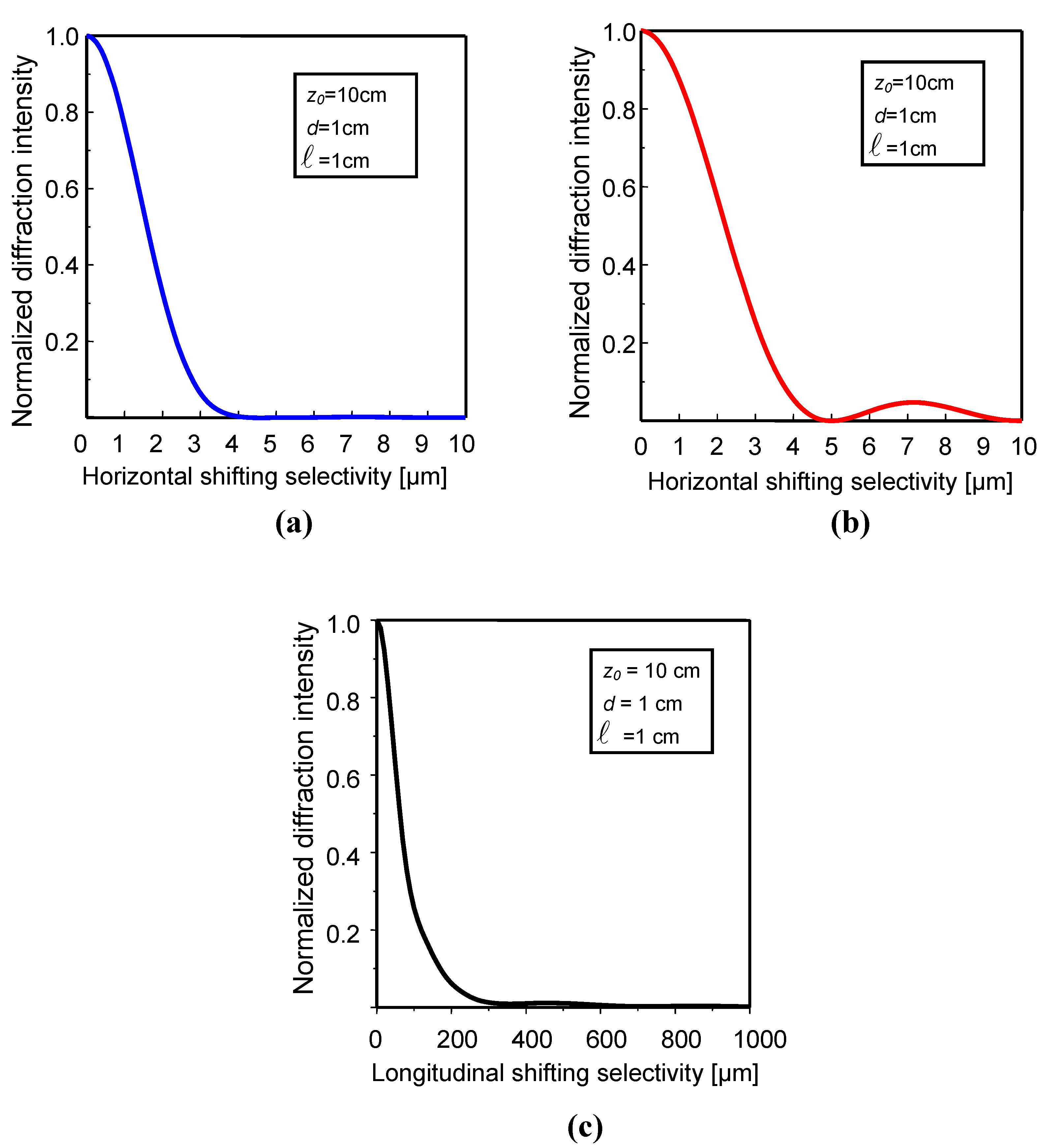
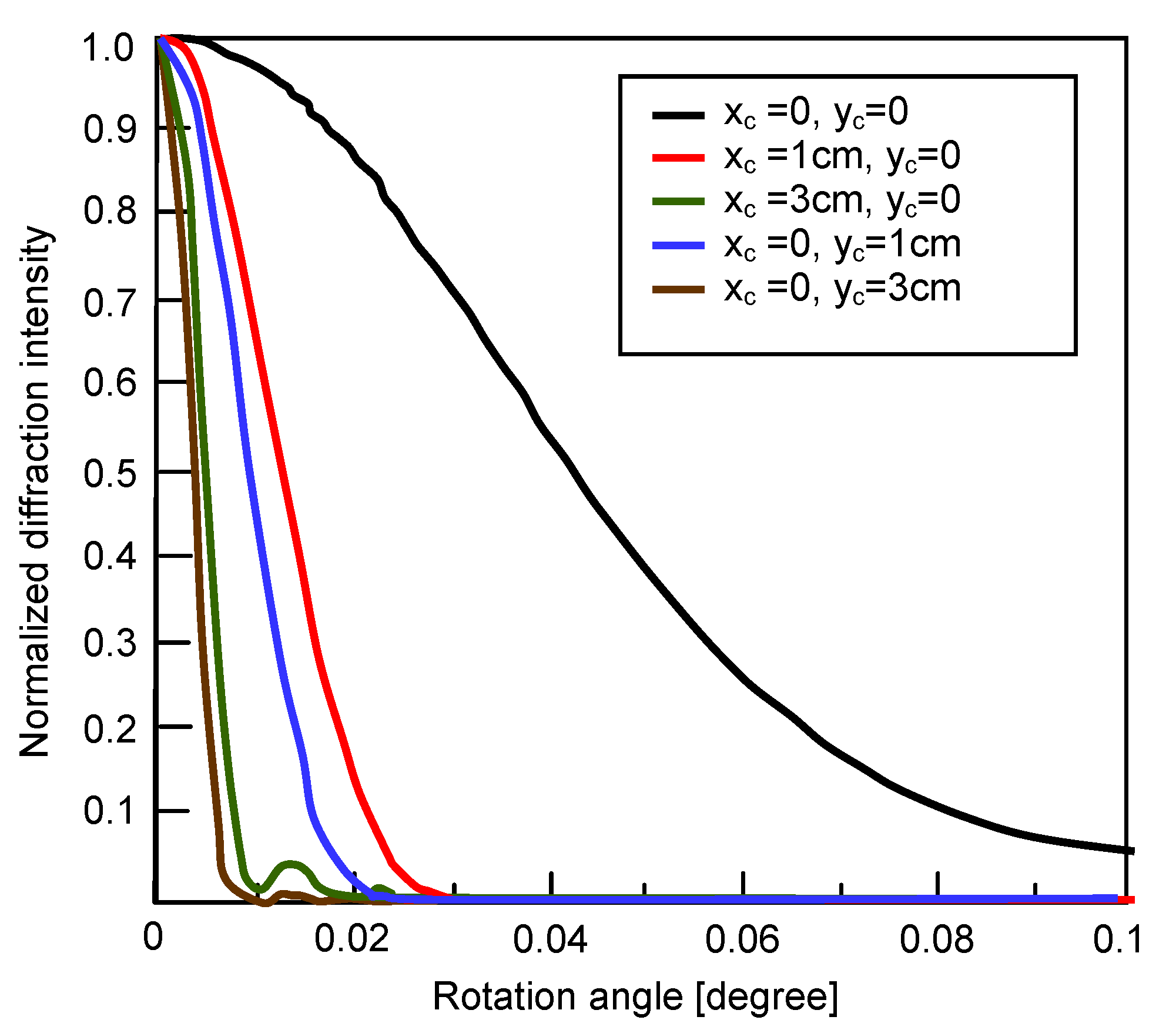
2.2. Rotational Selectivity
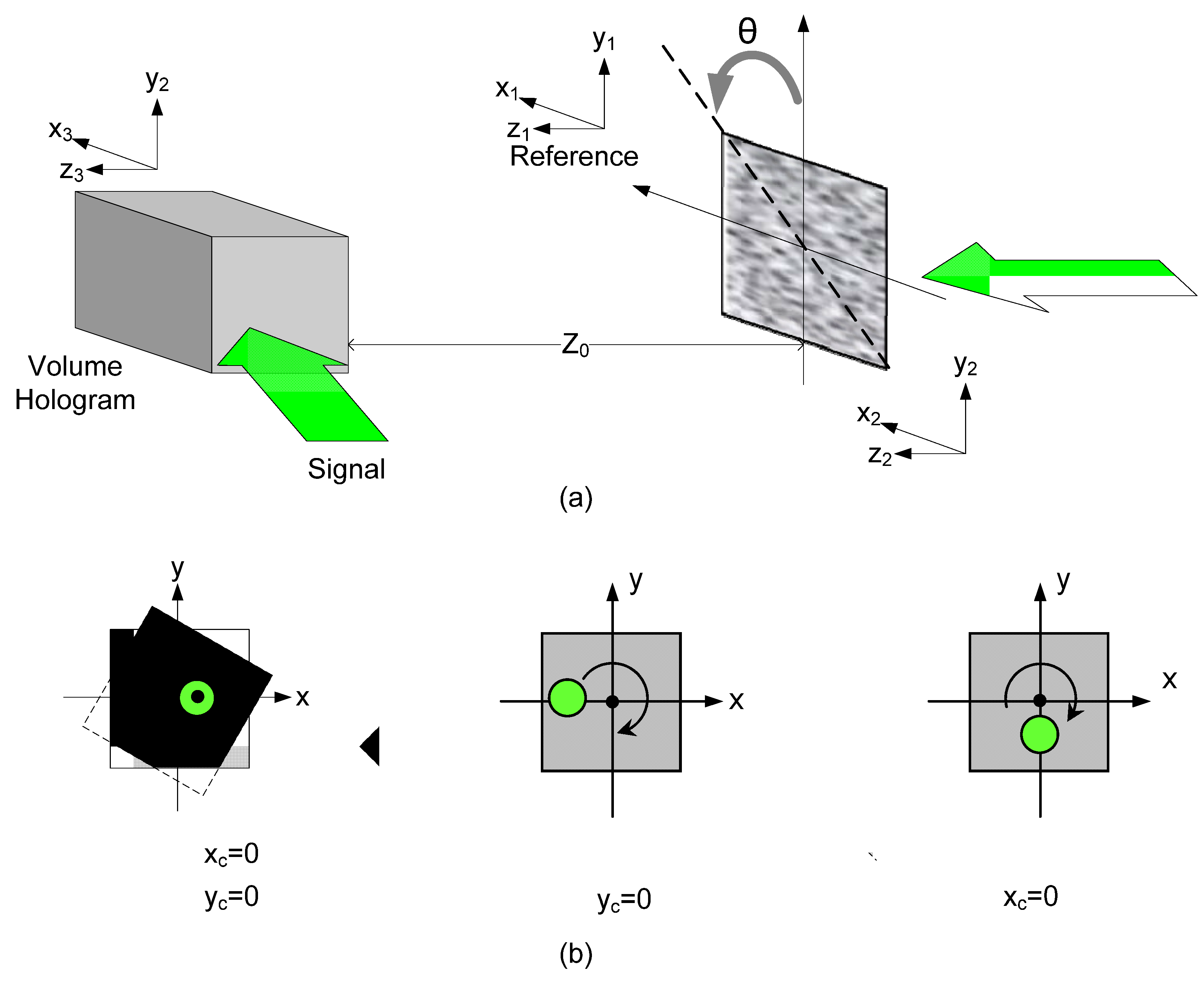
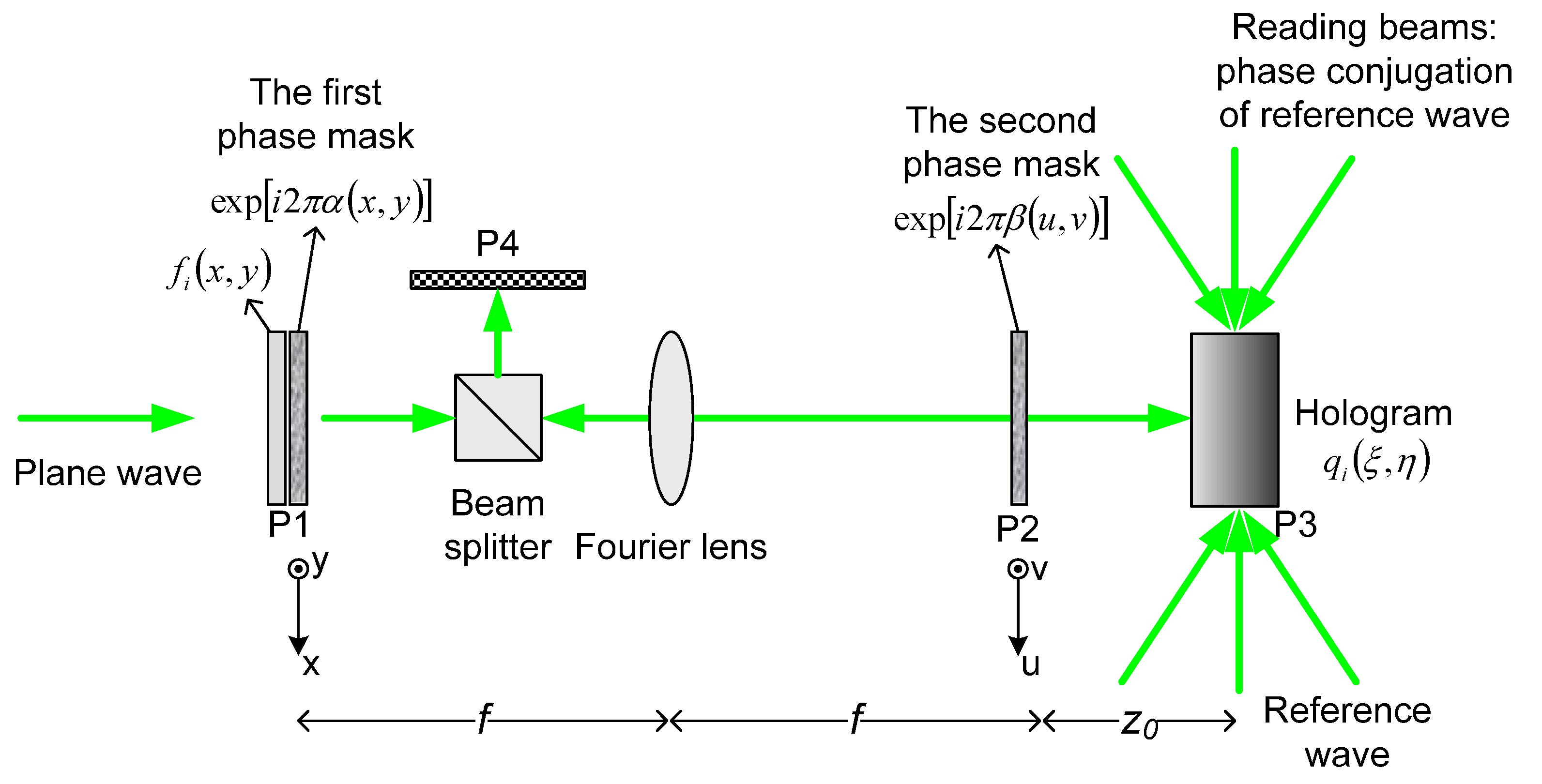
3. Image Encryption for Volume Holographic Storage
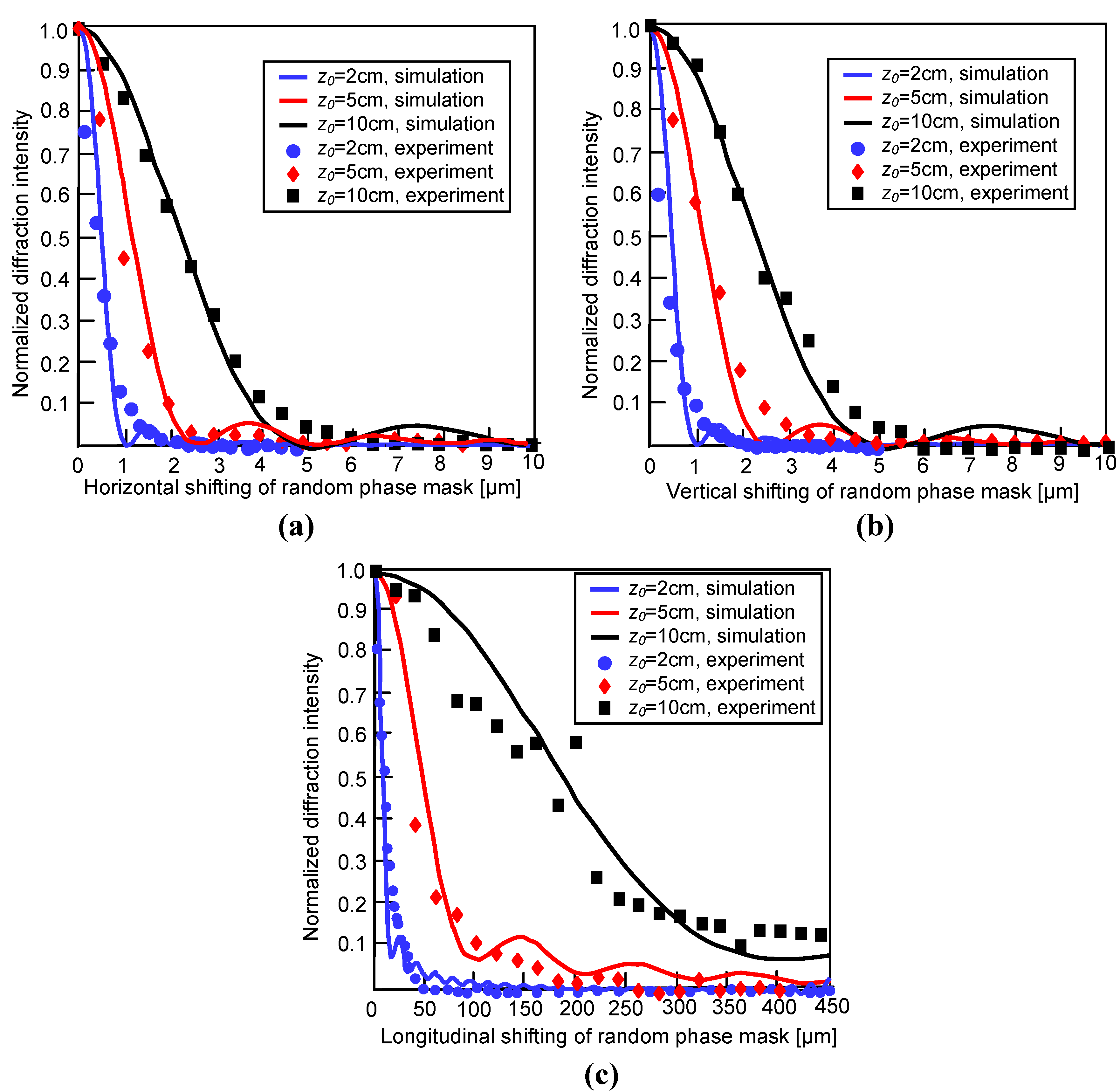
4. All Optical Fiber Sensors
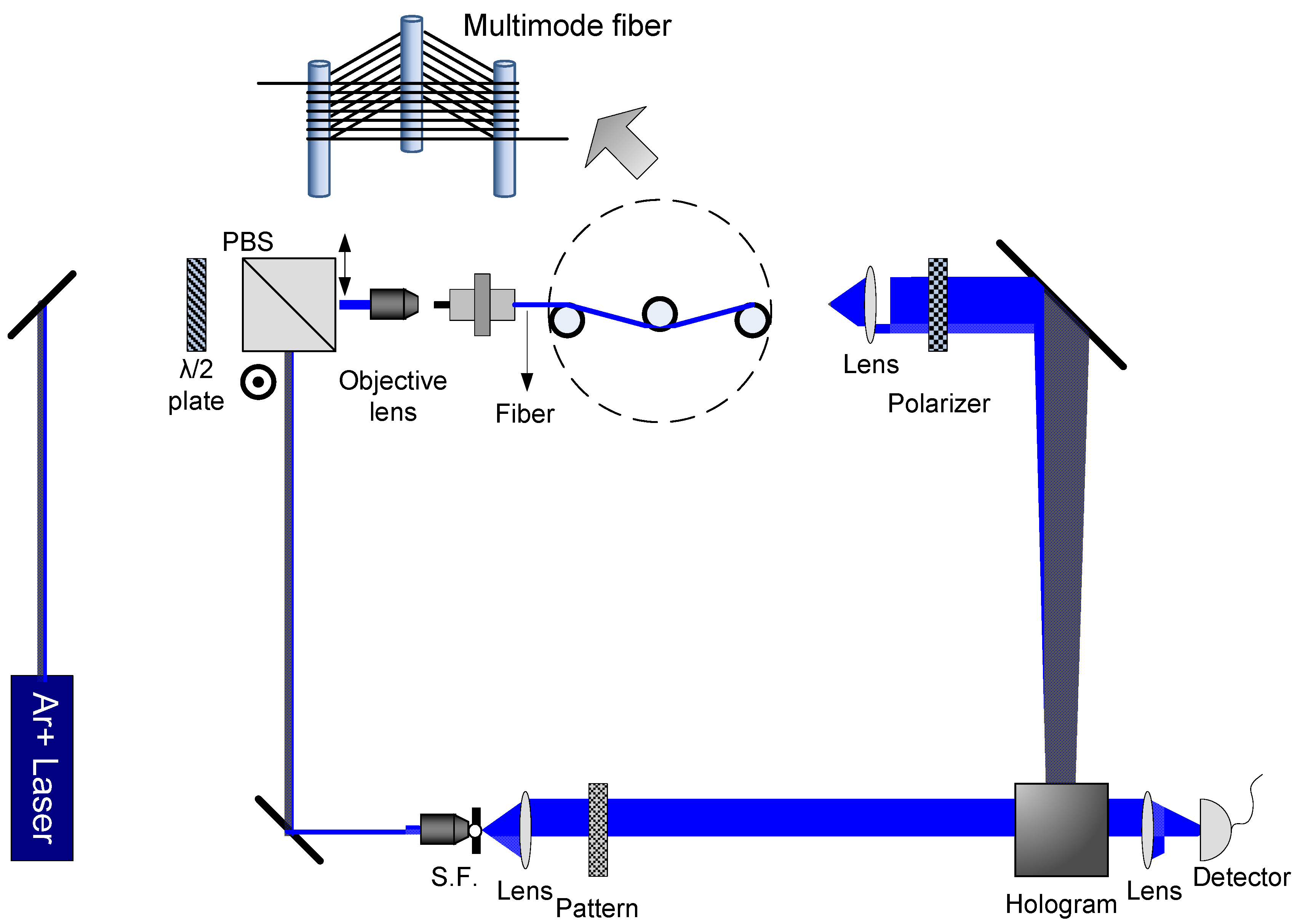

5. Conclusions
Acknowledgment
References
- Leith, E.N.; Kozma, A.; Upatnieks, J.; Marks, J.; Massey, N. Holographic data storage in three-dimensional media. Appl. Opt. 1966, 5, 1303–1311. [Google Scholar]
- Burr, G.W.; Jefferson, C.M.; Coufal, H.; Jurich, M.; Hoffnagle, J.A.; Macfarlane, R.M.; Shelby, R.M. Volume holographic data-Storage at areal density of 250-Gigapixels/in2. Opt. Lett. 2001, 26, 444–446. [Google Scholar]
- Anderson, K.; Curtis, K. Polytopic multiplexing. Opt. Lett. 2004, 29, 1402–1404. [Google Scholar]
- Orlov, S.S.; Phillips, W.; Bjornson, E.; Takashima, Y.; Sundaram, P.; Hesselink, L.; Okas, R.; Kwan, D.; Snyder, R. High-transfer-rate high-capacity holographic diskdata-storage system. Appl. Opt. 2004, 43, 4902–4914. [Google Scholar]
- Mok, F.H. Angle-multiplexed storage of 5000 holograms in lithium niobate. Opt. Lett. 1993, 18, 915–917. [Google Scholar]
- Yu, F.T.S.; Wu, S.; Mayers, A.W.; Rajan, S. Wavelength multiplexed reflection matched spatial filters using LiNbO3. Opt. Commun. 1991, 81, 343–347. [Google Scholar]
- Rakuljic, G.A.; Leyva, V.; Yariv, A. Optical data storage by using orthogonal wavelength-multiplexed volume hologram. Opt. Lett. 1992, 17, 1471–1473. [Google Scholar]
- Denz, C.; Pauliat, G.; Roosen, G. Volume hologram multiplexing using a deterministic phase encoding method. Opt. Commun. 1991, 85, 171–176. [Google Scholar]
- Barbastathis, G.; Levene, M.; Psaltis, D. Shift multiplexing with spherical reference waves. Appl. Opt. 1996, 35, 2403–2417. [Google Scholar]
- Curtis, K.; Pu, A.; Psaltis, D. Method for holographic storage using peristrophic multiplexing. Opt. Lett. 1994, 19, 993–995. [Google Scholar]
- LaMacchia, J.T.; White, D.L. Coded multiple exposure holograms. Appl. Opt. 1968, 7, 91–94. [Google Scholar]
- He, Q.; Wang, J.; Zhang, P.; Wang, J.; Wu, M.; Jin, G. Dynamic speckle multiplexing scheme in volume holographic data storage and its realization. Opt. Exp. 2003, 11, 366–370. [Google Scholar]
- Sun, C.C.; Su, W.C. Three-dimensional shifting selectivity of random phase encoding in volume holograms. Appl. Opt. 2001, 40, 1253–1260. [Google Scholar]
- Sun, C.C.; Su, W.C.; Wang, B.; OuYang, Y. Diffraction selectivity of holograms with random phase encoding. Opt. Commun. 2000, 175, 67–74. [Google Scholar]
- Sun, C.C.; Tsou, R.H.; Chang, W.; Chang, J.Y.; Chang, M.W. Random phase-coded multiplexing in LiNbO3 for volume hologram storage by using a ground-glass. Opt. Quantum Electron. 1996, 28, 1551–1561. [Google Scholar]
- Heanue, J.F.; Bashaw, M.C.; Hesselink, L. Encrypted holographic data storage based on orthogonal-phase-code multiplexing. Appl. Opt. 1995, 34, 6012–6015. [Google Scholar]
- Denz, C.; Muller, K-O.; Visinka, F.; Tschudi, T. Digital volume holographic data storage using phase-coded holographic memory system. Proc. SPIE 1999, 3802, 142–147. [Google Scholar]
- Yu, Y.W.; Cheng, C.Y.; Hsieh, S.C.; Teng, T.C.; Sun, C.C. Point spread function by random phase reference in collinear holographic storage. Opt. Eng. 2009, 48, 020501:1–020501:2. [Google Scholar]
- Sun, C.C.; Su, W.C.; Wang, B.; Chiou, A.E.T. Lateral shifting sensitivity of a ground glass for holographic encryption and multiplexing using phase conjugate readout algorithm. Opt. Commun. 2001, 191, 209–224. [Google Scholar]
- Su, W.C.; Chen, Y.W.; Chen, Y.J.; Lin, S.H.; Wang, L.K. Security optical data storage in Fourier holograms. Appl. Opt. 2012, 51, 1297–1303. [Google Scholar]
- Su, W.C.; Sun, C.C.; Su, W.C. Selective-encrypted holographic storage in LiNbO3 with angular multiplexing. Microw. Opt. Technol. Lett. 2004, 36, 227–230. [Google Scholar]
- Wang, B.; Chang, J.Y.; Su, W.C.; Sun, C.C. Optical security using a random binary phase code in volume holograms. Opt. Eng. 2004, 43, 2048–2052. [Google Scholar]
- Han, S.; Jeong, Y.; Paek, J.; Kim, T.; Lee, B. Characteristics of remote hologram multiplexing with random pattern references from multimode fiber bundle. Opt. Eng. 2004, 43, 2040–2047. [Google Scholar]
- Lee, B.; Han, S.; Jeong, Y.; Paek, J. Remote multiplexing of holograms with random patterns from multimode fiber bundles. Opt. Lett. 2004, 29, 116–118. [Google Scholar]
- Inoue, A.; Takayama, Y.; Kodate, K. Multiwavelength recording with a random pattern reference scheme. Appl. Opt. 2010, 49, 2403–2408. [Google Scholar]
- Lee, H.S.; Kim, Y.H.; Han, D.; Lee, B. Cross-talk noise analysis in hologram memory with hybrid multiplexing of the Hadamard phase code and wavelength. J. Opt. Soc. Am. A 1999, 16, 563–567. [Google Scholar]
- Zhu, Y.; Zhang, J.; Yi, T.; Gong, Q. Signal and reference wave dually encrypted holographic memory with shift multiplexing. Optics Commun. 2008, 281, 1450–1454. [Google Scholar]
- Su, W.C.; Sun, C.C.; Chen, Y.C.; Ouyang, Y. Duplication of phase key for random-phase-encrypted volume holograms. Appl. Opt. 2004, 43, 1728–1733. [Google Scholar]
- Su, W.H.; Su, W.C.; Kao, H.J.; Chen, C.Y. Correlator-aided alignment of phase key in encrypted holographic storage systems. Opt. Commun. 2007, 280, 27–32. [Google Scholar]
- Bashaw, M.C.; Heanue, J.F.; Aharoni, A.; Walkup, J.F.; Hesselink, L. Cross-talk considerations for angular and phase-encoded multiplexing in volume holography. J. Opt. Soc. Am. B 1994, 11, 1820–1836. [Google Scholar]
- Refregier, P.; Javidi, B. Optical image encryption based on input plane and Fourier plane random phase encoding. Opt. Lett. 1995, 20, 767–769. [Google Scholar]
- Javidi, B.; Zhang, G.; Li, J. Encrypted optical memory using double-random phase encoding. Appl. Opt. 1997, 36, 1054–1058. [Google Scholar]
- Unnikrishnan, G.; Joseph, J.; Singh, K. Optical encryption system that uses phase conjugation in a photorefractive crystal. Appl. Opt. 1998, 37, 8181–8186. [Google Scholar]
- Matoba, O.; Javidi, B. Encrypted optical memory system using three-dimensional keys in the Fresnel domain. Opt. Lett. 1999, 24, 762–764. [Google Scholar]
- Unnikrishnan, G.; Joseph, J.; Singh, K. Optical encryption by double-random phase encoding in the fractional Fourier domain. Opt. Lett. 2000, 25, 887–889. [Google Scholar]
- Matoba, O.; Javidi, B. Encrypted optical storage with angular multiplexing. Appl. Opt. 1999, 38, 7288–7293. [Google Scholar]
- Su, W.C.; Lin, C.H. Three-dimensional shifting selectivity of decryption phase mask in double random phase encoding holographic memory. Opt. Commun. 2004, 241, 29–41. [Google Scholar]
- Su, W.C.; Lin, C.H. Enhancement of angular selectivity in encrypted holographic memories. Appl. Opt. 2004, 43, 2298–2304. [Google Scholar]
- Sun, C.C.; Chen, Y.M.; Su, W.C. An all-optical fiber sensing system based on random phase encoding and holographic interconnection. Opt. Eng. 2001, 40, 160–161. [Google Scholar]
- Lee, H.; Jin, S.K. Experimental study of volume holographic interconnects using random patterns. Appl. Phys. Lett. 1993, 62, 2191–2193. [Google Scholar]
- Su, W.C.; Sun, C.C. Optical pattern interconnections using random phase encoding in volume holograms. Opt. Commun. 2002, 213, 259–265. [Google Scholar]
- Sun, C.C.; Hsu, C.Y.; Ouyang, Y.; Su, W.C.; Chiou, A.E.T. All-optical angular sensing based on holography multiplexing with spherical waves. Opt. Eng. 2002, 41, 2809–2813. [Google Scholar]
- Su, W.C.; Chen, Y.W.; Ouyang, Y.; Sun, C.C.; Wang, B. Optical identification using a random phase mask. Opt. Commun. 2003, 219, 117–123. [Google Scholar]
- Sun, C.C.; Su, W.C.; Ouyang, Y.; Sun, W.S. Applications of random phase encoding in volume holograms. Opt. Mem. Neural Netw. 2001, 10, 25–34. [Google Scholar]
- Yeh, P.; Chiou, A.E.T.; Hong, J. Optical interconnection using photorefractive dynamic holograms. Appl. Opt. 1988, 27, 2093–2096. [Google Scholar]
- Lee, H.; Gu, X.G.; Psaltis, D. Volume holographic interconnections with maximal capacity and minimal cross talk. J. Appl. Phys. 1989, 65, 2191–2194. [Google Scholar]
- Jin, S.K.; Lee, H. Optical connections using irregular patterns as object waves in a volume hologram. Opt. Quantum Electron. 1995, 27, 503–510. [Google Scholar]
- Kang, Y.H.; Kim, K.H.; Lee, B. Volume hologram scheme using optical fiber for spatial multiplexing. Opt. Lett. 1997, 22, 739–741. [Google Scholar]
- Curtis, K.; Wilson, W.L. Phase Correlation Multiplex Holography. U.S. Patent 5,719,691, 17 February 1998. [Google Scholar]
- Markov, V.; Millerd, J.; Trolinger, J.; Norrie, M. Multilayer volume holographic optical memory. Opt. Lett. 1999, 24, 265–267. [Google Scholar]
- Jeong, Y.; Lee, B. Effect of a random pattern through a multimode-fiber bundle on angular and spatial selectivity in volume: Experiments and theory. Appl. Opt. 2002, 41, 4085–4091. [Google Scholar]
- Su, W.C.; Sun, C.C.; Kukhtarev, N. Multiplexed edge-lit holograms. Opt. Eng. 2003, 42, 1871–1872. [Google Scholar]
- Sun, C.C.; Lin, C.C.; Yu, Y.W.; Lee, X.H.; Teng, T.C. Improving longitudinal shifting selectivity by introducing a light Pipe. Opt. Commun. 2011, 284, 4408–4411. [Google Scholar]
- Markov, V. Spatial-angular selectivity of 3-D speckle-wave holograms and information storage. J. Imaging Sci. Technol. 1997, 41, 383–388. [Google Scholar]
- Su, W.C.; Chen, C.M.; Lee, X.H. Enhanced angular selectivity in volume holograms with speckle reference waves. Opt. Commun. 2006, 266, 450–455. [Google Scholar]
- Kim, K.H.; Lee, H.S.; Lee, B. Enhancement of the wavelength selectivity of a volume hologram by use of multimode optical fiber referencing. Opt. Lett. 1998, 23, 1224–1225. [Google Scholar]
- Sun, C.C. A simplified model for diffraction analysis of volume holograms. Opt. Eng. 2003, 42, 1184–1185. [Google Scholar]
- Chang, C.C.; Russel, K.L.; Wu, G.K. Optical holographic memory using angular-rotationally phase-coded multiplexing in a LiNbO3:Fe crystal. Appl. Phys. B 2001, 72, 307–310. [Google Scholar]
- Sun, C.C.; Hsu, C.Y.; Ma, S.H.; Su, W.C. Rotation selectivity of random phase encoding in volume holograms. Opt. Commun. 2007, 276, 62–66. [Google Scholar]
- Sun, C.C.; Hsu, C.Y.; Wu, C.H.; Su, W.C. Spatial filtering of three-dimensional objects based on volume holography. Opt. Eng. 2003, 42, 2788–2789. [Google Scholar]
- Teng, T.C.; Zhong, W.J.; Ma, S.H.; Sun, C.C. Volume holographic filters for rotational sensing of 3D objects. Appl. Opt. 2007, 46, 1456–1459. [Google Scholar]
- Ma, S.H.; Lee, X.H.; Teng, T.C.; Yu, Y.W.; Sun, C.C. Enhanced rotational bragg selectivity by use of random phase encoding in volume holographic filter. Appl. Opt. 2007, 46, 5430–5434. [Google Scholar]
- Wang, R.K.; Watson, I.A.; Chatwin, C. Random phase encoding for optical security. Opt. Eng. 1996, 35, 2464–2469. [Google Scholar]
- Javidi, B.; Ahouzi, E. Optical security system with Fourier plane encoding. Appl. Opt. 1998, 37, 6247–6255. [Google Scholar]
- Javidi, B.; Sergent, A.; Zhang, G.; Guibert, L. Fault tolerance properties of a double random phase encoding encryption technique. Opt. Eng. 1997, 36, 992–998. [Google Scholar]
- Javidi, B.; Sergent, A.; Ahouzi, E. Performance of double random phase encoding encryption technique using binarized encrypted images. Opt. Eng. 1998, 37, 565–569. [Google Scholar]
- Wang, B.; Sun, C.C.; Su, W.C.; Chiou, A.E.T. Shift tolerance of a double random phase encryption system. Appl. Opt. 2000, 39, 4788–4793. [Google Scholar]
- Wang, B.; Sun, C.C. Enhancement of signal-to-noise ratio of a double random phase encoding encryption system. Opt. Eng. 2001, 40, 1502–1506. [Google Scholar]
- Wu, S.; Yin, S.; Yu, F.T.S. Sensing with fiber specklegrams. Appl. Opt. 1991, 30, 4468–4470. [Google Scholar]
- Yu, F.T.S.; Yin, S.; Zhang, J.; Guo, R. Application of a fiber-speckle hologram to fiber sensing. Appl. Opt. 1994, 33, 5202–5203. [Google Scholar]
- Yin, S.; Purwosumarto, P.; Yu, F.T.S. Application of fiber specklergram sensor to fine angular alignment. Opt. Commun. 1999, 170, 15–21. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Su, W.-C.; Sun, C.-C. Review of Random Phase Encoding in Volume Holographic Storage. Materials 2012, 5, 1635-1653. https://doi.org/10.3390/ma5091635
Su W-C, Sun C-C. Review of Random Phase Encoding in Volume Holographic Storage. Materials. 2012; 5(9):1635-1653. https://doi.org/10.3390/ma5091635
Chicago/Turabian StyleSu, Wei-Chia, and Ching-Cherng Sun. 2012. "Review of Random Phase Encoding in Volume Holographic Storage" Materials 5, no. 9: 1635-1653. https://doi.org/10.3390/ma5091635
APA StyleSu, W.-C., & Sun, C.-C. (2012). Review of Random Phase Encoding in Volume Holographic Storage. Materials, 5(9), 1635-1653. https://doi.org/10.3390/ma5091635




