Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories
Abstract
1. Introduction
2. Theoretical Background
3. Gratings Recorded in Photopolymers
3.1. Theoretical Simulations
| Refractive index modulation | f = 350 lines/mm | f = 500 lines/mm | f = 750 lines/mm |
|---|---|---|---|
| n1 = 0.004 | Ω ~ 8 | Ω ~ 17 | Ω ~ 38 |
| n1 = 0.011 | Ω ~ 3 | Ω ~ 6 | Ω ~ 14 |
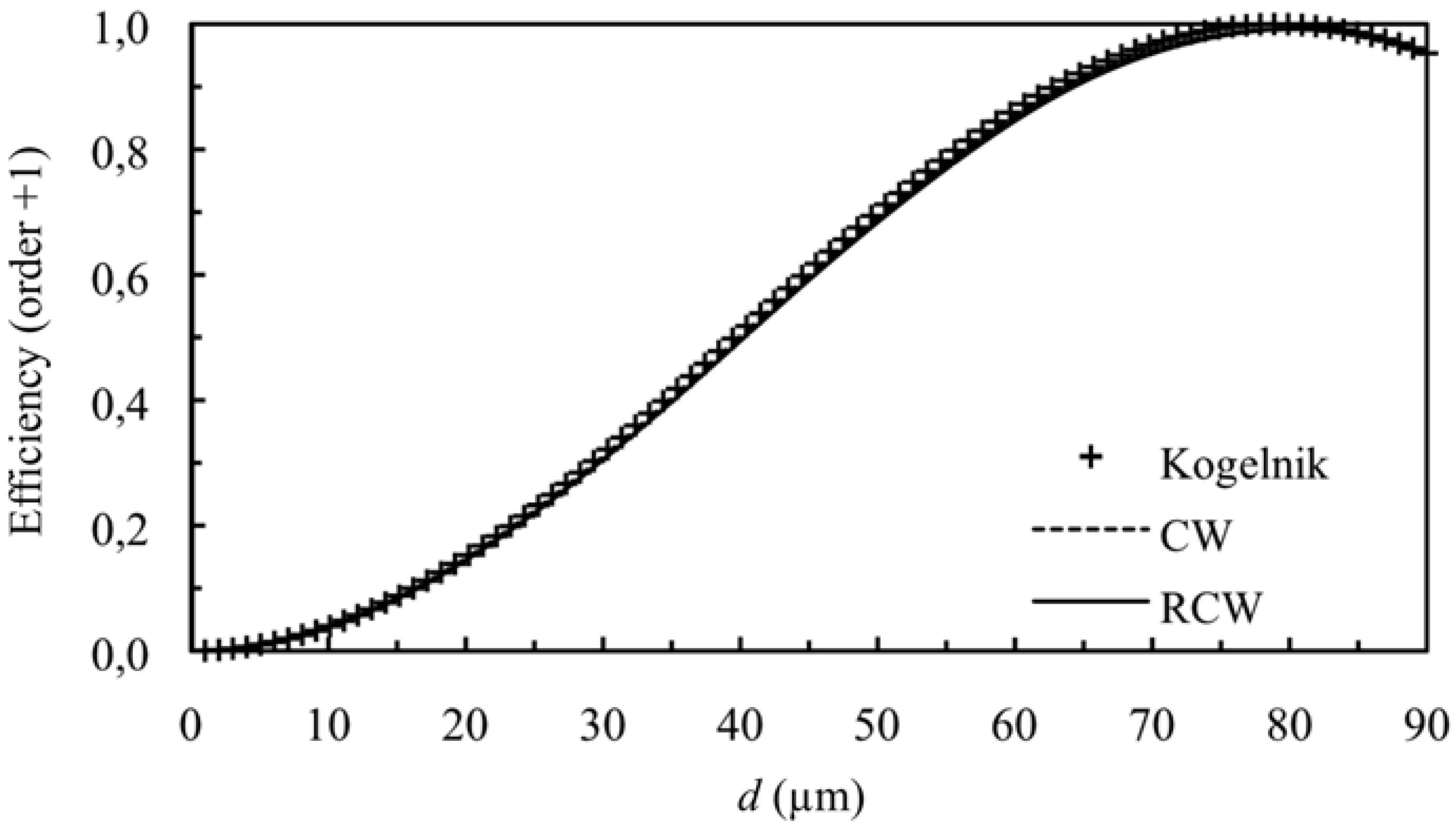
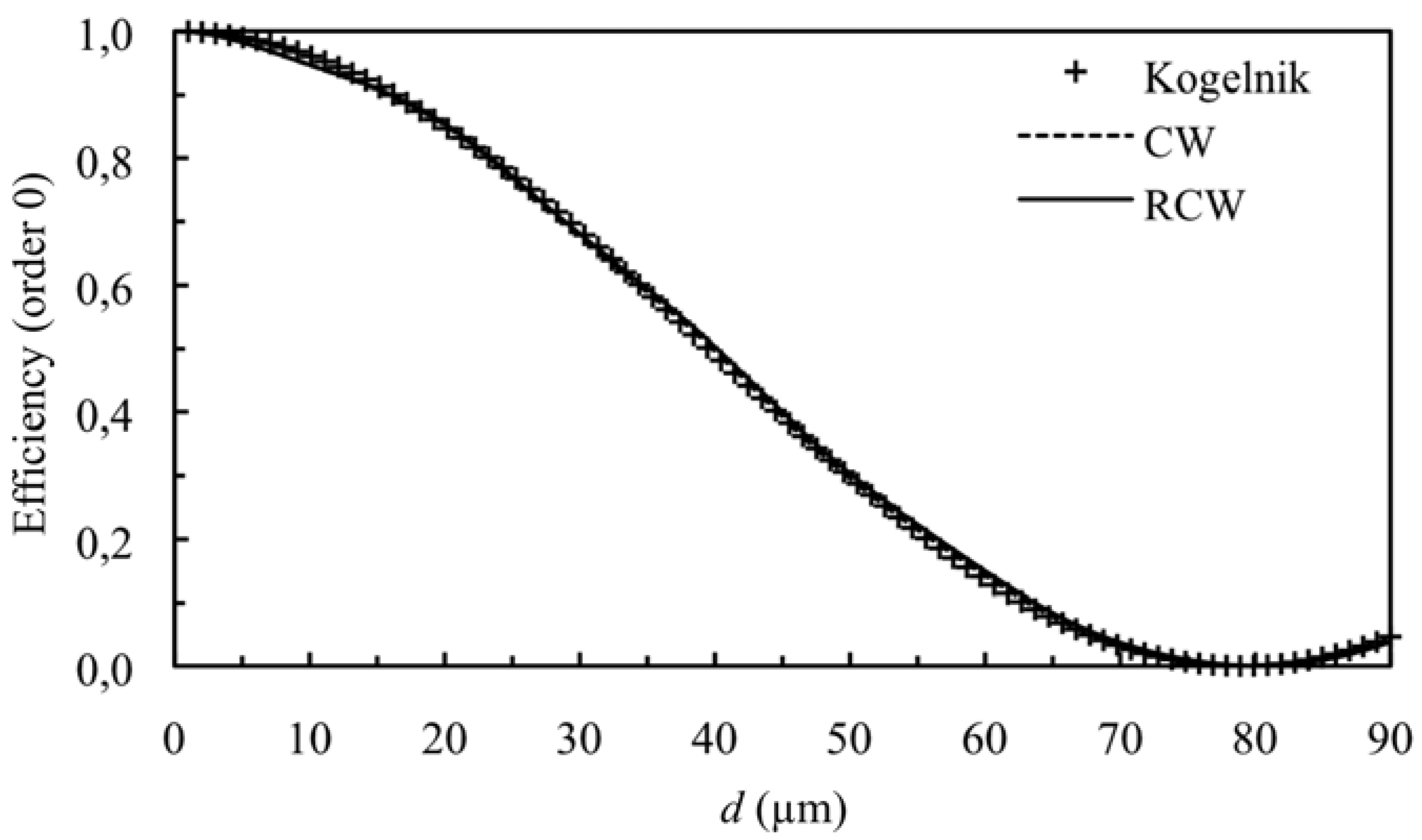
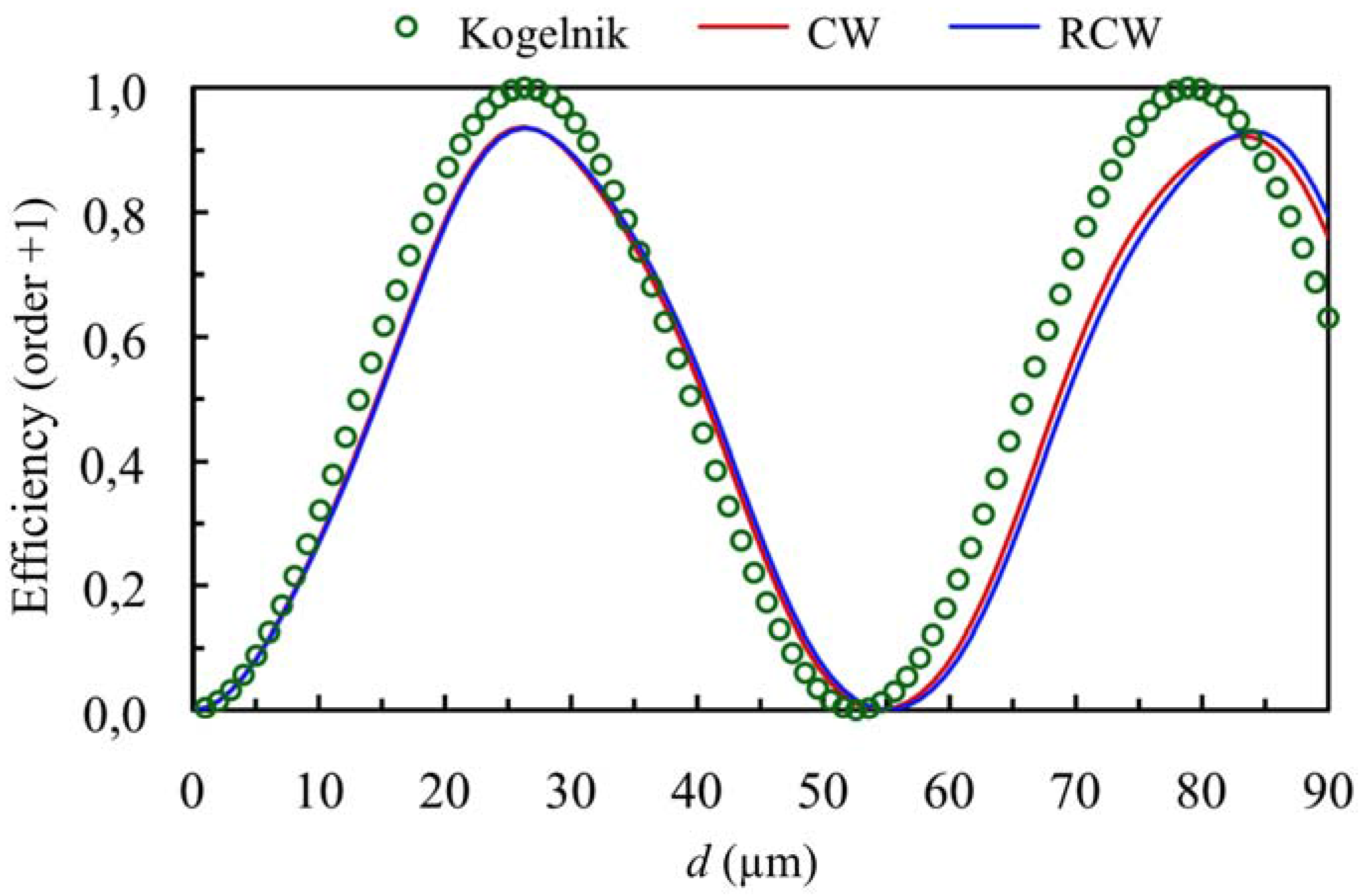
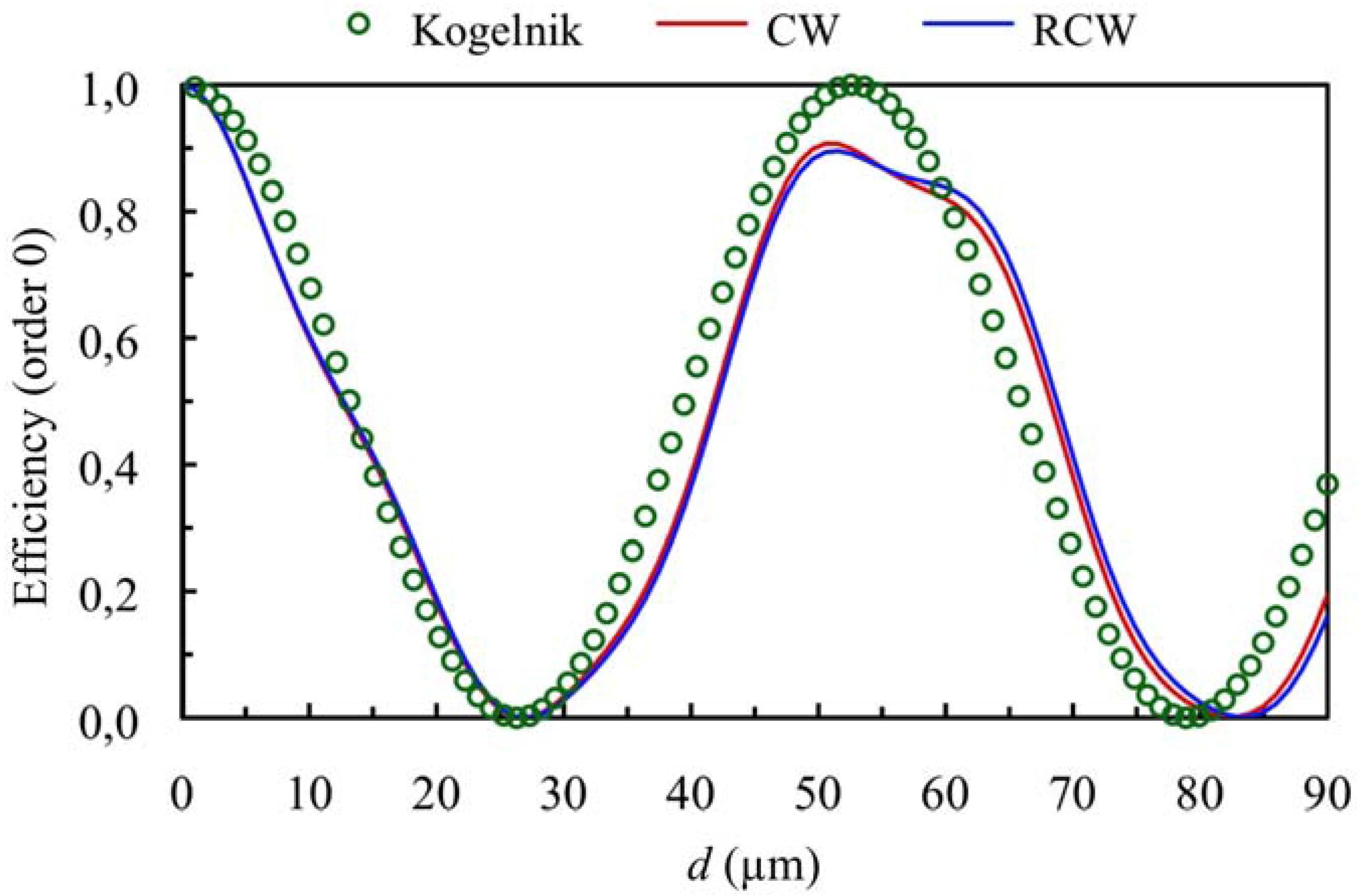
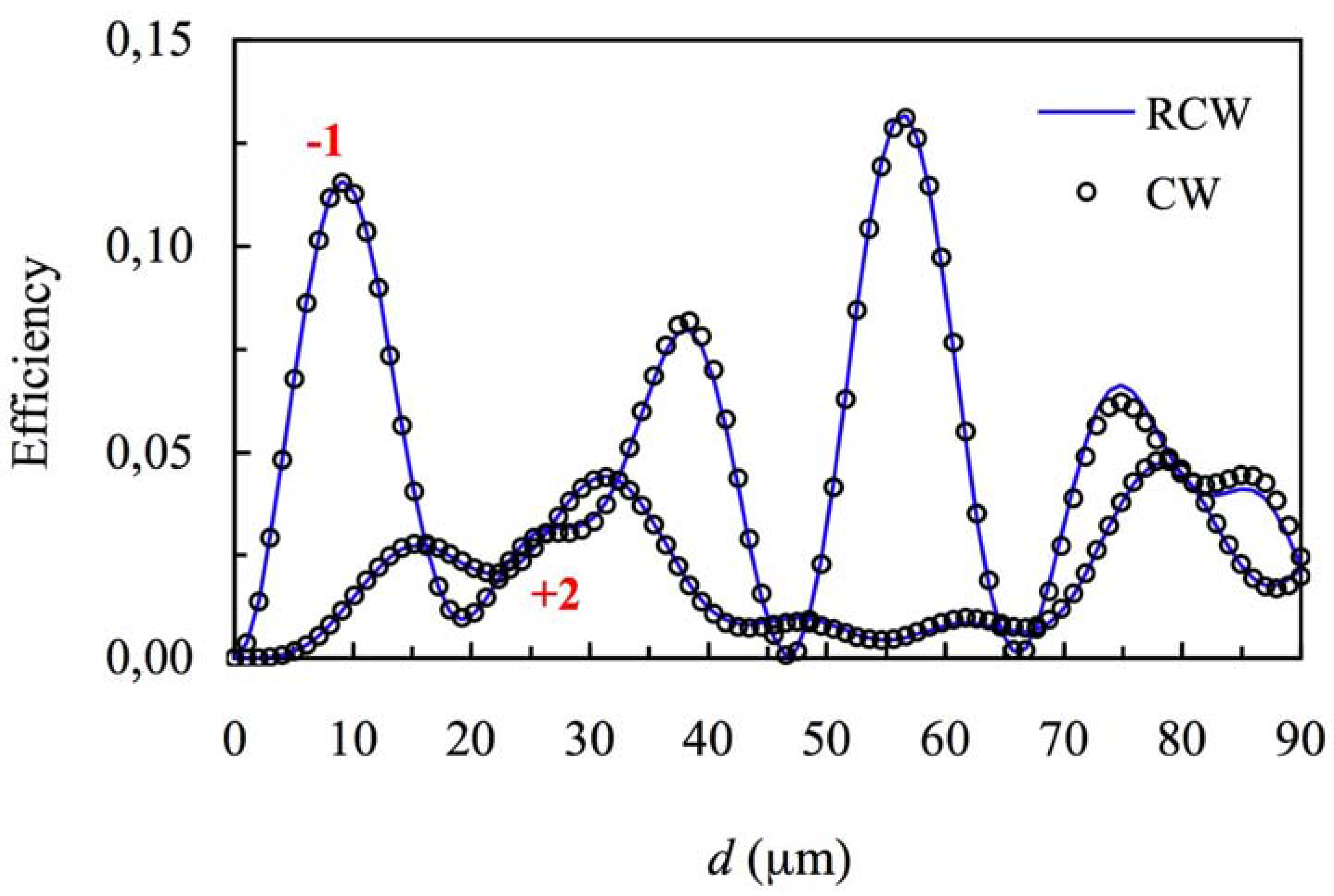
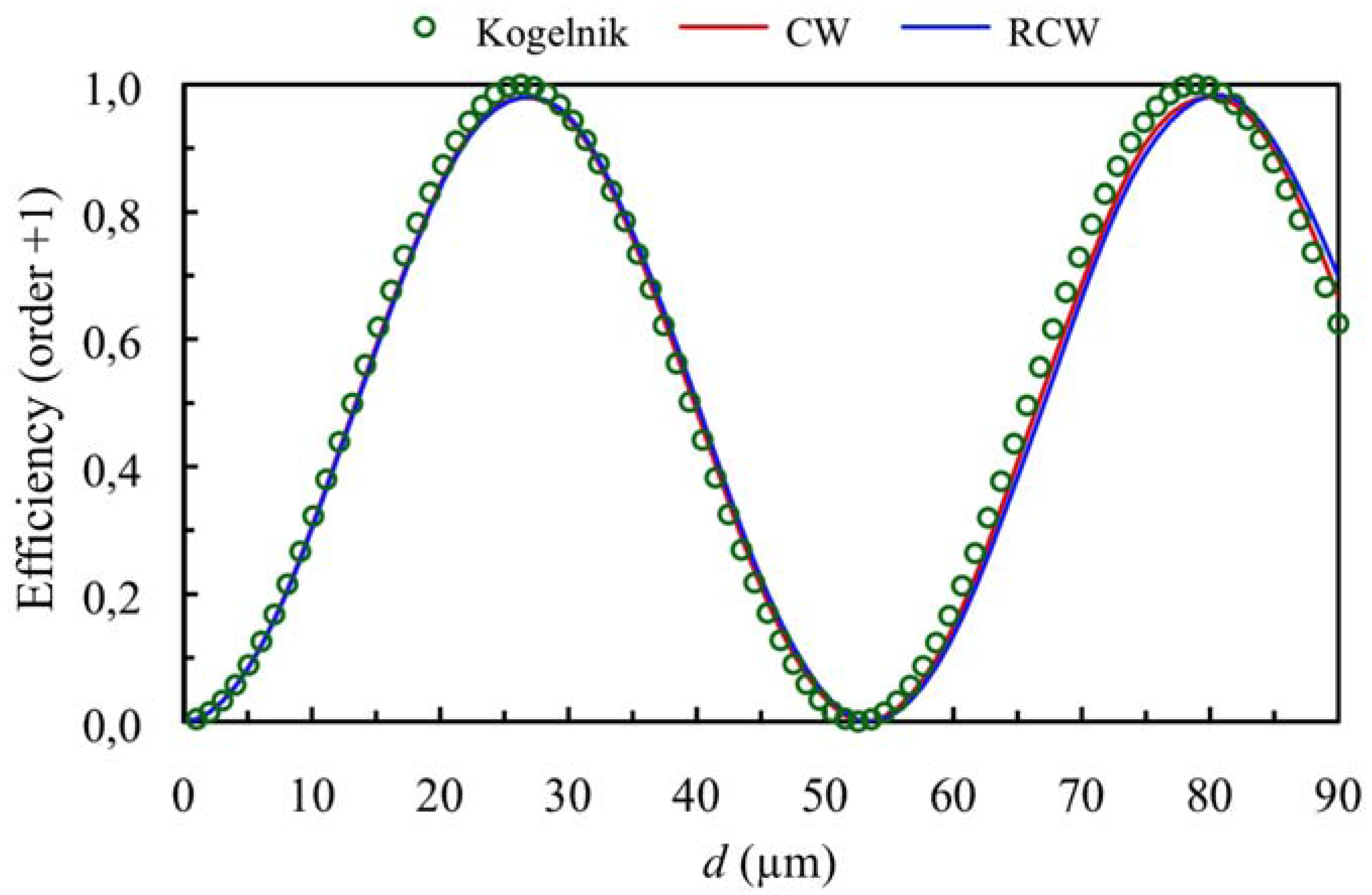
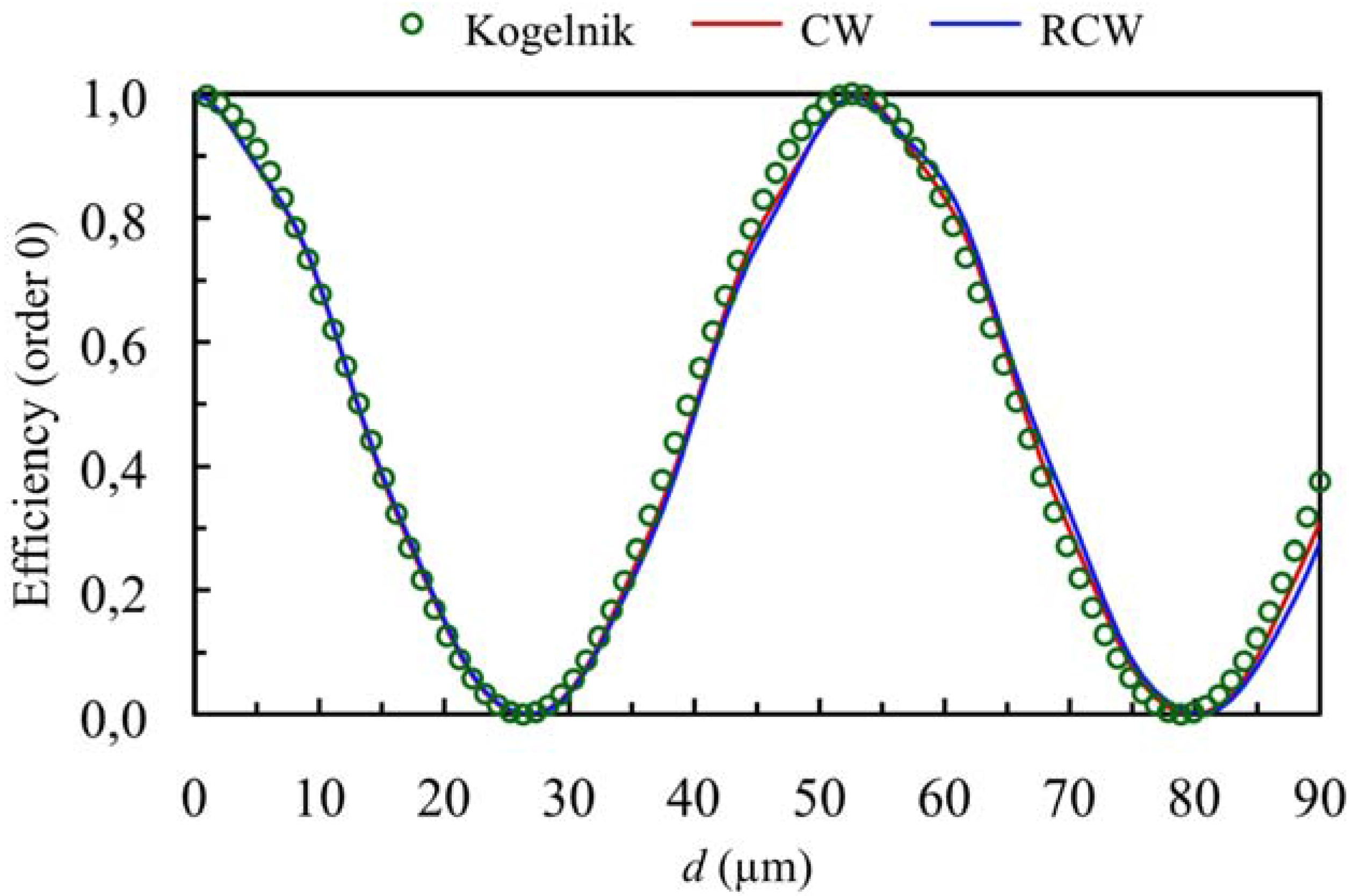
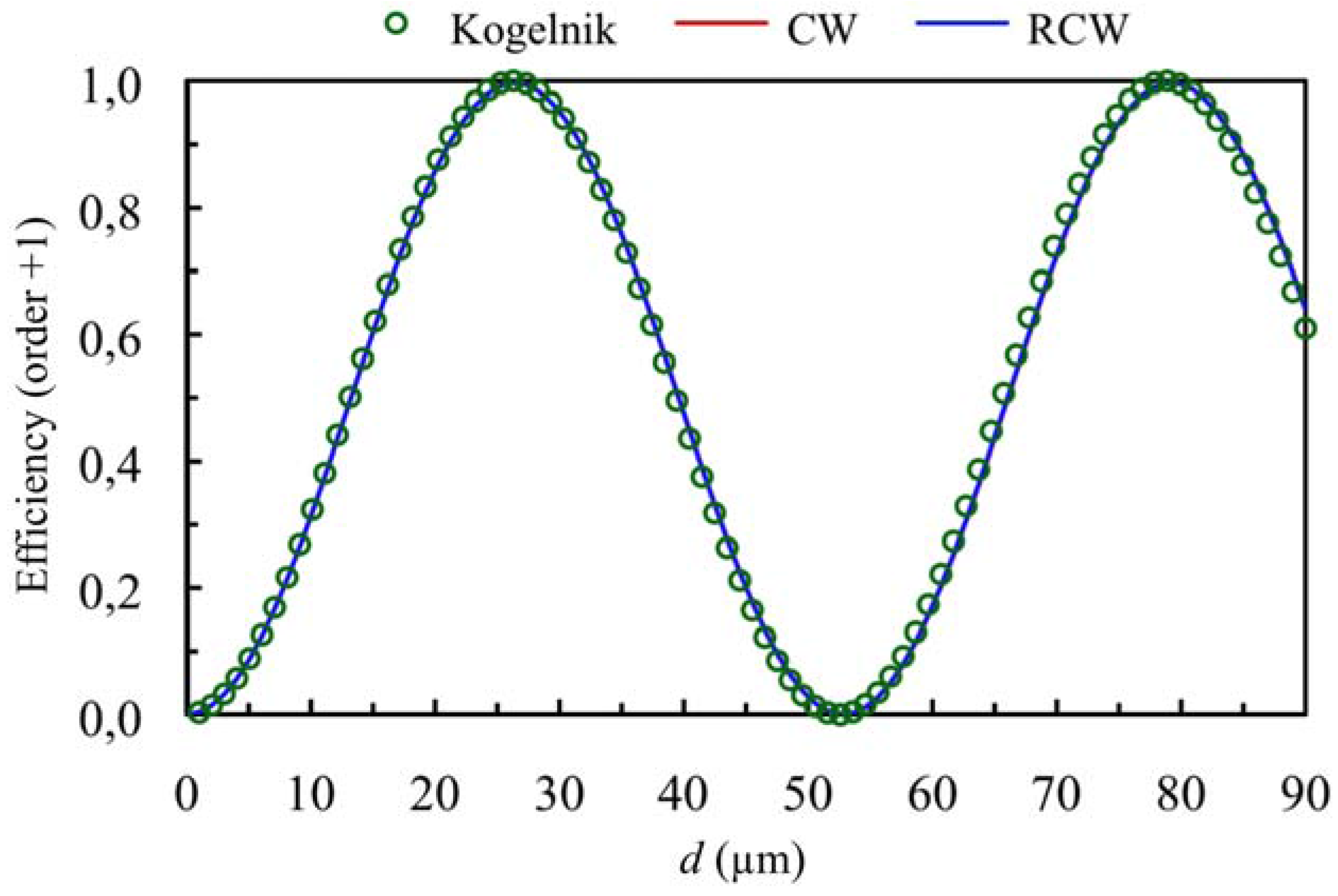
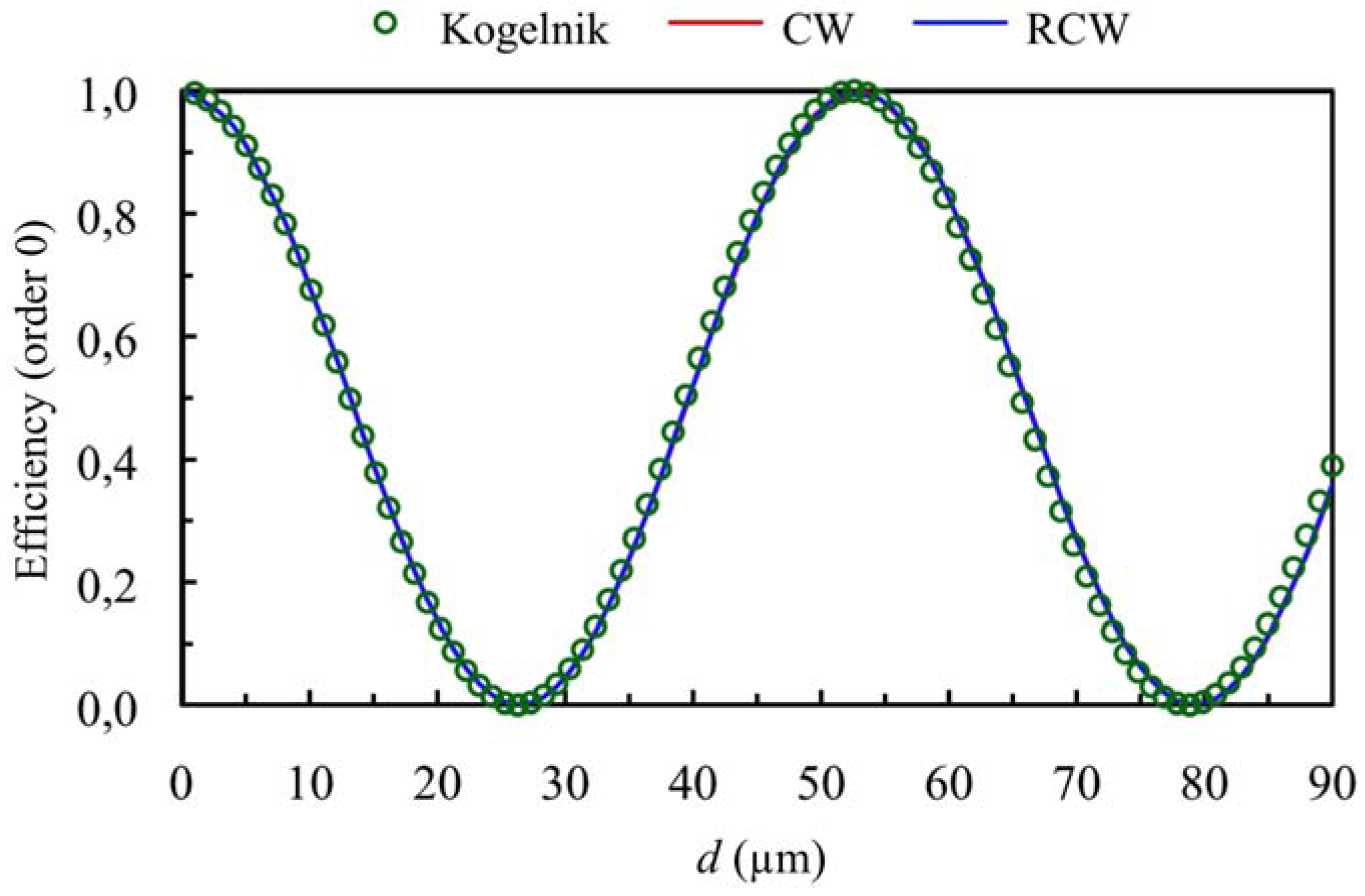
3.2. Experimental Results
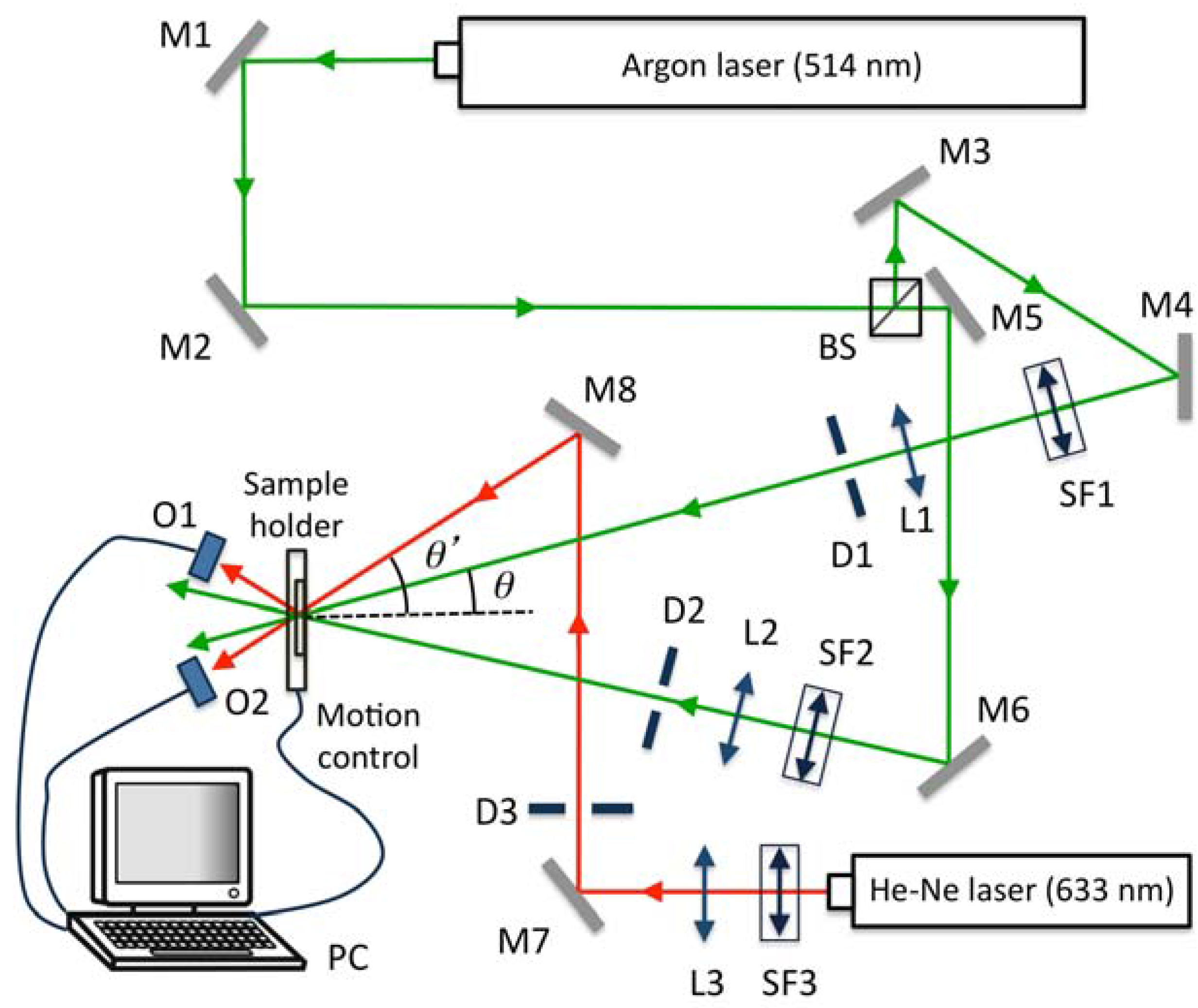

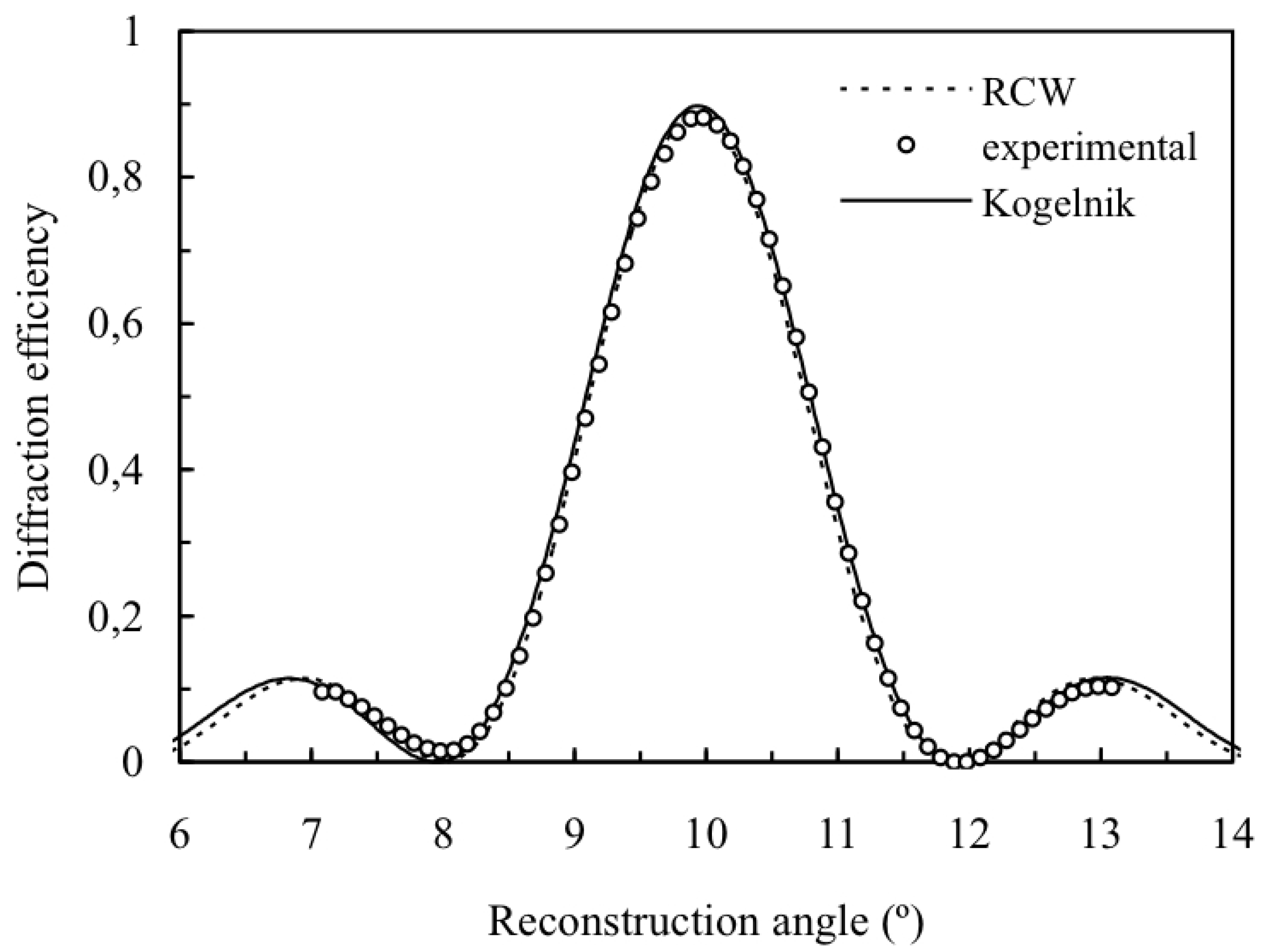

4. Conclusions
Acknowledgments
References
- Neumann, J.; Wieking, K.S.; Kip, D. Direct laser writing of surface reliefs in dry, self-developing photopolymer films. Appl. Opt. 1999, 38, 5418–5421. [Google Scholar] [CrossRef] [PubMed]
- Li, X.T.; Natansohn, A.; Rochon, P. Photoinduced liquid crystal alignment based on a surface relief grating in an assembled cell. Appl. Phys. Lett. 1999, 74, 3791–3793. [Google Scholar] [CrossRef]
- Márquez, A.; Gallego, S.; Ortuño, M.; Fernández, E.; Alvarez, M.L.; Beléndez, A.; Pascual, I. Generation of diffractive optical elements onto a photopolymer using a liquid crystal display. Proc. SPIE 2010, 7717. Available online: http://rua.ua.es/dspace/bitstream/10045/14247/1/SPIE_vol7717_art7717-12_2010.pdf (accessed on 2 August 2012). [Google Scholar] [CrossRef]
- Lechner, M.D. Photopolymers for optical memories and waveguides. Electron. Prop. Polym. Relat. Compd. 1985, 63, 301–308. [Google Scholar]
- Coufal, H.J.; Psaltis, D.; Sincerbox, G.T. Holographic Data Storage; Springer-Verlag: Berlin, Germany, 2000. [Google Scholar]
- Márquez, A.; Neipp, C.; Beléndez, A.; Gallego, S.; Ortuño, M.; Pascual, I. Edge-enhanced imaging with polyvinyl alcohol/acrylamide photopolymer gratings. Opt. Lett. 2003, 28, 1510–1512. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Manivannan, G.; Lessard, R.A. Trends in holographic recording materials. Trends Polym. Sci. 1994, 2, 282–290. [Google Scholar]
- Curtis, K.; Dhar, L.; Murphy, L.; Hill, A. Future Developments in Holographic Data Storage: From Theory to Practical Systems; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Martin, S.; Leclere, P.E.; Renotte, Y.L.; Toal, V.; Lion, Y.F. Characterization of an acrylamide-based dry photopolymer holographic recording material. Opt. Eng. 1994, 33, 3942–3946. [Google Scholar] [CrossRef]
- Curtis, K.; Psaltis, D. Characterization of the Du-Pont photopolymer for 3-dimensional holographic storage. Appl. Opt. 1994, 33, 5396–5399. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Ortuño, M.; Neipp, C.; Márquez, A.; Beléndez, A.; Pascual, I.; Kelly, J.V.; Sheridan, J.T. Physical and effective optical thickness of the holographic diffraction gratings recorded in photopolymers. Opt. Express 2005, 13, 3543–3557. [Google Scholar] [CrossRef] [PubMed]
- Gallego, S.; Ortuño, M.; Neipp, C.; Fernández, E.; Beléndez, A.; Pascual, I. Improved maximum uniformity and capacity of multiple holograms recorded in absorbent photopolymers. Opt. Express 2007, 15, 9308–9319. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.; Feely, C.A.; Toal, V. Holographic recording characteristics of an acrylamide-based photopolymer. Appl. Opt. 1994, 36, 5757–5768. [Google Scholar] [CrossRef]
- O’Neill, F.T.; Lawrence, J.R.; Sheridan, J.T. Thickness variation of self-processing acrylamide-based photopolymer and reflection holography. Opt. Eng. 2001, 40, 533–539. [Google Scholar] [CrossRef]
- Close, C.E.; Gleeson, M.R.; Sheridan, J.T. Monomer diffusion rates in photopolymer material: Part I: Low spatial frequency holographic gratings. J. Opt. Soc. Am. B 2011, 28, 658–666. [Google Scholar] [CrossRef]
- Gallego, S.; Márquez, A.; Méndez, D.I.; Marini, S.; Beléndez, A.; Pascual, I. Spatial-phase-modulation-based study of polyvinyl-alcohol/acrylamide photopolymers in the low spatial frequency range. Appl. Opt. 2009, 48, 4403–4413. [Google Scholar] [CrossRef] [PubMed]
- Naydenova, I.; Mihaylova, E.; Martin, S.; Toal, V. Holographic patterning of acrylamide-based photopolymer surface. Opt. Express 2005, 13, 4878–4889. [Google Scholar] [CrossRef] [PubMed]
- Kogelnik, H. Coupled wave theory for thick hologram gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Gallego, S.; Ortuño, M.; Neipp, C.; García, C.; Beléndez, I.; Pascual, I. Overmodulation effects in volume holograms recorded on photopolymers. Opt. Commun. 2003, 215, 263–269. [Google Scholar] [CrossRef]
- Gallego, S.; Ortuño, M.; Neipp, C.; García, C.; Beléndez, I.; Pascual, I. Temporal evolution of the angular response of a holographic diffraction grating in PVA/acrylamide photopolymer. Opt. Express 2003, 11, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of planar-grating diffraction. J. Opt. Soc. Am. 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Neipp, C.; Beléndez, A.; Gallego, S.; Ortuño, M.; Pascual, I.; Sheridan, J.T. Angular responses of the first and second diffracted orders in transmission diffraction grating recorded on photopolymer material. Opt. Express 2003, 11, 1835–1843. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wu, S.; Glytsis, E.N. Holographic gratings formation in photopolymers: analysis and experimental results based on a non-local diffusion based model and rigorous couple-wave analysis. J. Opt. Soc. Am. B 2003, 20, 1177–1188. [Google Scholar] [CrossRef]
- Moharam, M.G.; Young, L. Criteria for Bragg and Raman-Nath regimes. Appl. Opt. 1978, 17, 1757–1759. [Google Scholar] [CrossRef] [PubMed]
- Moharam, M.G.; Gaylord, T.K.; Magnusson, R. Criteria for Raman-Nath regime diffraction by phase gratings. Opt. Commun. 1980, 32, 19–23. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K.; Magnusson, R. Criteria for Bragg regime diffraction by phase gratings. Opt. Commun. 1980, 32, 14–18. [Google Scholar] [CrossRef]
- Solymar, L.; Cooke, D.J. Volume Holography and Volume Gratings; Academic Press: London, UK, 1981. [Google Scholar]
- Solymar, L.; Jordan, M.P. Finite beams in large volume holograms microwaves. Opt. Acoust. 1977, 1, 89–92. [Google Scholar] [CrossRef]
- Solymar, L.; Sheppard, C.J.R. A two-dimensional theory of volume holograms with electric polarization in the plane of the grating. J. Opt. Soc. Am. 1979, 69, 491–495. [Google Scholar] [CrossRef]
- Fally, M.; Klepp, J.; Tomita, Y. An experimental study to discriminate between the validity of diffraction theories for off-Bragg replay. Appl. Phys. B 2012, in press. [Google Scholar]
- Neipp, C.; Alvarez, M.L.; Gallego, S.; Ortuño, M.; Sheridan, J.T.; Pascual, I.; Beléndez, A. Angular responses of the first diffracted order in overmodulated diffraction grating. J. Modern Opt. 2004, 51, 1149–1162. [Google Scholar] [CrossRef]
- Syms, R.R.A. Practical Volume Holography; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Moharam, M.G.; Gaylord, T.K. Rigorous coupled-wave analysis of gratings diffraction TE-mode polarization and losses. J. Opt. Soc. Am. 1983, 73, 451–455. [Google Scholar] [CrossRef]
- Kamiya, N. Rigorous coupled-wave analysis for practical planar dielectric gratings: 1. Thickness-changed holograms and some characteristics of diffraction efficiency. Appl. Opt. 1998, 37, 5843–5853. [Google Scholar] [CrossRef] [PubMed]
- Moharam, M.G.; Grann, E.B.; Pommet, D.A.; Gaylord, T.K. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. J. Opt. Soc. Am. A 1995, 12, 1068–1076. [Google Scholar] [CrossRef]
- Neipp, C.; Gallego, S.; Ortuño, M.; Márquez, A.; Beléndez, A.; Pascual, I. Characterization of a PVA/acrylamide photopolymer. Influence of a cross-linking monomer in the final characteristics of the hologram. Opt. Commun. 2003, 224, 27–34. [Google Scholar] [CrossRef]
- Gallego, S.; Neipp, C.; Ortuño, M.; Beléndez, A.; Pascual, I. Stabilization of volume gratings recorded in PVA/acrylamide photopolymers with diffraction efficiencies higher than 90%. J. Modern Opt. 2004, 51, 491–503. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gallego, S.; Neipp, C.; Estepa, L.A.; Ortuño, M.; Márquez, A.; Francés, J.; Pascual, I.; Beléndez, A. Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories. Materials 2012, 5, 1373-1388. https://doi.org/10.3390/ma5081373
Gallego S, Neipp C, Estepa LA, Ortuño M, Márquez A, Francés J, Pascual I, Beléndez A. Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories. Materials. 2012; 5(8):1373-1388. https://doi.org/10.3390/ma5081373
Chicago/Turabian StyleGallego, Sergi, Cristian Neipp, Luis A. Estepa, Manuel Ortuño, Andrés Márquez, Jorge Francés, Inmaculada Pascual, and Augusto Beléndez. 2012. "Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories" Materials 5, no. 8: 1373-1388. https://doi.org/10.3390/ma5081373
APA StyleGallego, S., Neipp, C., Estepa, L. A., Ortuño, M., Márquez, A., Francés, J., Pascual, I., & Beléndez, A. (2012). Volume Holograms in Photopolymers: Comparison between Analytical and Rigorous Theories. Materials, 5(8), 1373-1388. https://doi.org/10.3390/ma5081373









