Micro-Imaging by Interference Microscopy: A Case Study of Orientation-Dependent Guest Diffusion in MFI-Type Zeolite Host Crystals
Abstract
:1. Introduction
2. Experimental Section
2.1. Synthesis
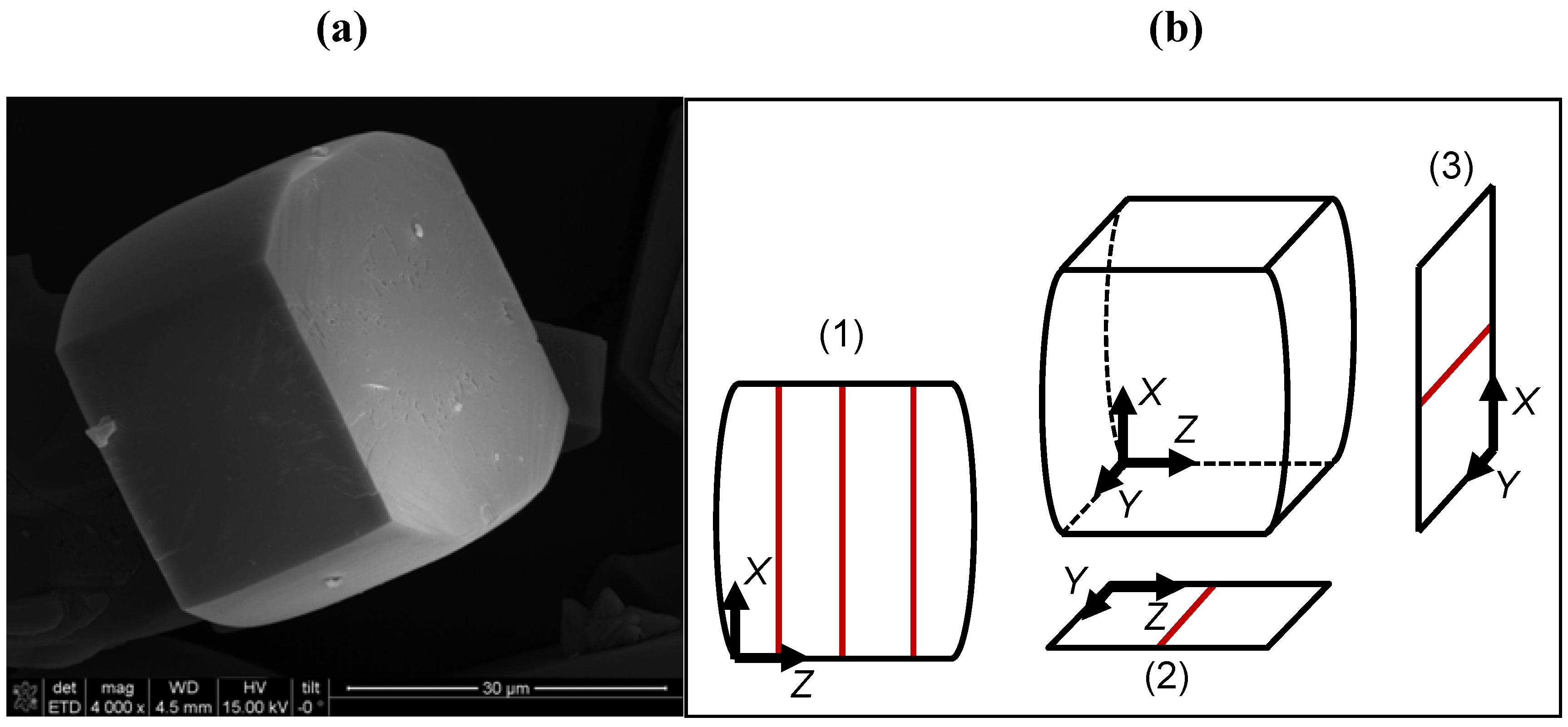
2.2. Micro-Imaging by Interference Microscopy
2.3. The Guest Molecules under Study
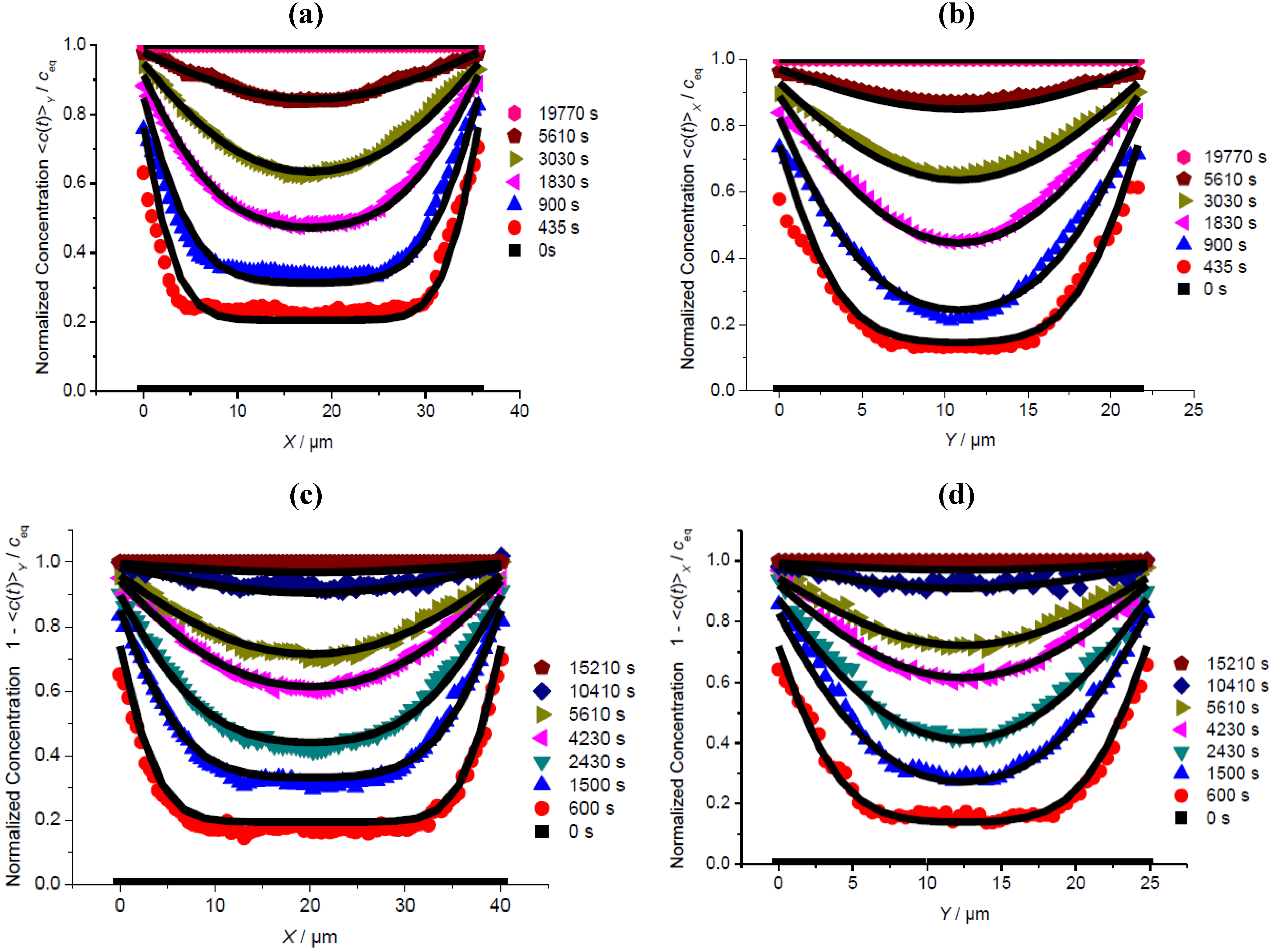
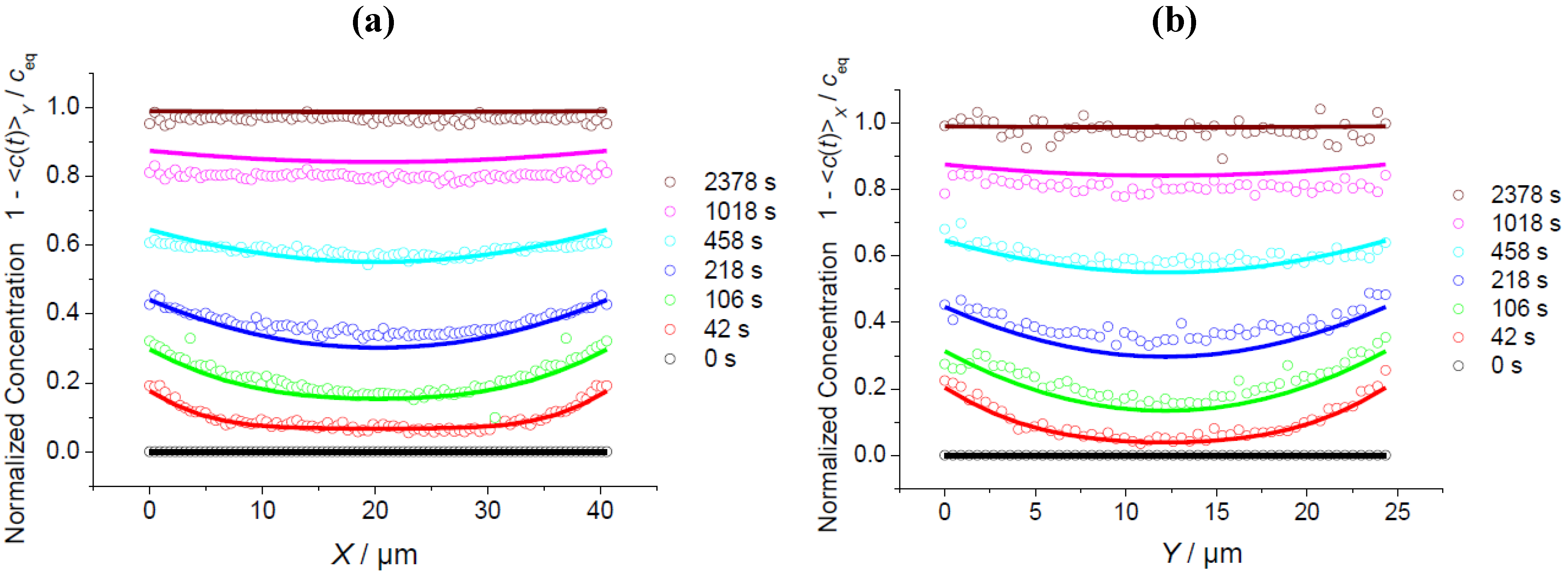
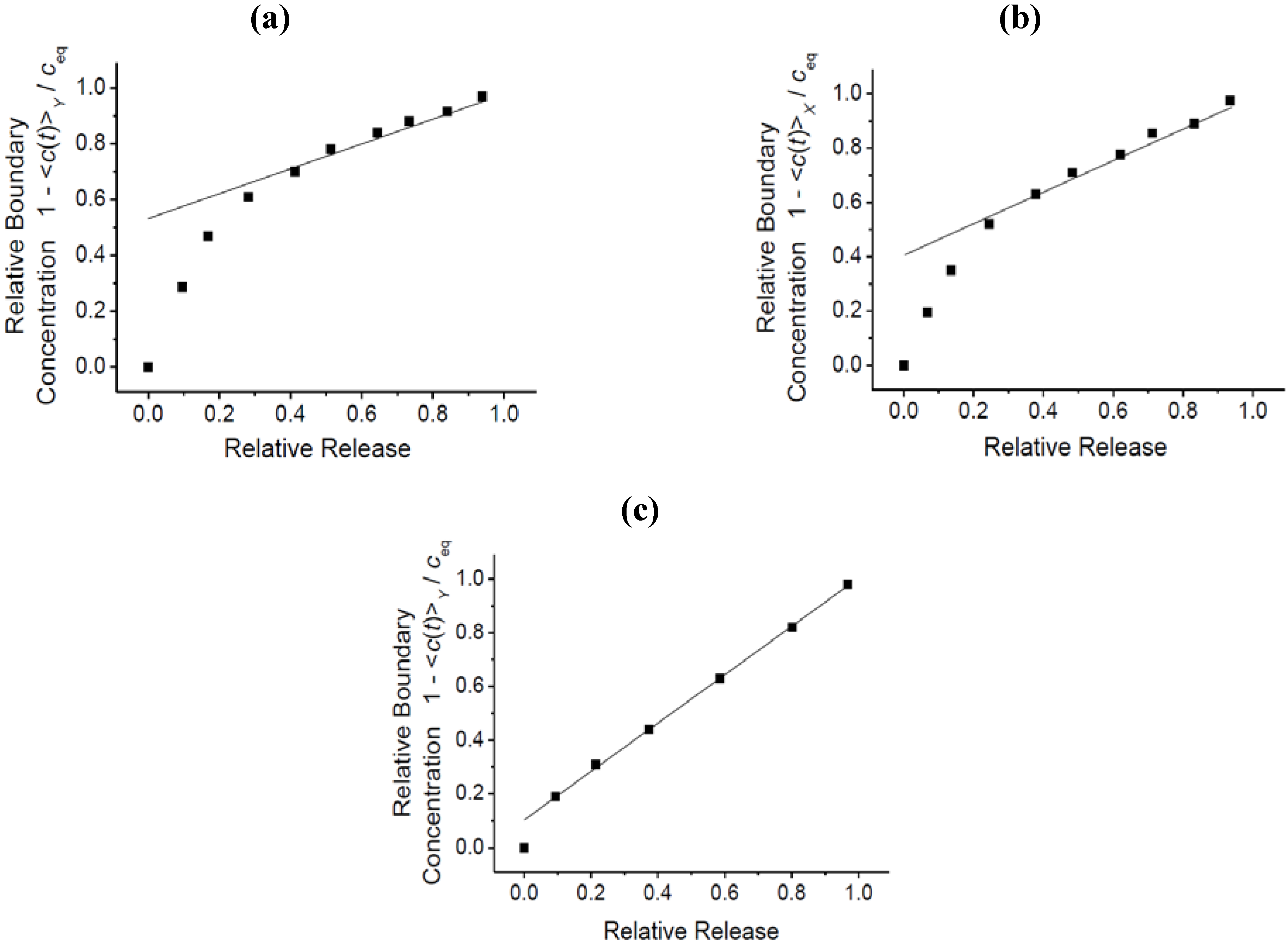
3. Results and Discussion
| Ads/Des, pressure (mbar) | Direction | D (m2 s−1) | α (m s−1) | |
|---|---|---|---|---|
| Methyl-butane | Ads, 0–1 | X,Y | 2.4 × 10−13 | 1.5 × 10−7 |
| Des, 1–0 | X,Y | 2.6 × 10−13 | 5.0 × 10−8 | |
| Benzene | Ads, 0–0.5 | X,Y | 1.5 × 10−14 | 9.5 × 10−9 |
| Des, 1–0 | X,Y | 1.4 × 10−14 | 7.0 × 10−9 | |
| 4-Methyl-2-pentyne | Des, 1–0 | X | 4.4 × 10−13 | 1.9 × 10−8 |
| Des, 1–0 | Y | 5.2 × 10−13 | 1.3 × 10−8 |
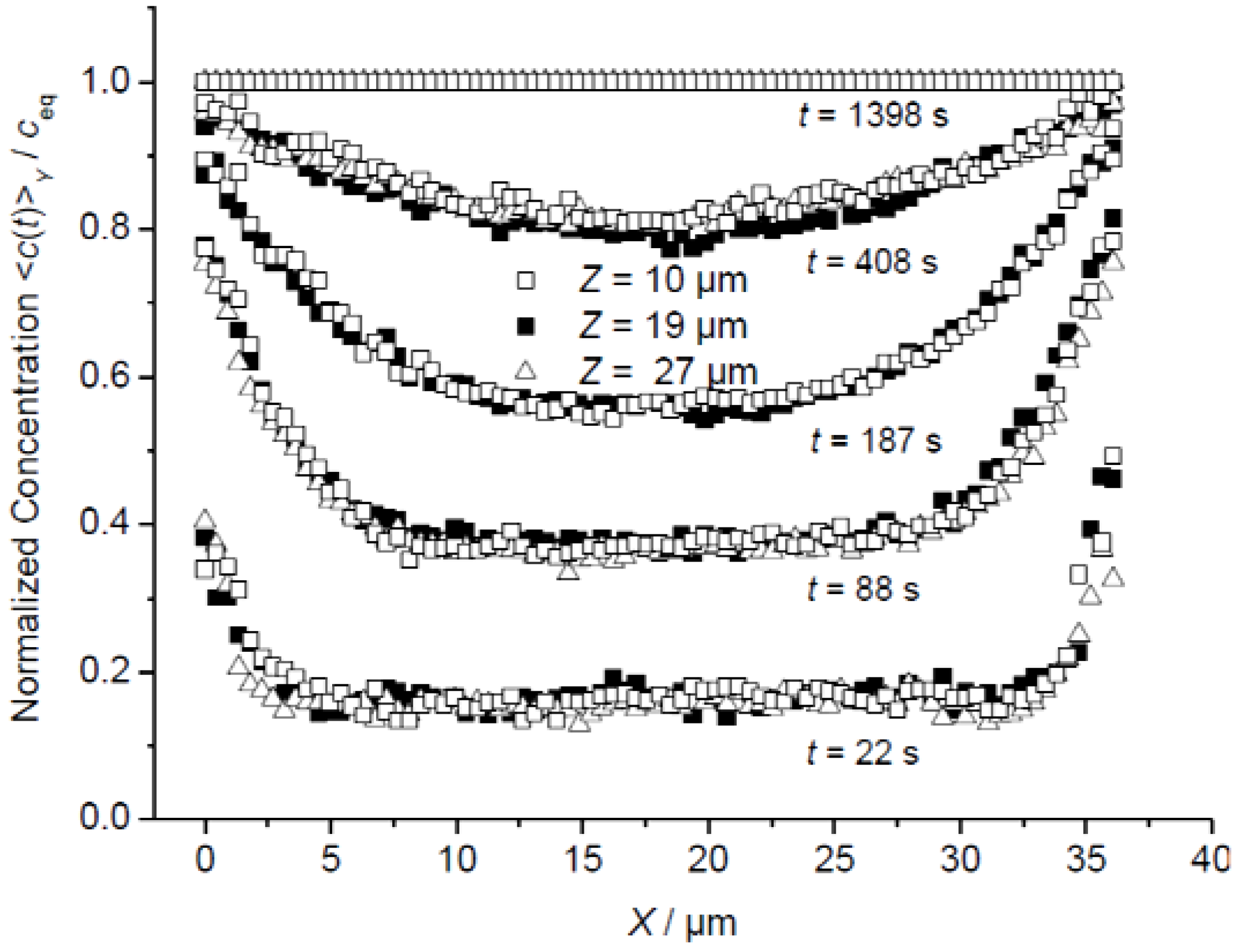
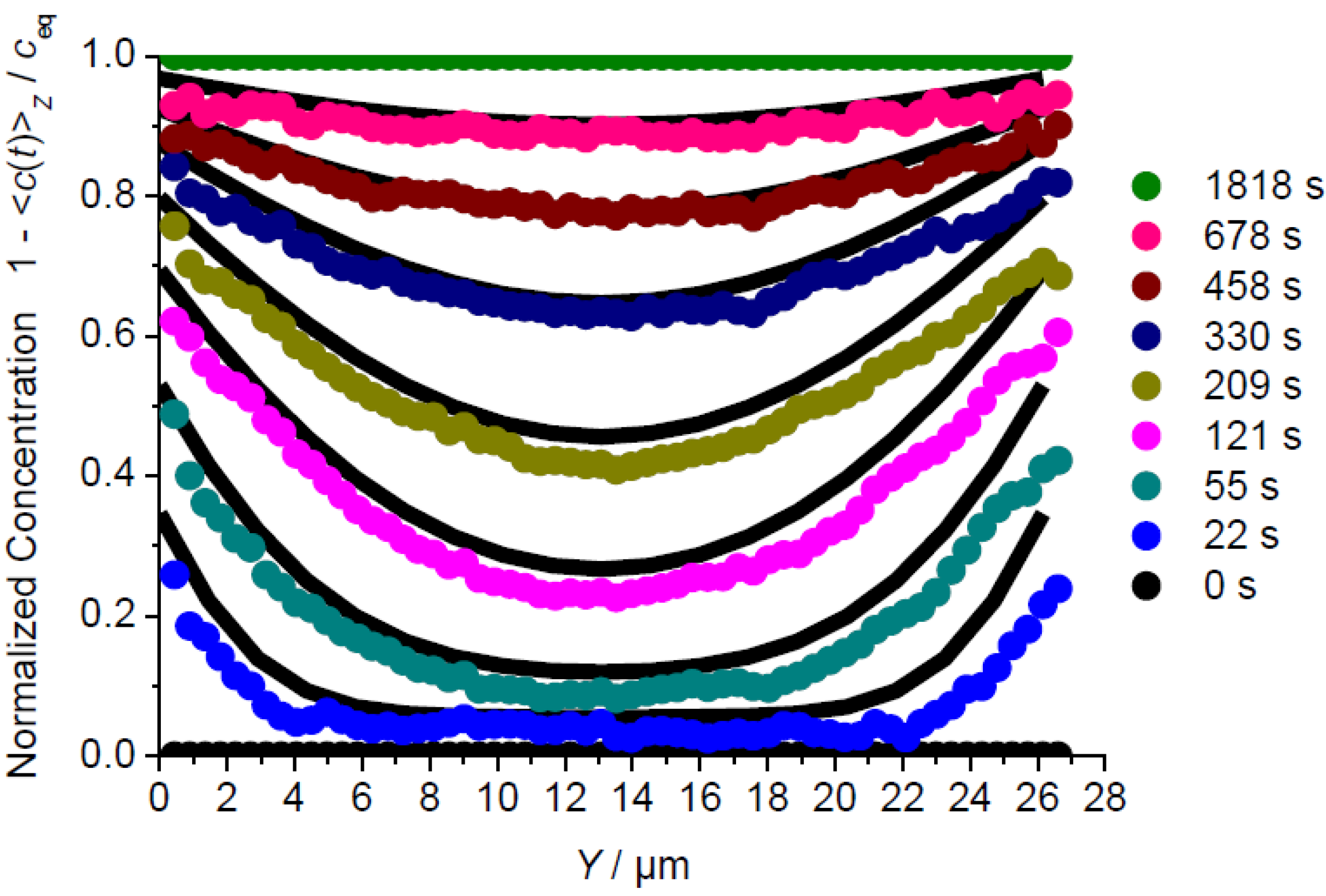
3.1. Mass Transfer in Z Direction
3.2. A Check of Diffusion Anisotropy in the XY Plane
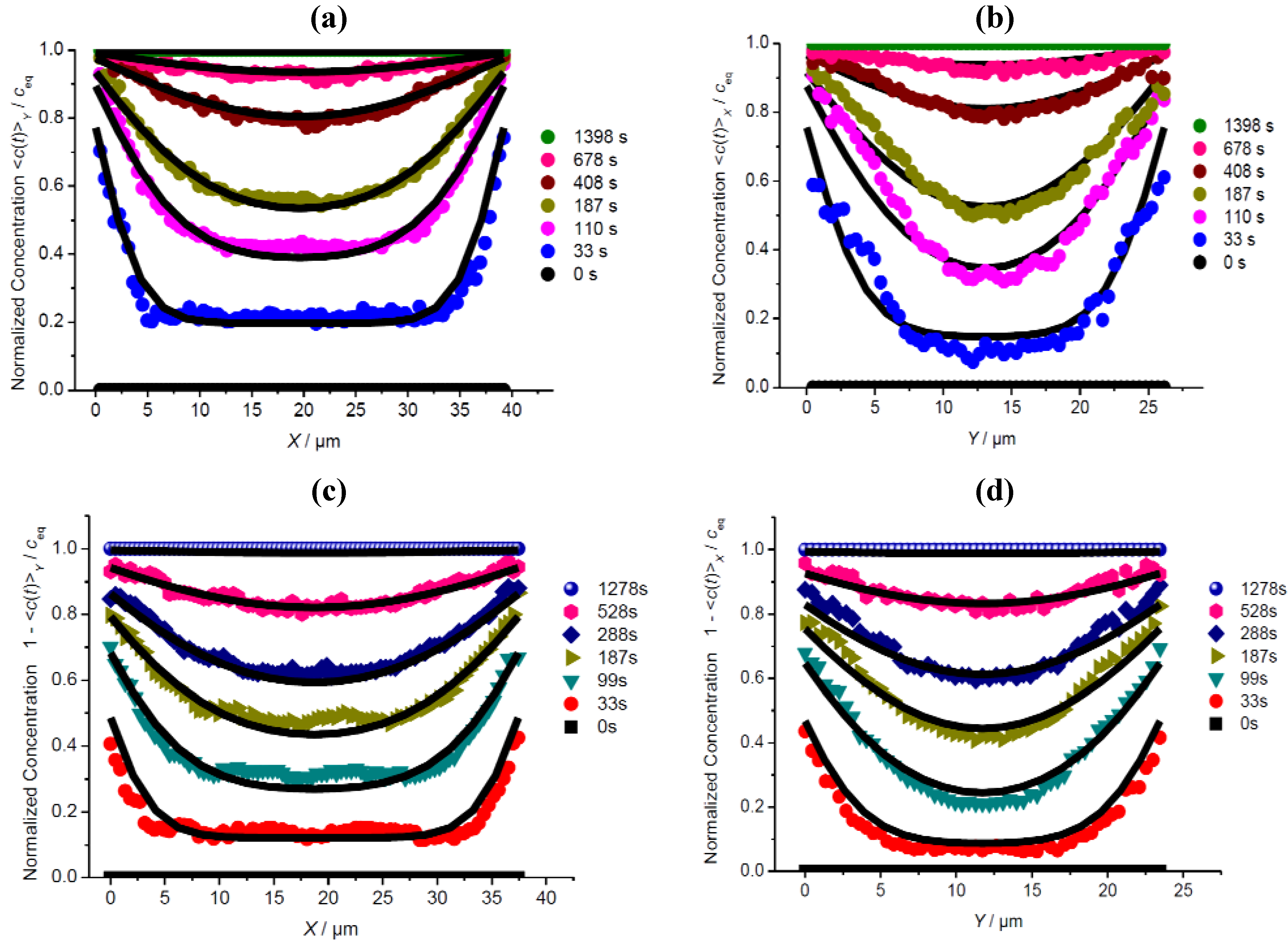
3.3. Comparison of Different Guest Molecules
3.4. Impact of Surface Resistances
4. Conclusions
Acknowledgments
References
- Chen, N.Y.; Degnan, T.F.; Smith, C.M. Molecular Transport and Reaction in Zeolites; Wiley-VCH: New York, NY, USA, 1994. [Google Scholar]
- Schüth, F.; Sing, K.S.W.; Weitkamp, J. Handbook of Porous Solids; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Auerbach, S.M.; Carrado, K.A.; Dutta, P.K. (Eds.) Handbook of Zeolite Science and Technology; CRC Press: Boca Raton, FL, USA, 2003.
- Laeri, F.; Schüth, F.; Simon, U.; Wark, M. (Eds.) Host-Guest-Systems Based on Nanoporous Crystals; Wiley-VCH: Weinheim, Germany, 2003.
- Ertl, G.; Knözinger, H.; Schüth, F.; Weitkamp, J. (Eds.) Handbook of Heterogeneous Catalysis; Wiley-VCH: Weinheim, Germany, 2008.
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Klages, R.; Radons, G.; Sokolov, I.M. Anomalous Transport; Weinheim, Germany, 2008. [Google Scholar]
- Kärger, J.; Ruthven, D.M.; Theodorou, D.N. Diffusion in Nanporous Materials; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Treacy, M.M.J.; Higgins, J.B. Collection of Simulated XRD Powder Patterns for Zeolites; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Flanigen, E.M.; Bennett, J.M.; Grose, R.W.; Cohen, J.P.; Patton, R.L.; Kirchner, R.M.; Smith, J.V. Silicalite, a new hydrophobic crystalline silica molecular-sieve. Nature 1978, 271, 512–514. [Google Scholar] [CrossRef]
- Kokotailo, G.T.; Lawton, S.L.; Olson, D.H.; Meier, W.M. Structure of synthetic zeolite ZSM-5. Nature 1978, 272, 437–438. [Google Scholar] [CrossRef]
- Theodorou, D.N.; Snurr, R.Q.; Bell, A.T. Molecular dynamics and diffusion in microporous materials. In Comprehensive Supramolecular Chemistry; Alberti, G., Bein, T., Eds.; Pergamon: Oxford, NY, USA, 1996; pp. 507–548. [Google Scholar]
- Haberlandt, R.; Fritzsche, S.; Vörtler, H.L. Simulation of microporous systems: Confined fluids in equilibrium and diffusion in zeolites. In Handbook of Surfaces and Interfaces of Materials; Nalwa, H.S., Ed.; Academic Press: New York, NY, USA, 2001; Volume 5, pp. 357–443. [Google Scholar]
- Dubbeldam, D.; Calero, S.; Vlugt, T.J.H.; Krishna, R.; Maesen, T.L.M.; Beerdsen, E.; Smit, B. Force field parametrization through fitting on inflection points in isotherms. Phys. Rev. Lett. 2004, 93, 088302:1–088302:4. [Google Scholar] [CrossRef]
- Saengsawang, O.; Schüring, A.; Remsungnen, T.; Loisruangsin, A.; Hannongbua, S.; Magusin, P.C.M.; Fritzsche, S. Rotational motion of pentane in the flat gamma cages of zeolite KFI. J. Phys. Chem. C 2008, 112, 5922–5929. [Google Scholar] [CrossRef]
- June, R.L.; Bell, A.T.; Theodorou, D.N. Prediction of low occupancy sorption of alkanes in silicalite prediction of low occupancy sorption of alkanes in silicalite. J. Phys. Chem. 1990, 94, 1508–1516. [Google Scholar] [CrossRef]
- June, R.L.; Bell, A.T.; Theodorou, D.N. A molecular dynamics study of mehane and xenon in silicalite. J. Phys. Chem. 1990, 94, 8232–8240. [Google Scholar] [CrossRef]
- June, R.L.; Bell, A.T.; Theodorou, D.N. Molecular dynamics studies of butane and hexane in silicalite. J. Phys. Chem. 1992, 96, 1051–1059. [Google Scholar] [CrossRef]
- Hernandez, E.; Catlow, C.R.A. Molecular dynamics simulations of n-butane and n-hexane diffusion in silicalite. In Proceedings: Mathematical and Physical Science; The Royal Society: London, UK, 1995; Volume 448, pp. 143–160. [Google Scholar]
- Demontis, P.; Fris, E.S.; Suffritti, G. Molecular dynamics studies on zeolite: 6. Temperature dependence of diffusion of methane in silicalite. J. Phys. Chem. 1992, 96, 1482–1490. [Google Scholar] [CrossRef]
- Gergidis, L.N.; Theodorou, D.N. Molecular dynamics simulation of n-butane-methane mixtures in silicalite. J. Phys. Chem. B 1999, 103, 3380–3390. [Google Scholar] [CrossRef]
- Bussai, C.; Fritzsche, S.; Haberlandt, R.; Hannongbua, S. A molecular dynamics (MD) study of methane in silicalite-1: A novel moller-plesset potential energy surface. In Recent Advances in the Science and Technology of Zeolites and Related Materials; van Steen, E., Callanan, L.H., Claeys, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; Volume 154, pp. 2104–2109. [Google Scholar]
- Schüring, A.; Fritzsche, S.; Haberlandt, R.; Vasenkov, S.; Kärger, J. Modelling molecular diffusion in channel networks via displacements between the channelsegments. Phys. Chem. Chem. Phys. 2004, 6, 3676–3679. [Google Scholar] [CrossRef]
- Jost, S.; Biswas, P.; Schuring, A.; Karger, J.; Bopp, P.A.; Haberlandt, R.; Fritzsche, S. Structure and self-diffusion of water molecules in chabazite: A molecular dynamics study. J. Phys. Chem. C 2007, 111, 14707–14712. [Google Scholar] [CrossRef]
- Chanajaree, R.; Bopp, P.A.; Fritzsche, S.; Kärger, J. Water dynamics in chabazite. Microp. Mesop. Mat. 2011, 146, 106–118. [Google Scholar] [CrossRef]
- Kärger, J. Random walk through two-channel networks: A simple means to correlate the coefficients of anisotropic diffusion in ZSM-5 type zeolite. J. Phys. Chem. 1991, 95, 5558–5560. [Google Scholar] [CrossRef]
- Kärger, J.; Pfeifer, H. On the interdependence of the principal values of the diffusion tensor in zeolites with channel networks. Zeolites 1992, 12, 872–873. [Google Scholar] [CrossRef]
- Bär, N.K.; Kärger, J.; Pfeifer, H.; Schäfer, H.; Schmitz, W. Diffusion anisotropy in natural chabazite. Microporous Mesoporous Mat. 1998, 22, 289–295. [Google Scholar] [CrossRef]
- Kocirik, M.; Kornatowski, J.; Masarik, V.; Novak, P.; Zikanova, A.; Maixner, J. Investigation of sorption and transport of sorbate molecules in crystals of MFI structure type by iodine indicator technique. Microporous Mesoporous Mat. 1998, 23, 295–308. [Google Scholar] [CrossRef]
- Schmidt, W.; Wilczok, U.; Weidenthaler, C.; Medenbach, O.; Goddard, R.; Buth, G.; Cepak, A. Preparation and morphology of pyramidal MFI single crystal segments. J. Phys. Chem. B 2007, 111, 13538–13543. [Google Scholar] [CrossRef] [PubMed]
- Tzoulaki, D.; Schmidt, W.; Wilczok, U.; Kärger, J. Formation of surface barriers on silicalite-1 crystal fragments by residual water vapour as probed with isobutane by interference microscopy. Microporous Mesoporous Mat. 2008, 110, 72–76. [Google Scholar] [CrossRef]
- Hong, U.; Kärger, J.; Pfeifer, H.; Müller, U.; Unger, K.K. Observing diffusion anisotropy in zeolites by pulsed field gradient NMR. Z. Phys. Chem. 1991, 173, 225–234. [Google Scholar] [CrossRef]
- Hong, U.; Kärger, J.; Kramer, R.; Pfeifer, H.; Seiffert, G.; Müller, U.; Unger, K.K.; Lück, H.B.; Ito, T. PFG NMR study of diffusion anisotropy in oriented ZSM-5 type zeolite crystallies. Zeolites 1991, 11, 816–821. [Google Scholar] [CrossRef]
- Caro, J.; Noack, M.; Marlow, F.; Peterson, D.; Griepenstrog, M.; Kornatowksi, J.J. Selective sorption uptake kinetics of n-hexane on zsm-5: A new method for measuring anitsotropic diffusivities. J. Phys. Chem. 1993, 97, 13685–13690. [Google Scholar] [CrossRef]
- Hayhurst, D.T.; Paravar, A. Direct measurement of diffusivity for butane across a single large silicalite crystal. In Proceeding of the Sixth International Zeolite Conference, Reno, NV, USA, 1983; Olson, D., Bisio, A., Eds.; Butterworths: Guildford, UK, 1984; pp. 217–224. [Google Scholar]
- Hayhurst, D.T.; Paravar, A.R. Diffusion of C1 to C5 normal paraffins in silicalite. Zeolites 1988, 8, 27–29. [Google Scholar] [CrossRef]
- Shah, D.B.; Chokchai, S.; Hayhurst, D. Measurements of transport rates of C4 hydrocarbons across a single-crystal silicalite membrane. J. Chem. Soc. Faraday Trans. 1993, 89, 3161–3167. [Google Scholar] [CrossRef]
- Eic, M.; Ruthven, D.M. Intracrystalline diffusion of linear paraffins and benzene in silicalite studied by the ZLC method. In Zeolites: Facts, Figures, Future; Jacobs, P.A., van Santen, R.A., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 897–906. [Google Scholar]
- Hufton, J.R.; Ruthven, D.M.; Danner, R.P. Adsorption and diffusion of hydrocarbons in silicalite at very low concentration: Effect of Defect Sites. Microporous Mater. 1995, 5, 39–52. [Google Scholar] [CrossRef]
- Cavalcante, C.L.; Ruthven, D.M. Adsorption of branched and cyclic paraffins in silicalite. 2: Kinetics. Ind. Eng. Chem. Res. 1995, 34, 185–191. [Google Scholar] [CrossRef]
- Brandani, S.; Jama, M.; Ruthven, D. Diffusion, Self-diffusion and counter-diffusion of benzene and p-xylene in silicalite. Microporous Mesoporous Mat. 2000, 6, 283–300. [Google Scholar] [CrossRef]
- Brandani, S.; Ruthven, D.M. Analysis of ZLC desorption curves for gaseous systems. Adsorpt. 1996, 2, 133–143. [Google Scholar] [CrossRef]
- Ruthven, D.M.; Brandani, S.; Eic, M. Measurement of diffusion in microporous solids by macroscopic methods. In Adsorption and Diffusion; Karge, H.G., Weitkamp, J., Eds.; Springer: Berlin, Germany, 2008; Volume 7, pp. 45–85. [Google Scholar]
- Ruthven, D.M.; Brandani, S. Measurement of diffusion in porous solids by zero length column (ZLC) methods. In Recent Advances in Gas Separation by Microporous Ceramic Membranes; Kanellopoulos, N.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2000; pp. 187–212. [Google Scholar]
- Chmelik, C.; Heinke, L.; Kortunov, P.; Li, J.; Olson, D.; Tzoulaki, D.; Weitkamp, J.; Kärger, J. Ensemble measurement of diffusion: Novel beauty and evidence. Chem. Phys. Chem. 2009, 10, 2623–2627. [Google Scholar] [PubMed]
- Chmelik, C.; Hibbe, F.; Tzoulaki, D.; Heinke, L.; Caro, J.; Li, J.; Kärger, J. Exploring the nature of surface barriers on MOF Zn(tbip) by applying IR microscopy in high temporal and spatial resolution. Microporous Mesoporous Mater. 2010, 129, 340–344. [Google Scholar] [CrossRef]
- Heinke, L.; Tzoulaki, D.; Chmelik, C.; Hibbe, F.; van Baten, J.; Lim, H.; Li, J.; Krishna, R.; Kärger, J. Assessing guest diffusivities in porous hosts from transient concentration profiles. Phys. Rev. Lett. 2009, 102, 065901: 1–065901: 4. [Google Scholar] [CrossRef] [PubMed]
- Hibbe, F.; Chmelik, C.; Heinke, L.; Pramanik, S.; Li, J.; Ruthven, D.M.; Tzoulaki, D.; Kärger, J. The nature of surface barriers on nanoporous solids explored by microimaging of transient guest distributions. J. Am. Chem. Soc. 2011, 133, 2804–2807. [Google Scholar] [CrossRef] [PubMed]
- Tzoulaki, D.; Heinke, L.; Li, J.; Lim, H.; Olson, D.; Caro, J.; Krishna, R.; Chmelik, C.; Kärger, J. Assessing surface permeabilities from transient guest profiles in nanoporous materials. Angew. Chem. Int. Ed. 2009, 48, 3525–3528. [Google Scholar] [CrossRef]
- Heinke, L.; Kärger, J. Correlating surface permeability with intracrystalline diffusivity in nanoporous solids. Phys. Rev. Lett. 2011, 106, 074501: 1–074501: 4. [Google Scholar] [CrossRef] [PubMed]
- Hibbe, F.; Marthala, R.; Chmelik, C.; Weitkamp, J.; Kärger, J. Micro-imaging of transient guest profiles in nanochannels. J. Chem. Phys. 2011, 135, 184201:1–184201:5. [Google Scholar] [CrossRef]
- Kärger, J.; Kortunov, P.; Vasenkov, S.; Heinke, L.; Shah, D.B.; Rakoczy, R.A.; Traa, Y.; Weitkamp, J. Unprecedented insight into diffusion by monitoring concentration of guest molecules in nanoporous host materials. Angew. Chem. Int. Edit. 2006, 45, 7846–7849. [Google Scholar] [CrossRef]
- Geier, O.; Vasenkov, S.; Lehmann, E.; Kärger, J.; Schemmert, U.; Rakoczy, R.A.; Weitkamp, J. Interference microscopy investigation of the influence of regular intergrowth effects in MFI-type zeolites on molecular uptake. J. Phys. Chem. B 2001, 105, 10217–10222. [Google Scholar] [CrossRef]
- Kortunov, P.; Heinke, L.; Vasenkov, S.; Chmelik, C.; Shah, D.B.; Kärger, J.; Rakoczy, R.A.; Traa, Y.; Weitkamp, J. Internal concentration gradients of guest molecules in nanoporous host materials: Measurement and microscopic analysis. J. Phys. Chem. B 2006, 110, 23821–23828. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, E.; Chmelik, C.; Scheidt, H.; Vasenkov, S.; Staudte, B.; Kärger, J.; Kremer, F.; Zadrozna, G.; Kornatowski, J. Regular intergrowth in the AFI type crystals: Influence on the intracrystalline adsorbate distribution as observed by interference and FTIR-microscopy. J. Amer. Chem. Soc. 2002, 124, 8690–8692. [Google Scholar] [CrossRef]
- Wright, P.A.; Maple, M.J.; Slawin, A.M.Z.; Patinek, V.; Aitken, R.A.; Welsh, S.; Cox, P.A. Cation-directed syntheses of novel zeolite-like metalloaluminophosphates STA-6 and STA-7 in the presence of azamacrocycle templates. J. Chem. Soc. Dalton Trans. 2000, 1243–1248. [Google Scholar]
- Castro, M.; Garcia, R.; Warrender, S.J.; Slawin, A.M.Z.; Wright, P.A.; Cox, P.A.; Fecant, C.; Mellot-Dranznieksd, C.; Bats, N. Co-templating and modelling in the rational synthesis of zeolitic solids. Chem. Commun. 2007, 3470–3472. [Google Scholar]
- Tzoulaki, D.; Heinke, L.; Schmidt, W.; Wilczok, U.; Kärger, J. Exploring crystal morphology of nanoporous hosts from transient guest profiles. Angew. Chem. Int. Ed. 2008, 47, 3954–3957. [Google Scholar] [CrossRef]
- Karwacki, L.; Stavitski, E.; Kox, M.H.F.; Kornatowski, J.; Weckhuysen, B.M. Intergrowth structure of zeolite crystals as determined by optical and fluorescence microscopy of the template-removal process. Angew. Chem.-Int. Edit. 2007, 46, 7228–7231. [Google Scholar] [CrossRef]
- Karwacki, L.; Kox, M.H.F.; Winter, D.A.M.; de Drury, M.R.; Meeldijk, J.D.; Stavitski, E.; Schmidt, W.; Mertens, M.; Cubillas, P.; John, N.; et al. Morphology-dependent zeolite intergrowth structures leading to distinct internal and outer-surface molecular diffusion barriers. Nat. Mater. 2009, 8, 959–965. [Google Scholar] [CrossRef] [PubMed]
- Shao, C.; Li, X.; Qiu, S.; Xiao, F.-S.; Terasaki, O. Size-controlled synthesis of silicalite-1 single crystals in the presence of benzene-1,2-diol. Microporous Mesoporous Materials 2000, 39, 117–123. [Google Scholar] [CrossRef]
- Gueudré, L.; Jolimaîte, E.; Bats, N.; Dong, W. Diffusion in zeolites: is surface resistance a critical parameter? Adsorption 2010, 16, 17–27. [Google Scholar] [CrossRef]
- Gueudré, L.; Bats, N.; Jolimaître, E. Effect of surface resistance on cyclohexane uptake curves in Silicalite-1 crystals. Microporous Mesoporous Materials 2012, 147, 310–317. [Google Scholar] [CrossRef]
- Kärger, J.; Vasenkov, S. Quantitation of diffusion in zeolite catalysts. Microporous Mesoporous Mat. 2005, 85, 195–206. [Google Scholar] [CrossRef]
- Karge, H.G.; Kärger, J. Application of IR spectroscopy, IR microscopy, and optical interference microscopy to diffusion in zeolites. In Adsorption and Diffusion; Karge, H.G., Weitkamp, J., Eds.; Springer: Berlin, Germany, 2008; Volume 7, pp. 135–206. [Google Scholar]
- Chmelik, C.; Heinke, L.; Valiullin, R.; Kärger, J. New view of diffusion in nanoporous materials. Chem. Ing. Tech. 2010, 82, 779–804. [Google Scholar] [CrossRef]
- Chmelik, C.; Kärger, J. In-situ study on molecular diffusion phenomena in nanoporous catalytic solids. Chem. Soc. Rev. 2010, 39, 4864–4884. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Rees, L.V.C. Frequency response measurements of diffusion in microporous materials. In Adsorption and Diffusion; Karge, H.G., Weitkamp, J., Eds.; Springer: Berlin, Germany, 2008; Volume 7, pp. 235–276. [Google Scholar]
- Rees, L.V.C.; Song, L. Frequency response methods for the characterization of microporous solids. In Recent Advances in Gas Separation by Microporous Ceramic Membranes; Kanellopoulos, N.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2000; pp. 139–186. [Google Scholar]
- Song, L.J.; Sun, Z.L.; Rees, L.V.C. Experimental and molecular simulation studies of adsorption and diffusion of cyclic hydrocarbons in silicalite-1. Microporous Mesoporous Mat. 2002, 55, 31–49. [Google Scholar] [CrossRef]
- Förste, C.; Kärger, J.; Pfeifer, H.; Riekert, L.; Bulow, M.; Zikanova, A. Comparison of nuclear-magnetic-resonance tracer exchange and molecular uptake of benzene on pentasils. J. Chem. Soc. Faraday Trans. I 1990, 86, 881–885. [Google Scholar] [CrossRef]
- Qureshi, W.; Wei, J. One- and two-component diffusion in zeolite ZSM-5 I. Theoretical. J. Catal. 1990, 126, 126–146. [Google Scholar] [CrossRef]
- Beschmann, K.; Koktailo, G.; Riekert, L. Kinetics of sorption of aromatics in zeolite ZSM-5. Chem. Eng. Process 1987, 27, 223–229. [Google Scholar] [CrossRef]
- Eic, M.; Ruthven, D.M. Intracrystalline diffusion of linear paraffins and benzene in silicalite studied by the ZLC method. In 8th International Conference on Zeolites; Jacobs, P.A., van Santen, R.A., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 897–905. [Google Scholar]
- Zikanova, A.; Bülow, M.; Schlodder, H. Intracrystalline diffusion of benzene in ZSM-5 and silicalite. Zeolites 1987, 7, 115–118. [Google Scholar] [CrossRef]
- Doelle, H.-J.; Heering, J.; Riekert, L.; Marosi, L. Sorption and catalytic reaction in pentasil zeolites. Influence of preparation and crystal size on equilibria and kinetics. J. Catal. 1981, 71, 27–40. [Google Scholar] [CrossRef]
- Stavitski, E.; Drury, M.R.; Winter, D.A.M.; de Kox, M.H.F.; Weckhuysen, B.M. Intergrowth structure of zeolite crystals and pore orientation of individual subunits revealed by electron backscatter diffraction/focused ion beam experiments. Angew. Chem. Int. Edit. 2008, 47, 5637–5640. [Google Scholar] [CrossRef]
- Heinke, L.; Kortunov, P.; Tzoulaki, D.; Kärger, J. The options of interference microscopy to explore the significance of intracrystalline diffusion and surface permeation for overall mass transfer on nanoporous materials. Adsorpt. J. Int. Adsorpt. Soc. 2007, 13, 215–223. [Google Scholar] [CrossRef]
- Heinke, L. Significance of concentration-dependent intracrystalline diffusion and surface permeation for overall mass transfer. Diffusion Fundam. 2007, 4, 12.1–12.11. [Google Scholar]
- Heinke, L.; Kärger, J. Discriminating the molecular pathways during uptake and release on nanoporous host systems. J. Chem. Phys. 2009, 130, 044707: 1–044707: 8. [Google Scholar] [CrossRef] [PubMed]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gueudré, L.; Binder, T.; Chmelik, C.; Hibbe, F.; Ruthven, D.M.; Kärger, J. Micro-Imaging by Interference Microscopy: A Case Study of Orientation-Dependent Guest Diffusion in MFI-Type Zeolite Host Crystals. Materials 2012, 5, 721-740. https://doi.org/10.3390/ma5040721
Gueudré L, Binder T, Chmelik C, Hibbe F, Ruthven DM, Kärger J. Micro-Imaging by Interference Microscopy: A Case Study of Orientation-Dependent Guest Diffusion in MFI-Type Zeolite Host Crystals. Materials. 2012; 5(4):721-740. https://doi.org/10.3390/ma5040721
Chicago/Turabian StyleGueudré, Laurent, Tomas Binder, Christian Chmelik, Florian Hibbe, Douglas M. Ruthven, and Jörg Kärger. 2012. "Micro-Imaging by Interference Microscopy: A Case Study of Orientation-Dependent Guest Diffusion in MFI-Type Zeolite Host Crystals" Materials 5, no. 4: 721-740. https://doi.org/10.3390/ma5040721
APA StyleGueudré, L., Binder, T., Chmelik, C., Hibbe, F., Ruthven, D. M., & Kärger, J. (2012). Micro-Imaging by Interference Microscopy: A Case Study of Orientation-Dependent Guest Diffusion in MFI-Type Zeolite Host Crystals. Materials, 5(4), 721-740. https://doi.org/10.3390/ma5040721




