Abstract
This paper presents the stress and displacement fields in a functionally graded material (FGM) caused by a load. The FGM is a graded material of Si3N4-based ceramics and is assumed to be of semi-infinite extent. The load is a distributed loading over a rectangular area that is parallel to the external surface of the FGM and either on its external surface or within its interior space. The point-load analytical solutions or so-called Yue’s solutions are used for the numerical integration over the distributed loaded area. The loaded area is discretized into 200 small equal-sized rectangular elements. The numerical integration is carried out with the regular Gaussian quadrature. Weak and strong singular integrations encountered when the field points are located on the loaded plane, are resolved with the classical methods in boundary element analysis. The numerical integration results have high accuracy.
1. Introduction
Functionally graded materials (FGMs), also known as graded materials, are generally multi-phase composites with continuously varying mechanical properties. They are primarily used as coatings and interfacial zones to reduce stresses resulting from the material property mismatch, to improve the surface properties and to provide protection against severe loading, thermal and chemical environments. At present, FGMs are usually associated with particulate composites where the volume fraction of particles varies in one or several directions. With the wide use of FGMs in engineering, much attention has been paid to the mechanical behavior of FGMs due to different loadings.
Significant efforts have been made in the study of the mechanical responses of FGMs. These studies include the investigation of elastic fields, crack and contact problems in FGMs. For example, Gibson [1], Booker et al. [2], Oner [3] and Butter et al. [4] analyzed the elastic behavior of non-homogeneous half-spaces. Kassir [5], Giannakopoulos et al. [6] and Suresh [7] discussed the contact problems between punches and graded materials. Chen et al. [8] presented a semianalytical approach to solve the time-dependent response of a multilayered pavement. Delale et al. [9] analyzed the fracture mechanics of crack problems in FGMs. Chan et al. [10] and Martin et al. [11] presented Green’s functions for 2D and 3D exponentially-graded elastic solids, respectively. Birman et al. [12] presented a review of the principal developments in FGMs and the critical areas where further research is needed for a successful implementation of FGM in design. In particular, Carrera and his co-workers [13,14,15] developed the unified formulation for analysis of classical layered structures and extended it for FGM structures by using a set of functions which are indicated as thickness functions.
More recently, Xiao et al. [16] developed a numerical method in analyzing the contact between the rectangular rigid plate and the graded material of semi-infinite extent. Xiao et al. [17] further developed the numerical method for analysis of the elastic fields in heterogeneous rocks due to reservoir water impoundment. The numerical method has high accuracy and efficiency by using the generalized Kelvin solution of a multilayered medium of infinite extent, which is adoptable to a layered medium of infinite extent.
In this paper, the numerical method is used for the analysis of elastic behaviors of FGM half-space. Referring to the results in Pender et al. [18], the graded material of Si3N4-based ceramics of semi-infinite extent is used as the FGM for the stress and displacement analysis. The rectangular loading area is parallel to the boundary of the semi-infinite FGM space and the uniform normal loads are chosen. The displacements and stresses induced in the graded materials are presented. The comparison of elastic fields is made for two different positions of the rectangular loads.
2. Numerical Method for Analysis of Mechanical States in FGMs
2.1. The Point-Load Solution Suitable for the FGM
Yue [19] presented the point-load analytical solutions for multilayer elastic solids. This point-load solution is an extension of the classical Kelvin solution for a point-load in a homogeneous elastic space and is for the stress and displacement fields in a layered elastic solid of infinite extent caused by the action of point loads. Each layer is a homogeneous elastic solid of finite thickness and infinite lateral extension. The total number of the dissimilar elastic layers is an arbitrary integer. The internal layers adhere to the first homogeneous elastic solid of upper semi-infinite extent and the last homogeneous elastic solid of lower semi-infinite extent. The interface between any two connected dissimilar layers is planar and fully bonded. All the layer interfaces are parallel to each other.
The FGM shown in Figure 1 has its isotropic elastic properties variable in depth and the layered technique is used along the depth. For this FGM problem of semi-infinite extent, the shear modulus of the first solid of upper semi-infinite extent is assigned a zero value (or an infinitesimal value, e.g., 10–15 MPa). Consequently, the first elastic solid becomes a void space of upper semi-infinite extent. The Yue’s solution for a point load in a multilayered elastic solid of infinite extent is automatically degenerated into the generalized Mindlin solution for a point load in a layered half-space.
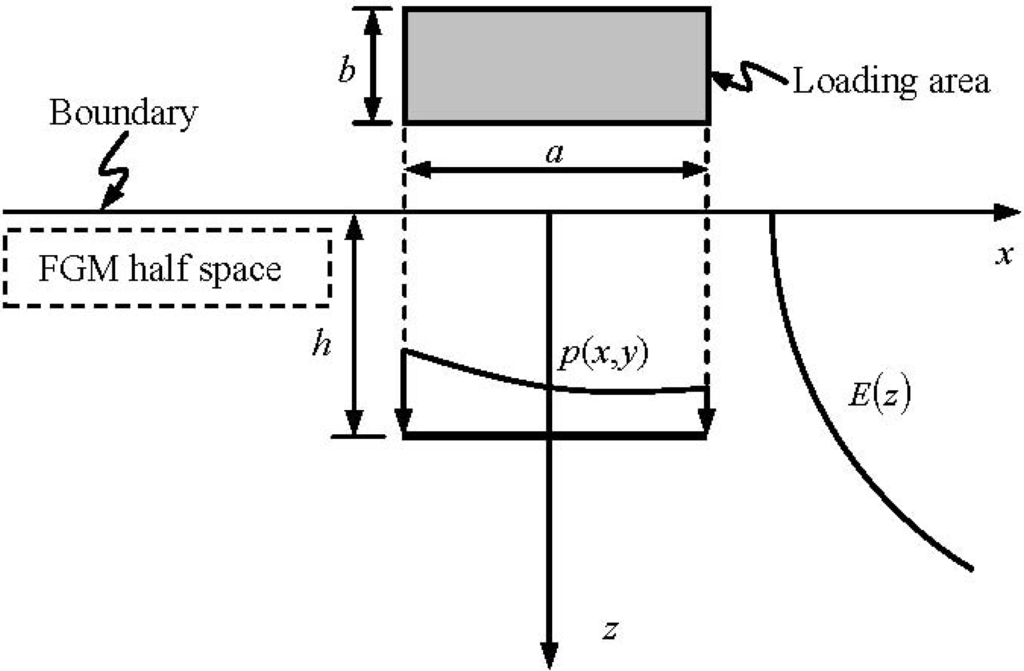
Figure 1.
Functionally Graded Material (FGM) half-space subjected to loads on a rectangular area (a = 2 mm, b = 1 mm).
Figure 1.
Functionally Graded Material (FGM) half-space subjected to loads on a rectangular area (a = 2 mm, b = 1 mm).
2.2. The Numerical Method for Analysis of the FGM due to Distributed Loadings
By using Yue’s solution, Xiao et al. [16,20] presented the numerical analysis of contact problems between rigid punch and the graded materials and elastic fields in heterogeneous rocks induced by reservoir water impoundment, respectively. The accuracy and effectiveness of the numerical integration method have been verified by comparing the numerical results with the existing analytical ones. The numerical integration method is again used in the analysis of the stress and displacement fields in the FGM as shown in Figure 1. It is also noted that Yue et al. [21] used the similar numerical integration method and analyzed the effects of tire-pavement contact pressure distributions on the response of asphalts concrete pavements.
Therefore, the mathematical formulation and computational procedures of the numerical integration method are not presented here in detail. Basically, the numerical integration method needs to discretize an FGM layer as a system of n number of fully bonded dissimilar sublayers. Thus, it uses Yue’s solution [19] for the elastostatic field in a layered solid of infinite extent due to the action of concentrated point loads. Figure 2 shows the discretization approach for FGMs. The Yue’s solution is used as the point-load solution to replace the classical Mindlin point-load solution in conventional numerical integration method for a homogeneous medium of semi-infinite extent. As a result, any FGMs with arbitrary property gradient in depth can be examined using this numerical method.
As shown in Figure 1, the surface S of the layered medium of semi-infinite extent is subjected to loads in the x, y and/or z directions. The total number of the dissimilar layers is an arbitrary integer. The stresses and displacements at any points of the layered medium are described as
where σijk*(Q, P) and uik*(Q, P) are the point-load solutions of the layered medium; σijk*(Q, P) are stresses for the field point Q due to the unit force along the k direction at the source point P; uik*(Q, P) displacements for the field point Q along the i direction due to the unit force along the k direction at the source point P; tk(P) is the traction at the source point P.
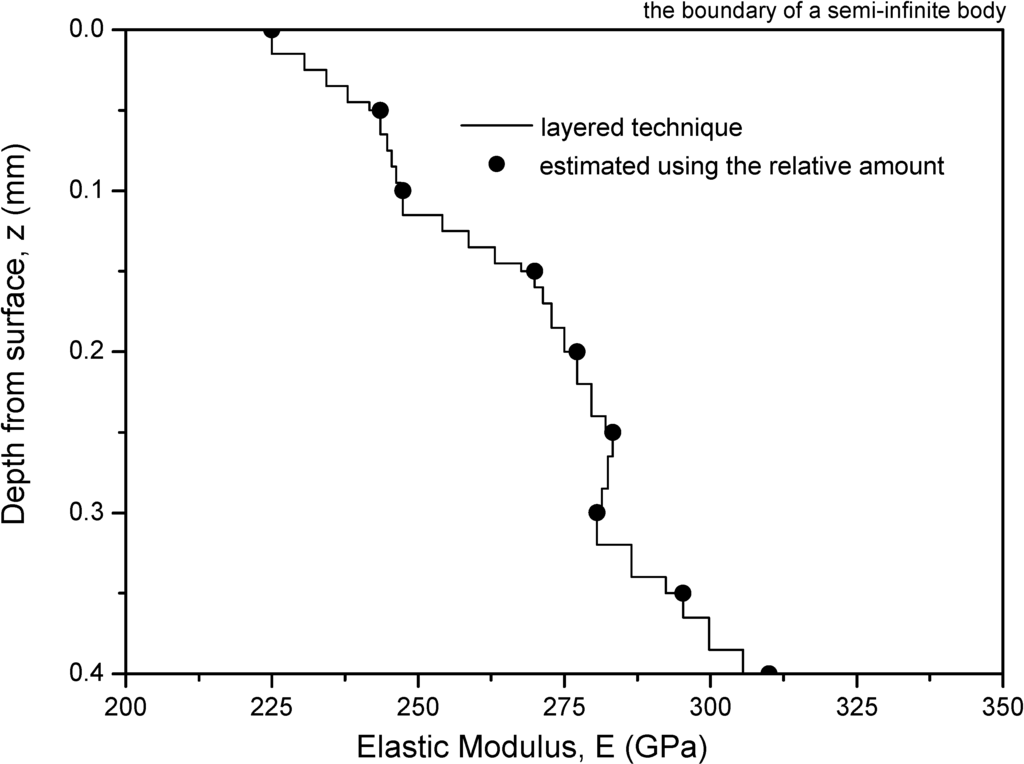
Figure 2.
Variation of elastic modulus in layers for actual measured modulus.
Figure 2.
Variation of elastic modulus in layers for actual measured modulus.
Due to the irregular shapes of a loading area and the non-uniform distribution of the traction tk(P), the integrals shown in Expressions (1) and (2) cannot be integrated into analytical forms. The 2D integrals in (1) and (2) have to be calculated numerically. A discretization technique, similar to that used in boundary element methods [16], is adopted. The loading area S is discretized into quadrilateral elements. In each element, the interpolation functions between the global and local coordinates are introduced. Thus, the integral on each element is executed in local coordinates and is calculated by using the regular Gaussian quadrature.
If the source point Q is located at the integral element, the integrand of Expression (1) is strongly singular and the integrand of Expression (2) is weakly singular. The strongly singular integral of Expression (1) is calculated by using the indirect method and the weakly singular integral of Expression (2) is calculated by dividing an element into several triangular sub-elements and using the coordinate transformation.
3. Displacements and Stresses in FGMs under Rectangular Loadings
3.1. General
In most of existing solutions to problems relating to FGMs, it is assumed that the material is isotropic, the Poisson’s ratio is constant, and Young’s (or shear) modulus is either an exponential or a power function of a space variable. In the studies described in Delale et al. [9], the shear modulus is assumed to be μ = μ0exp(αy) where y = 0 is either the boundary of the half plane or the plane of the crack. In Kassir [5], it is assumed that μ = μ0׀y׀m, (0 < m < 1).Generally, it is easy to obtain the analytical solutions of FGMs for the above-mentioned assumption of the material properties. Actually, the properties of FGMs are distributed in complex forms. Thus, the proposed numerical method is used much effectively to analyze the mechanical response of the actual FGMs because it can also take into account the depth variations in both Young’s modulus and Poisson’s ratio.
Herein, the Si3N4-based materials given in Pender et al. [18] are further used for the stress analysis. The Si3N4-based graded materials were fabricated with controlled, unidirectional gradients in elastic modulus from the surface to the interior. The elastic parameters shown in Figure 2 were estimated by using several photomicrographs and image analysis software. The FGM had a constant Poisson’s ratio 0.22 and its elastic modulus is described by a piecewise linear interpolation as follows
where the unit of elastic modulus is GPa and z is the depth coordinate, as shown in Figure 2.
The FGM from the depth z = 0 mm to 0.4 mm is discretized into 30 thin layers, as shown in Figure 2. Each layer has a constant modulus from Equation (3). The FGM from the depth z = 0.4 mm to ∞ is modeled as a homogeneous elastic solid of lower half-space extent. The above-mentioned FGMs will be referred to as Case 1. For reference and comparison, a homogeneous medium of semi-infinite extent is chosen and will be referred to as Case 2. The Young’s modulus and the Poisson’s ratio of the homogeneous elastic solid are assumed to be 225.1 GPa and 0.22, respectively, (i.e., E0 = 225.1 GPa and ν = 0.22). This modulus value is equal to the average value of the FGM modulus.
The loaded area (a × b) is a rectangular, where a and b are the length and width, respectively. It is assumed that a = 2 mm and b = 1 mm. The loaded area is parallel to the boundary of FGMs at z = 0 mm. The loaded area is subjected to the uniform vertical load p(x,y), where –a/2 ≤ x ≤ a/2 and –b/2 ≤ y ≤ b/2. The rectangular loaded area is discretized into the mesh of 200 eight-noded elements and 661 nodes, as shown in Figure 3.
Figure 3.
The mesh of loading area with 200 eight-noded elements and 661 nodes.
Figure 3.
The mesh of loading area with 200 eight-noded elements and 661 nodes.
Lankford [22] measured hardness and compressive strength of several strong ceramics from room temperature to 1,000 °C and gave the tensile and compressive strengths of the ceramic Si3N4. It can be found that the tensile strength of Si3N4 is 810 MPa and the compressive strength of Si3N4 is more than 1.5 GPa. Herein, it is assumed that p(x,y) = 100 MPa. For this case, the FGMs may be in the elastic state and the proposed method can be used for analysis of the displacement and stress fields.
For the FGM half-space subjected to the rectangular loading, the distribution characteristics of the elastic fields at the loaded plane are in general similar to those of the elastic fields in two bonded rocks of infinite extent induced by the rectangular loadings [17]. In Xiao et al. [17], the closed-form solutions were presented for the elastic fields in two bonded rocks of infinite extent induced by the uniform rectangular loadings. The continuities of the stresses and displacements across the loading plane and the material interface were discussed in detail. In the ensuing, distributions of the elastic fields for Cases 1 and 2 at different depths are presented and discussed in detail.
3.2. The Loading Area at h = 0 mm
The rectangular loading on the plane h = 0 mm is examined in this section. In this case, the loading is applied on the boundary of the FGMs of semi-infinite extent. Figure 4 shows the variations of the three normalized displacements ux, uy and uz along y = 0.5 mm at the depths z = 0, 0.125 and 0.225 mm. From these figures, it can be observed that the absolute values of displacements decrease as the depth increased for the two cases. At a given depth, the absolute values of the displacements of Case 1 are smaller than the ones of Case 2.
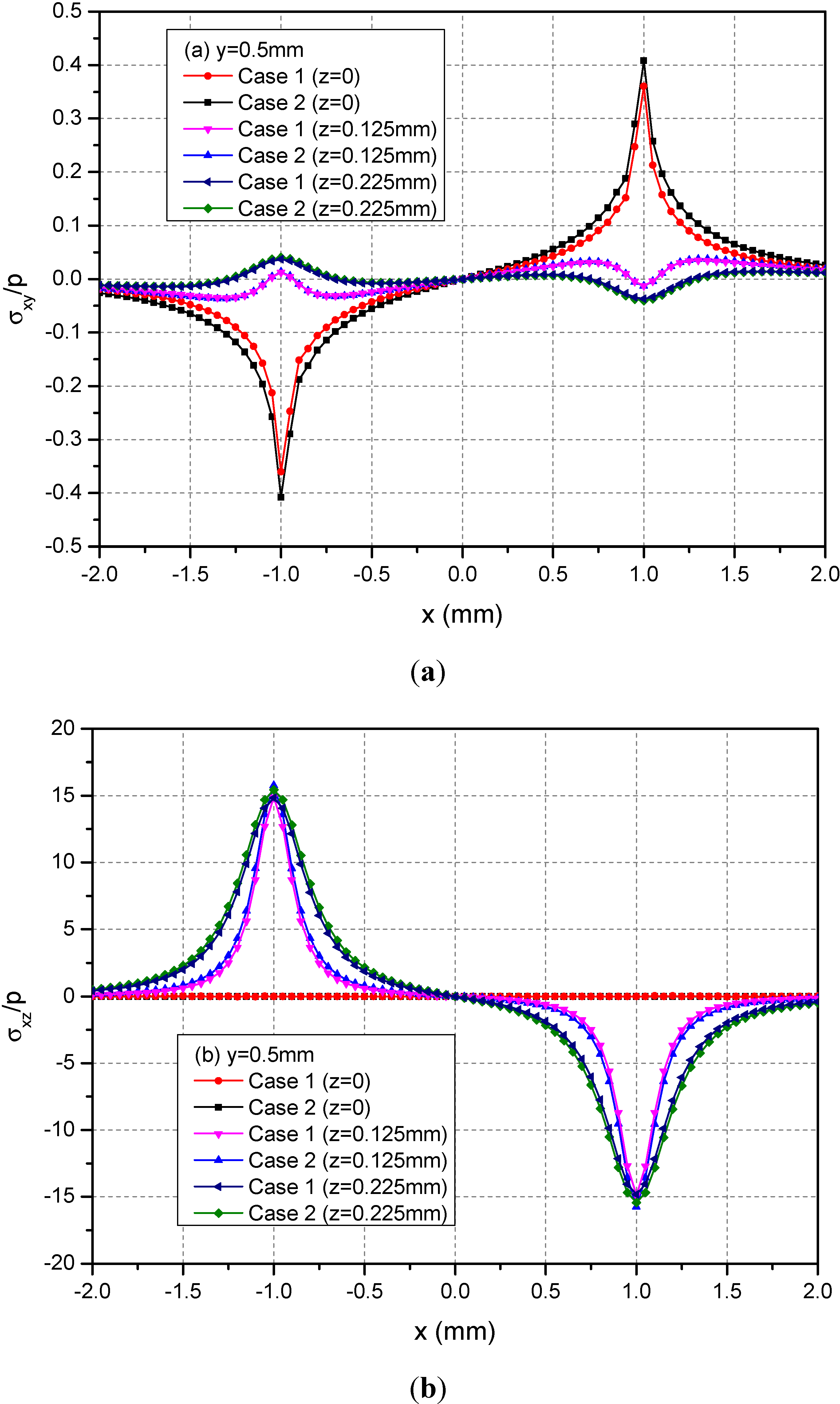
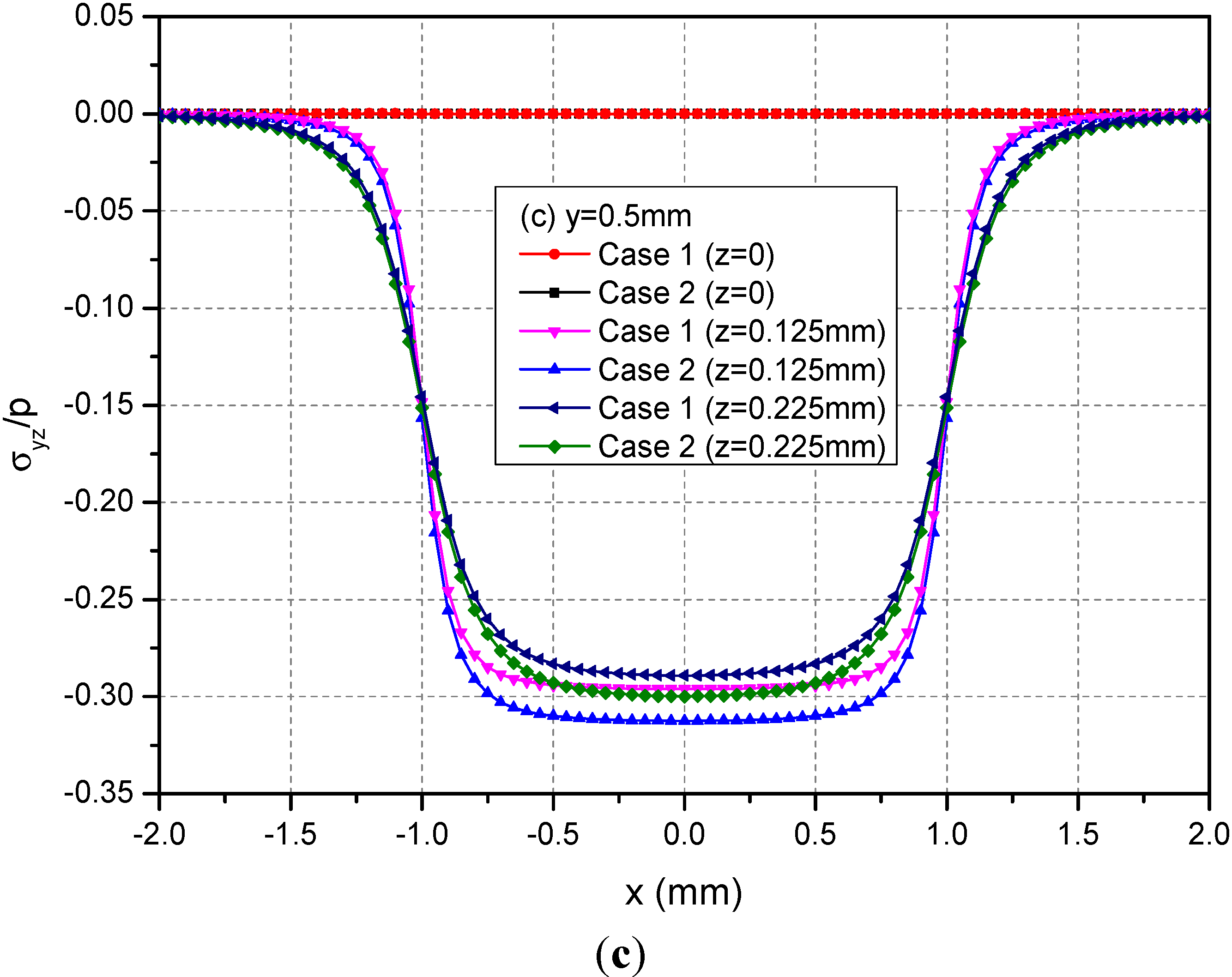
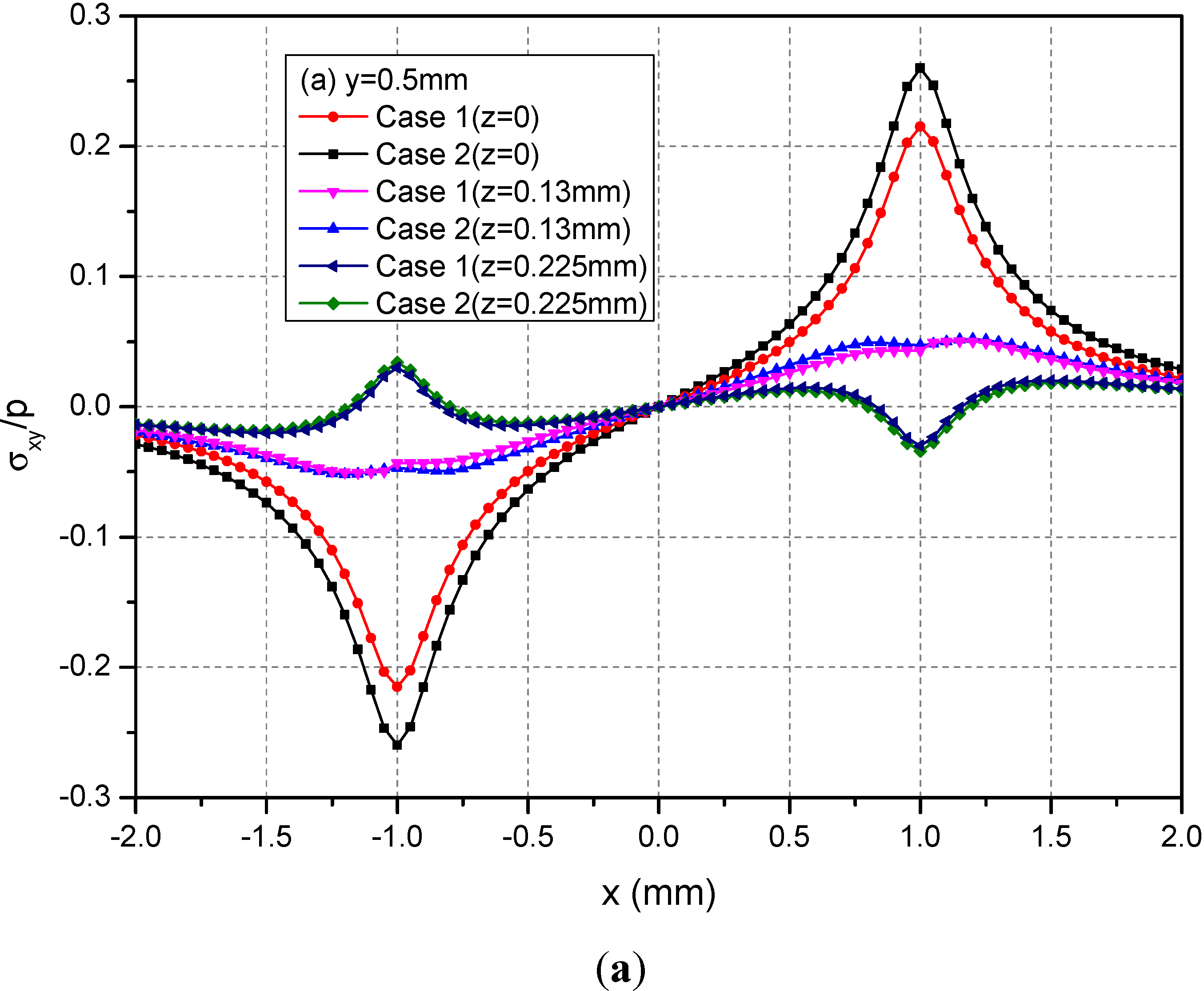
Figure 5 shows the variations of the three normalized normal stresses σxx, σyy and σzz along y = 0.5 mm at depths z = 0, 0.125 and 0.225 mm. It can be observed that the normal stresses are discontinuous at the points x = ± 1.0 mm and z = 0 mm across the loading area. At a given depth and among −1.0 mm < x < 1.0 mm, the absolute values of σxx and σyy for Case 1 are smaller than the those of the corresponding normal stresses for Case 2. At the depth z = 0.225 mm, this influence is not obvious. Figure 6 shows the variations of the three normalized shear stresses σxy, σxz and σyz along y = 0.5 mm at the depths z = 0, 0.125 or 0.225 mm. It can be observed that there are no obvious influences of material heterogeneities on the distributions of stresses except σyz. At the depth z = 0.225 mm and among −1.0 mm < x < 1.0 mm, the σyz values have obvious differences between Cases 1 and 2.
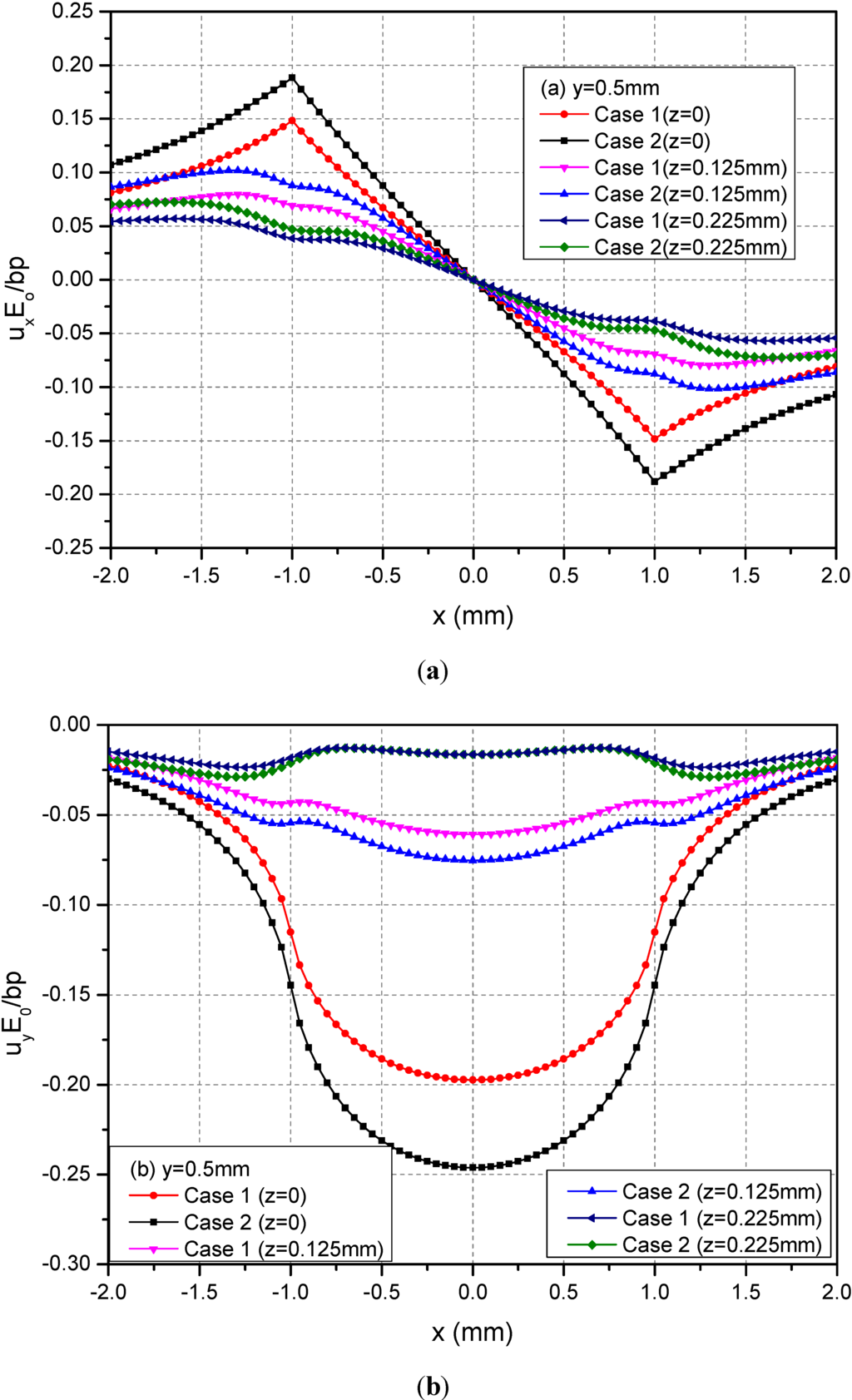
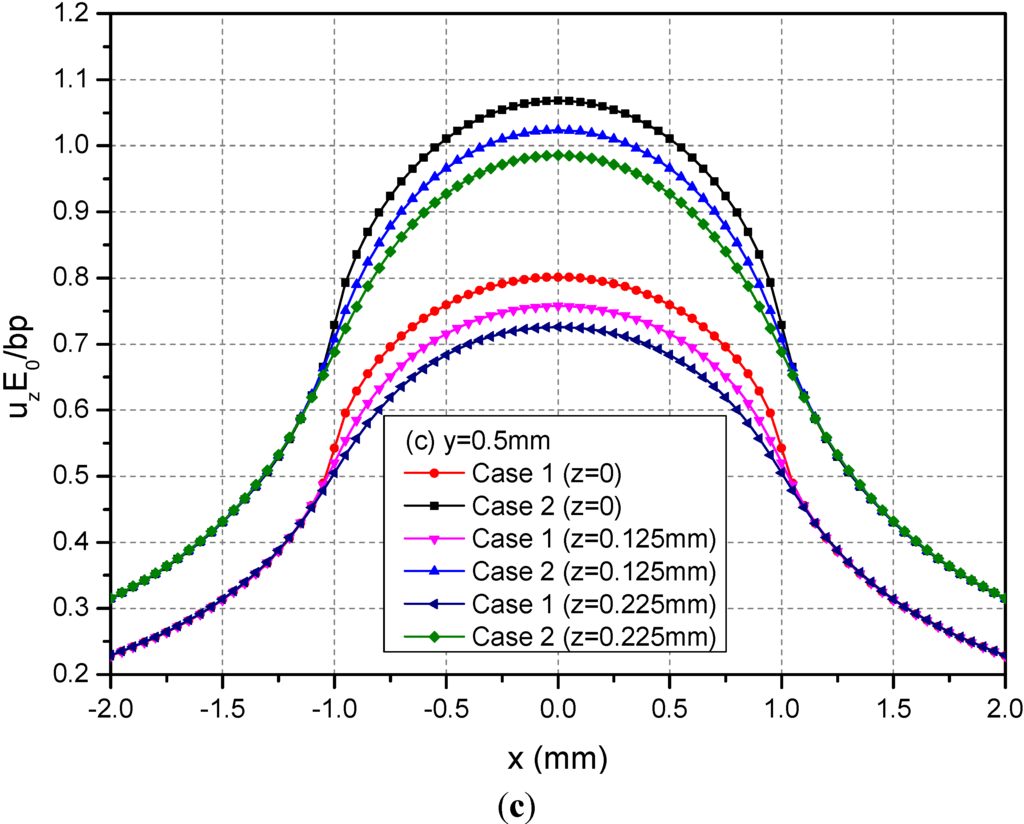
Figure 4.
Normalized displacements (a) ux; (b) uy; (c) uz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
Figure 4.
Normalized displacements (a) ux; (b) uy; (c) uz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
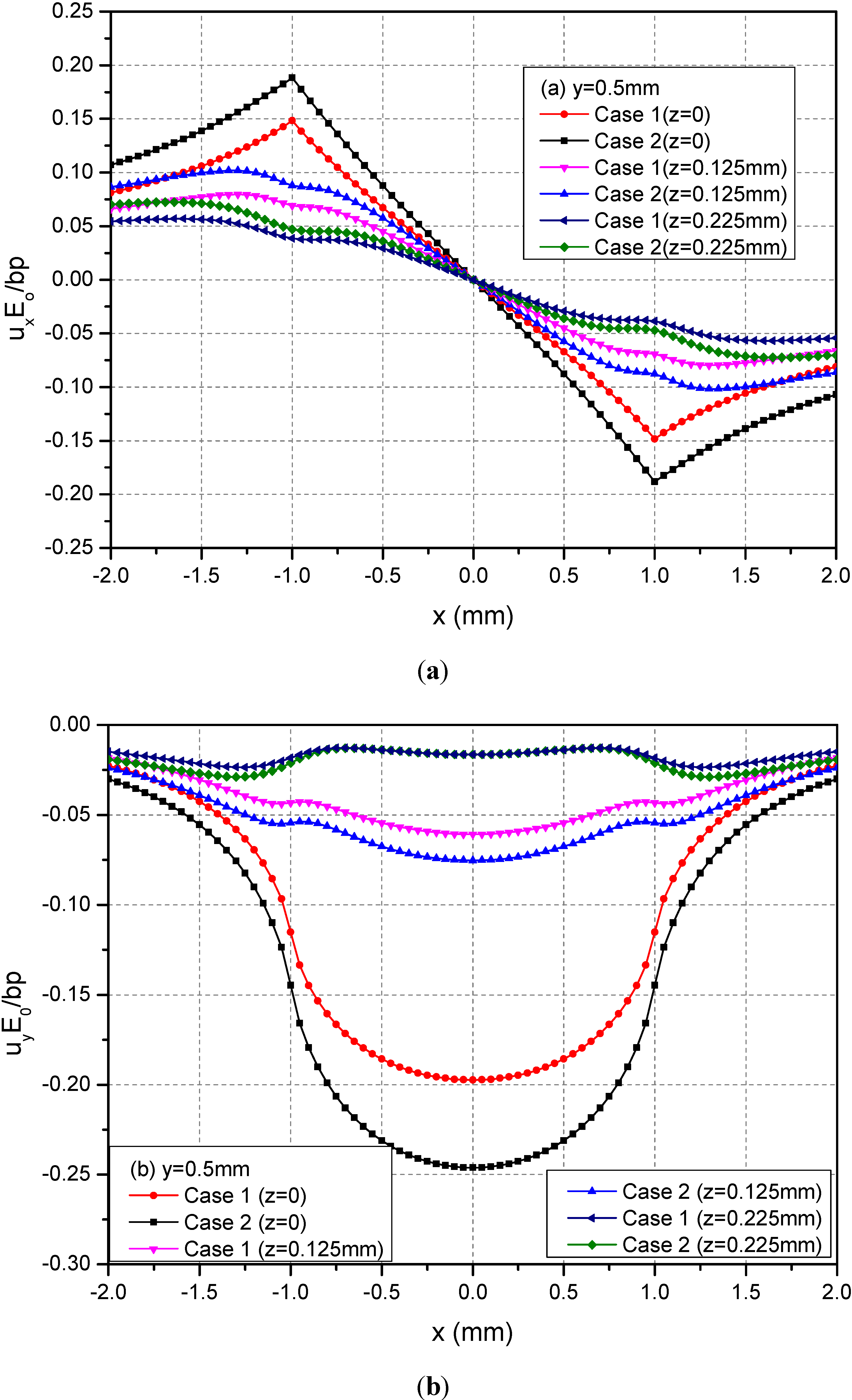
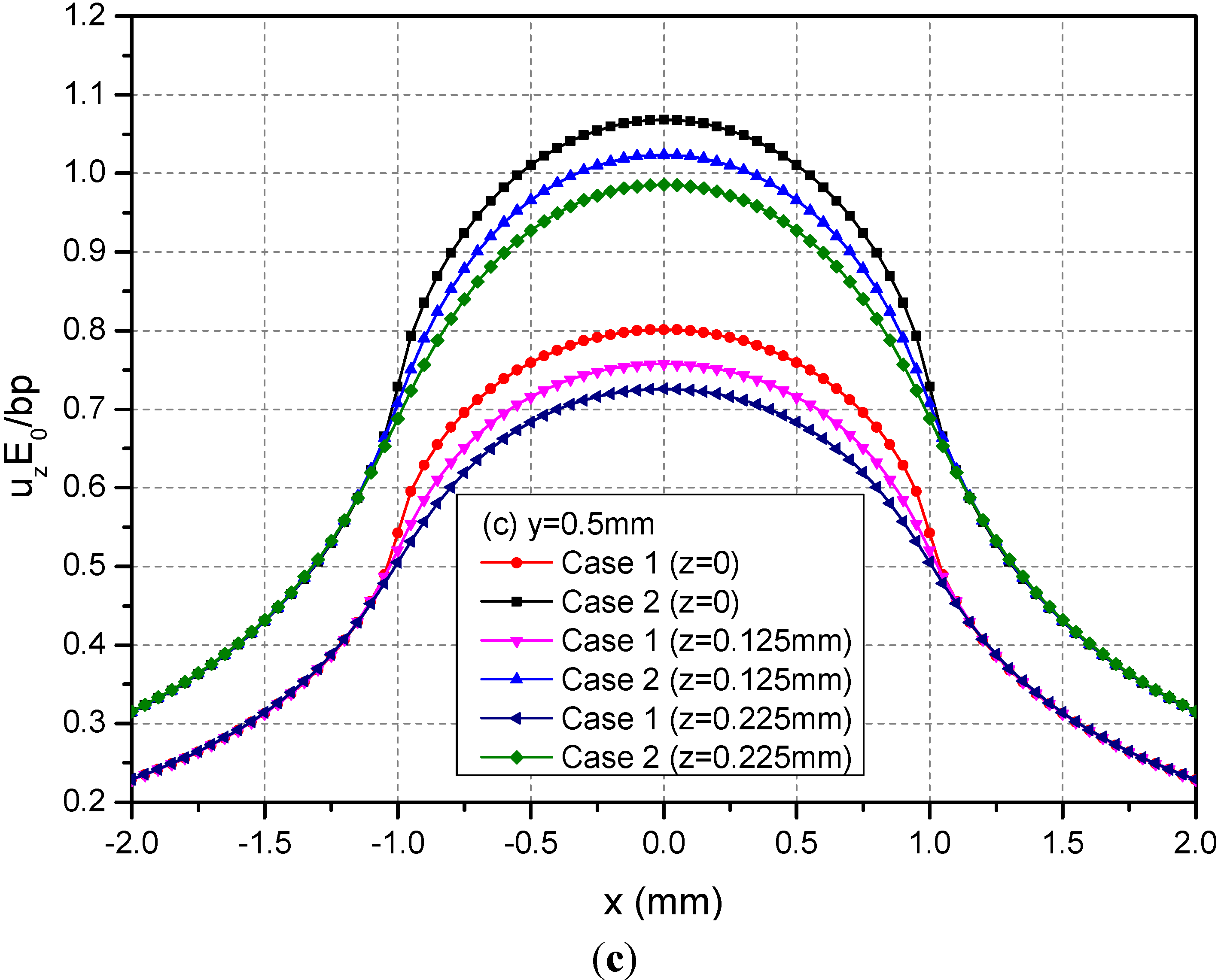
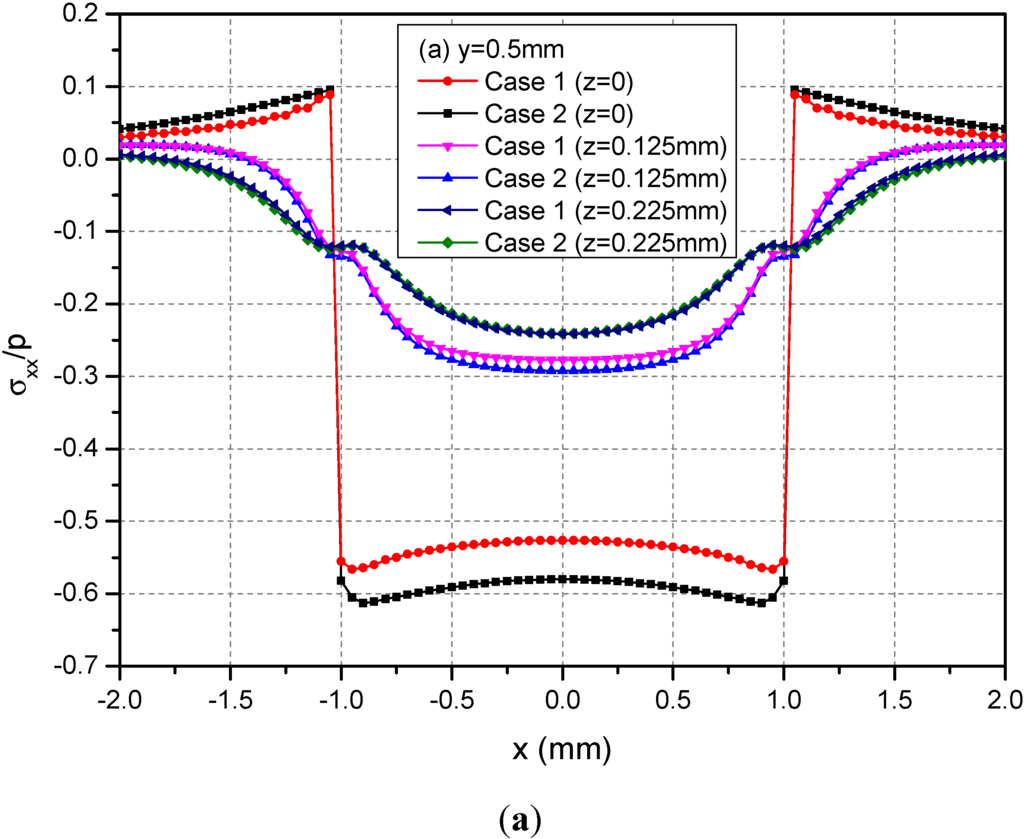
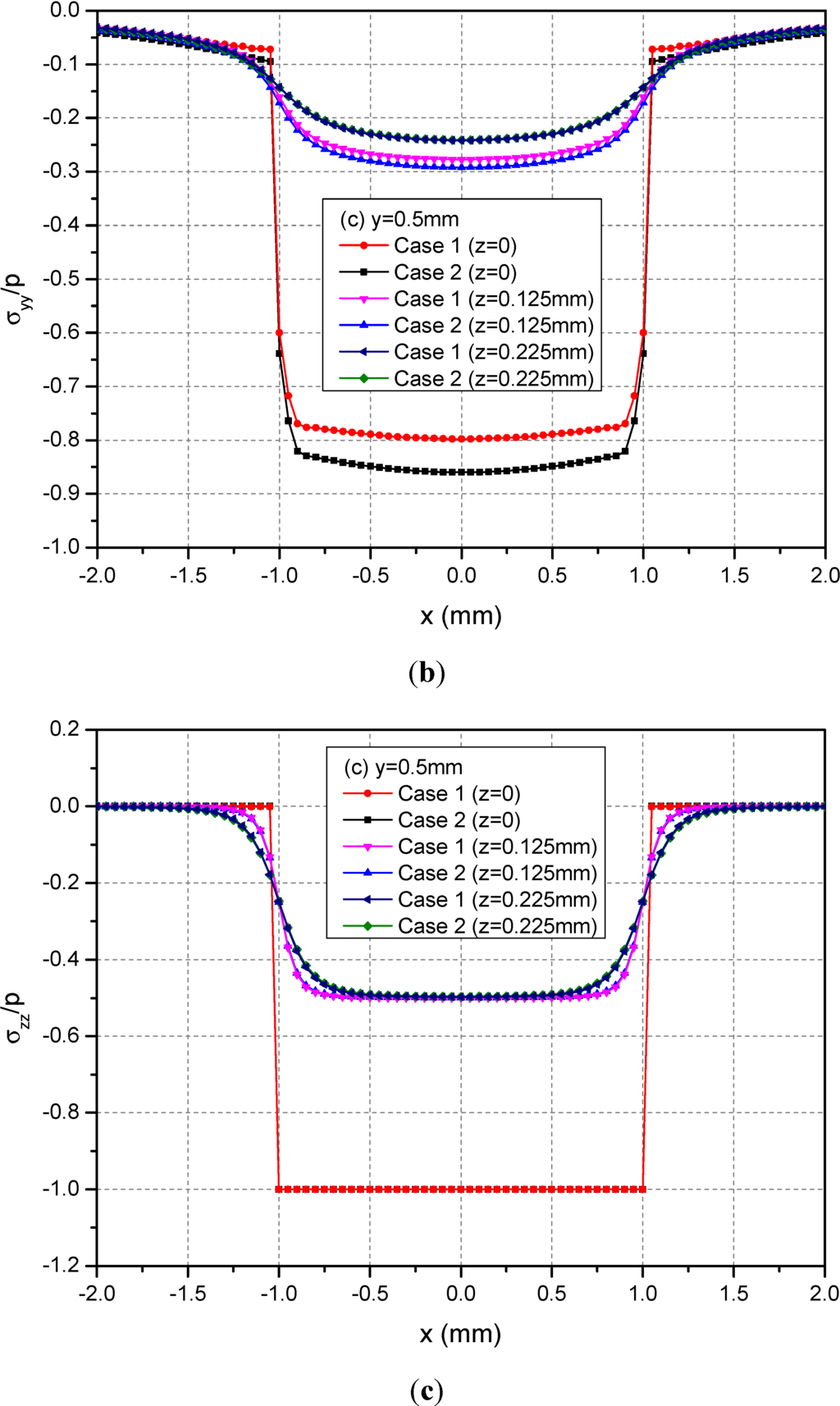
Figure 5.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
Figure 5.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
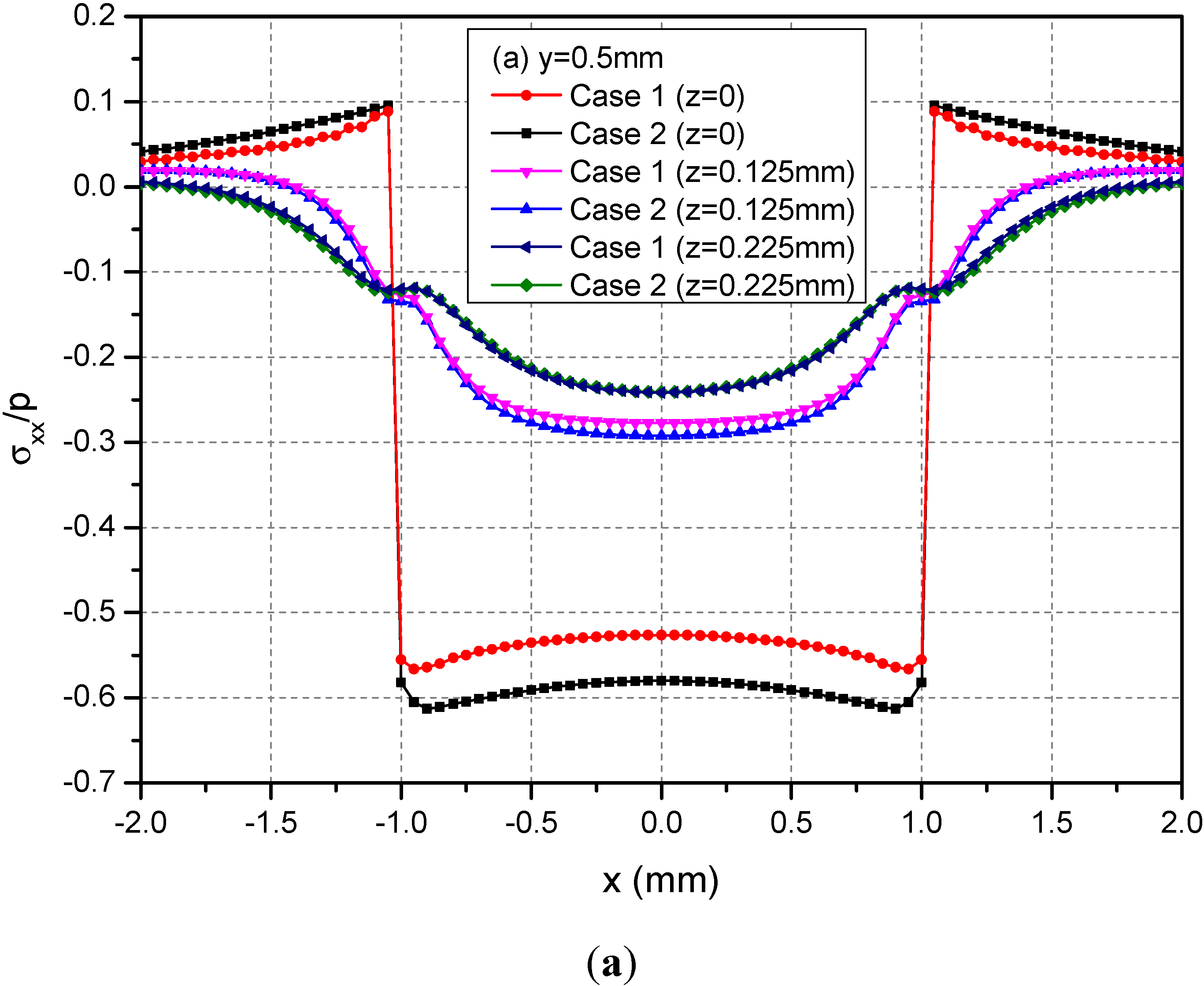
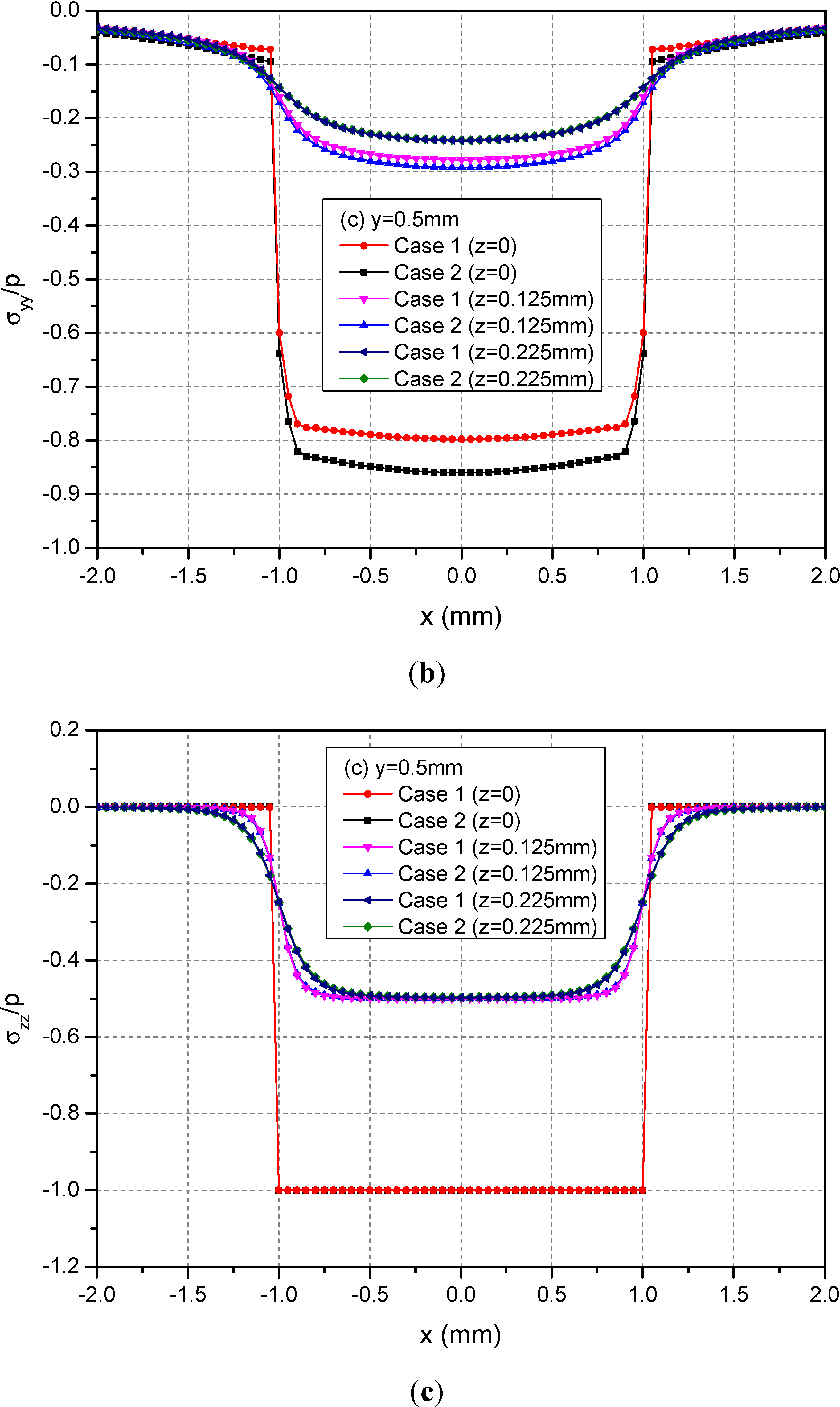
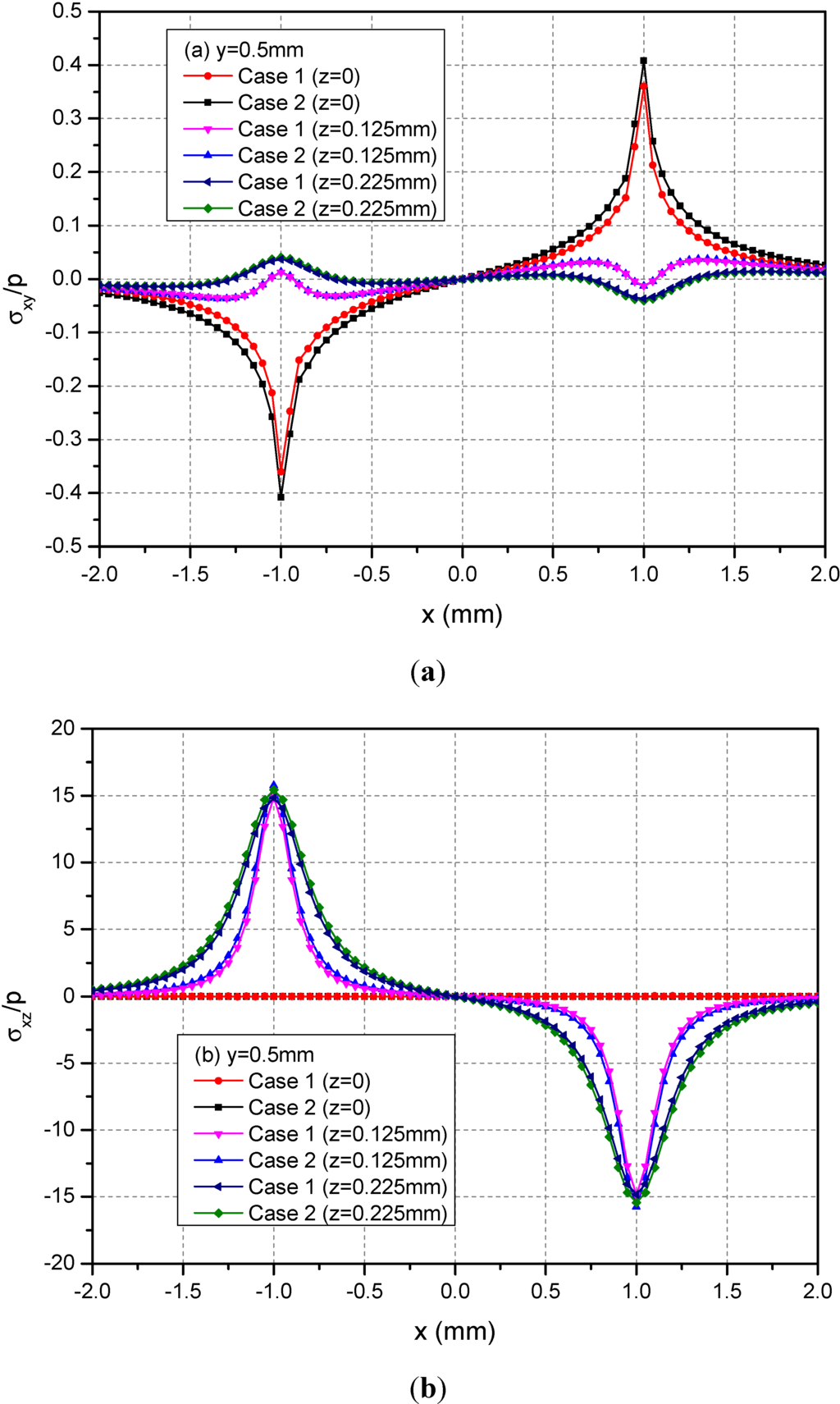
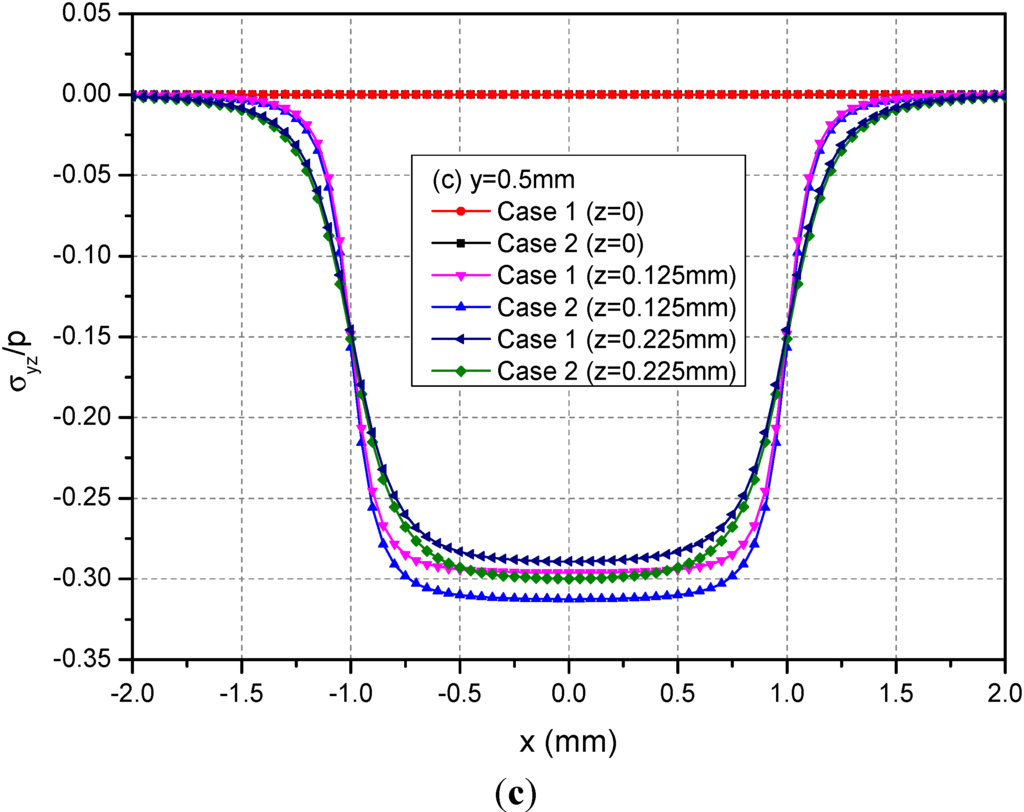
Figure 6.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
Figure 6.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.125, 0.225 mm for the loading area h = 0 mm.
3.3. The Loading Area at h = 0.13 mm
The rectangular loading on the plane h = 0.13 mm is examined in this section. In this case, the loading is applied within the FGMs of semi-infinite extent. Figure 7 shows the variations of normalized displacements along y = 0.5 mm for the depths z = 0, 0.13 and 0.225 mm. It can be observed that the absolute values of the three displacements at a given depth for Case 1 are smaller than those of the corresponding displacements for Case 2. The phenomenon is more obvious in the neighborhood of x = ±1.0 mm for ux and among −1.0 mm ≤ x ≤ 1.0 mm for uy and uz.
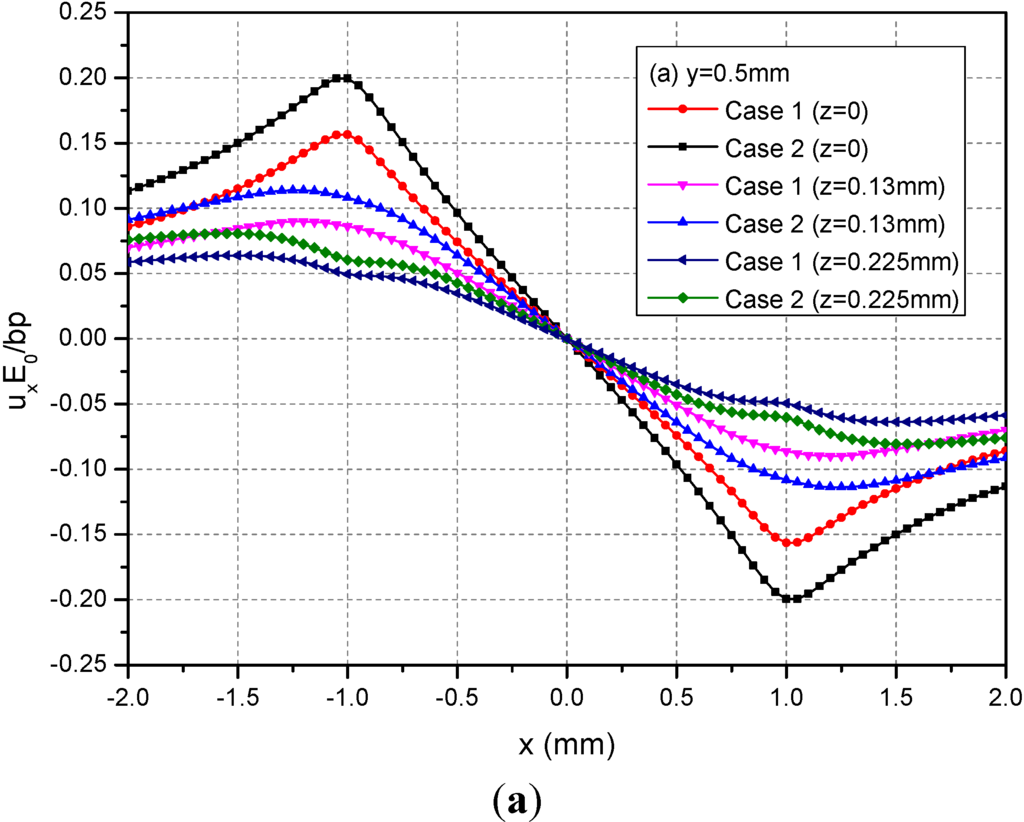
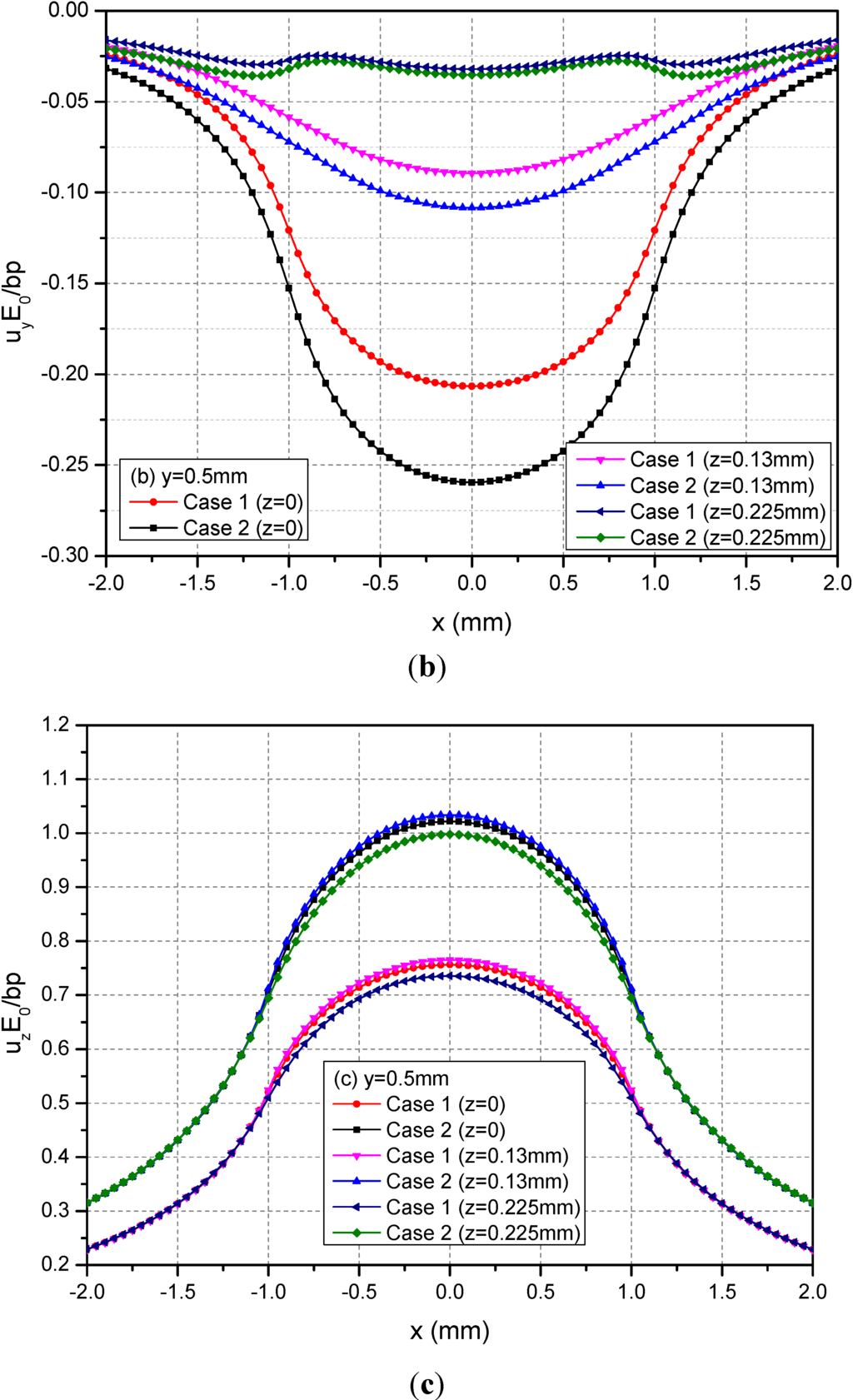
Figure 7.
Normalized displacements (a) ux; (b) uy; (c) uz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
Figure 7.
Normalized displacements (a) ux; (b) uy; (c) uz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
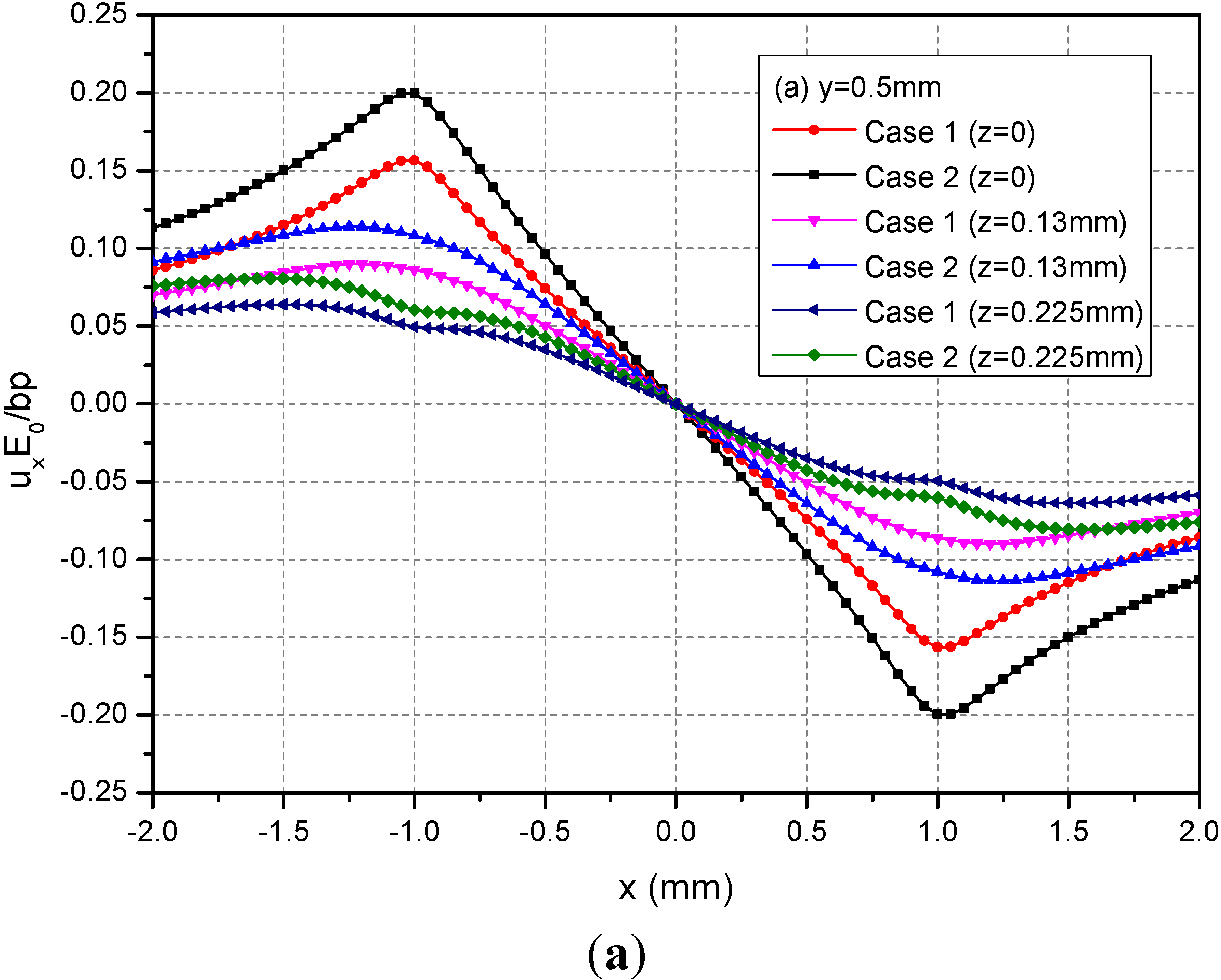
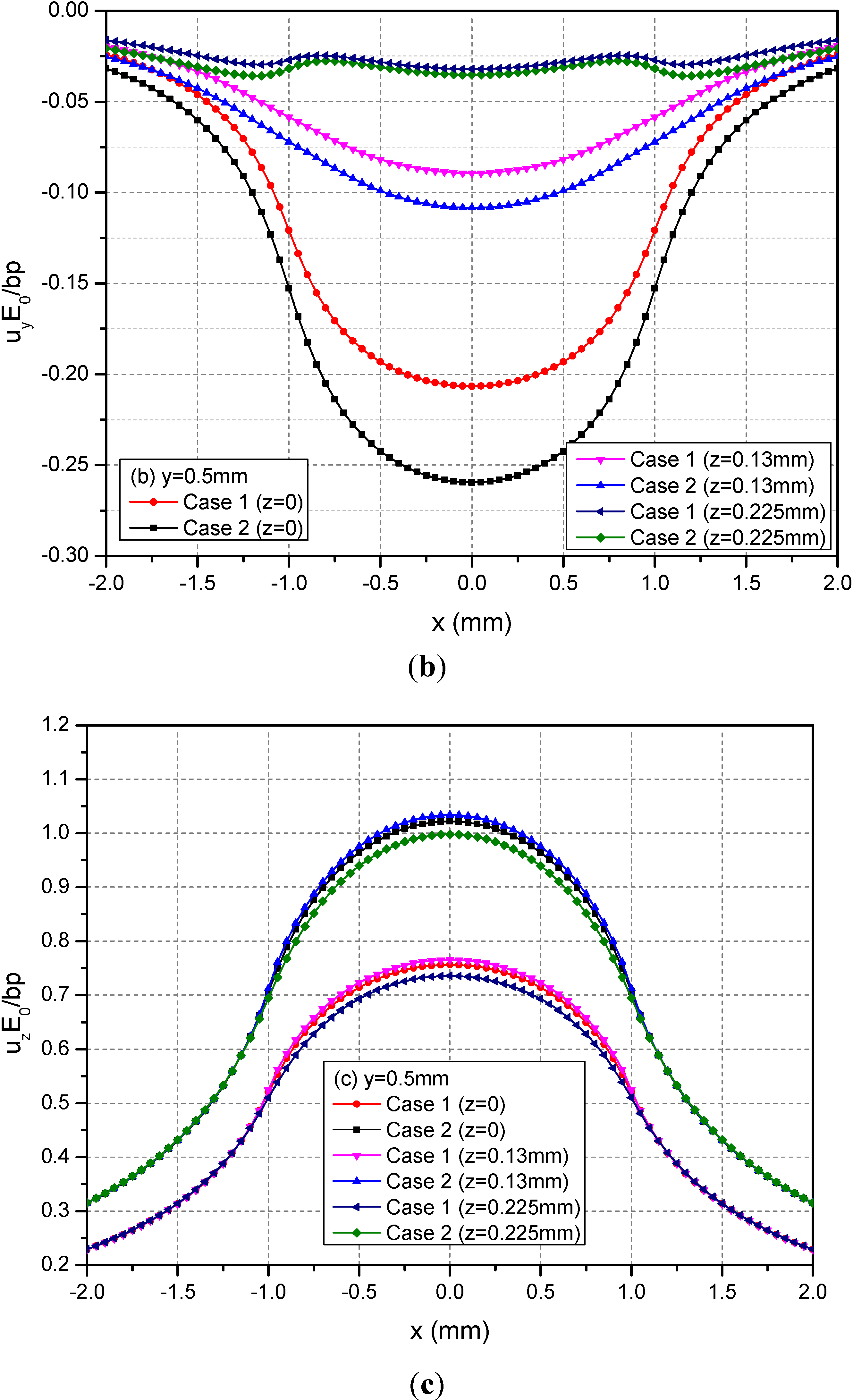
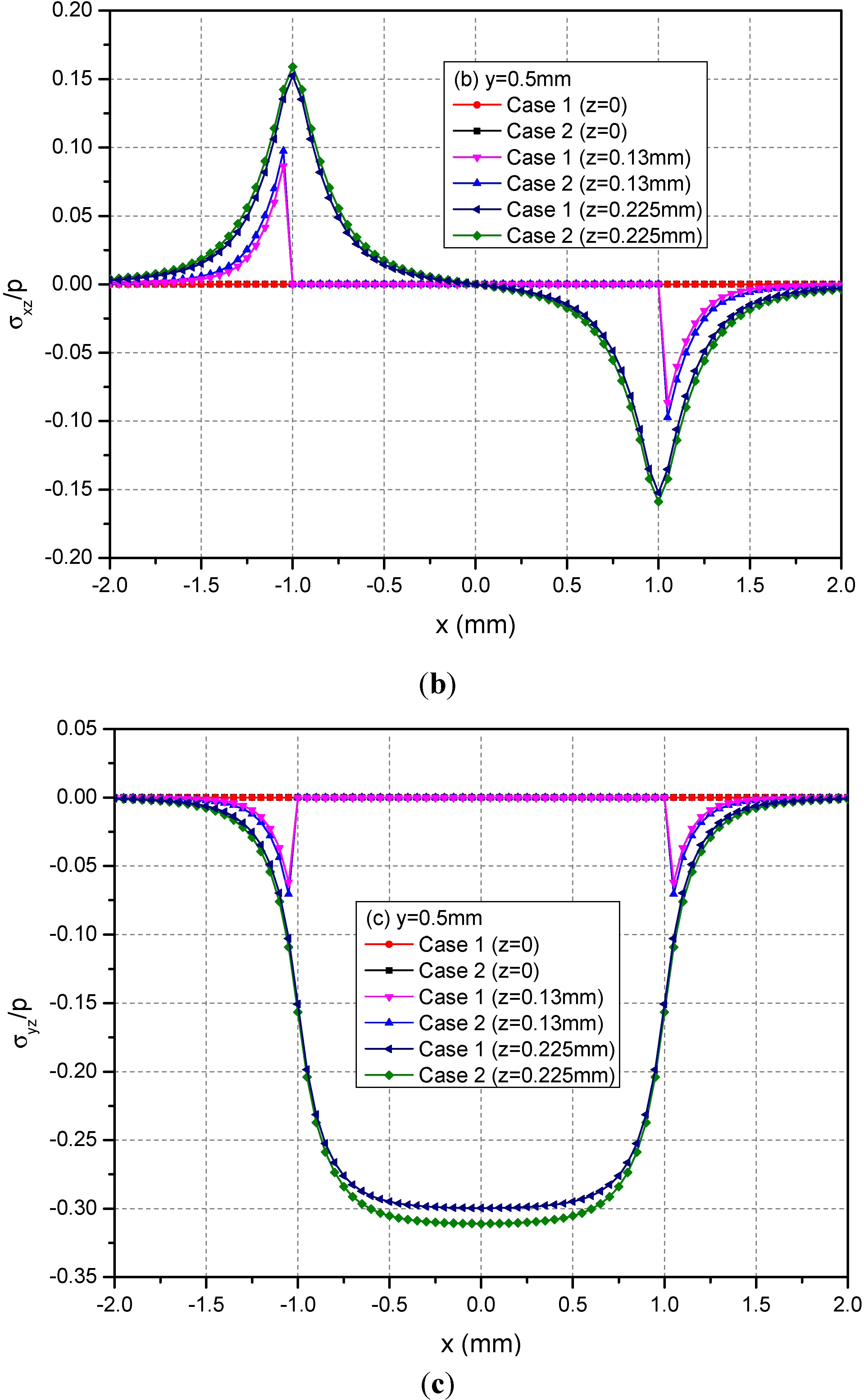
Figure 8 shows the variations of the three normalized normal stresses along y = 0.5 mm at the depths z = 0, 0.13 and 0.225 mm. It can be found that the normal stresses σxx and σyy for Cases 1 and 2 have obvious differences for −1.0 mm ≤ x ≤ 1.0 mm at the depths z = 0 mm and 0.13 mm while the stresses has negligible differences at z = 0.225 mm. However, the values of σzz at any depths for Cases 1 and 2 have no obvious differences. Figure 9 shows the variations of the three normalized shear stresses along y = 0.5 mm for different depths z = 0, 0.13 and 0.225 mm. It can be found that there are small differences between Cases 1 and 2 except the shear stress σxy. The σxy values have large differences between Cases 1 and 2.
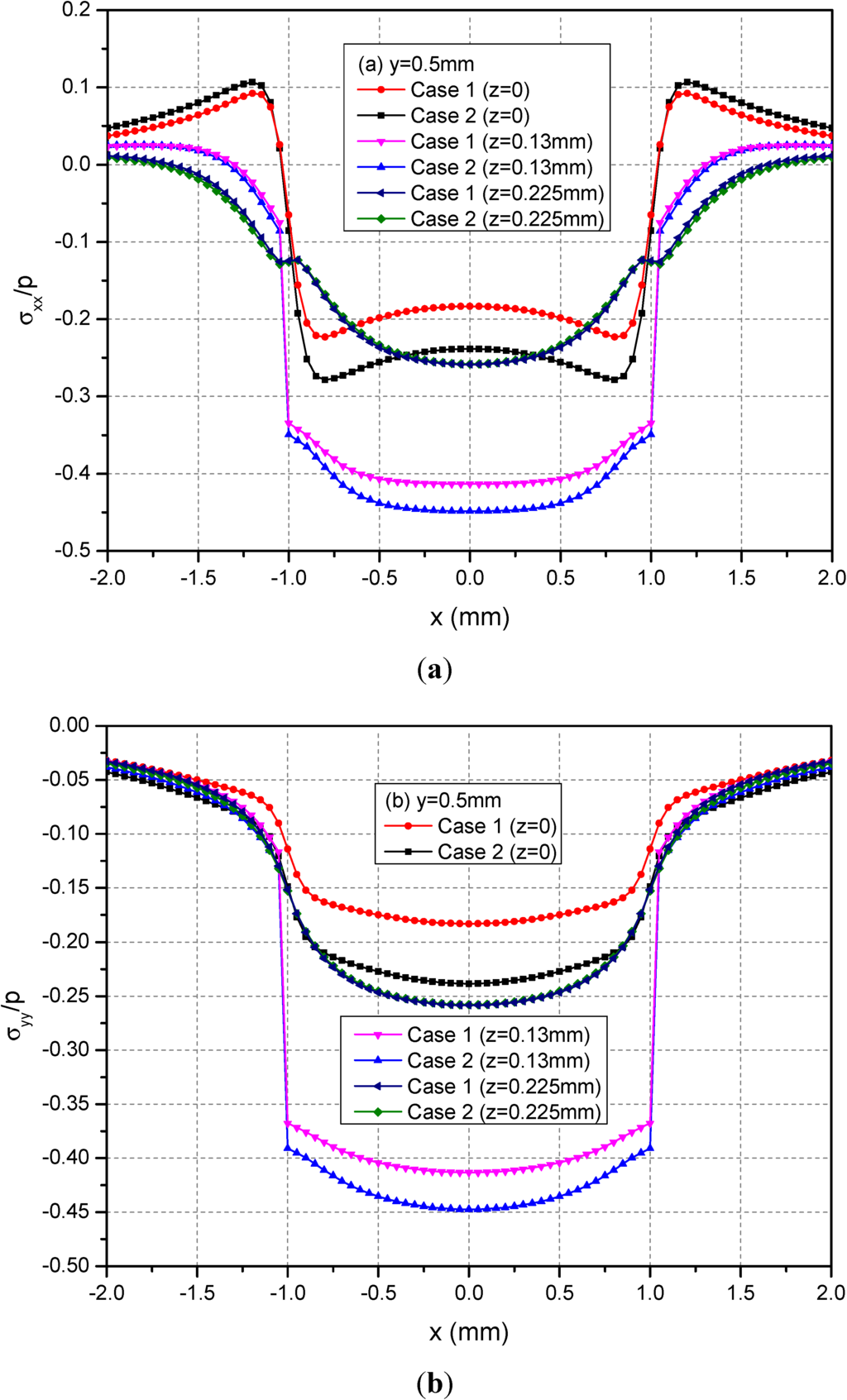
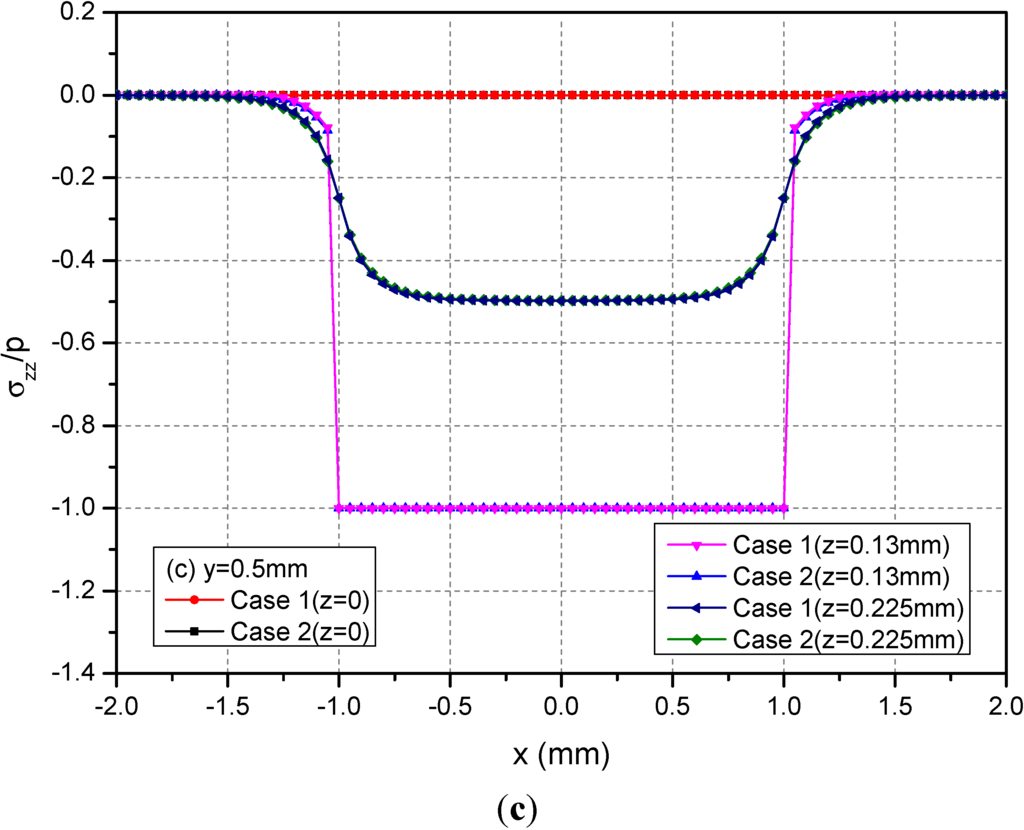
Figure 8.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
Figure 8.
Normalized stresses (a) σxx; (b) σyy; (c) σzz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
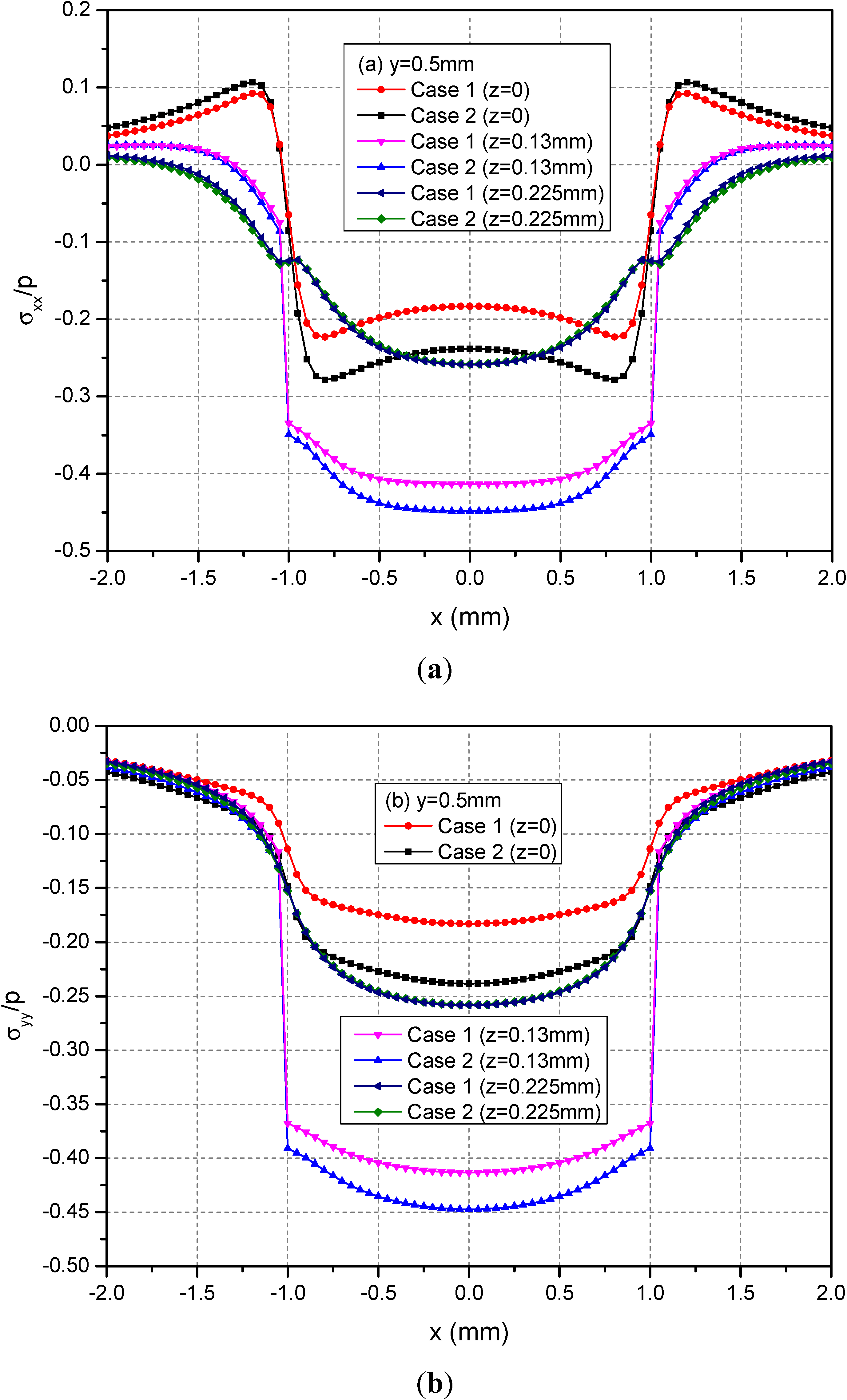
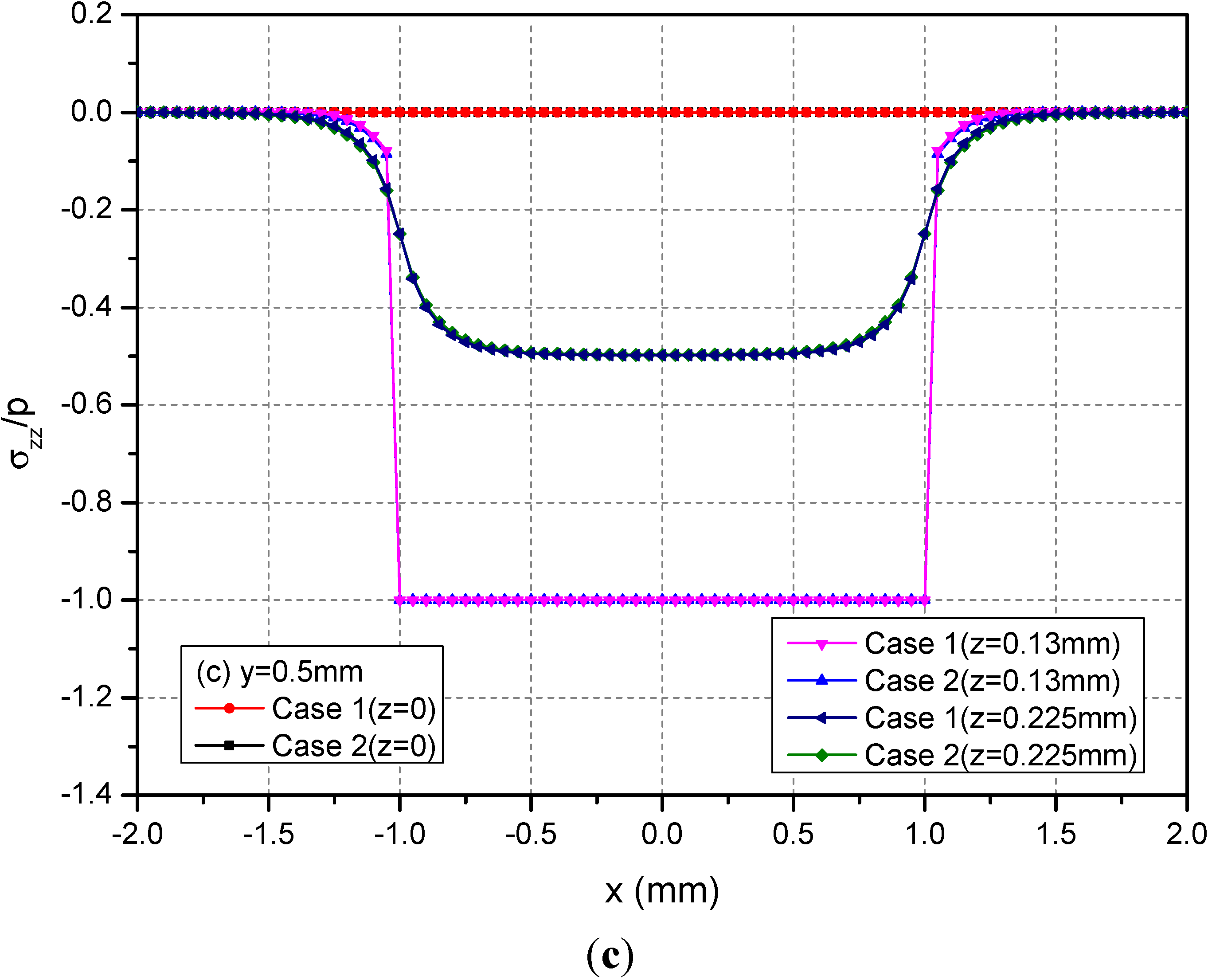
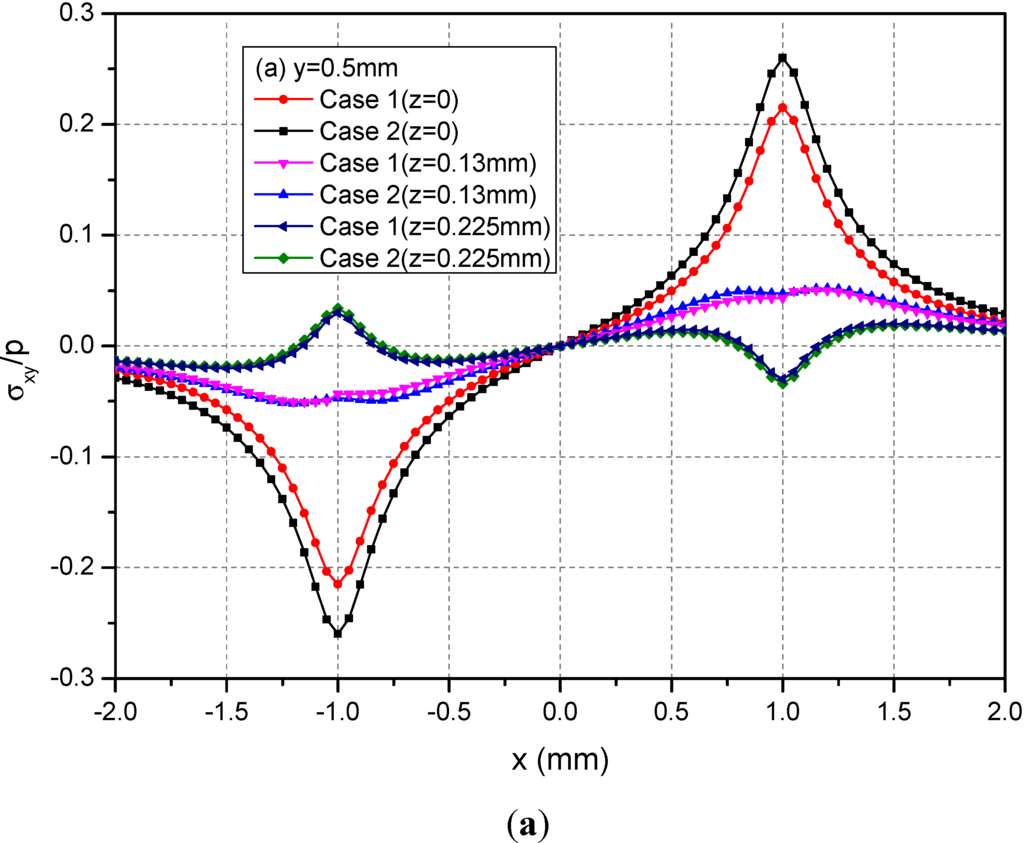
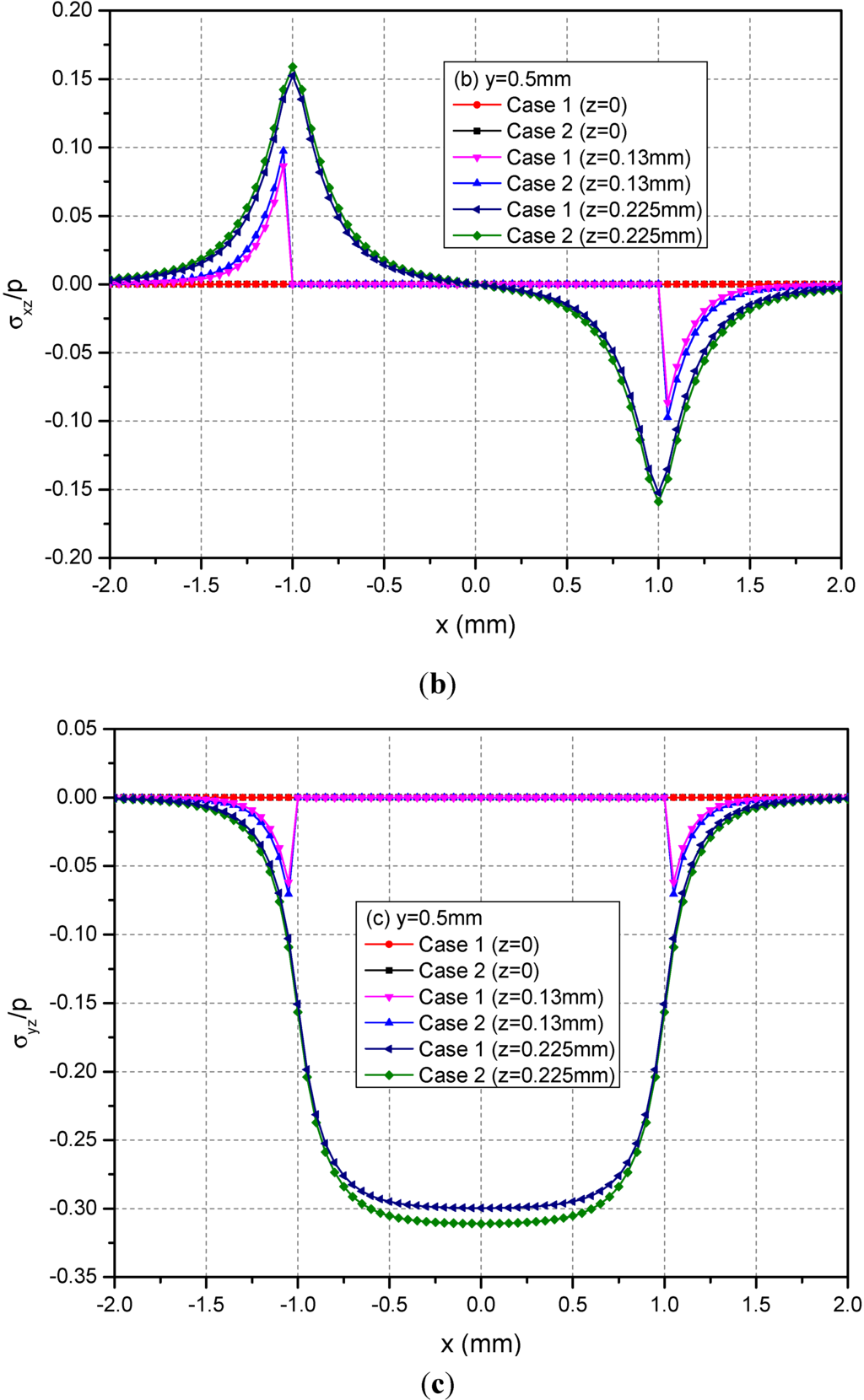
Figure 9.
Normalized stresses (a) σxy; (b) σxz; (c) σyz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
Figure 9.
Normalized stresses (a) σxy; (b) σxz; (c) σyz along y = 0.5 mm at z = 0, 0.13, 0.225 mm for the loading area h = 0.13 mm.
3.4. Comparison of Elastic Fields for the Two Loading Positions
Among the displacement components, the uz values for h = 0.13 mm are smaller than the ones for h = 0 mm. This is because the materials above the loading plane h = 0.13 mm constrain the deformation of the FGMs. However, ux and uy have small differences for two loading positions.
For two loading positions, σxx, σyy and σzz are the maximums at loading plane positions h = 0 mm and h = 0.13 mm, respectively. Away from the loading plane positions, the values of these stress components become small. For the two loading positions, the absolute values of σxy are the maximums at z = 0 mm, i.e., the boundary of semi-infinite extent. At x = ±1.0 mm, σxz = 0 and σyz = 0 for the loading position h = 0 mm while σxz and σyz has a jump for the loading position h = 0.13 mm.
4. Conclusions
This paper has analyzed the stress and displacement fields in a functionally graded material of semi-infinite extent induced by rectangular loading. The FGM can have their elastic properties exhibiting the variation in depth while keeping constant in lateral directions. This paper has examined the theoretical stress and displacement fields in the Si3N4-based ceramics due to the rectangular loading. The displacements and stresses are presented and compared to those of a homogeneous elastic solid of semi-infinite extent. It was found that the heterogeneity of FGM has an evident influence on the elastic fields of the semi-infinite elastic solids. This capability to exactly calculate the complete elastic field induced in FGM is important to the understanding of the FGM mechanical behavior and in the design of FGM properties with depth.
Acknowledgements
The authors would like to thank the financial supports from the Committee on Research and Conference Grants of The University of Hong Kong and the National Natural Science Foundation of China (Grant Nos. 51079081 and 41172242).
References
- Gibson, R.E. Some results concerning displacements and stresses in a non-homogeneous elastic half space. Geotechnique 1967, 17, 58–67. [Google Scholar] [CrossRef]
- Booker, J.R.; Balaam, N.P.; Davis, E.H. The behavior of an elastic non-homogeneous half-space. Part I—Line and point load. Int. J. Numer. Anal. Meth. Geomech. 1985, 9, 353–367. [Google Scholar] [CrossRef]
- Oner, M. Vertical and horizontal deformation of an inhomogeneous elastic half-space. Int. J. Numer. Anal. Meth. Geomech. 1990, 14, 613–629. [Google Scholar] [CrossRef]
- Butter, W.G.; Paulino, G.H.; Song, S.H. Application of gradient finite elements for asphalt pavements. J. Eng. Mech. 2006, 132, 240–249. [Google Scholar] [CrossRef]
- Kassir, M.K. Boussineq problems for a non-homogeneous solid. J. Eng. Mech. 1972, 98, 457–470. [Google Scholar]
- Giannakopoulos, A.E.; Suresh, S. Indentation of solids with gradients in elastic properties: Part I. point force. Int. J. Solids Struct. 1997, 34, 2357–2392. [Google Scholar] [CrossRef]
- Suresh, S. Graded materials for resistance to contact deformation and damage. Science 2001, 292, 2447–2451. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.G.; Pan, E.; Green, R. Surface loading of a multilayered viscoelastic pavement: Semianalytical solution. J. Eng. Mech. 2009, 135, 517–528. [Google Scholar] [CrossRef]
- Delale, F.; Erdogan, F. The crack problem for a nonhomogeneous plane. J. Appl. Mech. 1983, 50, 609–614. [Google Scholar] [CrossRef]
- Chan, Y.S.; Gray, L.J.; Kaplan, T.; Paulino, G.H. Green’s function for a two-dimensional exponentially graded elastic medium. Proc. R. Soc. 2004, 460, 1689–1706. [Google Scholar] [CrossRef]
- Martin, P.A.; Richardson, J.D.; Gray, L.J.; Berger, J.R. On Green’s function for a three-dimensional exponentially-graded elastic solid. Proc. R. Soc. 2002, A458, 1931–1947. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Carrera, E. Evaluation of layer-wise mixed theories for laminated plates analysis. AIAA J. 1998, 26, 830–839. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Robaldo, A. Variable kinematic model for the analysis of functionally graded material plates. AIAA J. 2008, 46, 194–203. [Google Scholar] [CrossRef]
- Cinefra, M.; Belouettar, S.; Soave, M.; Carrera, E. Variable kinematic models applied to free vibration analysis of functionally graded materials shells. Eur. J. Mech. A 2010, 29, 1078–1087. [Google Scholar] [CrossRef]
- Xiao, H.T.; Yue, Z.Q. A generalized Kelvin solution based BEM for contact problems of elastic indenter on functionally graded materials. CMES Comput. Model. Eng. Sci. 2009, 52, 159–179. [Google Scholar]
- Xiao, H.T.; Yue, Z.Q. Elastic fields in two joined transversely isotropic media if infinite extent as a result of rectangular loading. Int. J. Numer. Analy. Meth. Geomech. 2011. [Google Scholar] [CrossRef]
- Pender, D.C.; Padture, N.P.; Giannakopoulos, A.E. Gradients in elastic modulus for improved contact-damage resistance: Part I. Acta Mater. 2001, 49, 3255–3262. [Google Scholar] [CrossRef]
- Yue, Z.Q. On generalized Kelvin solutions in a multilayered elastic medium. J. Elast. 1995, 40, 1–43. [Google Scholar] [CrossRef]
- Xiao, H.T.; Yue, Z.Q.; Zhao, X.M. A generalized Kelvin solution based method for analyzing elastic fields in heterogeneous rocks due to reservoir water impoundment. Comput. Geosci. 2011, in press. [Google Scholar]
- Yue, Z.Q.; Svec, O.J. Effects of tire-pavement contact pressure distributions on the response of asphalts concrete pavements. Can. J. Civ. Eng. 1995, 22, 849–860. [Google Scholar] [CrossRef]
- Lankford, J. Comparative study of the temperature dependence of hardness and compressive strength in ceramics. J. Mater. Sci. 1983, 18, 1666–1674. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
