Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage †
Abstract
:1. Introduction
| Composition | Dielectric permittivity |
|---|---|
| BaTiO3 | 1,700 |
| PMN-PT (65/35) | 3,640 |
| PbNb2O6 | 225 |
| PLZT (7/60/40) | 2,590 |
| SiO2 | 3.9 |
| Al2O3 | 9 |
| Ta2O5 | 22 |
| TiO2 | 80 |
| SrTiO3 | 2,000 |
| ZrO2 | 25 |
| HfO2 | 25 |
| HfSiO4 | 11 |
| La2O3 | 30 |
| Y2O3 | 15 |
| α-LaAlO3 | 30 |
| CaCu3Ti4O12 | ~60,000 |
| La1.8Sr0.2NiO4 | ~100,000 |
| Polymer | Dielectric permittivity |
|---|---|
| Nonfluorinated aromatic polyimides | 3.2-3.6 |
| Fluorinated polyimide | 2.6-2.8 |
| Poly(phenyl quinoxaline) | 2.8 |
| Poly(arylene ether oxazole) | 2.6-2.8 |
| Poly(arylene ether) | 2.9 |
| Polyquinoline | 2.8 |
| Silsesquioxane | 2.8-3.0 |
| Poly(norborene) | 2.4 |
| Perfluorocyclobutane polyether | 2.4 |
| Fluorinated poly(arylene ether) | 2.7 |
| Polynaphthalene | 2.2 |
| Poly(tetrafluoroethylene) | 1.9 |
| Polystyrene | 2.6 |
| Poly(vinylidene fluoride-co-hexafluoropropylene) | ~12 |
| Poly(ether ketone ketone) | ~3.5 |
1.1. Dielectric Permittivity
1.1.1. Polymer Composite Dielectrics
1.1.2. Models for Effective Dielectric Constant
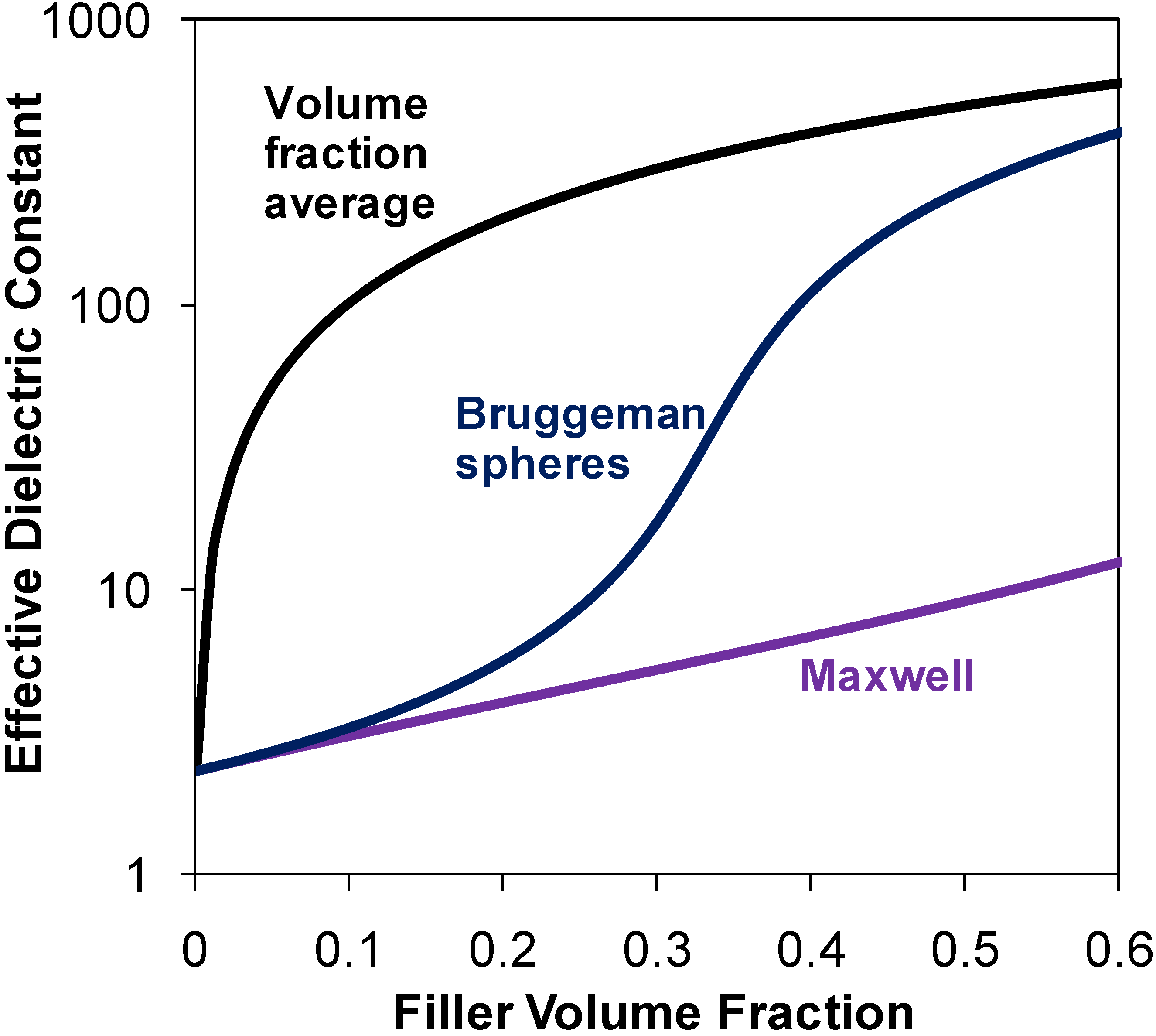
1.1.3. Nanocomposite Dielectric Concepts
1.2. Dielectric Breakdown
1.2.1. Breakdown Behavior of Polymers
| Polymer | Dielectric Strength (V/μm) |
|---|---|
| Polyethylene (LD) | 200 |
| Polyethylene (HD) | 200 |
| Polyethylene (XL) | 220 |
| Polypropylene (Biaxially oriented) | 200 |
| Polystyrene | 200 |
| Polytetrafluoroethylene | 88-176 |
| Poly(vinylidene fluoride) | 10.2 |
| Polycarbonate | 252 |
| Polyester | 300 |
| Polyimide | 280 |
| Epoxy resin | 25-45 |
1.2.2. Breakdown Behavior of Polymer Composites and Nanocomposites
1.2.3. Statistical Analysis of Breakdown Data
2. Inorganic Additives for Polymer Composite Dielectrics
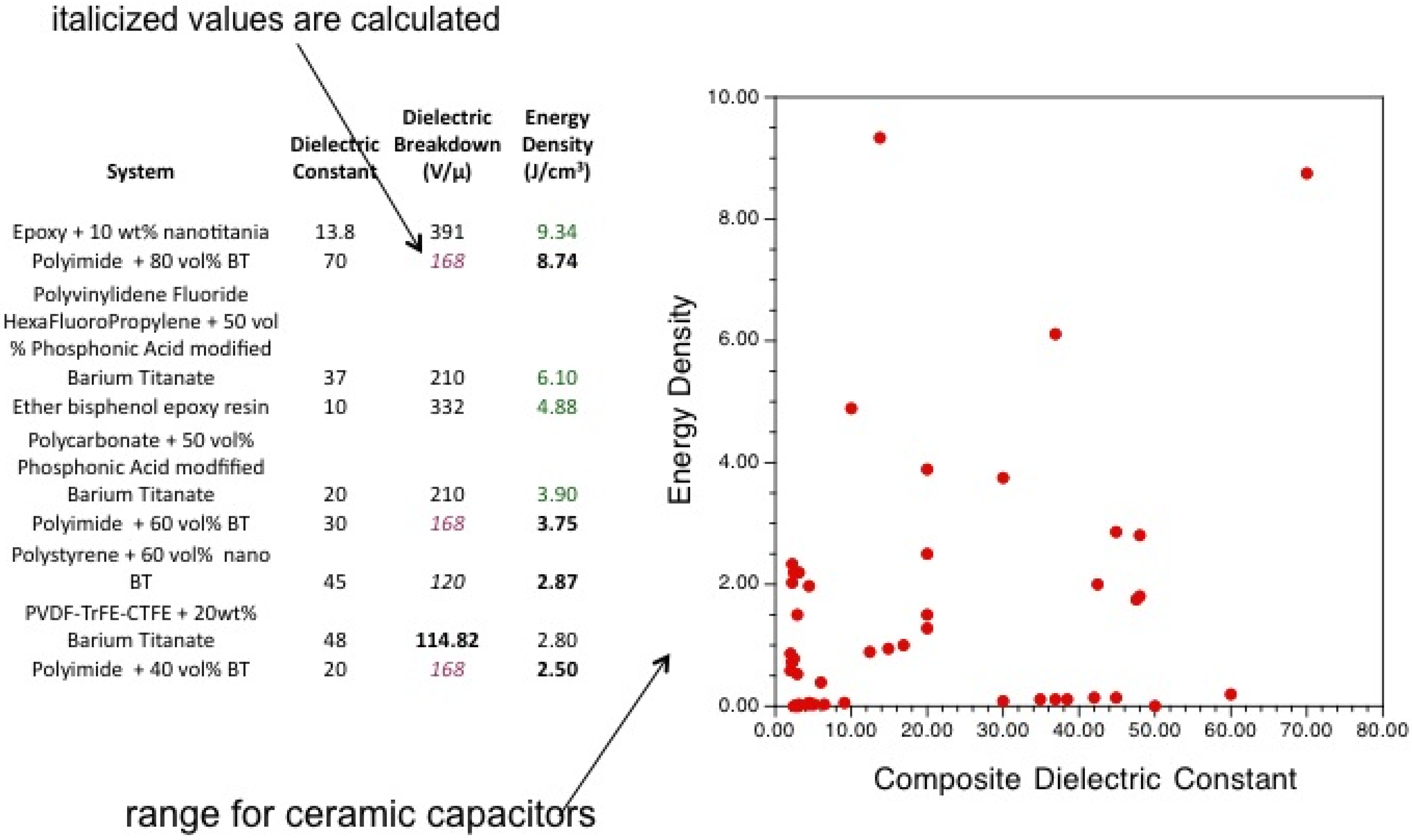
2.1. Barium Titanate (BaTiO3) Composites
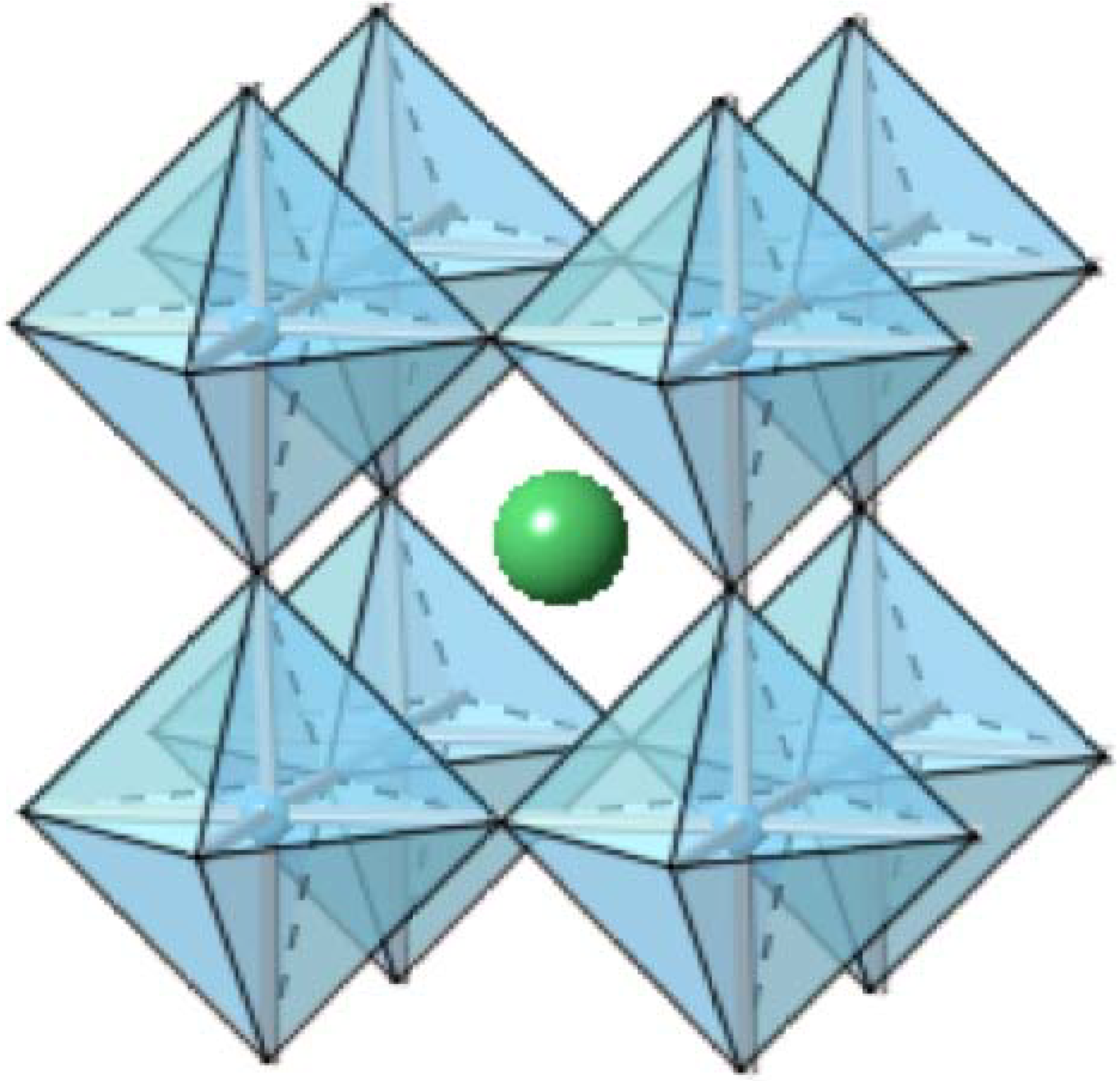
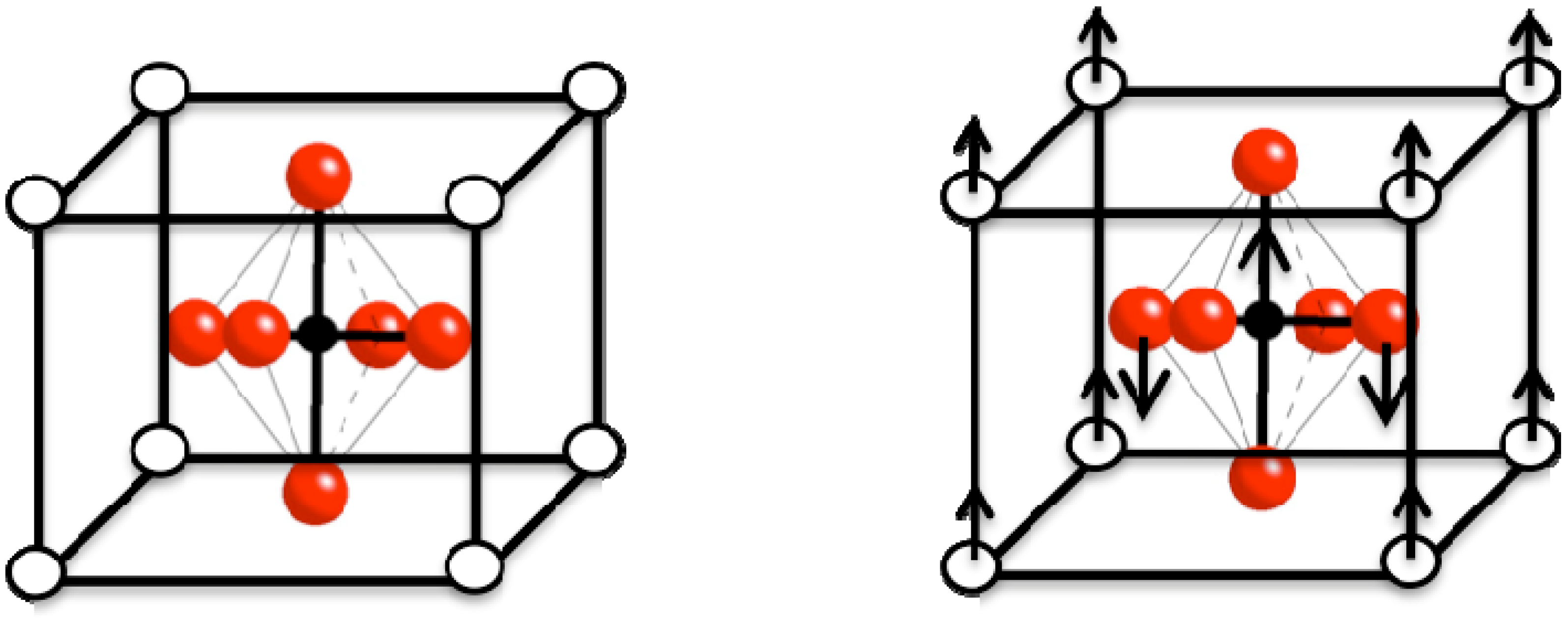
2.1.1. Barium Titanate (BaTiO3)
2.1.2. BT Polymer Composites
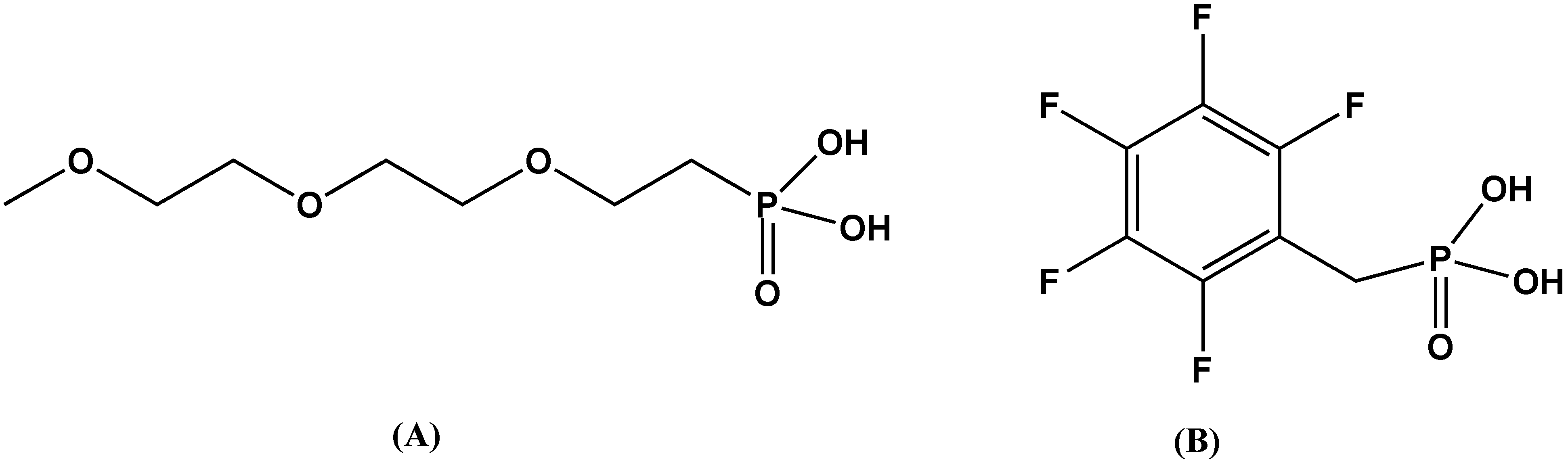

| 50 vol % PEGBA-BT in PC | 50 vol % PFBPA-BT in PVDF-HFP | |
|---|---|---|
| Film Thickness (μm) | 3.89 | 3.84 |
| Capacitance density (nF/cm) | 4.6 ± 0.6 | 8.6 ± 0.4 |
| Relative permittivity at 1kHz | 20 ± 2 | 37 ± 2 |
| Dielectric Loss at 1MHz | <0.01 | <0.07 |
| Leakage current density (nA/cm2) | 30 | 60 |
| Dielectric Strength (V/μm) | 210 ± 20 | 210 ± 50 |
| Max energy density (J/cm3) | 3.9 | 6.1 |
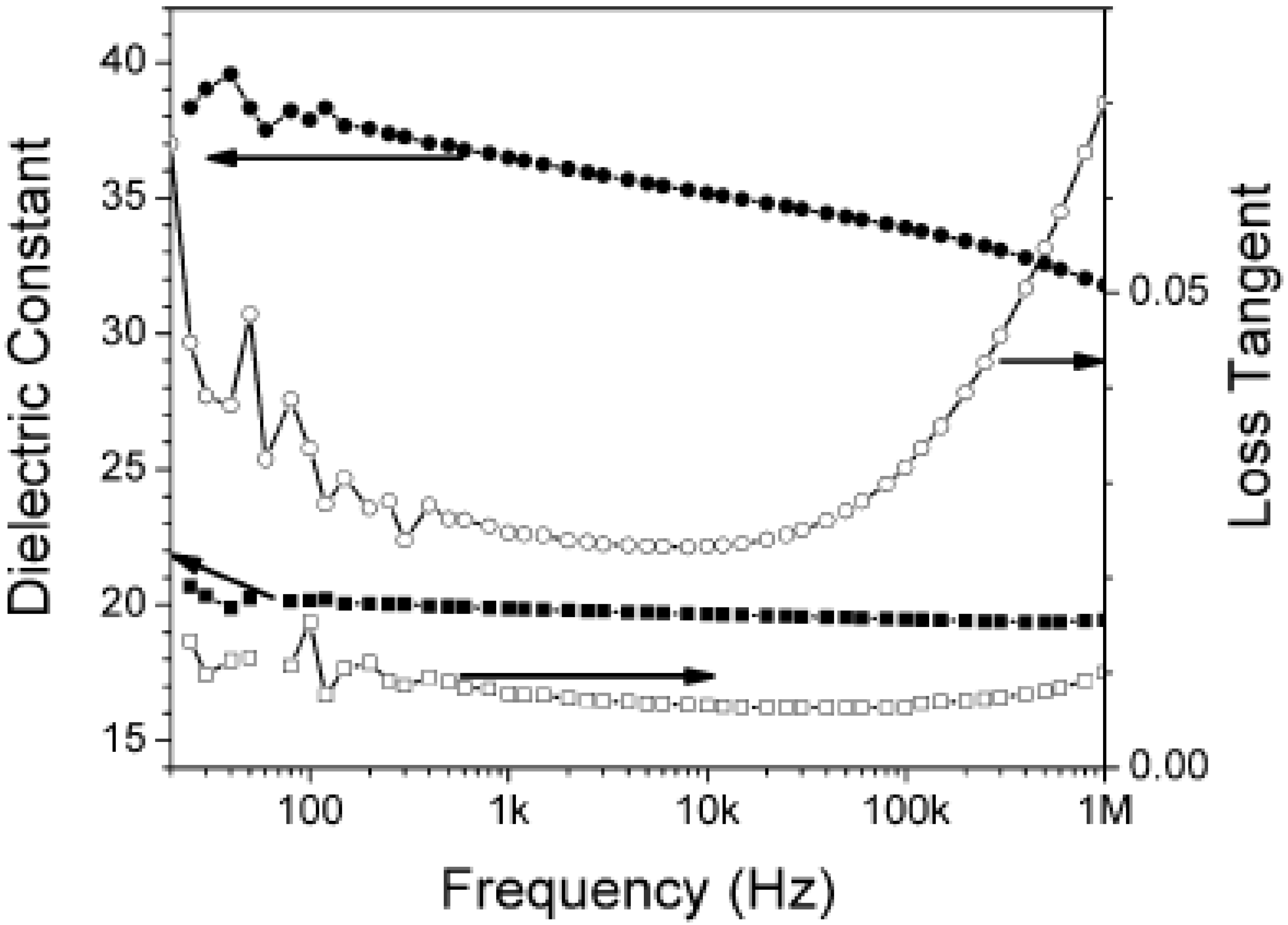
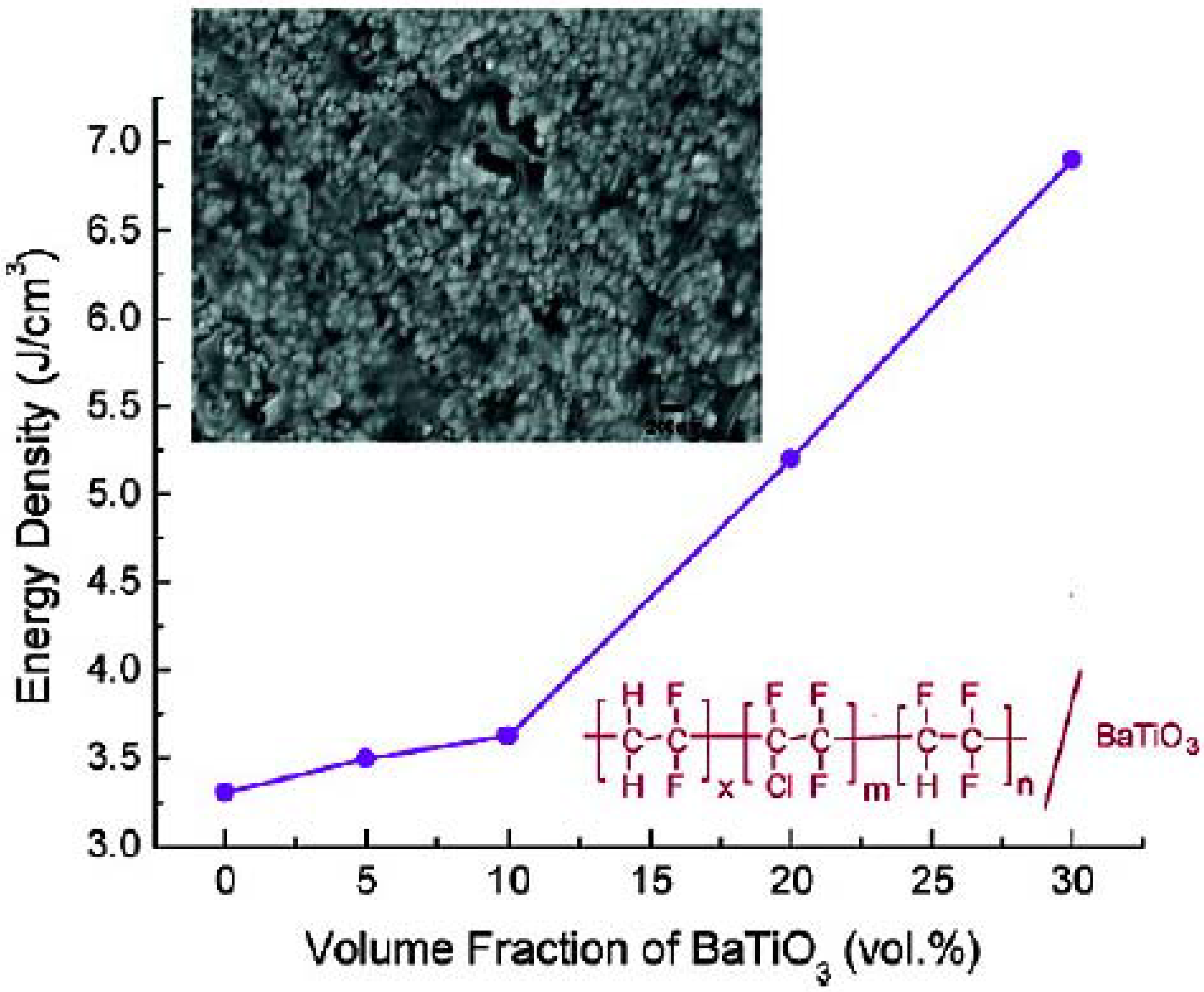
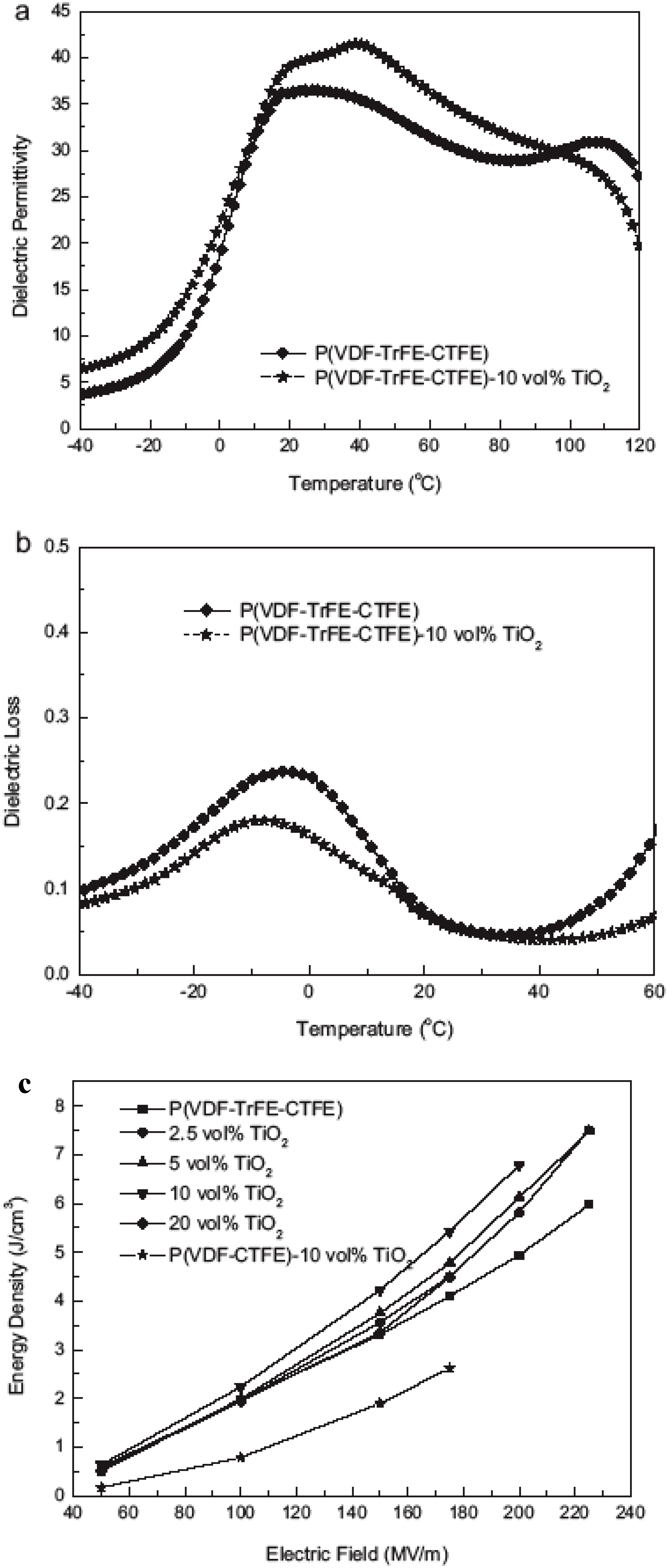
2.2. Titania (TiO2, TO) and TO Polymer Composites

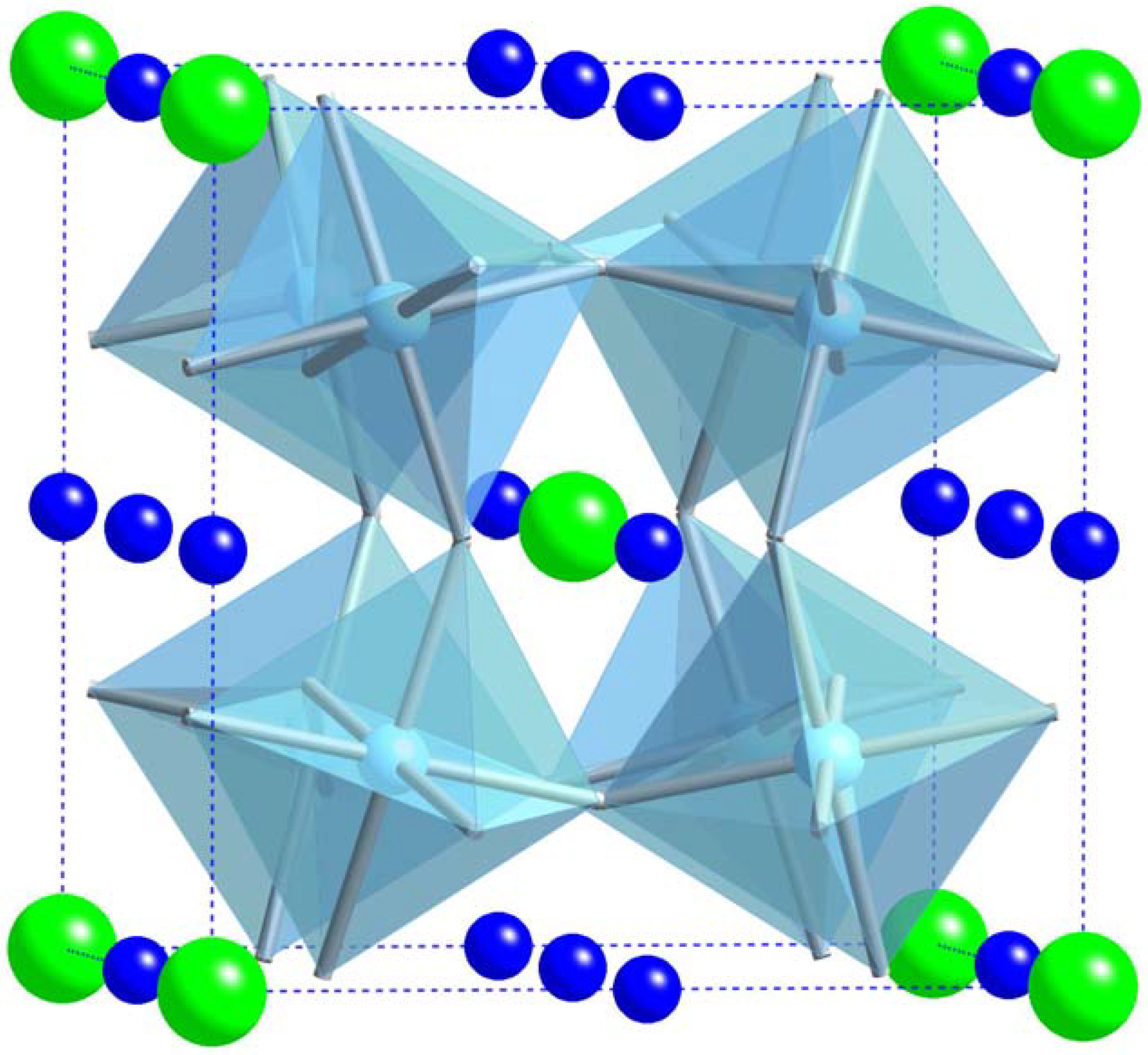
2.3. CaCu3Ti4O12 (CCTO) and CCTO Polymer Composites
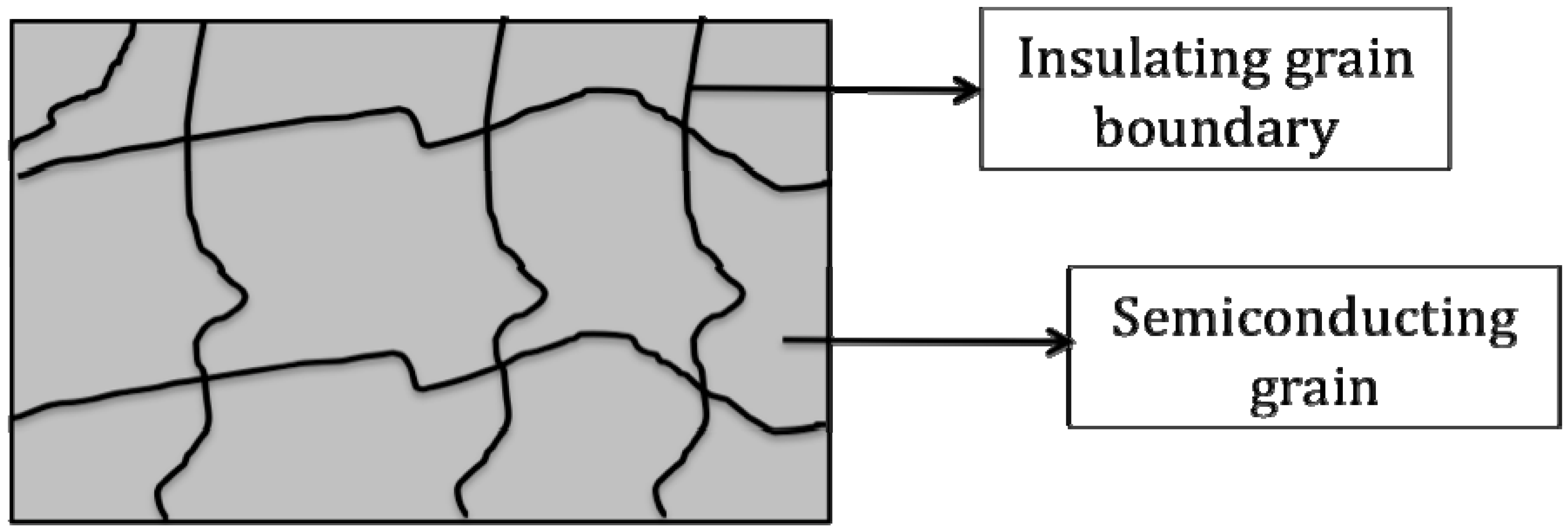
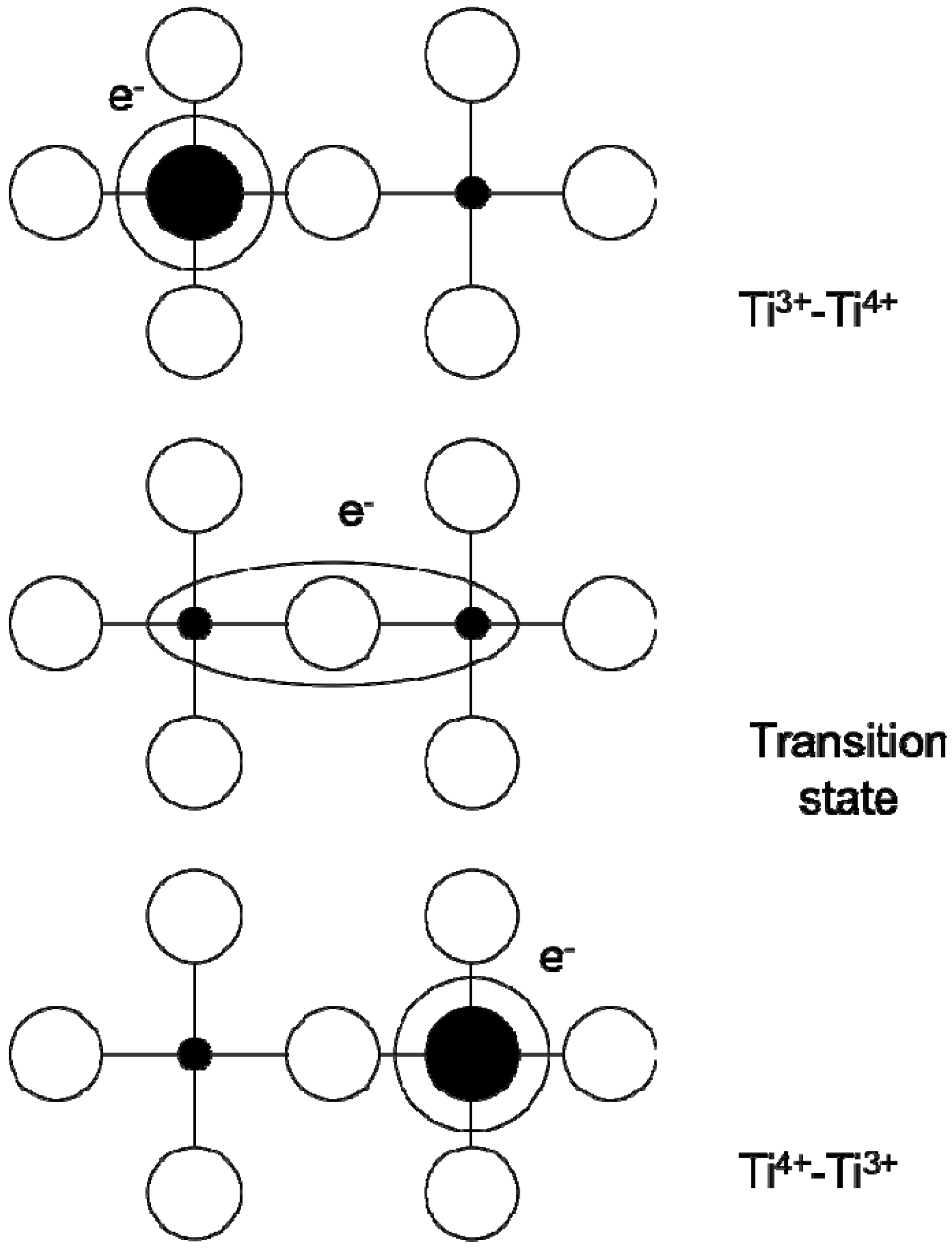
2.4. La2-xSrxNiO4 (LSNO) and LSNO Polymer Composites

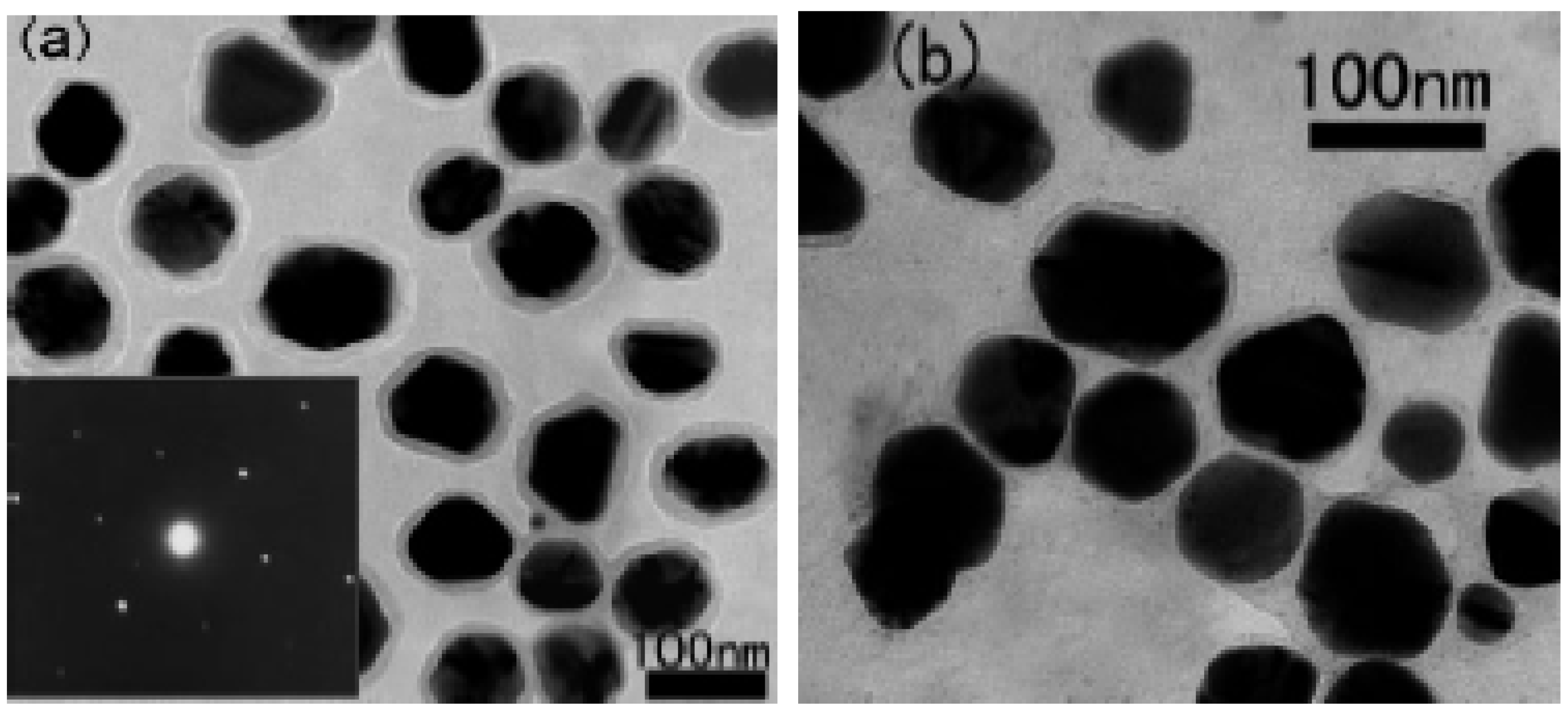
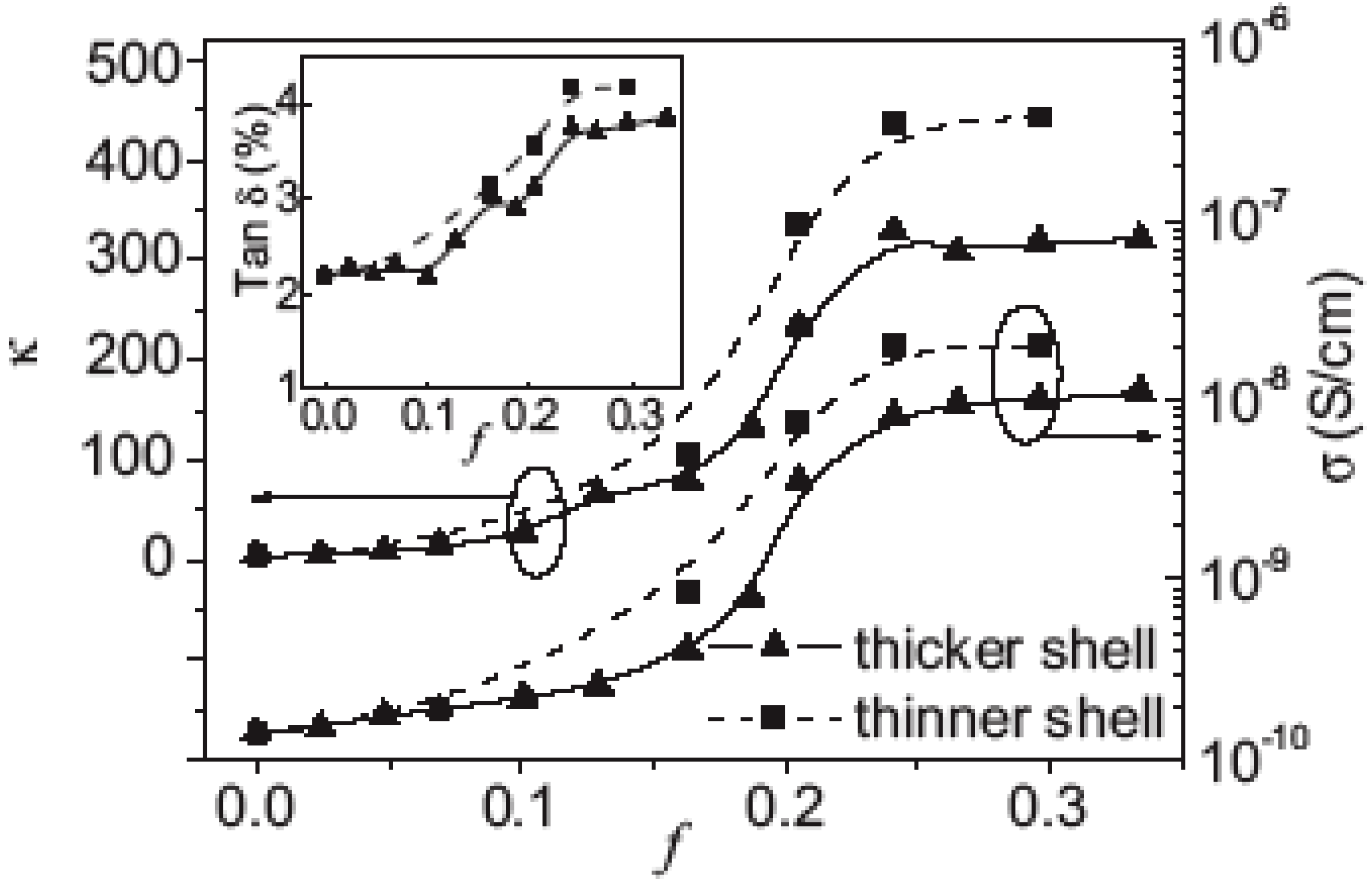
3. Core Shell Nanoparticles and Percolating Inter-Particle Barrier Layering
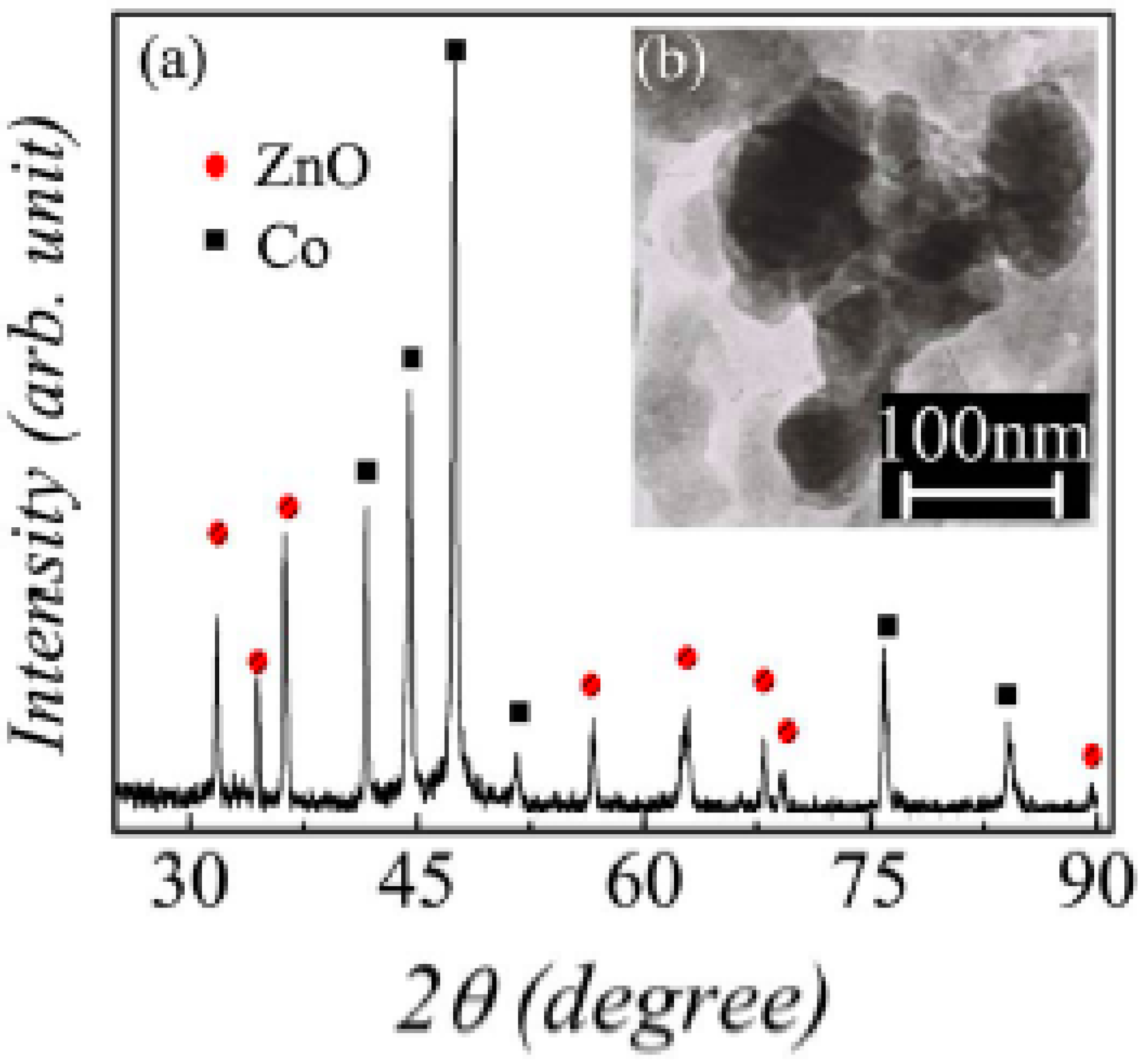
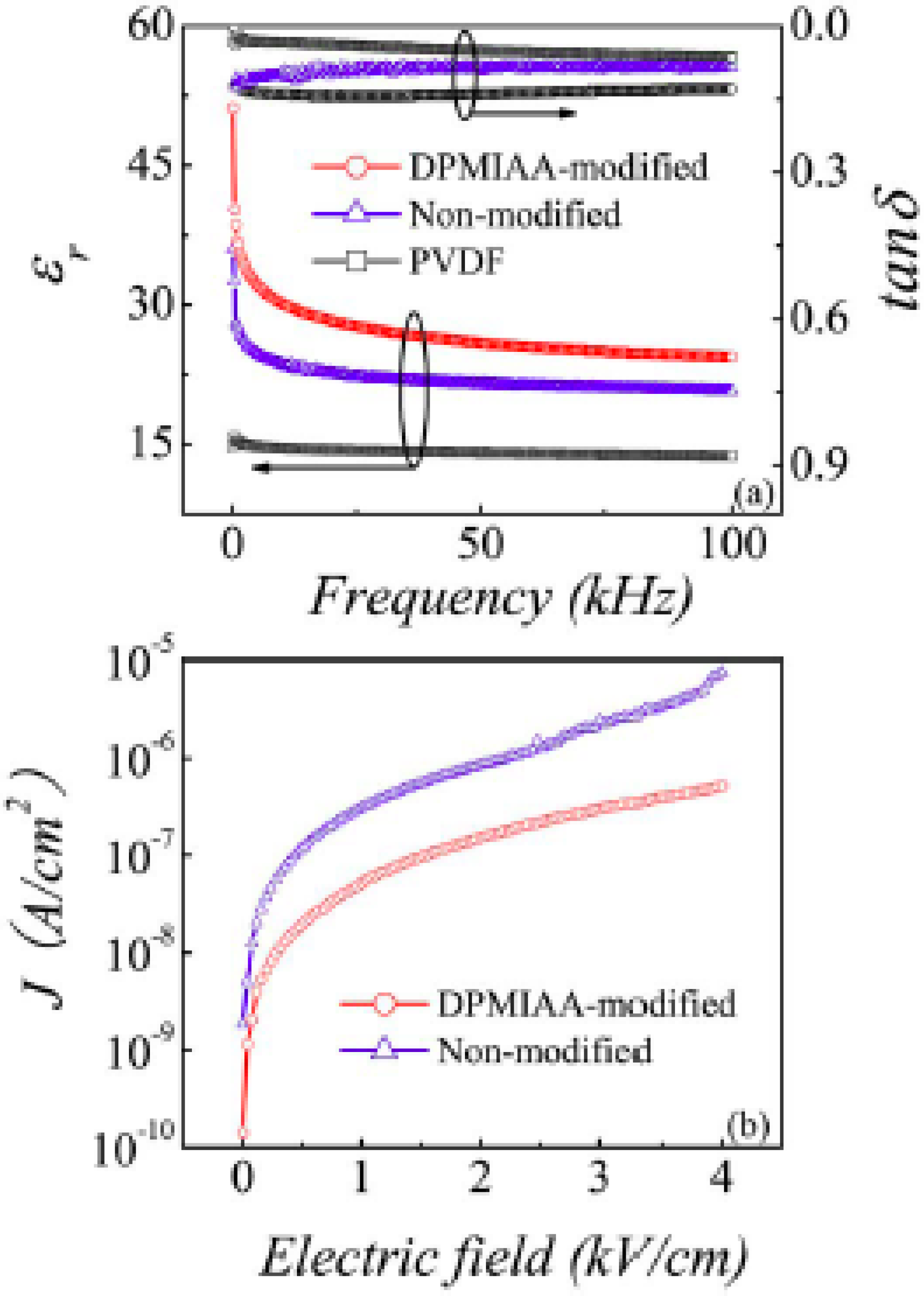
4. Non-Oxide Dielectric Materials: Mixed-Metal Phenyl Phosphonates

5. Conclusions
References
- Nalwa, H. Handbook of Low and High Dielectric Constant Materials and Their Applications; Academic Press: London, UK, 1999. [Google Scholar]
- Osaka, T.; Datta, M. Energy Storage Systems for Electronics; Gordon and Breach: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Brosseau, C. Modellilng and simulation of dielectric heterostructures: A physical survey from an historical perspective. J. Phys. D: Appl. Phys. 2006, 39, 1277–1294. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Brosseau, C. Finite-element modeling method for the prediciton of the complex effective permittivity of two-phase random statistically isotropic heterostructures. J. Appl. Phys. 2005, 97, 044101. [Google Scholar] [CrossRef]
- Rao, Y.; Qu, J.; Marinis, T.; Wong, C.P. A precise numerical prediction of the effective dielectric constant for polymer-ceramic composite based on effective-medium theory. IEEE Trans. Comp. Pack. Tech. 2000, 23, 680–683. [Google Scholar] [CrossRef]
- Ying, K.L.; Hsieh, T.E. Sintering behaviors and dielectric properties of nanocrystalline barium titanate. Mater. Sci. Eng. B-Sol. St. Mater. Adv. Technol. 2007, 138, 241–245. [Google Scholar] [CrossRef]
- Yoon, D.-H.; Zhang, J.; Lee, B.I. Dielectric constant and mixing model of barium titanate composite thick films. Mater. Res. Bull. 2003, 38, 765–772. [Google Scholar] [CrossRef]
- Rao, Y.; Wong, C.P. Material characterization of a high-dielectric constant polymer-ceramic composite for embedded capacitor for RF applications. J. Appl. Polym. Sci. 2004, 92, 2228–2231. [Google Scholar] [CrossRef]
- Todd, M.G.; Shi, F.G. Complex permittivity of composite systems: A comprehensive interphase approach. IEEE Dielect. El. In. 2005, 12, 601–611. [Google Scholar] [CrossRef]
- Vo, H.T.; Shi, F.G. Towards model-based engineering of optoelectronic packaging materials: Dielectric constant modeling. Microelectronics 2002, 33, 409–415. [Google Scholar] [CrossRef]
- Murugaraj, P.; Mainwaring, D.; Mora-Huertas, N. Dielectric enhancement of polymer-nanoparticle through interphase polarizability. J. App. Phy. 2005, 98, 054304. [Google Scholar] [CrossRef]
- Tuncer, E. Signs of low frequency dispersions in disordered binary dielectric mixtures (50-50). J. Phys. D: Appl. Phys. 2004, 37, 334–342. [Google Scholar] [CrossRef]
- Tuncer, E.; Nettelblad, B.; Gubanski, S.M. Non-Debye relaxation of binary dielectric mixtures (50-50): Randomness and regularity in mixture topology. J. Appl. Phys. 2002, 92, 4612–4624. [Google Scholar] [CrossRef]
- Lewis, T.J. Interfaces are the dominant feature of dielectrics at the nanometric level. IEEE Dielect. El. In. 2004, 11, 739–753. [Google Scholar] [CrossRef]
- Lewis, T.J. Interfaces: Nanometric dielectrics. J. Phys. D: Appl. Phys. 2005, 38, 202–212. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Wong, C.P. Influence of interphase and moisture on the dielectric spectroscopy of epoxy/silica composites. Polymer 2005, 46, 2297–2305. [Google Scholar] [CrossRef]
- Tanaka, T.; Kozaka, M.; Fuse, N.; Ohki, Y. Proposal of a multi-core model for polymer nanocomposite dielectrics. IEEE Dielect. El. In. 2005, 12, 669–681. [Google Scholar] [CrossRef]
- Tuncer, E.; Rondinone, A.J.; Woodward, J.; Sauers, I.; James, D.R.; Ellis, A.R. Cobalt iron-oxide nanoparticle modified poly(methyl methacrylate) nanodielectrics. Appl. Phys. A 2009, 94, 843–852. [Google Scholar] [CrossRef]
- Raju, G.G. Dielectrics in Electric Field; Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar]
- Vorob'ev, A.A. Excitation and electrical breakdown of solid insulators. Russ. Phys. J. 1980, 23, 382–386. [Google Scholar]
- Bunget, I.; Popescu, M. Physics of Solid Dielectrics; Elsevier: Amsterdam, The Netherlands, 1984; Vol. 19. [Google Scholar]
- Kuffel, E.; Zaengl, W.S. High Voltage Engineering Fundamental; Pergamon: New York, NY, USA, 1984. [Google Scholar]
- Artbauer, J. Electric strength of polymers. J. Phys. D: Appl. Phys. 1996, 29, 446–456. [Google Scholar] [CrossRef]
- Sabuni, M.H.; Nelson, J.K. The effects of plasticizer on the electric strength of polystyrene. J. Mater. Sci. 1979, 14, 2791–2796. [Google Scholar] [CrossRef]
- Wiacek, K.J. Synthesis and Electrical Properties of Fluorenyl Polyesters Incorporating Diamond Fragments. MS Thesis, Wright State University, Dayton, OH, USA, 2007. [Google Scholar]
- Hosier, I.L.; Vaughan, A.S.; Swingler, S.G. The effects of measuring techniques and sample preparation on the breakdown strength of polyethylene. IEEE Dielect. El. In. 2002, 9, 353–361. [Google Scholar] [CrossRef]
- Schneuwly, A.; Groning, P.; Schlapbach, L.; Irrang, C.; Vogt, J. Breakdown behavior of oil-impregnated polyproplyene as dielectric in film capacitors. IEEE Dielect. El. In. 1998, 5, 862–868. [Google Scholar] [CrossRef]
- Job, A.E.; Alves, N.; Zanin, M.; Ueki, M.M.; Mattoso, L.H.; Teruya, M.Y.; Giacometti, J.A. Increasing the dielectric breakdown strength of poly(ethylene terephthalate) films using a coated polyaniline layer. J. Phys. D: Appl. Phys. 2003, 36, 1414–1417. [Google Scholar] [CrossRef]
- Zakrevski, V.A.; Sudar, N.T.; Zappo, A.; Dubitsky, Y.A. Mechanism of electrical degradation and breakdown of insulating polymers. J. Appl. Phys. 2003, 93, 2135–2139. [Google Scholar] [CrossRef]
- Ieda, M. Dielectric breakdown process of polymers. IEEE Electr. Insul. 1980, 15, 206–224. [Google Scholar] [CrossRef]
- Shen, Y.; Lin, Y.; Li, M.; Nan, C.W. High dielectric performance of polymer composite films induced by a percolating interparticle barrier layer. Adv. Mater. 2007, 19, 1418–1422. [Google Scholar] [CrossRef]
- Chen, G.; Davies, A.E. The influence of defects on the short-term breakdown characteristics and long-term dc performance of LDPE insulation. IEEE Dielect. El. In. 2000, 7, 401–407. [Google Scholar] [CrossRef]
- Lewis, T.J. Nanometric dielectrics. IEEE Dielect. El. In. 1994, 1, 812–825. [Google Scholar] [CrossRef]
- Tanaka, T.; Montanari, G.C.; Mulhaupt, R. Polymer nanocomposites as dielectrics and electrical insulation-perspectives for processing technologies, material characterization, and future applications. IEEE Dielect. El. In. 2004, 11, 763–784. [Google Scholar] [CrossRef]
- Ma, D.; Hugener, T.A.; Siegel, R.W.; Christerson, A.; Martensson, E.; Onneby, C.; Schadler, L. Influence of nanoparticle surface modification on the electrical behavior of polyethylene nanocomposites. Nanotechnology 2005, 16, 724–731. [Google Scholar] [CrossRef]
- Montanari, G.C.; Fabiani, D.; Palmieri, F.; Kaempfer, D.; Thomann, R.; Mulhaupt, R. Modification of electrical properties and perfomance of EVA and PP insulation through nanostructure by organophillic silicates. IEEE Dielect. El. In. 2004, 11, 754–762. [Google Scholar] [CrossRef]
- Smith, R.C.; Liang, C.; Landry, M.; Nelson, J.K.; Schadler, L.S. The mechanisms leading to the useful electrical properties of polmyer nanodielectrics. IEEE Dielect. El. In. 2008, 15, 187–196. [Google Scholar] [CrossRef]
- Kim, P.J.; Simon, C.; Hotchkiss, P.J.; Joshua, N.; Kippelen, B.; Marder, S.R.; Perry, J.W. Phosphonic acid-modified barium titanate polymer nanocomposites with high permittivity and dielectric strength. Adv. Mater. 2007, 19, 1001–1005. [Google Scholar] [CrossRef]
- Li, J.; Claude, J.; Norena-Franco, L.E.; Seok, S.I.; Wang, Q. Electrical energy storage in ferroelectric polymer nanocomposites containing surface-functionalized BaTiO3 nanoparticles. Chem. Mater. 2008, 20, 6304–6306. [Google Scholar] [CrossRef]
- Roy, M.; Nelson, J.K.; MacCrone, R.K.; Schadler, L.S. Candidate mechanisms controlling the electrical characteristics of silica/XLPE nanodielectrics. J. Mater. Sci. 2007, 42, 3789–3799. [Google Scholar] [CrossRef]
- Nelson, W. Applied Life Data Analysis; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Tuncer, E.; James, D.R.; Sauers, I.; Ellis, A.R.; Pace, M.O. On dielectric breakdown statistics. J. Phys. D: Appl. Phys. 2006, 39, 4257–4268. [Google Scholar] [CrossRef]
- Laihonen, S.J.; Gafvert, U.; Schutte, T.; Gedde, U.W. Breakdown strength of polypropylene films: Area dependence and statistical behavior. IEEE Dielect. El. In. 2007, 14, 275–286. [Google Scholar] [CrossRef]
- Fothergill, J.C. Estimating the cumulative probability of failure data points to be plotted on Weibull and other probability paper. IEEE Dielect. El. In. 1990, 25, 489–492. [Google Scholar]
- Jackson, W.; Reddish, W. High permittivity crystalline aggregates. Nature 1945, 156, 717. [Google Scholar] [CrossRef]
- Mitsui, T.; Westphal, W.B. Dielectric and X-Ray Studies of CaxBa1-xTiO3 and CaxSr1-xTiO3. Phys. Rev. 1961, 124, 1354–1359. [Google Scholar] [CrossRef]
- Bell, A.J. Grain size effects on barium titanate-revisted. In Proc. 9th IEEE Int. Symp. Appl. Ferroelectrics, Piscataway, NJ, USA, August 7-10, 1994.
- Hennings, D.; Rosenstein, G. Temperature stable dielectrics based on chemically inhomogeneous barium titanate. J. Am. Ceram. Soc. 1984, 67, 249–254. [Google Scholar] [CrossRef]
- Swartz, S.L. Topics in electronic ceramics. IEEE Dielect. El. In. 1990, 25, 935–987. [Google Scholar]
- Buessem, W.R.; Cross, L.E.; Goswami, A.K. Effect of Two-Dimensional Pressure on the Permittivity of Fine- and Coarse-Grained Barium Titanate. J. Am. Ceram. Soc. 1992, 75, 2926–2929. [Google Scholar] [CrossRef]
- Ihlefeld, J.; Laughlin, B.; Hunt-Lowery, A.; Borland, W.; Kingon, A.; Maria, J.-P. Copper compatible barium titanate thin films for embedded passives. J. Electroceram. 2005, 14, 95–102. [Google Scholar] [CrossRef]
- Dang, Z.M. Novel ferroelectric polymer composites with high dielectric constants. Adv. Mater. 2003, 15, 1625–1629. [Google Scholar] [CrossRef]
- Pecharroman, C.; Esteban-Betegon, F.; Bartolome, J.F.; Lopes-Esteban, S.; Moya, J.S. New percolative BaTiO3-Ni composites with a high and frequency-independent dielectric constant. Adv. Mater. 2001, 13, 1541–1544. [Google Scholar] [CrossRef]
- Qi, L. High dielectric constant silver epoxy composites as embedded dielectrics. Adv. Mater 2005, 17, 1777–1781. [Google Scholar] [CrossRef]
- Ogitani, S. Factors influencing the permittivity of polymer/ceramic composites for embedded capacitors. IEEE Trans. Adv. Pack. 2000, 23, 313–322. [Google Scholar] [CrossRef]
- Cho, S.-D.; Paik, K.-W. Relationships between suspension formulations and the properties of BaTiO3/epoxy composite films for integral capacitors. In Proc. 51st IEEE Electronic Components and Technology, Orlando, FL, USA, 29 May – 1 June, 2001; p. 1418.
- Ramesh, S.; Shutzberg, B.A.; Huang, C.; Gao, J.; Giannelis, E.P. Dielectric nanocomposites for integral thin films capacitors: Materials design, fabrication, and integration issues. IEEE Trans. Adv. Pack. 2003, 26, 17–24. [Google Scholar] [CrossRef]
- Lovinger, A.J. Ferroelectric polymers. Science 1983, 220, 1115–1121. [Google Scholar] [CrossRef] [PubMed]
- An, L.; Boggs, S.A.; Calame, J.P. Energy storage in polymer films with high dielectric constant fillers. IEEE Electr. Insul. M. 2008, 24, 5–10. [Google Scholar] [CrossRef]
- Li, J.J.; Seok, S.I.; Chu, B.J.; Dogan, F.; Zhang, Q.M.; Wang, Q. Nanocomposites of ferroelectric polymers with TiO2 nanoparticles exhibiting significantly enhanced electrical energy density. Adv. Mater. 2009, 21, 217–221. [Google Scholar] [CrossRef]
- Lunkenheimer, P.; Bobnar, V.; Pronin, A.V.; Ritus, A.I.; Volkov, A.A.; Loidl, A. Guoy-Chapman Diffuse Layer. Phys. Rev. B: Condens. Mater. 2002, 66, 052105. [Google Scholar] [CrossRef]
- Nelson, J.K.; Fothergill, J.C. Internal charge behavior of nanocomposites. Nanotechnology 2004, 15, 586–595. [Google Scholar] [CrossRef]
- Fujita, S.; Ruike, M.; Baba, M. Annual Report of the Conf. on Electrical Insulation and Dielectric Phenomena, Piscataway, NJ, USA, 20-23 October 1996; p. 738.
- Khalil, M.S. The role of barium titanate in modifying the dc breakdown strength of LDPE. IEEE Dielect. El. In. 2000, 7, 261–268. [Google Scholar] [CrossRef]
- Tuncer, E.; Sauers, I.; James, D.R.; Ellis, A.R.; Duckworth, R.C. Nanodielectric system for cryogenic applications: Barium titanate filled polyvinyl alcohol. IEEE Dielect. El. In. 2008, 15, 237–242. [Google Scholar]
- Tuncer, E.; Sauers, I.; James, D.R.; Ellis, A.R.; Paranthaman, M.P.; Goyal, A.; Moore, K.L. Enhancement of dielectric strength in nanocomposites. Nanotechnology 2007, 18, 325704. [Google Scholar] [PubMed]
- Cross, L.E. Relaxor ferroelectrics. Ferroelectrics 1987, 76, 241–267. [Google Scholar] [CrossRef]
- Kim, B.-G.; Cho, S.M.; Kim, T.-Y.; Jang, H.M. Giant dielectric permittivity observed in Pb-based perovskite ferroelectrics. Phys. Rev. Lett. 2001, 86, 3404–3406. [Google Scholar] [CrossRef] [PubMed]
- Edon, V.; Li, Z.; Hugon, M.-C.; Agius, B.; Krug, C.; Baumvol, I.J.R.; Durand, O.; Eypert, C. Electrical characteristics and interface structure of HfAlO/SiON/Si(001) stacks. Appl. Phys. Lett. 2007, 90, 122905. [Google Scholar] [CrossRef]
- Homes, C.C.; Vogt, T.; Shapiro, S.M.; Wakimoto, S.; Ramirez, A.P. Optical response of high dielectric constant perovskite related oxide. Science 2001, 293, 673–676. [Google Scholar] [CrossRef] [PubMed]
- Ni, L.; Chen, X.M. Dielectric relaxations and formation mechanism of giant dielectric constant step in CaCu3Ti4O12 ceramics. Appl. Phys. Lett. 2007, 91, 122905. [Google Scholar]
- Raevski, I.P.; Prosandeev, S.A.; Bogatin, A.S.; Malitskaya, M.A.; Jastrabik, L. High dielectric permittivity in AFe0.5B0.5O3 nonferroelectric perovskite ceramics (A = Ba,Sr; B = Nb, Ta, Sb). J. Appl. Phys. 2003, 93, 4130–4136. [Google Scholar]
- Wang, Z.; Chen, X.M.; Ni, L.; Liu, X.Q. Dielectric abnormalities of complex perovskite Ba(Fe0.5Nb0.5)O3 ceramics over broad temperature and frequency range. Appl. Phys. Lett. 2007, 90, 022904. [Google Scholar]
- Wu, J.B.; Nan, C.W.; Lin, Y.H.; Deng, Y. Giant dielectric permittivity observed in Li and Ti doped NiO. Phys. Rev. Lett. 2002, 89, 217601. [Google Scholar] [PubMed]
- Zhu, Y.; Zheng, J.C.; Wu, L.; Frenkel, A.I.; Hanson, J.; Northup, P.; Ku, W. Nanoscale disorder in CaCu3Ti4O12: A new route to the enhanced dielectric response. Phys. Rev. Lett. 2007, 99, 037602. [Google Scholar] [PubMed]
- Masingboon, C.; Thongbai, P.; Maensiri, S.; Yamwong, T.; Seraphin, S. Synthesis and giant dielectric behavior of CaCu3Ti4O12 ceramics prepared by polymerized complex method. Mater. Chem. Phys. 2008, 109, 262–270. [Google Scholar] [CrossRef]
- Ramirez, A.P.; Subramanian, M.A.; Gardel, M.; Li, D.; Vogt, T.; Shapiro, S.M. Giant dielectric constant response in a copper-titanate. Solid State Commun. 2000, 115, 217–220. [Google Scholar] [CrossRef]
- Subramanian, M.A.; Li, D.; Duan, N.; Reisner, B.A.; Sleight, A.W. High dielectric constant in ACu3Ti4O12 and ACu3Ti3FeO12 phases. J. Solid State Chem. 2000, 151, 323–325. [Google Scholar] [CrossRef]
- Singh, R.; Ulrich, R.K. High and low dielectric constant materials. Electrochem. Soc. Interface 1999, 8, 26–30. [Google Scholar]
- Sinclair, D.C.; Adams, T.B.; Morrison, F.D.; West, A.R. CaCu3Ti4O12: One-step internal barrier layer capacitor. Appl. Phys. Lett. 2002, 80, 2153–2155. [Google Scholar] [CrossRef]
- Dang, Z.-M.; Zhou, T.; Yao, S.-H.; Yuan, J.-K.; Zha, J.-W.; Song, H.-T.; Li, J.-Y.; Chen, Q.; Yang, W.-T.; Bai, J. Advanced calcium copper titanate/polyimide functional hybrid films with high dielectric permittivity. Adv. Mater. 2009, 21, 2077–2082. [Google Scholar] [CrossRef]
- Prakash, B.S.; Varma, K.B.R. Dielectric behavior of CCTO/epoxy and Al-CCTO/epoxy composites. Comp. Sci. Tech. 2007, 67, 2363–2368. [Google Scholar] [CrossRef]
- Tuncer, E.; Sauers, I.; James, D.R.; Ellis, A.R.; Paranthaman, M.P.; Aytug, T.; Sathyamurthy, S.; Moore, K.L.; Li, J.; Goyal, A. Electrical properties of epoxy resin based nanocomposites. Nanotechnology 2007, 18, 025703. [Google Scholar] [PubMed]
- Liu, X.Q.; Wu, Y.J.; Chen, X.M.; Zhu, H.Y. Temperature-stable giant dielectric response in orthorhombic samarium strontium nickelate ceramics. J. Appl Phys. 2009, 105, 0541041. [Google Scholar]
- Krohns, S.; Lunkenheimer, P.; Kant, C.; Pronin, A.V.; Brom, H.B.; Nugroho, A.A.; Diantoro, M.; Loidl, A. Colossal dielectric constant up to gigahertz at room temperature. Appl. Phys. Lett. 2009, 94, 122903. [Google Scholar] [CrossRef]
- Kajimoto, R.; Ishizaka, K.; Yoshizawa, H.; Tokura, Y. Spontaneous rearrangement of the checkerboard charge order to stripe order in La1.5Sr0.5NiO4. Phys. Rev. B 2003, 67, 0145111. [Google Scholar]
- Deskins, N.A.; Dupuis, M. Electron transport via polaron hopping in bulk TiO2. A density functional theory characterization. Phys. Rev. B 2007, 75, 1952121. [Google Scholar]
- Rivas, J.; Rivas-Murias, B.; Fondado, A.; Mira, J.; Senaris-Rodriguez, M.A. Dielectric response of the charge-ordered two-dimensional nickelate La1.5Sr0.5NiO4. Appl. Phys. Lett. 2008, 85, 6224–6226. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Q.M.; de Botton, G.; Bhattacharya, K. All-organic dielectric-percolative three-component composite materials with high electromechanical response. Appl. Phys. Lett. 2004, 84, 4391–4393. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, Q.M.; Su, J. High-dielectric constant all-polymer percolative composites. Appl. Phys. Lett. 2003, 82, 3502–3504. [Google Scholar] [CrossRef]
- Nan, C.W. Physics of inhomogeneous inorganic materials. Prog. Mater. Sci. 1993, 37, 1–116. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor and Francis: London, UK, 1992. [Google Scholar]
- McLachlan, D.S.; Heaney, M.B. Complex ac conductivity of a carbon black composite as a function of frequency, composition, and temperature. Phys. Rev. B 1999, 60, 12746–12751. [Google Scholar] [CrossRef]
- Wei, T.; Jin, C.Q.; Zhong, W.; Liu, J.-M. High permittivity polymer embedded with Co/ZnO core/shell nanoparticles modified by organophosphorous acid. Appl. Phys. Lett. 2007, 91, 222907. [Google Scholar]
- Xu, J.; Wong, C.P. Low-loss peroclative dielectric composite. Appl. Phys. Lett. 2005, 87, 082907. [Google Scholar]
- Barber, P.; Houghton, H.; Balasubramanian, S.; Anguchamy, Y.K.; Ploehn, H.J.; zur Loye, H.-C. New layered mixed metal phosphonates for high dielectric-polymer composite materials. Chem. Mater. 2009, 21, 1303–1310. [Google Scholar] [CrossRef]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barber, P.; Balasubramanian, S.; Anguchamy, Y.; Gong, S.; Wibowo, A.; Gao, H.; Ploehn, H.J.; Zur Loye, H.-C. Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage. Materials 2009, 2, 1697-1733. https://doi.org/10.3390/ma2041697
Barber P, Balasubramanian S, Anguchamy Y, Gong S, Wibowo A, Gao H, Ploehn HJ, Zur Loye H-C. Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage. Materials. 2009; 2(4):1697-1733. https://doi.org/10.3390/ma2041697
Chicago/Turabian StyleBarber, Peter, Shiva Balasubramanian, Yogesh Anguchamy, Shushan Gong, Arief Wibowo, Hongsheng Gao, Harry J. Ploehn, and Hans-Conrad Zur Loye. 2009. "Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage" Materials 2, no. 4: 1697-1733. https://doi.org/10.3390/ma2041697
APA StyleBarber, P., Balasubramanian, S., Anguchamy, Y., Gong, S., Wibowo, A., Gao, H., Ploehn, H. J., & Zur Loye, H.-C. (2009). Polymer Composite and Nanocomposite Dielectric Materials for Pulse Power Energy Storage. Materials, 2(4), 1697-1733. https://doi.org/10.3390/ma2041697




